B
PA PC PD PB
即 PA•PB =PC•PD
A
C
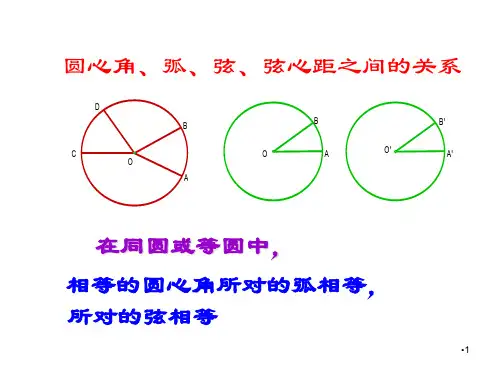
1、同弧或等弧所对的圆周角相等
2、直径所对的圆周角是直角;
B
90°的圆周角所对的弦是直径.
定理的运用
1、常用于证明角相等或弧、弦相等;
2、常利用直径所对的圆周角是直角来 A 解决有关问题 !
O E
D
C
B
第|一章 整式的乘除
4 整式的乘法〔第1课时〕
3、在你探索单项式乘法运算法那么的 过程中 ,运用了哪些运算律和运算法那 么?
探索规律:
单项式乘法的法那么: 单项式与单项式相乘 ,把它们的系
数、相同字母的幂分别相乘 ,其余字母 连同它的指数不变 ,作为积的因式 .
例题解析:
例1 计算:
(1)2 xy 2 ( 1 xy ) 3
(2) 2a2b3 (3a)
〔3〕单项式乘法法那么对于三个以上 的单项式相乘同样适用;
〔4〕单项式乘以单项式 ,结果仍为单项 式.
完成课本15页:随堂练习
延伸拓展:
一家住房的结构如图
y
2y
示 ,房子的主人打算把 卧室以外的局部全都铺
卫生间
卧室
上地砖 ,至||少需要多
x
厨房
4x
少平方米的地砖 ?如果
某种地砖的价格是a元/ 2x
E
8
7 6
5C
角形吗 ?
34
∠1 =∠4 ,∠2 =∠7 , △AEB∽△DEC B
∠3 =∠6 ,∠5 =∠8 , △AED∽△BEC
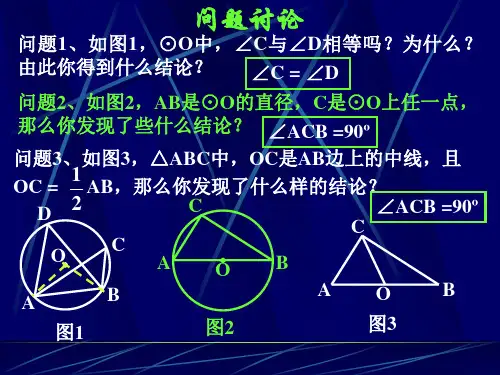
如图 ,弦AB与CD相交于点P ,
D A
求证:PA•PB =PC•PD
证明:连接AC ,BD.