SPC计量值之中位数全距控制图(M-R)
- 格式:pdf
- 大小:347.35 KB
- 文档页数:3


SPC所有公式详细解释及分析SPC统计制程管制计量值管制图:Xbar-R(平均-全距)、Xbar-S(平均-标准差)、X-MR(个别值-移动全距)、EWMA、CUSUM等管制图。
计数值管制图:不良率p、不良数np、良率1-p、缺点数c、单位缺点数u等管制图。
常用分析工具:直方图、柏拉图、散布图、推移图、%GRR...等。
公式解说制程能力指数制程能力分析制程能力研究在于确认这些特性符合规格的程度,以保证制程成品不符规格的不良率在要求的水准之上,作为制程持续改善的依据。
制程能力研究的时机分短期制程能力研究及长期制程能力研究,短期着重在新产品及新制程的试作、初期生产、工程变更或制程设备改变等阶段;长期以量产期间为主。
制程能力指针Cp 或Cpk 之值在一产品或制程特性分配为常态且在管制状态下时,可经由常态分配之机率计算,换算为该产品或制程特性的良率或不良率,同时亦可以几Sigma 来对照。
计数值统计数据的数量表示缺点及不良(Defects VS. Defectives)缺点代表一单位产品不符要求的点数,一单位产品不良可能有一个缺点或多个缺点,此为计点的品质指针。
例如描述一匹布或一铸件的品质,可用每公尺棉布有几个疵点,一铸件表面有几个气孔或砂眼来表达,无尘室中每立方公尺含微粒之个数,一片PCB有几个零件及几个焊点有缺点,一片按键有几个杂质、包风、印刷等缺点,这些都是以计点方式表示一单位产品的特性值。
不良代表一单位产品有不符要求的缺点,可能有一个或一个以上,此将产品分类为好与坏、良与不良及合格与不合格等所谓的通过-不通过(Go-NoGo)的衡量方式称为计件的品质指针。
例如单位产品必须以二分法来判定品质,不良的单位产品必须报废或重修,这是以计件方式来表示一单位产品的特值。
每单位缺点数及每百万机会缺点数(DPU VS. DPMO)一单位产品或制程的复杂程度与其发生缺点的机会有直接的关系,越复杂容易出现缺点;反之越简单越不容易出现缺点。

SPC培训试题
一、填空题。
1.制程是SPC 的焦点。
2.CL表示管制中心线UCL表示上控制界限LCL表示下控制界限
3.Ca表示准确度Cp表示精密度CPK表示制程能力
4.X(bar)表示平均数R表示极差
5.PPM是指制程中所产生之百万分之不良数
DPM是指制程中所产生之百万分之缺点数
6.控制图的基本类型按数据类型分为计数值控制图、计量值控制图
7.若直方图出现孤岛型、偏向型等非正态分布说明过程中有异常因素作用
8.影响过程的主要因素有人、机、料、法、环、测
9.计算CP,CPK数据量不得少于25组
10.控制产品平均值与极差采用X(bar)-R控制图
二、判断题。
1.生产出来的产品相差越少,越接近产品中心值,产品的工序能力越大(√)
2.没有超出控制界限的点过程能力是可接受的(×)
3.因为X(bar)-R图最为精确和敏感,较其它方法优势更强,因此大多数企业
都选择使用该方法(×)
4.当过程能力较高时,为降低成本,采取方法使之降低(×)
5.正确使用统计技术,能达到早期预防或及时提出矫正措施并得以及时改善的
目的(√)
三、简答题
1.写出依据数据性质分类四种计量型控制图、四种计数型控制图
计量型控制图
(1)平均值与极差管制图(X-R)
(2)平均值与标准差管制图(X- σ)
(3)中位值与全距管制图( -R)
(4)个别值与移动全距管制图(X-Rm)
计数值控制
(1)不良率管制图(P)
(2)不良数管制图(pn)
(3)缺点数管制图(C)
(4)单位缺点数管制图(μ)。



SPC常用计算方法SPC基础知识及常用计算方法SPC基础知识一、 SPC定义:1、 SPC——统计制程管制:是指一套自制程中去搜集资料,并加以统计分析,从分析中去发气掘制程的异常,立即采取修正行动,使制程恢复正常的方法。
也就是说:品质不应再依赖进料及出货的抽样检验,而应该采取在生产过程中,认良好的管理方法,未获得良好的品质。
2、良好品质,必须做到下面几点:①变异性低②耐用度③吸引力④合理的价格3、变异的来源:大概来自5个方面:①机器②材料③方法④环境⑤作业人员应先从机器,材料方法,环境找变异,最后考虑人。
4、 SPC不是一个观念,而是要行动的步骤一、确立制程流程——首先制程程序要明确,依据制程程序给制造流程图,并依据流程图订定工程品质管理表。
步骤二、决定管制项目——如果把所有对品质有影响的项目不论大小,轻重缓急一律列入或把客户不很重视的特性一并管制时,徒增管制成本浪费资料且得不赏失,反之如果重要的项目未加以管制时,则不能满足设计者,后工程及客户的需求,则先去管制的意义。
步骤三、实施标准化——欲求制程管制首先即得要求制程安定,例如:在风浪很大的船上比赛乒乓球,试部能否确定谁技高一筹,帮制程作业的安定是最重要的先决条件,所以对于制程上影响产品口质的重要原因,应先建立作业标准,并透过教育训练使作业能经标准进行。
步骤四、制程能力调查——为了设计、生产、销售客户满意且愿意购买的产品,制造该产品的制程能力务必符合客户的要求。
因此制程的能力不足时,必顺进行制程能力的改善,而且在制程能力充足后还必须能继续,所以在品质管理的系统中制程能力的掌握很重要。
步骤五、管制图运用——SPC的一个基本工具就是管制图,而管制图又分计量值管制图与计数值管制图。
步骤六、问题分析解决——制程能力调查与管制图是可筛提供问题的原因系由遇原因或非机遇原因所造成,但无法告知你确切的原因为何及如何解决决问题?解决问题?而问题的解决技巧,在于依据事实找出造成变异的确切原因,并提此对策加以改善,及如何防止再发生。
SPC之I-MR控制图概述1924年,美国的休哈特博士应用统计数学理论将3Sigma原理运用于生产过程中,并发表了著名的“控制图法”,对产品特性和过程变量进行控制,开启了统计过程控制新时代。
01什么是控制图控制图指示过程何时不受控制,有助于标识是否存在特殊原因变异。
如果存在特殊原因变异,则说明过程不稳定且有必要采取纠正措施。
控制图是按时间排序顺序绘制过程数据的图。
大多数控制图都包括一条中心线、一个控制上限和一个控制下限。
中心线表示过程均值。
控制限表示过程变异。
默认情况下,控制限绘制在中心线上下3σ的位置。
随机位于控制限内的点指示过程受控制且仅显示常见原因变异。
位于控制限外部或者显示非随机模式的点指示过程不受控制且存在特殊原因变异。
02如何选择合适的控制图随着控制图的发展,它的类型也是越来越多,那么这时候对于使用Minitab的朋友来说,经常会纠结如何去选择一个合适的控制图。
在Minitab19中,协助菜单可以很好的帮助我们去选择一个合适的控制图。
今天,我们来绘制一下I-MR控制图。
问题背景:某质量工程师监控了液体洗涤剂的生产过程,想要评估该过程是否受控制。
这位工程师测量了25个连续批次的洗涤剂的pH值。
由于pH值的数据类型是连续型数据,而且是每批次只取一个样品(子组大小等于1),故这位工程师创建了一张I-MR控制图,以监控洗涤剂的生产过程。
Minitab结果解释首先解释移动极差控制图(MR控制图)以检查过程变异。
没有位于控制限外部的点且所有的点都显示出随机模式。
因此,过程变异受控制,质量工程师可以检查单值控制图(I控制图)上的过程中心。
I控制图上的一个观测值在检验1中失败,因为观测值在中心线上方且距离中心线超过3个标准差。
I-MR控制图的控制限计算(手动)对于I-MR控制图,包含两张图单值控制图(I控制图)和移动极差控制图(MR控制图),我们首先来认识一下这两张图形上的X轴、Y轴、点和线分别表示什么含义。

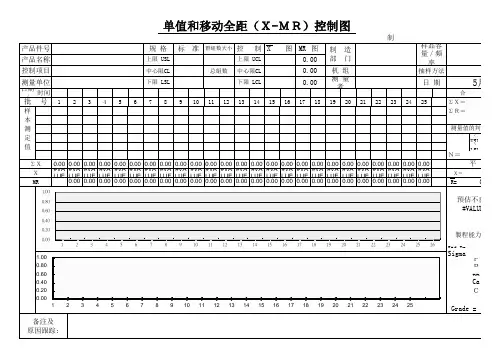
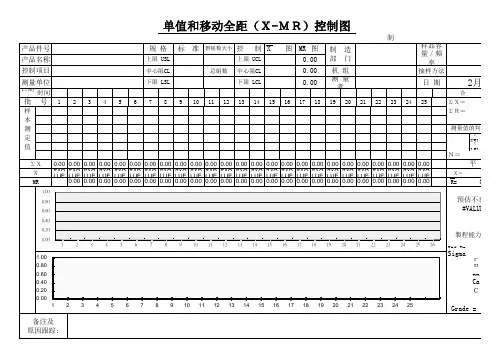
X-Rm(个别值与移动全距管制图)
摘要:计量值作为SPC管制图中的一种,其中包括X-R、X-δ、X-Rm以及Mo-R四种常用的管制图。
下面本文主要针对X-Rm(个别值移动全距管制图)进行介绍。
X-Rm(个别值移动全距管制图)的意义
以不分组的方式描点作管制图,要求每次或每组的样本数为1。
在计量值中,当每次取样为1时,不能用以上三种管制图,只能用X-Rm(个别值移动全距管制图)来做。
X-Rm(个别值移动全距管制图)使用场合
∙一次只能收集到一个样本数据,如损耗率;
∙制程的品质极为均匀,不需要多取样本,如液体浓度、PH值等;
∙取得测定值既费时成本又高,如复杂的化学分析及破坏性试验等。
X-Rm管制图注意事项
∙X-Rm在检查过程变化时不如Xbar-R图敏感;
∙X-Rm图不能区分过程的零件间重复性,因些在很多情况下最好还是使用常规的子组样本容量较小(2-4)的Xbar-R图。
应用案例
某电子厂对每批苡片研磨制程进行管制,其厚度规格化为3±0.1u,希望建立管制图,以在量产时对制程上的厚度进行有效的管制。
因同一批差异很小,所以每一批次取一个样本量测,记录如下:
最终得出的X-Rm管制图如下:。

RX -一、 管制图公式说明1. 计量值公式管制图 1.1 X 管制图:n 为组内样本量,m 为抽样组数;中心线 ✍ R CL = 管制下限 ✍ R D d R d R R U C L R 323)(33=-=-=σ 其中 23331d d D -= , 23431d d D += 第i 组之标准偏差1)(12--=∑=n x x S n i i i x nx x x x mn++=21......估计标准偏差 4C S =σ管制上限 ✍ S A X S n C X U C L 343(+=+=中心线 ✍ X CL =管制下限 ✍ S A X S n C X L C L 34)3(-=-= 其中n C A 433=S 管制图:管制上限 ✍ S B U C L s 4=中心线 ✍ ∑==Ki i P K P 11 管制上限 ✍ ) 1 , )1(3min(n P P P UCL -+= 管制下限 ✍ ) 0 , )1(3max(nP P P LCL --= 当各组之样本数不相同时:中心线 ✍ ∑==Ni i i P n N P 11 , 其中 k n n n N +++= (21)各组管制上下限分别为管制上限 ✍ ) 1 , )1(3min(i n P P P UCL -+= 管制下限 ✍ ) 0 , )1(3max(i n P P P LCL --=n 管制上限 ✍ )1(3P P P U C L n n -+=管制下限 ✍ )1(3P P P L C Ln n --= 其中 n P 为各组之不合格数。
★ ),max ()(LSL SL SL USL SL Ca ---=μ ; 其中 μ:平均值 SL :规格标准USL :规格上限LSL :规格下限★ σ6LSL)-(USL Cp = ; σ:估计标准偏差 ( Capability Sigma )。
★ σμ3)-(USL Cpu = ; σ:估计标准偏差 ( Capability Sigma )。
关于s p c的专业名词准确度Accuracy成品改善ActiononOutput制程中对策ActionontheProcess人员变异AppraiserVariation计数值AttributeData平均数Average中位数平均AverageofMedian全距平均AverageofRange标准差平均AverageofStandardDeviation平均数-全距管制图Average-RangeControlChart二项分配BinomialDistribution平均数-标准差制图Average-StandardDeviationControlChart 中心线CenterLine;CL中央极限定理CentralLimitTheorem管制界限ControlLimits持续改善ContinualImprovement管制图ControlChart分散Dispersion管制计划ControlPlan计件CountbyPieces计点CountbyPoints关键制程特性CriticalProcessCharacteristics共同原因CommonCause每百万缺点数管制图DefectPartsPerMillionControlChart分配Distribution关键产品特性CriticalProductParameter仪器变异EquipmentVariation连续随机变数ContinuousRandomVariable估计平均数EstimatedAverage离散随机变数DiscreteRandomVariable单位缺点数DefectsPerUnit单位缺点数管制图DefectsPerUnitControChart指数分配ExponentialDistribution估计不良率EstimatedProcessPercentDefectives次数分配FrequencyDistribution估计标准差EstimatedStandardDeviation漏斗实验FunnelExperiment个别值-移动全距管制图Individual-MovingRangeControlChart 仪器设备Gauge每百万缺点数DefectsPartPerMillion;dppm仪器设备能力研究GRRStudy绩效报告InformationaboutPerformance直方图Histogram固有制程变异InherentProcessVariation个别值Individual短期制程能力研究ShortTermProcessCapabilityStudy 中心位置Location管制下限LowerControlLimit;LCL管制上限UpperControlLimit;UCL中位数Median规格下限LowerSpecificationLimit;LSL混批MixedLot量测系统误差MeasurementSystemError标称植Nominal中位数-全距管制图Median-RangeControlChart常态分配NormalDistribution不良数管制图NumberofDefectivesControlChart缺点数NumberofDefects缺点数管制图NumberofDefectsControlChart不良数NumberofDefectives每百万不良数PartsPerMillion;ppm不在管制状态下OutofControl制程能力图ProcessCapabilityChart过度调整Overadjustment制程绩效指数ProcessPerformanceIndex柏拉图ParetoDiagram不良率管制图PercentDefectivesControlChart不良率PercentDefectives制造流程图ProcessCapabilityChart卜氏分析PoissionDistribution长期制程能力研究LongTermProcessCapabilityStudy 群体Population简单随机抽样SimpleRandomSampling精密度Precision分段随机抽样StageRandomSampling制程系统Process统计制程管制StstisticalProcessControl;SPC制程能力ProcessCapability制程能力图RunChart样本Sample全距Range抽样Sampling抽样分配SamplingDistribution合理的分组RationalSubgrouping偏态Skewness再生性Reproducibility再现性Repeatability特殊原因SpecialCause稳定性Stabiity规格界限SpecificationLimits标准差StandardDevivation分层分析Stratification分层批StratifiedLot分层随机抽样StratifiedRandomSampling 组平均数SubgroupAverage组标准差SubgroupStandardDeviation组全距SubgroupRange规格上限UpperSpecificationLimit;USL 系统抽样SystematicSampling组间变异VariationbetweenGroups总平均数TotalAverage组内变异VariationwithinGroup干预Tempering计量值VariableData良率Yield总制程变异TotalProcessVariation组中位数SubgroupMedian中心值Target总变异TotaVariation均匀分配UniformDistribution管制状态下UnderControl推移图TrendChart变异Variation良率管制图YieldControlChart。
SPC管制图做法及应用(精华内容)常规操纵图的作法及其应用一:管制图的概论任何产品或事物均有变异存在,即没有任何两件产品是完全相同的,因此如何操纵变异使之在我们能够同意的范畴内,乃是产品生产过程中的重要品管工作.管制图是极具有功效的管制工具之一,用以侦测品质变异的缘故,然后采取计策以排除其缘故,使生产过程复原正常.管制图是由三条管制界限,即中心线,上管制界限及下管制界限组成的图形,并将生产过程中所获得的统计量绘入图中,以判定其为管制中抑管制外,假如其状况是属于管制中时,显示生产过程的变异行为把握在我们的预知中,连续生产.但假设其状况是属于管制外,那么显示其变异情形已超出我们的操纵外,必须控讨其发生的缘故,采取计策以矫正之.为发探讨管制图.必须注意下面三项要紧因素:变异的缘故:管制图的目的在于探讨变异的行为及缘故,以便排除之,其缘故通常可分为机遇缘故及非机遇缘故.管制图的设计:即决定管制界限的宽度以给制其上管制界限,中心线及下管制界限.此外尚须决定样本大小及抽样间距.管制图的讯号:管制图是透过异行为来判定其为管制中或管制外,其发生缘故为何,如保采取计策,也是管制图的核心.1. 所谓管制图:管制图上均包含有中心线(Central line (CL)) 及上下两条管制界线[Uppe r and Lowe r Control Lim i ts, (UCL)(LCL)],用以测知制程是否在正常状态。
2. 管制图系于1924 年由美国品管大师W. A . S h e w h a r t 博士发明。
3. 管制图最要紧之用途为察觉制程有无产生变异之〝非机遇缘故〞,所谓非机遇缘故,确实是引起质量大变动之缘故。
4. 管制图与一样统计图不同,因其不仅能将数值以曲线表示出来,以观其变异之趋势,且能显示变异系属于机遇性或非机遇性者,以指示某种现象是否正常,而备采取适当之措施。
二.管制图原理1. 变异―机遇及非机遇缘故1.1 量度产品时,假如制程专门稳固,那么将形成㆒种固定形状,称为分配。
SPC(Cpk、Ppk)等⼯程能⼒计算公式均值X图均值X图n A2d2D3D4A3c4B3B42 1.880 1.128- 3.267 2.6590.7979- 3.2763 1.023 1.693- 2.571 1.9540.8862-2.56840.729 2.059- 2.282 1.6280.9213- 2.26650.577 2.326- 2.114 1.4270.9400- 2.08960.483 2.543- 2.0041.2870.95150.030 1.97070.4192.7040.076 1.924 1.1820.95940.118 1.88280.373 2.8470.136 1.864 1.0990.96500.1851.81590.3372.9700.184 1.816 1.0320.96930.239 1.761100.3083.0780.223 1.7770.9750.97270.284 1.716110.2853.1730.256 1.7440.9270.97540.321 1.679120.266 3.2580.283 1.7170.8860.97760.354 1.640130.249 3.3360.3071.6930.8500.97940.382 1.618140.235 3.4070.328 1.6720.8170.98100.406 1.594150.223 3.4720.3471.6530.7890.98230.428 1.572160.212 3.5320.363 1.6370.7630.98350.448 1.552170.203 3.5880.3781.6220.7390.98450.446 1.534180.194 3.6400.391 1.6080.7180.98540.482 1.518190.187 3.6890.4031.5970.6980.98620.497 1.503200.180 3.7350.415 1.5850.6800.98690.510 1.490210.173 3.7780.4251.5750.6630.98760.523 1.477220.167 3.8190.434 1.5660.6470.98820.534 1.466230.162 3.8580.4431.5570.6330.98870.545 1.455240.157 3.8950.451 1.5480.6190.98920.555 1.445250.153 3.9310.4591.5410.6060.98960.565 1.435X±A 2R X±A 2R中位数X图单值X图n A 2d 2D 3D 4E 2d 2D 3D 42 1.880 1.128- 3.267 2.660 1.128- 3.2673 1.187 1.693- 2.574 1.772 1.693-2.57440.796 2.059- 2.282 1.457 2.059- 2.282标准差估计值的除数UCL X ,LCL X = 全距R图全距R图中位数图计算控制限⽤的系数单值图LCL S = B 3s标准差估计值的除数计算控制限⽤的系数全距R图⼦组容量计算控制限⽤的系数标准差估计值的除数计算控制限⽤的系数X-R图标准差S图X-s图计算控制限⽤的系数计算控制限⽤的系数UCL S = B 4s控制图的常数和公式表δ=R/D 2δ= s/c 4⼦组容量计算控制限⽤的系数标准差估计值的除数计算控制限⽤的系数UCL X ,LCL X =UCL R = D 4R LCL R = D 3R50.691 2.326-2.114 1.290 2.326- 2.11460.548 2.534-2.004 1.184 2.534- 2.00470.508 2.7040.0761.924 1.1092.7040.076 1.92480.433 2.8470.1361.864 1.0542.8470.136 1.86490.412 2.9700.1841.816 1.0102.9700.184 1.816100.3623.0780.2231.7770.975 3.0780.223 1.777X±A 2RX±E 2R δ=R/d 2δ= R/d 2UCL R = D 4RUCL MR = D 4R LCL R = D 3RLCL MR = D 3R UCL ,LCL =UCL X ,LCL X =UCL P ,LCL P ==UCL np ,LCL np =UCL C ,LCL C =UCL U ,LCL U =Cpk=( 1 - k ) x Cp 或 MIN {CPU,CPL}Ppk=( 1 - k )x Pp 或 MIN {PPU,PPL}单边规格(设计规格)因没有规格上限或下限,没有规格下限 Cp = CPU = Cpk,没有规格上限 Cp = ()n P P P /13-±=()n P P P -±=13()P P n P n -±=13nUU 3±=CC 3±=格上限 Cp = CPL = Cpk。
统计过程控制(SPC)一统计过程控制(SPC)的涵义统计过程控制(Statistical Process Control,简称SPC)是为了贯彻预防原则,应用统计技术对过程中的各个阶段进行评估和监察,建立并保持过程处于可接受的并且稳定的水平,从而保证产品符合规定的要求的一种技术。
二SPC的特点1、强调全员参加,而不是只依靠少数质量管理人员;2、强调应用统计方法来保证预防原则的实现;3、SPC不是用来解决个别工序采用什么控制的问题,SPC强调从整个过程,整个体系出发来解决问题。
SPC的重点就在于“P(Process,过程);4、SPC中的主要统计技术为控制图,SPC可以判断过程的异常,对过程中的各个阶段阶段监控与诊断,针对异常迅速采取纠正措施,减少损失、降低成本、以达到保证产品质量、持续改进的目的。
5.过程的定义:将各项输入资源按一定要求组合起来并能转化为输出产品及其质量特性的活动。
任何一个产品的制造可分解为若干个过程通过并联或串联组成。
过程能力指数CPK评价一个过程的质量以及过程满足顾客要求的能力。
三控制图1.定义:控制图是生产过程质量的一种记录图形,图上有中心线和上下控制界限,并有按时间顺序抽取的各样本统计量的数值。
2.作用:利用控制图所提供的信息,把一个过程维持在受控状态;一旦发现异常波动,就分析对质量不利的原因,采取措施加以消除,使质量不断提高,并把一个过程从失控状态变为受控状态,以保持质量稳定。
3.常规控制图的种类(1)计量值控制图均值-极差控制图( Xbar-R 图)。
均值-标准差控制图(Xbar-s 图)。
X-s控制图与X-R图相似,只是用标准差s图代替极差R图而已。
极差计算简便,故R图得到广泛应用,但当样本量n>10,这时应用极差估计总体标准差的效率减低,需要应用s图来代替R图。
中位数-极差控制图( X~ -R 图,也有用Me-R图表示)单值-移动极差控制图(X-Rs 图)2)计数值控制图不合格品率控制图(p 图)不合格品数控制图(pn 图)单位缺陷数控制图(u 图)缺陷数控制图(c 图)3、控制图的构造控制上限(记为UCL)为μ+3σ控制下限(记为LCL)为μ-3σ控制中心线(记为CL)为μ将这三条水平线画在一张坐标纸上,其横轴为时间或样本序号,纵轴为过程变量的观察值这就形成了一张控制图。
1以顾客为关注焦点:组织依存于其顾客。
因此组织应理解顾客当前和未来的需求,满足顾客并争取超越顾客期望。
2领导作用:领导者确立本组织统一的宗旨和方向。
他们应该创造并保持使员工能充分参与实现组织目标的内部环境。
3全员参与:各级人员是组织之本,只有他们的充分参与,才能使他们的才干为组织获益。
4过程方法:将相关的活动和资源作为过程进行管理,可以更高效地得到期望的结果。
5管理的系统方法:识别、理解和管理作为体系的相互关联的过程,有助于组织实现其目标的效率和有效性。
6持续改进:组织总体业绩的持续改进应是组织的一个永恒的目标。
7基于事实的决策方法:有效决策是建立在数据和信息分析基础上。
8互利的供方关系:组织与其供方是相互依存的,互利的关系可增强双方创造价值的能力。
这八项质量管理原则形成了ISO 9000族质量管理体系标准的基础。
一、质量管理八项原则产生的背景随着全球竞争的不断加剧,质量管理越来越成为所有组织管理工作的重点。
一个组织应具有怎样的组织文化,以保证向顾客提供高质量的产品呢?ISO/TC176/SC2/WG15结合ISO9000标准2000年版制订工作的需要,通过广泛的顾客调查制订成了质量管理八项原则。
质量管理八项原则最初以ISO/TC176/SC2/WG/N125号文件《质量管理原则及其应用指南》发布,在ISO/TC176召开的特拉维夫会议前以绝对多数的赞同票得到通过。
为了能对质量管理原则的定义取得高度的一致,又编制了仅包含质量管理八项原则的新文件ISO/TC176/SC2/WG15/N130《质量管理原则》。
在1997年9月27日至29日召开的哥本哈根会议上,36个投票国以32票赞同4票反对通过了该文件,并由ISO/TC176/SC2/N376号文件予以发布。
二、质量管理八项原则及其应用指南原则1—以顾客为中心组织依存于他们的顾客,因而组织应理解顾客当前和未来的需求,满足顾客需求并争取超过顾客的期望。
SPC计量值之中位数全距控制图(M-R)
摘要:中位数全距控制图(M-R)是属于SPC计量值控制图中的一种,用以侦测品质变异的原因,然后采取对策以消除其原因,使生产过程恢复正常一种管理工具。
中位数全距控制图(M-R)的意义
中位数全距控制图(M-R)主要用来对产品初期品质进行测定和监控,以了解在现有环境中品质的制程能力。
∙优点:易于使用,并不要求很多计算,使车间工人易于接受的一种控制图方法。
∙缺点:中位数在统计意义上没有均值理想。
中位数全距控制图(M-R)的图形制作步骤
1)中位数的算法:先将数据按大小顺序排序,再取中间的一个数据;
2)计算管制中心线及管制上、下限;
3)图形分析:通过图形来直接判断制程是否受控时;
中位数全距控制图(M-R)的应用案例
分别计算出它们的中位数(如遇偶数个数据,建议统一取前面或后面一个数据)
1.计算出控制图的中心线及管制上、下限:
2.最后得出中位数全距控制图(M-R)的图形如下:。