切应力τ的计算公式剪切强度条件挤压强度条件

切应力τ的计算公式剪切强度条件挤压强度条件
切应力τ是一种刻画物体内部材料抗剪能力的物理量，它代表了物
体内部单位面积上所受到的切割作用力。

在弹性力学中，切应力可以通过
以下公式进行计算：
τ=F/A
其中，τ表示切应力，F表示作用在物体上的切割力，A表示受力面
的面积。

剪切强度条件是指材料在受到切应力时能够抵抗剪切破坏的能力。

剪
切强度是材料的一个重要参数，也是材料设计和工程应用中需要考虑的一
个关键因素。

一般情况下，剪切强度与材料的直接抗拉强度有一定的关联。

根据材料的性质和试验数据，可以得到剪切强度与抗拉强度之间的经验关系。

挤压强度条件是指材料在受到纵向挤压应力时能够抵抗挤压破坏的能力。

挤压强度是材料设计和工程应用中常常需要考虑的一个参数。

在挤压
过程中，由于材料在横截面上受到侧向作用力，会引起横截面上的应力分布。

根据材料的性质和试验数据，可以得到挤压强度与抗拉强度之间的经
验关系。

在考虑剪切强度和挤压强度条件时，常常需要考虑材料的塑性变形特性。

材料在受到外界应力作用时，会发生塑性变形，形成塑性流动区域。

在塑性流动区域内，材料的应力和应变之间存在一定的关系，常用应力应
变曲线来表征材料的塑性形变特性。

总结起来，剪切应力τ可以通过公式τ=F/A来计算，剪切强度和挤压强度是材料在受到剪切和挤压应力时抵抗破坏的能力。

在实际应用中，常常需要考虑材料的塑性变形特性来确定剪切强度和挤压强度的条件。

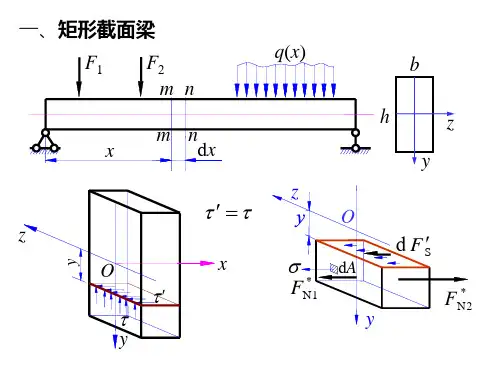
一、拉（压）杆强度条件：--------（1）二、（剪切）切应力条件和挤压强度条件1.切应力强度条件：τ --------（2）2.挤压强度条件：--------（3）三、圆轴扭转时的强度和刚度条件资料个人收集整理，勿做商业用途1.扭转强度条件：-----------（4）----------------（5）2.扭转刚度条件：-----------（6）----------------（7）四：弯曲正应力强度条件：------(8)符号释义：1.：正应力2. τ：切应力3.T：扭矩4.：轴力5.：剪切力6.7.A：剪切截面面积8.：抗扭截面系数9.：横截面对圆心的极惯性矩10.y: 正应力到中性轴的距离11.ε：正应变(线应变) 三个弹性材料的关系：1.E：弹性模量（GN/m²）2. μ：为泊松比（钢材的μ为0.25-0.33）3.G：剪切弹性模量（GN/m²）剪切胡可定律：τ=Gγ16.E：抗拉刚度17.胡可定律：σ=Eεσ=E18.ρ：曲率半径19.：梁弯曲变形后的曲率20.M：弯矩轴力、剪切力、均为内力求内力的方法-截面法：1.假想沿m-m横截面将杆件切开2.留下左半端或右半段3.将弃去部分对留下部分的作用(力)用内力代替4.对留下部分写平衡方程，求出内力的值。

当你选择好研究对象时，建立坐标系，这个对象的所有受力的x方向的代数和，和y方向的代数和为零，这就建立平衡方程，【me=o】，就是你在研究对象上选取一个点作为支点，然后所有力对这个点取矩，顺时针和逆时针方向的代数和为零，这样就分别建立三个平衡方程，可以联立接触其中未知数，这种情况只是用于解决静定结构的。

12.γ：切应变(角应变)21.：外力偶矩13.EA：抗拉强度(钢材的EA约为200GPa)14.δ：断后伸长率15.ψ：断面收缩率/相对扭转角梁受力有：轴力、剪切力和弯矩M。

一、材料力学的几个基本感念1.构件：工程结构或机械的每一组成部分。

2.剪切强度计算 (1) 剪切强度条件剪切强度条件就是使构件的实际剪应力不超过材料的许用剪应力。

[]sF A ττ=≤(5-6)这里[τ]为许用剪应力，单价为Pa 或MPa 。

由于剪应力并非均匀分布，式(5-2)、(5-6)算出的只是剪切面上的平均剪应力，所以在使用实验的方式建立强度条件时，应使试件受力尽可能地接近实际联接件的情况，以确定试样失效时的极限载荷τ0，再除以安全系数n ，得许用剪应力[τ]。

[]n ττ=(5-7)各种材料的剪切许用应力应尽量从相关规范中查取。

一般来说，材料的剪切许用应力[τ]与材料的许用拉应力[σ]之间，存在如下关系： 对塑性材料：[]0.60.8[]τσ= 对脆性材料：[]0.8 1.0[]τσ=(2) 剪切实用计算剪切计算相应地也可分为强度校核、截面设计、确定许可载荷等三类问题，这里就不展开论述了。

但在剪切计算中要正确判断剪切面积，在铆钉联接中还要正确判断单剪切和双剪切。

下面通过几个简单的例题来说明。

例5-1 图5-12(a)所示电瓶车挂钩中的销钉材料为20号钢，[τ]＝30MPa ，直径d=20mm 。

挂钩及被连接板件的厚度分别为t ＝8mm 和t 1＝12mm 。

牵引力F=15kN 。

试校核销钉的剪切强度。

图5-12 电瓶车挂钩及其销钉受力分析示意图解：销钉受力如图5-12(b)所示。

根据受力情况，销钉中段相对于上、下两段沿m-m 和n-n 两个面向左错动。

所以有两个剪切面，是一个双剪切问题。

由平衡方程容易求出：2s F F =销钉横截面上的剪应力为：332151023.9MPa<[]2(2010)4s F A ττπ-⨯===⨯⨯故销钉满足剪切强度要求。

例5-2 如图5-13所示冲床，F max =400KN ，冲头[σ]=400MPa ，冲剪钢板的极限剪应力τb =360 MPa 。

试设计冲头的最小直径及钢板最大厚度。

图5-13 冲床冲剪钢板及冲剪部分受力示意图解：(1) 按冲头压缩强度计算dmax max2=[]4F F d Aσσπ=≤所以0.034 3.4d m cm≥===(2) 钢板的剪切面是直径为d 高为t 的柱表面。

剪切及挤压应力计算剪切应力的计算公式如下：τ=F/A其中，τ表示剪切应力，F表示剪力，A表示剪切面积。

剪切面积的计算取决于物体的几何形状。

对于一个长方形截面，剪切面积为宽度乘以高度（A=b*h）；对于一个圆形截面，剪切面积为π乘以半径的平方（A=π*r²）。

挤压应力的计算公式如下：σ=F/A其中，σ表示挤压应力，F表示挤压力，A表示挤压面积。

挤压面积的计算方法与剪切应力类似，取决于物体的几何形状。

在实际应用中，剪切应力和挤压应力的计算是密切相关的。

当物体受到外部力的作用时，如果该力的方向与物体表面的切线方向垂直，则产生挤压应力；如果该力的方向与物体表面的切线方向平行，则产生剪切应力。

因此，可以通过计算剪切应力和挤压应力来评估物体在受力下的变形和稳定性。

剪切应力和挤压应力的计算在工程领域具有重要的应用，例如材料力学、结构力学以及机械设计等。

通过对剪切应力和挤压应力的分析和计算，可以确定材料的承载能力、抗变形能力、抗压能力等重要参数，从而保证工程结构的安全性、稳定性和可靠性。

总之，剪切应力和挤压应力的计算是工程领域中的重要内容，通过合理的计算和分析可以更好地了解材料和结构受力状态，从而指导工程设计与实施。

1. Hibbeler, R. C. (2024). Mechanics of materials. Pearson Education.2. Beer, F. P., Johnston, E. R., DeWolf, J. T., & Mazurek, D.F. (2024). Mechanics of materials. McGraw-Hill Education.3. Timoshenko, S., & Gere, J. M. (2004). Theory of elastic stability. Courier Corporation.。

拉伸、压缩与剪切1基本概念及知识要点1.1 基本概念轴力、拉（压）应力、力学性能、强度失效、拉压变形、胡克定律、应变、变形能、静不定问题、剪切、挤压。

以上概念是进行轴向拉压及剪切变形分析的基础，应准确掌握和理解这些基本概念。

1.2 轴向拉压 的内力、应力及变形1．横截面上的内力：由截面法求得横截面上内力的合力沿杆的轴线方向，故定义为轴力F N ，符号规定：拉力为正，压力为负。

工程上常以轴力图表示杆件轴力沿杆长的变化。

2．轴力在横截面上均匀分布，引起了正应力，其值为F Aσ=N正应力的符号规定：拉应力为正，压应力为负。

常用的单位为MPa 、Pa 。

3．强度条件强度计算是材料力学研究的主要问题之一。

轴向拉压时，构件的强度条件是[]F Aσσ=≤N可解决三个方面的工程问题，即强度校核、设计截面尺寸及确定许用载荷。

4．胡克定律线弹性范围内，杆的变形量与杆截面上的轴力F N 、杆的长度l 成正比，与截面尺寸A成反比；或描述为线弹性范围内，应力应变成正比，即F l l E EAσε∆==N式中的E 称为材料的弹性模量，EA 称为抗拉压刚度。

胡克定律揭示在比例极限内，应力和应变成正比，是材料力学最基本的定律之一，一定要熟练掌握。

1.3 材料在拉压时的力学性能材料的力学性能的研究是解决强度和刚度问题的一个重要方面。

材料力学性能的研究一般是通过实验方法实现的，其中拉压试验是最主要、最基本的一种试验，由它所测定的材料性能指标有：E —材料抵抗弹性变形能力的指标；b s σσ,—材料的强度指标；ψδ,—材料的塑性指标。

低碳钢的拉伸试验是一个典型的试验。

详见教材，应理解本部分知识。

1.4 简单拉压静不定问题1． 未知力的个数超过静力平衡方程个数的问题为静不定问题，其中未知力可以是结构的约束反力或构件的内力。

2． 解决静不定问题，除列出静力平衡方程外，还需列出一定数量的补充方程，这些补充方程可由结构各部分变形之间的几何关系以及变形和力之间的物理关系求得，将补充方程和静力平衡方程联立求解，即可得出全部未知力。

剪切及挤压应力计算剪切应力是物体内部的应力状态之一，指物体内部各部分相对于其它部分的平动趋势。

挤压应力则是指物体受到外部挤压力作用后内部产生的应力。

剪切及挤压应力计算需要考虑物体的形状、尺寸以及施加力的方向和大小。

对于剪切应力的计算，可以通过剪切力与剪切面积之比来求得。

假设一个物体受到平行于其中一平面的剪切力作用，剪切力的大小为F，剪切面的积为A。

剪切应力可以表示为τ=F/A。

其中τ表示剪切应力。

如果物体的形状不规则，可以将其划分为多个小面元，然后求和计算得到总的剪切应力。

对于挤压应力的计算，可以通过挤压力与挤压面积之比来求得。

假设一个物体受到垂直于其中一平面的挤压力作用，挤压力的大小为P，挤压面的积为A。

挤压应力可以表示为σ=P/A。

其中σ表示挤压应力。

如果物体的形状不规则，可以将其划分为多个小面元，然后求和计算得到总的挤压应力。

剪切应力和挤压应力的计算都需要明确给定施加力的方向和大小，以及物体的面积。

对于规则形状的物体，可以通过几何方法直接计算得到。

对于不规则形状的物体，需要采用数值方法进行近似计算。

除了这种简单情况外，对于复杂的物体形状和受力情况，需要运用工程力学的知识，通过应力分析、协调方程等方法来进行计算。

在这种情况下，需要考虑物体的几何形状、材料的性质、受力的位置和大小等因素，以得到更精确的剪切应力和挤压应力的计算结果。

最后，需要注意的是，剪切应力和挤压应力是物体内部的应力状态，其大小与物体的尺寸和形状有关。

在工程设计中，需要根据所需的应力状态来选择合适的材料和设计结构，以保证物体在受力情况下不会发生破坏或变形。

总之，剪切应力和挤压应力的计算是工程力学中重要的内容之一，需要综合运用几何学、力学、材料学等知识，通过适当的数值计算或工程分析方法来进行。

这样可以为工程设计提供可靠的理论基础，以保证物体的强度和稳定性。

切应力τ的计算公式剪切强度条件挤压强度条件
切应力τ是描述材料内部剪切力作用下产生的单位面积上的应力。

它可以用来衡量材料承受剪切负载的能力。

下面将介绍一些常用的切应力
计算公式以及剪切强度条件和挤压强度条件。

1.切应力计算公式：
在一般情况下，切应力τ可以根据以下公式进行计算：
τ=F/A
其中，τ为切应力，F为作用在材料上的剪切力，A为剪切面积。

2.剪切强度条件：
剪切强度是指材料能够承受的最大切应力。

剪切强度条件可以通过以
下公式表示：
τ<τ_s
其中，τ为切应力，τ_s为材料的剪切强度。

当切应力小于剪切强
度时，材料是稳定的，不会发生破坏。

3.挤压强度条件：
挤压强度是指材料在挤压过程中能够承受的最大应力。

挤压强度条件
可以通过以下公式表示：
σ<σ_c
其中，σ为应力，σ_c为材料的挤压强度。

当应力小于挤压强度时，材料是稳定的，不会发生破坏。

需要注意的是，切应力计算公式、剪切强度条件和挤压强度条件并不
是所有材料都适用，不同材料可能有不同的计算公式和强度条件。

此外，
对于复合材料和非均质材料，切应力计算和强度条件的确定可能更加复杂。

总结起来，切应力的计算公式可以使用τ=F/A进行计算。

而切应力
的强度条件根据具体情况可以使用剪切强度条件：τ<τ_s或者挤压强度
条件：σ<σ_c进行判断。

在设计结构或选择材料时，需要根据具体要求
和实际情况来确定切应力和强度条件的数值。

- 1 - 材料力学常用公式1、胡克定律：EA l F l N ⋅=∆或εσ⋅=E 2、杆件轴向拉、压强度条件：[]σσ≤=⋅AFN nax max 3、剪切强度条件：[]ττ≤=AF S；挤压强度条件：[]bc bc bc bc F A σσ=≤4、外力偶矩计算公式：min/||||9550||r kWm N n P M =⋅5、圆轴扭转切应力：pI T ρτρ⋅=；扭转强度条件：[]max max t T W ττ=≤6、圆轴扭转变形：p I G lT ⋅⋅=ϕ；扭转刚度条件：[]θπθ≤⋅=0max max 180p GI T7、极惯性矩：Dd,)1(32;32444=-==ααππD I D I p p 空心实心； 扭转截面系数：)1(16;16433αππ-==D W D W p p 空心实心8、梁弯曲正应力：z I yM ⋅=σ；弯曲正应力强度条件：[]σσ≤=zW M max max 9、惯性矩：1212；)1(64;6433444hb I bh I D I D I y z z z ==-==或矩形空心圆实心圆αππ 10、弯曲截面系数：66)1(32;3222433hb W bh W ；D W D W y z z z ==-==或矩形空心圆实心圆αππ11、拉压-弯曲组合变形强度条件：[]][,max max ,max max ,c zN c t z N t W M A F W M A F σσσσ≤-=≤+=12、圆轴弯扭组合变形强度条件：[][]σσσσ≤+=≤+=zr z r W T M W T M 22422375.0或13、压杆临界应力公式：欧拉公式()2222;cr cr EI EF L ππσλμ==；直线公式λσb a cr -= 14、柔度i l μλ=；惯性半径：AI i = 15、压杆的稳定条件：[]cr cr st st A Fn n F F σ==≥ 16、平面应力状态下斜截面应力的一般公式 cos 2sin 222sin 2cos 22x y x yαxy x y xy σσσσσσσαατατατα+-⎧=+-⎪⎪⎨-⎪=+⎪⎩- 2 -17、最大最小正应力：18、主平面方位计算公式：19、面内最大切应力： 20、20、三向应力状态最大切应力：21、胡克定律：21四大强度理论：max 13()2τσσ=-max min 2x y σσσσ+⎫=±⎬⎭132σσσ⎫=±⎬⎭()11231E εσμσσ=-+⎡⎤⎣⎦()22311E εσμσσ=-+⎡⎤⎣⎦()33121Eεσμσσ=-+⎡⎤⎣⎦,11[]r σσσ=≤,313[]r σσσσ=-≤,2123()[]r σσμσσσ=-+≤,4[]r σσ=≤。

材料力学重点及其公式外力偶矩传动轴所受的外力偶矩通常不是直接给出，而是根据轴的转速n 与传递的功率P 来计算。

当功率P 单位为千瓦（kW ），转速为n （r/min）时，外力偶矩为Me=9549P n P n(N. m)当功率P 单位为马力（PS ），转速为n （r/min）时，外力偶矩为Me=7024(N. m)2.5.2切应力计算公式横截面上某一点切应力大小为τp =T ρI p(3-12)式中I p 为该截面对圆心的极惯性矩，ρ为欲求的点至圆心的距离。

圆截面周边上的切应力为τm a x =I p RT W t(3-13)式中W t =称为扭转截面系数，R 为圆截面半径。

2.5.3 切应力公式讨论（1）切应力公式（3-12）和式（3-13）适用于材料在线弹性范围内、小变形时的等圆截面直杆；对小锥度圆截面直杆以及阶梯形圆轴亦可近似应用，其误差在工程允许范围内。

（2）极惯性矩I p 和扭转截面系数W t 是截面几何特征量，计算公式见表3-3。

在面积不变情况下，材料离散程度高，其值愈大；反映出轴抵抗扭转破坏和变形的能力愈强。

因此，设计空心轴比实心轴更为合理。

2.5.4强度条件圆轴扭转时，全轴中最大切应力不得超过材料允许极限值，否则将发生破坏。

因此，强度条件为τm a x =⎛T ⎫≤[τ] (3-14) 对等圆截面直杆τm ⎪W ⎝t ⎭m a xa=xT m W ta x≤[τ] （3-15）式中[τ]为材料的许用切应力。

3.1.1中性层的曲率与弯矩的关系1ρ=M EI z(3-16)式中，ρ是变形后梁轴线的曲率半径；E 是材料的弹性模量；I E 是横截面对中性轴Z 轴的惯性矩。

3.1.2横截面上各点弯曲正应力计算公式σ=M I Zy(3-17)式中，M 是横截面上的弯矩；I Z 的意义同上；y 是欲求正应力的点到中性轴的距离最大正应力出现在距中性轴最远点处σm a x =I z y m axM m I za x∙y=m a xM W zm a x（3-18）π32式中，W z =称为抗弯截面系数。

切应力的计算公式适用于
切应力的计算公式通常应用于材料力学领域，特别是用于研究材料的强度和变形特性。

切应力是指材料在受到外力作用下产生的切变应力。

切应力的计算公式可以通过以下方式得到：
切应力（τ）= 外力的剪切力（F）/ 剪切面积（A）
其中，外力的剪切力指的是施加在材料上的剪切力，剪切面积是受力面积的大小。

切应力的单位通常为帕斯卡（Pa）或兆帕（MPa）。

切应力的计算公式是非常重要的，在工程领域中广泛应用。

它可以帮助工程师和研究人员更好地理解材料的强度和变形特性，以便设计出更安全可靠的结构和机件。

切应力的计算公式可以应用于各种材料，包括金属、塑料、混凝土等。

在工程实践中，切应力的计算公式常常与材料的弹性模量和变形率等参数一起使用，以更全面地评估材料的力学性质。

除了计算切应力，这个公式还可用于材料强度的评估。

当切应力超过材料的极限强度时，材料会发生破裂或变形。

因此，通过计算切应力，可以判断材料是否能够承受外力的作用并保持结构的完整性。

在材料设计和工程实践中，切应力的计算公式为工程师提供了重要的指导。

通过了解材料的切应力分布和变化情况，工程师可以优化
结构设计，减少材料的浪费和成本，并确保结构在工作负荷下的稳定性和安全性。

总之，切应力的计算公式对于材料力学的研究和工程实践非常重要。

它提供了一种评估材料强度和变形特性的方法，为工程师设计更安全可靠的结构和机件提供了指导。

在今后的工作中，我们应该进一步深入研究和应用切应力的计算公式，以推动材料力学领域的发展和进步。