2.3平行线的性质

平行线的性质及推导方法平行线，是指在同一个平面内，永不相交的两条直线。

平行线的性质与推导方法是几何学中的重要内容，下面我们将详细介绍平行线的性质及推导方法。

一、平行线的性质1. 平行线定理：如果一条直线与两条平行线相交，那么这条直线将被两条平行线所截成的锐角和钝角互补。

证明：设直线l与平行线m和n相交于A点，BC与m、n平行。

由平行线的性质可知∠ABC=∠ACD，又∠ABC+∠ACD=180°（线l与m、n相交，∠ABC和∠ACD互补），所以∠ABC和∠ACD互补。

2. 平行线的性质之间的关系：如果两条平行线被一条交线所截，那么它们与这条交线所构成的内错角、内外错角、对顶角以及同位角是相等的。

证明：设直线l与平行线m和n相交于点O，AB与m平行，CD与n平行。

先证明内错角相等，连接AC、BD。

由三角形的内角和为180°可知∠ACB+∠BCA+∠CDA+∠DAB=180°，∠ACB+∠BCA+∠ADB=180°（∠CDA和∠DAB互补），所以∠ACB+∠BCA+∠CDA+∠DAB=∠ACB+∠BCA+∠ADB，化简得∠CDA=∠ADB。

同理可证∠ACD=∠ABC，∠BAC=∠DCB，∠ADC=∠BCD。

二、平行线的推导方法1. 利用平行线的性质证明线段比例关系。

证明：设AB与CD分别是平行线m和n上的两个点，交线AC与BD相交于E点。

若已知AE:EC=BD:DE，要证明AB:BC=BD:DC（即证明∆ABD∽∆CBD）。

由已知的比例关系可得：AE/EC=BD/DE，即AE/BD=EC/DE。

又因为∠AEB和∠CDE为同位角，根据同位角定理可知∠AEB=∠CDE。

由此可得∆ABE∽∆CDE，进一步得出AB:BE=CD:DE。

同理可证∆CBD∽∆ADE，从而得出BC:BD=DE:DA。

综合上述比例关系，可以得出AB:BC=BD:DC，证明了平行线性质下的线段比例关系。

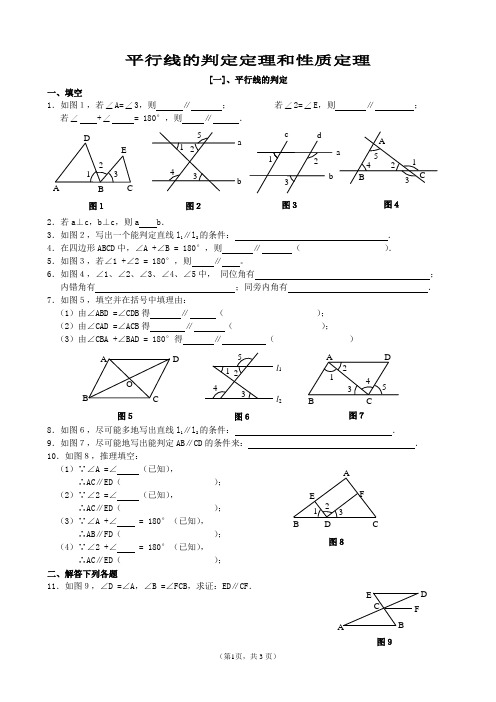
平行线的判定定理和性质定理[一]、平行线的判定一、填空1．如图１，若∠A=∠3，则 ∥ ； 若∠2=∠E ，则 ∥ ； 若∠ +∠ = 180°，则 ∥ ．2．若a⊥c，b⊥c，则a b ．3．如图２，写出一个能判定直线l 1∥l 2的条件： ． 4．在四边形ABCD 中，∠A +∠B = 180°，则 ∥ （ ）． 5．如图３，若∠1 +∠2 = 180°，则 ∥ 。

6．如图４，∠1、∠2、∠3、∠4、∠5中， 同位角有 ； 内错角有 ；同旁内角有 ． 7．如图５，填空并在括号中填理由：（1）由∠ABD =∠CDB 得 ∥ （ ）； （2）由∠CAD =∠ACB 得 ∥ （ ）；（3）由∠CBA +∠BAD = 180°得 ∥ （ ）8．如图６，尽可能多地写出直线l 1∥l 2的条件： ．9．如图７，尽可能地写出能判定AB∥CD 的条件来： ． 10．如图８，推理填空：（1）∵∠A =∠ （已知）， ∴AC∥ED（ ）；（2）∵∠2 =∠ （已知）， ∴AC∥ED（ ）； （3）∵∠A +∠ = 180°（已知）， ∴AB∥FD（ ）；（4）∵∠2 +∠ = 180°（已知）， ∴AC∥ED（ ）； 二、解答下列各题11．如图９，∠D =∠A，∠B =∠FCB，求证：E D∥CF．A CB 4 1 2 3 5 图４ a b c d 1 2 3 图３ A BC ED 1 2 3 图１ 图２ 4 3 2 1 5 a b 1 2 3A F C DB E图８EB AF D C 图９A D CB O 图５ 图６ 5 1 24 3 l 1 l 2 图７5 4 3 2 1 A D C B12．如图10，∠1∶∠2∶∠3 = 2∶3∶4， ∠AFE = 60°，∠BDE =120°，写出图中平行的直线，并说明理由．13．如图11，直线AB 、CD 被EF 所截，∠1 =∠2，∠CNF =∠BME。

平行线与平行线的性质定理平行线是几何学中的重要概念，自古以来就引起人们的关注与探索。

在欧几里得的《几何原本》中，有关平行线的性质定理被详细地论述。

本文将对平行线及其性质定理进行探讨。

1. 平行线的定义及基本性质平行线的定义：在平面几何中，如果两条直线在同一个平面内且永不相交，那么这两条直线被称为平行线。

记作AB || CD。

平行线的基本性质：- 平行线之间的距离是恒定的，任意一点到平行线的距离相等。

- 平行线的斜率相等或者相互垂直的直线之间的斜率乘积为-1。

2. 平行线的性质定理2.1. 平行线的传递性：如果一条直线与另外两条直线分别平行，那么这两条直线也是平行的。

2.2. 平行线的对应角定理：当一条直线与两条平行线相交时，所形成的对应角相等。

2.3. 平行线的同位角定理：当一条直线与两条平行线相交时，所形成的同位角互为对应角，且相等。

2.4. 平行线的内错角定理：当两条平行线被一条截断时，所形成的内错角互为对应角，且相等。

2.5. 平行线的外错角定理：当两条平行线被一条截断时，所形成的外错角互为对应角，且相等。

2.6. 平行线的平行截线定理：当一条直线与两条平行线相交时，所形成的截线与平行线的交线段成比例。

3. 平行线定理的应用平行线定理是几何学中重要的基础理论，在实际应用中有着广泛的运用，例如：3.1. 建筑设计中，利用平行线定理可以确保建筑结构的平衡和稳定性。

3.2. 地图制作中，通过研究平行线定理可以实现地图的精确绘制与测量。

3.3. 工程规划中，运用平行线定理可以合理安排道路、桥梁等建设。

4. 总结平行线与平行线的性质定理是几何学中的基础理论，对于理解和应用几何知识具有重要意义。

通过对平行线的定义及性质定理的论述，我们可以深入了解平行线的特点以及其在实际中的应用价值。

温习这些性质定理有助于提升几何学的理解能力，培养逻辑思维和分析问题的能力。

同时，我们也可以发现平行线定理对于解决实际问题具有指导作用，能够有效地应用于各个领域的设计与规划中。

人教版初中数学教案第一篇：人教版初中数学平行线的性质教案2.3平行线的性质一、教材分析：本节课是人民教育出版社义务教育课程标准实验教科书（五四学制）七年级上册第2章第3节平行线的性质，它是平行线及直线平行的继续，是后面研究平移等内容的基础，是?空间与图形?的重要组成部分。

二、教学目标：1.知识与技能：掌握平行线的性质，能应用性质解决相关问题。

数学思考：在平行线的性质的探究过程中，让学生经历观察、比较、联想、分析、归纳、猜想、概括的全过程。

2.解决问题：通过探究平行线的性质，使学生形成数形结合的数学思想方法，以及建模能力、创新意识和创新精神。

3.情感态度与价值观：在探究活动中，让学生获得亲自参与研究的情感体验，从而增强学生学习数学的热情和勇于探索、锲而不舍的精神。

三、教学重、难点：重点：平行线的性质难点：?性质1?的探究过程四、教学方法：引导发现法?与?动像探索法?五、教具、学具：教具：多媒体课件学具：三角板、量角器。

六、教学媒体：大屏幕、实物投影七、教学过程：（一）创设情境，设疑激思：1．播放一组幻灯片。

内容：①火车行驶在铁轨上；②游泳池；③横格纸。

2．声音：日常生活中我们经常会遇到平行线，你能说出直线平行的条件吗？学生活动：思考回答。

①同位角相等两直线平行；②内错角相等两直线平行；③同旁内角互补两直线平行；教师：首先肯定学生的回答，然后提出问题。

问题：若两直线平行，那么同位角、内错角、同旁内角各有什么关系呢？引出课题——平行线的性质。

（二）数形结合，探究性质1．画图探究，归纳猜想任意画出两条平行线（a‖b），画一条截线c与这两条平行线相交，标出8个角（如图）。

问题一：指出图中的同位角，并度量这些角，把结果填入下表：第一组第二组第三组第四组同位角∠1∠5角的度数数量关系学生活动：画图——度量——填表——猜想结论：两直线平行，同位角相等。

问题二：再画出一条截线d，看你的猜想结论是否仍然成立？学生：探究、讨论，最后得出结论：仍然成立。

平行线的性质知识点1平行线的性质平行线的性质：性质1 两条平行线被第三条直线所截，同位角相等.简单说成：两直线平行，同位角相等.如图1，∵a∥b，∴∠4=∠2.性质2 两条平行线被第三条直线所截，内错角相等.简单说成：两直线平行，内错角相等.如图2，∵a∥b，∴∠4=∠5.性质3 两条平行线被第三条直线所截，同旁内角互补.简单说成：同旁内角互补，两直线平行.如图3，∵a∥b，∴∠4+∠1=180°.【典例】1.如图1，对于直线MN同侧的两个点A，B，若直线MN上的点P满足∠APM=∠BPN，则称点P为A，B在直线MN上的反射点．已知如图2，MN∥HG，AP∥BQ，点P为A，B在直线MN上的反射点，判断点B是否为P，Q在直线HG上的反射点，并说明理由．【方法总结】依据点P为A，B在直线MN上的反射点，即可得到∠APM=∠BPQ，再根据平行线的性质，即可得到∠PAB=∠PBA，经过等量代换可得∠PBA=∠QBG，所以点B是P，Q在直线HG 上的反射点．本题是新定义题，正确理解“反射点”的概念和特征，并熟练应用平行线的性质是解题的关键.【随堂练习】1．如图，已知AM∥BN，∠A＝80°，点P是射线AM上动点（与A不重合），BC、BD分别平分∠ABP和∠PBN，交射线AM于C、D．（1）求∠CBD的度数；（2）当点P运动时，那么∠APB：∠ADB的度数比值是否随之发生变化？若不变，请求出这个比值；若变化，请找出变化规律；（3）当点P运动到使∠ACB＝∠ABD时，求∠ABC的度数．2．如图1，AM∥CN，点B为平面内一点，AB⊥BC于B，过B作BD⊥AM．（1）求证：∠ABD＝∠C；（2）如图2，在（1）问的条件下，分别作∠ABD、∠DBC的平分线交DM于E、F，若∠BFC＝1.5∠ABF，∠FCB＝2.5∠BCN，①求证：∠ABF＝∠AFB；②求∠CBE的度数．3．已知直线l1∥l2，直线l3与l1、l2分别交于C、D两点，点P是直线l3上的一动点，如图①，若动点P在线段CD之间运动（不与C、D两点重合），问在点P的运动过程中是否始终具有∠3+∠1＝∠2这一相等关系？试说明理由；如图②，当动点P在线段CD之外且在CD的上方运动（不与C、D两点重合），则上述结论是否仍成立？若不成立，试写出新的结论，并说明理由．知识点2 平行线的判定与性质的综合运用两直线平行⇔同位角相等.两直线平行⇔内错角相等.同旁内角互补⇔两直线平行.“⇔”叫做“等价于”，即由左边能推出右边，由右边也能推出左边.【典例】1.如图，已知∠1=∠2，∠3=∠4，∠5=∠A，试说明：BE∥CF．2.学习完平行线的性质与判定之后，我们发现借助构造平行线的方法可以帮我们解决许多问题．（1）小明遇到了下面的问题：如图1，l1∥l2，点P在l1、l2内部，探究∠A，∠APB，∠B的关系．小明过点P作l1的平行线，可证∠APB，∠A，∠B之间的数量关系是：∠APB=____________________．（2）如图2，若AC∥BD，点P在AC、BD外部，∠A，∠B，∠APB的数量关系是否发生变化？（3）已知：如图3，三角形ABC，试说明：∠A+∠B+∠C=180°．【方法总结】平行线的判定是由角的关系得到两直线平行，平形线的性质是由两直线平行得到角之间的关系，他们都可以作为说理的依据.其他常见的说理依据有：已知、等量代换、对顶角相等、等角的余角相等、等角的补角相等、平行于同一条直线的两条直线互相平行、三角形的内角和等于180°等.【随堂练习】1．阅读下列材料：已知：如图1，直线AB∥CD，点E是AB、CD之间的一点，连接BE、DE得到∠BED．求证：∠BED＝∠B+∠D．小冰是这样做的：证明：过点E作EF∥AB，则有∠BEF＝∠B．∵AB∥CD，∴EF∥CD．∴∠FED＝∠D．∴∠BEF+∠FED＝∠B+∠D．图1即∠BED＝∠B+∠D．请利用材料中的结论，完成下面的问题：已知：直线AB∥CD，直线MN分别与AB、CD交于点E、F．（1）如图2，∠BEF和∠EFD的平分线交于点G．猜想∠G的度数，并证明你的猜想；（2）如图3，EG1和EG2为∠BEF内满足∠1＝∠2的两条线，分别与∠EFD的平分线交于点G1和G2．求证：∠FG1E+∠G2＝180°．2．先阅读下面的解题过程，再解答问题：如图①，已知AB∥CD，∠B＝40°，∠D＝30°，求∠BED的度数．解：过点E作EF∥AB，则AB∥CD∥EF，因为EF∥AB，所以∠1＝∠B＝40°又因为CD∥EF，所以∠2＝∠D＝30°所以∠BED＝∠1+∠2＝40°+30°＝70°．如图②是小军设计的智力拼图玩具的一部分，现在小军遇到两个问题，请你帮他解决：（1）如图②∠B＝45°，∠BED＝75°，为了保证AB∥CD，∠D必须是多少度？请写出理由．（2）如图②，当∠G、∠GFP、∠P满足什么关系时，GH∥PQ，请直接写出满足关系的式子，并在如图②中画出需要添加的辅助线．。

2．3平行线的性质1．理解平行线的性质；(重点)2．能运用平行线的性质进行推理证明．(重点、难点)一、情境导入窗户的内窗的两条竖直的边是平行的，在推动过程中，两条竖直的边与窗户外框形成的两个角∠1、∠2有什么数量关系？二、合作探究探究点：平行线的性质【类型一】两直线平行，同位角相等如图，直线a，b与直线c，d相交，若∠1＝∠2，∠3＝70°，则∠4的度数是()A．35°B．70°C．90°D．110°解析：由∠1＝∠2，可根据“同位角相等，两直线平行”判断出a∥b，可得∠3＝∠5.再根据邻补角互补可以计算出∠4的度数．∵∠1＝∠2，∴a∥b，∴∠3＝∠5.∵∠3＝70°，∴∠5＝70°，∴∠4＝180°－70°＝110°.故选D.方法总结：此题主要考查了平行线的判定方法与性质1，关键是掌握平行线的判定定理与性质定理，平行线的判定是由角的数量关系判断两直线的位置关系．平行线的性质是由平行关系来寻找角的数量关系．【类型二】两直线平行，内错角相等如图，∠A＝∠D，如果∠B＝20°，那么∠C为()A．40°B．20°C．60°D．70°解析：∵∠A＝∠D，∴AB∥CD.∵AB∥CD，∠B＝20°，∴∠C＝∠B＝20°.故选B.【类型三】两直线平行，同旁内角互补如图，已知∠1＝85°，∠2＝95°，∠4＝125°，则∠3的度数为()A．95°B．85°C．70°D．55°解析：根据“对顶角相等”得到∠5＝∠1＝85°，再由“同旁内角互补，两直线平行”得到a∥b，最后根据“两直线平行，同旁内角互补”即可得到结论．如图，∵∠5＝∠1＝85°，∴∠5＋∠2＝85°＋95°＝180°，∴a∥b，∴∠3＋∠4＝180°.∵∠4＝125°，∴∠3＝55°.故选D.【类型四】平行线性质的实际应用一大门的栏杆如图所示，BA垂直于地面AE于A，CD平行于地面AE，则∠ABC＋∠BCD＝________度．解析：过B作BF∥AE，则CD∥BF∥AE.根据平行线的性质即可求解．过B作BF∥AE，则CD∥BF∥AE，∴∠BCD＋∠1＝180°.又∵AB⊥AE，∴AB⊥BF，∴∠ABF＝90°，∴∠ABC＋∠BCD＝90°＋180°＝270°.故答案为270.【类型五】平行线性质与判定中的探究型问题如图，AB∥CD，E，F分别是AB，CD之间的两点，且∠BAF＝2∠EAF，∠CDF＝2∠EDF.(1)判定∠BAE，∠CDE与∠AED之间的数量关系，并说明理由；(2)求出∠AFD与∠AED之间的数量关系．解析：平行线中的拐点问题，通常需过拐点作平行线．解：(1)∠AED＝∠BAE＋∠CDE.理由如下：过点E作EG∥AB.∵AB∥CD，∴AB∥EG ∥CD，∴∠AEG＝∠BAE，∠DEG＝∠CDE.∵∠AED＝∠AEG＋∠DEG，∴∠AED＝∠BAE＋∠CDE ；(2)同(1)可得∠AFD ＝∠BAF ＋∠CDF .∵∠BAF ＝2∠EAF ，∠CDF ＝2∠EDF ，∴∠BAE＋∠CDE ＝32∠BAF ＋32∠CDF ，∴∠AED ＝32∠AFD . 方法总结：无论平行线中的何种问题，都可转化到基本模型中去解决，把复杂的问题分解到简单模型中，问题便迎刃而解．三、板书设计平行线的性质：性质1：两条平行线被第三条直线所截，同位角相等；性质2：两条平行线被第三条直线所截，内错角相等；性质3：两条平行线被第三条直线所截，同旁内角互补．平行线的性质是几何证明的基础，教学中注意基本的推理格式的书写，培养学生的逻辑思维能力，鼓励学生勇于尝试．在课堂上，力求体现学生的主体地位，把课堂交给学生，让学生在动口、动手、动脑中学数学。