当前位置：文档之家 › 材料力学07应力与应变分析 强度理论

材料力学07应力与应变分析 强度理论

  • 格式：ppt
  • 大小：2.57 MB
  • 文档页数：65

下载文档原格式

  / 65

合集下载

材料力学第7章应力状态

材料力学第7章应力状态

y
2

2 xy

m m
ax in




m
ax
2

m
in
极值切应力等于极值正应力差的一半。
§7.2 平面应力状态分析的解析法
三、极值切应力和主平面夹角
注意到 则 所以
tan
2 0

2 xy x
y
tan
21


x 2 xy
y
tan
20


1
tan 21
§7.2 平面应力状态分析的解析法
7.2.3 极值切应力及其作用面 一、极值切应力方位角
d 0 d
( x y ) cos 2 2 xy sin 2 0
得
tan
21


x 2 xy
y
二、最大、最小切应力

m m
ax
in




x
2



x
y
2
sin 2
xy cos 2
§7.2 平面应力状态分析的解析法
7.2.2 主应力 主方向 一、主应力
正应力是求极值
d d
x
y
2
(2sin 2 ) xy(2cos2 ) 0
得极值条件为

x

2
y
sin
2
xy
cos
2

0
(1) 极值正应力所在的斜面，恰好是切应力等于零的
平面，即主平面。
(2) 极值正应力就是主应力。
§7.2 平面应力状态分析的解析法

材料力学第七章应力状态和强度理论

材料力学第七章应力状态和强度理论
2
x y 2 a 0 2
x y x y 2
x y
2
) x
2
2
例题1: 已知:单元体各侧面应力 x=60MPa,
求: (1) = - 450斜截面上的应力,(2)主应力和主平面
dA
y

x y
2
sin 2 xy cos2
y
yx
应力圆
y
1 R 2

x
y

2
4 2 xy
x
yx xy x
y
R c

x y
2
2
x
xy
x´
dA
yx
y´
y
x y 1 2 2 2

40

x y
2 0.431MPa
sin( 80 ) xy cos(80 )

C
C

C
例题3：已知梁上的M、Q，试用单元体表示截面上1、2、
3、4点的应力状态。
1
2 0
2
1点 2点
1 2 0 3
3Q ＝ 2A
M x Wz
2 xy
x y
2 20.6 0.69 60 0
17.2
x y
2 (
6.4MPa
2 34.4
max(min)
x
17.20
x y
2
) xy
2
2
x
66.4MPa
60 0 60 0 2 ( ) 20.6 2 2 2 66.4(6.4) MPa

材料力学带答疑

材料力学带答疑

第七章应力和应变分析强度理论1.单元体最大剪应力作用面上必无正应力答案此说法错误（在最大、最小正应力作用面上剪应力一定为零；在最大剪应力作用面上正应力不一定为零。

拉伸变形时，最大正应力发生在横截面上，在横截面上剪应力为零；最大剪应力发生在45度角的斜截面上，在此斜截面上正应力为σ/2。

）2. 单向应力状态有一个主平面，二向应力状态有两个主平面答案此说法错误（无论几向应力状态均有三个主平面，单向应力状态中有一个主平面上的正应力不为零；二向应力状态中有两个主平面上的正应力不为零）3. 弯曲变形时梁中最大正应力所在的点处于单向应力状态答案此说法正确（最大正应力位于横截面的最上端和最下端，在此处剪应力为零。

）4. 在受力物体中一点的应力状态，最大正应力作用面上切应力一定是零答案此说法正确（最大正应力就是主应力，主应力所在的面剪应力一定是零）5.应力超过材料的比例极限后，广义虎克定律不再成立答案此说法正确（广义虎克定律的适用范围是各向同性的线弹性材料。

）6. 材料的破坏形式由材料的种类而定答案此说法错误（材料的破坏形式由危险点所处的应力状态和材料的种类综合决定的）7. 不同强度理论的破坏原因不同答案此说法正确（不同的强度理论的破坏原因分别为：最大拉应力、最大线应变、最大剪应力、形状比能。

）二、选择1.滚珠轴承中，滚珠与外圆接触点为应力状态。

A：二向； B：单向C：三向D：纯剪切答案正确选择C（接触点在铅垂方向受压，使单元体向周围膨胀，于是引起周围材料对接触点在前后、左右方向的约束应力。

）2.厚玻璃杯因沸水倒入而发生破裂，裂纹起始于。

A：内壁 B：外壁 C：内外壁同时 D：壁厚的中间答案正确选择：B （厚玻璃杯倒入沸水，使得内壁受热膨胀，外壁对内壁产生压应力的作用；内壁膨胀使得外壁受拉，固裂纹起始于外壁。

）3. 受内压作用的封闭薄壁圆筒，在通过其壁上任意一点的纵、横两个截面中。

A：纵、横两截面均不是主平面； B：横截面是主平面、纵截面不是主平面；C：纵、横二截面均是主平面； D：纵截面是主平面，横截面不是主平面；答案正确选择：C （在受内压作用的封闭薄壁圆筒的壁上任意取一点的应力状态为二向不等值拉伸，其σx =pD/4t、σy=pD/2t。

材料力学 第07章 应力状态分析与强度理论

材料力学 第07章 应力状态分析与强度理论
2
sin2a t xy cos2a
18/95
7.2 平面应力状态分析 主应力 7.2.3 主平面的方位及极值正应力 s x s y s x s y sa cos2a t xy sin2a 2 2 s x s y ds a 上式对a 求导 2 sin2a t xy cos2a da 2 s x s y 若a a0时，导数为 0 sin2a 0 t xy cos2a 0 0 2 2t xy tan2a 0 s x s y
7.2.5 应力圆
t
sx
tyx
sy
sx txy sy
D(sx,txy) 1. 确定点 D (s ,t ) x xy
O
D'(sy,tyx)
C
s
2. 确定点D' (sy,tyx) tyx= －txy 3. 连接DD'与s 轴交于点C 4. 以 C 为圆心，CD（CD'） 为半径画圆。
26/95
7.2 平面应力状态分析 主应力 7.2.5 应力圆
sx sy sz
sxs1 100 MPas 2
0 MPas 3 120 MPa
11/95
7.1 一点的应力状态的概念 单向、二向(平面)、三向(空间)应力状态 三个主应力中仅有一个主应力不为零 单向应力状态
s1
s1
F
A
F
12/95
7.1 一点的应力状态的概念 单向、二向(平面)、三向(空间)应力状态
O
D'(sy,tyx)
C sx－ sx sy/2
s
27/95
7.2 平面应力状态分析 主应力 7.2.5 应力圆 利用应力圆确定角a 斜截面上的正应力和切应力

工程力学c材料力学部分第七章 应力状态和强度理论

工程力学c材料力学部分第七章 应力状态和强度理论

无论是强度分析还是刚度分析，都需要求出应力的极值， 无论是强度分析还是刚度分析，都需要求出应力的极值，为了找 到构件内最大应力的位置和方向 需要对各点的应力情况做出分析。 最大应力的位置和方向， 到构件内最大应力的位置和方向，需要对各点的应力情况做出分析。
受力构件内一点处所有方位截面上应力的集合，称为一点的 受力构件内一点处所有方位截面上应力的集合，称为一点的 研究一点的应力状态时， 应力状态 。研究一点的应力状态时，往往围绕该点取一个无限小 的正六面体—单元体来研究。 单元体来研究 的正六面体 单元体来研究。
σ2
σ2
σ1
σ1
σ
σ
σ3
三向应力状态
双向应力状态
单向应力状态 简单应力状态
复杂应力状态 主应力符号按代数值的大小规定： 主应力符号按代数值的大小规定：
σ1 ≥ σ 2 ≥ σ 3
平面应力状态的应力分析—解析法 §7−2 平面应力状态的应力分析 解析法
图(a)所示平面应力单元体常用平面图形(b)来表示。现欲求 )所示平面应力单元体常用平面图形( )来表示。现欲求 垂直于平面xy的任意斜截面 上的应力 垂直于平面 的任意斜截面ef上的应力。 的任意斜截面 上的应力。
二、最大正应力和最大剪应力
σα =
σ x +σ y
2
+
σ x −σ y
2
cos 2α − τ x sin 2α
τα =
令
σ x −σ y
2
sin 2α + τ x cos 2α
dσ α =0 dα
σ x −σ y
2
sin 2α +τ x cos2α = 0
可见在 τ α
=0

材料力学应力和应变分析强度理论

材料力学应力和应变分析强度理论

§7–5 广义虎克定律
y
一、单拉下旳应力--应变关系
x
x
E
y
E
x
ij 0 (i,j x,y,z)
二、纯剪旳应力--应变关系
z
E
x
z
y
xy
xy
G
i 0 (i x,y,z)
z
yz zx 0
x
x
xy
x
三、复杂状态下旳应力 --- 应变关系
y
y
x
y x
z
xy
z
x
依叠加原理,得:
x
1
(MPa)
解法2—解析法：分析——建立坐标系如图
45 25 3
95
60°
i j
x
2
y
（
x
2
y
）2
2 xy
y
1
25 3 y 45MPa
° 5
0
Ox
6095MPa 6025 3MPa
yx 25 3MPa xy
x ?
x
y
2
sin 2
xy cos 2
25 3 x 45 sin 120o 25 3 cos120o
y
z
z
y
证明: 单元体平衡 M z 0
xy x
x
( xydydz)dx( yxdzdx)dy0
xy yx
五、取单元体： 例1 画出下图中旳A、B、C点旳已知单元体。
F
A
y
F x
x
A
B
C z
x B x
zx
xz
F
Mex
yx
C
xy
FP

材料力学应力理论

材料力学应力理论

例 单向拉伸状态
σx
45º
σx'
τx'y'
B
45º A
σy'
E
τy'x'
D
τα
b
2×45º
d
c
σα
o
a
2×45º
e
σx
¾45º斜面同有正应力、切应力；但正应力不是最大，切应力最大
例 纯剪切状态
D
σy'＝τ
y
O
x
τα
a (0,τ )
τ σx'＝τ
2×45º
2×45º
E
τ
e
c
b σα
o B
Α
d(0,-τ )
σy τyx
τyx
σy
σx
σz
τxy
σx
σz
τxy
平面应力三维看： σ1≥σ2 ≥σ3
τ
τ
o
σ2
σ
σ1
σ3 o
σ
σ1
σ3
τ
σ
σ2
o
200 300 50
τα
τmax
σ3
σ2
σα
o
σ1
σ3
200 300 50
τα
τα
σ3 σ2
O
σ2
σ1 σα
O
300 50
σα
σ1
例 求图示单元体的主应力和最大剪应力。(MPa)
τ τ
45°
τ
τ
7.5 三向应力状态－应力圆法
设三个主应力已知
σ2
τα
τmax
y
σ3
z
x

材料力学 第七章 应力状态和强度理论

材料力学 第七章 应力状态和强度理论

y
2
2 xy
tan 2a0
2 xy x
y
max
1
2
3
主应力符号与规定： 1 2 3 （按代数值）
§7-3 空间应力状态
与任一截面相对应 的点，或位于应力 圆上，或位于由应 力圆所构成的阴影 区域内
max 1 min 3
max
1
3
2
最大切应力位于与 1 及 3 均成45的截面上
针转为正，顺时针转为负。
tg 2a 0
2 x x
y
在主值区间，2a0有两个解，与此对应的a0也有两个解，其中落
在剪应力箭头所指象限内的解为真解，另一解舍掉。
三、应力圆
由解析法知，任意斜截面的应力为
a
x y
2
a x
x
y
2
y cos2a
2
sin 2a x c
x s os2a
in
2a
广义胡克定律
1、基本变形时的胡克定律
1）轴向拉压胡克定律
x E x
横向变形
y
x
x
E
2）纯剪切胡克定律
G
y
x x
2、三向应力状态的广义胡克定律－叠加法
2
2
1
1
3
3
1
1
E
2
E
3
E
1
1 E
1
2
3
同理
2
1 E
2
3
1
广义胡克定律
3
1 E
3
1
2
7-5, 7-6
§7-4 材料的破坏形式
⒈ 上述公式中各项均为代数量，应用公式解题时，首先应写清已 知条件。

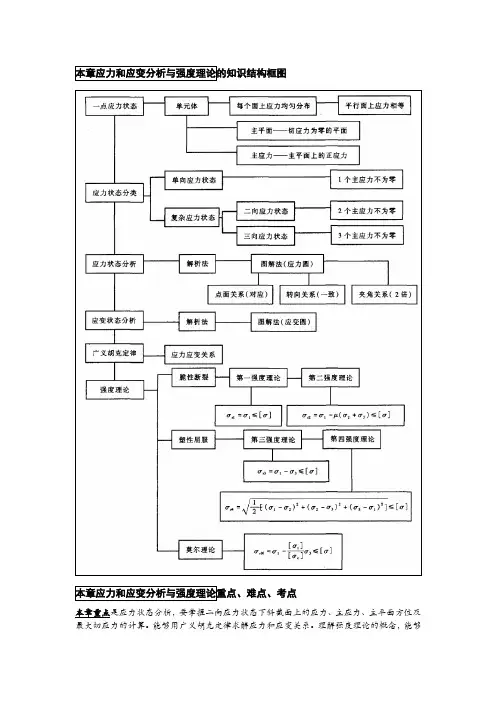
本章应力和应变分析与强度理论的知识结构框图

本章应力和应变分析与强度理论的知识结构框图

本章应力和应变分析与强度理论的知识结构框图本章应力和应变分析与强度理论重点、难点、考点本章重点是应力状态分析，要掌握二向应力状态下斜截面上的应力、主应力、主平面方位及最大切应力的计算。

能够用广义胡克定律求解应力和应变关系。

理解强度理论的概念，能够按材料可能发生的破坏形式，选择适当的强度理论。

难点主要有 ① 主平面方位的判断。

当由解析法求主平面方位时，结果有两个相差 90 ”的方位角，一般不容易直接判断出它们分别对应哪一个主应力，除去直接将两个方位角代人式中验算确定的方法外，最简明直观的方法是利用应力圆判定，即使用应力圆草图。

还可约定y x σσ≥，则两个方位中绝对值较小的角度对应max σ所在平面。

② 最大切应力。

无论何种应力状态，最大切应力均为2/)(31max σστ-=，而由式（ 7 一 l ）中第二式取导数0d d =ατα得到的切应力只是单元体的极值切应力，也称为面内最大切应力，它仅对垂直于Oxy 坐标平面的方向而言。

面内最大切应力不一定是一点的所有方位面中切应力的最大值，在解题时要特别注意，不要掉人“陷阱”中。

本章主要考点： ① 建立一点应力状态的概念，能够准确地从构件中截取单元体。

② 二向应力状态下求解主应力、主平面方位，并会用主单元体表示。

会计算任意斜截面上的应力分量。

③ 计算单元体的最大切应力。

④ 广义胡克定律的应用。

⑤ 能够选择适当的强度理论进行复杂应力状态下的强度计算，会分析简单强度破坏问题的原因。

本章应力和应变分析与强度理论的习题分类及解题要点：本章习题大致可分为四类：( l ）从构件中截取单元体这类题一般沿构件截面截取一正六面体，根据轴力、弯矩判断横截面上的正应力方向，由扭矩、剪力判断切应力方向，单元体其他侧面上的应力分量由力平衡和切应力互等定理画完整。

特别是当单元体包括构件表面（自由面）时，其上应力分量为零。

( 2 ）复杂应力状态分析一般考题都不限制采用哪一种方法解题，故最好采用应力圆分析，它常常能快速而有效地解决一些复杂的问题。

材料力学刘鸿文第六版最新课件第七章 应力和应变分析 强度理论

材料力学刘鸿文第六版最新课件第七章 应力和应变分析 强度理论
不相同，此即应力的点的概念。
5
7-1 应力状态的概述
直杆拉伸斜截面上的应力
k
F
{ F
p cos cos2
k
F
k p
k
p sin cos sin sin 2
2
直杆拉伸应力分析结果表明：即 使同一点不同方向面上的应力也是各
不相同的，此即应力的面的概念。
6
7-1 应力状态的概述
点的应力状态：
虚线：主压应力迹线 实线：主拉应力迹线
思考：在钢筋混泥土梁中，钢筋怎么放置最佳。 30
内容小结：
（1）根据已知点的应力状态求任意截面的应力。 （2）根据已知点的应力状态求主应力、主平面。 （3）结合前五章内容，掌握梁在拉、压、剪、扭、弯 等状态下，求某点的应力，并计算主应力和主平面。
31
第七章 应力和应变分析
58.3MPa 22
7-3 二向应力状态分析-解析法
（2）主应力、主平面
y xy
max
x
y
2
(
x
y
)2
2 xy
2
68.3MPa
x
min
x
y
2
(
x
y
)2
2 xy
2
48.3MPa
1 68.3MPa, 2 0, 3 48.3MPa
23
7-3 二向应力状态分析-解析法
y
主平面的方位：
2
2sin cos sin2
并注意到 yx xy （切应力互等）
化简得出：
1 2
( x
y)
1 2
(
x
y ) cos 2
xy
sin
2

材料力学第七章知识点总结

材料力学第七章知识点总结
研究应力状态的目的：找出一点处沿不同方向应力的变化
规律，确定出最大应力，从而全面考虑构件破坏的原因，建 立适当的强度条件。
材料力学
3、一点的应力状态的描述
研究一点的应力状态，可对一个 包围该点的微小正六面体——单 元体进行分析
在单元体各面上标上应力 各边边长 dx , dy , dz
——应力单元体
三、几个对应关系
点面对应——应力圆上某一点的坐标值对应着单元体某一截面
上的正应力和切应力；
y
σy
n
τ
H (σα ,τα )
τ yxHτ xy来自αxσx
(σy ,Dτyx)
2α A (σx ,τxy)
c
σ
σx +σ y
2
转向对应——半径旋转方向与截面法线的旋转方向一致； 二倍角对应——半径转过的角度是截面法线旋转角度的两倍。
α =α0
=
−2⎢⎡σ x
⎣
−σ y
2
sin 2α0
+τ xy
cos
2α
0
⎤ ⎥
⎦
=0
=
−2τ α 0
τα0 = 0
tg
2α 0
=
− 2τ xy σx −σ y
可以确定出两个相互垂直的平面——主平面，分别为
最大正应力和最小正应力所在平面。
主平面的方位
(α0 ; α0′ = α0 ± 900 )
主应力的大小
材料力学
四、在应力圆上标出极值应力
τ
τ max
x
R
O σ min
2α12α0A(σx ,τxy)
c
σ
σ
max
(σy ,τyx) D

第七章 应力与应变分析 强度理论4

第七章 应力与应变分析 强度理论4

2 x
29.8MPa 3.72 MPa
(单位 MPa)
1 29.28MPa， 2 3.72MPa， 3 0
1 29.28MPa < 30MPa
某结构上危险点处的应力状态如图所示，其中σ＝ 116.7MPa，τ＝46.3MPa。材料为钢，许用应力［σ］＝ 160MPa。试校核此结构是否安全。
3）强度理论：
材料的破坏与上述因素有关（某一方面），在长期的实践 中，对材料失效的原因提出各种不同的假设，形成各种不 同的判断准则，统称为强度理论（关于构件失效的假说） 4）意义： 找出失效原因 解决实际问题 提出强度理论
用简单的试验模拟
四、介绍四种强度理论
1、关于断裂失效的强度理论 ------适用于脆性材料 1）最大拉应力理论 十七世纪（1638年）由伽利略提出来的关于强度判断 的理论，亦称第一强度理论 认为： 材料失效的原因是由于材料内部的最大拉应力引 起的，无论应力状态如何，只要拉应力达到某一 限值，材料断裂。 模拟： 用简单的试验模拟，如单向拉伸。
2 50MPa
max 1 3
2
3 50MPa
65MPa
例2 已知如图所示过一点两个平
面上的应力。试求：
(1)该点的主应力及主平面；
(2)两平面的夹角。
1.四个常用的古典强度理论的相当表达式分 为 、 、 、 。 2.当矩形截面钢拉伸试样的轴向拉力F ＝ 20 kN时，
三向拉应力， 1 2 3>0且相差不大时，发生脆 性破坏，尽管材料可能是塑性的。选择第一、二强度 理论。 三向压应力， 1 2 3<0 且相差不大时，发生 塑性破坏，尽管材料可能是脆性的。选择第三、四强 度理论。

材料力学应力和应变分析强度理论

材料力学应力和应变分析强度理论
l
y
S平面
SF
a
1
T
4
z
x
2
T
Fa
M
Fl
1
T
Wt
σ
Mz Wz
3 Mz 3
T
Wt
σ
Mz Wz
目录
7—1 应力状态的概念
一、单元体的取法
S平面
F
S平面
F
5
2
4
l/2
l/2
3
Mz
Fl 4
2 1
1 1
2
2
2
3 3
10
二、单元体的特征
2 3
1、单元体特征 单元体的尺寸无限小，
1
1
每个面上应力均匀分布
3
任意一对平行平面上的应力相等
x = -40MPa
大小
y =60 MPa
max min
x
2
y
(
x
2
y
)2
2 x
80.7MPa 60.7MPa
x = -50MPa =-30°
1 80.7MPa 2 0 3 60.7MPa
方位
tan 20
2 xy x
y
2 (50) 40 60
1
20
45 135
0
22.5 67.5
三个主应力1 、2 、3 均不等于零
三个主应力1 、2 、3 中有两个不等于零
3、单向应力状态
三个主应力 1 、2 、3 中只有一个不等于零
2 3
2
1
1
1
1
1
3 2
2
1
7-2 二向应力状态分析-解析法

刘鸿文《材料力学》(第5版)笔记和课后习题(含考研真题)详解-应力和应变分析强度理论(圣才出品)

刘鸿文《材料力学》(第5版)笔记和课后习题(含考研真题)详解-应力和应变分析强度理论(圣才出品)

OA1
= OC + CA1
= x
+ y 2
+
(
x
− y )2 2
+
2 xy
= max = 1
OB1
= OC − CB1
=
x
+ 2
y
−
(
x
− 2
y
)2
+
2 xy
= min
=2
b．确定主平面方位的方法
如图 7-3（b）（c）所示，将半径 CD 旋转 20 到 CA1 处，单元体 x 轴沿 20 旋转方向
图 7-2 应力圆 （2）应力圆的应用 ①应力圆与单元体应力间的关系 点面之间的对应关系：单元体某一面上的应力，必对应于应力圆上某一点的坐标； 夹角关系：圆周上任意两点所引半径的夹角等于单元体上对应两截面夹角的两倍，且两 者的转向一致。 ②求单元体上任一截面上的应力 从应力圆的半径 CD 按方位角 α 的转向转动 2α 得到半径 CE，圆周上 E 点的坐标就是
任意两个互相垂直的截面上的正应力之和为常数，即 + +90 = x + y 。
③最大切应力和最小切应力 切应力的大小
max min
=
x
− y 2
2
+ 2xy
=
1 2
(max
− min )
切应力极值所在截面方位角
tan
21
=
x − y 2 xy
最大和最小切应力所在平面与主平面的夹角为 45°，即1 = 0 + 45。
圣才电子书 十万种考研考证电子书、题库视频学习平台

第 7 章 应力和应变分析强度理论

材料力学 第七章 应力状态与强度理论

材料力学 第七章 应力状态与强度理论

取三角形单元建立静力平衡方程
n 0
dA ( xdA cos ) sin ( xdA cos ) cos ( y dA sin ) cos ( y dA sin ) sin 0
t 0
dA ( xdA cos ) cos ( xdA cos ) sin ( y dA sin ) sin ( y dA sin ) cos 0
2 2

cos 2 x sin 2
2 x y 2 x y ( ) ( cos 2 x sin 2 )2
2
2

x y
sin 2 x cos 2
( 0) (
x y
2
2
sin 2 x cos 2 )
max x y x y 2 x 2 2 min
2
max
1 3
2
例7-2 试求例7-1中所示单元体的主应力和最大剪应力。
（1）求主应力的值
x 10MPa, y 30MPa, x 20MPa max x y x y 2 2 x min 2
复杂应力状态下（只就主应力状态说明） 有三个主应力
1 , 2 , 3
1
E
由 1引起的线段 1应变 1
由 2引起的线段 1应变 1
2
由 3引起的线段1应变 1
3
E
E
沿主应力1的方向的总应变为：
1 1 1 1
1 42.4 1 3 2 0 MPa 由 max 3 2.4 2

应力和应变分析和强度理论

应力和应变分析和强度理论

机械设计
01
02
03
零件强度校核
通过应力和应变分析，可 以校核机械零件的强度， 确保零件在正常工作载荷 下不会发生破坏。
优化装配设计
通过应力和应变分析，可 以优化机械装配设计，减 少装配误差和应力集中， 提高装配质量和可靠性。
振动和噪声控制
通过应力和应变分析，可 以预测和控制机械系统的 振动和噪声，提高机械系 统的性能和舒适性。
总结词
最大拉应力理论
详细描述
该理论认为最大拉应力是导致材料破坏的主要因素，当最大 拉应力达到材料的极限抗拉强度时，材料发生断裂。
第二强度理论
总结词
最大伸长应变理论
详细描述
该理论认为最大伸长应变是导致材料 破坏的主要因素，当最大伸长应变达 到材料的极限抗拉应变时，材料发生 断裂。
第三强度理论
总结词
03
应力和应变的应用
结构分析
结构稳定性
01
通过应力和应变分析，可以评估结构的稳定性，预测结构在不
同载荷下的变形和破坏模式。
结构优化设计
02
通过对应力和应变的精确计算，可以优化结构设计，降低结构
重量，提高结构效率。
结构疲劳寿命预测
03
通过应力和应变分析，可以预测结构的疲劳寿命，为结构的维
护和更换提供依据。
能量法
总结词
能量法是一种基于能量守恒和变分原理 的数值分析方法，通过将问题转化为能 量泛函的极值问题，并采用变分法或有 限元法进行求解。
VS
详细描述
在应力和应变分析中，能量法可以用于求 解各种力学问题，如弹性力学、塑性力学 等。通过构造合适的能量泛函和约束条件 ，能量法能够提供精确和高效的数值解。 同时，能量法还可以用于优化设计、稳定 性分析和控制等领域。

材料力学第七章__应力和应变分析__强度理论(2).ppt

材料力学第七章__应力和应变分析__强度理论(2).ppt

所以
m Wtt
d 3
16Biblioteka 1E45o
例 边长为10mm的铝质方块，紧密无隙 地嵌入一个深度和宽度都是10mm的钢槽 中，如图所示。当铝块受到P=60MPa的
• 在小变形及线弹性范围内，线应变 只与正应力有关，而与剪应力无关；
• 剪应变只与剪应力有关，而与正应 力无关，满足应用叠加原理的条件。
• 所以，我们利用单向应力状态和纯 剪切应力状态的虎克定律，分别求 出各应力分量相对应的应变，
• 然后，再进行叠加。
正应力分量在不同方向对应的应变
sx
s y
sz
s 1
(s 2
s 3 )
2
1 E
s 2
(s 3
s 1 )
3
1 E
s 3
(s 1
s 2 )
二、体积应变及应力的关系 1．体积应变
变形前单元体的体积为
V dxdydz
变形后，三个棱边的长度变为
dx 1dx (1 1)dx dy 2dy (1 2 )dy dz 3dz (1 3 )dz
x
y
xy
x
y
sin 2
xy
cos 2
22
2
二、应变圆
x
y
x
y cos2 xy sin 2
2
2
2
x
y
sin 2
xy
cos 2
22
2
(
x
y
)2
(
)2
x
y
sin
2
(
xy
)
2
22
2
t x'y'
R 1 2
sx s y

材料力学-07-应力分析和强度理论

材料力学-07-应力分析和强度理论

§7-2 平面应力状态 平面应力状态--解析法 平面应力状态 解析法： 解析法
1.斜截面上的应力 1.斜截面上的应力
y
σx
a
τ yx
τ xy
σx α
τa
n
τ xy
σa
dA
x
σy
n
τ yx
σy
t
t
∑F = 0
∑F =0
13
§7-2 平面应力状态 平面应力状态--解析法 平面应力状态 解析法： 解析法
tan 2α0 = − 2τ xy
σ x −σ y
由上式可以确定出两个相互垂直的平面， 由上式可以确定出两个相互垂直的平面，分别 为最大正应力和最小正应力所在平面。 为最大正应力和最小正应力所在平面。 所以，最大和最小正应力分别为： 所以，最大和最小正应力分别为：
σmax = σ x +σ y
2 1 + 2 − 1 2
单元体
单元体——构件内的点的代表物， 单元体——构件内的点的代表物，是包围被研究点的 ——构件内的点的代表物 无限小的几何体。 常用的是正六面体。 无限小的几何体。 常用的是正六面体。 单元体的性质—— 平行面上，应力均布； 单元体的性质——1) 平行面上，应力均布； —— 2) 平行面上，应力相等。 平行面上，应力相等。
2 2
σy
τ xy
α
60 − 40 60 + 40 = + cos(−60o ) + 30 sin(−60o ) 2 2
σx
= 9.02 MPa
τα =
σ x −σ y
2 60 + 40 = sin(−60o ) − 30 cos(−60o ) 2

材料力学第七章应力应变分析

材料力学第七章应力应变分析

x
y
2
x
2
y
cos 2
xy sin 2
x
y
2
sin 2
xy cos 2
1、最大正应力的方位
令
d d
2[
x
y sin 2
2
xy cos 2 ] 0
tg 2 0
2 xy x
y
0 0
90
0 和 0+90°确定两个互相垂直的平面，一个是最大正应 力所在的平面，另一个是最小正应力所在的平面.
的方位.
m
m a
A
l
解： 把从A点处截取的单元体放大如图
x 70, y 0, xy 50
A
tan 20
2 xy x y
2 50 1.429
1
3
(70) 0
0
A
x
0
27.5 62.5
3
1
因为 x < y ，所以 0= 27.5° 与 min 对应
max min
x
2
y
(
x
2
y )2
三、应力状态的分类
1、空间应力状态
三个主应力1 、2 、3 均不等于零
2、平面应力状态
三个主应力1 、2 、3 中有两个不等于零
3、单向应力状态
三个主应力 1 、2 、3 中只有一个不等于零
2 3
2
1
1
1
1
1
3 2
2
1
例题 1 画出如图所示梁S截面的应力状态单元体.
F
5
S平面
4
3
l/2
2
l/2 1
任意一对平行平面上的应力相等
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

x
y O
y
x
xy

x y 2
n
x y 2 2
2
2 xy
2
此方程曲线为圆—应力圆（或莫尔圆， 由德国工程师：Otto Mohr引入）

y

y x n D( , C O 2 O
x 1 tg 0 xy
x 95MPa
0 30
例6 如图，已知梁发生剪切弯曲（横力弯曲），某截面上M、
FS>0，试确定此截面上各点主应力大小及主平面位置。 F1 F2 q
解：由梁弯曲应力公式：
1 2 3 4 5
My x Iz
xy
FS S z b Iz
yx
C Me C
解：确定危险点并画单元体
xy
x y 0
xy
T WP
xy
求主应力及最大切应力
yx
y O
x y 2 i x y 2 （ ） xy 2 2 j
x

2 xy
1 ; 2 0; 3
25 3
2
45 B
150°
95
A
0
25 3
1
0 30
(MPa)
B A 20MPa
3
20
C
O 2
1
(MPa)

解法2—解析法：分析——建立坐标系如图
25 3
y
45
150°
95
60°
x y 2 2 i x y （ ） xy 2 2 j
n
二、应力圆的画法 建立应力坐标系，如下图所示，

x
（注意选好比例尺） 在坐标系内画出点A( x，xy)和 B(y，yx) AB与 轴的交点C便是圆心。
xy
x
A(x ,xy)
以C为圆心，以AC为半径画 圆——应力圆；

B(y ,yx)
y

y x n D( , C O 2 O
O

y x
y
考虑切应力互等和三角变换，得：
xy
x
图1
x y x y cos2 xy sin 2 2 2
同理： F 0
O

x
y
y
x
xy
图2

x y sin 2 xy cos2 2
n
O

二、极值应力 2 xy d 令: x y sin2 0 2 xy cos2 0 0 tg2 0 d x y 0
40 44.14 arctg 22.5o 10 1 3 max 22.07MPa 2
1
22.5o
2 )2 xy
10MPa
x 40 MPa xy 10 MPa
y 20 MPa
i, j
x y
2
2 44.14MPa 30 10 2 15.86MPa
离。
y
y
证明 : 单元体平衡
M
z
0
z
z
xy
x
x
( xydydz)dx( yxdzdx)dy0
xy yx
五、取单元体：
例1 F y B F x Me 画出下列图中的A、B、C点的已知单元体。 A F
x
A
x
z
C
FP
S平面
x
zx
yx
B
xz
x
C
xy
l/2
铸 铁 扭 转
F
铸
铁 压 缩
y'
yx
x'
xy xy
x'y'
yx
x'
切中有拉
重要结论
不仅横截面上存在应力，斜截 面上也存在应力；不仅要研究横 截面上的应力，而且也要研究斜 截面上的应力。
FS
Mz
横截面上正应力分析和切应力分析 的结果表明：同一面上不同点的应力 各不相同，此即 应力的点的概念 。
1 x x 2 2 （ ） xy 2 3 2
2 0
yx
xy
x
1

3 3
D1 A2 C A1 D2 O

D1
A2
D1 D1
20 C O

A1
D2
1
3
0 3
–45°


20= –90°
C O D2

A2 O
D2 20 C
1
3 0
l/2
六、主单元体、主平面、主应力：
y
y x
主单元体(Principal bidy)： 各侧面上切应力均为零的单元体。 主平面(Principal Plane)： x
z
z
切应力为零的截面。
主应力(Principal Stress ）：
2 1
主平面上的正应力。
主应力排列规定：按代数值大小，
max 1 3
2
主 单元体
x 1 tg 0 1 0 45 xy
3 xy
0
x y tg21 0 10 2 xy
破坏分析
yx 1
低碳钢 : s 240 MPa; s 200 MPa
灰口铸铁 : tb 98 ~ 280 MPa
cos2 xy sin2

x y
2 21.65MPa
si n2 xy cos2
例4 用解析法确定图示应力状态的主应力大小、主平面方位、最大切应力。
解：
20MPa
1 44.14MPa 2 15.86MPa 3 0 1 1 arctg x xy 40MPa
(
x y
x
2
§7–3
平面应力状态分析——图解法
一、应力圆（ Stress Circle）
y x
y O x
xy

x y x y cos2 xy sin2 2 2 x y sin2 cos2 xy 2 对上述方程消去参数（2），得：
D2 A2 C O
D1 A1

1
5
1
A1 D1
x A(x ,xy)
i OC R j
x y
2
（
x y
2
2 2 ） xy
3 2
1

min
max 1 3 R 2 min
例5 求图示单元体的主应力及主平面的位置。(单位：MPa) 解：主应力坐标系如图 在坐标系内画出点
y
y
yx
xy
x
x
单元体的性质 a、任意面上，应力均布； b、平行面上，应力相等。
z
z
四、切应力互等定理（Theorem of Conjugate Shearing Stress): 过一点的两个正交面上,如果有与相交边垂直的切应力分
量,则两个面上的这两个切应力分量一定等值、方向相对或相
由此得两个驻点：
0、（ 0 ）和两个极值：
2
i j
0

y x

x y
2
±（
x y
2
2 ） xy 2
y O x
xy
0
极值正应力就是主应力 ！
三、主应力大小及方向
(1) i j 0 (2) 0 i j (3) i 0; j 0
y x
y
一、任意斜截面上的应力 规定： 截面外法线同向为正；
xy
x
图1
绕研究对象顺时针转为正；
逆时针为正。 设：斜截面面积为S，由分离体平衡得：
O

x
y
y
x
xy
图2

F 0
n
n
S x S cos2 xy S cos sin
y Ssin 2 yx Ssin cos 0
' i j max ' 2 min 空间应力状态： max 1 3 2 min
y O x
xy 1
max
1 3
2
0 1

4
0 , 即 极 值 剪 应 力 面 与 主面 平 成45
例2 分析受扭构件的破坏规律。
一个主应力不为零的应力状态。
z
z
zy yz
zx
x
x
xz
x
y
xy yx
y
zx
B
xz
x
x
A
x
§7–2 平面应力状态分析——解析法 y
y
等价
y x
y x O x
xy
z
x
xy
应力状态分析的任务： 1.任意斜截面上的应力。 2.主应力的大小及主平面的方位。 3.最大切应力。
n
三、单元体与应力圆的对应关系 面上的应力( ， ) 应力圆上一点( ， )

x
xy
面的法线
两面夹角 且转向一致。
应力圆的半径
两半径夹角2 ；
x
A(x ,xy)

B(y ,yx)
四、在应力圆上标出极值应力

max
21 O C B(y ,yx) 2 0
3
1 2 3