当前位置：文档之家 › 材料力学B试题7应力状态_强度理论.docx

材料力学B试题7应力状态_强度理论.docx

  • 格式：docx
  • 大小：279.17 KB
  • 文档页数：11

下载文档原格式

  / 11

合集下载

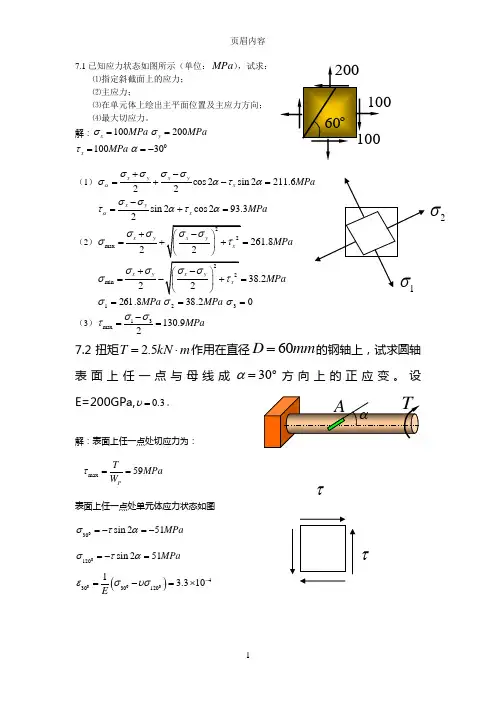
第7章应力状态和强度理论(答案)

第7章应力状态和强度理论(答案)

17.1已知应力状态如图所示（单位：MPa ），试求：⑴指定斜截面上的应力； ⑵主应力；⑶在单元体上绘出主平面位置及主应力方向； ⑷最大切应力。

解：100x MPa σ=200y MPa σ=100x MPa τ=030α=-（1）cos 2sin 2211.622x yx yxασσσσσατα+-=+-=sin 2cos 293.32x yx MPa ασστατα-=+=（2）max 261.82x yMPa σσσ+==min 38.22x yMPa σσσ+==MPa 8.2611=σMPa 2.382=σ03=σ（3）13max 130.92MPa σστ-==7.2扭矩m kN T ⋅=5.2作用在直径mm D 60=的钢轴上，试求圆轴表面上任一点与母线成ο30=α方向上的正应变。

设E=200GPa,0.3υ=。

解：表面上任一点处切应力为：max 59PTMPa W τ== 表面上任一点处单元体应力状态如图30sin 251MPa στα=-=-120sin 251MPa στα=-=()004303012013.310Eεσυσ-=-=⨯2σττ7.3用电阻应变仪测得空心钢轴表面某点与母线成ο45方向上的正应变4100.2-⨯=ε，已知转速min /120r ，G=80GPa ，试求轴所传递的功率。

解：表面任一点处应力为max 9550PPP T n W W τ==max 9550P W nP τ∴=纯剪切应力状态下，045斜截面上三个主应力为：1στ=20σ=3στ=-由广义胡克定律 ()11311E E υεσυστ+=-=又()21E G υ=+Q V 2G τε∴= 代入max 9550P W nP τ=，得109.4P KW =7.4图示为一钢质圆杆，直径mm D 20=，已知A 点与水平线成ο60方向上的正应变460101.4-⨯=οε，E=200GPa ，0.3υ=，试求荷载P 。

材料力学第七章应力状态和强度理论

材料力学第七章应力状态和强度理论
2
x y 2 a 0 2
x y x y 2
x y
2
) x
2
2
例题1: 已知:单元体各侧面应力 x=60MPa,
求: (1) = - 450斜截面上的应力,(2)主应力和主平面
dA
y

x y
2
sin 2 xy cos2
y
yx
应力圆
y
1 R 2

x
y

2
4 2 xy
x
yx xy x
y
R c

x y
2
2
x
xy
x´
dA
yx
y´
y
x y 1 2 2 2

40

x y
2 0.431MPa
sin( 80 ) xy cos(80 )

C
C

C
例题3：已知梁上的M、Q，试用单元体表示截面上1、2、
3、4点的应力状态。
1
2 0
2
1点 2点
1 2 0 3
3Q ＝ 2A
M x Wz
2 xy
x y
2 20.6 0.69 60 0
17.2
x y
2 (
6.4MPa
2 34.4
max(min)
x
17.20
x y
2
) xy
2
2
x
66.4MPa
60 0 60 0 2 ( ) 20.6 2 2 2 66.4(6.4) MPa

材料力学习题册参考答案

材料力学习题册参考答案

材料力学习题册参考答案材料力学习题册参考答案（无计算题）第1章：轴向拉伸与压缩一：1（ABE ）2（ABD ）3（DE ）4（AEB ）5（C ）6（ＣＥ）７（ABD ）8（C ）9（BD ）10（ADE ）11（ACE ）12（D ）13（CE ）14（D ）15（ＡＢ）１６（BE ）17（D ）二：1对2错3错4错5对6对7错8错9错10错11错12错13对14错15错三：1：钢铸铁 2：比例极限p σ 弹性极限e σ 屈服极限s σ 强度极限b σ3.横截面 45度斜截面4. εσE =， EAFl l =5.强度，刚度，稳定性；6.轴向拉伸（或压缩）；7. llb b ?μ?=8. 1MPa=106 N/m 2 =1012 N/mm 2 9. 抵抗伸缩弹性变形，加载方式 10. 正正、剪 11.极限应力 12. >5% <5% 13. 破坏s σ b σ 14.强度校核截面设计荷载设计15. 线弹性变形弹性变形 16.拉应力 45度 17.无明显屈服阶段的塑性材料力学性能参考答案：1. A 2. C 3. C 4. C 5. C 6. 5d ; 10d 7. 弹塑8. s2s 9. 0.1 10. 压缩11. b 0.4σ 12. <；< 剪切挤压答案：一：1.（C ），2.（B ），3.（A ），二：1. 2bh db 2. b(d+a) bc 3. 4a δ a 2 4. F第2章：扭转一：1.（B ） 2.（C D ） 3.（C D ） 4. （C ） 5. （A E ） 6. （A ）7. （D ）8. （B D ） 9.（C ） 10. （B ） 11.（D ） 12.（C ）13.（B ）14.（A ） 15.（A E ）二：1错 2对 3对 4错 5错 6 对三：1. 垂直 2. 扭矩剪应力 3.最外缘为零4. p ττ< 抗扭刚度材料抵抗扭转变形的能力5. 不变不变增大一倍6. 1.5879τ7.实心空心圆8. 3241)(α- 9. m ax m in αττ= 10. 长边的中点中心角点 11.形成回路（剪力流）第3章：平面图形的几何性质一：1.（C ），2.（A ），3.（C ），4.（C ），5.（A ），6.（C ），7.（C ），8.（A ），9.（D ）二：1）. 1；无穷多；2）4)4/5(a ； 3），84p R I π=p 4z y I 16R I I ===π4）12/312bh I I z z ==；5）)/(/H 6bh 6BH W 32z -= 6）12/)(2211h b bh I I I I z y z y +=+=+；7）各分部图形对同一轴静矩8）两轴交点的极惯性矩；9）距形心最近的；10）惯性主轴；11）图形对其惯性积为零三：1：64/πd 114； 2.（0 , 14.09cm ）(a 22，a 62)3： 4447.9cm 4， 4：0.00686d 4 ，5: 77500 mm 4 ;6: 64640039.110 23.410C C C C y y z z I I mm I I mm ==?==?第4章：弯曲内力一：1.（A B ）2.（D ）3.（B ）4.（A B E ）5.（A B D ）6.（ACE ） 7.（ABDE ） 8.（ABE ）9. （D ） 10. （D ） 11.（ACBE ） 12.（D ） 13.（ABCDE ）二：1错 2错 3错 4对 5错 6对 7对三：1. 以弯曲变形 2.集中力 3. KNm 2512M .max =4. m KN 2q = 向下 KN 9P = 向上5.中性轴6.荷载支撑力7. 小8. 悬臂简支外伸9. 零第5章：弯曲应力一：1（ＡＢＤ）２．（C ）3.（BE ）4.（A ）5.（C ）6.（C ）7.（B ）8.（C ）9.（BC ）二：1对 2错 3错 4 对 5 错 6错 7 对三：1.满足强度要求更经济、更省料2. 变成曲面，既不伸长也不缩短3.中性轴4.形心主轴5.最大正应力6.剪力方向7.相等8.平面弯曲发生在最大弯矩处9.平面弯曲第6章：弯曲变形一：1（B ），2（B ），3（A ），4（D ），5（C ），6（A ），7（C ），8（B ），9（A ）10（B ），11（A ）二：1对2错3错4错5错6对7错8错9错10对11错12对三：1.（转角小量:θθtan ≈）（未考虑高阶小量对曲率的影响）2. 挠曲线采用近似微分方程导致的。

材料力学 第07章 应力状态分析与强度理论

材料力学 第07章 应力状态分析与强度理论
2
sin2a t xy cos2a
18/95
7.2 平面应力状态分析 主应力 7.2.3 主平面的方位及极值正应力 s x s y s x s y sa cos2a t xy sin2a 2 2 s x s y ds a 上式对a 求导 2 sin2a t xy cos2a da 2 s x s y 若a a0时，导数为 0 sin2a 0 t xy cos2a 0 0 2 2t xy tan2a 0 s x s y
7.2.5 应力圆
t
sx
tyx
sy
sx txy sy
D(sx,txy) 1. 确定点 D (s ,t ) x xy
O
D'(sy,tyx)
C
s
2. 确定点D' (sy,tyx) tyx= －txy 3. 连接DD'与s 轴交于点C 4. 以 C 为圆心，CD（CD'） 为半径画圆。
26/95
7.2 平面应力状态分析 主应力 7.2.5 应力圆
sx sy sz
sxs1 100 MPas 2
0 MPas 3 120 MPa
11/95
7.1 一点的应力状态的概念 单向、二向(平面)、三向(空间)应力状态 三个主应力中仅有一个主应力不为零 单向应力状态
s1
s1
F
A
F
12/95
7.1 一点的应力状态的概念 单向、二向(平面)、三向(空间)应力状态
O
D'(sy,tyx)
C sx－ sx sy/2
s
27/95
7.2 平面应力状态分析 主应力 7.2.5 应力圆 利用应力圆确定角a 斜截面上的正应力和切应力

材料力学习题册答案_第7章_应力状态

材料力学习题册答案_第7章_应力状态

第 七 章 应力状态 强度理论一、 判断题1、平面应力状态即二向应力状态，空间应力状态即三向应力状态。

(√)2、单元体中正应力为最大值的截面上，剪应力必定为零。

(√)3、单元体中剪应力为最大值的截面上，正应力必定为零。

(×) 原因：正应力一般不为零。

4、单向应力状态的应力圆和三向均匀拉伸或压缩应力状态的应力圆相同，且均为应力轴 上的一个点。

(×) 原因：单向应力状态的应力圆不为一个点，而是一个圆。

三向等拉或等压倒是为一个点。

5、纯剪应力状态的单元体，最大正应力和最大剪应力值相等，且作用在同一平面上。

(×) 原因：最大正应力和最大剪应力值相等，但不在同一平面上6、材料在静载作用下的失效形式主要有断裂和屈服两种。

(√)7、砖,石等脆性材料式样压缩时沿横截面断裂。

(×)8、塑性材料制成的杆件，其危险点必须用第三或第四强度理论所建立的强度条件来校核强度。

(×) 原因：塑性材料也会表现出脆性，比如三向受拉时，此时，就应用第一强度理论9、纯剪应力状态的单元体既在体积改变，又有形状改变。

(×) 原因：只形状改变，体积不变10、铸铁水管冬天结冰时会因冰膨胀被胀裂，而管的冰不会被破坏，只是因为冰的强度比铸铁的强度高。

(×) 原因：铸铁的强度显然高于冰，其破坏原因是受到复杂应力状态二、 选择题1、危险截面是（ C ）所在的截面。

A 最大面积B 最小面积C 最大应力D 最大力2、关于用单元体表示一点处的应力状态，如下论述中正确的一种是( D )。

A 单元体的形状可以是任意的B 单元体的形状不是任意的，只能是六面体微元C 不一定是六面体，五面体也可以，其他形状则不行D 单元体的形状可以是任意的，但其上已知的应力分量足以确定任意方向面上的硬力 3、受力构件任意一点，随着所截取截面方位不同，一般来说（ D ） A 正应力相同，剪应力不同 B 正应力不同，剪应力相同 C 正应力和剪应力均相同 D 正应力和剪应力均不同 4、圆轴受扭时，轴表面各点处于（ B ）A 单向应力状态B 二向应力状态C 三向应力状态D 各向等应力状态 5、分析处于平面应力状态的一点，说确的是（ B ）。

工程力学c材料力学部分第七章 应力状态和强度理论

工程力学c材料力学部分第七章 应力状态和强度理论

无论是强度分析还是刚度分析，都需要求出应力的极值， 无论是强度分析还是刚度分析，都需要求出应力的极值，为了找 到构件内最大应力的位置和方向 需要对各点的应力情况做出分析。 最大应力的位置和方向， 到构件内最大应力的位置和方向，需要对各点的应力情况做出分析。
受力构件内一点处所有方位截面上应力的集合，称为一点的 受力构件内一点处所有方位截面上应力的集合，称为一点的 研究一点的应力状态时， 应力状态 。研究一点的应力状态时，往往围绕该点取一个无限小 的正六面体—单元体来研究。 单元体来研究 的正六面体 单元体来研究。
σ2
σ2
σ1
σ1
σ
σ
σ3
三向应力状态
双向应力状态
单向应力状态 简单应力状态
复杂应力状态 主应力符号按代数值的大小规定： 主应力符号按代数值的大小规定：
σ1 ≥ σ 2 ≥ σ 3
平面应力状态的应力分析—解析法 §7−2 平面应力状态的应力分析 解析法
图(a)所示平面应力单元体常用平面图形(b)来表示。现欲求 )所示平面应力单元体常用平面图形( )来表示。现欲求 垂直于平面xy的任意斜截面 上的应力 垂直于平面 的任意斜截面ef上的应力。 的任意斜截面 上的应力。
二、最大正应力和最大剪应力
σα =
σ x +σ y
2
+
σ x −σ y
2
cos 2α − τ x sin 2α
τα =
令
σ x −σ y
2
sin 2α + τ x cos 2α
dσ α =0 dα
σ x −σ y
2
sin 2α +τ x cos2α = 0
可见在 τ α
=0

材料力学习题参考答案2011年7月-第22章应力状态和强度理论

材料力学习题参考答案2011年7月-第22章应力状态和强度理论

22-６ 图示受力板件，试证明A 点处各截面的正应力、剪应力均为零证明：若在尖点A 处沿自由边界取三角形单元体如图所示，设单元体 、面上的应力分量为、和、，自由边界上的应力分量为，则有由于、，因此，必有、、。

这时，代表A 点应力状态的应力圆缩为 坐标的原点，所以A 点为零应力状态。

22-7 图示槽形刚体，在槽内放置一边长为10mm 、的立方钢块，钢块顶面受到合力为P=8kN 的均布压力作用，试求钢块的三个主应力和最大剪应力。

已知材料的弹性模量GPa E 200=，泊松比3.0=μ。

解： 选取坐标轴x 、y 、z 如图。

x σ＝0， σz ＝－10101083⨯⨯＝－80MPa ，εy ＝1E 〔σy －μ（σz ＋σx ）〕＝1E〔σy －μσz 〕＝0 由此得 σy ＝μσz ＝0.3×（－80）=－24 MPa 。

Ｐxzyo将x σ、y σ、z σ按代数值大小排列，得三个主应力为 σ1＝0 、σ2 ＝－24 MPa 、σ3=－80 MPa 。

最大剪应力 τm a x =σσ132-＝280＝40 MPa 。

22-12 试比较图示正方形棱柱体在下列两种情况下的相当应力3xd σ：(a )棱柱体自由受压：(b )棱柱体在刚性方模内受压。

弹性常数E 、μ均为已知.解：对于图（a ）中的情况，应力状态如图（c ）对于图（b ）中的情况，应力状态如图（d ）所以，，22-20 N O.28a普通热轧工字钢简支梁如图所示。

今由贴在中性层上某点K处、与轴线夹45º角方向上的应变片测得ε45º=-260×10-6。

已知钢材的E=210GPa，μ=0.28。

求作用在梁上的载荷F P。

材料力学应力状态分析强度理论

材料力学应力状态分析强度理论
断裂力学
断裂力学用于研究材料发生断裂时的力学行为，包括断裂韧性和断裂韧性指标。
断裂模式分析
通过对材料断裂模式的分析，了解材料在受到外力作用时如何发生破裂。
材料的强度
应力。 材料在受力过程中开始产生塑性变形的应力值。
材料在受到大幅度应力作用时发生破裂的强度。
由强度理论推导的材料设计
根据材料的强度特性，可以进行材料设计，以确保材料在使用过程中不超过其强度极限。
考虑材料疲劳的应力分析
1
疲劳寿命评估
扭转应力分析
扭转应力是材料在受扭转力作 用下的应力分布，对材料的扭 转能力和疲劳寿命影响较大。
应力分布分析
1 梁的应力分布
梁的应力分布分析可以 帮助了解梁在受力过程 中的强度和变形情况。
2 压力容器的应力分析 3 板的应力分布
压力容器的应力分析是 为了确保容器在承受压 力时不会发生破裂或变 形。
板的应力分布分析可用 于评估板在受力状态下 的强度和变形性能。
材料力学应力状态分析强 度理论
材料力学应力状态分析强度理论是研究材料受力情况及其强度特性的理论体 系，包括弹性理论、横向状态分析、应力分布分析等内容。
弹性理论
基本原理
材料在受力过程中 会发生变形，弹性 理论用于描述材料 的弹性性质和应变 的产生与传递。
弹性模量
弹性模量是衡量材 料对应力的响应能 力，不同材料具有 不同的弹性模量。
应力-应变关 系
弹性理论可以通过 应力-应变关系来描 述材料受力后的变 形情况。
限制条件
弹性理论是在一定 条件下适用的，需 要考虑材料的线性 弹性和小变形假设。
横向状态分析
横向力
横向状态分析用于研究材料在 受横向力作用下的变形和应力 分布。

《材料力学》第7章-应力状态和强度理论-习题解

《材料力学》第7章-应力状态和强度理论-习题解
解：左支座为A，右支座为B，左集中力作用点为C，右集中力作用点为D。
支座反力: (↑)
=
（1）梁内最大正应力发生在跨中截面的上、下边缘
超过 的5。3％，在工程上是允许的。
（2）梁内最大剪应力发生在支承截面的中性轴处
(3)在集中力作用处偏外侧横截面上校核点a的强度
超过 的3.53%，在工程上是允许的。
解：坐标面应力:X（—0。05，0);Y（-0.2,0）
。根据以上数据作出如图所示的应
力圆。图中比例尺为 代表 。
按比例尺量得斜面的应力为：
按习题7—5得到的公式计算如下：
作图法(应力圆法)与解析法（公式法）的结果一致。
［习题7-7]试用应力圆的几何关系求图示悬臂梁距离自由端为 的截面上，在顶面以下 的一点处的最大及最小主应力,并求最大主应力与 轴之间的夹角。
解：
…………(1)
…………（2)
（1)、(2)联立,可解得 和 。
至此,三个面的应力均为已知：X（ ，0），Y（ ，0）（ , 均为负值）;
( ）。由X，Y面的应力就可以作出应力圆。
[习题7-12]一焊接钢板梁的尺寸及受力情况如图所示,梁的自重略去不计。试示 上 三点处的主应力。
解:（1）求 点的主应力
解：坐标面应力：X（15,15）,Y(0，-15）
第一强度理论：
因为 ， ，即 ，
所以 符合第一强度理论的强度条件，构件不会破坏，即安全.
第二强度理论：
因为 ,
，即 ，
所以 符合第二强度理论的强度条件，构件不会破坏，即安全。
[习题7—25]一简支钢板梁承受荷载如图a所示，其截面尺寸见图b。已知钢材的许用应力为 , .试校核梁内的最大正应力和最大切应力。并按第四强度理论校核危险截面上的a点的强度。注:通常在计算a点处的应力时，近似地按 点的位置计算。

材料力学 第七章 应力状态和强度理论

材料力学 第七章 应力状态和强度理论

y
2
2 xy
tan 2a0
2 xy x
y
max
1
2
3
主应力符号与规定： 1 2 3 （按代数值）
§7-3 空间应力状态
与任一截面相对应 的点，或位于应力 圆上，或位于由应 力圆所构成的阴影 区域内
max 1 min 3
max
1
3
2
最大切应力位于与 1 及 3 均成45的截面上
针转为正，顺时针转为负。
tg 2a 0
2 x x
y
在主值区间，2a0有两个解，与此对应的a0也有两个解，其中落
在剪应力箭头所指象限内的解为真解，另一解舍掉。
三、应力圆
由解析法知，任意斜截面的应力为
a
x y
2
a x
x
y
2
y cos2a
2
sin 2a x c
x s os2a
in
2a
广义胡克定律
1、基本变形时的胡克定律
1）轴向拉压胡克定律
x E x
横向变形
y
x
x
E
2）纯剪切胡克定律
G
y
x x
2、三向应力状态的广义胡克定律－叠加法
2
2
1
1
3
3
1
1
E
2
E
3
E
1
1 E
1
2
3
同理
2
1 E
2
3
1
广义胡克定律
3
1 E
3
1
2
7-5, 7-6
§7-4 材料的破坏形式
⒈ 上述公式中各项均为代数量，应用公式解题时，首先应写清已 知条件。

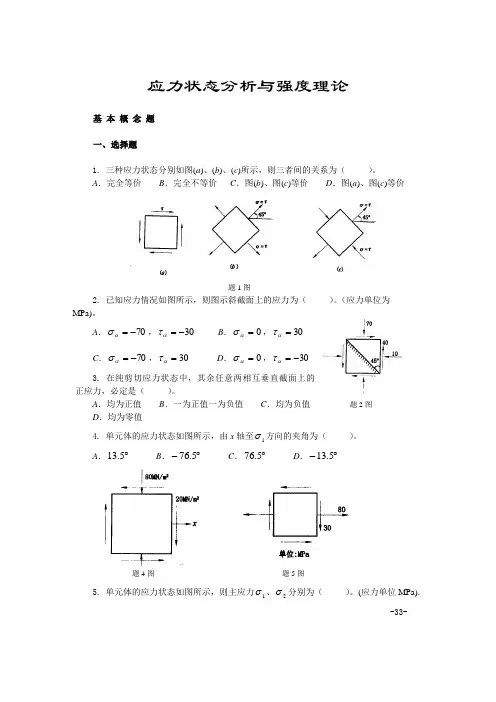
材料力学习题应力状态和强度理论

材料力学习题应力状态和强度理论

应力状态分析与强度理论基 本 概 念 题一、选择题1. 三种应力状态分别如图(a )、(b )、(c )所示，则三者间的关系为（ ）。

A ．完全等价B ．完全不等价C ．图(b )、图(c )等价D ．图(a )、图(c )等价题1图2. 已知应力情况如图所示，则图示斜截面上的应力为（ ）。

（应力单位为 MPa)。

A ．70-=ασ，30-=ατB ．0=ασ，30=ατC ．70-=ασ，30=ατD ．0=ασ，30-=ατ3. 在纯剪切应力状态中，其余任意两相互垂直截面上的 正应力，必定是（ ）。

A ．均为正值B ．一为正值一为负值C ．均为负值 题2图D ．均为零值4. 单元体的应力状态如图所示，由x 轴至1σ方向的夹角为（ ）。

A ．︒5.13 B ．︒-5.76 C ．︒5.76 D ．︒-5.13题4图 题5图5. 单元体的应力状态如图所示，则主应力1σ、2σ分别为（ ）。

(应力单位MPa). -33-A ．901=σ，102-=σB ．1001=σ，102-=σC ．901=σ，02=σD ．1001=σ，02=σ 6. 如图6所示单元体最大剪应力max τ为（ ）。

A ．100 MPaB ．50 MPaC ．25 MPaD ．0题6图 题7图7. 单元体如图所示，关于其主应力有下列四种答案，正确的是（ ）。

A ．1σ＞2σ，03=σ B ．3σ＜2σ＜0，03=σ01=σ C ．1σ＞0，2σ= 0，3σ＜0，1σ＜3σ D ．1σ＞0，2σ= 0，3σ＜0，1σ＞3σ8. 已知应力圆如图7-22所示，图(a )、(b )、(c )、(d )分别表示单元体的应力状态和A 截面的应力，则与应力圆所对应的单元体为( )。

A ．图(a )B ．图(b )C ．图(c )D ．图(d )题8图9. 在图示四种应力状态中，其应力圆具有相同的圆心和相同的半径是（ ）。

-34-题9图A ．图(a )、图(d )B ．图(b )、图(c )C ．图(a )、图(b )、图(c ) 、图(d )D ．图(a )、图(d )、图(b )、图(c )10. 如图所示，较大体积的钢块上开有一贯穿的槽，槽内嵌入一铝质立方体，铝块受到均布压力P 作用，假设钢块不变形，铝块处于（ ）。

材料力学-第七章-强度理论

材料力学-第七章-强度理论
脆性断裂,最大拉应力准则
r1 = max= 1 [] 其次确定主应力
ma xx 2y 1 2 xy2 4x 2y 2.2 9 M 8 P
m inx 2y 1 2 xy2 4x 2y 3 .7M 2 P
1＝29.28MPa,2＝3.72MPa, 3＝0
r113M 0 Pa
根据常温静力拉伸和压缩试验,已建立起单向应力状态下的弹 性失效准则;
考虑安全系数后，其强度条件
根据薄壁圆筒扭转实验,可建立起纯剪应力状态下的弹性失 效准则;
考虑安全系数后，强度条件
建立常温静载复杂应力状态下的弹性失效准则: 强度理论的基本思想是:
确认引起材料失效存在共同的力学原因,提出关于这一 共同力学原因的假设;
像铸铁一类脆性材料均具有 bc bt 的性能，
可选择莫尔强度理论。
思考题:把经过冷却的钢质实心球体,放入沸腾的热油锅 中,将引起钢球的爆裂,试分析原因。
答:经过冷却的钢质实心球体,放入沸腾的热油锅中, 钢 球的外部因骤热而迅速膨胀,其内芯受拉且处于三向均 匀拉伸的应力状态因而发生脆性爆裂。
思考题: 水管在寒冬低温条件下,由于管内水结冰引起体 积膨胀,而导致水管爆裂。由作用反作用定律可知,水 管与冰块所受的压力相等,试问为什么冰不破裂,而水管 发生爆裂。
局限性:
1、未考虑 2 的影响，试验证实最大影响达15%。
2、不能解释三向均拉下可能发生断裂的现象, 此准则也称特雷斯卡（Tresca）屈服准则
4. 畸变能密度理论（第四强度理论） 材料发生塑性屈服的主要因素是 畸变能密度;
无论处于什么应力状态,只要危险点处畸变能密度达到 与材料性质有关的某一极限值,材料就发生屈服。
具有屈服极限 s
铸铁拉伸破坏

家电公司研发部资料材料力学习题答案(七)

家电公司研发部资料材料力学习题答案(七)

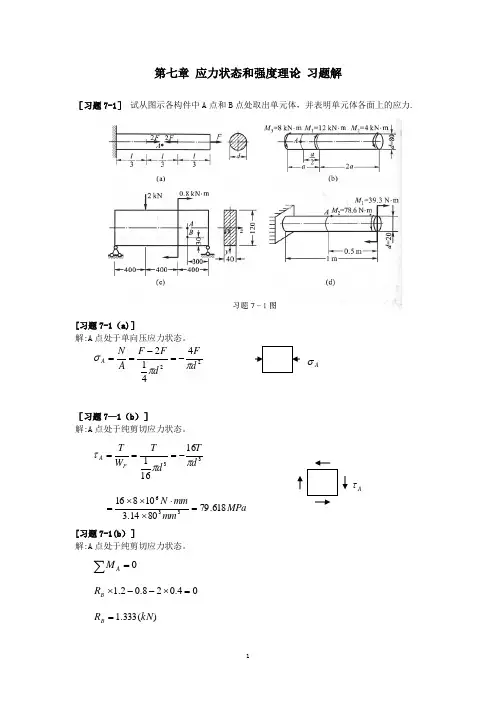
第七章 应力状态和强度理论7-1 围绕受力构件内某点处取出的微棱柱体的平面图如图所示，已知该点处于平面应力状态，AC 面上的正应力σ＝－14MPa ，切应力为零，试从平衡方程确定σx 和τx 值。

答：σx ＝37.9MPa ,τx ＝74.2MPa 解：利用公式求解x x x x x cos 2sin 222sin 2cos 22yyyαασσσσσατασστατα+-=+--=+代入数据得x x x x x 9292140.3430.94229200.940.3432σστστ+--=+⨯-⨯-=⨯+⨯σx ＝37.9MPa ,τx ＝74.2MPa7-2 试绘出图示水坝内A 、B 、C 三小块各截面上的应力（只考虑平面内受力情况）。

A: B: C:7-3 已知平面应力状态如图所示，已知σx ＝100MPa ，σy =40MPa,以及该点处的最大主应力σ1＝120MPa ，试用应力圆求该点处的τx 及另外两个主应力σ2，σ3和最大剪应力τmax。

答：MPa,60,0MPa,20max 32===τσσx τ＝40 MPa 解：由应力圆分析可得A BC题 7 - 2 图题 7 - 1 图111(100,),(40,),(,0)x x c D D C ττσ'-x 121004070MPa221207050MPa 705020MPayc c c r r σσσσσσσ++====-=-=∴=-=-=是平面应力状态3=0σ∴222x x 13max (100)40MPa120060MPa 22c r σττσστ∴=-+⇒=--===7-4 已知平面应力状态一点处互相垂直平面上作用有拉应力90MPa 和压应力50MPa ，这些面上还有剪应力，如果最大主应力为拉应力100MPa ，试求：(1) 上述面上的切应力； (2) 此平面上另一主应力； (3) 最大切应力平面上的正应力； (4) 最大切应力。

[材料力学]材料力学试题库精选题解精选题8_应力状态_强度理论.docx

[材料力学]材料力学试题库精选题解精选题8_应力状态_强度理论.docx

应力状态强度理论1.图示单元体，试求 (1) 指定斜截而丄的应力；(2) 主应力大小及主平而位置，并将主平而标在单元体上。

F<T r — CT V解：(1) (y (/ = — ----- + ---------- cos 2a 一 g sin 2& = 76.6 MPar r/ = ----- sin + r v cos2a =-32.7 MPaCc£X-50 ± 加 +(—129.9)2 = _50 ±1506=100 MPa, (r 2 = 0 , 6=-200 MPa解：b 、=150 MPa,「=—120 MPayx由 r = ----------- sin 2Q +「cos 2a = —~~— = -804522得 6 =-10 MPa3.—点处两个互成45°平面上的应力如图所示,其屮<7未知，求该点主应力。

max bmin81.98 MPa-121.98a = 81.98 MPa, <r 2 = 0 , cr 3 = -121.98 MPa^0=larctan(^^) = l arctan2 CT X -cr v 2402.某点应力状态如图示。

试求该点的主应力。

解：取合适坐标轴令6=25 MPa, r x =-129.9 MPa120"-- ----- sin 2a + T cos 2a = 0 得 = -125 MPa 2 -100MPa-200150 MPacr cr + cr所以max= __ ±2214.22MPa一74.226=214.22 MPa, cr2 = 0, <r3 = -74.22 MPa4.图示封闭薄壁圆筒，内径d=100 mm,壁厚f = 2 mm,承受内床“ =4 MPa, 外力偶矩M“=0・192 kN-mo求靠圆筒内壁任一点处的主应力。

解・・r常九严停32a=^- = 5Q MPax 4t<r v二四= 100 MPa、2tmax bmin 100.7MPa 49.356=100.7 MPa, 6=49.35 MPa, (r3 = -4 MPa5.受力体某点平面JL的应力如图示，求其主应力大小。

材料力学--应力状态(强度理论)

材料力学--应力状态(强度理论)

1 B 76.9MPa 2 0 3 B 76.9MPa
r3 1 3 2 B 153.8MPa [ ]
B max
F S S max
* z max
dI z
75.08MPa
r3 150.16MPa [ ]
性 材 料
1 2 0纵向开裂 第二强度理论
3 0
斜截面开裂 直接实验 [ ]
三向受压： 1＜0 , 3
1
,
max
1
2
3
＞
s
第三强度理论
塑
性 一般应力状态下 第三、第四强度理论
材 三向等拉状态 r3 r4 0 第一强度理论
料 三向等压状态，无论脆性材料还是塑性
材料均不发生破坏。
1 b
1
b
n
铸铁拉伸
2020/4/13
铸铁扭转
7
2. 最大伸长拉应变理论（第二强度理论） 无论材料处于什么应力状态,, 最大拉伸
线变形 1 0 发生脆性断裂
1－构件危险点的最大伸长线应变
1 [ 1 ( 2 3 )]/ E
0 －极限伸长线应E
3、校核A点强度：
A
| M |max Iz
yA
17.5 103 1073 108
75 103
122.3MPa
1 122.3MPa 2 3 0
r3 A 122.3MPa [ ]
4、校核B点强度：
B
B
max
| FS |max A腹板
50 103 130 5 106
76.9MPa
2020/4/13
2
max max
满足
max [ ] max [ ]
是否强度就没有问题了？

7工程力学(下)—应力状态和强度理论1

7工程力学(下)—应力状态和强度理论1

σα =
σx +σ y
2
+
σ x −σ y
2
cos 2α − τ x sin 2α
7.2 平面应力状态
对于斜截面的切线t参考轴列平衡方程为 对于斜截面的切线 参考轴列平衡方程为 ΣFt = 0, τ α d A − (σ x d A cos α ) sin α − (τ x d A cos α ) cos α + (σ y d A sin α ) cos α
σα =
σ x + σ y σ x −σ y
2 + 2
cos 2α −τ x sin 2α
τα =
σ x −σ y
2
sin2α +τ x cos2α
2 求正应力的极值
σ x −σ y dσ α = −2[ sin 2α + τ x cos 2α ] = 0 令: dα 2
比较可知, 极值正应力所在的平面, 比较可知 极值正应力所在的平面 就是切应力 τα为零的平面。这个切应力等于零的平面 叫做 为零的平面。这个切应力等于零的平面, 主平面, 主平面上的正应力, 叫做主应力。也就 主平面 主平面上的正应力 叫做主应力。 主应力 是说, 在通过某点的各个平面上, 是说 在通过某点的各个平面上 其中的最大正 应力和最小正应力就是该点处的主应力。 应力和最小正应力就是该点处的主应力。 表示主平面的法线n与 轴间的夹角 轴间的夹角, 以α0表示主平面的法线 与x轴间的夹角 由上式 可得 −2τ x tan 2α 0 = σ x −σ y
σ α = σ x cos 2 α + σ y sin 2 α − 2τ x sin α cos α
又由三角关系: 又由三角关系

材料力学 第七章 应力状态与强度理论

材料力学 第七章 应力状态与强度理论

取三角形单元建立静力平衡方程
n 0
dA ( xdA cos ) sin ( xdA cos ) cos ( y dA sin ) cos ( y dA sin ) sin 0
t 0
dA ( xdA cos ) cos ( xdA cos ) sin ( y dA sin ) sin ( y dA sin ) cos 0
2 2

cos 2 x sin 2
2 x y 2 x y ( ) ( cos 2 x sin 2 )2
2
2

x y
sin 2 x cos 2
( 0) (
x y
2
2
sin 2 x cos 2 )
max x y x y 2 x 2 2 min
2
max
1 3
2
例7-2 试求例7-1中所示单元体的主应力和最大剪应力。
（1）求主应力的值
x 10MPa, y 30MPa, x 20MPa max x y x y 2 2 x min 2
复杂应力状态下（只就主应力状态说明） 有三个主应力
1 , 2 , 3
1
E
由 1引起的线段 1应变 1
由 2引起的线段 1应变 1
2
由 3引起的线段1应变 1
3
E
E
沿主应力1的方向的总应变为：
1 1 1 1
1 42.4 1 3 2 0 MPa 由 max 3 2.4 2

材料力学-07-应力分析和强度理论

材料力学-07-应力分析和强度理论

§7-2 平面应力状态 平面应力状态--解析法 平面应力状态 解析法： 解析法
1.斜截面上的应力 1.斜截面上的应力
y
σx
a
τ yx
τ xy
σx α
τa
n
τ xy
σa
dA
x
σy
n
τ yx
σy
t
t
∑F = 0
∑F =0
13
§7-2 平面应力状态 平面应力状态--解析法 平面应力状态 解析法： 解析法
tan 2α0 = − 2τ xy
σ x −σ y
由上式可以确定出两个相互垂直的平面， 由上式可以确定出两个相互垂直的平面，分别 为最大正应力和最小正应力所在平面。 为最大正应力和最小正应力所在平面。 所以，最大和最小正应力分别为： 所以，最大和最小正应力分别为：
σmax = σ x +σ y
2 1 + 2 − 1 2
单元体
单元体——构件内的点的代表物， 单元体——构件内的点的代表物，是包围被研究点的 ——构件内的点的代表物 无限小的几何体。 常用的是正六面体。 无限小的几何体。 常用的是正六面体。 单元体的性质—— 平行面上，应力均布； 单元体的性质——1) 平行面上，应力均布； —— 2) 平行面上，应力相等。 平行面上，应力相等。
2 2
σy
τ xy
α
60 − 40 60 + 40 = + cos(−60o ) + 30 sin(−60o ) 2 2
σx
= 9.02 MPa
τα =
σ x −σ y
2 60 + 40 = sin(−60o ) − 30 cos(−60o ) 2
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

40 MPa.word 可编辑 .应力状态强度理论1. 图示单元体，试求60100 MPa(1)指定斜截面上的应力；(2)主应力大小及主平面位置，并将主平面标在单元体上。

解： (1)x y xy cos 2x sin 276.6 MPa22xy sin 2x cos232.7 MPa231 (2)max xy( x y) 2xy281.98MPa39.35min22121.98181.98MPa，2，3121.98MPa12xy12000arctan()arctan39.352x y24020060602. 某点应力状态如图示。

试求该点的主应力。

129.9129.9解：取合适坐标轴令x25 MPa，x由120xy sin 2xy cos20 得y2所以m axx y( xy ) 2xy 2m in 22129.9 MPa2525(MPa)125MPa50752( 129.9)250 150100 MPa2001 100MPa，20 ，3200MPa3. 一点处两个互成45 平面上的应力如图所示，其中未知，求该点主应力。

解：y150 MPa，x120 MPa.word 可编辑 .由得45xy sin 2xy cos 2x 15080 22x10MPa所以max xy(x y)2222xy min yx454545214.22 MPa 74.221214.22 MPa，20 ，45374.22MPa4.图示封闭薄壁圆筒，内径 d 100 mm，壁厚 t 2 mm，承受内压 p 4 MPa，外力偶矩 M e 0.192 kN·m。

求靠圆筒内壁任一点处的主应力。

0.19210 3解：xπ(0.10440.14)0.05 5.75MPat32x y pd MPa504tpd MPa1002tM e p M emax x y(x y ) 2xy2min22100.7 MPa 49.351100.7MPa，249.35 MPa，3 4 MPa5.受力体某点平面上的应力如图示，求其主应力大小。

解：取坐标轴使x100 MPa，x 20MPa40 MPa100 MPaxy x y12020 MPa22cos2x sin 2100y 100y22得y43.1MPa.word 可编辑 .cos120 20 sin120 40maxxyxy22() xymin22106.33 MPa36.771106.33 MPa ， 236.77 MPa ，3206. 某点的应力状态如图示，求该点的主应力及最大切应力。

解：maxxy( xy )2xy 24010min223030 20252 4025 47.1652.16 MPa(MPa)242.16所以 152.2 MPa ， 2 10 MPa ， 342.16 MPa1347.2 MPamax27. 图示工字形截面梁 AB ，截50 kNB面的惯性矩 I z 72.56 10 6m 4 ， A0.75 m求固定端截面翼缘和腹板交 界处点 a 的主应力和主方向。

解：50 103 0.75 0.0736.17MPa （压应力）72.5610 650 103150 30 85 10 98.8 MPa0.0372.56 10 6y3030 z 140a 30150177.05a 3amax x y( xy )2xy 2min222. 03MPa38.21 2.03MPa ， 20 ， 338.2 MPa 12 xy)1 2 8.8 0arctan(arctan 77.052xy236.17.word 可编辑 .8.图示矩形截面拉杆受轴向拉力 F ，若截面尺寸 b 、 h 和材料的弹性模量 E ，泊松比均已知，试求杆表面45方向线段AB 的改变量L AB？解：x FbhF2bh ，，y0，xy0AF45h F（45 ）B b 22bh所以45 1 ( F F )F(1 v)E 2bh2bh2EbhL AB AB 45F(12F (1 ) 2h)2Ebh2Eb9.一边长为 50 mm 的正方形硬铝板处于纯剪切状态，若切应力80MPa，并已知材料的弹性模量 E 72 GPa，泊松比0.34 。

试求对角线 AC 的伸长量。

解：4580 MPa，13580 MPa31145729(800.3480) 1.4810345 10LAC52L AC52 1.4810 30.00105 mm10.一变形体 A 四周和底边均与刚性边界光滑接触，上边受均布压力0 。

已知材料的的弹性模量 E ，泊松比，求竖向和y水平方向上的应变和应力。

0解：y0 ，x z ， xz0A x x1 [x( y z )]0 ，得到x z0E1y 1 [y( x z )]1[ 0(20 )]0 (1 2 2)E E1E1.word 可编辑 .11. 设地层由石灰岩组成，其密度2.5 103 kg/m 3 ，泊松比0.2 。

计算离地面200m 深处的地压应力。

解： y2.5 103 9.8200 4.9 MPay200 mxz， x z1[ x0.2 ( 4.9z )] 0xxEz得到 xz1.22 MPa12. 一体积为 10 10 10 mm 3 的立方铝块，将其放入宽为10 mm的刚性槽中。

已知铝的泊松比 0.33 ，求铝块的三个主应力。

F =6 kN解：6 103MPa,13 0.01600.01由 21 (2 0.33 60) 0得 219.8 MPaE13. 直径为 D 的实心圆轴，受外力偶 M e 作用如图。

测得轴表面点 A 与轴线成45 方向的线应变为，试导出用 M e 、 D 、 表示的切变弹性模量 G 的表达式。

解： 45，451 (1) ，所以 2Gd45A45EM eM e又16M e，所以 G8M eD 3 3ED14. 直径 d 100 mm 的圆轴，受轴向拉力 F 和力偶矩 M e 作用。

材料的弹性模量 E 200 GPa ，泊松比 0.3。

现测得圆轴表面.word 可编辑 .的轴向线应变50010 6 ， 方向的线应变45400 10 6，求 F45和 M e 。

解： FEA785 kNM eM e 设力偶矩引起的切应力为F45F4550 ， 4550451 ( 4545 )110 9 [( 50 ) 1060.3 (50 ) 106 ]E200400 10 6234.6 MPa ，又16Mπ (0.1)345M e 6.8kN ·m215. 直径 d 100 mm 的实心钢球， 受静水压力 p 42 MPa 作用。

求直径和体积的缩减量。

设钢球的弹性模量E 210 GPa ，泊松比0.3 。

解：因为123q42 MPa所以1 2 ( 123 )(1 2 0.3) 3 420.24 10 311E16.8 210 103[ 1(23 )]3 810 5E210 10得VV0.24 10 3 ( ) 1003 1.257 10 2mm 36d1d8 10 5 1008 10 3 mm16. 边长 a 10 0 mm 的立方体，已知弹性模量 E 200 GPa ，泊松比0.3 。

如将立方体沉入100 m 深的水中， 求其体积变化。

解：因为123gh1 MPa1 2 (1 23 )1 0.6 ( 3) 6 10 6E200 103VV610 6 0.10.1 0.16mm 3.word 可编辑 .17. 图示拉杆， F ，b ，h 及材料的弹性常数 E 、 均为已知。

试求线段 AB 的正应变和转角。

解： xF ， 45 135Fbh2bh所以!(45F(1 )AB135)E2bhE又因为 x F ， y FvbhE bhE所以 AB45(FvF )F (1 v)bhE bhEbhEF18. 图示曲拐 ABC 在水平面内，悬臂端 C 处作用铅垂集中力 F 。

在上表面E45CE 处，沿与母线成45 方向贴一应变片，已测得线应变 45 ，求载荷 F 值。

已知长度 l、 直径 d及材料的常数a 、AdalBE 、v 。

解：应力状态如图示，32 Fl ，16Fad 3d 3/2452，! (所以 45E45 245 v45 )E45d3/2所以 F16a(1 v)16l (1 v)19. 三个弹性常数之间的关系： G E /[ 2(1 )] 适用于 (A) 任何材料在任何变形阶段； (B) 各向同性材 料在任何变形阶段； (C) 各向同性材料应力在比例极限范围内； (D) 任何材料在 弹性变形范围内。

答： C20. 一实心均质钢球，当其外表面处迅速均匀加热，则球心O 点处的应力状态。

(A) 单向拉伸应力状态； (B) 二向拉伸应力状态；(C) 三向等值拉伸应力状态； (D) 三向压缩应力状态。

答： C.word 可编辑 .21. 混凝土立方体试样作单向压缩试验时，若在其上、下压板面上涂有润滑剂，则试样破坏时将沿纵向剖面裂开的主要原因。

(A) 最大压应力； (B) 最大切应力； (C) 最大伸长线应变；(D) 存在横向拉应力。

答： C22. 已知单元体的主应力为1 ， 2 ，推证两相互垂直的截面上的正应力之和为常数。

2证：1 2 12cos22211212cos2(90 )2212常数 得证。

23. 受内压的薄壁圆筒， 已知内压为p ，平均直径为 D ，壁厚为 t ，弹性常数为 E 、 。

试确定圆筒薄壁上任一点的主应力、主应变及第三、 第四强度理论的相当应力。

解： 1 pD ， 2 pD， 3 02t4t1 2 )1 pD pD pD(2 ) 1(1(2t)4tE EE4t21 ( 21 )1 ( pD pD ) pD(1 2 )EE 4t2t4tE31[0(12 )]1[03 pD ] 3 pDEE4t4tEr313pD2tr41[( 12 )2( 23 )2( 31 )2]2Dp3 p D4t24.图示正方形截面棱柱体，弹性常数 E 、均为已知。

试比较在下列两种情况下的相当应力r3 。

(a)棱柱体自由受压；(b)棱柱体在刚性方模内受压。

解： (a)120，3r313(b),0(a)(b)312所以12(1 v)所以r313(1 2))(1)y(11 m 25.图示重W 1800 N的信号牌，受最大水平风力 F 400 N，立柱直径 d 60 mm。

试用第三强度理论计算立柱危险点处的相当应力。

W M F P解：102.68MPa 3 mA W z9.43 MPax2z MPar31322242104.4426.纯剪切状态的单元体如图，则其第三强度理论相当应力为。

答：r 3227.图示单元体所示的应力状态按第四强度理论，其相当应力r4为：/2 (A) 3 / 2；(B)/ 2 ；(C)7 / 2 ；(D)5/ 2 。