2019高考数学真题汇编 椭圆 双曲线 抛物线

2019年高考数学试题分项版——解析几何（解析版）一、选择题1．(2019·全国Ⅰ文，10)双曲线C：－＝1(a>0，b>0)的一条渐近线的倾斜角为130°，则C的离心率为()A．2sin 40°B．2cos 40° C. D.答案 D解析由题意可得－＝tan 130°，所以e＝＝＝＝＝.2．(2019·全国Ⅰ文，12)已知椭圆C的焦点为F1(－1,0)，F2(1,0)，过F2的直线与C交于A，B两点．若|AF2|＝2|F2B|，|AB|＝|BF1|，则C的方程为()A.＋y2＝1B.＋＝1C.＋＝1D.＋＝1答案 B解析由题意设椭圆的方程为＋＝1(a>b>0)，连接F1A，令|F2B|＝m，则|AF2|＝2m，|BF1|＝3m.由椭圆的定义知，4m＝2a，得m＝，故|F2A|＝a＝|F1A|，则点A为椭圆C的上顶点或下顶点．令∠OAF2＝θ(O为坐标原点)，则sin θ＝＝.在等腰三角形ABF1中，cos 2θ＝＝，因为cos 2θ＝1－2sin2θ，所以＝1－22，得a2＝3.又c2＝1，所以b2＝a2－c2＝2，椭圆C的方程为＋＝1，故选B.3．(2019·全国Ⅱ文，9)若抛物线y2＝2px(p>0)的焦点是椭圆＋＝1的一个焦点，则p等于()A．2 B．3 C．4 D．8答案 D解析由题意知，抛物线的焦点坐标为，椭圆的焦点坐标为(±，0)，所以＝，解得p＝8，故选D.4．(2019·全国Ⅱ文，12)设F为双曲线C：－＝1(a>0，b>0)的右焦点，O为坐标原点，以OF为直径的圆与圆x2＋y2＝a2交于P，Q两点．若|PQ|＝|OF|，则C的离心率为() A. B.C．2 D.答案 A解析如图，由题意知，以OF为直径的圆的方程为2＋y2＝①，将x2＋y2＝a2记为②式，①－②得x＝，则以OF为直径的圆与圆x2＋y2＝a2的相交弦所在直线的方程为x ＝，所以|PQ|＝2.由|PQ|＝|OF|，得2＝c，整理得c4－4a2c2＋4a4＝0，即e4－4e2＋4＝0，解得e ＝，故选A.5．(2019·全国Ⅲ文，10)已知F是双曲线C：－＝1的一个焦点，点P在C上，O为坐标原点．若|OP|＝|OF|，则△OPF的面积为()A. B. C. D.答案 B解析由F是双曲线－＝1的一个焦点，知|OF|＝3，所以|OP|＝|OF|＝3.不妨设点P在第一象限，P(x0，y0)，x0>0，y0>0，则解得所以P，所以S△OPF＝|OF|·y0＝×3×＝.6．(2019·北京文，5已知双曲线－y2＝1(a>0)的离心率是，则a等于()A.B．4 C．2 D.答案 D解析由双曲线方程－y2＝1，得b2＝1，∴c2＝a2＋1.∴5＝e2＝＝＝1＋.结合a>0，解得a＝.7．(2019·天津文，6)已知抛物线y2＝4x的焦点为F，准线为l.若l与双曲线－＝1(a＞0，b＞0)的两条渐近线分别交于点A和点B，且|AB|＝4|OF|(O为原点)，则双曲线的离心率为()A. B.C．2 D.答案 D解析由题意，可得F(1,0)，直线l的方程为x＝－1，双曲线的渐近线方程为y＝±x.将x＝－1代入y＝±x，得y＝±，所以点A，B的纵坐标的绝对值均为.由|AB|＝4|OF|可得＝4，即b＝2a，b2＝4a2，故双曲线的离心率e＝＝＝.8．(2019·浙江，2)渐近线方程为x±y＝0的双曲线的离心率是()A.B．1C.D．2答案 C解析因为双曲线的渐近线方程为x±y＝0，所以无论双曲线的焦点在x轴上还是在y轴上，都满足a＝b，所以c＝a，所以双曲线的离心率e＝＝.9．(2019·全国Ⅰ理，10)已知椭圆C的焦点为F1(－1,0)，F2(1,0)，过F2的直线与C交于A，B两点．若|AF2|＝2|F2B|，|AB|＝|BF1|，则C的方程为()A.＋y2＝1B.＋＝1C.＋＝1D.＋＝1答案 B解析由题意设椭圆的方程为＋＝1(a>b>0)，连接F1A，令|F2B|＝m，则|AF2|＝2m，|BF1|＝3m.由椭圆的定义知，4m＝2a，得m＝，故|F2A|＝a＝|F1A|，则点A为椭圆C的上顶点或下顶点．令∠OAF2＝θ(O为坐标原点)，则sin θ＝＝.在等腰三角形ABF1中，cos 2θ＝＝，因为cos 2θ＝1－2sin2θ，所以＝1－22，得a2＝3.又c2＝1，所以b2＝a2－c2＝2，椭圆C的方程为＋＝1，故选B.10．(2019·全国Ⅱ理，8)若抛物线y2＝2px(p>0)的焦点是椭圆＋＝1的一个焦点，则p 等于()A．2 B．3 C．4 D．8答案 D解析由题意知，抛物线的焦点坐标为，椭圆的焦点坐标为(±，0)，所以＝，解得p＝8，故选D.11．(2019·全国Ⅱ理，11)设F 为双曲线C ：－＝1(a >0，b >0)的右焦点，O 为坐标原点，以OF 为直径的圆与圆x 2＋y 2＝a 2交于P ，Q 两点．若|PQ |＝|OF |，则C 的离心率为( ) A. B. C ．2 D. 答案 A 解析 如图，由题意知，以OF 为直径的圆的方程为2＋y 2＝①，将x 2＋y 2＝a 2记为②式，①－②得x ＝ ，则以OF 为直径的圆与圆x 2＋y 2＝a 2的相交弦所在直线的方程为x ＝，所以|PQ |＝2.由|PQ |＝|OF |，得2＝c ，整理得c 4－4a 2c 2＋4a 4＝0，即e 4－4e 2＋4＝0，解得e＝ ，故选A.12．(2019·全国Ⅲ理，10)双曲线C ：－＝1的右焦点为F ，点P 在C 的一条渐近线上，O 为坐标原点．若|PO |＝|PF |，则△PFO 的面积为( ) A.B.C ．2D ．3答案 A解析 不妨设点P 在第一象限，根据题意可知c 2＝6， 所以|OF |＝ .又tan ∠POF ＝＝，所以等腰△POF 的高h ＝ ×＝，所以S △PFO ＝× ×＝. 13．(2019·北京理，4)已知椭圆22221(0)x y a b a b +=>>的离心率为12，则( )A ．222a b =B ．2234a b =C ．2a b =D ．34a b =【思路分析】由椭圆离心率及隐含条件222a b c =+得答案．【解析】：由题意，12c a =，得2214c a =，则22214a b a -=，22244a b a ∴-=，即2234a b =．故选：B ．【归纳与总结】本题考查椭圆的简单性质，熟记隐含条件是关键，是基础题．14．(2019·北京理，8)数学中有许多形状优美、寓意美好的曲线，曲线22:1||C x y x y +=+就是其中之一（如图）．给出下列三个结论：①曲线C 恰好经过6个整点（即横、纵坐标均为整数的点）；②曲线C ③曲线C 所围成的“心形”区域的面积小于3． 其中，所有正确结论的序号是( )A ．①B ．②C ．①②D ．①②③【思路分析】将x 换成x -方程不变，所以图形关于y 轴对称，根据对称性讨论y 轴右边的图形可得．【解析】：将x 换成x -方程不变，所以图形关于y 轴对称， 当0x =时，代入得21y =，1y ∴=±，即曲线经过(0,1)，(0,1)-；当0x >时，方程变为2210y xy x -+-=，所以△224(1)0x x =--…，解得(0x ∈， 所以x 只能取整数1，当1x =时，20y y -=，解得0y =或1y =，即曲线经过(1,0)，(1,1)， 根据对称性可得曲线还经过(1,0)-，(1,1)-， 故曲线一共经过6个整点，故①正确．当0x >时，由221x y xy +=+得222212x y x y xy ++-=…，（当x y =时取等），222x y ∴+…，∴C 上y ，根据对称性可得：曲线C在x 轴上图形面积大于矩形面积122=⨯=，x 轴下方的面积大于等腰直角三角形的面积12112=⨯⨯=，因此曲线C 所围成的“心形”区域的面积大于213+=，故③错误． 故选：C ．【归纳与总结】本题考查了命题的真假判断与应用，属中档题．15．(2019·天津理，5)已知抛物线y2＝4x的焦点为F，准线为l.若l与双曲线－＝1(a ＞0，b＞0)的两条渐近线分别交于点A和点B，且|AB|＝4|OF|(O为原点)，则双曲线的离心率为()A. B.C．2 D.答案 D解析由题意，可得F(1,0)，直线l的方程为x＝－1，双曲线的渐近线方程为y＝±x.将x ＝－1代入y＝±x，得y＝±，所以点A，B的纵坐标的绝对值均为.由|AB|＝4|OF|可得＝4，即b＝2a，b2＝4a2，故双曲线的离心率e＝＝＝.二、填空题1．(2019·全国Ⅲ文，15)设F1，F2为椭圆C：＋＝1的两个焦点，M为C上一点且在第一象限．若△MF1F2为等腰三角形，则M的坐标为________．答案(3，)解析不妨令F1，F2分别为椭圆C的左、右焦点，根据题意可知c＝＝4.因为△MF1F2为等腰三角形，所以易知|F1M|＝2c＝8，所以|F2M|＝2a－8＝4.设M(x，y)，则得所以M的坐标为(3，)．2．(2019·北京文，11)设抛物线y2＝4x的焦点为F，准线为l.则以F为圆心，且与l相切的圆的方程为________．答案(x－1)2＋y2＝4解析∵抛物线y2＝4x的焦点F的坐标为(1,0)，准线l为直线x＝－1，∴圆的圆心坐标为(1,0)．又∵圆与l相切，∴圆心到l的距离为圆的半径，∴r＝2.∴圆的方程为(x－1)2＋y2＝4.3．(2019·浙江，12)已知圆C的圆心坐标是(0，m)，半径长是r.若直线2x－y＋3＝0与圆C 相切于点A(－2，－1)，则m＝________，r＝________.答案－2解析 方法一 设过点A (－2，－1)且与直线2x －y ＋3＝0垂直的直线方程为l ：x ＋2y ＋t ＝0，所以－2－2＋t ＝0，所以t ＝4，所以l ：x ＋2y ＋4＝0，令x ＝0，得m ＝－2，则r ＝ ＝ .方法二 因为直线2x －y ＋3＝0与以点(0，m )为圆心的圆相切，且切点为A (－2，－1)，所以×2＝－1，所以m ＝－2，r ＝ ＝ .4．(2019·浙江，15)已知椭圆＋＝1的左焦点为F ，点P 在椭圆上且在x 轴的上方．若线段PF 的中点在以原点O 为圆心 ，|OF |为半径的圆上，则直线PF 的斜率是________． 答案解析 依题意，设点P (m ，n )(n ＞0)，由题意知F (－2,0)，|OF |＝2，所以线段FP 的中点M在圆x 2＋y 2＝4上，所以2＋2＝4，又点P (m ，n )在椭圆 ＋＝1上，所以＋＝1，所以4m 2－36m －63＝0，所以m ＝－或m ＝(舍去)，当m ＝－时，n ＝，所以k PF ＝＝ .5．(2019·江苏，7)在平面直角坐标系xOy 中，若双曲线x 2－＝1(b >0)经过点(3,4)，则该双曲线的渐近线方程是_________________． 答案 y ＝± x解析 因为双曲线x 2－＝1(b >0)经过点(3,4)，所以9－＝1，得b ＝ ，所以该双曲线的渐近线方程是y ＝±bx ＝± x .6．(2019·江苏，10)在平面直角坐标系xOy 中，P 是曲线y ＝x ＋(x >0)上的一个动点，则点P 到直线x ＋y ＝0的距离的最小值是________． 答案 4解析 设P，x >0，则点P 到直线x ＋y ＝0的距离d ＝＝≥＝4，当且仅当2x ＝，即x ＝ 时取等号，故点P 到直线x ＋y ＝0的距离的最小值是4.7．(2019·全国Ⅰ理，16)已知双曲线C ：－＝1(a >0，b >0)的左、右焦点分别为F 1，F 2，过F 1的直线与C 的两条渐近线分别交于A ，B 两点．若 ＝ ， · ＝0，则C 的离心率为________． 答案 2解析 因为F 1B →·F 2B →＝0，所以F 1B ⊥F 2B ，如图．因为＝，所以点A为F1B的中点，又点O为F1F2的中点，所以OA∥BF2，所以F1B⊥OA，所以|OF1|＝|OB|，所以∠BF1O＝∠F1BO，所以∠BOF2＝2∠BF1O.因为直线OA，OB为双曲线C的两条渐近线，所以tan∠BOF2＝，tan∠BF1O＝.因为tan∠BOF2＝tan(2∠BF1O)，所以＝，所以b2＝3a2，所以c2－a2＝3a2，即2a＝c，所以双曲线的离心率e＝＝2.8．(2019·全国Ⅲ理，15)设F1，F2为椭圆C：＋＝1的两个焦点，M为C上一点且在第一象限．若△MF1F2为等腰三角形，则M的坐标为________．答案(3，)解析不妨令F1，F2分别为椭圆C的左、右焦点，根据题意可知c＝＝4.因为△MF1F2为等腰三角形，所以易知|F1M|＝2c＝8，所以|F2M|＝2a－8＝4.设M(x，y)，则＝，＝，，，得所以M的坐标为(3，)．三、解答题1．(2019·全国Ⅰ文，21)已知点A，B关于坐标原点O对称，|AB|＝4，⊙M过点A，B且与直线x＋2＝0相切．(1)若A在直线x＋y＝0上，求⊙M的半径；(2)是否存在定点P，使得当A运动时，|MA|－|MP|为定值？并说明理由．解(1)因为⊙M过点A，B，所以圆心M在AB的垂直平分线上．由已知A在直线x＋y＝0上，且A，B关于坐标原点O对称，所以M在直线y＝x上，故可设M(a，a)．因为⊙M与直线x＋2＝0相切，所以⊙M的半径为r＝|a＋2|.由已知得|AO|＝2.又MO⊥AO，故可得2a2＋4＝(a＋2)2，解得a＝0或a＝4.故⊙M的半径r＝2或r＝6.(2)存在定点P(1,0)，使得|MA|－|MP|为定值．理由如下：设M(x，y)，由已知得⊙M的半径为r＝|x＋2|，|AO|＝2.由于MO⊥AO，故可得x2＋y2＋4＝(x＋2)2，化简得M的轨迹方程为y2＝4x.因为曲线C：y2＝4x是以点P(1,0)为焦点，以直线x＝－1为准线的抛物线，所以|MP|＝x＋1.因为|MA|－|MP|＝r－|MP|＝x＋2－(x＋1)＝1，所以存在满足条件的定点P.2．(2019·全国Ⅱ文，20)已知F1，F2是椭圆C：＋＝1(a>b>0)的两个焦点，P为C上的点，O为坐标原点．(1)若△POF2为等边三角形，求C的离心率；(2)如果存在点P，使得PF1⊥PF2，且△F1PF2的面积等于16，求b的值和a的取值范围．解(1)连接PF1.由△POF2为等边三角形可知在△F1PF2中，∠F1PF2＝90°，|PF2|＝c，|PF1|＝c，于是2a＝|PF1|＋|PF2|＝(＋1)c，故C的离心率为e＝＝－1.(2)由题意可知，若满足条件的点P(x，y)存在，则|y|·2c＝16，·＝－1，即c|y|＝16，①x2＋y2＝c2，②又＋＝1.③由②③及a2＝b2＋c2得y2＝.又由①知y2＝，故b＝4.由②③及a2＝b2＋c2得x2＝(c2－b2)，所以c2≥b2，从而a2＝b2＋c2≥2b2＝32，故a≥4.当b＝4，a≥4时，存在满足条件的点P.所以b＝4，a的取值范围为[4，＋∞)．3．(2019·全国Ⅲ文，21)已知曲线C：y＝，D为直线y＝－上的动点，过D作C的两条切线，切点分别为A，B.(1)证明：直线AB过定点；(2)若以E为圆心的圆与直线AB相切，且切点为线段AB的中点，求该圆的方程．(1)证明设D，A(x1，y1)，则＝2y1.由于y′＝x，所以切线DA的斜率为x1，故＝x1，整理得2tx1－2y1＋1＝0.设B(x2，y2)，同理可得2tx2－2y2＋1＝0.所以直线AB的方程为2tx－2y＋1＝0.所以直线AB过定点.(2)解由(1)得直线AB的方程为y＝tx＋.由可得x2－2tx－1＝0，于是x1＋x2＝2t，y1＋y2＝t(x1＋x2)＋1＝2t2＋1.设M为线段AB的中点，则M.由于⊥，而＝(t，t2－2)，与向量(1，t)平行，所以t＋(t2－2)t＝0.解得t＝0或t＝±1.当t＝0时，||＝2，所求圆的方程为x2＋2＝4；当t＝±1时，||＝，所求圆的方程为x2＋2＝2.4．(2019·北京文，19)已知椭圆C：＋＝1的右焦点为(1,0)，且经过点A(0,1)．(1)求椭圆C的方程；(2)设O为原点，直线l：y＝kx＋t(t≠±1)与椭圆C交于两个不同点P，Q，直线AP与x轴交于点M，直线AQ与x轴交于点N.若|OM|·|ON|＝2，求证：直线l经过定点．(1)解由题意，得b2＝1，c＝1，所以a2＝b2＋c2＝2.所以椭圆C的方程为＋y2＝1.(2)证明设P(x1，y1)，Q(x2，y2)，则直线AP的方程为y＝x＋1.令y＝0，得点M的横坐标x M＝－.又y1＝kx1＋t，从而|OM|＝|x M|＝.同理，|ON|＝.由得(1＋2k2)x2＋4ktx＋2t2－2＝0，则x1＋x2＝－，x1x2＝.所以|OM|·|ON|＝·＝＝＝2.又|OM|·|ON|＝2，所以2＝2.解得t＝0，所以直线l经过定点(0,0)．5．(2019·天津文，19)设椭圆＋＝1(a＞b＞0)的左焦点为F，左顶点为A，上顶点为B.已知|OA|＝2|OB|(O为原点)．(1)求椭圆的离心率；(2)设经过点F且斜率为的直线l与椭圆在x轴上方的交点为P，圆C同时与x轴和直线l 相切，圆心C在直线x＝4上，且OC∥AP.求椭圆的方程．解(1)设椭圆的半焦距为c，由已知有a＝2b，又由a2＝b2＋c2，消去b得a2＝2＋c2，解得＝.所以椭圆的离心率为.(2)由(1)知，a＝2c，b＝c，故椭圆方程为＋＝1.由题意，F(－c,0)，则直线l的方程为y＝(x＋c)．点P的坐标满足消去y并化简，得到7x2＋6cx－13c2＝0，解得x1＝c，x2＝－.代入到l的方程，解得y1＝c，y2＝－c.因为点P在x轴上方，所以P.由圆心C在直线x＝4上，可设C(4，t)．因为OC∥AP，且由(1)知A(－2c,0)，故＝，解得t＝2.因为圆C与x轴相切，所以圆C的半径为2.又由圆C与l相切，得＝2，可得c＝2.所以，椭圆的方程为＋＝1.6.(2019·浙江，21)如图，已知点F(1,0)为抛物线y2＝2px(p＞0)的焦点．过点F的直线交抛物线于A，B两点，点C在抛物线上，使得△ABC的重心G在x轴上，直线AC交x轴于点Q，且Q在点F的右侧．记△AFG，△CQG的面积分别为S1，S2.(1)求p的值及抛物线的准线方程；(2)求的最小值及此时点G的坐标．解(1)由题意得＝1，即p＝2.所以，抛物线的准线方程为x＝－1.(2)设A(x A，y A)，B(x B，y B)，C(x C，y C)，重心G(x G，y G)．令y A＝2t，t≠0，则x A＝t2.由于直线AB过点F，故直线AB的方程为x＝y＋1，代入y2＝4x，得y2－y－4＝0，故2ty B＝－4，即y B＝－，所以B.又由于x G＝(x A＋x B＋x C)，y G＝(y A＋y B＋y C)及重心G在x轴上，故2t－＋y C＝0.即C，G.所以，直线AC的方程为y－2t＝2t(x－t2)，得Q(t2－1,0)．由于Q在焦点F的右侧，故t2＞2.从而＝＝＝＝2－.令m＝t2－2，则m＞0，＝2－＝2－≥2－＝1＋.当且仅当m＝时，取得最小值1＋，此时G(2,0)．7.(2019·江苏，17)如图，在平面直角坐标系xOy中，椭圆C：＋＝1(a>b>0)的焦点为F1(－1,0)，F2(1,0)．过F2作x轴的垂线l，在x轴的上方，l与圆F2：(x－1)2＋y2＝4a2交于点A，与椭圆C交于点D.连接AF1并延长交圆F2于点B，连接BF2交椭圆C于点E，连接DF1.已知DF1＝.(1)求椭圆C的标准方程；(2)求点E的坐标．解(1)设椭圆C的焦距为2c.因为F1(－1,0)，F2(1,0)，所以F1F2＝2，则c＝1.又因为DF1＝，AF2⊥x轴，所以DF2＝＝＝.因此2a＝DF1＋DF2＝4，所以a＝2.由b2＝a2－c2，得b2＝3.所以椭圆C的标准方程为＋＝1.(2)方法一由(1)知，椭圆C：＋＝1，a＝2.因为AF2⊥x轴，所以点A的横坐标为1.将x＝1代入圆F2方程(x－1)2＋y2＝16，解得y＝±4.因为点A在x轴上方，所以A(1,4)．又F1(－1,0)，所以直线AF1：y＝2x＋2.由得5x2＋6x－11＝0，解得x＝1或x＝－.将x＝－代入y＝2x＋2，得y＝－.因此B.又F2(1,0)，所以直线BF2：y＝(x－1)．由得7x2－6x－13＝0，解得x＝－1或x＝.又因为E是线段BF2与椭圆的交点，所以x＝－1.将x＝－1代入y＝(x－1)，得y＝－.因此E.方法二由(1)知，椭圆C：＋＝1.如图，连接EF1.因为BF2＝2a，EF1＋EF2＝2a，所以EF1＝EB，从而∠BF1E＝∠B.因为F2A＝F2B，所以∠A＝∠B.所以∠A＝∠BF1E，从而EF1∥F2A.因为AF2⊥x轴，所以EF1⊥x轴．因为F1(－1,0)，由得y＝±.又因为E是线段BF2与椭圆的交点，所以y＝－.因此E.8．(2019·江苏，18)如图，一个湖的边界是圆心为O的圆，湖的一侧有一条直线型公路l，湖上有桥AB(AB是圆O的直径)．规划在公路l上选两个点P，Q，并修建两段直线型道路PB，QA，规划要求：线段PB，QA上的所有点到点O的距离均不小于圆O的半径．已知点A，B到直线l的距离分别为AC和BD(C，D为垂足)，测得AB＝10，AC＝6，BD＝12(单位：百米)．(1)若道路PB与桥AB垂直，求道路PB的长；(2)在规划要求下，P和Q中能否有一个点选在D处？并说明理由；(3)在规划要求下，若道路PB和QA的长度均为d(单位：百米)，求当d最小时，P，Q两点间的距离．解方法一(1)过A作AE⊥BD，垂足为E.由已知条件得，四边形ACDE为矩形，DE＝BE＝AC＝6，AE＝CD＝8.因为PB⊥AB，所以cos∠PBD＝sin∠ABE＝＝＝.所以PB＝＝＝15.因此道路PB的长为15(百米)．(2)①若P在D处，由(1)可得E在圆上，则线段BE上的点(除B，E)到点O的距离均小于圆O的半径，所以P选在D处不满足规划要求．②若Q在D处，连接AD，由(1)知AD＝＝10，从而cos∠BAD＝＝>0，所以∠BAD为锐角．所以线段AD上存在点到点O的距离小于圆O的半径．因此Q选在D处也不满足规划要求．综上，P和Q均不能选在D处．(3)先讨论点P的位置．当∠OBP<90°时，线段PB上存在点到点O的距离小于圆O的半径，点P不符合规划要求；当∠OBP≥90°时，对线段PB上任意一点F，OF≥OB，即线段PB上所有点到点O的距离均不小于圆O的半径，点P符合规划要求．设P1为l上一点，且P1B⊥AB，由(1)知，P1B＝15，此时P1D＝P1B sin∠P1BD＝P1B cos∠EBA ＝15×＝9；当∠OBP>90°时，在△PP1B中，PB>P1B＝15.由上可知，d≥15.再讨论点Q的位置．由(2)知，要使得QA≥15，点Q只有位于点C的右侧，才能符合规划要求．当QA＝15时，CQ＝＝＝3.此时，线段QA上所有点到点O的距离均不小于圆O 的半径．综上，当PB⊥AB，点Q位于点C右侧，且CQ＝3时，d最小，此时P，Q两点间的距离PQ＝PD＋CD＋CQ＝17＋3.因此，d最小时，P，Q两点间的距离为17＋3(百米)．方法二(1)如图，过O作OH⊥l，垂足为H.以O为坐标原点，直线OH为y轴，建立如图所示的平面直角坐标系．因为BD＝12，AC＝6，所以OH＝9，直线l的方程为y＝9，点A，B的纵坐标分别为3，－3.因为AB为圆O的直径，AB＝10，所以圆O的方程为x2＋y2＝25.从而A(4,3)，B(－4，－3)，直线AB的斜率为.因为PB⊥AB，所以直线PB的斜率为－，直线PB的方程为y＝－x－.所以P(－13,9)，PB＝＝15.所以道路PB的长为15(百米)．(2)①若P在D处，取线段BD上一点E(－4,0)，则EO＝4<5，所以P选在D处不满足规划要求．②若Q在D处，连接AD，由(1)知D(－4,9)，又A(4,3)，所以线段AD：y＝－x＋6(－4≤x≤4)．在线段AD上取点M，因为OM＝<＝5，所以线段AD上存在点到点O的距离小于圆O的半径．因此Q选在D处也不满足规划要求．综上，P和Q均不能选在D处．(3)先讨论点P的位置．当∠OBP<90°时，线段PB上存在点到点O的距离小于圆O的半径，点P不符合规划要求；当∠OBP≥90°时，对线段PB上任意一点F，OF≥OB，即线段PB上所有点到点O的距离均不小于圆O的半径，点P符合规划要求．设P1为l上一点，且P1B⊥AB，由(1)知，P1B＝15，此时P1(－13,9)；当∠OBP>90°时，在△PP1B中，PB>P1B＝15.由上可知，d≥15.再讨论点Q的位置．由(2)知，要使得QA≥15，点Q只有位于点C的右侧，才能符合规划要求．当QA＝15时，设Q(a,9)，由AQ＝＝15(a>4)，得a＝4＋3，所以Q(4＋3，9)．此时，线段QA上所有点到点O的距离均不小于圆O的半径．综上，当P(－13,9)，Q(4＋3，9)时，d最小，此时P，Q两点间的距离PQ＝4＋3－(－13)＝17＋3.因此，d最小时，P，Q两点间的距离为17＋3(百米)．9．(2019·全国Ⅰ理，19)已知抛物线C：y2＝3x的焦点为F，斜率为的直线l与C的交点为A，B，与x轴的交点为P.(1)若|AF|＋|BF|＝4，求l的方程；(2)若＝3，求|AB|.解设直线l：y＝x＋t，A(x1，y1)，B(x2，y2)．(1)由题设得F，故|AF|＋|BF|＝x1＋x2＋，由题设可得x1＋x2＝.由可得9x2＋12(t－1)x＋4t2＝0，令Δ>0，得t<，则x1＋x2＝－.从而－＝，得t＝－.所以l的方程为y＝x－.(2)由＝3可得y1＝－3y2，由可得y2－2y＋2t＝0，所以y1＋y2＝2，从而－3y2＋y2＝2，故y2＝－1，y1＝3，代入C的方程得x1＝3，x2＝，即A(3,3)，B，故|AB|＝.10．(2019·全国Ⅱ理，21)已知点A(－2,0)，B(2,0)，动点M(x，y)满足直线AM与BM的斜率之积为－.记M的轨迹为曲线C.(1)求C的方程，并说明C是什么曲线；(2)过坐标原点的直线交C于P，Q两点，点P在第一象限，PE⊥x轴，垂足为E，连接QE 并延长交C于点G.(ⅰ)证明：△PQG是直角三角形；(ⅱ)求△PQG面积的最大值．(1)解由题设得·＝－，化简得＋＝1(|x|≠2)，所以C为中心在坐标原点，焦点在x轴上的椭圆，不含左右顶点．(2)(ⅰ)证明设直线PQ的斜率为k，则其方程为y＝kx(k>0)．由得x＝±.记u＝，则P(u，uk)，Q(－u，－uk)，E(u,0)．于是直线QG的斜率为，方程为y＝(x－u)．由得(2＋k2)x2－2uk2x＋k2u2－8＝0.①设G(x G，y G)，则－u和x G是方程①的解，故x G＝，由此得y G＝.从而直线PG的斜率为＝－，因为k PQ·k PG＝－1.所以PQ⊥PG，即△PQG是直角三角形．(ⅱ)解由(ⅰ)得|PQ|＝2u，|PG|＝，所以△PQG的面积S＝|PQ||PG|＝＝.设t＝k＋，则由k>0得t≥2，当且仅当k＝1时取等号．因为S＝在[2，＋∞)上单调递减，所以当t＝2，即k＝1时，S取得最大值，最大值为. 因此，△PQG面积的最大值为.11．(2019·全国Ⅲ理，21)已知曲线C：y＝，D为直线y＝－上的动点，过D作C的两条切线，切点分别为A，B.(1)证明：直线AB过定点；(2)若以E为圆心的圆与直线AB 相切，且切点为线段AB 的中点，求四边形ADBE 的面积．(1)证明 设D，A (x 1，y 1)，则＝2y 1.由y ′＝x ，所以切线DA 的斜率为x 1，故＝x 1.整理得2tx 1－2y 1＋1＝0.设B (x 2，y 2)，同理可得2tx 2－2y 2＋1＝0. 故直线AB 的方程为2tx －2y ＋1＝0. 所以直线AB 过定点.(2)解 由(1)得直线AB 的方程为y ＝tx ＋. 由可得x 2－2tx －1＝0，Δ＝4t 2＋4>0， 于是x 1＋x 2＝2t ，x 1x 2＝－1，y 1＋y 2 ＝t (x 1＋x 2)＋1＝2t 2＋1， |AB |＝ |x 1－x 2|＝ ＝2(t 2＋1)． 设d 1，d 2分别为点D ，E 到直线AB 的距离， 则d 1＝ ，d 2＝，因此，四边形ADBE 的面积S ＝|AB |(d 1＋d 2) ＝(t 2＋3) .设M 为线段AB 的中点，则M. 由于⊥ ，而 ＝(t ，t 2－2)，与坐标为(1，t )的向量平行，所以t ＋(t 2－2)t ＝0. 解得t ＝0或t ＝±1.当t ＝0时，S ＝3；当t ＝±1时，S ＝4 . 因此，四边形ADBE 的面积为3或4 .12．(2019·北京理，18)（14分）已知抛物线2:2C x py =-经过点(2,1)-． （Ⅰ）求抛物线C 的方程及其准线方程；（Ⅱ）设O 为原点，过抛物线C 的焦点作斜率不为0的直线l 交抛物线C 于两点M ，N ，直线1y =-分别交直线OM ，ON 于点A 和点B ．求证：以AB 为直径的圆经过y 轴上的两个定点．【思路分析】（Ⅰ）代入点(2,1)-，解方程可得p ，求得抛物线的方程和准线方程；（Ⅱ）抛物线24x y =-的焦点为(0,1)F -，设直线方程为1y kx =-，联立抛物线方程，运用韦达定理，以及直线的斜率和方程，求得A ，B 的坐标，可得AB 为直径的圆方程，可令0x =，解方程，即可得到所求定点．【解析】：（Ⅰ）抛物线2:2C x py =-经过点(2,1)-．可得42p =，即2p =， 可得抛物线C 的方程为24x y =-，准线方程为1y =； （Ⅱ）证明：抛物线24x y =-的焦点为(0,1)F -，设直线方程为1y kx =-，联立抛物线方程，可得2440x kx +-=， 设1(M x ，1)y ，2(N x ，2)y ， 可得124x x k +=-，124x x =-， 直线OM 的方程为11y y x x =，即14xy x =-， 直线ON 的方程为22y y x x =，即24xy x =-， 可得14(A x ，1)-，24(B x ，1)-， 可得AB 的中点的横坐标为121142()224kk x x -+==-， 即有AB 为直径的圆心为(2,1)k -，半径为212||1441616||222AB k x x +=-==， 可得圆的方程为222(2)(1)4(1)x k y k -++=+， 化为224(1)4x kx y -++=， 由0x =，可得1y =或3-．则以AB 为直径的圆经过y 轴上的两个定点(0,1)，(0,3)-．【归纳与总结】本题考查抛物线的定义和方程、性质，以及圆方程的求法，考查直线和抛物线方程联立，运用韦达定理，考查化简整理的运算能力，属于中档题．13．(2019·天津理，18)设椭圆＋＝1(a ＞b ＞0)的左焦点为F ，上顶点为B .已知椭圆的短轴长为4，离心率为. (1)求椭圆的方程；(2)设点P 在椭圆上，且异于椭圆的上、下顶点，点M 为直线PB 与x 轴的交点，点N 在y 轴的负半轴上．若|ON |＝|OF |(O 为原点)，且OP ⊥MN ，求直线PB 的斜率．解(1)设椭圆的半焦距为c，依题意，2b＝4，＝，又a2＝b2＋c2，可得a＝，b＝2，c ＝1.所以椭圆的方程为＋＝1.(2)由题意，设P(x P，y P)(x P≠0)，M(x M,0)，直线PB的斜率为k(k≠0)，又B(0,2)，则直线PB 的方程为y＝kx＋2，与椭圆方程联立得整理得(4＋5k2)x2＋20kx＝0，可得x P＝－，代入y＝kx＋2得y P＝.所以直线OP的斜率为＝.在y＝kx＋2中，令y＝0，得x M＝－.由题意得N(0，－1)，所以直线MN的斜率为－.由OP⊥MN，得·＝－1，化简得k2＝，从解得k＝±.所以直线PB的斜率为或－.。

高考真题（2019•全国II 卷（文））若抛物线y 2=2px （p >0）的焦点是椭圆的一个焦点，则p =A ．2B ．3C ．4D ．8【解析】因为抛物线的焦点是椭圆的一个焦点，所以，解得，故选D ． 【答案】D（2019•全国III 卷（文））设为椭圆的两个焦点，为上一点且在第一象限.若为等腰三角形，则的坐标为___________.【解析】由已知可得，．∴．设点的坐标为，则， 又，解得， ，解得（舍去）， 的坐标为．【答案】2231x y pp+=22(0)y px p =>(,0)2p 2231x y p p +=23()2p p p -=8p =12F F ，22:+13620x y C =M C 12MF F △M 2222236,20,16,4a b c a b c ==∴=-=∴=11228MF F F c ∴===24MF =M ()()0000,0,0x y x y >>121200142MF F S F F y y =⋅⋅=△1201442MF F S y =⨯=∴=△0y=22013620x ∴+=03x =03x =-M ((（2019•全国II 卷（文））已知是椭圆的两个焦点，P 为C 上一点，O 为坐标原点．（1）若为等边三角形，求C 的离心率；（2）如果存在点P ，使得，且的面积等于16，求b 的值和a 的取值范围. 【答案标记】【解析】（1）连结，由为等边三角形可知：在中，，，，于是， 故椭圆C 的离心率为； （2）由题意可知，满足条件的点存在，当且仅当，，， 即 ①②③ 由②③以及得，又由①知，故；由②③得，所以，从而，故；当，时，存在满足条件的点. 故，a 的取值范围为.【答案】（1）；（2），a 的取值范围为.（2019•天津卷（文））设椭圆的左焦点为，左顶点为，上顶点为B ．已知（为原点）.12,F F 2222:1(0)x y C a b a b+=>>2POF 12PF PF ⊥12F PF △1PF 2POF 12F PF △1290F PF ∠=2PF c =1PF =122a PF PF c=+=1c e a ===(,)P x y 12162y c ⋅=1y y x c x c ⋅=-+-22221x y a b+=16c y =222x y c +=22221x y a b+=222a b c =+422b y c =22216y c=4b =22222()a x c b c=-22c b ≥2222232a b c b =+≥=a ≥4b =a ≥P 4b =)+∞1e =4b =)+∞22221(0)x y a b a b+=>>F A |2||OA OB =O（Ⅰ）求椭圆的离心率； （Ⅱ）设经过点且斜率为的直线与椭圆在轴上方的交点为，圆同时与轴和直线相切，圆心在直线上，且，求椭圆的方程. 【答案标记】【解析】（I ）解：设椭圆的半焦距为， 又由，消去得，解得，所以，椭圆的离心率为. （II ）解：由（I ）知，，故椭圆方程为，由题意，，则直线的方程为， 点的坐标满足，消去并化简，得到，解得， 代入到的方程，解得， 因为点在轴的上方，所以， 由圆心在直线上，可设，因为，且由（I ）知，故，解得， 因为圆与轴相切，所以圆的半径为2，F 34l x P C x l C 4x =OC AP ∥c 2b =222a b c =+b 222)2a a c =+12c a =122,a c b ==2222143x y c c+=(,0)F c -l 3()4y x c =+P 22221433()4x y c c y x c ⎧+=⎪⎪⎨⎪=+⎪⎩y 2276130x cx c +-=1213,7cx c x ==-l 1239,214y c y c ==-P x 3(,)2P c c 4x =(4,)C t OC AP ∥(2,0)A c -3242ct c c=+2t =C x又由圆与，解得， 所以椭圆的方程为：.【答案】（I ）；（II ）.C l 2=2c =2211612x y +=122211612x y +=。

2019年高考数学试题分项版——解析几何（原卷版）一、选择题1．(2019·全国Ⅰ文，10)双曲线C：－＝1(a>0，b>0)的一条渐近线的倾斜角为130°，则C的离心率为()A．2sin 40°B．2cos 40° C. D.2．(2019·全国Ⅰ文，12)已知椭圆C的焦点为F1(－1,0)，F2(1,0)，过F2的直线与C交于A，B两点．若|AF2|＝2|F2B|，|AB|＝|BF1|，则C的方程为()A.＋y2＝1B.＋＝1C.＋＝1D.＋＝13．(2019·全国Ⅱ文，9)若抛物线y2＝2px(p>0)的焦点是椭圆＋＝1的一个焦点，则p等于()A．2 B．3 C．4 D．84．(2019·全国Ⅱ文，12)设F为双曲线C：－＝1(a>0，b>0)的右焦点，O为坐标原点，以OF为直径的圆与圆x2＋y2＝a2交于P，Q两点．若|PQ|＝|OF|，则C的离心率为() A. B.C．2 D.5．(2019·全国Ⅲ文，10)已知F是双曲线C：－＝1的一个焦点，点P在C上，O为坐标原点．若|OP|＝|OF|，则△OPF的面积为()A. B. C. D.6．(2019·北京文，5已知双曲线－y2＝1(a>0)的离心率是，则a等于()A.B．4 C．2 D.7．(2019·天津文，6)已知抛物线y2＝4x的焦点为F，准线为l.若l与双曲线－＝1(a＞0，b＞0)的两条渐近线分别交于点A和点B，且|AB|＝4|OF|(O为原点)，则双曲线的离心率为()A. B.C．2 D.8．(2019·浙江，2)渐近线方程为x±y＝0的双曲线的离心率是()A.B．1C.D．29．(2019·全国Ⅰ理，10)已知椭圆C的焦点为F1(－1,0)，F2(1,0)，过F2的直线与C交于A，B两点．若|AF2|＝2|F2B|，|AB|＝|BF1|，则C的方程为()A.＋y2＝1B.＋＝1C.＋＝1D.＋＝110．(2019·全国Ⅱ理，8)若抛物线y 2＝2px (p >0)的焦点是椭圆＋ ＝1的一个焦点，则p 等于( )A ．2B ．3C ．4D ．811．(2019·全国Ⅱ理，11)设F 为双曲线C ：－＝1(a >0，b >0)的右焦点，O 为坐标原点，以OF 为直径的圆与圆x 2＋y 2＝a 2交于P ，Q 两点．若|PQ |＝|OF |，则C 的离心率为( ) A. B. C ．2 D.12．(2019·全国Ⅲ理，10)双曲线C ：－＝1的右焦点为F ，点P 在C 的一条渐近线上，O 为坐标原点．若|PO |＝|PF |，则△PFO 的面积为( ) A.B.C ．2D ．313．(2019·北京理，4)已知椭圆22221(0)x y a b a b +=>>的离心率为12，则( )A ．222a b =B ．2234a b =C ．2a b =D ．34a b =14．(2019·北京理，8)数学中有许多形状优美、寓意美好的曲线，曲线22:1||C x y x y +=+就是其中之一（如图）．给出下列三个结论：①曲线C 恰好经过6个整点（即横、纵坐标均为整数的点）；②曲线C ③曲线C 所围成的“心形”区域的面积小于3． 其中，所有正确结论的序号是( )A ．①B ．②C ．①②D ．①②③15．(2019·天津理，5)已知抛物线y 2＝4x 的焦点为F ，准线为l .若l 与双曲线－＝1(a ＞0，b ＞0)的两条渐近线分别交于点A 和点B ，且|AB |＝4|OF |(O 为原点)，则双曲线的离心率为( )A. B. C ．2 D. 二、填空题1．(2019·全国Ⅲ文，15)设F1，F2为椭圆C：＋＝1的两个焦点，M为C上一点且在第一象限．若△MF1F2为等腰三角形，则M的坐标为________．2．(2019·北京文，11)设抛物线y2＝4x的焦点为F，准线为l.则以F为圆心，且与l相切的圆的方程为________．3．(2019·浙江，12)已知圆C的圆心坐标是(0，m)，半径长是r.若直线2x－y＋3＝0与圆C 相切于点A(－2，－1)，则m＝________，r＝________.4．(2019·浙江，15)已知椭圆＋＝1的左焦点为F，点P在椭圆上且在x轴的上方．若线段PF的中点在以原点O为圆心，|OF|为半径的圆上，则直线PF的斜率是________．5．(2019·江苏，7)在平面直角坐标系xOy中，若双曲线x2－＝1(b>0)经过点(3,4)，则该双曲线的渐近线方程是_________________．6．(2019·江苏，10)在平面直角坐标系xOy中，P是曲线y＝x＋(x>0)上的一个动点，则点P到直线x＋y＝0的距离的最小值是________．7．(2019·全国Ⅰ理，16)已知双曲线C：－＝1(a>0，b>0)的左、右焦点分别为F1，F2，过F1的直线与C的两条渐近线分别交于A，B两点．若＝，·＝0，则C的离心率为________．8．(2019·全国Ⅲ理，15)设F1，F2为椭圆C：＋＝1的两个焦点，M为C上一点且在第一象限．若△MF1F2为等腰三角形，则M的坐标为________．三、解答题1．(2019·全国Ⅰ文，21)已知点A，B关于坐标原点O对称，|AB|＝4，⊙M过点A，B且与直线x＋2＝0相切．(1)若A在直线x＋y＝0上，求⊙M的半径；(2)是否存在定点P，使得当A运动时，|MA|－|MP|为定值？并说明理由．2．(2019·全国Ⅱ文，20)已知F1，F2是椭圆C：＋＝1(a>b>0)的两个焦点，P为C上的点，O为坐标原点．(1)若△POF2为等边三角形，求C的离心率；(2)如果存在点P，使得PF1⊥PF2，且△F1PF2的面积等于16，求b的值和a的取值范围．3．(2019·全国Ⅲ文，21)已知曲线C：y＝，D为直线y＝－上的动点，过D作C的两条切线，切点分别为A，B.(1)证明：直线AB过定点；(2)若以E为圆心的圆与直线AB相切，且切点为线段AB的中点，求该圆的方程．4．(2019·北京文，19)已知椭圆C：＋＝1的右焦点为(1,0)，且经过点A(0,1)．(1)求椭圆C的方程；(2)设O为原点，直线l：y＝kx＋t(t≠±1)与椭圆C交于两个不同点P，Q，直线AP与x轴交于点M，直线AQ与x轴交于点N.若|OM|·|ON|＝2，求证：直线l经过定点．5．(2019·天津文，19)设椭圆＋＝1(a＞b＞0)的左焦点为F，左顶点为A，上顶点为B.已知|OA|＝2|OB|(O为原点)．(1)求椭圆的离心率；(2)设经过点F且斜率为的直线l与椭圆在x轴上方的交点为P，圆C同时与x轴和直线l 相切，圆心C在直线x＝4上，且OC∥AP.求椭圆的方程．6.(2019·浙江，21)如图，已知点F(1,0)为抛物线y2＝2px(p＞0)的焦点．过点F的直线交抛物线于A，B两点，点C在抛物线上，使得△ABC的重心G在x轴上，直线AC交x轴于点Q，且Q在点F的右侧．记△AFG，△CQG的面积分别为S1，S2.(1)求p的值及抛物线的准线方程；(2)求的最小值及此时点G的坐标．7.(2019·江苏，17)如图，在平面直角坐标系xOy中，椭圆C：＋＝1(a>b>0)的焦点为F1(－1,0)，F2(1,0)．过F2作x轴的垂线l，在x轴的上方，l与圆F2：(x－1)2＋y2＝4a2交于点A，与椭圆C交于点D.连接AF1并延长交圆F2于点B，连接BF2交椭圆C于点E，连接DF1.已知DF1＝.(1)求椭圆C的标准方程；(2)求点E的坐标．8．(2019·江苏，18)如图，一个湖的边界是圆心为O的圆，湖的一侧有一条直线型公路l，湖上有桥AB(AB是圆O的直径)．规划在公路l上选两个点P，Q，并修建两段直线型道路PB，QA，规划要求：线段PB，QA上的所有点到点O的距离均不小于圆O的半径．已知点A，B到直线l的距离分别为AC和BD(C，D为垂足)，测得AB＝10，AC＝6，BD＝12(单位：百米)．(1)若道路PB与桥AB垂直，求道路PB的长；(2)在规划要求下，P和Q中能否有一个点选在D处？并说明理由；(3)在规划要求下，若道路PB和QA的长度均为d(单位：百米)，求当d最小时，P，Q两点间的距离．9．(2019·全国Ⅰ理，19)已知抛物线C：y2＝3x的焦点为F，斜率为的直线l与C的交点为A，B，与x轴的交点为P.(1)若|AF|＋|BF|＝4，求l的方程；(2)若＝3，求|AB|.10．(2019·全国Ⅱ理，21)已知点A(－2,0)，B(2,0)，动点M(x，y)满足直线AM与BM的斜率之积为－.记M的轨迹为曲线C.(1)求C的方程，并说明C是什么曲线；(2)过坐标原点的直线交C于P，Q两点，点P在第一象限，PE⊥x轴，垂足为E，连接QE 并延长交C于点G.(ⅰ)证明：△PQG是直角三角形；(ⅱ)求△PQG面积的最大值．11．(2019·全国Ⅲ理，21)已知曲线C ：y ＝，D 为直线y ＝－上的动点，过D 作C 的两条切线，切点分别为A ，B . (1)证明：直线AB 过定点；(2)若以E为圆心的圆与直线AB 相切，且切点为线段AB 的中点，求四边形ADBE 的面积．12．(2019·北京理，18)（14分）已知抛物线2:2C x py =-经过点(2,1)-． （Ⅰ）求抛物线C 的方程及其准线方程；（Ⅱ）设O 为原点，过抛物线C 的焦点作斜率不为0的直线l 交抛物线C 于两点M ，N ，直线1y =-分别交直线OM ，ON 于点A 和点B ．求证：以AB 为直径的圆经过y 轴上的两个定点．13．(2019·天津理，18)设椭圆＋＝1(a ＞b ＞0)的左焦点为F ，上顶点为B .已知椭圆的短轴长为4，离心率为. (1)求椭圆的方程；(2)设点P 在椭圆上，且异于椭圆的上、下顶点，点M 为直线PB 与x 轴的交点，点N 在y 轴的负半轴上．若|ON |＝|OF |(O 为原点)，且OP ⊥MN ，求直线PB 的斜率．。

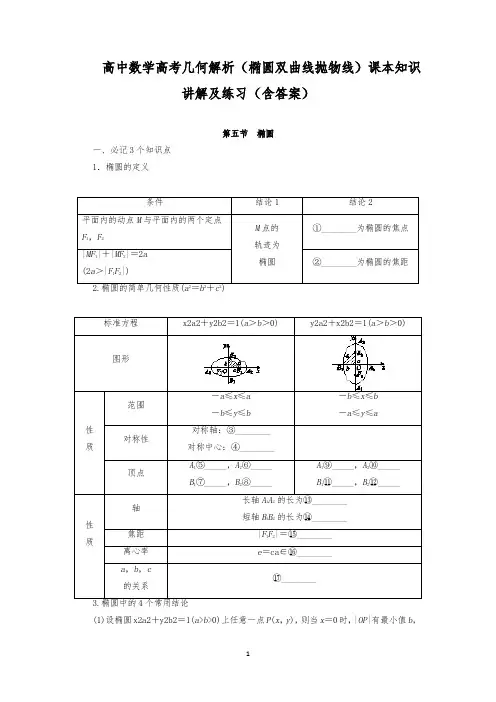
高中数学高考几何解析（椭圆双曲线抛物线）课本知识讲解及练习（含答案）第五节椭圆一、必记3个知识点1．椭圆的定义(1)设椭圆x2a2＋y2b2＝1(a>b>0)上任意一点P(x，y)，则当x＝0时，|OP|有最小值b，这时，P在短轴端点处；当x＝±a时，|OP|有最大值a，这时，P在长轴端点处．(2)椭圆的一个焦点、中心和短轴的一个端点构成直角三角形，其中a是斜边长，a2＝b2＋c2.(3)已知过焦点F1的弦AB，则△ABF2的周长为4a.(4)若P为椭圆上任一点，F为其焦点，则a－c≤|PF|≤a＋c.二、必明3个易误点1．椭圆的定义中易忽视2a>|F1F2|这一条件，当2a＝|F1F2|其轨迹为线段F1F2，当2a<|F1F2|不存在轨迹．2．求椭圆的标准方程时易忽视判断焦点的位置，而直接设方程为x2a2＋y2b2＝1(a>b>0)．3．注意椭圆的范围，在设椭圆x2a2＋y2b2＝1(a>b>0)上点的坐标为P(x，y)时，则|x|≤a，这往往在求与点P有关的最值问题中特别有用，也是容易被忽略而导致求最值错误的原因．三、技法1.求椭圆标准方程的2种常用方法(1)直接求出a，c来求解e.通过已知条件列方程组，解出a，c的值．(2)构造a，c的齐次式，解出e.由已知条件得出关于a，c的二元齐次方程，然后转化为关于离心率e的一元二次方程求解．(3)通过取特殊值或特殊位置，求出离心率．提醒：在解关于离心率e的二次方程时，要注意利用椭圆的离心率e∈(0,1)进行根的取舍，否则将产生增根.3.求解最值、取值范围问题的技巧(1)与椭圆几何性质有关的问题要结合图形进行分析，即使画不出图形，思考时也要联想到一个图形．(2)椭圆的范围或最值问题常常涉及一些不等式．例如，－a≤x≤a，－b≤y≤b,0<e<1，在求椭圆的相关量的范围时，要注意应用这些不等关系．(3)最值问题，将所求列出表达式，构造基本不等式或利用函数单调性求解.4.判断直线与椭圆位置关系的四个步骤第一步：确定直线与椭圆的方程．第二步：联立直线方程与椭圆方程．第三步：消元得出关于x(或y)的一元二次方程．第四步：当Δ>0时，直线与椭圆相交；当Δ＝0时，直线与椭圆相切；当Δ<0时，直线与椭圆相离．5．直线被椭圆截得的弦长公式设直线与椭圆的交点坐标为A(x1，y1)，B(x2，y2)，则|AB|＝(1＋k2)[(x1＋x2)2－4x1x2])＝(y1＋y2)2－4y1y2])(k为直线斜率).参考答案①F1，F2②|F1F2|③x轴，y轴④坐标原点⑤(－a,0)⑥(a,0)⑦(0，－b)⑧(0，b)⑨(0，－a)⑩(0，a)⑪(－b,0)⑫(b,0)⑬2a⑭2b⑮2c⑯(0,1)⑰c2＝a2－b2第六节双曲线一、必记3个知识点1．双曲线的定义(1)平面内与两个定点F1、F2(|F1F2|＝2c>0)的距离①________________为非零常数2a(2a<2c)的点的轨迹叫做双曲线．这两个定点叫做双曲线的②________，两焦点间的距离叫做③________.(2)集合P＝{M|||MF1|－|MF2||＝2a}，|F1F2|＝2c，其中a，c为常数且a>0，c>0.(ⅰ)当④________________时，M点的轨迹是双曲线；(ⅱ)当⑤________________时，M点的轨迹是两条射线；(ⅲ)当⑥________________时，M点不存在．2．双曲线的标准方程和几何性质⑧________x ∈对称轴：⑪________对称中心：⑫________顶点坐标：A 1⑮______，A 2⑯________⑱____________c ＝⑳________|＝21________；线段________；a 叫做双曲线的虚半轴长＞b ＞0)(1)双曲线为等轴双曲线⇔双曲线的离心率e ＝2⇔双曲线的两条渐近线互相垂直．(2)渐近线的斜率与双曲线的焦点位置的关系：当焦点在x 轴上时，渐近线斜率为±ba，当焦点在y 轴上时，渐近线斜率为±ab.(3)渐近线与离心率．x2a2－y2b2＝1(a >0，b >0)的一条渐近线的斜率为ba＝e2－1.(4)若P 为双曲线上一点，F 为其对应焦点，则|PF |≥c －a .二、必明4个易误点1．双曲线的定义中易忽视2a <|F 1F 2|这一条件．若2a ＝|F 1F 2|，则轨迹是以F 1，F 2为端点的两条射线，若2a >|F 1F 2|则轨迹不存在．2．双曲线的标准方程中对a ，b 的要求只是a >0，b >0，易误认为与椭圆标准方程中a ，b 的要求相同．若a >b >0，则双曲线的离心率e ∈(1，2)；若a ＝b >0，则双曲线的离心率e ＝2；若0<a <b ，则双曲线的离心率e >2.3．注意区分双曲线中的a ，b ，c 大小关系与椭圆a ，b ，c 关系，在椭圆中a 2＝b 2＋c 2，而在双曲线中c2＝a2＋b2.4．易忽视渐近线的斜率与双曲线的焦点位置关系．当焦点在x轴上，渐近线斜率为±ba，当焦点在y轴上，渐近线斜率为±ab.三、技法1.双曲线定义的应用(1)判定满足某条件的平面内动点的轨迹是否为双曲线，进而根据要求可求出曲线方程；(2)在“焦点三角形”中，常利用正弦定理、余弦定理，经常结合||PF1|－|PF2||＝2a，运用平方的方法，建立|PF1|与|PF2|的关系．[注意]在应用双曲线定义时，要注意定义中的条件，搞清所求轨迹是双曲线，还是双曲线的一支，若是双曲线的一支，则需确定是哪一支.2.求双曲线标准方程的一般方法(1)待定系数法：设出双曲线方程的标准形式，根据已知条件，列出参数a，b，c的方程并求出a，b，c的值．与双曲线x2a2－y2b2＝1有相同渐近线时，可设所求双曲线方程为：x2a2－y2b2＝λ(λ≠0)．(2)定义法：依定义得出距离之差的等量关系式，求出a的值，由定点位置确定c的值.3.求双曲线离心率或其范围的方法(1)求a，b，c的值，由c2a2＝a2＋b2a2＝1＋b2a2直接求e.(2)列出含有a，b，c的齐次方程(或不等式)，借助于b2＝c2－a2消去b，然后转化成关于e的方程(或不等式)求解．4．求双曲线的渐近线方程的方法求双曲线x2a2－y2b2＝1(a>0，b>0)的渐近线的方法是令x2a2－y2b2＝0，即得两渐近线方程为：xa±yb＝0.参考答案①之差的绝对值②焦点③焦距④2a<|F1F2|⑤2a＝|F1F2|⑥2a>|F1F2|⑦x≥a或x≤－a⑧y≥a或y≤－a⑨x轴，y轴⑩坐标原点⑪x轴，y轴⑫坐标原点⑬(－a,0)⑭(a,0)⑮(0，－a)⑯(0，a)⑰y＝±ba x⑱y＝±ab x⑲ca⑳a2＋b2212a222b23a2＋b2第七节抛物线一、必记2个知识点1．抛物线定义、标准方程及几何性质x轴⑤________y轴⑥________O(0,0)O(0,0)O(0,0)O(0,0)F⑦________⑧________⑨________设AB是过抛物线y2＝2px(p>0)的焦点F的弦，若A(x1，y1)，B(x2，y2)，则(1)x1x2＝p24，y1y2＝－p2.(2)弦长|AB|＝x1＋x2＋p＝2psin2α(α为弦AB的倾斜角)．(3)以弦AB为直径的圆与准线相切．(4)通径：过焦点且垂直于对称轴的弦，长等于2p.二、必明2个易误点1．抛物线的定义中易忽视“定点不在定直线上”这一条件，当定点在定直线上时，动点的轨迹是过定点且与直线垂直的直线．2．抛物线标准方程中参数p易忽视，只有p>0，才能证明其几何意义是焦点F到准线l 的距离，否则无几何意义．三、技法1.应用抛物线定义的2个关键点(1)由抛物线定义，把抛物线上点到焦点距离与到准线距离相互转化．(2)注意灵活运用抛物线上一点P(x，y)到焦点F的距离|PF|＝|x|＋p2或|PF|＝|y|＋p2.2.求抛物线的标准方程的方法(1)求抛物线的标准方程常用待定系数法，因为未知数只有p，所以只需一个条件确定p值即可．(2)因为抛物线方程有四种标准形式，因此求抛物线方程时，需先定位，再定量．3．确定及应用抛物线性质的技巧(1)利用抛物线方程确定及应用其焦点、准线等性质时，关键是将抛物线方程化为标准方程．(2)要结合图形分析，灵活运用平面几何的性质以图助解.4.解决直线与抛物线位置关系问题的常用方法(1)直线与抛物线的位置关系和直线与椭圆、双曲线的位置关系类似，一般要用到根与系数的关系．(2)有关直线与抛物线的弦长问题，要注意直线是否过抛物线的焦点，若过抛物线的焦点，可直接使用公式|AB|＝x1＋x2＋p，若不过焦点，则必须用一般弦长公式．(3)涉及抛物线的弦长、中点、距离等相关问题时，一般利用根与系数的关系采用“设而不求”“整体代入”等解法．提醒：涉及弦的中点、斜率时，一般用“点差法”求解.参考答案①相等②y2＝－2px(p＞0)③x2＝－2py(p＞0)④x2＝2py(p＞0)⑤x轴⑥y轴⑦F(－p2，0)⑧F(0，－p2)⑨F(0，p2)⑩e＝1⑪x＝－p2⑫y＝－p2⑬－y0＋p2⑭y0＋p2⑮y≤0⑯y≥0。

2019年高考数学理试题分类汇编：圆锥曲线(含答案)2019年高考数学理试题分类汇编——圆锥曲线一、选择题1.（2019年四川高考）设O为坐标原点，P是以F为焦点的抛物线y=2px(p>0)上任意一点，M是线段PF上的点，且PM=2MF，则直线OM的斜率的最大值为2/3.（答案：C）2.（2019年天津高考）已知双曲线x^2/4 - y^2/9 = 1（b>0），以原点为圆心，双曲线的实半轴长为半径长的圆与双曲线的两条渐近线相交于A、B、C、D四点，四边形ABCD的面积为2b，则双曲线的方程为x^2/4 - y^2/9 = 1.（答案：D）3.（2019年全国I高考）已知方程x^2/n^2 - y^2/m^2 = 1表示双曲线，且该双曲线两焦点间的距离为4，则n的取值范围是(-1,3)。

（答案：A）4.（2019年全国I高考）以抛物线C的顶点为圆心的圆交C于A、B两点，交C的准线于D、E两点。

已知|AB|=42，|DE|=25，则C的焦点到准线的距离为4.（答案：B）5.（2019年全国II高考）圆(x-1)^2 + (y-4)^2 = 13的圆心到直线ax+y-1=0的距离为1，则a=-2/3.（答案：A）6.（2019年全国II高考）已知F1,F2是双曲线E:x^2/4 -y^2/2 = 1的左、右焦点，点M在E上，MF1与x轴垂直，sin∠MF2F1=1/3，则E的离心率为2/3.（答案：A）7.（2019年全国III高考）已知O为坐标原点，F是椭圆C:x^2/a^2 + y^2/b^2 = 1(a>b>0)的左焦点，A、B分别为C的左、右顶点。

P为C上一点，且PF⊥x轴。

过点A的直线l与线段PF交于点M，与y轴交于点E。

若直线BM经过OE的中点，则C的离心率为1/3.（答案：A）8.（2019年浙江高考）已知椭圆 + y^2/(m^2-1) = 1(m>1)与双曲线- y^2/(n^2-1) = 1(n>0)的焦点重合，e1，e2分别为m，n，则e1+e2=3.（答案：C）解析】Ⅰ）由题意可知，椭圆C的离心率为$\frac{\sqrt{3}}{2}$，根据离心率的定义可得：$\frac{c}{a}=\frac{\sqrt{3}}{2}$，其中$c$为椭圆的焦距之一，即$2c$为椭圆的长轴长度，$a$为椭圆的半长轴长度，$b$为椭圆的半短轴长度，则有：$$\frac{2c}{2a}=\frac{\sqrt{3}}{2}$$ 即：$$\frac{c}{a}=\frac{\sqrt{3}}{4}$$ 又因为焦点$F$在椭圆的一个顶点上，所以该顶点的坐标为$(a,0)$，即$2c=2a$，代入上式可得：$$\frac{b}{a}=\frac{1}{2}$$ 又因为椭圆的方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$，代入$\frac{b}{a}=\frac{1}{2}$可得：$$\frac{x^2}{a^2}+\frac{4y^2}{a^2}=1$$ 即：$$x^2+4y^2=a^2$$ （Ⅱ）（i）设椭圆C的另一个顶点为$V$，则$OV$为椭圆的长轴，$OF$为椭圆的短轴，且$OV=2a$，$OF=\sqrt{3}a$。

2|F2B|，|AB|＝|BF1|，则 C 的方程为( )
A.x2＋y2＝1 2
B.x2＋y2＝1 32
C.x2＋y2＝1 43
D.x2＋y2＝1 54
【训练 1】 (1)已知双曲线ax22－by22＝1(a>0，b>0)的离心率为 2，过右焦点且垂直于 x 轴的直线与双曲线交于 A，
B 两点.设 A，B 到双曲线的同一条渐近线的距离分别为 d1 和 d2，且 d1＋d2＝6，则双曲线的方程为( )
Hale Waihona Puke (2)过 B1 作直线 l 交椭圆于 P，Q 两点，使得 PB2⊥QB2，求直线 l 的
方程.
【训练 3】 在直角坐标系 xOy 中，直线 l：y＝t(t≠0)交 y 轴于点 M，交抛物线 C：y2＝2px(p>0)于点 P，M 关于点 P 的对称点为 N，连接 ON 并延长交 C 于点 H. (1)求|OH|；
(1)(2019·河南八市联考)设双曲线
C：x2－y2＝1 8m
的左、右焦点分别为
F1，F2，过
F1
的直线与双曲
线 C 交于 M，N 两点，其中 M 在左支上，N 在右支上.若∠F2MN＝∠F2NM，则|MN|＝( )
A.8
B.4
C.8 2
D.4 2
(2)(2019·全国Ⅰ卷)已知椭圆 C 的焦点为 F1(－1，0)，F2(1，0)，过 F2 的直线与 C 交于 A，B 两点.若|AF2|＝
第 2 讲 椭圆、双曲线、抛物线
真题感悟
1.(2019·全国Ⅱ卷)若抛物线 y2＝2px(p>0)的焦点是椭圆 x2 ＋y2＝1 的一个焦点，则 p＝( ) 3p p
A.2 B.3 C.4

椭圆2019年1.（2019全国1文12）已知椭圆C 的焦点为12(1,0),(1,0)F F -，过F 2的直线与C 交于A ，B 两点.若22||2||AF F B =，1||||AB BF =，则C 的方程为A ．2212x y +=B ．22132x y +=C ．22143x y +=D ．22154x y +=2.（2019全国II 文9）若抛物线y 2=2px （p >0）的焦点是椭圆2213x y p p+=的一个焦点，则p = A ．2 B ．3C ．4D ．83.（2019北京文19）已知椭圆2222:1x y C a b+=的右焦点为(1,0)，且经过点(0,1)A ．（Ⅰ）求椭圆C 的方程；（Ⅱ）设O 为原点，直线:(1)l y kx t t =+≠±与椭圆C 交于两个不同点P ，Q ，直线AP 与x 轴交于点M ，直线AQ 与x 轴交于点N ，若|OM |·|ON |=2，求证：直线l 经过定点．4.（2019江苏16）如图，在平面直角坐标系xOy 中，椭圆C :22221(0)x y a b a b+=>>的焦点为F 1（–1、0），F 2（1，0）．过F 2作x 轴的垂线l ，在x 轴的上方，l 与圆F 2:222(1)4x y a-+=交于点A ，与椭圆C 交于点D .连结AF 1并延长交圆F 2于点B ，连结BF 2交椭圆C 于点E ，连结DF 1．已知DF 1=52． （1）求椭圆C 的标准方程； （2）求点E 的坐标．5.（2019浙江15）已知椭圆22195x y +=的左焦点为F ，点P 在椭圆上且在x 轴的上方，若线段PF 的中点在以原点O 为圆心，OF 为半径的圆上，则直线PF 的斜率是_______.6.（2019全国II 文20）已知12,F F 是椭圆2222:1(0)x y C a b a b+=>>的两个焦点，P 为C 上一点，O 为坐标原点．（1）若2POF △为等边三角形，求C 的离心率；（2）如果存在点P ，使得12PF PF ⊥，且12F PF △的面积等于16，求b 的值和a 的取值范围.7.（2019天津文19）设椭圆22221(0)x y a b a b+=>>的左焦点为F ，左顶点为A ，顶点为B .3|2||OA OB =（O 为原点）.（Ⅰ）求椭圆的离心率； （Ⅱ）设经过点F 且斜率为34的直线l 与椭圆在x 轴上方的交点为P ，圆C 同时与x 轴和直线l 相切，圆心C 在直线4x =上，且OC AP ∥，求椭圆的方程.8.(2019全国III 文15）设12F F ，为椭圆C :22+13620x y =的两个焦点，M 为C 上一点且在第一象限.若12MF F △为等腰三角形，则M 的坐标为___________.9.（2019北京文19）已知椭圆2222:1x y C a b+=的右焦点为(1,0)，且经过点(0,1)A ．（Ⅰ）求椭圆C 的方程；（Ⅱ）设O 为原点，直线:(1)l y kx t t =+≠±与椭圆C 交于两个不同点P ，Q ，直线AP 与x 轴交于点M ，直线AQ 与x 轴交于点N ，若|OM |·|ON |=2，求证：直线l 经过定点．2010-2019年一、选择题1．(2018全国卷Ⅰ)已知椭圆C ：22214x y a +=的一个焦点为(20)，，则C 的离心率为A ．13B ．12CD 2．(2018全国卷Ⅱ)已知1F ，2F 是椭圆C 的两个焦点，P 是C 上的一点，若12PF PF ⊥，且2160PF F ∠=︒，则C 的离心率为A ．1B ．2CD 13．(2018上海)设P 是椭圆22153x y +=上的动点，则P 到该椭圆的两个焦点的距离之和为A ．B ．C ．D ．4．（2017浙江）椭圆22194x y +=的离心率是A ．B C ．23D ．59 5．（2017新课标Ⅲ）已知椭圆C ：22221(0)x y a b a b+=>>的左、右顶点分别为1A ，2A ，且以线段12A A 为直径的圆与直线20bx ay ab -+=相切，则C 的离心率为A B C ．3 D ．136．（2017新课标Ⅰ）设A 、B 是椭圆C ：2213x y m+=长轴的两个端点，若C 上存在点M 满足AMB ∠ =120°，则m 的取值范围是A ．(0,1][9,)+∞B ．[9,)+∞C ．(0,1][4,)+∞D ．[4,)+∞7．（2016年全国I 卷）直线l 经过椭圆的一个顶点和一个焦点，若椭圆中心到l 的距离为其短轴长的14，则该椭圆的离心率为 A ．13 B ．12 C ．23 D ．348．（2016年全国III 卷）已知O 为坐标原点，F 是椭圆C ：22221(0)x y a b a b+=>>的左焦点，A ，B 分别为C 的左，右顶点.P 为C 上一点，且PF x ⊥轴.过点A 的直线l 与线段PF 交于点M ，与y 轴交于点E .若直线BM 经过OE 的中点，则C 的离心率为A ．13B ．12C ．23D ．349．（2015新课标1）已知椭圆E 的中心为坐标原点，离心率为12，E 的右焦点与抛物线C ：28y x =的焦点重合，A B 、是C 的准线与E 的两个交点，则AB =A ．3B ．6C ．9D ．1210．（2015广东）已知椭圆222125x y m+=（0m >）的左焦点为()14,0F -，则m = A ．2 B ．3 C ．4 D ．911．（2015福建）已知椭圆2222:1(0)x y E a b a b+=>>的右焦点为F ．短轴的一个端点为M ，直线:340l x y -=交椭圆E 于,A B 两点．若4AF BF +=，点M 到直线l 的距离不小于45，则椭圆E 的离心率的取值范围是A ．B ．3(0,]4C ．D ．3[,1)412．(2014福建)设Q P ,分别为()2622=-+y x 和椭圆11022=+y x 上的点，则Q P ,两点间的最大距离是A ．25B ．246+C ．27+D ．2613．（2013新课标1）已知椭圆22221(0)x y a b a b+=>>的右焦点为F (3,0)，过点F 的直线交椭圆于A 、B 两点．若AB 的中点坐标为(1，－1)，则E 的方程为 A ．x 245＋y 236＝1B ．x 236＋y 227＝1C ．x 227＋y 218＝1D ．x 218＋y 29＝114．（2013广东）已知中心在原点的椭圆C 的右焦点为(1,0)F ，离心率等于21，则C 的方程是A ．14322=+y x B ．13422=+y x C ．12422=+y x D ．13422=+y x 15．(2012新课标)设1F 、2F 是椭圆E ：)0(12222>>=+b a by a x 的左、右焦点，P 为直线23a x =上一点，12PF F ∆ 是底角为o30的等腰三角形，则E 的离心率为 A 、21 B 、32 C 、43 D 、54二、填空题16．(2018浙江)已知点(0,1)P ，椭圆224x y m +=(1m >)上两点A ，B 满足2AP PB =，则当m =___时，点B 横坐标的绝对值最大．17．（2015浙江）椭圆22221x y a b +=（0a b >>）的右焦点(),0F c 关于直线by x c=的对称点Q 在椭圆上，则椭圆的离心率是 ．18．（2014江西）过点(1,1)M 作斜率为12-的直线与椭圆C ：22221(0)x y a b a b +=>>相交于,A B 两点，若M 是线段AB 的中点，则椭圆C 的离心率等于 ．19．（2014辽宁）已知椭圆C ：22194x y +=，点M 与C 的焦点不重合，若M 关于C 的焦点的对称点分别为A ，B ，线段MN 的中点在C 上，则||||AN BN += ．20．（2014江西）设椭圆()01:2222>>=+b a by a x C 的左右焦点为21F F ，，作2F 作x 轴的垂线与C 交于B A ，两点，B F 1与y 轴相交于点D ，若B F AD 1⊥，则椭圆C 的离心率等于________．21．（2014安徽）设21,F F 分别是椭圆)10(1:222<<=+b by x E 的左、右焦点，过点1F 的直线交椭圆E 于B A ,两点，若x AF BF AF ⊥=211,3轴，则椭圆E 的方程为____．22．（2013福建）椭圆)0(1:2222>>=+Γb a by a x 的左、右焦点分别为21,F F ，焦距为c 2．若直线)y x c =+与椭圆Γ的一个交点M 满足12212F MF F MF ∠=∠，则该椭圆的离心率等于 ．23．（2012江西）椭圆22221(0)x y a b a b+=>>的左、右顶点分别是,A B ，左、右焦点分别是12,F F ．若1121||,||,||AF F F F B 成等比数列，则此椭圆的离心率为_________．24．（2011浙江）设12,F F 分别为椭圆2213x y +=的左、右焦点，点,A B 在椭圆上，若125F A F B =；则点A 的坐标是 ．三、解答题25．（2018江苏）如图，在平面直角坐标系xOy 中，椭圆C 过点1)2，焦点12(F F ，圆O 的直径为12F F ．(1)求椭圆C 及圆O 的方程；(2)设直线l 与圆O 相切于第一象限内的点P ．①若直线l 与椭圆C 有且只有一个公共点，求点P 的坐标；②直线l 与椭圆C 交于,A B 两点．若OAB △，求直线l 的方程． 26．（2018全国卷Ⅲ）已知斜率为k 的直线l 与椭圆22143x y C +=：交于A ，B 两点．线段AB 的中点为(1,)(0)M m m >．(1)证明：12k <-； (2)设F 为C 的右焦点，P 为C 上一点，且FP FA FB ++=0．证明：2||||||FP FA FB =+．27．（2018北京）已知椭圆2222:1(0)x y M a b a b+=>>的离心率为3，焦距为．斜率为k 的直线l 与椭圆M 有两个不同的交点A ，B ． (1)求椭圆M 的方程；(2)若1k =，求||AB 的最大值；(3)设(2,0)P -，直线PA 与椭圆M 的另一个交点为C ，直线PB 与椭圆M 的另一个交点为D ．若C ，D 和点71(,)42Q - 共线，求k ．28．（2018天津）设椭圆22221(0)x y a b a b+=>>的右顶点为A ，上顶点为B ．已知椭圆的离心率为3||AB = (1)求椭圆的方程；(2)设直线:(0)l y kx k =<与椭圆交于,P Q 两点，l 与直线AB 交于点M ，且点P ，M 均在第四象限．若BPM △的面积是BPQ △面积的2倍，求k 的值．29．（2017新课标Ⅱ）设O 为坐标原点，动点M 在椭圆C ：2212x y +=上，过M 做x 轴的垂线，垂足为N ，点P 满足2NP NM =．（1）求点P 的轨迹方程；（2）设点Q 在直线3x =-上，且1OP PQ ⋅=．证明：过点P 且垂直于OQ 的直线l 过C 的左焦点F ．30．（2017天津）已知椭圆22221(0)x y a b a b+=>>的左焦点为,()0F c -，右顶点为A ，点E的坐标为(0,)c ，EFA △的面积为22b ．（Ⅰ）求椭圆的离心率；（Ⅱ）设点Q 在线段AE 上，3||2FQ c =，延长线段FQ 与椭圆交于点P ，点M ，N 在x 轴上，PM QN ∥，且直线PM 与直线QN 间的距离为c ，四边形PQNM 的面积为3c ．（i ）求直线FP 的斜率； （ii ）求椭圆的方程．31．（2017山东）在平面直角坐标系xOy 中，已知椭圆C :22221x y a b+=(0)a b >>的离心率为2，椭圆C 截直线1y =所得线段的长度为 (Ⅰ)求椭圆C 的方程；(Ⅱ)动直线l ：(0)y kx m m =+≠交椭圆C 于A ，B 两点，交y 轴于点M ．点N 是M 关于O 的对称点，N 的半径为||NO ． 设D 为AB 的中点，DE ，DF 与N 分别相切于点E ，F ，求EDF ∠的最小值．x32．（2017北京）已知椭圆C 的两个顶点分别为(2,0)A -，(2,0)B ，焦点在x 轴上，离心． （Ⅰ）求椭圆C 的方程；（Ⅱ）点D 为x 轴上一点，过D 作x 轴的垂线交椭圆C 于不同的两点M ，N ，过D 作AM 的垂线交BN 于点E ．求证：BDE ∆与BDN ∆的面积之比为4:5．33．（2017江苏）如图，在平面直角坐标系xOy 中，椭圆E ：22221(0)x y a b a b+=>>的左、右焦点分别为1F ，2F ，离心率为12，两准线之间的距离为8．点P 在椭圆E 上，且位于第一象限，过点1F 作直线1PF 的垂线1l ，过点2F 作直线2PF 的垂线2l ． （1）求椭圆E 的标准方程；（2）若直线1l ，2l 的交点Q 在椭圆E 上，求点P 的坐标．34．（2016年北京）已知椭圆C ：22221x y a b+=过(2,0)A ，(0,1)B 两点．（Ⅰ）求椭圆C 的方程及离心率；（Ⅱ）设P 为第三象限内一点且在椭圆C 上，直线PA 与y 轴交于点M ，直线PB 与x轴交于点N ，求证：四边形ABNM 的面积为定值．35．（2016年全国II 卷）已知A 是椭圆E ：22143x y +=的左顶点，斜率为()0k k ＞的直线交E 与A ，M 两点，点N 在E 上，MA NA ⊥. （Ⅰ）当AM AN =时，求AMN ∆的面积； （Ⅱ）当AM AN =时，证明：32k <<.36．（2016年山东）已知椭圆C ：22221(0)x y a b a b+=>>的长轴长为4，焦距为2．（Ⅰ）求椭圆C 的方程；（Ⅱ）过动点M (0，m )(m >0)的直线交x 轴与点N ，交C 于点A ，P (P 在第一象限)，且M 是线段PN 的中点．过点P 作x 轴的垂线交C 于另一点Q ，延长线QM 交C 于点B ．(i)设直线PM 、QM 的斜率分别为k 、k'，证明k k'为定值； (ii)求直线AB 的斜率的最小值．37．（2016年天津）设椭圆13222=+y a x （3>a ）的右焦点为F ，右顶点为A ，已知||3||1||1FA eOA OF =+，其中O 为原点，e 为椭圆的离心率. （Ⅰ）求椭圆的方程；（Ⅱ）设过点A 的直线l 与椭圆交于点B （B 不在x 轴上），垂直于l 的直线与l 交于点M ，与y 轴交于点H ，若HF BF ⊥，且MAO MOA ∠=∠，求直线的l 斜率.38．（2015新课标2）已知椭圆C ：22221(0)x y a b a b+=>>的离心率为2，点在C 上．（Ⅰ）求C 的方程；（Ⅱ）直线l 不过原点O 且不平行于坐标轴，l 与C 有两个交点,A B ，线段AB 的中点为M ．证明：直线OM 的斜率与直线l 的斜率的乘积为定值．39．（2015天津）已知椭圆22221(0)x y a b a b+=>>的上顶点为B ，左焦点为F ，离心率为5． （Ⅰ）求直线BF 的斜率；（Ⅱ）设直线BF 与椭圆交于点P （P 异于点B ），故点B 且垂直于BP 的直线与椭圆交于点Q （Q 异于点B ）直线PQ 与y 轴交于点M ，||=||PM MQ λ． （i ）求λ的值；（ii ）若||sin =9PM BQP ∠，求椭圆的方程．40．（2015陕西）如图，椭圆E ：22221x y a b+=（a >b >0）经过点(0,1)A -，且离心率为22．（Ⅰ）求椭圆E 的方程；（Ⅱ）经过点(1,1)，且斜率为k 的直线与椭圆E 交于不同的两点,P Q （均异于点A ），证明：直线AP 与AQ 的斜率之和为2．41．(2015重庆)如图，椭圆22221x y a b+=（a >b >0）的左、右焦点分别为1F ,2F ，且过2F 的直线交椭圆于,P Q 两点，且PQ ⊥1PF ．（Ⅰ）若122PF =+|，222PF =-|，求椭圆的标准方程； （Ⅱ）若|1PQ PF λ=，且3443λ≤≤，试确定椭圆离心率e 的取值范围．42． (2014新课标1) 已知点A (0,2)-，椭圆E ：22221(0)x y a b a b+=>>3F 是椭圆E 的右焦点，直线AF 23，O 为坐标原点． （Ⅰ)求E 的方程；（Ⅱ）设过点A 的动直线l 与E 相交于,P Q 两点，当OPQ ∆的面积最大时，求l 的方程．43．(2014浙江)如图，设椭圆(),01:2222>>=+b a by a x C 动直线l 与椭圆C 只有一个公共点P ，且点P 在第一象限．（Ⅰ）已知直线l 的斜率为k ，用k b a ,,表示点P 的坐标；（Ⅱ）若过原点O 的直线1l 与l 垂直，证明：点P 到直线1l 的距离的最大值为b a -．44．（2014新课标2）设1F ，2F 分别是椭圆C ：()222210y x a b a b+=>>的左，右焦点，M 是C 上一点且2MF 与x 轴垂直，直线1MF 与C 的另一个交点为N ． （Ⅰ）若直线MN 的斜率为34，求C 的离心率；（Ⅱ）若直线MN 在y 轴上的截距为2，且15MN F N =，求,a b ．45．（2014安徽）设1F ,2F 分别是椭圆E ：22221(0)x y a b a b+=>>的左、右焦点，过点1F的直线交椭圆E 于,A B 两点，11||3||AF BF = （Ⅰ）若2||4,AB ABF =∆的周长为16，求2||AF ； （Ⅱ）若23cos 5AF B ∠=，求椭圆E 的离心率． 46．（2014山东）在平面直角坐标系xOy 中，椭圆2222:1(0)x y C a b ab+=>>，直线y x =被椭圆C ． （Ｉ）求椭圆C 的方程；（Ⅱ）过原点的直线与椭圆C 交于A ，B 两点（A ，B 不是椭圆C 的顶点）．点D 在椭圆C 上，且AD AB ⊥，直线BD 与x 轴、y 轴分别交于M ，N 两点．(ⅰ)设直线BD ，AM 的斜率分别为12,k k ，证明存在常数λ使得12k k λ=，并求出λ的值；(ⅱ)求OMN ∆面积的最大值．47．（2014湖南）如图5，O 为坐标原点，双曲线221112211:1(0,0)x y C a b a b -=>>和椭圆222222222:1(0)x y C a b a b +=>>均过点23(,1)3P ，且以1C 的两个顶点和2C 的两个焦点为顶点的四边形是面积为2的正方形． （Ｉ）求12,C C 的方程；（Ⅱ）是否存在直线l ，使得l 与1C 交于,A B 两点，与2C 只有一个公共点，且||||OA OB AB +=证明你的结论．48．（2014四川）已知椭圆C ：22221x y a b+=（0a b >>）的焦距为4，其短轴的两个端点与长轴的一个端点构成正三角形． （Ⅰ）求椭圆C 的标准方程；（Ⅱ）设F 为椭圆C 的左焦点，T 为直线3x =-上任意一点，过F 作TF 的垂线交椭圆C 于点P ，Q ．（i ）证明：OT 平分线段PQ （其中O 为坐标原点）； （ii ）当||||TF PQ 最小时，求点T 的坐标． 49．（2013安徽）已知椭圆2222:1(0)x y C a b a b+=>>的焦距为4，且过点23)P ，.（Ⅰ）求椭圆C 的方程；（Ⅱ）设0000(,)(0)Q x y x y ≠为椭圆C 上一点，过点Q 作x 轴的垂线，垂足为E ．取点(0,22)A ,连接AE ，过点A 作AE 的垂线交x 轴于点D ．点G 是点D 关于y 轴的对称点，作直线QG ，问这样作出的直线QG 是否与椭圆C 一定有唯一的公共点？并说明理由.50．（2013湖北）如图，已知椭圆1C 与2C 的中心在坐标原点O ，长轴均为MN 且在x 轴上，短轴长分别为2m ，2()n m n >，过原点且不与x 轴重合的直线l 与1C ，2C 的四个交点按纵坐标从大到小依次为A ，B ，C ，D ．记mnλ=，△BDM 和△ABN 的面积分别为1S 和2S ．（Ⅰ）当直线l 与y 轴重合时，若12S S λ=，求λ的值；（Ⅱ）当λ变化时，是否存在与坐标轴不重合的直线l ，使得12S S λ=？并说明理由．51． (2013天津)设椭圆22221(0)x y a b a b+=>>的左焦点为F ， 3， 过点F 且与x43(Ⅰ) 求椭圆的方程；(Ⅱ) 设A ，B 分别为椭圆的左、右顶点， 过点F 且斜率为k 的直线与椭圆交于C ，D两点．若··8AC DB AD CB +=， 求k 的值．52．（2013山东）椭圆2222:1(0)x y C a b a b+=>>的左、右焦点分别是12,F F ，离心率为32，过1F 且垂直于x 轴的直线被椭圆C 截得的线段长为l ． （Ⅰ）求椭圆C 的方程；（Ⅱ）点P 是椭圆C 上除长轴端点外的任一点，连接12,PF PF ．设12F PF ∠的角平分线PM 交C 的长轴于点(),0M m ，求m 的取值范围；（Ⅲ）在（Ⅱ）的条件下，过点P 作斜率为k 的直线l ，使得l 与椭圆C 有且只有一个公共点．设直线12,PF PF 的斜率分别为12,k k ，若0k ≠，试证明1211kk kk +为定值，并求出这个定值．53．（2012北京）已知椭圆C :22221(0)x y a b a b+=>>的一个顶点为(2,0)A ，离心率为2.直线(1y k x =-）与椭圆C 交于不同的两点M ,N . （Ⅰ）求椭圆C 的方程； （Ⅱ）当△AMNk 的值. 54．（2013安徽）如图，21,F F 分别是椭圆C ：22a x +22by =1（0>>b a ）的左、右焦点，A是椭圆C 的顶点，B 是直线2AF 与椭圆C 的另一个交点，1F ∠A 2F =60°．（Ⅰ）求椭圆C 的离心率；（Ⅱ）已知△A B F 1的面积为403，求a , b 的值．55．（2012广东）在平面直角坐标系xOy 中，已知椭圆C ：22221(0)x y a b a b+=>>的离心率e =C 上的点到(0,2)Q 的距离的最大值为3． （Ⅰ）求椭圆C 的方程；（Ⅱ）在椭圆C 上，是否存在点(,)M m n 使得直线l ：1mx ny +=与圆O ：221x y +=相交于不同的两点,A B ，且OAB ∆的面积最大？若存在，求出点M 的坐标及相对应的OAB ∆的面积；若不存在，请说明理由．56．（2011陕西）设椭圆C : ()222210x y a b a b +=>>过点(0，4)，离心率为35．（Ⅰ）求C 的方程； （Ⅱ）求过点(3，0)且斜率为45的直线被C 所截线段的中点坐标． 57．（2011山东）在平面直角坐标系xOy 中，已知椭圆22:13x C y +=．如图所示，斜率为(0)k k ＞且不过原点的直线l 交椭圆C 于A ，B 两点，线段AB 的中点为E ，射线OE交椭圆C 于点G ，交直线3x =-于点(3,)D m -． （Ⅰ）求22m k +的最小值； （Ⅱ）若2OG OD =∙OE ，（i ）求证：直线l 过定点；（ii ）试问点B ，G 能否关于x 轴对称？若能，求出此时ABG 的外接圆方程；若不能，请说明理由．58．（2010新课标）设1F ,2F 分别是椭圆E ：2x +22y b=1（0﹤b ﹤1）的左、右焦点，过1F的直线l 与E 相交于A 、B 两点，且2AF ，AB ，2BF 成等差数列． （Ⅰ）求AB ；（Ⅱ）若直线l 的斜率为1，求b 的值．59．（2010辽宁）设椭圆C ：22221(0)x y a b a b+=>>的左焦点为F ，过点F 的直线与椭圆C相交于A ，B 两点，直线l 的倾斜角为60o ，2AF FB ． （Ⅰ）求椭圆C 的离心率； （Ⅱ）如果||AB =154，求椭圆C 的方程．。

专题9.4 双曲线1．（2021·江苏高考真题）已知双曲线()222210,0x y a b a b-=>>的一条渐近线与直线230x y -+=平行，则该双曲线的离心率是（ ）ABC ．2D【答案】D 【分析】写出渐近线，再利用斜率相等，进而得到离心率【详解】双曲线的渐近线为b y x a =±，易知by x a=与直线230x y -+=平行，所以=2b e a ⇒==故选：D.2．（2021·北京高考真题）若双曲线2222:1x y C a b-=离心率为2，过点，则该双曲线的程为（）A ．2221x y -=B ．2213y x -=C ．22531x y -=D ．22126x y -=【答案】B 【分析】分析可得b =，再将点代入双曲线的方程，求出a 的值，即可得出双曲线的标准方程.【详解】2c e a == ，则2c a =，b =，则双曲线的方程为222213x y a a-=，将点的坐标代入双曲线的方程可得22223113a a a-==，解得1a =，故b ，因此，双曲线的方程为2213y x -=.故选：B3．（2021·山东高考真题）已知1F 是双曲线22221x y a b-=（0a >，0b >）的左焦点，点P 在双曲线上，直线1PF 与x 轴垂直，且1PF a =，那么双曲线的离心率是（）练基础A B C ．2D ．3【答案】A 【分析】易得1F 的坐标为(),0c -，设P 点坐标为()0,c y -，求得20by a=，由1PF a =可得a b =，然后由a ，b ，c 的关系求得222c a =，最后求得离心率即可.【详解】1F 的坐标为(),0c -，设P 点坐标为()0,c y -，易得()22221c y a b--=，解得20b y a =，因为直线1PF 与x 轴垂直，且1PF a =，所以可得2b a a=，则22a b =，即a b =，所以22222c a b a =+=，离心率为e =故选：A .4．（2021·天津高考真题）已知双曲线22221(0,0)x y a b a b-=>>的右焦点与抛物线22(0)y px p =>的焦点重合，抛物线的准线交双曲线于A ，B 两点，交双曲线的渐近线于C 、D |AB ．则双曲线的离心率为（ ）A B C ．2D ．3【答案】A 【分析】设公共焦点为(),0c ，进而可得准线为x c =-，代入双曲线及渐近线方程，结合线段长度比值可得2212a c =，再由双曲线离心率公式即可得解.【详解】设双曲线22221(0,0)x y a b a b-=>>与抛物线22(0)y px p =>的公共焦点为(),0c ，则抛物线22(0)y px p =>的准线为x c =-，令x c =-，则22221c y a b -=，解得2b y a =±，所以22bAB a=,又因为双曲线的渐近线方程为b y x a =±，所以2bcCD a=，所以2bc a =c =，所以222212a c b c =-=，所以双曲线的离心率ce a==故选：A.5．（2019·北京高考真题（文））已知双曲线2221x y a-=（a ＞0）a =（ ）AB ．4C ．2D ．12【答案】D 【解析】∵双曲线的离心率ce a==，c = ，=，解得12a = ，故选D.6．（全国高考真题（文））双曲线2222:1(0,0)x y C a b a b -=>>的离心率为2，焦点到渐近线的，则C 的焦距等于（ ）．A.2B. C.4D.【答案】C 【解析】设双曲线的焦距为2c ，双曲线的渐进线方程为，由条件可知，，又，解得，故答案选C ．7.（2017·天津高考真题（文））已知双曲线的左焦点为，点在双曲线的渐近线上，是边长为2的等边三角形（为原点），则双曲线的方程为（ ）A. B. C. D.【答案】D 【解析】22221(0,0)x y a b a b -=>>F A OAF △O 221412x y -=221124x y -=2213x y -=2213y x -=由题意结合双曲线的渐近线方程可得：，解得：，双曲线方程为：.本题选择D选项.8．（2021·全国高考真题（理））已知双曲线22:1(0)xC y mm-=>的一条渐近线为my+=，则C的焦距为_________．【答案】4【分析】将渐近线方程化成斜截式，得出,a b的关系，再结合双曲线中22,a b对应关系，联立求解m，再由关系式求得c，即可求解.【详解】my+=化简得y=，即ba，同时平方得2223ba m=，又双曲线中22,1a m b==，故231m m=，解得3,0m m==（舍去），2223142c a b c=+=+=⇒=，故焦距24c=.故答案为：4.9．（2019·江苏高考真题）在平面直角坐标系xOy中，若双曲线2221(0)yx bb-=>经过点（3，4)，则该双曲线的渐近线方程是_____.【答案】y=.【解析】由已知得222431b-=，解得b=或b=，因为0b>，所以b=.因为1a=，所以双曲线的渐近线方程为y=.10.（2020·全国高考真题（文））设双曲线C：22221x ya b-= (a>0，b>0)的一条渐近线为y= 2222tan60cc a bba⎧⎪=⎪=+⎨⎪⎪==⎩221,3a b==2213yx-=x ，则C 的离心率为_________．【解析】由双曲线方程22221x y a b-=可得其焦点在x 轴上，因为其一条渐近线为y =，所以b a =c e a ===1.（2018·全国高考真题（理））设,是双曲线（）的左、右焦点，是坐标原点．过作的一条渐近线的垂线，垂足为．若则的离心率为( )ABC ．D【答案】B 【解析】由题可知在中，在中,故选B.2．（2020·云南文山·高三其他（理））已知双曲线2221(0)x y a a-=>上关于原点对称的两个点P ，Q ，右顶点为A ，线段AP 的中点为E ，直线QE 交x 轴于(1,0)M ，则双曲线的离心1F 2F 2222:1x y C a b-=O 2F C P 1PF =C222,PF b OF c==PO a∴=2Rt POF V 222cos P O PF b F OF c∠==12PF F △22221212212cos P O 2PF F F PF b F PF F F c+-∠==223bc a c=⇒=e ∴=练提升率为（ ）A B ．C D 【答案】D 【解析】由已知得M 为APQ V 的重心，∴3||3a OM ==，又1b =，∴c ==，即c e a ==.故选:D.3．（2020·广东天河·华南师大附中高三月考（文））已知平行于x 轴的直线l 与双曲线C ：()222210,0x y a b a b-=>>的两条渐近线分别交于P 、Q 两点，O 为坐标原点，若OPQ △为等边三角形，则双曲线C 的离心率为（ ）A ．2B ．C D 【答案】A 【解析】因为OPQ △为等边三角形，所以渐近线的倾斜角为3π，所以22,3,bb b a a=∴=∴=所以2222223,4,4,2c a a c a e e -=∴=∴=∴=.故选：A4．（2021·广东广州市·高三月考）已知1F ，2F 分别是双曲线C ：2213xy -=的左、右焦点，点P 是其一条渐近线上一点，且以线段12F F 为直径的圆经过点P ，则点P 的横坐标为（ ）A ．±1B ．C ．D ．2±【答案】C 【分析】由题意可设00(,)P x ，根据圆的性质有120F P F P ⋅= ，利用向量垂直的坐标表示，列方程求0x 即可.【详解】由题设，渐近线为y =，可令00(,)P x x ，而1(2,0)F -，2(2,0)F ，∴100(2,)F P x x =+ ，200(2,)F P x =- ，又220120403x F P F P x ⋅=-+= ，∴0x =故选：C5.（2020·广西南宁三中其他（理））圆22:10160+-+=C x y y 上有且仅有两点到双曲线22221(0,0)x y a b a b -=>>的一条渐近线的距离为1，则该双曲线离心率的取值范围是（ ）A ．B ．55(,)32C ．55(,42D ．1)【答案】C 【解析】双曲线22221x y a b-=的一条渐近线为0bx ay -=，圆22:10160C x y y +-+=，圆心()0,5，半径3因为圆C 上有且仅有两点到0bx ay -=的距离为1，所以圆心()0,5到0bx ay -=的距离d 的范围为24d <<即24<<，而222+=a b c 所以524a c <<，即5542e <<故选C 项.6．【多选题】（2021·湖南高三）已知双曲线2222:1x y C a b-=（0a >，0b >）的左，右焦点为1F ，2F ，右顶点为A ，则下列结论中，正确的有（ ）A ．若a b =，则CB ．若以1F 为圆心，b 为半径作圆1F ，则圆1F 与C 的渐近线相切C ．若P 为C 上不与顶点重合的一点，则12PF F △的内切圆圆心的横坐标x a =D ．若M 为直线2a x c=（c =0的一点，则当M 的纵坐标为2MAF V 外接圆的面积最小【答案】ABD 【分析】由a b =，得到222a c =，利用离心率的定义，可判定A 正确；由双曲线的几何性质和点到直线的距离公式，可判定B 正确；由双曲线的定义和内心的性质，可判定C 不正确；由正弦定理得到2MAF V 外接圆的半径为222sin AF R AMF =∠，得出2sin AMF ∠最大时，R 最小，只需2tan AMF ∠最大，设2,a M t c ⎛⎫⎪⎝⎭，得到22tan tan()AMF NMF NMA ∠=∠-∠，结合基本不等式，可判定D 正确．【详解】对于A 中，因为a b =，所以222a c =，故C 的离心率ce a==A 正确；对于B 中，因为()1,0F c -到渐近线0bx ay -=的距离为d b ==，所以B 正确；对于C 中，设内切圆与12PF F △的边1221,,FF F P FP 分别切于点1,,A B C ，设切点1A (,0)x ，当点P 在双曲线的右支上时，可得121212PF PF PC CF PB BF CF BF -=+--=-1112A F A F =-()()22c x c x x a =+--==，解得x a =，当点P 在双曲线的左支上时，可得x a =-，所以12PF F △的内切圆圆心的横坐标x a =±，所以C 不正确；对于D 中，由正弦定理，可知2MAF V 外接圆的半径为222sin AF R AMF =∠，所以当2sin AMF ∠最大时，R 最小，因为2a a c<，所以2AMF ∠为锐角，故2sin AMF ∠最大，只需2tan AMF ∠最大．由对称性，不妨设2,a M t c ⎛⎫ ⎪⎝⎭（0t >），设直线2a x c =与x 轴的交点为N ，在直角2NMF △中，可得222=tan a c NF c NM t NMF -∠=，在直角NMA △中，可得2=tan a a NA c NM tMA N -∠=，又由22222222tan tan tan tan()1tan tan 1NMF NMA AMF NMF NMA NMF NMAa a c a c ct t a a c a c c t t--∠-∠∠=∠-∠==+∠∠--⨯+-⋅22()c a ab c a t c t-=≤-+当且仅当()22ab c a t c t -=，即t =2tan AMF ∠取最大值，由双曲线的对称性可知，当t =2tan AMF ∠也取得最大值，所以D 正确．故选：ABD ．7．【多选题】（2021·重庆巴蜀中学高三月考）已知点Q 是圆M ：()2224x y ++=上一动点，点()2,0N ，若线段NQ 的垂直平分线交直线MQ 于点P ，则下列结论正确的是（ ）A ．点P 的轨迹是椭圆B ．点P 的轨迹是双曲线C ．当点P 满足PM PN ⊥时，PMN V 的面积3PMN S =△D ．当点P 满足PM MN ⊥时，PMN V 的面积6PMN S =V 【答案】BCD 【分析】根据PM PN -的结果先判断出点P 的轨迹是双曲线，由此判断AB 选项；然后根据双曲线的定义以及垂直对应的勾股定理分别求解出PM PN ⋅的值，即可求解出PMN S △，据此可判断CD 选项.【详解】依题意，2MQ =，4MN =，因线段NQ 的垂直平分线交直线MQ 于点P ，于是得PQ PN =，当点P 在线段MQ 的延长线上时，2PM PN PM PQ MQ -=-==，当点P 在线段QM 的延长线上时，2PN PM PQ PM MQ -=-==，从而得24PM PN MN -=<=，由双曲线的定义知，点M 的轨迹是双曲线，故A 错，B 对；选项C ，点P 的轨迹方程为2213y x -=，当PM PN ⊥时，2222616PM PN PM PN PM PN MN ⎧-=⎪⇒⋅=⎨+==⎪⎩，所以132PMN S PM PN ==△，故C 对；选项D ，当PM MN ⊥时，2222316PM PN PM PN PM MN ⎧-=-⎪⇒=⎨-==⎪⎩，所以162PMN S PM MN ==△，故D 对，故选：BCD.8．（2021·全国高二课时练习）双曲线()22122:10,0x y C a b a b-=>>的焦距为4，且其渐近线与圆()222:21C x y -+=相切，则双曲线1C 的标准方程为______．【答案】2213x y -=【分析】根据焦距，可求得c 值，根据渐近线与圆2C 相切，可得圆心到直线的距离等于半径1，根据a ，b ，c 的关系，即可求得a ，b 值，即可得答案.【详解】因为双曲线()22122:10,0x y C a b a b-=>>的焦距为4，所以2c =．由双曲线1C 的两条渐近线b y x a=±与圆()222:21C x y -+=相切，可得1=又224a b +=，所以1b =，a =所以双曲线1C 的标准方程为2213x y -=．故答案为：2213x y -=9．（2021·全国高二单元测试）已知双曲线2213y x -=的左、右焦点分别为1F ，2F ，离心率为e ，若双曲线上一点P 使2160PF F ∠=︒，则221F P F F ⋅的值为______．【答案】3【分析】在12PF F △中，设2PF x =，则12PF x =+或12PF x =-．分别运用余弦定理可求得答案.【详解】解：由已知得2124F F c ==．在12PF F △中，设2PF x =，则12PF x =+或12PF x =-．当12PF x =+时，由余弦定理，得()222124242x x x +=+-⨯⨯，解得32x =，所以221314322F P F F ⋅=⨯⨯= ．当12PF x =-时，由余弦定理，得()222124242x x x -=+-⨯⨯，无解．故2213F P F F ⋅=．故答案为：3.10．（2021·全国高二课时练习）如图，以AB 为直径的圆有一内接梯形ABCD ，且//AB CD ．若双曲线1C 以A ，B 为焦点，且过C ，D 两点，则当梯形的周长最大时，双曲线1C 的离心率为______．1【分析】连接AC ，设BAC θ∠=，将梯形的周长表示成关于θ的函数，求出当30θ=︒时，l 有最大值，即可得到答案；【详解】连接AC ，设BAC θ∠=，2AB R c R ==，，作CE AB ⊥于点E ，则||2sin BC R θ=，()2||||cos 902sin EB BC R θθ=︒-=，所以2||24sin CD R R θ=-，梯形的周长221||2||||24sin 24sin 4sin 52l AB BC CD R R R R R R θθθ⎛⎫=++=++-=--+ ⎪⎝⎭．当1sin 2θ=，即30θ=︒时，l 有最大值5R ，这时，||BC R =，||AC =，1(||||)2a AC BC =-=，1=c e a ．1+1. （2021·全国高考真题（理））已知12,F F 是双曲线C 的两个焦点，P 为C 上一点，且121260,3F PF PF PF ∠=︒=，则C 的离心率为（ ）ABCD【答案】A 【分析】根据双曲线的定义及条件，表示出12,PF PF ，结合余弦定理可得答案.【详解】因为213PF PF =，由双曲线的定义可得12222PF PF PF a -==，所以2PF a =，13PF a =；因为1260F PF ∠=︒,由余弦定理可得2224923cos 60c a a a a =+-⨯⋅⋅︒，整理可得2247c a =，所以22274a c e ==，即e =故选：A2．（2020·浙江省高考真题）已知点O （0，0），A （–2，0），B （2，0）．设点P 满足|PA |–|PB |=2，且P 为函数y=|OP |=（ ）ABCD【答案】D 【解析】因为||||24PA PB -=<，所以点P 在以,A B 为焦点，实轴长为2，焦距为4的双曲线的右支上，由2,1c a ==可得，222413b c a=-=-=，即双曲线的右支方程为()22103y x x -=>，而点P还在函数y =练真题由()22103y x x y ⎧⎪⎨->==⎪⎩，解得x y ⎧=⎪⎪⎨⎪=⎪⎩，即OP ==．故选：D.3.（2019·全国高考真题（理））设F 为双曲线C ：22221x y a b-=（a >0，b >0）的右焦点，O为坐标原点，以OF 为直径的圆与圆x 2+y 2=a 2交于P 、Q 两点．若|PQ |=|OF |，则C 的离心率为（ ）ABC ．2D【答案】A 【解析】设PQ 与x 轴交于点A ，由对称性可知PQ x ⊥轴，又||PQ OF c == ，||,2cPA PA ∴=∴为以OF 为直径的圆的半径，A ∴为圆心||2c OA =．,22c c P ⎛⎫∴ ⎪⎝⎭，又P 点在圆222x y a +=上，22244c c a ∴+=，即22222,22c c a e a=∴==．e ∴=，故选A ．4.（2019·全国高考真题（理））双曲线C ：2242x y -=1的右焦点为F ，点P 在C的一条渐近线上，O 为坐标原点，若=PO PF ，则△PFO 的面积为（ ）A B C ．D ．【答案】A 【解析】由2,,,a b c ====．,P PO PF x =∴=，又P 在C 的一条渐近线上，不妨设为在y x =上，1122PFO P S OF y ∴=⋅==△，故选A ．5. （2021·全国高考真题（文））双曲线22145x y -=的右焦点到直线280x y +-=的距离为________．【分析】先求出右焦点坐标，再利用点到直线的距离公式求解.【详解】由已知，3c ===，所以双曲线的右焦点为(3,0)，所以右焦点(3,0)到直线280x y +-===.6．（2019·全国高考真题（理））已知双曲线C ：22221(0,0)x y a b a b-=>>的左、右焦点分别为F 1，F 2，过F 1的直线与C 的两条渐近线分别交于A ，B 两点．若1F A AB = ，120F B F B ⋅=，则C 的离心率为____________．【答案】2.【解析】如图，由1,F A AB =得1.F A AB =又12,OF OF =得OA 是三角形12F F B 的中位线，即22//,2.BF OA BF OA =由120F B F B =g ，得121,,F B F B OA F A ⊥⊥则1OB OF =有1AOB AOF ∠=∠，又OA 与OB 都是渐近线，得21,BOF AOF ∠=∠又21BOF AOB AOF π∠+∠+∠=，得02160,BOF AOF BOA ∠=∠=∠=．又渐近线OB 的斜率为0tan 60ba==，所以该双曲线的离心率为2c e a ====．。

2019年高考数学试题分类汇编解析几何一、选择题.1、（2019年高考全国I 卷理科10）双曲线C ：22221(0,0)x y a b a b-=>>的一条渐近线的倾斜角为130°，则C 的离心率为 A ．2sin40° B ．2cos40°C ．1sin50︒D ．1cos50︒答案：C解析：由题可知,130tan ︒=-a b 即,50tan ︒=a b 则有︒︒=50cos 50sin 2222a b ，即︒︒=-50cos 50sin 22222a a c 所以︒︒=-50cos 50sin 1222e ，︒=50cos 12e ，故选D 2、（2019年高考全国I 卷理科10，文科12）已知椭圆C 的焦点为12(1,0),(1,0)F F -，过F 2的直线与C交于A ，B 两点.若22||2||AF F B =，1||||AB BF =，则C 的方程为A ．2212x y +=B ．22132x y +=C ．22143x y +=D ．22154x y +=答案：B解析：设x B F =||2，则x B F B F AF AB B F 3||3||||||||2221==+== 由椭圆定义得x a B F B F 42||||21==+，故,23||,2||12aB F a B F ==a AF a AF a AF =-==||2||,||212在21F AF ∆和21F BF ∆中，由余弦定理得a c a a c a F AF 1224cos 22221=⨯⨯-+=∠ a a c a a c a F BF 2222212221249441cos -=⨯⨯-+=∠ 21F AF ∠、21F BF ∠互补得a a a 122=-，解得32=a ，22=b ，方程为12322=+y x 。

故选B 3、（2019年高考全国II 卷理科8，文科9）若抛物线y 2=2px (p >0)的焦点是椭圆2231x y pp+=的一个焦点，则p=A ．2B ．3C ．4D ．8 答案：D解析：易知抛物线的焦点为)0,2(p,故椭圆焦点在x 轴上 由p p p b a c 23222=-=-=,则p p 2)2(2=,解得p=8。

高考数学总复习 椭圆、双曲线、抛物线单元测试题一.选择题(1) 抛物线24x y =上一点A 的纵坐标为4，则点A 与抛物线焦点的距离为 ( )A 2B 3C 4D 5 (2) 若焦点在x轴上的椭圆2212x y m +=的离心率为12，则m=( )Ａ Ｂ32 Ｃ83Ｄ23(3) 若方程x 2+ky 2=2表示焦点在y 轴上的椭圆, 那么实数k 的取值范围是 ( )A (0, +∞)B (0, 2)C (1, +∞)D (0, 1)(4) 设P 是双曲线19222=-y ax 上一点，双曲线的一条渐近线方程为023=-y x ,F 1、F 2分别是双曲线的左、右焦点，若3||1=PF ，则=||2PF( )A 1或 5B 6C 7D 9(5) 对于抛物线y 2=2x 上任意一点Q, 点P(a, 0)都满足|PQ|≥|a |, 则a 的取值范围是( )A [0, 1]B (0, 1)C (]1，∞- D (-∞, 0)(6) 若椭圆)0(12222〉〉=+b a by a x 的左、右焦点分别为F 1、F 2，线段F 1F 2被抛物线y 2=2bx 的焦点分成5：3两段，则此椭圆的离心率为( )A1716B 17174C 54D 552(7) 已知双曲线)0(1222>=-a y ax 的一条准线与抛物线x y 62-=的准线重合，则该双曲线的离心率为 ( )A23 B23C 26D 332(8) 设A(x 1,y 1),B(x 2,y 2)是抛物线y 2=2px(p>0)上的两点,并且满足OA ⊥OB. 则y 1y 2等于( )A – 4p 2B 4p 2C – 2p 2D 2p 2(9) 已知双曲线1222=-y x 的焦点为F 1、F 2，点M 在双曲线上且120,MF MF ⋅=则点M 到x 轴的距离为( )A43B53C 3 (10) 设椭圆的两个焦点分别为F 1、、F 2，过F 2作椭圆长轴的垂线交椭圆于点P ， 若△F 1PF 2为等腰直角三角形，则椭圆的离心率是( )A2B C 2 1 二.填空题(11) 若双曲线的渐近线方程为x y 3±=，它的一个焦点是()0,10，则双曲线的方程是__________.(12)设中心在原点的椭圆与双曲线2 x 2-2y 2=1有公共的焦点,且它们的离心率互为倒数,则该椭圆的方程是 .(13) 过双曲线22221x y a b-=(a ＞0，b ＞0)的左焦点且垂直于x 轴的直线与双曲线相交于M 、N两点，以MN 为直径的圆恰好过双曲线的右顶点，则双曲线的离心率等于_________．(14) 以下同个关于圆锥曲线的命题中 ①设A 、B 为两个定点，k 为非零常数，k PB PA =-||||，则动点P 的轨迹为双曲线；②过定圆C 上一定点A 作圆的动弦AB ，O 为坐标原点，若),(21OB OA OP +=则动点P 的轨迹为椭圆； ③方程02522=+-x x 的两根可分别作为椭圆和双曲线的离心率；④双曲线13519252222=+=-y x y x 与椭圆有相同的焦点.其中真命题的序号为 （写出所有真命题的序号） 三.解答题(15)点A 、B 分别是椭圆1203622=+y x 长轴的左、右端点，点F 是椭圆的右焦点，点P 在椭圆上，且位于x 轴上方，PF PA ⊥.求点P 的坐标； .(16) 已知抛物线C: y=-21x 2+6, 点P （2, 4）、A 、B 在抛物线上, 且直线PA 、PB 的倾斜角互补. (Ⅰ)证明:直线AB 的斜率为定值;(Ⅱ)当直线AB 在y 轴上的截距为正数时, 求△PAB 面积的最大值及此时直线AB 的方程.(17) 双曲线12222=-by a x (a>1,b>0)的焦距为2c,直线l 过点(a,0)和(0,b),且点(1,0)到直线l 的距离与点(-1,0)到直线l 的距离之和s ≥54c.求双曲线的离心率e 的取值范围(18) 已知抛物线)0(22>=p px y 的焦点为F ，A 是抛物线上横坐标为4、且位于x 轴上方的点，A 到抛物线准线的距离等于5.过A 作AB 垂直于y 轴，垂足为B ，OB 的中点为M.（1）求抛物线方程；（2）过M 作FA MN ⊥，垂足为N ，求点N 的坐标；（3）以M 为圆心，MB 为半径作圆M ，当)0,(m K 是x 轴上一动点时，讨论直线AK 与圆M 的位置关系.参考答案一选择题:1.D[解析]：点A 与抛物线焦点的距离就是点A 与抛物线准线的距离，即5)1(4=-- 2.B[解析]：∵焦点在x 轴上的椭圆2212x y m +=的离心率为12，∴2122=-m 则m=233.D[解析]： ∵方程x 2+ky 2=2，即12222=+ky x 表示焦点在y 轴上的椭圆 ∴22>k故10<<k 4.C[解析]：双曲线19222=-y ax 的一条渐近线方程为023=-y x ，故2=a 又P 是双曲线上一点，故4||||||21=-PF PF ，而3||1=PF ，则=||2PF 75.C[解析]：对于抛物线y 2=2x 上任意一点Q, 点P(a, 0)都满足|PQ|≥|a |,若,0≤a 显然适合若0>a ，点P(a, 0)都满足|PQ|≥|a |就是2222)2(y y a a +-≤ 即1142≤+≤y a ，此时10≤<a 则a 的取值范围是(]1，∞- 6.D[解析]：3522=-+b c bc ，5245222==∴=∴=a c e a c b c 7.D[解析]：双曲线)0(1222>=-a y a x 的准线为122+±=a a x抛物线x y 62-=的准线为23=x 因为两准线重合，故122+a a =23，2a =3，则该双曲线的离心率为328.A[解析]：∵A(x 1,y 1),B(x 2,y 2)是抛物线y 2=2px(p>0)上的两点,并且满足OA ⊥OB.∴04)(0,12122212121=+∴=+∴-=⋅y y py y y y x x k k OBOA 则y 1y 2 = – 4p 29.C[解析]：∵120,MF MF ⋅=∴点M 在以F 1F 2为直径的圆322=+y x 上故由32||1232222=⎪⎩⎪⎨⎧=-=+y y x y x 得 则点M 到x 轴的距离为332 10.D[解析]：不妨设点P 在 x 轴上方，坐标为),(2ab c ,∵△F 1PF 2为等腰直角三角形∴|PF 2|=|F 1F 2|，即c a b 22=，即e e a c ac a 2122222=-∴=- 故椭圆的离心率e1二填空题:11. 1922=-y x [解析]： 因为双曲线的渐近线方程为x y 3±=，则设双曲线的方程是λ=-922y x ，又它的一个焦点是()0,10 故1109=∴=+λλλ12. 1222=+y x [解析]：双曲线2 x 2-2y 2=1的焦点为（)0,1±，离心率为2故椭圆的焦点为（)0,1±，离心率为22, 则1,2,1===b a c ，因此该椭圆的方程是1222=+y x 13. 2[解析]：设双曲线22221x y a b-=(a ＞0，b ＞0)的左焦点F 1，右顶点为A ，因为以MN 为直径的圆恰好过双曲线的右顶点， 故|F 1M|=|F 1A|，∴c a ab +=2∴2112=∴+=-e e e 14. ③④[解析]：根据双曲线的定义必须有||||AB k ≤，动点P 的轨迹才为双曲线，故①错 ∵),(21OB OA OP +=∴P 为弦AB 的中点，故090=∠APC 则动点P 的轨迹为以线段AC 为直径的圆。

专题九 解析几何第二十五讲 椭圆2019年1.（2019全国1文12）已知椭圆C 的焦点为12(1,0),(1,0)F F -，过F 2的直线与C 交于A ，B 两点.若22||2||AF F B =，1||||AB BF =，则C 的方程为A ．2212x y +=B ．22132x y +=C ．22143x y +=D ．22154x y +=2.（2019全国II 文9）若抛物线y 2=2px （p >0）的焦点是椭圆2213x y p p+=的一个焦点，则p = A ．2 B ．3C ．4D ．83.（2019北京文19）已知椭圆2222:1x y C a b+=的右焦点为(1,0)，且经过点(0,1)A ．（Ⅰ）求椭圆C 的方程；（Ⅱ）设O 为原点，直线:(1)l y kx t t =+≠±与椭圆C 交于两个不同点P ，Q ，直线AP 与x 轴交于点M ，直线AQ 与x 轴交于点N ，若|OM |·|ON |=2，求证：直线l 经过定点．4.（2019江苏16）如图，在平面直角坐标系xOy 中，椭圆C :22221(0)x y a b a b+=>>的焦点为F 1（–1、0），F 2（1，0）．过F 2作x 轴的垂线l ，在x 轴的上方，l 与圆F 2:222(1)4x y a-+=交于点A ，与椭圆C 交于点D .连结AF 1并延长交圆F 2于点B ，连结BF 2交椭圆C 于点E ，连结DF 1．已知DF 1=52． （1）求椭圆C 的标准方程； （2）求点E 的坐标．5.（2019浙江15）已知椭圆22195x y +=的左焦点为F ，点P 在椭圆上且在x 轴的上方，若线段PF 的中点在以原点O 为圆心，OF 为半径的圆上，则直线PF 的斜率是_______.6.（2019全国II 文20）已知12,F F 是椭圆2222:1(0)x y C a b a b+=>>的两个焦点，P 为C 上一点，O 为坐标原点．（1）若2POF △为等边三角形，求C 的离心率；（2）如果存在点P ，使得12PF PF ⊥，且12F PF △的面积等于16，求b 的值和a 的取值范围.7.（2019天津文19）设椭圆22221(0)x y a b a b+=>>的左焦点为F ，左顶点为A ，顶点为B .|2||OA OB =（O 为原点）.（Ⅰ）求椭圆的离心率； （Ⅱ）设经过点F 且斜率为34的直线l 与椭圆在x 轴上方的交点为P ，圆C 同时与x 轴和直线l 相切，圆心C 在直线4x =上，且OC AP ∥，求椭圆的方程.8.(2019全国III 文15）设12F F ，为椭圆C :22+13620x y =的两个焦点，M 为C 上一点且在第一象限.若12MF F △为等腰三角形，则M 的坐标为___________.9.（2019北京文19）已知椭圆2222:1x y C a b+=的右焦点为(1,0)，且经过点(0,1)A ．（Ⅰ）求椭圆C 的方程；（Ⅱ）设O 为原点，直线:(1)l y kx t t =+≠±与椭圆C 交于两个不同点P ，Q ，直线AP 与x 轴交于点M ，直线AQ 与x 轴交于点N ，若|OM |·|ON |=2，求证：直线l 经过定点．2010-2019年一、选择题1．(2018全国卷Ⅰ)已知椭圆C ：22214x y a +=的一个焦点为(20)，，则C 的离心率为A ．13B ．12CD 2．(2018全国卷Ⅱ)已知1F ，2F 是椭圆C 的两个焦点，P 是C 上的一点，若12PF PF ⊥，且2160PF F ∠=︒，则C 的离心率为A ．1B ．2CD 13．(2018上海)设P 是椭圆22153x y +=上的动点，则P 到该椭圆的两个焦点的距离之和为A ．B ．C ．D ．4．（2017浙江）椭圆22194x y +=的离心率是A ．3 B ．3 C ．23 D ．595．（2017新课标Ⅲ）已知椭圆C ：22221(0)x y a b a b+=>>的左、右顶点分别为1A ，2A ，且以线段12A A 为直径的圆与直线20bx ay ab -+=相切，则C 的离心率为A B C ．3 D ．136．（2017新课标Ⅰ）设A 、B 是椭圆C ：2213x y m+=长轴的两个端点，若C 上存在点M 满足AMB ∠ =120°，则m 的取值范围是A ．(0,1][9,)+∞B ．[9,)+∞C ．(0,1][4,)+∞D ．[4,)+∞7．（2016年全国I 卷）直线l 经过椭圆的一个顶点和一个焦点，若椭圆中心到l 的距离为其短轴长的14，则该椭圆的离心率为 A ．13 B ．12 C ．23 D ．348．（2016年全国III 卷）已知O 为坐标原点，F 是椭圆C ：22221(0)x y a b a b+=>>的左焦点，A ，B 分别为C 的左，右顶点.P 为C 上一点，且PF x ⊥轴.过点A 的直线l 与线段PF 交于点M ，与y 轴交于点E .若直线BM 经过OE 的中点，则C 的离心率为A ．13B ．12C ．23D ．349．（2015新课标1）已知椭圆E 的中心为坐标原点，离心率为12，E 的右焦点与抛物线C ：28y x =的焦点重合，A B 、是C 的准线与E 的两个交点，则AB =A ．3B ．6C ．9D ．1210．（2015广东）已知椭圆222125x y m+=（0m >）的左焦点为()14,0F -，则m = A ．2 B ．3 C ．4 D ．911．（2015福建）已知椭圆2222:1(0)x y E a b a b+=>>的右焦点为F ．短轴的一个端点为M ，直线:340l x y -=交椭圆E 于,A B 两点．若4A F B F +=，点M 到直线l 的距离不小于45，则椭圆E 的离心率的取值范围是A ．B ．3(0,]4C ．D ．3[,1)412．(2014福建)设Q P ,分别为()2622=-+y x 和椭圆11022=+y x 上的点，则Q P ,两点间的最大距离是A ．25B ．246+C ．27+D ．2613．（2013新课标1）已知椭圆22221(0)x y a b a b+=>>的右焦点为F (3,0)，过点F 的直线交椭圆于A 、B 两点．若AB 的中点坐标为(1，－1)，则E 的方程为 A ．x 245＋y 236＝1B ．x 236＋y 227＝1C ．x 227＋y 218＝1D ．x 218＋y 29＝114．（2013广东）已知中心在原点的椭圆C 的右焦点为(1,0)F ，离心率等于21，则C 的方程是A ．14322=+y x B ．13422=+y x C ．12422=+y x D ．13422=+y x 15．(2012新课标)设1F 、2F 是椭圆E ：)0(12222>>=+b a by a x 的左、右焦点，P 为直线23a x =上一点，12PF F ∆ 是底角为o30的等腰三角形，则E 的离心率为 A 、21 B 、32 C 、43 D 、54二、填空题16．(2018浙江)已知点(0,1)P ，椭圆224x y m +=(1m >)上两点A ，B 满足2AP PB =，则当m =___时，点B 横坐标的绝对值最大．17．（2015浙江）椭圆22221x y a b +=（0a b >>）的右焦点(),0F c 关于直线by x c=的对称点Q 在椭圆上，则椭圆的离心率是 ．18．（2014江西）过点(1,1)M 作斜率为12-的直线与椭圆C ：22221(0)x y a b a b +=>>相交于,A B 两点，若M 是线段AB 的中点，则椭圆C 的离心率等于 ．19．（2014辽宁）已知椭圆C ：22194x y +=，点M 与C 的焦点不重合，若M 关于C 的焦点的对称点分别为A ，B ，线段MN 的中点在C 上，则||||AN BN += ．20．（2014江西）设椭圆()01:2222>>=+b a by a x C 的左右焦点为21F F ，，作2F 作x 轴的垂线与C 交于B A ，两点，B F 1与y 轴相交于点D ，若B F AD 1⊥，则椭圆C 的离心率等于________．21．（2014安徽）设21,F F 分别是椭圆)10(1:222<<=+b by x E 的左、右焦点，过点1F 的直线交椭圆E 于B A ,两点，若x AF BF AF ⊥=211,3轴，则椭圆E 的方程为____．22．（2013福建）椭圆)0(1:2222>>=+Γb a by a x 的左、右焦点分别为21,F F ，焦距为c 2．若直线)y x c =+与椭圆Γ的一个交点M 满足12212F MF F MF ∠=∠，则该椭圆的离心率等于 ．23．（2012江西）椭圆22221(0)x y a b a b+=>>的左、右顶点分别是,A B ，左、右焦点分别是12,F F ．若1121||,||,||AF F F F B 成等比数列，则此椭圆的离心率为_________．24．（2011浙江）设12,F F 分别为椭圆2213x y +=的左、右焦点，点,A B 在椭圆上，若125F A F B =；则点A 的坐标是 ．三、解答题25．（2018江苏）如图，在平面直角坐标系xOy 中，椭圆C 过点1,)2，焦点12(F F ，圆O 的直径为12F F ．(1)求椭圆C 及圆O 的方程；(2)设直线l 与圆O 相切于第一象限内的点P ．①若直线l 与椭圆C 有且只有一个公共点，求点P 的坐标；②直线l 与椭圆C 交于,A B 两点．若OAB △，求直线l 的方程． 26．（2018全国卷Ⅲ）已知斜率为k 的直线l 与椭圆22143x y C +=：交于A ，B 两点．线段AB 的中点为(1,)(0)M m m >．(1)证明：12k <-； (2)设F 为C 的右焦点，P 为C 上一点，且FP FA FB ++=0．证明：2||||||FP FA FB =+．27．（2018北京）已知椭圆2222:1(0)x y M a b a b+=>>的离心率为3，焦距为．斜率为k 的直线l 与椭圆M 有两个不同的交点A ，B ． (1)求椭圆M 的方程；(2)若1k =，求||AB 的最大值；(3)设(2,0)P -，直线PA 与椭圆M 的另一个交点为C ，直线PB 与椭圆M 的另一个交点为D ．若C ，D 和点71(,)42Q - 共线，求k ．28．（2018天津）设椭圆22221(0)x y a b a b+=>>的右顶点为A ，上顶点为B ．已知椭圆的离心率为3||AB = (1)求椭圆的方程；(2)设直线:(0)l y kx k =<与椭圆交于,P Q 两点，l 与直线AB 交于点M ，且点P ，M 均在第四象限．若BPM △的面积是BPQ △面积的2倍，求k 的值．29．（2017新课标Ⅱ）设O 为坐标原点，动点M 在椭圆C ：2212x y +=上，过M 做x 轴的垂线，垂足为N ，点P 满足2NP NM =．（1）求点P 的轨迹方程；（2）设点Q 在直线3x =-上，且1OP PQ ⋅=．证明：过点P 且垂直于OQ 的直线l 过C 的左焦点F ．30．（2017天津）已知椭圆22221(0)x y a b a b+=>>的左焦点为,()0F c -，右顶点为A ，点E的坐标为(0,)c ，EFA △的面积为22b ．（Ⅰ）求椭圆的离心率；（Ⅱ）设点Q 在线段AE 上，3||2FQ c =，延长线段FQ 与椭圆交于点P ，点M ，N 在x 轴上，PM QN ∥，且直线PM 与直线QN 间的距离为c ，四边形PQNM 的面积为3c ．（i ）求直线FP 的斜率； （ii ）求椭圆的方程．31．（2017山东）在平面直角坐标系xOy 中，已知椭圆C :22221x y a b+=(0)a b >>的离心率为2，椭圆C 截直线1y =所得线段的长度为 (Ⅰ)求椭圆C 的方程；(Ⅱ)动直线l ：(0)y kx m m =+≠交椭圆C 于A ，B 两点，交y 轴于点M ．点N 是M 关于O 的对称点，N 的半径为||NO ． 设D 为AB 的中点，DE ，DF 与N 分别相切于点E ，F ，求EDF ∠的最小值．x32．（2017北京）已知椭圆C 的两个顶点分别为(2,0)A -，(2,0)B ，焦点在x 轴上，离心． （Ⅰ）求椭圆C 的方程；（Ⅱ）点D 为x 轴上一点，过D 作x 轴的垂线交椭圆C 于不同的两点M ，N ，过D 作AM 的垂线交BN 于点E ．求证：BDE ∆与BDN ∆的面积之比为4:5．33．（2017江苏）如图，在平面直角坐标系xOy 中，椭圆E ：22221(0)x y a b a b+=>>的左、右焦点分别为1F ，2F ，离心率为12，两准线之间的距离为8．点P 在椭圆E 上，且位于第一象限，过点1F 作直线1PF 的垂线1l ，过点2F 作直线2PF 的垂线2l ． （1）求椭圆E 的标准方程；（2）若直线1l ，2l 的交点Q 在椭圆E 上，求点P 的坐标．34．（2016年北京）已知椭圆C ：22221x y a b+=过(2,0)A ，(0,1)B 两点．（Ⅰ）求椭圆C 的方程及离心率；（Ⅱ）设P 为第三象限内一点且在椭圆C 上，直线PA 与y 轴交于点M ，直线PB 与x轴交于点N ，求证：四边形ABNM 的面积为定值．35．（2016年全国II 卷）已知A 是椭圆E ：22143x y +=的左顶点，斜率为()0k k ＞的直线交E 与A ，M 两点，点N 在E 上，MA NA ⊥. （Ⅰ）当AM AN =时，求AMN ∆的面积；（Ⅱ）当AM AN =2k <<.36．（2016年山东）已知椭圆C ：22221(0)x y a b a b+=>>的长轴长为4，焦距为2．（Ⅰ）求椭圆C 的方程；（Ⅱ）过动点M (0，m )(m >0)的直线交x 轴与点N ，交C 于点A ，P (P 在第一象限)，且M 是线段PN 的中点．过点P 作x 轴的垂线交C 于另一点Q ，延长线QM 交C 于点B ．(i)设直线PM 、QM 的斜率分别为k 、k'，证明k k'为定值； (ii)求直线AB 的斜率的最小值．37．（2016年天津）设椭圆13222=+y a x （3>a ）的右焦点为F ，右顶点为A ，已知||3||1||1FA eOA OF =+，其中O 为原点，e 为椭圆的离心率. （Ⅰ）求椭圆的方程；（Ⅱ）设过点A 的直线l 与椭圆交于点B （B 不在x 轴上），垂直于l 的直线与l 交于点M ，与y 轴交于点H ，若HF BF ⊥，且MAO MOA ∠=∠，求直线的l 斜率.38．（2015新课标2）已知椭圆C ：22221(0)x y a b a b+=>>的离心率为2，点在C 上．（Ⅰ）求C 的方程；（Ⅱ）直线l 不过原点O 且不平行于坐标轴，l 与C 有两个交点,A B ，线段AB 的中点为M ．证明：直线OM 的斜率与直线l 的斜率的乘积为定值．39．（2015天津）已知椭圆22221(0)x y a b a b+=>>的上顶点为B ，左焦点为F ，离心率为（Ⅰ）求直线BF 的斜率；（Ⅱ）设直线BF 与椭圆交于点P （P 异于点B ），故点B 且垂直于BP 的直线与椭圆交于点Q （Q 异于点B ）直线PQ 与y 轴交于点M ，||=||PM MQ λ． （i ）求λ的值；（ii ）若||sin =9PM BQP ∠，求椭圆的方程．40．（2015陕西）如图，椭圆E （Ⅰ）求椭圆E 的方程；（Ⅱ）经过点(1,1)，且斜率为k 的直线与椭圆E 交于不同的两点,P Q （均异于点A ），证明：直线AP 与AQ 的斜率之和为2．41．(2015重庆)直线交椭圆于,P Q 两点，且PQ ⊥1PF ．42． (2014新课标1) 已知点A (0,2)-，椭圆E ：22221(0)x y a b a b+=>>，F 是椭圆E 的右焦点，直线AF ，O 为坐标原点． （Ⅰ)求E 的方程；（Ⅱ）设过点A 的动直线l 与E 相交于,P Q 两点，当OPQ ∆的面积最大时，求l 的方程．43．(2014浙江)如图，设椭圆(),01:2222>>=+b a by a x C 动直线l 与椭圆C 只有一个公共点P ，且点P 在第一象限．（Ⅰ）已知直线l 的斜率为k ，用k b a ,,表示点P 的坐标；（Ⅱ）若过原点O 的直线1l 与l 垂直，证明：点P 到直线1l 的距离的最大值为b a -．44．（2014新课标2）设1F ，2F 分别是椭圆C ：()222210y x a b a b+=>>的左，右焦点，M 是C 上一点且2MF 与x 轴垂直，直线1MF 与C 的另一个交点为N ． （Ⅰ）若直线MN 的斜率为34，求C 的离心率；（Ⅱ）若直线MN 在y 轴上的截距为2，且15MN F N =，求,a b ．45．（2014安徽）设1F ,2F 分别是椭圆E ：22221(0)x y a b a b+=>>的左、右焦点，过点1F的直线交椭圆E 于,A B 两点，11||3||AF BF = （Ⅰ）若2||4,AB ABF =∆的周长为16，求2||AF ； （Ⅱ）若23cos 5AF B ∠=，求椭圆E 的离心率． 46．（2014山东）在平面直角坐标系xOy 中，椭圆2222:1(0)x y C ab a b+=>>的离心率为2，直线y x =被椭圆C ． （Ｉ）求椭圆C 的方程；（Ⅱ）过原点的直线与椭圆C 交于A ，B 两点（A ，B 不是椭圆C 的顶点）．点D 在椭圆C 上，且AD AB ⊥，直线BD 与x 轴、y 轴分别交于M ，N 两点．(ⅰ)设直线BD ，AM 的斜率分别为12,k k ，证明存在常数λ使得12k k λ=，并求出λ的值；(ⅱ)求OMN ∆面积的最大值．47．（2014湖南）如图5，O 为坐标原点，双曲线221112211:1(0,0)x y C a b a b -=>>和椭圆222222222:1(0)x y C a b a b +=>>均过点(,1)3P ，且以1C 的两个顶点和2C 的两个焦点为顶点的四边形是面积为2的正方形． （Ｉ）求12,C C 的方程；（Ⅱ）是否存在直线l ，使得l 与1C 交于,A B 两点，与2C 只有一个公共点，且||||OA OB AB +=？证明你的结论．48．（2014四川）已知椭圆C ：22221x y a b+=（0a b >>）的焦距为4，其短轴的两个端点与长轴的一个端点构成正三角形． （Ⅰ）求椭圆C 的标准方程；（Ⅱ）设F 为椭圆C 的左焦点，T 为直线3x =-上任意一点，过F 作TF 的垂线交椭圆C 于点P ，Q ．（i ）证明：OT 平分线段PQ （其中O 为坐标原点）； （ii ）当||||TF PQ 最小时，求点T 的坐标．49．（2013安徽）已知椭圆2222:1(0)x y C a b a b+=>>的焦距为4，且过点P .12短轴长分别为2m ，2()n m n >，过原点且不与x 轴重合的直线l 与1C ，2C 的四个交点按纵坐标从大到小依次为A ，B ，C ，D ．记mnλ=，△B D M 和△ABN 的面积分别为1S 和2S ．（Ⅰ）当直线l 与y 轴重合时，若12S S λ=，求λ的值；（Ⅱ）当λ变化时，是否存在与坐标轴不重合的直线l ，使得12S S λ=？并说明理由．51． (2013天津)设椭圆22221(0)x y a b a b+=>>的左焦点为F ， ， 过点F 且与x(Ⅰ) 求椭圆的方程；(Ⅱ) 设A ，B 分别为椭圆的左、右顶点， 过点F 且斜率为k 的直线与椭圆交于C ，D两点．若··8AC DB AD CB +=， 求k 的值．52．（2013山东）椭圆2222:1(0)x y C a b a b+=>>的左、右焦点分别是12,F F ，，过1F 且垂直于x 轴的直线被椭圆C 截得的线段长为l ． （Ⅰ）求椭圆C 的方程；（Ⅱ）点P 是椭圆C 上除长轴端点外的任一点，连接12,PF PF ．设12F PF ∠的角平分线PM 交C 的长轴于点(),0M m ，求m 的取值范围；（Ⅲ）在（Ⅱ）的条件下，过点P 作斜率为k 的直线l ，使得l 与椭圆C 有且只有一个公共点．设直线12,PF PF 的斜率分别为12,k k ，若0k ≠，试证明1211kk kk +为定值，并求出这个定值．53．（2012北京）已知椭圆C :22221(0)x y a b a b+=>>的一个顶点为(2,0)A ，离心率为2.直线(1y k x =-）与椭圆C 交于不同的两点M ,N . （Ⅰ）求椭圆C 的方程； （Ⅱ）当△AMN得面积为3时，求k 的值. 54．（2013安徽）如图，21,F F 分别是椭圆C ：22a x +22by =1（0>>b a ）的左、右焦点，A是椭圆C 的顶点，B 是直线2AF 与椭圆C 的另一个交点，1F ∠A 2F =60°．（Ⅰ）求椭圆C 的离心率；（Ⅱ）已知△A B F 1的面积为403，求a , b 的值．55．（2012广东）在平面直角坐标系xOy 中，已知椭圆C ：22221(0)x y a b a b+=>>的离心率e =C 上的点到(0,2)Q 的距离的最大值为3． （Ⅰ）求椭圆C 的方程；（Ⅱ）在椭圆C 上，是否存在点(,)M m n 使得直线l ：1mx ny +=与圆O ：221x y +=相交于不同的两点,A B ，且OAB ∆的面积最大？若存在，求出点M 的坐标及相对应的OAB ∆的面积；若不存在，请说明理由．56．（2011陕西）设椭圆C : ()222210x y a b a b +=>>过点(0，4)，离心率为35．（Ⅰ）求C 的方程； （Ⅱ）求过点(3，0)且斜率为45的直线被C 所截线段的中点坐标． 57．（2011山东）在平面直角坐标系xOy 中，已知椭圆22:13x C y +=．如图所示，斜率为(0)k k ＞且不过原点的直线l 交椭圆C 于A ，B 两点，线段AB 的中点为E ，射线OE交椭圆C 于点G ，交直线3x =-于点(3,)D m -． （Ⅰ）求22m k +的最小值； （Ⅱ）若2OG OD =∙OE ，（i ）求证：直线l 过定点；（ii ）试问点B ，G 能否关于x 轴对称？若能，求出此时ABG 的外接圆方程；若不能，请说明理由．58．（2010新课标）设1F ,2F 分别是椭圆E ：2x +22y b=1（0﹤b ﹤1）的左、右焦点，过1F的直线l 与E 相交于A 、B 两点，且2AF ，AB ，2BF 成等差数列． （Ⅰ）求AB ；（Ⅱ）若直线l 的斜率为1，求b 的值．59．（2010辽宁）设椭圆C ：22221(0)x y a b a b+=>>的左焦点为F ，过点F 的直线与椭圆C相交于A ，B 两点，直线l 的倾斜角为60o ，2AF FB ． （Ⅰ）求椭圆C 的离心率； （Ⅱ）如果||AB =154，求椭圆C 的方程．。

【母题原题1】【2019年高考全国Ⅲ卷理数】双曲线C：2242x y-=1的右焦点为F，点P在C的一条渐近线上，O为坐标原点，若=PO PF，则△PFO的面积为A．4B．2C．D．【答案】A【解析】由2,,a b c===,2PPO PF x=∴=Q，又P在C的一条渐近线上，不妨设为在by xa=上，则222P Pby xa=⋅==，11224PFO PS OF y∴=⋅==△，故选A．【名师点睛】忽视圆锥曲线方程和两点间的距离公式的联系导致求解不畅，采取列方程组的方式解出三角形的高，便可求三角形面积．【母题原题2】【2018年高考全国Ⅲ卷理数】设12F F，是双曲线22221x yCa b-=：（00a b>>，）的左，右焦点，O是坐标原点．过2F作C的一条渐近线的垂线，垂足为P．若1PF=，则C的离心率为AB．2专题10 双曲CD【答案】B【解析】由题可知22,PF b OF c ==，∴||PO a =， 在2Rt POF △中，222cos PF bPF O OF c∠==， ∵在12PF F △中，22221212212cos 2PF F F PF b F PF F P O F c+-∠==，∴)222224322b c bc a b cc+-=⇒=⋅，∴e =，故选C ． 【名师点睛】本题主要考查双曲线的相关知识，考查了双曲线的离心率和余弦定理的应用，属于中档题．【命题意图】高考对双曲线内容的考查以基础知识为主，重点考查双曲线的几何性质、方程思想及运算能力．2019年高考题考查了以双曲线为载体的三角形面积的求法，渗透了直观想象、逻辑推理和数学运算素养．采取公式法，利用数形结合、转化与化归和方程思想解题．【命题规律】主要考查双曲线的定义、标准方程和几何性质，其中离心率和渐近线问题是高考考查的重点，以选择题和填空题为主，难度中等． 【答题模板】1．求双曲线的离心率的值或范围一般考虑如下三步：第一步：将提供的双曲线的几何关系转化为关于双曲线基本量a ，b ，c 的方程或不等式； 第二步：利用222b c a +=和ce a=转化为关于e 的方程或不等式； 第三步：通过解方程或不等式求得离心率的值或取值范围． 2．其他问题：（1）双曲线的焦点到其渐近线的距离为b ．（2）若P 是双曲线右支上一点，F 1，F 2分别为双曲线的左、右焦点，则|PF 1|min =a+c ，|PF 2|min =c –a ．（3）同支的焦点弦中最短的为通径(过焦点且垂直于长轴的弦)，其长为22b a；异支的弦中最短的为实轴，其长为2a ．（4）若P 是双曲线上不同于实轴两端点的任意一点，F 1，F 2分别为双曲线的左、右焦点，则12PF F S △=2tan 2b θ，其中θ为∠F 1PF 2．（5）若P 是双曲线22x a22y b -=1(a>0，b>0)右支上不同于实轴端点的任意一点，F 1，F 2分别为双曲线的左、右焦点，I 为△PF 1F 2内切圆的圆心，则圆心I 的横坐标为定值a ． 【方法总结】1．双曲线定义的应用策略（1）根据动点与两定点的距离的差判断动点的轨迹是否为双曲线．（2）利用双曲线的定义解决与双曲线的焦点有关的问题，如最值问题、距离问题． （3）利用双曲线的定义解决问题时应注意三点：①距离之差的绝对值；②2a <|F 1F 2|；③焦点所在坐标轴的位置． 2．求双曲线的标准方程的方法 （1）定义法根据双曲线的定义确定a 2，b 2的值，再结合焦点位置，求出双曲线方程，常用的关系有： ①c 2=a 2+b 2；②双曲线上任意一点到双曲线两焦点的距离的差的绝对值等于2a ．求轨迹方程时，满足条件：|PF 1|–|PF 2|=2a （0<2a <|F 1F 2|）的双曲线为双曲线的一支，应注意合理取舍． （2）待定系数法 一般步骤为①判断：根据已知条件，确定双曲线的焦点是在x 轴上，还是在y 轴上，还是两个坐标轴都有可能； ②设：根据①中的判断结果，设出所需的未知数或者标准方程； ③列：根据题意，列出关于a ，b ，c 的方程或者方程组； ④解：求解得到方程． 常见设法有①与双曲线22x a –22y b =1共渐近线的双曲线方程可设为22x a –22y b=λ（λ≠0）；②若双曲线的渐近线方程为y =±ba x ，则双曲线方程可设为22x a –22yb =λ（λ≠0）；③若双曲线过两个已知点，则双曲线方程可设为2x m +2y n=1（mn <0）；④与双曲线22x a –22y b =1共焦点的双曲线方程可设为22x a k -–22y b k+=1（–b 2<k <a 2）；⑤与椭圆22x a +22y b =1（a >b >0）有共同焦点的双曲线方程可设为22x a λ-+22y b λ-=1（b 2<λ<a 2）．注意：当焦点位置不确定时，有两种方法来解决：一种是分类讨论，注意考虑要全面；另一种是如果已知中心在原点，但不能确定焦点的具体位置，可以设双曲线的方程为mx 2+ny 2=1（mn <0）． 3．求双曲线离心率的值（1）直接求出c a ,，求解e ：已知标准方程或a ，c 易求时，可利用离心率公式e ＝ca求解； （2）变用公式，整体求e ：如利用e，e； 4．双曲线的离心率与渐近线方程之间有着密切的联系，二者之间可以互求．已知渐近线方程时，可得b a的值，于是e 2＝22c a ＝222a b a +＝1＋2()b a ，因此可求出离心率e 的值；而已知离心率的值，也可求出渐近线的方程，即b a个解．1．【广西壮族自治区南宁、梧州等八市2019届高三4月联合调研考试数学】已知双曲线222:1(0)3x y C a a -=>的一个焦点为（2，0），则双曲线C 的渐近线方程为A ．y x =±B ．y =C ．y =D ．2y x =±【答案】C【解析】因为双曲线222:1(0)3x y C a a -=>的一个焦点为（2，0），所以234a +=，故21a =，因此双曲线的方程为2213y x -=，所以其渐近线方程为y =．故选C ．【名师点睛】本题主要考查双曲线的渐近线方程，熟记双曲线的性质即可，属于基础题型．2．【广西壮族自治区柳州市2019届高三毕业班3月模拟考试数学】已知双曲线22221(0,0)x y a b a b-=>>的左、右焦点为1F 、2F ，双曲线上的点P 满足121243PF PF F F +≥u u u v u u u u v u u u u v恒成立，则双曲线的离心率的取值范围是A ．312e <≤B ．32e ≥C ．413e <≤D ．43e ≥【答案】C【解析】∵OP 是12F PF △的边12F F 上的中线，∴122PF PF PO+=u u u v u u u u v u u u v． ∵121243PF PF F F u u u v u u u u v u u u u v +≥，∴1283PO F F ≥u u u v u u u u v，当且仅当12,,F P F 三点共线时等号成立． 又PO a ≥u u u v ，122F F c =u u u u v ，∴86a c ≥，∴43c e a =≤，又1e >，∴413e <≤．故离心率的取值范围为41,3⎛⎤⎥⎝⎦．故选C ． 【名师点睛】解答本题时注意两点：一是注意数形结合在解题中的应用，特别是由题意得到PO a ≥u u u v；二是根据题意得到,,a b c 间的关系，再根据离心率的定义求解，属于基础题．3．【四川省华文大教育联盟2019届高三第二次质量检测考试数学】已知双曲线()222210,0x y a b a b-=>>的左、右焦点分别为()()12,0,,0F c F c -，过点2F 作x 轴的垂线，与双曲线的渐近线在第一象限的交点为P ，线段2PF 的中点M ，则此双曲线的渐近线方程为 A ．2y x =± B ．12y x =±C ．4y x =±D ．14y x =±【答案】A【解析】由题意知，双曲线的渐近线方程为b y x a =±，易求点P 的坐标为,bc c a ⎛⎫ ⎪⎝⎭，中点M 的坐标为,2bc c a ⎛⎫ ⎪⎝⎭，∵2222)2bc OM c a ⎛⎫=+= ⎪⎝⎭，∴224a b =，即2b a =．故选A ． 【名师点睛】本题考查双曲线的方程与简单的几何性质，考查计算能力与转化能力，属于基础题． 4．【四川省棠湖中学2019届高三高考适应性考试数学】已知双曲线的中心在原点，焦点在坐标轴上，一条渐近线方程为340x y +=，则该双曲线的离心率是A ．53 B ．54C ．43或53D ．53或54【答案】D【解析】33404x y y x +=⇒=-，当焦点位于横轴时，2239416b b a a =⇒=，而222c a b =+，所以22295164c a c e a a -=⇒==； 当焦点位于纵轴时，22222222416165,,3993b bc a c c a b e a a a a -=⇒==+⇒=⇒==故选D ． 【名师点睛】本题考查了通过双曲线的渐近线方程求离心率问题，解题的关键是对焦点的位置进行分类．5．【四川省棠湖中学2019届高三高考适应性考试数学】已知双曲线()2222:10,0x y C a b a b-=>>的左，右焦点分别为12,F F ，抛物线()220=>y px p 与双曲线C 有相同的焦点．设P 为抛物线与双曲线C 的一个交点，且12sin PF F ∠=，则双曲线C 的离心率为AB或3 C ．2D ．2或3【答案】D【解析】不妨设P 在第一象限且()00,P x y ，则1,02p F ⎛⎫- ⎪⎝⎭，2,02p F ⎛⎫⎪⎝⎭， 过P 作直线2px =-（抛物线的准线）的垂线，垂足为E ， 则112F PE PF F ∠=∠，故112sin sin 7F PE PF F ∠=∠=， 因1F PE △为直角三角形，故可设,2p E ⎛⎫- ⎪⎝⎭，()0P x ， 且25PE PF k ==，17PF k =，所以02052242p x k k px ⎧+=⎪⎨⎪=⎩，解得043p k x k =⎧⎨=⎩或062p k x k =⎧⎨=⎩， 若043p k x k =⎧⎨=⎩，则124F F k =，22752ke k k ==-； 若062p k x k =⎧⎨=⎩，则126F F k =，33752ke k k ==-． 综上可得，选D ．【名师点睛】离心率的计算关键在于构建,,a b c 的一个等量关系，构建时可依据圆锥曲线的几何性质来转化，有两个转化的角度：（1）利用圆锥曲线的定义转化为与另一个焦点；（2）利用圆锥曲线的统一定义把问题转化为与曲线上的点到相应准线的距离．6．【四川省成都七中2019届高三5月高考模拟测试数学】已知双曲线1C ：22142-=x y ，双曲线2C 的焦点在y 轴上，它的渐近线与双曲线1C 相同，则双曲线2C 的离心率为 A ．3 B ．2 CD ．1【解析】由题意，双曲线2C 的焦点在y 轴上，它的渐近线与双曲线1C 相同，设双曲线2C 的方程为22(0)24y x λλ-=>，则双曲线2C =A ． 【名师点睛】本题主要考查了双曲线的离心率的求解，其中解答中根据双曲线2C 的焦点在y 轴上，它的渐近线与双曲线1C 相同，得出双曲线2C 的方程的形式，再根据离心率的定义求解是解答的关键，着重考查了运算与求解能力，属于基础题．7．【四川省华文大教育联盟2019届高三第二次质量检测数学】已知双曲线的左、右焦点分别为()1,0F c -，()2,0F c ，过点2F 作x 轴的垂线，与双曲线的渐近线在第一象限内的交点为P ，线段2PF 的中点M 到，则双曲线的渐近线方程为 A ．2y x =± B ．12y x =±C ．4y x =±D ．14y x =±【答案】A【解析】设双曲线的渐近线方程为()0,0by x a b a=±>>， 根据题意可知P 点坐标,bc c a ⎛⎫ ⎪⎝⎭，M为2PF 中点，所以可得,2bc M c a ⎛⎫⎪⎝⎭， 所以222222bc OM c c a ⎛⎫=+= ⎪⎝⎭，所以224a b =，即2b a =， 所以双曲线的渐近线方程为2y x =±，故选A ．【名师点睛】本题考查通过双曲线中，线段的几何关系求双曲线渐近线方程，属于简单题．8．【四川省雅安市2019届高三第三次诊断考试数学】双曲线2212x y -=的离心率为A BCD【解析】由双曲线的方程2212x y -=可得：222,1a b ==，所以2223c a b =+=，所以2c e a ===．故选D ． 【名师点睛】本题主要考查了双曲线的简单性质，考查计算能力，属于基础题．9．【四川省内江市2019届高三第三次模拟考试数学】双曲线22221(0,0)x y a b a b-=>>的一条渐近线方程为34y x =，则该双曲线的离心率为 A ．43 B ．53C ．54D ．2【答案】C【解析】双曲线()2222100x y a b a b-=>>，的一条渐近线方程为34y x =，可得34b a =，即222916c a a -=，解得e 22516=，e 54=．故选C ． 【名师点睛】本题考查双曲线的简单性质的应用，涉及双曲线的渐近线方程，离心率等知识，考查计算能力．10．【四川省双流中学2019届高三第一次模拟考试数学】已知M 为双曲线2222:1(0,0)x y C a b a b-=>>的右支上一点，,A F 分别为双曲线C 的左顶点和右焦点，线段FA 的垂直平分线过点M ，60MFA ∠=︒，则双曲线C 的离心率为A B ．2 C ．3 D ．4【答案】D【解析】设双曲线另一个焦点为F '，如下图所示．因为线段FA 的垂直平分线过点M ，60MFA ∠=︒，所以MFA △是等边三角形，边长为a c +，M 为双曲线2222:1(0,0)x y C a b a b-=>>的右支上一点，所以有23MF MF a MF a c -=⇒='+'，在MFF '△中，由余弦定理可得：'2222cos60MF MF FF MF FF ︒=+-'⋅'， 即22430a ac c +-=，解得4a c =，即4ca=，双曲线的离心率为4，故选D ． 【名师点睛】本题考查了双曲线的定义、离心率，考查了转化思想、数形结合思想．11．【四川省宜宾市2019届高三第三次诊断性考试数学】已知双曲线22213x y a -=的左右焦点分别为12,F F ，以它的一个焦点为圆心，半径为a 的圆恰好与双曲线的两条渐近线分别切于,A B 两点，则四边形12F AF B 的面积为A ．3B ．4C ．5D ．6【答案】D【解析】因为双曲线22213x y a -=的左右焦点分别为()()12,0,0F c F c -，，双曲线的渐近线方程为y x a=±0ay -=， 以它的一个焦点为圆心，半径为a 的圆恰好与双曲线的两条渐近线分别切于A ，B 两点， 根据焦点到渐近线的距离及双曲线中a b c 、、的关系，可得223a c a ==+⎪⎩，解得a c ==A ⎝⎭，则四边形12F AF B的面积为1212122622F AF B F AF S S ==⨯⨯=．故选D ． 【名师点睛】本题考查双曲线的简单性质以及圆与双曲线的位置关系的应用，考查转化思想以及计算能力，属于中档题．12．【四川省成都市外国语学校2019届高三一诊模拟考试数学】过双曲线C ：22221x y a b-=的右顶点作x 轴的垂线，与C 的一条渐近线相交于点A ．若以C 的右焦点为圆心、半径为4的圆经过A ，O 两点（O 为坐标原点），则双曲线C 的方程为A ．221124x y -=B ．22179x y -=C ．22188x y -=D ．221412x y -=【答案】D【解析】∵以C 的右焦点为圆心、半径为4的圆经过A ，O 两点（O 为坐标原点）， ∴半径4R c ==，则圆的标准方程为()22416x y -+=，(),0A a ，b y a b a=⋅=，即(),B a b ，则()22416a b -+=，即2281616a a b -++=，即280c a -=，即816a =，则2a =，216412b =-=，则双曲线C 的方程为221412x y -=，故选D ．【名师点睛】本题主要考查双曲线方程的求解，根据圆的性质先求出半径4c =是解决本题的关键．属于简单题．13．【四川省成都市2019届高三毕业班第二次诊断性检测数学】已知双曲线()222:10y C x b b-=>的焦距为4，则双曲线C 的渐近线方程为 A．y =B ．2y x =±C ．3y x =± D．y =【答案】D【解析】双曲线C ：()22210y x b b-=>的焦距为4，则2c ＝4，即c ＝2，∵1+b 2＝c 2＝4，∴b =C 的渐近线方程为y =x ，故选D ．【名师点睛】本题考查双曲线的方程和性质，考查双曲线的渐近线方程的运用，属于基础题．14．【四川省2019届高三联合诊断数学】已知双曲线()222:103x y C a a -=>的右焦点为F ，则点F 到C的渐近线的距离为 A ．3 BC ．a D【答案】B【解析】因为双曲线()222:103x y C a a -=>的右焦点为()0F c ，，渐近线y x =， 所以点F到渐近线y x ===B ． 【名师点睛】本题主要考查利用双曲线的方程求焦点坐标与渐近线方程，以及点到直线距离公式的应用，属于基础题．若双曲线方程为22221x y a b-=，则渐近线方程为b y x a =±．15．【四川省广安、眉山、内江、遂宁2019届高三第一次诊断性考试数学】若双曲线221x y m-=的一条渐近线为20x y -=，则实数m = A ．2 B ．4 C ．6 D ．8【答案】B【解析】∵双曲线的方程为221x y m-=，∴双曲线的渐近线方程为yx ，又∵一条渐近线方程为y =12x ，∴m =4．故选B ． 【名师点睛】本题给出双曲线的方程和一条渐近线方程，求参数m 的值，属于基础题．16．【四川省高2019届高三第一次诊断性测试数学】中心在原点，对称轴为坐标轴的双曲线C 的两条渐近线与圆()2221x y -+=都相切，则双曲线C 的离心率是A ．2B ．2C2D．3或2【答案】A【解析】设双曲线C 的渐近线方程为y =kx，∴k =，得双曲线的一条渐近线的方程为3y =，∴焦点在x 、y 轴上两种情况讨论： ①当焦点在x轴上时有：b c e a a ==②当焦点在y轴上时有：23a c e b a ==＝．∴求得双曲线的离心率2A ． 【名师点睛】本小题主要考查直线与圆的位置关系、双曲线的简单性质等基础知识，考查运算求解能力，考查数形结合思想．解题的关键是：由圆的切线求得直线的方程，再由双曲线中渐近线的方程的关系建立等式，从而解出双曲线的离心率的值．此题易忽视两解得出错误答案． 17．【贵州省遵义航天高级中学2019届高三第十一模（最后一卷）数学】设12,F F 是双曲线22221(0,0)x y a b a b-=>>的左、右焦点，P 为双曲线右支上一点，若1290F PF ︒∠=，c =2，213PF F S =△，则双曲线的两条渐近线的夹角为 A ．5π B ．4πC ．π6D ．π3【答案】D【解析】由题意可得22121216132PF PF PF PF ⎧+=⎪⎨=⎪⎩，可得212)4PF PF -=（， 可得1222PF PF a -==，可得a =1，b所以双曲线的渐近线方程为y =，可得双曲线的渐近线的夹角为π3，故选D ． 【名师点睛】本题主要考察双曲线的性质及渐近线的方程，熟练掌握其性质是解题的关键．18．【贵州省凯里市第一中学2019届高三下学期模拟考试《黄金卷三》数学】已知抛物线2y =的焦点为双曲线2221(0)x y a a-=>的一个焦点，那么双曲线的渐近线方程是A．3y x =±B．y =C．2y x =± D．y =【答案】C【解析】抛物线2y =的焦点为)，所以双曲线中c =，由双曲线方程2221x y a-=，222+=a b c，所以a =因此双曲线的渐近线方程为2y x =±，故选C ． 【名师点睛】本题考查抛物线的焦点，根据焦点求双曲线的方程和渐近线方程，属于简单题． 19．【贵州省凯里市第一中学2019届高三下学期模拟考试《黄金卷三》数学】已知A 为双曲线22221(0,0)x y a b a b-=>>的右顶点，P 为双曲线右支上一点，若点P 关于双曲线中心O 的对称点Q 满足AP k ⨯14AQ k =，则双曲线的离心率为 A1BCD1【答案】B【解析】设(,),(,),P x y Q x y --∵AP k ⨯14AQ k =， ∴222000014y y y y y x a x a x a x a x a -----⋅=⋅==----+-， ∵22221x y a b -=，∴22222=()b y x a a-，∴222222()14b x a ax a -=-， ∴a =2b ，∴222244()a b c a ==-，∴2254a c =，∴2e =．故选B ． 20．【云南省昆明市2019届高三高考模拟（第四次统测）数学】已知双曲线C的一个焦点坐标为0)，渐近线方程为2y x =±，则C 的方程是 A ．2212y x -=B ．2212x y -=C ．2212y x -=D ．2212x y -=【答案】B【解析】因为双曲线C的一个焦点坐标为),所以c =又因为双曲线C的渐近线方程为2y x =±，所以有2b a=a ⇒=，c =而c =1a b ==，因此双曲线方程为2212x y -=，故选B ．【名师点睛】本题考查了求双曲线的标准方程，考查了解方程、运算能力．21．【云南省2019届高三第一次毕业生复习统一检测数学】双曲线M 的焦点是1F ，2F ，若双曲线M 上存在点P ，使12PF F △是有一个内角为23π的等腰三角形，则M 的离心率是 A1B1C D 【答案】C【解析】不妨设P 在第一象限，由于12PF F △是有一个内角为23π的等腰三角形，故()2P c ，代入双曲线方程得2222431c c a b -=，化简得4224480c a c a -+=，42810e e -+=，解得2e =，故e =C ． 【名师点睛】本小题主要考查双曲线离心率的求法，考查等腰三角形的知识，属于基础题．22．【西藏山南市第二高级中学2019届高三下学期第一次模拟考试数学】已知椭圆22221x y a b+=左右焦点分别为12,F F ，双曲线22221x y m n-=的一条渐近线交椭圆于点P ，且满足12PF PF ⊥，已知椭圆的离心率为134e =，则双曲线的离心率2e =AB ．8C ．4D ．2【答案】B【解析】椭圆22221x y a b+=左右焦点分别为12,F F ，椭圆的离心率为134e =，不妨令4,3a c ==，则b =221167x y +=，双曲线22221x y m n-=的一条渐近线交椭圆于点P ，且满足12PF PF ⊥，可设(),,0,0P s t s t >>，可得()13,PF s t =---u u u r ，()23,PF s t =--u u u u r ，则222291167s t s t ⎧+=⎪⎨+=⎪⎩，解得22329499s t ⎧=⎪⎪⎨⎪=⎪⎩， 代入双曲线方程渐近线方程n y x m =±，可得224932n m =，双曲线的离心率为：28e ===．故选B ． 【名师点睛】本题考查椭圆的简单性质以及双曲线的简单性质的应用，利用垂直关系和点在椭圆上建立方程组，求得双曲线,a b 之间满足的关系是解题关键．23．【广西柳州市2019届高三毕业班1月模拟考试高三数学】已知双曲线()2222100x y C a b a b-=>>：，的离心率为2，左焦点为1F ，点()0Q （c 为半焦距）．P 是双曲线C 的右支上的动点，且1PF PQ +的最小值为6．则双曲线C 的方程为___________．【答案】2213y x -=【解析】设双曲线右焦点为2F ，则122PF PF a -=，所以122PF PQ a PF PQ +=++， 而2PF PQ +的最小值为22QF c ==，所以1PF PQ +最小值为226a c +=，又2c a =，解得12a c ==，，于是23b =，故双曲线方程为2213y x -=． 【点睛】本题考查了双曲线的方程，双曲线的定义，及双曲线的离心率，考查了计算能力，属于中档题．24．【西藏拉萨市2019届高三第三次模拟考试数学】已知双曲线C ：()222210,0x y a b a b-=>>的左、右焦点为1F 、2F ，过1F 且斜率为2的直线l 与C 的一条渐近线在第一象限相交于A 点，若21AF AF ⊥，则该双曲线的离心率为___________． 【答案】3【解析】∵21AF AF ⊥，∴12AF F △是直角三角形，又O 是12F F 中点，∴AO c =，又A 在双曲线渐近线上，∴(,)A a b ，∴12tan AF F ∠=2b ac =+， 变形可得：22230c ac a --=，()(3)0c a c a +-=，∴3c a =，3ce a==．故答案为：3． 【点睛】本题考查双曲线的几何性质，解题关键是掌握双曲线的性质：即过双曲线22221x y a b -=(0,0)a b >>的右顶点A 作x 轴垂线，交渐近线于点P ，则OP c =，AP b =．。

专题九 解析几何第二十七讲 双曲线2019年1.（2019全国III 理10）双曲线C ：2242x y -=1的右焦点为F ，点P 在C 的一条渐进线上，O 为坐标原点，若=PO PF ，则△PFO 的面积为A B C ． D ．2.（2019江苏7）在平面直角坐标系xOy 中，若双曲线2221(0)y x b b-=>经过点（3，4)，则该双曲线的渐近线方程是 .3.（2019全国I 理16）已知双曲线C ：22221(0,0)x y a b a b-=>>的左、右焦点分别为F 1，F 2，过F 1的直线与C 的两条渐近线分别交于A ，B 两点．若1F A AB =，120F B F B ⋅=，则C 的离心率为____________．4.（2019年全国II 理11）设F 为双曲线C ：22221(0,0)x y a b a b-=>>的右焦点，O 为坐标原点，以OF 为直径的圆与圆222x y a +=交于P ，Q 两点.若PQ OF =，则C 的离心率为ABC ．2D 5．（2019浙江2）渐近线方程为x ±y =0的双曲线的离心率是A B ．1CD ．26.（2019天津理5）已知抛物线24y x =的焦点为F ，准线为l ，若l 与双曲线22221(0,0)x y a b a b-=>>的两条渐近线分别交于点A 和点B ，且||4||AB OF =（O 为原点），则双曲线的离心率为C.22010-2018年一、选择题1．(2018浙江)双曲线2213x y -=的焦点坐标是A ．(，B ．(2,0)-，(2,0)C ．(0,，D ．(0,2)-，(0,2)2．(2018全国卷Ⅰ)已知双曲线C ：2213-=x y ，O 为坐标原点，F 为C 的右焦点，过F 的直线与C 的两条渐近线的交点分别为M 、N ．若∆OMN 为直角三角形，则||MN =A ．32B ．3C ．D ．43．(2018全国卷Ⅱ)双曲线22221(0,0)-=>>x y a b a bA ．=yB ．=yC ．2=±y x D ．2=±y x 4．(2018全国卷Ⅲ)设1F ，2F 是双曲线C ：22221(0,0)x y a b a b-=>>的左、右焦点，O 是坐标原点．过2F 作C 的一条渐近线的垂线，垂足为P ．若1|||PF OP =，则C 的离心率为AB ．2CD5．(2018天津)已知双曲线22221(0,0)x y a b a b-=>>的离心率为2，过右焦点且垂直于x 轴的直线与双曲线交于A ，B 两点．设A ，B 到双曲线同一条渐近线的距离分别为1d 和2d ， 且126d d +=，则双曲线的方程为A ．221412x y -= B ．221124x y -= C ．22139x y -= D ．22193x y -=6．（2017新课标Ⅱ）若双曲线C ：22221(0,0)x y a b a b-=>>的一条渐近线被圆22(2)4x y -+=所截得的弦长为2，则C 的离心率为A ．2BCD ．37．（2017新课标Ⅲ）已知双曲线C ：22221(0,0)x y a b a b-=>>的一条渐近线方程为2y x =,且与椭圆221123x y +=有公共焦点，则C 的方程为 A ．221810x y -= B ．22145x y -= C ．22154x y -= D ．22143x y -=8．（2017天津）已知双曲线22221(0,0)x y a b a b-=>>的左焦点为F ．若经过F 和(0,4)P 两点的直线平行于双曲线的一条渐近线，则双曲线的方程为A ．22144x y -=B ．22188x y -=C ．22148x y -=D ．22184x y -= 9．(2016天津)已知双曲线222=1(0)4x y b b->，以原点为圆心，双曲线的实半轴长为半径长的圆与双曲线的两条渐近线相交于A 、B 、C 、D 四点，四边形的ABCD 的面积为2b ，则双曲线的方程为A ．22443=1y x -B ．22344=1y x -C ．2224=1x y b -D ．2224=11x y - 10．(2016年全国I)已知方程222213x y m n m n-=+-表示双曲线，且该双曲线两焦点间的距离为4，则n 的取值范围是A ．(–1,3)B ．(–1,3)C ．(0,3)D ．(0,3)11．(2016全国II)已知1F ,2F 是双曲线E ：22221x y a b-=的左、右焦点，点M 在E 上，1MF 与x 轴垂直，211sin 3MF F ∠=,则E 的离心率为A B ．32C D ．2 12．（2015四川）过双曲线2213y x -=的右焦点且与x 轴垂直的直线，交该双曲线的两条渐近线于,A B 两点，则AB =A B ． C ．6 D ．13．（2015福建）若双曲线22:1916x y E -= 的左、右焦点分别为12,F F ，点P 在双曲线E 上，且13PF =，则2PF 等于A ．11B ．9C ．5D ．314．（2015湖北）将离心率为1e 的双曲线1C 的实半轴长a 和虚半轴长()b a b ≠同时增加(0)m m >个单位长度，得到离心率为2e 的双曲线2C ，则A ．对任意的,a b ，12e e >B ．当a b >时，12e e >；当a b <时，12e e <C ．对任意的,a b ，12e e <D ．当a b >时，12e e <；当a b <时，12e e > 15．（2015安徽）下列双曲线中，焦点在y 轴上且渐近线方程为2y x =±的是A ．2214y x -= B ．2214x y -= C ．2214y x -= D ．2214x y -= 16．（2015新课标1）已知00(,)M x y 是双曲线C ：2212x y -=上的一点，12,F F 是C 的两个焦点，若120MF MF ⋅<，则0y 的取值范围是A ．(B ．(C ．(,33-D ．(33- 17．（2015重庆）设双曲线22221x y a b-=（0,0a b >>）的右焦点为F ，右顶点为A ，过F作AF 的垂线与双曲线交于,B C 两点，过,B C 分别作,AC AB 的垂线，两垂线交于点D ．若D 到直线BC 的距离小于a 则该双曲线的渐近线斜率的取值范围是A ．(1,0)(0,1)-∪B ．(,1)(1,)-∞-+∞∪C ．∪D ．(,1))-∞-∞∪18．（2014新课标1）已知F 是双曲线C ：223(0)x my m m -=>的一个焦点，则点F 到C的一条渐近线的距离为A B ．3 C D ．3m19．（2014广东）若实数k 满足09k <<，则曲线221259x y k-=-与曲线221259x y k -=-的 A ．焦距相等 B ．实半轴长相等 C ．虚半轴长相等 D ．离心率相等20．（2014天津）已知双曲线22221x y a b 0,0a b 的一条渐近线平行于直线l ：210y x ，双曲线的一个焦点在直线l 上，则双曲线的方程为 A ．221520x y B ．221205x yC ．2233125100x y D ．2233110025x y21．（2014重庆）设21F F ，分别为双曲线)0,0(12222>>=-b a by a x 的左、右焦点，双曲线上存在一点P 使得,49||||,3||||2121ab PF PF b PF PF =⋅=+则该双曲线的离心率为 A ．34 B ．35 C ．49D ．322．（2013新课标1）已知双曲线C ：22221x y a b-=（0,0a b >>C的渐近线方程为A ．14y x =± B ．13y x =± C ．12y x =± D ．y x =± 23．(2013湖北)已知04πθ<<，则双曲线1C ：22221cos sin x y θθ-=与2C ：22sin y θ2221sin tan y θθ-=的 A ．实轴长相等 B ．虚轴长相等 C ．焦距相等 D ． 离心率相等 24．（2013重庆）设双曲线C 的中心为点O ，若有且只有一对相较于点O 、所成的角为060的直线11A B 和22A B ，使1122A B A B =，其中1A 、1B 和2A 、2B 分别是这对直线与双曲线C 的交点，则该双曲线的离心率的取值范围是A ．(2]3 B ．[,2)3 C ．()3+∞ D ．[)3+∞ 25．（2012福建）已知双曲线22215x y a -=的右焦点为(3,0)，则该双曲线的离心率等于A ．14B ．4 C ．32D ．4326．（2012湖南）已知双曲线C ：22x a -22y b=1的焦距为10 ，点P （2,1）在C 的渐近线上，则C 的方程为A ．220x -25y =1B ．25x -220y =1C ．280x -220y =1 D ．220x -280y =1 27．（2011安徽）双曲线x y 222-=8的实轴长是A ．2B ．C ．4D ．28．（2011山东）已知双曲线22221(0,0)x y a b a b-=>>的两条渐近线均和圆22:650C x y x +-+=相切，且双曲线的右焦点为圆C 的圆心，则该双曲线的方程为A ．22154x y -=B ．22145x y -=C ．22136x y -=D ．22163x y -= 29．（2011湖南）设双曲线2221(0)9x y a a -=>的渐近线方程为320x y ±=，则a 的值为 A ．4 B ．3 C ．2 D ．130．（2011天津）已知双曲线22221(0,0)x y a b a b-=>>的左顶点与抛物线22(0)y px p =>的焦点的距离为4，且双曲线的一条渐近线与抛物线的准线的交点坐标为(2,1)--，则双曲线的焦距为A ．B ．C ．D ．31．（2010新课标）已知双曲线E 的中心为原点，(3,0)P 是E 的焦点，过F 的直线l 与E 相交于A ，B 两点，且AB 的中点为(12,15)N --,则E 的方程式为A ．22136x y -= B ．22145x y -= C ．22163x y -= D ．22154x y -= 32．（2010新课标）中心在原点，焦点在x 轴上的双曲线的一条渐近线经过点(4,2)-，则它的离心率为A B C ．2 D ．233．（2010福建）若点O 和点F 分别为椭圆22143x y +=的中心和左焦点，点P 为椭圆上的任意一点，则OP FP ⋅的最大值为A ．2B ．3C ．6D ．8 二、填空题34．(2018上海)双曲线2214x y -=的渐近线方程为 ． 35．(2018江苏)在平面直角坐标系xOy 中，若双曲线22221(0,0)x y a b a b-=>>的右焦点(,0)F c 到一条渐近线的距离为2c ，则其离心率的值是 ． 36．（2017江苏）在平面直角坐标系xOy 中 ，双曲线2213x y -=的右准线与它的两条渐近线分别交于点P ，Q ，其焦点是1F ，2F ，则四边形12F PF Q 的面积是 ．37．（2017新课标Ⅰ）已知双曲线C ：22221(0,0)x y a b a b-=>>的右顶点为A ，以A 为圆心，b 为半径做圆A ，圆A 与双曲线C 的一条渐近线交于M 、N 两点．若MAN ∠=60°，则C 的离心率为________．38．（2017山东）在平面直角坐标系xOy 中，双曲线22221(00)x y a b a b-=>>，的右支与焦点为F 的抛物线22(0)x py p =>交于A ，B 两点，若||||4||AF BF OF +=，则该双曲线的渐近线方程为 ．39．（2017北京）若双曲线221y x m-=m =_________．40．(2016年北京)双曲线22221(0,0)x y a b a b-=>>的渐近线为正方形OABC 的边,OA OC所在的直线，点B 为该双曲线的焦点．若正方形OABC 的边长为2，则a =______．41．(2016山东)已知双曲线E ：22221x y a b-=(0,0)a b >>，若矩形ABCD 的四个顶点在E上，AB ，CD 的中点为E 的两个焦点，且2||3||AB BC =，则E 的离心率是 .42．（2015北京）已知双曲线()22210x y a a-=>0y +=，则a = ．43．（2015江苏）在平面直角坐标系xOy 中，P 为双曲线122=-y x 右支上的一个动点．若点P 到直线01=+-y x 的距离大于c 恒成立，则是实数c 的最大值为 ．44．（2015山东）平面直角坐标系xOy 中，双曲线1C ：22221x y a b-=(0,0)a b >>的渐近线与抛物线2C ：22x py =(0p >)交于,,O A B ，若△OAB 的垂心为2C 的焦点，则1C 的离心率为_______．45．（2014山东）已知双曲线22221(0,0)x y a b a b-=>>的焦距为2c ，右顶点为A ，抛物线22(0)x py p =>的焦点为F ，若双曲线截抛物线的准线所得线段长为2c ，且||FA c =，则双曲线的渐近线方程为 ．46．（2014浙江）设直线30(0)x y m m -+=≠与双曲线22221(0,0)x y a b a b-=>>的两条渐近线分别交于点A ，B ，若点(,0)P m 满足||||PA PB =，则该双曲线的离心率是____．47．（2014北京）设双曲线C 经过点()2,2，且与2214y x -=具有相同渐近线，则C 的方程为________；渐近线方程为________．48．（2013陕西）双曲线221169x y -=的离心率为 ．49．（2014湖南）设F 1，F 2是双曲线C ：22221(0,0)x y a b a b-=>>的两个焦点．若在C 上存在一点P ，使PF 1⊥PF 2，且∠PF 1F 2=30°，则C 的离心率为_________．50．（2013辽宁）已知F 为双曲线22:1916x y C -=的左焦点，,P Q 为C 上的点，若PQ 的长等于虚轴长的2倍，点(5,0)A 在线段PQ ，则PQF ∆的周长为 ．51．（2012辽宁）已知双曲线122=-y x ，点21,F F 为其两个焦点，点P 为双曲线上一点，若21PF PF ⊥，则21PF PF +的值为 ．52．（2012天津）已知双曲线)0,0(1:22221>>=-b a by a x C 与双曲线1164:222=-y x C 有相同的渐近线，且1C 的右焦点为F ,则a = b = ．53．（2012江苏）在平面直角坐标系xOy 中，若双曲线22214x y m m -=+则m 的值为 ．54．（2011山东）已知双曲线22221(0,0)x y a b a b -=>>和椭圆221169x y +=有相同的焦点，且双曲线的离心率是椭圆离心率的两倍，则双曲线的方程为 ．55．(2011北京)已知双曲线2221(0)y x b b-=>的一条渐近线的方程为2y x =，则b = ．三、解答题56．（2014江西）如图，已知双曲线C ：2221x y a-=(0a >)的右焦点F ，点B A ,分别在C的两条渐近线上，x AF ⊥轴，BF OB AB ,⊥∥OA (O 为坐标原点）．（1）求双曲线C 的方程；（2）过C 上一点)0)((00,0≠y y x P 的直线1:020=-y y axx l 与直线AF 相交于点M ，与直线23=x 相交于点N ，证明：当点P 在C 上移动时，NFMF 恒为定值，并求此定值．57．（2011广东）设圆C 与两圆2222(5)4,(5)4x y x y ++=+=中的一个内切，另一个外切．（1）求C 的圆心轨迹L 的方程； （2）已知点M 3545(,5,0)55F ，且P 为L 上动点，求MP FP -的最大值及此时点P 的坐标．专题九 解析几何第二十七讲 双曲线答案部分2019年1. 解析 双曲线22:142x y C -=的右焦点为6,0)F ，渐近线方程为：22y x =±，不妨设点P 在第一象限，可得2tan POF ∠=63P ，所以PFO △的面积为： 133262=．故选A ．2. 解析 因为双曲线2221(0)y x b b-=>经过点(3,4)，所以221631b-=，解得22b =，即2b =． 又1a =，所以该双曲线的渐近线方程是2y x =±． 3.解析 如图所示，因为1F A AB =,所以A 为1F B 的中点. 又O 为12F F 的中点，所以212AOBF ，212AO BF =. 因为120F B F B ⋅=，所以1290F BF ∠=︒， 且O 为12F F 的中点，所以12212OB F F OF c ===. 由212AOBF 得2121BOF AOF BF F ∠=∠=∠，所以2OB BF =， 因此2OPF △为等边三角形，260BOF ∠=︒，即渐近线的斜率为3，也即3ba=， 所以2212b e a=+=.4．A 解析：解法一：由题意，把2c x =代入222x y a +=，得2224c PQ a =-，再由PQ OF =，得2224ca c -=，即222a c =，所以222c a=，解得2c e a ==.故选A ．解法二：如图所示，由PQ OF =可知PQ 为以OF 为直径圆的另一条直径，所以,22c c P ⎛⎫± ⎪⎝⎭，代入222x y a +=得222a c =， 所以222c a=，解得2c e a ==.故选A ．解法三：由PQ OF =可知PQ 为以OF 为直径圆的另一条直径，则1222OP a OF ===，2c e a ==故选A ． 5．解析 根据渐进线方程为0x y ±=的双曲线，可得a b =，所以2c a =，则该双曲线的离心率为2ce a==C ． 6.解析 因为抛物线24y x =的焦点为F ，准线为l ，所以()1,0F ，准线l 的方程为1x =-.因为与双曲线()222210,0x y a b a b=>>的两条渐近线分别交于点A 和点B ，且4AB OF =（为原点），所以2b AB a =，1OF =，所以24b a=，即2b a =， 所以225c a b a +=，所以双曲线的离心率为5ca==．故选D ．2010-2018年1．B 【解析】由题可知双曲线的焦点在x 轴上，因为222314c a b =+=+=，所以2c =，故焦点坐标为(2,0)-，(2,0)．故选B ．2．B 【解析】因为双曲线2213-=x y 的渐近线方程为33=±y x ，所以60∠=MON ．不妨设过点F 的直线与直线3=y 交于点M ，由∆OMN 为直角三角形，不妨设90∠=OMN ，则60∠=MFO ，又直线MN 过点(2,0)F ，所以直线MN 的方程为3(2)=-y x ，由2)⎧=-⎪⎨=⎪⎩y x y x，得32⎧=⎪⎪⎨⎪=⎪⎩x y3(,22M ，所以||==OM所以|||3==MN OM ．故选B ． 3．A 【解析】解法一由题意知，==ce a，所以=c，所以=b ，所以=b a=±=by x a，故选A ．解法二由===c e a，得=ba，所以该双曲线的渐近线方程为=±=by x a．故选A ． 4．C 【解析】不妨设一条渐近线的方程为by x a=， 则2F 到by x a =的距离d b ==， 在2Rt F PO ∆中，2||F O c =，所以||PO a =，所以1||PF =，又1||F O c =，所以在1F PO ∆与2Rt F PO ∆中，根据余弦定理得22212)cos cos 2a c aPOF POF ac c+-∠==-∠=-，即2223)0a c +-=，得223a c =．所以ce a==．故选C ． 5．C 【解析】通解 因为直线AB 经过双曲线的右焦点，所以不妨取2(,)b A c a，2(,)b B c a -，取双曲线的一条渐近线为直线0bx ay -=，由点到直线的距离公式可得221bc b d c -==，222bc b d c +==， 因为126d d +=，所以226bc b bc b c c-++=，所以26b =，得3b =．因为双曲线22221(0,0)x y a b a b -=>>的离心率为2，所以2ca=，所以2224a b a+=，所以2294a a +=，解得23a =， 所以双曲线的方程为22139x y -=，故选C ． 优解 由126d d +=，得双曲线的右焦点到渐近线的距离为3，所以3b =．因为双曲线22221(0,0)x y a b a b -=>>的离心率为2，所以2ca=，所以2224a b a+=，所以2294a a +=，解得23a =， 所以双曲线的方程为22139x y -=，故选C ． 6．A 【解析】双曲线C 的渐近线方程为0bx ay ±=，圆心(2,0)到渐近线的距离为2bd c==，圆心(2,0)到弦的距离也为d ==所以2b c =222c a b =+，所以得2c a =，所以离心率2ce a==，选A ． 7．B【解析】由题意可得：b a =，3c =，又222a b c +=，解得24a =，25b =， 则C 的方程为2145x y 2-=．选B ． 8．B 【解析】设(,0)F c -，双曲线的渐近线方程为b y x a =±，由44PF k c c-==-，由题意有4bc a=，又c a =222c a b =+，得b =，a =．选B ．9．D 【解析】不妨设A 在第一象限，(,)A x y ，所以2242x y b y x ⎧+=⎪⎨=⎪⎩，解得x y ⎧=⎪⎪⎨⎪=⎪⎩， 故四边形ABCD的面积为2324424bxy b b ===+，解得212b =．故所求的双曲线方程为2224=11x y -，选D ． 10．A 【解析】由题意得22()(3)0m n m n +->，解得223m n m -<<，又由该双曲线两焦点间的距离为4，得M 2234m n m n ++-=，即21m =，所以13n -<<．11．A 【解析】设1(,0)F c -，将x c =-代入双曲线方程，得22221c y a b -=，化简得2by a=±，因为211sin 3MF F ∠=，所以222212112||tan ||222b MF b c a a MF F F F c ac ac -∠=====，12222c a e a c e -=-=210e --=，所以e =A ． 12．D 【解析】由双曲线的标准方程2213y x -=得，右焦点(2,0)F ，两条渐近线方程为y =，直线AB ：2x =，所以不妨设取(2,A，(2,B -，则||AB =，选D ．13．B 【解析】由双曲线定义得1226PF PF a -==，即236PF -=，解得29PF =，故选B ．14．D【解析】由题意1e ==2e ==∵()()b b m m b a a a m a a m +--=++，由于0m ，0a ，0b ， 所以当a b 时，01b a <<，01b m a m +<<+，b b m a a m +<+，22()()b b m a a m+<+， 所以12e e <；当a b <时，1ba>，1b m a m +>+，而b b m a a m +>+，22()()b b m a a m +>+， 所以12e e >．所以当a b >时，12e e <；当a b <时，12e e >．15．C 【解析】由题意，选项,A B 的焦点在x 轴，故排除,A B ，C 项的渐近线方程为2204y x -=，即2y x =±，故选C ． 16．A 【解析】由题意知22a，21b ，所以23c，不妨设1(F，2F ，所以100(,)=--MF x y ，200(3,)=-MF x y ，又∵00(,)M x y 在双曲线上，所以220012x y -=，即220022x y =+，222120003310MF MF x y y ⋅=-+=-<，所以033-<<y ，故选A ． 17．A 【解析】 由题意22(,0),(,),(,)b b A a B c C c a a-，由双曲线的对称性知D 在x 轴上，设(,0)D x ，由BD AC ⊥得221b b a a c x a c-⋅=---，解得42()b c x a c a -=-，所以42()b c x a a c a c a -=<=+-，所以42222b c a b a <-=221b a⇒<01b a ⇒<<，而双曲线的渐近性斜率为ba±，所以双曲线的渐近线的斜率取值范围是(1,0)(0,1)-，选A ．18．A 【解析】双曲线方程为22133x y m -=，焦点F 到一条渐近线的距离为b =A ． 19．A 【解析】∵09k <<，∴90,250k k ->->，本题两条曲线都是双曲线，又25(9)(25)9k k +-=-+，∴两双曲线的焦距相等，选A ．20．A 【解析】 依题意得22225ba cc a b ，所以25a，220b ，双曲线的方程为221520x y ．21．B 【解析】由双曲线的定义得12||||||2PF PF a -=，又12||||3PF PF b +=，所以22221212(||||)(||||)94PF PF PF PF b a +--=-，即124||||9PF PF ab =，因此22949b a ab -=，即299()40b b aa --=，则（31b a +）（34ba-）=0，解得41(33b b a a ==-舍去），则双曲线的离心率53e ==．22．C 【解析】由题知，2c a =，即54=22c a =222a b a +，∴22b a =14，∴b a =12±，∴C 的渐近线方程为12y x =±，故选C ． 23．D 【解析】双曲线1C 的离心率是11cos e θ=，双曲线2C 的离心率是21cos e θ==，故选D ． 24．A 【解析】设双曲线的焦点在x 轴上，则由作图易知双曲线的渐近线的离心率ba必须满足3b a <，所以21()33b a <≤，241()43b a<+≤，2<，又双曲线的离心率为c e a ==23e <≤． 25．C 【解析】∵双曲线22215x y a -=的右焦点为（3，0），∴2a +5=9，∴2a =4，∴a =2∵c =3，∴32c e a ==，故选C ． 26．A 【解析】设双曲线C ：22x a -22y b=1的半焦距为c ，则210,5c c ==．又C 的渐近线为b y x a =±，点P(2,1)在C 的渐近线上，12ba∴=，即2a b =．又222c a b =+，a ∴==，∴C 的方程为220x -25y =1．27．C 【解析】x y 222-=8可变形为22148x y -=，则24a =，2a =，24a =.故选C ． 28．A 【解析】圆22:(3)4C x y -+=，3,c =而32bc =，则22,5b a ==，应选A ． 29．C 【解析】由双曲线方程可知渐近线方程为3y x a=±，故可知2a =．30．B 【解析】双曲线22221(0,0)x y a b a b -=>>的渐近线为by x a=±，由双曲线的一条渐近线与抛物线的准线的交点坐标为（－2，－1）得22p-=-，即4p =， 又∵42p a +=，∴2a =，将（－2，－1）代入by x a=得1b =，∴c ==2c =31．B 【解析】由双曲线E 的中心为原点，(3,0)P 是E 的焦点可设双曲线的方程为2222221(9)x y a b a b -=+=，设1122(,),(,)A x y B x y ，即 2222112222221,1x y x y a b a b -=-= 则22121222121212015115312y y x x b b x x a y y a -+-+=⋅=⋅==-+-+，则22225,5,44b b a a ===，故E 的方程式为22145x y -=.应选B ． 32．D 【解析】设双曲线的方程为22221(0,0)x y a b a b -=>>，其渐近线为x aby ±=，∵点(4,2)-在渐近线上，所以12b a =，由2e ==． 33．C 【解析】由题意，F （－1，0），设点P 00(,)x y ，则有2200143x y +=, 解得22003(1)4x y =-， 因为00(1,)FP x y =+，00(,)OP x y =，所以2000(1)OP FP x x y ⋅=++=00(1)OP FP x x ⋅=++203(1)4x -=20034x x ++， 此二次函数对应的抛物线的对称轴为02x =-，因为022x -≤≤，所以当02x =时，OP FP ⋅取得最大值222364++=，选C ． 34．12y x =±【解析】由题意2a =，1b =，∴12b y x x a =±=±．35．2【解析】不妨设双曲线的一条渐近线方程为b y x a =2b ==，所以222234b c a c =-=，得2c a =，所以双曲线的离心率2ce a==． 36．232a x c ==，渐近线的方程为3y x =±，设3(,22P，则3(,22Q -，1(2,0)F -，2(2,0)F ， 所以四边形12F PF Q的面积为1211||||422F F PQ =⨯=． 37．3【解析】如图所示，AH MN ⊥，AM AN b ==，MAN ∠=60°， x所以30HAN ∠=，又MN 所在直线的方程为by x a=， (,0)A a 到MN的距离AH =，在Rt HAN ∆中，有cos HA HAN NA =，所以2==因为222c a b =+a c =，所以c e a ==．38．y x =【解析】设11(,)A x y ，22(,)B x y ，由抛物线的定义有1212||||22p p AF BF y y y y p +=+++=++，而||2p OF =， 所以1242py y p ++=⨯，即12y y p +=，由2222212x y a b x py⎧-=⎪⎨⎪=⎩得2222220a y pb y a b -+=，所以21222pb y y a +=， 所以222pb p a=，即a =，所以渐近性方程为2y x =±． 39．2【解析】221,a b m ==，所以1c a ==，解得2m =． 40．2【解析】不妨令B 为双曲线的右焦点，A 在第一象限，则双曲线图象如图∵OABC 为正方形，2=OA∴==c OB ，π4∠=AOB ∵直线OA 是渐近线，方程为=b y x a ，∴tan 1=∠=bAOB a又∵2228+==a b c ∴2=a41．2【解析】由题意||2BC c =，所以||3AB c =，于是点3(,)2cc 在双曲线E 上，代入方程，得2222914c c a b -=，在由222a b c +=得E 的离心率为2ce a==，应填2. 42．3【解析】因为双曲线()22210x y a a -=>的一条渐近线为y =，所以1a=故3a =． 43．2(,),(1)P x y x ≥，因为直线10x y -+=平行于渐近线0x y -=，所以c 的最大值为直线10x y -+=与渐近线0x y -== 44．32【解析】22122:1(0,0)x y C a b a b -=>>的渐近线为b y x a =±，则2222(,)pb pb A a a ，2222(,)pb pb B a a -，22:2(0)C x py p =>的焦点(0,)2p F ， 则22222AFpb pa a k pb b a-==，即2254b a =，2222294c a b a a +==，32c e a ==． 45．y x =±【解析】抛物线的准线2p y =-，与双曲线的方程联立得2222(1)4p x a b =+，根据已知得2222(1)4p a c b+= ①，由||AF c =得2224p a c += ②，由①②得22a b =，即a b =，所以所求双曲线的渐近线方程为y x =±．46．2【解析】联立直线方程与双曲线渐近线方程by x a=±可解得交点为(,)33am bm A b a b a --，(,)33am bm B b a b a -++，而13AB k =，由||||PA PB =，可得AB 的中点3333(,)22am am bm bmb a b a b a b a -+-+-+与点)0,(m P 连线的斜率为-3，可得224b a =，所以e =47．221312x y -= 2y x =±【解析】设与2214y x -=具有相同渐近线的双曲线C 的方程为224y x k -=，将点()2,2代入C 的方程中，得3k =-．∴双曲线的方程为221312x y -=，渐近线方程为2y x =±．48．45【解析】。

2019年高考数学（理）精品资料：
2.10 椭圆、双曲线、抛物线的几何性质的应用（练）
1.练高考
1.【2018年新课标I卷理】设抛物线C：y2=4x的焦点为F，过点（–2，0）且斜率为的直线与C交于M，N两点，则=
A．5 B．6 C．7 D．8
【答案】D
2.【2018年新课标I卷理】已知双曲线C：，O为坐标原点，F为C的右焦点，过F 的直线与C的两条渐近线的交点分别为M、N.若OMN为直角三角形，则|MN|=
A． B．3 C． D．4
【答案】B
【解析】
根据题意，可知其渐近线的斜率为，且右焦点为，
从而得到，所以直线的倾斜角为或，
根据双曲线的对称性，设其倾斜角为，
可以得出直线的方程为，
分别与两条渐近线和联立，
求得，
所以，故选B.
3.【2018年全国卷Ⅲ理】设,是双曲线（）的左、右焦点，是坐标
原点．过作的一条渐近线的垂线，垂足为．若，则的离心率为
A． B． C． D．
【答案】B
【解析】
由题可知
在中，
在中,
故选C.
4. 【2018年全国卷II理】已知，是椭圆的左，右焦点，是的
左顶点，点在过且斜率为的直线上，为等腰三角形，，则的离心率为
A． B． C． D．
【答案】D。

地地道道的达到 第二讲 椭圆、双曲线、抛物线的定义、方程与性质一、选择题x 2 y 21．(2018 ·广西南宁模拟 ) 双曲线 25－ 20＝ 1 的渐近线方程为 ()45A ． y ＝± 5xB ． y ＝± 4x12 5C ． y ＝± 5xD ． y ＝± 5 xx 2 y 2b分析：在双曲线 25－ 20＝1中， a ＝5， b ＝ 2 5，而其渐近线方程为 y ＝± a x ，∴其渐2 5近线方程为 y ＝± 5 x ，应选 D.答案： D22x y 22M 在 x 2．已知椭圆 C 的方程为 16＋ m ＝ 1( m ＞0) ，假如直线 y ＝ 2 x 与椭圆的一个交点 轴上的射影恰巧是椭圆的右焦点 F ，则 m 的值为 ( )A ． 2B ． 2 2C ． 8D ． 2 3分析：依据已知条件得c ＝222－ 2x 2y 216－ m ，则点16－ ，16 m 在椭圆＋ 2＝ 1( mm216m22＞0) 上，∴ 16－ m 16－ m＝ 22.＋2＝ 1，可得162mm答案： B3．(2018 ·张掖模拟 ) 双曲线 x 2 y 20) 的渐近线与圆 x 222－ 2＝ 1( a ＞ 0，b ＞＋ ( y － 2)＝1 相切，ab则双曲线的离心率为 ()A. 2B. 3C ．2 D ． 3x 2 y 2x 2y － 2)2相切，则圆心 (0,2) 到直线 －ay分析：双曲线 2－2＝1 的渐近线与圆＋(＝ 1abbx2a2ac＝0 的距离为 1，因此a 2＋b2＝1，即c＝1，因此双曲线的离心率e ＝a ＝ 2，应选 C.答案： Cx 2 y 24．(2017 ·高考全国卷Ⅲ ) 已知椭圆 C ： a 2＋ b 2＝ 1( a >b >0) 的左、右极点分别为 A 1、 A 2 ， 且以线段 A A 为直径的圆与直线 － ay ＋ 2 ＝ 0 相切，则 C 的离心率为 ()地地道道的达到6 3 2 1 A. 3B. 3C.3D. 3分析：以线段 A 1 A 2 为直径的圆的圆心为坐标原点O (0,0) ，半径为 a . 由题意，圆心到直线－ ＋ 2 2ab＝ ，即 2＝ 322b 2 2 6bx ＝ 0 的距离为a . 又e ＝ 1－2＝，因此＝ .ay aba 2＋ b2aba3e 3答案： Ax 2 y 25．已知双曲线 a 2－ b 2＝ 1( a ＞0， b ＞ 0) 的焦距为 4 5，渐近线方程为 2x ± y ＝ 0，则双曲线的方程为 ( )x 2y 2＝ 1x 2 y 2A. －B.－ ＝1416164x 2y 2x 2 y 2C. 16－ 64＝ 1D. 64－ 16＝ 122分析：易知双曲线x2－ y2＝ 1( ＞ 0， ＞ 0) 的焦点在x 轴上，因此由渐近线方程为 2 ±yababxb222＝0，得a ＝ 2，因为双曲线的焦距为 4 5，因此 c ＝25，联合 c ＝ a ＋ b ，可得 a ＝ 2，b ＝ 4，x 2 y 2因此双曲线的方程为4－ 16＝ 1，应选 A.答案： A6．(2018 ·长春模拟 ) 已知O 为坐标原点，设 1， 2 分别是双曲线 x 2－ y 2＝ 1 的左、右焦F F点， P 为双曲线上随意一点，过点F 作∠ F PF 的均分线的垂线，垂足为H ，则 | OH | ＝()112A ． 1B ． 21 C ． 4D. 2分析：不如设 P 在双曲线的左支，如图，延伸F 1H 交 PF 2于点 ，因为PH既是∠12的均分线又垂直于1，故△1M F PFF MPFM为等腰三角形， |PF | ＝| PM |且 H 为 F M 的中点，因此OH 为△111 2121212MFF 的中位线，因此 | OH |＝ 2| MF | ＝ 2(| PF | － | PM |) ＝ 2(| PF | － | PF 1|) ＝ 1. 应选 A.答案： Ax 2 y 27．(2018 ·高考全国卷Ⅲ ) 已知双曲线 C ：a 2－ b 2＝ 1( a ＞0， b ＞ 0) 的离心率为 2，则点 (4,0) 到 C 的渐近线的距离为 ()A. 2B ．23 2C. 2c分析：由题意，得e ＝ a ＝渐近线方程为 x ± y ＝ 0，点 (4,0) 应选 D.答案： DD ．2 22， c 2＝a 2＋b 2，得 a 2＝b 2 . 又因为 a ＞ 0， b ＞0，因此 a ＝ b ，4到渐近线的距离为＝2 2， 2x 2 y 28．(2018 ·石家庄一模 ) 已知直线 l ：y ＝2x ＋ 3 被椭圆 C ：a 2＋ b 2＝ 1( a ＞ b ＞ 0) 截得的弦 长为 7，有以下直线：① y ＝ 2x － 3；② y ＝ 2x ＋ 1；③ y ＝－ 2x － 3；④ y ＝－ 2x ＋ 3. 此中被椭 圆 C 截得的弦长必定为 7 的有 ()A ．1 条B ．2 条C ．3 条D ．4 条分析：易知直线 y ＝2x － 3 与直线 l 对于原点对称，直线 y ＝－ 2x － 3 与直线 l 对于 x轴对称，直线y ＝－ 2x ＋ 3 与直线 l 对于 y 轴对称，故由椭圆的对称性可知，有3 条直线被椭圆 C 截得的弦长必定为 7.选C.答案： Cx 2y 29．(2018 ·洛阳模拟 ) 设双曲线 C ：16－ 9 ＝ 1 的右焦点为 F ，过 F 作双曲线 C 的渐近线 的垂线，垂足分别为 M ，N ，若 d 是双曲线上随意一点d)P 到直线 MN 的距离，则 | | 的值为 (PF3 4 A. 4 B. 5C. 5D ．没法确立4x 2y 2分析：双曲线 C ： 16－ 9 ＝ 1 中， a ＝ 4， b ＝ 3， c ＝ 5，右焦点 F (5,0) ，渐近线方程为 y＝± 3 . 不如设 在直线 y ＝ 3 上， N 在直线 y ＝－ 3 上，则直线 的斜率为－4，其方程4xM4x4xMF3433416为 y ＝－ 3( x － 5) ，设 M ( t ， 4t ) ，代入直线 MF 的方程，得 4t ＝－ 3( t － 5) ，解得 t ＝ 5 ，即16 12 16 12 16M ( 5 ， 5 ) ．由对称性可得 N ( 5 ，－ 5 ) ，因此直线 MN 的方程为 x ＝ 5 . 设 P ( m ， n ) ，则 d ＝16 2291dm n 2 222|＝| m － 5 | ， 16－ 9 ＝ 1，即 n ＝ 16( m － 16) ，则 | PF | ＝m －＋n ＝ 4|5 m －16|. 故 |PF16| m － 5 |41＝ 5，应选 B.4|5 m － 16|答案： B2210．(2018 ·高考全国卷Ⅰ ) 设抛物线 C ： y ＝ 4 x 的焦点为 F ，过点 ( － 2,0) 且斜率为 3的 直线与C 交于 ， 两点，则 →· →＝ ()M NFM FNA ． 5B ． 6C ． 7D ． 82分析：由题意知直线MN 的方程为 y ＝ 3( x ＋2) ，2y ＝x ＋ ，联立直线与抛物线的方程，得3y 2＝ 4x ，x ＝ 1， x ＝ 4， 解得或y ＝ 4.y ＝ 2不如设 M 为 (1,2) ， N 为 (4,4) ．又∵抛物线焦点为 → →F (1,0) ，∴ FM ＝(0,2) ，FN ＝ (3,4) ， → → ∴ FM ·FN ＝0×3＋2×4＝ 8. 应选 D. 答案： Dx 2 y 211．(2018 ·广西五校联考 ) 已知点 F 1，F 2 分别是双曲线 a 2－ b 2 ＝1( a ＞ 0，b ＞ 0) 的左、右焦点，过 F 且垂直于 x 轴的直线与双曲线交于→ → M ， N 两点，若 MF · NF ＞0，则该双曲线的离21 1心率 e 的取值范围是 ()A ．( 2， 2＋1)B ．(1， 2＋1)C ．(1， 3)D ． ( 3，＋∞)分析：设 F 1( － c, 0) ， F 2( c, 0) ，c 2 y 2 b 2依题意可得 a 2－ b 2＝ 1，获得 y ＝ a ，b 2b 2不如设 M c ， a ，N c ，－ a ，则 → → ＝ － 2c ，－ b 2 · － 2c ， b 2 ＝ 4c2 b 41·1－2＞，MFNFa aa2 2 2 2 2获得 4a c － ( c － a ) ＞ 0，即 a 4＋ c 4－6a 2c 2＜ 0，故 e 4－ 6e 2＋ 1＜ 0，解得 3－ 2 2 ＜e 2＜ 3＋ 2 2，又 e ＞1，因此 1＜ e 2＜ 3＋2 2，解得 1＜ e ＜ 1＋ 2答案： B21 12 212．(2018 ·南昌模拟 ) 抛物线 y ＝ 8x 的焦点为 F ，设 A ( x ， y ) ， B ( x ， y ) 是抛物线上的两个动点，若 x 1＋ 2 3 的最大值为 ( )2＋4＝ | |，则∠x AB AFB 3π3πA.B.3 4 5π2πC. 6D. 3分析：由抛物线的定义可得2 3| AF | ＝ x ＋ 2， | BF | ＝ x ＋ 2，又 x ＋ x ＋ 4＝3 | AB|，12122 3得|AF |＋|BF |＝ 3 |AB |，3因此 | AB | ＝ 2 (| AF | ＋| BF |) ．| AF | 2＋| BF | 2－| AB | 2因此 cos ∠ AFB ＝2| AF | ·|BF || AF 2＋ BF 2－ 3AF ＋ BF2|||2 ( |||| )＝2| AF | ·|BF |121 2 3 4| AF | ＋4| BF | － 2| AF | ·|BF |＝2| |·| |AFBF1 ||| |3 1| AF | | BF | 3 1AF BF ＜ π ，＝＋－≥×2·－＝－，而0＜∠8 | BF || AF |4 8| BF | | AF |42AFB2π因此∠ AFB 的最大值为 3 .答案： D二、填空题x 2 y 2213．(2018 ·成都模拟 ) 已知双曲线 a 2－ 2 ＝ 1( a ＞ 0) 和抛物线 y ＝ 8x 有同样的焦点，则双曲线的离心率为 ________．2x 2 y 2分析：易知抛物线 y ＝ 8x 的焦点为 (2,0) ，因此双曲线 a 2 － 2 ＝ 1 的一个焦点为 (2,0) ，2 2c 2 则 a ＋ 2＝ 2 ，即 a ＝ 2，因此双曲线的离心率e ＝ a ＝ 2 ＝ 2.答案：2y 2 x 214．(2018 ·武汉调研 ) 双曲线 Γ ： a 2－ b 2＝1( a ＞ 0，b ＞ 0) 的焦距为10，焦点到渐近线的距离为 3，则 Γ 的实轴长等于 ________．a|5 b | 5b分析：双曲线的焦点 (0,5) 到渐近线 y ＝ b x ，即 ax －by ＝ 0 的距离为a2＋ b2＝ c ＝b ＝ 3，因此 a ＝ 4,2 a ＝ 8.答案： 815．(2018 ·唐山模拟 ) 过抛物线 y 2＝2px ( p ＞ 0) 的焦点 F 作直线交抛物线于 A ， B 两点，若| AF | ＝ 2| BF | ＝ 6，则 p ＝ ________.分析：设 AB 的方程为 x ＝ my ＋2， A ( x ， y ) ， B ( x ， y ) ，且 x ＞ x ，将直线 AB 的方程p1 12212代入抛物线方程得22y y2,4x x2l ，过 Ay － 2pmy －p ＝ 0，因此＝－ p＝p . 设抛物线的准线为1 212作 AC ⊥ l ，垂足为 C ，过 B 作 BD ⊥ l ，垂足为 D ，因为 | AF | ＝2| BF | ＝6，依据抛物线的定义知，| AF | ＝ | AC | ＝ x ＋pp＋2＝ 6， | BF| ＝| BD| ＝ x ＋ 2＝ 3，因此 x － x ＝ 3，x ＋ x ＝ 9－p ，因此 ( x12121212 2 12 21 2 2x ) －( x － x ) ＝ 4x x ＝p ，即 18p －72＝ 0，解得 p ＝ 4.答案： 42216．(2017 ·高考全国卷Ⅰ改编 ) 设 ， B 是椭圆 ： x＋ y ＝ 1 长轴的两个端点．若 C 上A Cm3存在点 M 知足∠ AMB ＝120°，则m 的取值范围是 ________．分析：当 0＜ m ＜ 3 时，焦点在 x 轴上，要使 C 上存在点 M 知足∠ AMB ＝120°，a 3，即3则 ≥tan 60 °＝≥ 3，bm解得 0＜ m ≤1.当 m ＞3 时，焦点在 y 轴上，要使 C 上存在点 M 知足∠ AMB ＝120°，a 3，即m则 ≥tan 60 °＝≥ 3，解得 ≥9.bm3故 m 的取值范围为 (0,1] ∪ [9 ，＋∞ ) ．答案： (0,1] ∪ [9 ，＋∞)地地道道的达到 三、解答题17．(2018 ·辽宁五校联考 ) 已知椭圆 C ：x2 22＋ y2＝1( a ＞ b ＞0) 的左、右焦点分别为F 1，a bF 2，上极点为 B ，若△ BF 1F 2 的周长为 6，且点 F 1 到直线 BF 2 的距离为 b .(1) 求椭圆 C 的方程；(2) 设1 ， 2 是椭圆C 长轴的两个端点，P 是椭圆C 上不一样于1， 2 的随意一点，直线A A A AA 1P 交直线 x ＝m 于点 M ，若以 MP 为直径的圆过点 A 2，务实数 m 的值．分析： (1) 由题意得 F 1 ( － c, 0) ， F 2( c, 0) ， B (0 ，b ) ，则 2a ＋ 2c ＝ 6，①直线 BF 2 的方程为 bx ＋ cy －bc ＝ 0，| － bc － bc | 因此 22 ＝ b ，即 2c ＝ a ，② c ＋ b 又 a 2＝ b 2＋c 2，③因此由①②③可得 a ＝ 2，b ＝ 3，x 2 y 2因此椭圆 C 的方程为 4 ＋ 3 ＝1.(2) 不如设 A 1( － 2,0) ， A 2(2,0) ， P ( x 0， y 0) ，y 0则直线 A 1P 的方程为 y ＝ x 0＋ 2( x ＋ 2) ，y 0因此 M ( m ， x 0＋ 2( m ＋ 2)) ，22x 0又点 P 在椭圆 C 上，因此 y 0＝ 3(1－4)，→ →若以 MP 为直径的圆过点 A 2，则 A 2M ⊥ A 2P ， A 2M · A 2P ＝ 0，y 02因此 ( m － 2，( m ＋2)) ·(x 0－ 2， y 0) ＝ ( m － 2)( x 0－ 2) ＋y 0( m ＋ 2) ＝ ( m － 2)( x 0－x ＋ 2x ＋ 22x 0－1 742) ＋ x 0＋ 2 ( m ＋ 2) ＝ ( x 0－ 2)( 4m － 2) ＝ 0.又点 P 不一样于点 A 1， A 2，因此 x 0≠± 2，因此 m ＝ 14.18．(2018 ·福州模拟 ) 抛物线 C ： y ＝2x 2－ 4x ＋ a 与两坐标轴有三个交点，此中与y 轴的交点为 P .(1) 若点 Q ( x ， y )(1 ＜ x ＜4) 在 C 上，求直线 PQ 斜率的取值范围；(2) 证明：经过这三个交点的圆 E 过定点．分析： (1) 由题意得(0 ， )( ≠0)， (2 2－4 ＋ )(1 ＜ ＜4)，故 k PQ ＝ 2x 2－ 4x ＋ a －a ＝ 2x －4， x因为 1＜ x ＜ 4，因此－ 2＜k PQ ＜ 4，因此直线 PQ 的斜率的取值范围为 ( － 2,4) ．(2) 证明：法一： P (0 ， a )( a ≠0) ．令 2x 2－4 ＋ ＝ 0，则 ＝16－ 8 a ＞0， a ＜ 2，且 a ≠0，x a解得 x ＝1±4－ 2a，2故抛物线C 与 x 轴交于4－ 2a4－ 2a(1 －，0)， (1＋，0) 两点．A2B2故可设圆 E 的圆心为 M (1 ， t ) ，由 | | 2＝|| 2，得 12＋ ( t－ )2＝(4－ 2a ) 2＋2，解得 t ＝ a＋ 1， MPMAa2t2 4则圆 E 的半径 r ＝ | MP |＝1 a 21＋ 4－2.因此圆 E 的方程为 ( x － 1) 2a1 2 1 a 2，＋ ( y －2 － )＝1＋( － )44 2221a因此圆 E 的一般方程为 x ＋y － 2x － ( a ＋ 2) y ＋ 2＝ 0，即 x 2＋ y 2－2x － 1y ＋a ( － y ) ＝0.221x 2＋ y 2－2 －1＝ 0， x ＝ 0，x ＝ 2，x 2y由得1或11y ＝ 2y ＝ 2，2－ y ＝ 0，1 1 故圆 E 过定点 (0， ) ，(2， ) ．22法二： P (0 ，a )( a ≠0) ，设抛物线 C 与 x 轴的两个交点分别为A ( x 1, 0) ，B ( x 2, 0) ，圆 E 的一般方程为 x 2＋ y 2＋ Dx ＋Fy ＋ G ＝ 0，则x 12＋1＋ ＝0，Dx G2＋G ＝ 0，x 2＋ Dx 2a 2＋＋ ＝0.Fa G22a因为 x 1，x 2 是方程 2x － 4x ＋ a ＝ 0，即 x －2x ＋2＝ 0 的两根，2a2a因此 x 1－2x 1＋ 2＝ 0，x 2－ 2x 2 ＋2＝ 0，a因此 D ＝－ 2， G ＝ 2，2－ G － a1因此圆 E 的一般方程为221 ax ＋y － 2x － ( a ＋ ) y ＋ ＝ 0，222211即 x ＋ y －2x － 2y ＋a ( 2－ y ) ＝0.221x ＋ y － 2x － y ＝ 0，由得12－ y ＝ 0，11故圆 E 过定点 (0，2) ，(2，2) ．x ＝ 0，x ＝ 2，y ＝1 或12 y ＝ ，2y 2x 219．(2018 ·广州模拟 ) 如图，在直角坐标系xOy 中，椭圆 ： 2＋ 2 ＝ 1( ＞ ＞0)的上C aba b焦点为 F ，椭圆 C 的离心率为1 2 62，且过点 (1 ，3) ．1(1) 求椭圆 C 的方程；(2) 设过椭圆 C 的上极点 A 的直线 l 与椭圆 C 交于点 B ( B 不在 y 轴上 ) ，垂直于 l 的直线→ →与 l 交于点 M ，与 x 轴交于点H ，若 F 1B ·F 1H ＝ 0，且 | MO |＝ | MA | ，求直线 l 的方程．分析： (1) 因为椭圆C 的离心率为 1c 1a ＝2 .，因此 ＝ ，即2 a 2 c2222223 2y 2 x 2又 a ＝ b ＋c ，因此 b＝3c ，即 b ＝4a ，因此椭圆 C 的方程为 a 2 ＋3 2＝1.4a2 62＝ 4.把点 (1， ) 代入椭圆 C 的方程中，解得a3因此椭圆 C 的方程为y 2＋ x 2＝ 1.43(2) 由 (1) 知， A (0,2) ，设直线 l 的斜率为 k ( k ≠0) ，则直线 l 的方程为 y ＝kx ＋ 2，地地道道的达到y＝kx＋2，由 x2 y2 得 (3 k2＋ 4) x2＋ 12kx＝ 0.3＋4＝1，－12k设 B( x B，y B)，得 x B＝3k2＋4，－6k2＋ 8因此 y B＝3k2＋4，－12k－6k2＋ 8因此 B(3k2＋4，3k2＋4)．设 M( x M，y M)，因为| MO|＝| MA|，因此点 M在线段 OA的垂直均分线上，1 1因此 y M＝1，因为 y M＝ kx M＋2，因此 x M＝－k，即M(－k，1)．设 ( H,0)，又直线垂直于直线l ，因此k1 1 1MH＝－，即＝－ .H x HM k 1 k－k－ xH1 1因此 x ＝k－k，即 H( k－k，0)．H又 F (0,1) →－ 12k 4－ 9k2 → 1，因此 F B＝ 3k＋ 4， 3k＋ 4， F H＝ k－k，－1)．1 12 2 1→ →－ 12k 1 4－ 9k2因为 F1 B· F1H＝0，因此3k2＋4·(k－k)－3 k2＋4＝0，2 6解得 k＝±.32 6因此直线 l 的方程为 y＝±3 x＋2.。

(2019全国1)10.已知椭圆C 的焦点为)0,1(1-F ，)0,1(2F ，过2F 的直线与C 交于A ，B 两点.若||2||22B F AF =，||||1BF AB =，则C 的方程为（ ）A.1222=+y xB. 12322=+y xC.13422=+y xD.14522=+y x答案： B解答：由椭圆C 的焦点为)0,1(1-F ，)0,1(2F 可知1=c ，又 ||2||22B F AF =，||||1BF AB =，可设m BF =||2，则m AF 2||2=，m AB BF 3||||1==，根据椭圆的定义可知a m m BF BF 23||||21=+=+，得a m 21=，所以a BF 21||2=，a AF =||2，可知),0(b A -，根据相似可得)21,23(b B 代入椭圆的标准方程12222=+by a x ，得32=a ，2222=-=c a b ，∴椭圆C 的方程为12322=+yx . (2019全国1)16.已知双曲线C:22221(0,0)x y a b a b-=>>的左、右焦点分别为12,F F ，过1F 的直线与C 的两条渐近线分别交于,A B 两点.若112,0F A AB F B F B =⋅=，则C 的离心率为 . 答案：2解答：由112,0F A AB F B F B =⋅=知A 是1BF 的中点，12F B F B ⊥，又O 是12,F F 的中点，所以OA 为中位线且1OA BF ⊥，所以1OB OF =，因此1FOA BOA ∠=∠，又根据两渐近线对称，12FOA F OB ∠=∠，所以260F OB ∠=︒，221()1tan 602b e a=+=+︒=.(2019全国1) 19.已知抛物线x y C 3:2=的焦点为F ，斜率为23的直线l 与C 的交点为A ，B ，与x 轴的交点为P .（1）若4||||=+BF AF ，求l 的方程； （2）若3=，求||AB . 答案：（1）07128=+-x y ；（2）3134. 解答：（1）设直线l 的方程为b x y +=23，设),(11y x A ，),(22y x B ， 联立直线l 与抛物线的方程：⎪⎩⎪⎨⎧=+=xy b x y 3232消去y 化简整理得0)33(4922=+-+b x b x ，0494)33(22>⨯--=∆b b ，21<∴b ，9)33(421b x x -⨯=+，依题意4||||=+BF AF 可知42321=++x x ，即2521=+x x ，故259)33(4=-⨯b ，得87-=b ，满足0>∆，故直线l 的方程为8723-=x y ，即07128=+-x y .（2）联立方程组⎪⎩⎪⎨⎧=+=xy b x y 3232消去x 化简整理得0222=+-b y y ，084>-=∆b ，21<∴b ，221=+y y ，b y y 221=， 3=，可知213y y -=，则222=-y ，得12-=y ，31=y ，故可知23-=b 满足0>∆， ∴3134|13|941||11||212=+⨯+=-⋅+=y y k AB . （2019全国2）8. 若抛物线)0(22>=p px y 的焦点是椭圆1322=+py p x 的一个焦点，则=p （ ） A.2 B.3 C.4 D.8 答案：D 解答：抛物线)0(22>=p px y 的焦点是)0,2(p，椭圆1322=+p y p x 的焦点是)0,2(p ±，∴p p22=，∴8=p .（2019全国2）11. 设F 为双曲线2222:1(0,0)x y C a b a b-=>>的右焦点，O 为坐标原点，以OF 为直径的圆与圆222x y a +=交于,P Q 两点，若||||PQ OF = ，则C 的离心率为（ ） A.2 B.3 C.2 D.5 答案:A解答：∵||||PQ OF c ==，∴90POQ ∠=, 又||||OP OQ a ==，∴222a a c +=解得2ca=，即2e =.（2019全国2）21. 已知点(2,0),(2,0)A B -，动点(,)M x y 满足直线AM 和BM 的斜率之积为12-，记M 的轨迹为曲线C .（1）求C 的方程，并说明C 什么曲线；（2）过坐标原点的直线交C 于,P Q 两点，点P 在第一象限，PE x ⊥轴，垂足为E ，连结QE 并延长交C 于点G .①证明：PQG ∆是直角三角形； ②求PQG ∆的面积的最大值. 答案： 见解析 解答：(1)由题意得：1222y y x x ⋅=-+-，化简得： 221(2)42x y x +=≠±，表示焦点在x 轴上的椭圆（不含与x 轴的交点）.(2) ①依题意设111100(,),(,),(,)P x y Q x y G x y --，直线PQ 的斜率为k (0)k > ，则101010101010,PG GQ y y y y y y k k x x x x x x ---+===---+，∴2210221012PG GQy y k k x x -⋅==--， 又1111122GQ EQ y y kk k x x x -====--，∴1PG k k=-， ∴PG PQ ⊥，即PQG ∆是直角三角形.②直线PQ 的方程为(0)y kx x =>，联立22142y kx x y=⎧⎪⎨+=⎪⎩ ，得12122121x k y k ⎧=⎪+⎪⎨⎪=⎪+⎩ ， 则直线21111111111:()k PG y x x y x x kx x x k k k k k +=--+=-++=-+， 联立直线PG 和椭圆C ，可得222221122224(1)2(1)(1)40x k x k x x k k k +++-+-=， 则211024(1)2x k x x k ++=+，∴2111012114(1)()222PQGx k S y x x kx k ∆+=+=⋅+ 2222422218()8(1)8(1)1(2)(21)2522()5k k k k k k k k k k k k +++===++++++， 令1t k k=+，则2t ≥，∴2288812(2)5212PQG t t S t t t t∆===-+++， ∵min 19(2)2t t+=， ∴max 16()9PQG S ∆=. （2019全国3）10.双曲线C ：22142x y -=的右焦点为F ，点P 为C 的一条渐近线的点，O 为坐标原点.若||||PO PF =则PFO ∆的面积为（ ）A: 4B:2C:D:答案: A解析：由双曲线的方程22042x y -=可得一条渐近线方程为2y x =；在PFO ∆中||||PO PF =过点P 做PH 垂直OF因为tan ∠得到PO =;所以12S PFO ∆==;故选A;（2019全国3）15.设1F、2F 为椭圆1203622=+y x C ：的两个焦点，M 为C 上一点且在第一象限，若21F MF ∆为等腰三角形，则M 的坐标为________.答案：)15,3(解析：已知椭圆1203622=+y x C ：可知，6=a ，4=c ，由M 为C 上一点且在第一象限，故等腰三角形21F MF ∆中8211==F F MF ，4212=-=MF a MF ,415828sin 2221=-=∠M F F ,15sin 212=∠=M F F MF y M ，代入1203622=+y x C ：可得3=M x .故M 的坐标为)15,3(.（2019全国3）21.已知曲线2:2x C y =，D 为直线12y =-上的动点.过D 作C 的两条切线,切点分别是A ,B ,（1）证明：直线AB 过定点;（2）若以5(0,)2E 为圆心的圆与直线AB 相切,且切点为线段AB 的中点,求四边形ADBE 的面积. 答案：见解析； 解答：（1）当点D 在1(0,)2-时，设过D 的直线方程为012y k x =-，与曲线C 联立化简得 20210x k x -+=，由于直线与曲线相切，则有20440k ∆=-=，解得01k =±，并求得,A B 坐标分别为11(1,),(1,)22-，所以直线AB 的方程为12y =； 当点D 横坐标不为0时，设直线AB 的方程为y kx m =+（0k ≠），由已知可得直线AB 不过坐标原点即0m ≠，联立直线AB 方程与曲线C 的方程可得，22y kx mx y =+⎧⎪⎨=⎪⎩，消y 并化简得2220x kx m --=，∵有两个交点∴2480k m ∆=+>， 设11(,)A x y ，22(,)B x y ，根据韦达定理有，122x x k +=，122x x m =-，由已知可得曲线C 为抛物线等价于函数2()2x f x =的图像，则有()f x x '=，则抛物线在11(,)A x y 上的切线方程为111()y y x x x -=-①， 同理，抛物线在22(,)B x y 上的切线方程为222()y y x x x -=-②， 联立①，②并消去x 可得122112y y y y x x x x ---=-， 由已知可得两条切线的交点在直线12y =-上，则有 22122112112222x x x x x x -----=-，化简得，12212112(1)()2x x x x x x x x --=-，∵0k ≠，∴12x x ≠，即1212112x x x x -=，即为2114m m --=-，解得12m =，经检验12m =满足条件，所以直线AB 的方程为12y kx =+过定点1(0,)2， 综上所述，直线AB 过定点1(0,)2得证.（2）由（1）得直线AB 的方程为12y kx =+，当0k =时，即直线AB 方程为12y =，此时点D 的坐标为1(0,)2-，以5(0,)2E 为圆心的圆与直线AB 相切于1(0,)2F 恰为AB 中点，此时1123322ADBE S AB ED =⋅=⨯⨯=；当0k ≠时，直线AB 方程与曲线方程联立化简得2210x kx --=，122x x k +=，121x x =-，21221y y k +=+，则AB 中点坐标为21(,)2H k k +，由已知可得EH AB ⊥，即2152210EH k k k k k +-⋅=⋅=--， 解得，1k =±，由对称性不妨取1k =，则直线方程为12y x =+， 求得D 的坐标为1(1,)2-，4AB =，E 到直线AB距离1d ==D 到直线AB距离2d ==则121122ADBE S AB d AB d =⋅+⋅=， 综上所述，四边形ADBE 的面积为3或（2019北京）4.已知椭圆2222 1x y a b+=（a ＞b ＞0）的离心率为12，则A. a 2=2b 2B. 3a 2=4b 2C. a =2bD. 3a =4b【答案】B 【解析】【分析】由题意利用离心率的定义和,,a b c 的关系可得满足题意的等式. 【详解】椭圆的离心率2221,2c e c a b a ===-,化简得2234a b =, 故选B.【点睛】本题考查椭圆的标准方程与几何性质,属于容易题,注重基础知识､基本运算能力的考查.（2019北京）18.已知抛物线C ：x 2=−2py 经过点（2，−1）． （Ⅰ）求抛物线C 的方程及其准线方程；（Ⅱ）设O 为原点，过抛物线C 的焦点作斜率不为0的直线l 交抛物线C 于两点M ，N ，直线y =−1分别交直线OM ，ON 于点A 和点B .求证：以AB 为直径的圆经过y 轴上的两个定点． 【答案】(Ⅰ) 24x y =-，1y =； (Ⅱ)见解析. 【解析】【分析】(Ⅰ)由题意结合点的坐标可得抛物线方程，进一步可得准线方程；(Ⅱ)联立准线方程和抛物线方程，结合韦达定理可得圆心坐标和圆的半径，从而确定圆的方程，最后令x =0即可证得题中的结论.【详解】(Ⅰ)将点()2,1-代入抛物线方程：()2221p =⨯-可得：2p =，故抛物线方程：24x y =-，其准线方程为：1y =.(Ⅱ)很明显直线l 的斜率存在，焦点坐标为()0,1-，设直线方程为1y kx =-，与抛物线方程24x y =-联立可得：2440x kx +-=. 故：12124,4x x k x x +=-=-.设221212,,,44x x M x N x ⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭，则12,44OM ONx x k k =-=-， 直线OM 的方程为14x y x =-，与1y =-联立可得：14,1A x ⎛⎫- ⎪⎝⎭，同理可得24,1B x ⎛⎫- ⎪⎝⎭， 易知以AB 为直径的圆的圆心坐标为：1222,1x x ⎛⎫+- ⎪⎝⎭，圆的半径为：1222x x -，且：()1212122222x x k x x x x ++==，12222x x -==则圆的方程为：()()()2222141x k y k -++=+，令0x =整理可得：2230y y +-=，解得：123,1y y =-=，即以AB 为直径的圆经过y 轴上的两个定点()()0,3,0,1-.【点睛】本题主要考查抛物线方程的求解与准线方程的确定，直线与抛物线的位置关系，圆的方程的求解及其应用等知识，意在考查学生的转化能力和计算求解能力.（2019天津）5.已知抛物线24y x =的焦点为F ，准线为l .若与双曲线22221(0,0)x y a b a b-=>>的两条渐近线分别交于点A 和点B ，且||4||AB OF=（O 为原点），则双曲线的离心率为C. 2 【答案】D 【解析】 【分析】只需把4AB OF =用,,a b c 表示出来，即可根据双曲线离心率的定义求得离心率。

2019年高考数学真题分类汇编 专题10：平面解析几何（基础题）1.（2019•浙江）渐近线方程为0=±y x 的双曲线的离心率是（ ） A.22B.1C.2D.2 【答案】 C【考点】双曲线的简单性质【解析】【解答】解：根据双曲线的渐近线方程，得1=ab，所以离心率2==ac e . 故答案为：C.【分析】根据双曲线的渐近线方程，得到ab，即可求出离心率e.2.（2019•天津）已知抛物线的焦点为F ，准线为l.若与双曲线)0,0(12222>>=-b a by a x 的两条渐近线分别交于点A 和点B ， 且||4||OF AB =（O 为原点），则双曲线的离心率为（ ）A. 2B. 3C. 2D. 5 【答案】 D【考点】圆锥曲线的综合【解析】【解答】抛物线 的准线 ：抛物线 的准线为F ，∵抛物线的准线与双曲线)0,0(12222>>=-b a by a x 的两条渐近线分别交于A ，B 两点，且 ，∴，，将A 点坐标代入双曲线渐近线方程得 ，∴ ，∴ ，即 ，∴.故答案为：D.【分析】求出抛物线的准线方程，双曲线的渐近线方程，而得出A 、B 的坐标，||4||OF AB =得出弦长|AB|的值，将A 点坐标代入双曲线渐近线方程结合a,b,c 的关系式得出a,c 的关系，即可求得离心率。

3.（2019•天津）已知抛物线的焦点为F ，准线为l ，若l 与双曲线)0,0(12222>>=-b a by a x 的两条渐近线分别交于点A 和点B ，且||4||OF AB =（O 为原点），则双曲线的离心率为（ ）A. 2B. 3C. 2D. 5 【答案】 D【考点】圆锥曲线的综合 【解析】【解答】抛物线的准线 ：抛物线的准线为F ，∵抛物线的准线与双曲线)0,0(12222>>=-b aby a x 的两条渐近线分别交于A ，B 两点，且 ，∴，，将A 点坐标代入双曲线渐近线方程得 ，∴ ，∴ ，即 ，∴.故答案为：D.【分析】求出抛物线的准线方程，双曲线的渐近线方程，而得出A 、B 的坐标，||4||OF AB =得出弦长|AB|的值，将A 点坐标代入双曲线渐近线方程结合a,b,c 的关系式得出a,c 的关系，即可求得离心率。