陕西省榆林市2018届高考模拟第一次测试理科数学试题+Word版含答案
- 格式:doc
- 大小:873.89 KB
- 文档页数:9

XXX(XXX、XXX等)2018届高三第一次模拟考试数学(理)试题含答案2018年XXX一模考试数学理科答案如下:一、选择题:XXX二、填空题:13.1 14.三、解答题:17.(本题满分12分)解:(Ⅰ)令n=1,得4a1=a1/(2+2a1-3),且a1>0,解得a1=3.当n≥2时,4Sn-4Sn-1=a_n-a_n-1+2a_n-2-2a_n-3,即4a_n=a_n-a_n-1+2a_n-2-2a_n-3,整理得(a_n+a_n-1)(a_n-a_n-1-2)=1/2,Qa_n>0,故a_n-a_n-1=2,所以数列{a_n}是首项为3,公差为2的等差数列,故a_n=2n+1.Ⅱ)由(Ⅰ)知:bn=(-1)^n/(2an-14n+4n^2(n+1))。
Qa_n>0.于是Tn=b1+b2+。
+b_n=(1-1/2+1/3-1/4+。
+(-1)^(n-1)/n)/(2n-14n+4n^2(n+1))=(1-1/2+1/3-1/4+。
+(-1)^(n-1)/n)/(2(n-1)^2+2(n-1)+1).18.(本题满分12分)解:(1)由已知X的可能取值为100,200,300,X的分布列为:X P 100 0.2 200 0.4 300 0.4.2)由已知①当订购200台时,E(Y)=[200×100-50×(200-100)]×0.2+200×200×0.8=(元)。
②当订购250台时,E(Y)=[200×100-50×(250-100)]×0.2+[200×200-50×(250-200)]×0.4+[200×250]×0.4=(元)。
综上所求,当订购250台时,Y的数学期望最大,11月每日应订购250台。
19.(本题满分12分)解:(Ⅰ)取AD中点O,连接OE,交MN于点Q,连接FQ,则OP⊥AD。

数 学 试 卷(理科农医类)考试说明:本试卷分第I 卷(选择题)第II 卷(非选择题)两部分,满分150分。
考试时间为120分钟。
以下公式可供解题时参考:如果事件A 、B 互斥,那么P (A+B )=P (A )+P (B ),如果事件互相独立,那么P (A ·B )=P (A )·P (B ),如果事件A 在一次试验中发生的概率是P ,那么n 次独立重复试验中恰好发生k 次的概率k n k k n n p p C k P --=)1()(第Ⅰ卷(选择题,共60分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的) 1.z i z 则,215+== ( )A .i 31035-- B .i 31035+-C .1-2iD .1+2i 2.函数)4(sin )4(cos 22ππ+-+=x x y( )A .周期为π的奇函数B .周期为π的偶函数C .周期2π的奇函数D .周期为2π的偶函数3.设)2tan(,21)tan(),2(53sin βαβππαπα-=-<<=则的值等于 ( )A .-724B .-247C .724D .2474.正方形ABCD ,沿对角线BD 折成直二面角后不会成立的结论是 ( )A .AC ⊥BDB .△ADC 为等边三角形C .AB 、CD 所成角为60°D .AB 与平面BCD 所成角为60°5.已知向量)()53(,2||,3||,60,m -⊥+==若夹角为 ,则m 的值为 ( )A .2332 B .4223 C .4229 D .2942 哈尔滨三中 东北育才 大连育明 天津耀华2018年第一次高考模拟考试6.函数)1(11)(x x x f --=的最大值是( )A .54 B .45 C .43 D .34 7.关于直线a ,b,c 以及平面M ,N ,给出下面命题:①若a //M ,b//M, 则a //b ②若a //M, b ⊥M ,则b ⊥a ③若a ⊂M ,b ⊂M,且c ⊥a ,c⊥b,则c ⊥M ④若a ⊥M, a //N ,则M ⊥N ,其中正确命题的个数为 ( ) A .0个 B .1个 C .2个 D .3个8.用四种不同颜色给正方体ABCD —A 1B 1C 1D 1的六个面涂色,要求相邻两个面涂不同颜色,则共有涂色方法 ( ) A .24种 B .72种 C .96种 D .48种9. 已知a 1, a 2, a 3, a 4, a 5, a 6, a 7, a 8 各项都大于零的数列,命题①a 1, a 2, a 3, a 4, a 5, a 6, a 7, a 8不是等比数列;命题②:a 1+a 8<a 4+a 5则命题②是命题①的 ( ) A .充分且必要条件 B .充分但不必要条件 C .必要但不充分条件 D .既不充分也不必要条件10.袋中有编号为1,2,3,4,5的五只小球,从中任取3只球,以ξ表示取出的球的最大号码,则E (ξ)的值是 ( ) A .5 B .4.75 C .4.5 D .4 11.点P 的曲线323+-=x x y 上移动,在点P 处的切线的倾斜角为α,则α的取值范围是( ) A .]2,0[πB .),43[)2,0[πππC .),43[ππD .]43,2(ππ 12.直线3x+4y -12=0与椭圆C :191622=+y x 相交于A 、B 两点,C 上点P ,使得△PAB 的面积等于3,这样的点P 共有( )A .1个B .2个C .3个D .4个第Ⅱ卷(非选择题,共90分)二、填空题(本大题共4个小题,每小题4分,共16分) 13.若不等式|ax +2|<6的解集为(-1,2),则实数a 等于14.把直线133+-=x y 绕点(1,1)顺时针旋转,使它与圆x 2+y 2-2x =0相切,则直线转动的最小正角是15.已知9)222(-x的展开式的第7项为421,)(lim 32n n x x x x ++++∞→ 则的值为16.对于定义在R 上的函数f (x ),有下述命题:①若f (x )是奇函数,则f (x -1)的图象关于点A (1,0)对称 ②若对x ∈R ,有f (x +1)= f (x -1),则f (x )的图象关于直线x =1对称 ③若函数f (x -1)的图象关于直线x =1对称,则f (x )为偶函数 ④函数f (1+x )与函数f (1-x )的图象关于直线x =1对称其中正确命题的序号为三、解答题(本大题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤) 17.(本小题满分12分)已知定义在R 上的函数)0,0,0(cos sin )(>>>+=b a x b x a x f ωωω周期为.3)4(,2)(,=≤ππf x f(1)写出f (x )的表达式;(2)写出函数f (x )的单调递增区间;(3)说明f (x )的图象如何由函数y=2sin x 的图象经过变换得到.已知数列{a n}是公比为q的等比数列,S n是其前n项和,且S3,S9,S6成等差数列(1)求证:a2 , a8, a5也成等差数列(2)判断以a2, a8, a5为前三项的等差数列的第四项是否也是数列{a n}中的一项,若是求出这一项,若不是请说明理由.如图,在正三棱柱ABC —A 1B 1C 1中,各棱长都相等,D ,E 分别为AC 1,BB 1的中点.(1)求证:DE//平面A 1B 1C 1;(2)求二面角A 1—DE —B 1的大小.E A B B 1CD C 1A 1某职业联赛的总决赛在甲、乙两队之间角逐,采用七局四胜制,即有一队胜四场,则此队获胜,且比赛结束.在每场比赛中,甲队获胜的概率是,32乙队获胜的概率是31.根据以往资料统计,每场比赛组织者可获门票收入为30万元,两队决出胜负后,问:(1)组织者在此决赛中获门票收入为120万元的概率是多少? (2)组织者在此决赛中获门票收入不低于180万元的概率是多少?21.(本小题满分12分)已知定点F (1,0),动点P 在y 轴上运动,过点P 作PM 交x 轴于点M ,并延长MP 到点N ,且.||||,0PN PM PF PM ==⋅(1)动点N 的轨迹方程;(2)线l 与动点N 的轨迹交于A ,B 两点,若304||64,4≤≤-=⋅AB OB OA 且,求直线l 的斜率k 的取值范围.22.(本小题满分14分)如图所示,曲线段OMB 是函数f (x )=x 2(0<x <6)的图象,BA ⊥x 轴于A ,曲线段OMB 上一点M(t, f (t)处的切线PQ 交x 轴于P ,交线段AB 于Q.(1)试用t 表示切线PQ 的方程;(2)设△QAP 的面积为g(t),若函数g(t)在(m , n )上单调递减,试求出m 的最小值;(3)]64,4121[∈∆QAP S ,试求出点P 横坐标的取值范围.数 学 试 卷(理科农医类)答案一、选择题答案1.D 2.A 3.D 4.D 5.C 6.D 7.C 8.C 9.B 10.C 11.B 12.B 二、填空题答案 13.-4 14.3π15.41-16.①③三、解答题答案 17.(1)x x x f 2cos 2sin 3)(+=…………………………………………4分(2)在每个闭区间Z k k k ∈+-],6,3[ππππ…………………………8分(3)将函数y=2sin x 的图象向左平移6π个单位,再将得到的函数图象上的所有的点的纵坐标不变,横坐标缩短为原来的21………………………………………………12分18.证明:(1)S 3=3a 1, S 9=9a 1, S 6=6a 1, 而a 1≠0,所以S 3,S 9,S 6不可能成等差数列……2分所以q ≠1,则由公式qq a q q a q q a q q a S n n --+--=----=1)1(1)1(1)1(2,1)1(6131911得……4分 即2q 6=1+q 3 ∴2q 6a 1q=a 1q+q 3a 1q , ∴2a 8=a 2+a 5 所以a 2, a 8, a 5成等差数列…………6分 (2)由2q 6=1+q 3=-21……………………………………………………………………8分要以a 2, a 8, a 5为前三项的等差数列的第四项是数列{a n }中的第k 项,必有a k -a 5=a 8-a 2,所以1632-=-q q a a k 所以,45)21(,45,453222-=--=-=--k k k q a a 所以所以由k 是整数,所以45)21(32-=--k 不可能成立,所以a 2, a 8, a 5 为前三项的等差数列的第四项不可能也是数列{a n }中的一项.………………………………………………………12分 19.(1)取A 1C 1中点F ,连结B 1F ,DF ,∵D ,E 分别为AC 1和BB 1的中点,∴DF//AA 1,DF=1AA 1哈尔滨三中 东北育才 大连育明 天津耀华2018年第一次高考模拟考试B 1E//AA 1,B 1E=21AA 1,∴DF//B 1E ,DF=B 1E ,∴DEB 1F 为平行四边形,……………………2分∴DE//B 1F ,又∵B 1F ⊂平面A 1B 1C 1,DE ⊄平面A 1B 1C 1,∴DE//平面A 1B 1C 1.……4分 (2)连结A 1D ,A 1E ,在正三棱柱ABC —A 1B 1C 1中,∵平面A 1B 1C 1⊥平面ACC 1A 1,A 1C 1是平面A 1B 1C 1与平面ACC 1A 1的交线,又∵B 1F ⊂平面A 1B 1C 1,且B 1F ⊥A 1C 1,∴B 1F ⊥平面ACC 1A 1,又DE//B 1F ,∴DE ⊥平面ACC 1A 1, ∴∠FDA 1为二面角A 1—DE —B 1的平面角,…………8分 并且∠FDA 1=21∠A 1DC 1,设正三棱柱的棱长为1,∵∠AA 1C 1=90°,D 是AC 1中点,∴DC 1=22,A 1D=22,∠A 1DC 1=90°∴∠FDA 1=45°,即二面角A 1—DE —B 1为45°.………12分20.(1)①门票收入为120万元的概率为8117)31()32(44=+………………………15分(2)门票收入不低于180万元的概率814031)32()31(32)31()32(31)32()31(32)31()32(3336333623352335=⨯+⨯+⨯+⨯C C C C …12分 21.(1)设动点N 的坐标为(x ,y ),则 ),2,(),0)(2,0(),0,(y x PM x y P x M --=>-…………………2分040),2,1(2=+-=⋅-=y x y 得由,因此,动点的轨迹方程为 ).0(42>=x x y ……4分(2)设l 与抛物线交于点A (x 1,y 1),B(x 2,y 2),当l 与x 轴垂直时, 则由6424||,22,22,421<=-==-=⋅AB y y 得, 不合题意,故与l 与x 轴不垂直,可设直线l 的方程为y=k x +b(k ≠0),则由4,42121-=+-=⋅y y x x 得…6分由点A ,B 在抛物线.8,4,4,)0(4212221212-===>=y y x y x y x x y 故有上又y 2=4x , y=k x +b 得ky 2-4y+4b=0,……………………8分所以)3216(1||),21(16.2,8422222++=+=∆-=-=k k k AB k k b k b ……10分因为.480)3216(196,304||64222≤++≤≤≤kk k AB 所以解得直线l 的斜率的取值范围是]1,21[]21,1[⋃--.………………………………………………………………12分22.(1)).60(2),(2,2)(22<<-=-=-∴='=t t tx y t x t t y t t f k 即………2分 (2)令y=0得.12,6;22t t y x tx-===令 .124,03664)12)(26(21||||21)(232<<<+-=--==∴t t t t t AQ AP t g 得 又0<t<6,∴4<t<6,g(t)在(m, n)上单调递减,故(m, n ).4)().6,4(min =∴⊆m …………8分)(,0)(,40t g t g t ∴>'<<时,2.61)64,4121(.1)40(41213664,412154)6(,64)4(23t x t S t t t t t g g QAP =≤≤⇔∈∴=<<=+->==∆又点的横坐标得解方程∴P 的横坐标的取值范围为)3,21[.……………………………………………………14分。


市一中高三第一次模拟考试数学(理)试题命题人:孙丽荣一、选择题(每小题5分,共60分)1.已知i 为虚数单位,复数z 满足(1+i )z=(1﹣i )2,则|z|为( ) A .2B .1C .21D .222.若M={x|﹣2≤x ≤2},N={x|y=log 2(x ﹣1)},则M ∩N=( ) A .{x|﹣2≤x <0} B .{x|﹣1<x <0} C .{﹣2,0} D .{x|1<x ≤2}3.某几何体的三视图如图所示,则该几何体的体积为( )A .4+2πB .8+2πC .4+πD .8+π4.下列命题中:①“∃x 0∈R ,x 02﹣x 0+1≤0”的否定; ②“若x 2+x ﹣6≥0,则x >2”的否命题; ③命题“若x 2﹣5x+6=0,则x=2”的逆否命题; 其中真命题的个数是( ) A .0个 B .1个 C .2个 D .3个 5.设f (x )=⎪⎩⎪⎨⎧≥-<-2x ),1x (log 2x ,e 2231x ,则f (f (2))的值为( )A .0B .1C .2D .36.执行右上如图的程序框图,若程序运行中输出的一组数是(x ,﹣12),则x 的值为( )A .27B .81C .243D .729 7.已知函数f (x )=cos (2x ﹣)+2cos 2x ,将函数y=f (x )的图象向右平移个单位,得到函数y=g (x )的图象,则函数y=g (x )图象的一个对称中心是( ) A .(﹣,1) B .(﹣,1) C .(,1) D .(,0)8.已知向量与的夹角为,||=,则在方向上的投影为( )A .B .C .D .9.已知实数x ,y 满足不等式组,若目标函数z=kx+y 仅在点(1,1)处取得最小值,则实数k 的取值范围是 ( )A .(﹣1,+∞)B .(﹣∞,﹣1)C .(1,+∞)D .(﹣∞,1) 10.四个大学生分到两个单位,每个单位至少分一个的分配方案有( ) A .10种 B .14种 C .20种 D .24种11.在区间[0,1]上随机选取两个数x 和y ,则y >2x 的概率为( ) A .41 B .21 C .43 D .3112.已知双曲线1by a x 2222=-(a >0,b >0)的左、右焦点分别为F 1、F 2,且F 2为抛物线y 2=24x 的焦点,设点P 为两曲线的一个公共点,若△PF 1F 2的面积为366,则双曲线的方程为( )A .127y 9x 22=-B .19y 27x 22=-C .19y 16x 22=-D .116y 9x 22=-二、填空题(每小题5分,共20分) 13.已知幂函数y=x a 的图象过点(3,9),则的展开式中x 的系数为 .14.已知等差数列{a n }的公差d ≠0,且a 1,a 3,a 13成等比数列,若a 2+a 3=8,则数列{a n }的前n 项和S n = .为 . 16.定积分⎰-10(2x 1-+x)dx 的值为 .三、解答题(每小题12分,共70分. 解答应写出文字说明、证明过程或演算步骤)17. (本小题满分12分) 在锐角△ABC 中, =(1)求角A ; (2)若a=,求bc 的取值范围.18. (本小题满分12分)如图,三棱锥P ﹣ABC 中,PA=PC ,底面ABC 为正三角形. (Ⅰ)证明:AC ⊥PB ;(Ⅱ)若平面PAC ⊥平面ABC ,AC=PC=2,求二面角A ﹣PC ﹣B 的余弦值. 19.(本小题满分12分)甲乙两队参加奥运知识竞赛,每队3人,每人回答一个问题,答对者为本队赢得一分,答错得零分。

届榆林市高三数学模拟试卷及答案2018届榆林市高三数学模拟试卷及答案高考一直备受大家的关注,其中高考数学的题型基本上是保持不变的,只是逻辑性不同,我们可以通过多做一些高考数学模拟试卷来熟悉高考的题型,以下是店铺为你整理的2018届榆林市高三数学模拟试卷,希望能帮到你。
2018届榆林市高三数学模拟试卷题目一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合,则等于( )A. B. C. D.2.已知复数的实部与虚部之和为4,则复数在复平面上对应的点在( )A.第一象限B.第二象限C.第三象限D.第四象限3.已知,则等于( )A. B. C. D.4.已知向量与的夹角为60°,,,则在方向上的投影为( )A. B.2 C. D.35. 如果实数,,满足条件,则的最大值为( )A. B. C. D.6.已知,则等于( )A.0B.-240C.-480D.9607. 执行如图所示的程序框图,则下列说法正确的是( )A. ,输出的值为5B. ,输出的值为5C. ,输出的值为5D. ,输出的值为58. 已知函数是奇函数,其中,则函数的图像( )A.点对称B.可由函数的图像向右平移个单位得到C.可由函数的图像向左平移个单位得到D.可由函数的图像向左平移个单位得到9. 已知函数的定义域为,对任意,有,且,则不等式的解集为( )A. B. C D.10. 一个几何体的三视图如图所示,则该几何体的体积为( )A. B.5 C. D.611. 已知点是抛物线与圆在第一象限的公共点,且点到抛物线焦点的距离为 .若抛物线上一动点到其准线与到点的距离之和的最小值为,为坐标原点,则直线被圆所截得的弦长为( )A.2B.C.D.12.已知函数,,实数,满足,若,,使得成立,则的最大值为( )A.4B.C.D.3第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.甲、乙、丙三人将独立参加某项体育达标测试.根据平时训练的经验,甲、乙、丙三人能达标的概率分别为、、,则三人中有人达标但没有全部达标的概率为_______.14. 过双曲线的右焦点作与轴垂直的直线,直线与双曲线交于两点,与双曲线的渐近线交于两点.若,则双曲线的离心率为_______.15.在四棱锥中,底面,底面是边长为2的正方形.若直线与平面所成的角为30°,则四棱锥的外接球的表面积为_______.16.在中,内角,,的对边分别为,,,,,是的中点,且,则的面积为_______.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17(本小题满分12分)已知公比小于1的等比数列的前项和为,且 .(1)求数列的通项公式;(2)设,求数列的前项和 .18.(本小题满分12分)如图,在直四棱柱中,底面是边长为1的正方形, ,点是侧棱的中点.(1)求证:平面 ;(2)求平面与平面所成锐二面角的余弦值.19. (本小题满分12分)为推行“新课堂”教学法,某化学老师分别用传统教学和“新课堂”两种不同的教学方式,在甲、乙两个平行进行教学实验,为了比较教学效果,期中考试后,分别从两个班级中各随机抽取20名学生的进行统计,结果如下表:记成绩不低于70分者为“成绩优良”.(1)由以上统计数据填写下面2×2列联表,并判断“成绩优良与教学方式是否有关”?附: .临界值表(2)现从上述40人中,学校按成绩是否优良采用分层抽样的方法抽取8人进行考核.在这8人中,记成绩不优良的乙班人数为,求的分布列及数学期望.20. (本小题满分12分)已知右焦点为的椭圆与直线相交于、两点,且 .(1)求椭圆的方程;(2) 为坐标原点,,,是椭圆上不同的三点,并且为的重心,试探究的面积是否为定值,若是,求出这个定值;若不是,说明理由.21. (本小题满分12分)已知函数,,且曲线与轴切于原点 .(1)求实数,的值;(2)若恒成立,求的值.请考生在22、23、24三题中任选一题作答,如果多做,则按所做的第一题记分.22.(本小题满分10分)选修4-1:几何证明选讲如图,在中,是的角平分线,的外接圆交于,(1)求证: ;(2)当时,求的长.23. (本小题满分10分)选修4-4:坐标系与参数方程已知曲线的极坐标方程为,以极点为原点,极轴为轴正半轴建立平面直角坐标系,设直线的参数方程为 ( 为参数).(1)求曲线的直角坐标方程与直线的普通方程;(2)设曲线与直线相交于两点,以为一条边作曲线的内接矩形,求该矩形的面积.24. (本小题满分10分)选修4-5:不等式选讲已知函数 .(1)求证: ;(2)若方程有解,求的取值范围.2018届榆林市高三数学模拟试卷答案一、选择题1. ,, .2. 实部与虚部之和为4,,则,故选 .3. 由已知得,化简得 .4. 向量,的夹角为60°,,,,则在方向上的投影为 .5. 根据约束条件画出可行域,可判断当时,取得最大值8,故的.最大值为 .6. , .7. 此时输出则且,即,故选 .9. 当时,即函数是在上的增函数,若,则且 .10. 该几何体的直观图如图所示,连接,则该几何体由直三棱柱和四棱锥组合而成,其体积为 .11. 抛物线上一动点到其准线与到点的距离之和的最小值为,又三点共线,且是线段的中点,则圆心到直线的距离为所求的弦长为12. ,则时, ;当时, .所以,,令,设,作函数的图像如图所示,由得或,的最大值为3.二、填空题13. 三人中有一人或两人达标,其概率为 .14. 化简得,则双曲线的离心率 .15. 连结交于,则可证得平面,连接,则就是直线与平面所成的角,即,,,,四棱锥的外接球的半径为,则所求外接球的表面积为 .16.6 由得,,,即,则 ,得,,则,又,,,解得,, ,则的面积为 .三、简答题17.解:(1)设等比数列的公比为,,,…………………………2分则,解得或 (舍去),…………………………4分故.…………………………5分(2) ,…………………………6分,①则,②…………………………7分①-②得:,…………………………10分解得.…………………………12分18.(1)证明:连接,底面是正方形,,…………………………1分又侧棱垂直于底面,,…………………………2分,平面,则.…………………………3分,,,,即.…………………………4分,平面.…………………………5分(2)解:以为坐标原点,建立如图所示的空间直角坐标系,则,,, .设平面的一个法向量为,则即…………………………8分令,则,,.…………………………9分向量是平面的一个法向量,…………………………10分,…………………………11分平面与平面所成锐二面角的余弦值为.…………………………12分19.解:(1)…………………………2分根据2×2列联表中的数据,得的观测值为,在犯错概率不超过0.05的前提下认为“成绩优良与教学方式有关”.…………………………5分(2)由表可知在8人中成绩不优良的人数为,则的可能取值为0,1,2,3.……………………6分; ;…………………………8分; .…………………………10分的分布列为:…………………………11分所以.…………………………12分20.解:(1)设,,则,…………………………1分,即,①…………………………2分,,即,②…………………………3分由①②得,又,,…………………………4分椭圆的方程为.…………………………5分(2)设直线方程为:,由得,为重心,,…………………………7分点在椭圆上,故有,可得,…………………………8分而,(或利用是()到距离的3倍得到),…………………………9分,………………………10分当直线斜率不存在时,,,,的面积为定值.…………………………12分21.解:(1),………………………………1分,又,.…………………………3分(2)不等式,整理得,即或,令,, .当时, ;当时,,在单调递减,在单调递增,,即,所以在上单调递增,而 ;故 ; .当或时, ;同理可得,当时, .由恒成立可得,当或时, ;当时,,故0和1是方程的两根,从而,,.………………………12分22.证明:(1)连结 ,为圆的内接四边形,又即,而 .又是的平分线,从而…………………………5分(2)由条件得设 .根据割线定理得即解得,即.…………………………10分23.解:(1)对于,由得进而对于,由 ( 为参数),得,即的普通方程为.…………………………5分(2)由(1)可知为圆,且圆心为(2,0),半径为2,则弦心距弦长,因此以为一条边的圆的内接矩形面积.…………………………10分24.解(1) …………………………5分(2)要使方程有解,只需,即或或解得,或 .故的取值范围是…………………………10分【2018届榆林市高三数学模拟试卷及答案】。

2018年全国一般高等学校招生高考数学模拟试卷(理科)(一)一、选择题:本大题共12个小题,每题5分,共60分.在每题给出的四个选项中,只有一项为哪一项符合题目要求的.1.(5分)已知集合A={x|2﹣x>0},B={x|()x<1},那么()A.A∩B={x|0<x≤2} B.A∩B={x|x<0} C.A∪B={x|x<2} D.A∪B=R2.(5分)已知i为虚数单位,a为实数,复数z知足z+3i=a+ai,假设复数z 是纯虚数,那么()A.a=3 B.a=0 C.a≠0 D.a<03.(5分)我国数学家邹元治利用如图证明勾股定理,该图顶用勾(a)和股(b)别离表示直角三角形的两条直角边,用弦(c)表示斜边,现已知该图中勾为3,股为4,假设从图中随机取一点,那么此点不落在中间小正方形中的概率是()A. B.C.D.4.(5分)已知等差数列{a n}的前n项和为S n,且S9=6π,那么tan a5=()A. B.C.﹣D.﹣5.(5分)已知函数f(x)=x+(a∈R),那么以下结论正确的选项是()A.∀a∈R,f(x)在区间(0,+∞)内单调递增B.∃a∈R,f(x)在区间(0,+∞)内单调递减C.∃a∈R,f(x)是偶函数D.∃a∈R,f(x)是奇函数,且f(x)在区间(0,+∞)内单调递增6.(5分)(1+x)(2﹣x)4的展开式中x项的系数为()A.﹣16 B.16 C.48 D.﹣487.(5分)如图是某个几何体的三视图,那么那个几何体的表面积是()A.π+4+4 B.2π+4+4 C.2π+4+2 D.2π+2+4 8.(5分)假设a>1,0<c<b<1,那么以下不等式不正确的选项是()A.log2018a>log2018b B.log b a<log c aC.(a﹣c)a c>(a﹣c)a b D.(c﹣b)a c>(c﹣b)a b9.(5分)执行如下图的程序框图,假设输出的n值为11,那么判定框中的条件能够是()A.S<1022?B.S<2018?C.S<4095?D.S>4095?10.(5分)已知函数f(x)=2sin(ωx+φ)(ω>0,|φ|≤)的部份图象如下图,将函数f(x)的图象向左平移个单位长度后,所得图象与函数y=g (x)的图象重合,那么()A.g(x)=2sin(2x+)B.g(x)=2sin(2x+)C.g(x)=2sin2x D.g(x)=2sin(2x﹣)11.(5分)已知抛物线C:y2=4x的核心为F,过点F作斜率为1的直线l交抛物线C与P、Q两点,那么+的值为()A.B.C.1 D.212.(5分)已知数列{an }中,a1=2,n(an+1﹣an)=an+1,n∈N*,假设关于任意的a∈[﹣2,2],n∈N*,不等式<2t2+at﹣1恒成立,那么实数t的取值范围为()A.(﹣∞,﹣2]∪[2,+∞)B.(﹣∞,﹣2]∪[1,+∞)C.(﹣∞,﹣1]∪[2,+∞)D.[﹣2,2]二、填空题(每题5分,总分值20分,将答案填在答题纸上)13.(5分)已知向量=(1,λ),=(3,1),假设向量2﹣与=(1,2)共线,那么向量在向量方向上的投影为.14.(5分)假设实数x,y知足,那么z=x﹣3y+1的最大值是.15.(5分)过双曲线﹣=1(a>0,b>0)的下核心F1作y轴的垂线,交双曲线于A,B两点,假设以AB为直径的圆恰好于其上核心F2,那么双曲线的离心率为.16.(5分)一底面为正方形的长方体各棱长之和为24,那么当该长方体体积最大时,其外接球的体积为.三、解答题(本大题共5小题,共70分.解许诺写出文字说明、证明进程或演算步骤.)17.(12分)如图,在△ABC中,角A,B,C所对的边别离为a,b,c,假设2acosA=bcosC+ccosB.(1)求角A的大小;(2)假设点D在边AC上,且BD是∠ABC的平分线,AB=2,BC=4,求AD的长.18.(12分)如图,在三棱柱ABC﹣A1B1C1中,侧棱CC1⊥地面ABC,且CC1=2AC=2BC,AC⊥BC,D是AB的中点,点M在侧棱CC1上运动.(1)当M是棱CC1的中点时,求证:CD∥平面MAB1;(2)当直线AM与平面ABC所成的角的正切值为时,求二面角A﹣MB1﹣C1的余弦值.19.(12分)第一届“一带一路”国际合作顶峰论坛于2017年5月14日至15日在北京举行,这是2017年我国重要的主场外交活动,对推动国际和地域合作具有重要意义.某高中政教处为了调查学生对“一带一路”的关注情形,在全校组织了“一带一路知多少”的知识问卷测试,并从中随机抽取了12份问卷,取得其测试成绩(百分制),如茎叶图所示.(1)写出该样本的众数、中位数,假设该校共有3000名学生,试估量该校测试成绩在70分以上的人数;(2)从所抽取的70分以上的学生中再随机选取1人.①记X表示选取4人的成绩的平均数,求P(X≥87);②记ξ表示测试成绩在80分以上的人数,求ξ的散布和数学期望.20.(12分)已知椭圆C:+=1(a>b>0)的左、右核心为F1,F2,离心率为,点P在椭圆C上,且△PF1F2的面积的最大值为2.(1)求椭圆C的方程;(2)已知直线l:y=kx+2(k≠0)与椭圆C交于不同的两点M,N,假设在x轴上存在点G,使得|GM|=|GN|,求点G的横坐标的取值范围.21.(12分)设函数f(x)=e x﹣2a﹣ln(x+a),a∈R,e为自然对数的底数.(1)假设a>0,且函数f(x)在区间[0,+∞)内单调递增,求实数a的取值范围;(2)假设0<a<,试判定函数f(x)的零点个数.请考生在2二、23两题中任选一题作答,若是多做,那么按所做的第一题记分.[选修4-4:坐标系与参数方程]22.(10分)已知在平面直角坐标系xOy中,椭圆C的方程为+=1,以O 为极点,x轴的非负半轴为极轴,取相同的长度单位成立极坐标系,直线l的极坐标方程为ρsin(θ+)=3.(1)求直线l的直角坐标方程和椭圆C的参数方程;(2)设M(x,y)为椭圆C上任意一点,求|2x+y﹣1|的最大值.[选修4-5:不等式选讲]23.已知函数f(x)=|x﹣2|.(1)求不等式f(x)+f(2+x)≤4的解集;(2)假设g(x)=f(x)﹣f(2﹣x)的最大值为m,对任意不相等的正实数a,b,证明:af(b)+bf(a)≥m|a﹣b|.2018年全国一般高等学校招生高考数学模拟试卷(理科)(一)参考答案与试题解析一、选择题:本大题共12个小题,每题5分,共60分.在每题给出的四个选项中,只有一项为哪一项符合题目要求的.1.(5分)已知集合A={x|2﹣x>0},B={x|()x<1},那么()A.A∩B={x|0<x≤2} B.A∩B={x|x<0} C.A∪B={x|x<2} D.A∪B=R【解答】解:集合A={x|2﹣x>0}={x|x<2},B={x|()x<1}={x|x>0},那么A∩B={x|0<x<2},A∪B=R.应选:D.2.(5分)已知i为虚数单位,a为实数,复数z知足z+3i=a+ai,假设复数z 是纯虚数,那么()A.a=3 B.a=0 C.a≠0 D.a<0【解答】解:由z+3i=a+ai,得z=a+(a﹣3)i,又∵复数z是纯虚数,∴,解得a=0.应选:B.3.(5分)我国数学家邹元治利用如图证明勾股定理,该图顶用勾(a)和股(b)别离表示直角三角形的两条直角边,用弦(c)表示斜边,现已知该图中勾为3,股为4,假设从图中随机取一点,那么此点不落在中间小正方形中的概率是()A. B. C.D.【解答】解:设直角三角形的长直角边为a=4,短直角边为b=3,由题意c=5,∵大方形的边长为a+b=3+4=7,小方形的边长为c=5,那么大正方形的面积为49,小正方形的面积为25,∴知足题意的概率值为:1﹣=.应选:B.4.(5分)已知等差数列{an }的前n项和为Sn,且S9=6π,那么tan a5=()A. B.C.﹣D.﹣【解答】解:由等差数列的性质可得:S9=6π==9a5,∴a=.5=tan=﹣.那么tan a5应选:C.5.(5分)已知函数f(x)=x+(a∈R),那么以下结论正确的选项是()A.∀a∈R,f(x)在区间(0,+∞)内单调递增B.∃a∈R,f(x)在区间(0,+∞)内单调递减C.∃a∈R,f(x)是偶函数D.∃a∈R,f(x)是奇函数,且f(x)在区间(0,+∞)内单调递增【解答】解:当a≤0时,函数f(x)=x+在区间(0,+∞)内单调递增,当a>0时,函数f(x)=x+在区间(0,]上单调递减,在[,+∞)内单调递增,故A,B均错误,∀a∈R,f(﹣x)=﹣f(x)均成立,故f(x)是奇函数,故C错误,应选:D.6.(5分)(1+x)(2﹣x)4的展开式中x项的系数为()A.﹣16 B.16 C.48 D.﹣48【解答】解:∵(2﹣x)4展开式的通项公式为 T=•24﹣r(﹣x)r,r+1∴(1+x)(2﹣x)4的展开式中x项的系数为﹣•23+24=﹣16,应选:A.7.(5分)如图是某个几何体的三视图,那么那个几何体的表面积是()A.π+4+4 B.2π+4+4 C.2π+4+2 D.2π+2+4【解答】解:由三视图可知:该几何体由一个半圆柱与三棱柱组成的几何体.其直观图如下所示:其表面积S=2×π•12+2××2×1++﹣2×1=2π+4+4,应选:B8.(5分)假设a>1,0<c<b<1,那么以下不等式不正确的选项是()A.log2018a>log2018b B.logba<logcaC.(a﹣c)a c>(a﹣c)a b D.(c﹣b)a c>(c﹣b)a b【解答】解:依照对数函数的单调性可得log2018a>log2018b正确,logba<logca正确,∵a>1,0<c<b<1,∴a c<a b,a﹣c>0,∴(a﹣c)a c<(a﹣c)a b,故C不正确,∵c﹣b<0,∴(c﹣b)a c>(c﹣b)a b正确,应选:C.9.(5分)执行如下图的程序框图,假设输出的n值为11,那么判定框中的条件能够是()A.S<1022?B.S<2018?C.S<4095?D.S>4095?【解答】解:第1次执行循环体,S=3,应不知足输出的条件,n=2,第2次执行循环体,S=7,应不知足输出的条件,n=3,第3次执行循环体,S=15,应不知足输出的条件,n=4,第4次执行循环体,S=31,应不知足输出的条件,n=5,第5次执行循环体,S=63,应不知足输出的条件,n=6,第6次执行循环体,S=127,应不知足输出的条件,n=7,第7次执行循环体,S=255,应不知足输出的条件,n=8,第8次执行循环体,S=511,应不知足输出的条件,n=9,第9次执行循环体,S=1023,应不知足输出的条件,n=10,第10次执行循环体,S=2047,应不知足输出的条件,n=11第11次执行循环体,S=4095,应知足输出的条件,故判定框中的条件能够是S<4095?,应选:C.10.(5分)已知函数f(x)=2sin(ωx+φ)(ω>0,|φ|≤)的部份图象如下图,将函数f(x)的图象向左平移个单位长度后,所得图象与函数y=g (x)的图象重合,那么()A.g(x)=2sin(2x+)B.g(x)=2sin(2x+)C.g(x)=2sin2x D.g(x)=2sin(2x﹣)【解答】解:依照函数f(x)=2sin(ωx+φ)(ω>0,|φ|≤)的部份图象,可得==+,∴ω=2,依照+φ=2•(﹣)+φ=0,∴φ=,故f(x)=2sin(2x+).将函数f(x)的图象向左平移个单位长度后,所得图象与函数y=g(x)的图象重合,故g(x)=2sin(2x++)=2sin(2x+).应选:A.11.(5分)已知抛物线C:y2=4x的核心为F,过点F作斜率为1的直线l交抛物线C与P、Q两点,那么+的值为()A.B.C.1 D.2【解答】解:抛物线C:y2=4x的核心为F(1,0),过点F作斜率为1的直线l:y=x﹣1,可得,消去y可得:x2﹣6x+1=0,可得xP +xQ=6,xPxQ=1,|PF|=xP +1,|QF|=xQ+1,|PF||QF|=xQ +xP+xPxQ+1=6+1+1=8,则+===1.应选:C.12.(5分)已知数列{an }中,a1=2,n(an+1﹣an)=an+1,n∈N*,假设关于任意的a∈[﹣2,2],n∈N*,不等式<2t2+at﹣1恒成立,那么实数t的取值范围为()A.(﹣∞,﹣2]∪[2,+∞)B.(﹣∞,﹣2]∪[1,+∞)C.(﹣∞,﹣1]∪[2,+∞)D.[﹣2,2]【解答】解:依照题意,数列{a n }中,n (a n+1﹣a n )=a n +1, 即na n+1﹣(n+1)a n =1,那么有﹣==﹣,那么有=(﹣)+(﹣)+(﹣)+…+(a 2﹣a 1)+a 1=(﹣)+(﹣)+(﹣)+…+(1﹣)+2=3﹣<3,<2t 2+at ﹣1即3﹣<2t 2+at ﹣1,∵关于任意的a ∈[﹣2,2],n ∈N *,不等式<2t 2+at ﹣1恒成立,∴2t 2+at ﹣1≥3, 化为:2t 2+at ﹣4≥0,设f (a )=2t 2+at ﹣4,a ∈[﹣2,2], 可得f (2)≥0且f (﹣2)≥0,即有即,可得t ≥2或t ≤﹣2,那么实数t 的取值范围是(﹣∞,﹣2]∪[2,+∞). 应选:A .二、填空题(每题5分,总分值20分,将答案填在答题纸上)13.(5分)已知向量=(1,λ),=(3,1),假设向量2﹣与=(1,2)共线,那么向量在向量方向上的投影为0 .【解答】解:向量=(1,λ),=(3,1),向量2﹣=(﹣1,2λ﹣1),∵向量2﹣与=(1,2)共线,∴2λ﹣1=﹣2,即λ=.∴向量=(1,﹣),∴向量在向量方向上的投影为||•cos<,>===0.故答案为:0.14.(5分)假设实数x,y知足,那么z=x﹣3y+1的最大值是.【解答】解:实数x,y知足,对应的可行域如图:线段AB,z=x﹣3y+1化为:y=,若是z最大,那么直线y=在y轴上的截距最小,作直线l:y=,平移直线y=至B点时,z=x﹣3y+1取得最大值,联立,解得B(,).因此z=x﹣3y+1的最大值是:.故答案为:﹣.15.(5分)过双曲线﹣=1(a>0,b>0)的下核心F作y轴的垂线,交1,那么双曲线的双曲线于A,B两点,假设以AB为直径的圆恰好于其上核心F2离心率为.作y轴的垂线,【解答】解:过双曲线﹣=1(a>0,b>0)的下核心F1交双曲线于A,B两点,那么|AB|=,,以AB为直径的圆恰好于其上核心F2可得:,∴c2﹣a2﹣2ac=0,可得e2﹣2e﹣1=0,解得e=1+,e=1﹣舍去.故答案为:1+.16.(5分)一底面为正方形的长方体各棱长之和为24,那么当该长方体体积最大时,其外接球的体积为4.【解答】解:设该项长方体底面边长为x米,由题意知其高是:=6﹣2x,(0<x<3)那么长方体的体积V(x)=x2(6﹣2x),(0<x<3),V′(x)=12x﹣6x2=6x(2﹣x),由V′(x)=0,得x=2,且当0<x<2时,V′(x)>0,V(x)单调递增;当2<x<3时,V′(x)<0,V(x)单调递减.∴体积函数V(x)在x=2处取得唯一的极大值,即为最大值,现在长方体的高为6﹣2x=2,∴其外接球的直径2R==2,∴R=,∴其外接球的体积V==4.故答案为:4.三、解答题(本大题共5小题,共70分.解许诺写出文字说明、证明进程或演算步骤.)17.(12分)如图,在△ABC中,角A,B,C所对的边别离为a,b,c,假设2acosA=bcosC+ccosB.(1)求角A的大小;(2)假设点D在边AC上,且BD是∠ABC的平分线,AB=2,BC=4,求AD的长.【解答】解:(1)∵2acosA=bcosC+ccosB,∴2sinAcosA=sinBcosC+sinCcosB=sin(B+C)=sinA,∵sinA≠0,∴cosA=,∴A=.(2)在△ABC中,由余弦定理的cosA==,解得AC=1+或AC=1﹣(舍).∵BD是∠ABC的平分线,∴=,∴AD=AC=.18.(12分)如图,在三棱柱ABC﹣A1B1C1中,侧棱CC1⊥地面ABC,且CC1=2AC=2BC,AC⊥BC,D是AB的中点,点M在侧棱CC1上运动.(1)当M是棱CC1的中点时,求证:CD∥平面MAB1;(2)当直线AM与平面ABC所成的角的正切值为时,求二面角A﹣MB1﹣C1的余弦值.【解答】证明:(1)取线段AB的中点E,连接DE,EM.∵AD=DB,AE=EB,∴DE∥BB1,ED=,又M为CC1的中点,∴.∴四边形CDEM是平行四边形.∴CD∥EM,又EM⊂MAB1,CD⊄MAB1∴CD∥平面MAB1;解(2)∵CA,CB,CC1两两垂直,∴以C为原点,CA,CB,CC1所在直线别离为x、y、z轴成立空间直角坐标系.∵在三棱柱ABC﹣A1B1C1中,侧棱CC1⊥地面ABC,可得∠MAC为直线AM与平面ABC所成的角,设AC=1,tan,得CM=∴C(0,0,0),A(1,0,0),B(0,1,0),B1(0,1,2),M(0,0,)设AMB1的法向量为,可取又平面B1C1CB的法向量为.cos==.∵二面角A﹣MB1﹣C1为钝角,∴二面角A﹣MB1﹣C1的余弦值为﹣.19.(12分)第一届“一带一路”国际合作顶峰论坛于2017年5月14日至15日在北京举行,这是2017年我国重要的主场外交活动,对推动国际和地域合作具有重要意义.某高中政教处为了调查学生对“一带一路”的关注情形,在全校组织了“一带一路知多少”的知识问卷测试,并从中随机抽取了12份问卷,取得其测试成绩(百分制),如茎叶图所示.(1)写出该样本的众数、中位数,假设该校共有3000名学生,试估量该校测试成绩在70分以上的人数;(2)从所抽取的70分以上的学生中再随机选取1人.①记X表示选取4人的成绩的平均数,求P(X≥87);②记ξ表示测试成绩在80分以上的人数,求ξ的散布和数学期望.【解答】解:(1)众数为76,中位数为76,抽取的12人中,70分以下的有4人,不低于70分的有8人,故从该校学生中任选1人,那个人测试成绩在70分以上的概率为=,∴该校这次测试成绩在70分以上的约有:3000×=2000人.(2)①由题意知70分以上的有72,76,76,76,82,88,93,94,当所选取的四个人的成绩的平均分大于87分时,有两类:一类是:82,88,93,94,共1种;另一类是:76,88,93,94,共3种.∴P(X≥87)==.②由题意得ξ的可能取值为0,1,2,3,4,P(ξ=0)==,P(ξ=1)==,P(ξ=2)==,P(ξ=3)==,P(ξ=4)==,∴ξ的散布列为:ξ 0 1 2 3 4P∴E(ξ)==2.20.(12分)已知椭圆C:+=1(a>b>0)的左、右核心为F1,F2,离心率为,点P在椭圆C上,且△PF1F2的面积的最大值为2.(1)求椭圆C的方程;(2)已知直线l:y=kx+2(k≠0)与椭圆C交于不同的两点M,N,假设在x轴上存在点G,使得|GM|=|GN|,求点G的横坐标的取值范围.【解答】解:(1)显然当点P位于短轴端点时,△PF1F2的面积取得最大值,∴,解得,∴椭圆的方程为=1.(2)联立方程组,消元得(8+9k2)x2+36kx﹣36=0,∵直线l恒过点(0,2),∴直线l与椭圆始终有两个交点,设M(x1,y1),N(x2,y2),那么x1+x2=,设MN的中点为E(x0,y),那么x=,y=kx+2=.∵|GM|=|GN|,∴GE⊥MN,设G(m,0),那么kGE==﹣,∴m==,当k>0时,9k+≥2=12.当且仅当9k=,即k=时取等号;∴﹣≤m<0,当k<0时,9k+≤﹣2=﹣12,当且仅当9k=,即k=﹣时取等号;∴0<m≤.∴点G的横坐标的取值范围是[﹣,0)∪(0,].21.(12分)设函数f(x)=e x﹣2a﹣ln(x+a),a∈R,e为自然对数的底数.(1)假设a>0,且函数f(x)在区间[0,+∞)内单调递增,求实数a的取值范围;(2)假设0<a<,试判定函数f(x)的零点个数.【解答】解:(1)∵函数f(x)在区间[0,+∞)内单调递增,∴f′(x)=e x﹣≥0在区间[0,+∞)恒成立,即a≥e﹣x﹣x在[0,+∞)恒成立,记g(x)=e﹣x﹣x,那么g′(x)=﹣e﹣x﹣1<0恒成立,故g(x)在[0,+∞)递减,故g(x)≤g(0)=1,a≥1,故实数a的范围是[1,+∞);(2)∵0<a<,f′(x)=e x﹣,记h(x)=f′(x),那么h′(x)=e x+>0,知f′(x)在区间(﹣a,+∞)递增,又∵f′(0)=1﹣<0,f′(1)=e﹣>0,,∴f′(x)在区间(﹣a,+∞)内存在唯一的零点x即f′(x)=﹣=0,于是x0=﹣ln(x+a),当﹣a<x<x时,f′(x)<0,f(x)递减,当x>x时,f′(x)>0,f(x)递增,故f(x)min =f(x)=﹣2a﹣ln(x+a)=x+a+﹣3a≥2﹣3a,当且仅当x+a=1时取“=”,由0<a<得2﹣3a>0,∴f(x)min =f(x)>0,即函数f(x)无零点.请考生在2二、23两题中任选一题作答,若是多做,那么按所做的第一题记分.[选修4-4:坐标系与参数方程]22.(10分)已知在平面直角坐标系xOy中,椭圆C的方程为+=1,以O 为极点,x轴的非负半轴为极轴,取相同的长度单位成立极坐标系,直线l的极坐标方程为ρsin(θ+)=3.(1)求直线l的直角坐标方程和椭圆C的参数方程;(2)设M(x,y)为椭圆C上任意一点,求|2x+y﹣1|的最大值.【解答】解:(1)依照题意,椭圆C的方程为+=1,那么其参数方程为,(α为参数);直线l的极坐标方程为ρsin(θ+)=3,变形可得ρsinθcos+ρcosθsin =3,即ρsinθ+ρcosθ=3,将x=ρcosθ,y=ρsinθ代入可得x+y﹣6=0,即直线l的一般方程为x+y﹣6=0;(2)依照题意,M(x,y)为椭圆一点,那么设M(2cosθ,4sinθ),|2x+y﹣1|=|4cosθ+4sinθ﹣1|=|8sin(θ+)﹣1|,分析可得,当sin(θ+)=﹣1时,|2x+y﹣1|取得最大值9.[选修4-5:不等式选讲]23.已知函数f(x)=|x﹣2|.(1)求不等式f(x)+f(2+x)≤4的解集;(2)假设g(x)=f(x)﹣f(2﹣x)的最大值为m,对任意不相等的正实数a,b,证明:af(b)+bf(a)≥m|a﹣b|.【解答】(1)解:不等式f(x)+f(2+x)≤4,即为|x﹣2|+|x|≤4,当x≥2时,2x﹣2≤4,即x≤3,那么2≤x≤3;当0<x<2时,2﹣x+x≤4,即2≤4,那么0<x<2;当x≤0时,2﹣x﹣x≤4,即x≥﹣1,那么﹣1≤x≤0.综上可得,不等式的解集为{x|﹣1≤x≤3};(2)证明:g(x)=f(x)﹣f(2﹣x)=|x﹣2|﹣|x|,由|x﹣2|﹣|x|≤|x﹣2﹣x|=2,当且仅当x≤0时,取得等号,即g(x)≤2,那么m=2,任意不相等的正实数a,b,可得af(b)+bf(a)=a|b﹣2|+b|a﹣2|=|ab﹣2a|+|ab﹣2b|≥|ab﹣2a﹣ab+2b|=|2a﹣2b|=2|a﹣b|=m|a﹣b|,当且仅当(a﹣2)(b﹣2)≤0时,取得等号,即af(b)+bf(a)≥m|a﹣b|.。


2018年高考数学一模试卷一、填空题(本大题共有12题,满分54分,其中1-6题每题4分,7-12题每题5分)1.已知集合A={1,2,5},B={2,a},若A∪B={1,2,3,5},则a= .2.抛物线y2=4x的焦点坐标为.30的解是.4.若复数z满足iz=1+i(i为虚数单位),则z= .5.在代数式(x7的展开式中,一次项的系数是.(用数字作答)6.若函数y=2sin(ωx+1(ω>0)的最小正周期是π,则ω= .7.(5分)若函数f(x)=x a,则a= .8.(5分)将一个正方形绕着它的一边所在的直线旋转一周,所得几何体的体积为27πcm3,则该几何体的侧面积为cm2.9.(5分)已知函数y=f(x)是奇函数,当x<0 时,f(x)=2x﹣ax,且f(2)=2,则a= .10.(5分)若无穷等比数列{a n}的各项和为S n,首项 a1=1,公比为a n=a,则a= .11.(5分)从5男3女共8名学生中选出队长1人,副队长1人,普通队员2人组成 4人志愿者服务队,要求服务队中至少有 1 名女生,共有种不同的选法.(用数字作答)12.(5分)在ABC中,BC边上的中垂线分别交BC,AC于点D,E,,则AC= .二、选择题(本大题共有4题,满分20分)13.(5分)展开式为ad﹣bc的行列式是()A14.(5分)设a,b∈R,若a>b,则()A B.lga>lgb C.sin a>sin b D.2a>2b15.(5分)已知等差数列{a n}的公差为d,前n项和为S n,则“d>0”是“S4+S6>2S5”的()A.充分不必要条件B.必要不充分条件C.充分必要条件 D.既不充分也不必要条件16.(5分)直线x=2与双曲线y2=1的渐近线交于A,B两点,设P为双曲线上任一点,a,b∈R,O为坐标原点),则下列不等式恒成立的是()A.a2+b2≥1 B.|ab|≥1 C.|a+b|≥1 D.|a﹣b|≥2三、解答题(本大题共有5题,满分76分)17.(14分)如图,长方体ABCD﹣A1B1C1D1中,AB=BC=2,A1C与底面ABCD所成的角为60°,(1)求四棱锥A1﹣ABCD的体积;(2)求异面直线A1B与 B1D1所成角的大小.18.(14分)已知f(x)2x﹣1.(1)求f(x)的最大值及该函数取得最大值时x的值;(2)在△ABC 中,a,b,c分别是角 A,B,C所对的边,若f求边c的值.19.(14分)2016 年崇明区政府投资 8 千万元启动休闲体育新乡村旅游项目.规划从 2017 年起,在今后的若干年内,每年继续投资 2 千万元用于此项目.2016 年该项目的净收入为 5 百万元,并预测在相当长的年份里,每年的净收入均为上一年的基础上增长50%.记 2016 年为第 1 年,f (n)为第 1 年至此后第 n (n∈N*)年的累计利润(注:含第 n 年,累计利润=累计净收入﹣累计投入,单位:千万元),且当 f (n)为正值时,认为该项目赢利.(1)试求 f (n)的表达式;(2)根据预测,该项目将从哪一年开始并持续赢利?请说明理由.20.(16分)在平面直角坐标系中,已知椭圆C2=1 (a>0,a≠1)的两个焦点分别是F1,F2,直线l:y=kx+m(k,m∈R)与椭圆交于A,B两点.(1)若M为椭圆短轴上的一个顶点,且△MF1F2是直角三角形,求a的值;(2)若k=1,且△OAB是以O为直角顶点的直角三角形,求a与m满足的关系;(3)若a=2,且k OA•k OB=OAB的面积为定值.21.(18分)若存在常数k(k>0),使得对定义域D内的任意x1,x2(x1≠x2),都有|f(x1)﹣f(x2)|≤k|x1﹣x2|成立,则称函数f(x)在其定义域 D上是“k﹣利普希兹条件函数”.(1)若函数f(x)(1≤x≤4)是“k﹣利普希兹条件函数”,求常数k的最小值;(2)判断函数f(x)=log2x 是否是“2﹣利普希兹条件函数”,若是,请证明,若不是,请说明理由;(3)若y=f(x)(x∈R )是周期为2的“1﹣利普希兹条件函数”,证明:对任意的实数x1,x2,都有|f(x1)﹣f(x2)|≤1.三、解答题(本大题共有5题,满分76分)17.解:(1)∵长方体ABCD﹣A1B1C1D1中,AB=BC=2,∴AA1⊥平面ABCD,=2∴∠A1CA是A1C与底面ABCD所成的角,∵A1C与底面ABCD所成的角为60°,∴∠A1CA=60°,∴AA1∵S正方形ABCD=AB×BC=2×2=4,∴四棱锥A1﹣ABCD的体积:(2)∵BD∥B1D1,∴∠A1BD是异面直线A1B与B1D1所成角(或所成角的补角).∵A1D=A1∴cos∠A1∴∠A1∴异面直线A1B与 B1D1所成角是18.解:f(x)2x﹣((1)当k∈Z),f(x)取得最大值为2;(2)由f2sin(可得sin(∵0<A<π∴∴当∵解得:c=4当∵解得:c=2.19.解:(1)由题意知,第1年至此后第n(n∈N*)年的累计投入为8+2(n﹣1)=2n+6(千万元),第1年至此后第n(n∈N*)….∴f(n)2n+6)2n﹣7(千万元).(2)方法一:∵f(n+1)﹣f(n)2(n+1)﹣7]﹣2n﹣﹣4],∴当n≤3时,f(n+1)﹣f(n)<0,故当n≤4时,f(n)递减;当n≥4时,f(n+1)﹣f(n)>0,故当n≥4时,f(n)递增.又f(1)=0,f(7)521=0,f(8)23≈25﹣23=2>0.∴该项目将从第8年开始并持续赢利.答:该项目将从2023年开始并持续赢利;方法二:设f(x)2x﹣7(x≥1),则f′(x)令f'(x)=0,∴x≈4.从而当x∈[1,4)时,f'(x)<0,f(x)递减;当x∈(4,+∞)时,f'(x)>0,f(x)递增.又f(1)=0,f(7)521=0,f(8)23≈25﹣23=2>0.∴该项目将从第8年开始并持续赢利.答:该项目将从2023年开始并持续赢利.20.解:(1)∵M为椭圆短轴上的一个顶点,且△MF1F2是直角三角形,∴△MF1F2为等腰直角三角形,∴OF1=OM,当a>1,解得当0<a<1,解得(2)当k=1时,y=x+m,设A(x1,y1),(x2,y2),1+a2)x2+2a2mx+a2m2﹣a2=0,∴x1+x2=x1x2∴y1y2=(x1+m)(x2+m)=x1x2+m(x1+x2)+m2∵△OAB是以O为直角顶点的直角三角形,,∴x1x2+y1y2=0,,∴a2m2﹣a2+m2﹣a2=0∴m2(a2+1)=2a2,(3)证明:当a=2时,x2+4y2=4,设A(x1,y1),(x2,y2),∵k OA•k OB=∴x1x2=﹣4y1y2,(1+4k2)x2+8kmx+4m2﹣4=0.∴x1+x2x1x2∴y1y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m22﹣4∴2m2﹣4k2=1,∴∵O到直线y=kx+m的距离∴S△OAB|AB|d=21.解:(1)若函数f(x)(1≤x≤4)是“k﹣利普希兹条件函数”,则对于定义域[1,4]上任意两个x1,x2(x1≠x2),均有|f(x1)﹣f(x2)|≤k|x1﹣x2|成立,不妨设x1>x2,则k∵1≤x2<x1≤4∴k的最小值为(2)f(x)=log2x的定义域为(0,+∞),令x1x2f f=log log﹣1﹣(﹣2)=1,而2|x1﹣x2f(x1)﹣f(x2)>2|x1﹣x2|,∴函数f(x)=log2x 不是“2﹣利普希兹条件函数”.证明:(3)设f(x)的最大值为M,最小值为m,在一个周期[0,2]内f(a)=M,f(b)=m,则|f(x1)﹣f(x2)|≤M﹣m=f(a)﹣f(b)≤|a﹣b|.若|a﹣b|≤1,显然有|f(x1)﹣f(x2)|≤|a﹣b|≤1.若|a﹣b|>1,不妨设a>b,则0<b+2﹣a<1,∴|f(x1)﹣f(x2)|≤M﹣m=f(a)﹣f(b+2)≤|a﹣b﹣2|<1.综上,|f(x1)﹣f(x2)|≤1.。
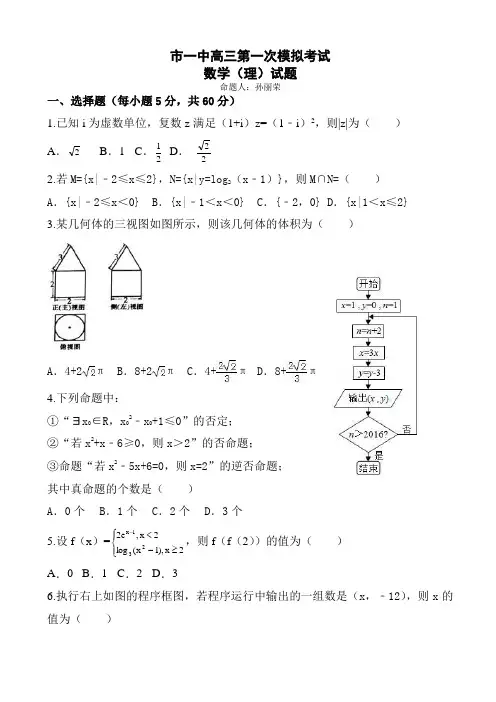
榆林市2018届高考模拟第一次测试 数学(理科)试题 第Ⅰ卷(共60分) 一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.设集合},21|{ZxxxA,集合}3,2{B,则BA等于( ) A.}2{ B.}3,2,1{ C.}3,2,1,0,1{ D.}3,2,1,0{ 2.若向量),3(),5,2(),1,1(xcba,满足30)8(cba,则x( ) A.6 B.5 C.4 D.3 3.设nS是等差数列}{na的前n项和,已知11,362aa,则7S等于( ) A.13 B.35 C.49 D.63 4.按下面的流程图进行计算.若输出的202x,则输出的正实数x值的个数最多为( )
A.5 B.4 C. 3 D.2 5.设21,FF分别是椭圆)0(1:2222babyaxC的左、右焦点,点P在椭圆C上,线段1
PF
的中点在y轴上,若3021FPF,则椭圆的离心率为( ) A.61 B.31 C. 63 D.33 6.已知曲线)6521cos(:,sin:21xyCxyC,则下列说法正确的是( ) A.把1C上各点横坐标伸长到原来的2倍,再把得到的曲线向右平移3,得到曲线2C B.把1C上各点横坐标伸长到原来的2倍,再把得到的曲线向右平移32,得到曲线2C C. 把1C向右平移3,再把得到的曲线上各点横坐标缩短到原来的21,得到曲线2C D.把1C向右平移6,再把得到的曲线上各点横坐标缩短到原来的21,得到曲线2C 7.《九章算术》卷五商功中有如下问题:今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高一丈,问积几何. 刍甍:底面为矩形的屋脊状的几何体(网络纸中粗线部分为其三视图,设网络纸上每个小正方形的边长为1丈),那么该刍甍的体积为( )
A.4立方丈 B.5立方丈 C. 6立方丈 D.12立方丈 8.曲线)0(1)(3xxxxf上一动点))(,(00xfxP处的切线斜率的最小值为( )
A.3 B.3 C. 32 D.6 9.已知直三棱柱111CBAABC的6个顶点都在球O的球面上,若12,,4,31AAACABACAB,则球O的直径为( )
A.13 B.104 C. 102 D.2172
10.设yx,满足约束条件1011yxxyx,若目标函数2xyz的取值范围],[nm恰好是函数)0(sin2xy的一个单调递增区间,则的值为( )
A.21 B.2 C. 4 D.8
11.已知21,FF是双曲线)0,0(12222babyax的左右两个焦点,过点2F与双曲线的一条渐近线平行的直线交双曲线另一条渐近线于点M,若点M在以线段21FF为直径的圆外,则该双曲线离心率的取值范围是( ) A.)2,1( B.)3,2( C. )2,3( D.),2( 12.对于函数)(xf和)(xg,设}0)(|{},0)(|{xgxxfxa,若存在,a,使得1||a,则称)(xf与)(xg互为“零点相邻函数”.若函数2)(1xexfx与
3)(2aaxxxg互为“零点相邻函数”,则实数a的取值范围是( ) A.]4,2[ B.]37,2[ C. ]3,37[ D.]3,2[ 第Ⅱ卷(共90分) 二、填空题(每题5分,满分20分,将答案填在答题纸上) 13.若角的终边经过点)54,53(P,则tansin的值是 . 14.有甲、乙、丙、丁四位歌手参加比赛,其中只有一位获奖,有人走访了四位歌手,甲说“是乙或丙获奖.”乙说:“甲、丙都未获奖.”丙说:“我获奖了”.丁说:“是乙获奖.”四位歌手的话只有两句是对的,则获奖的歌手是 . 15.设ml,是不同的直线,,,是不同的平面,则下列命题正确的是 . ①若mml,,则l或//l. ②若,l,则//l或l. ③若//,//ml,则ml//或l与m相交. ④若,//l,则l或l. 16.在平面直角坐标系xOy中,已知点P是函数)0()(xexfx的图象上的动点,该图象P在处的切线l交y轴于M点,过点P作l的垂线交y轴于点N,设线段MN的中点的纵
坐标为t,则t的最大值是 . 三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)
17. 在ABC中,角CBA,,所对的边分别为cba,,,已知AaBcbcoscos2. (1)求角A的大小; (2)若2a,求ABC的面积S的最大值. 18. 数列}{na满足*11),1()1(,1Nnnnannaann. (1)证明:数列}{nan是等差数列; (2)若nnnaaaaaT14321)1(,求nT2. 19. 在如图所示的几何体中,四边形ABCD为平行四边形,EBABD,90平面13,1,3,2,//,BCEFEBABABEFABCD,且M是BD的中点.
(1)求证://EM平面ADF; (2)求二面角BFDA的余弦值的大小. 20. 已知抛物线)0(2:2ppxyE的准线与x轴交于点k,过点k做圆9)5(:22yxC的两条切线,切点为33||,,MNNM.
(1)求抛物线E的方程; (2)若直线AB是讲过定点)0,2(Q的一条直线,且与抛物线E交于BA,两点,过定点Q作AB的垂线与抛物线交于DG,两点,求四边形AGBD面积的最小值.
21. 已知函数xexxgxxxf)(,ln)(,记)()()(xfxfxF. (1)求证:)(xF在区间),1(内有且仅有一个实数; (2)用},min{ba表示ba,中的最小值,设函数)}(),(min{)(xgxfxm,若方程cxm)(在区间),1(内有两个不相等的实根)(,2121xxxx,记)(xF在),1(内的实根为0x.求证:0212xxx. 请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分. 22.选修4-4:坐标系与参数方程 在平面直角坐标系中,以坐标原点为极点,x轴正半轴为极轴,建立极坐标系,点A的极坐标为)4,24(,直线l的极坐标方程为a)4cos(,且l过点A,曲线1C的参考
方程为sin3cos2yx(为参数). (1)求曲线1C上的点到直线l的距离的最大值与最小值; (2)过点)2,2(B与直线l平行的直线1l与曲1C线交于NM,两点,求||||BNBM的值. 23.选修4-5:不等式选讲 设0,0ba,且baba11.求证: (1)2ba; (2)22aa与22bb不可能同时成立.
试卷答案 一、选择题 1-5:DCCBD 6-10:BBCAC 11、12:DD 二、填空题
13. 1516 14.丙 15.② 16. )1(21ee 三、解答题
17.解:(1)由AaBcbcoscos2及正弦定理可得AABCBcossincossin2sin, 所以BAACABcossincossin2cossin, 所以)sin(cossin2BAAC, 所以CACsincossin2. 又因为0sinC,所以22cosA.故4A. (2)由余弦定理及(1)得,bccbbccba24cos2422222, 由基本不等式得:bc)22(4,当且仅当cb时等号成立, 所以)22(2224bc,
所以1222)22(221sin21AbcS. 所以ABC的面积S的最大值为12. 18.解:(1)由已知可得111nanann,即111nanann, 所以}{nan是以111a为首项,1为公差的等差数列. (2)由(1)得nnan,所以2nan,
nnnaaaaaT14321)1(,
nnnnnnnnnnnaaaaaaTnnn22222222124321222)143()1473()122)(122()34)(34()12)(12()2()12(4321
19.解:(1)解法一:取AD的中点N,连接NFMN,. 在DAB中,M是BD的中点,N是AD的中点, 所以ABMNABMN21,//,又因为ABEFABEF21,//, 所以EFMN//且EFMN. 所以四边形MNFE为平行四边形,所以FNEM//, 又因为FN平面EMADF,平面ADF,故//EM平面ADF. 解法二:因为EB平面BDABABD,, 故以B为原点,建立如图所示的空间直角坐标系xyzB.
由已知可得)3,1,0(),0,2,3(),3,0,23(AFADEM, 设平面ADF的一个法向量是),,(zyxn. 由00AFnADn得03023zyyx
令3y,则)3,3,2(n. 又因为0nEM,所以nEM,又EM平面ADF, 故//EM平面ADF.