三年级奥数第7讲——填数游戏

三年级奥数培训资料时间：2021.03.09 创作：欧阳法填数游戏一、知识要点小朋友都喜爱做游戏。

填数游戏不但非常有趣，而且能促使你积极地思考问题、分析问题、发展能力。

但有时也有一定的难度，不过，只要你掌握了填写方法，填起来就很轻松了。

填数时，要仔细观察图形，确定图形中关键的位置应填几，一般是图形的顶点及中间位置。

另外，要将所填的空与所提供的数字联系起来，一般要先计算所填数的总和与所提供数字的和之差，从而确定关键位置应填几。

关键位置的数确定好了，其他问题就迎刃而解了。

二、精讲精练【例题1】在下图中分别填入1——9，使两条直线上五个数的和相等，和是多少呢？【思路导航】我们可以这样想，把1——9中间的5填到中心的○内，剩下八个数，一大一小，搭配成和都是10的四组，这样两条直线上五个数的和都是5＋10×2=25。

如果把1填在中心的○内，这样剩下的八个数可以一大一小搭配成和都是11的四组，这时两条直线上五个数的和是1＋11×2=23。

想想：两条直线上五个数的和还可以是多少？练习1：1.在下图（左下）中填入2——10，使横行、竖行中的五个数的和相同。

和是多少呢？2.把1、4、7、10、13、16、19七个数填入图（中上图）中7朵花里，使每条直线上三个数的和相等。

3.把6、8、10、12、14、16、18七个数填在右上图的○中，使每排三个数及外圆上三个数的和都是32。

【例题2】把数字1——8分别填入下图的小圆圈内，使每个五边形上5个数的和都等于20。

【思路导航】题目中所给8个数字的和是1＋2＋3＋4＋5＋6＋7＋8=36，题中要使每个五边形上五个数的和等于20，那么两个五边形上数字的总和是20×2=40。

两个五边形上的数字总和比8个数的和多40－36=4，多4的原因是图中中间两个圆圈的数字算了两次，多算了一次。

1——8中只有1和3的和为4，所以先确定关键的中间两个圆圈中，一个填1.一个填3。

第7讲：填数游戏专题分析：小朋友都喜爱做游戏，填数游戏不但非常有趣，而且能促使你积极地思考问题、分析问题、但做填数游戏也有一定的难度，不过只要你掌握了方法，填起来就很轻松了。

填数时要仔细观察图形，确实图形中关键位置应填几，关键位置一般是图形的顶点或中间位置。

另外要将所填的空与所提供的数联系起来，一般要先计算所填数的总和与所提供的总和之差，进而确定关键位置应填几。

关键位置的数确定好了，其他问题就迎刃而解了。

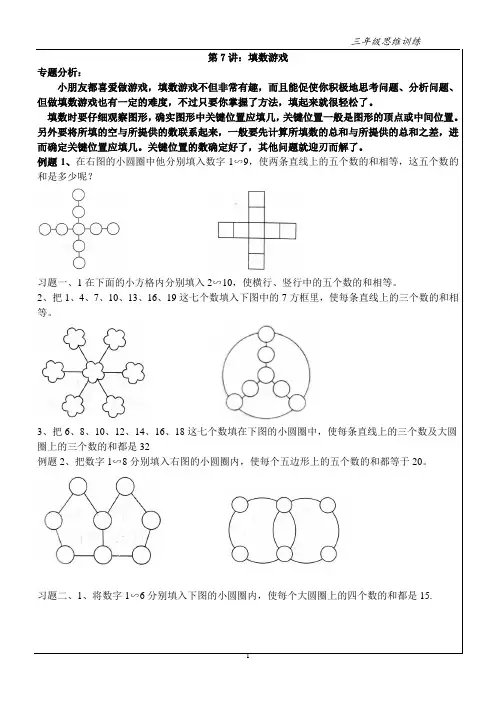
例题1、在右图的小圆圈中他分别填入数字1∽9，使两条直线上的五个数的和相等，这五个数的和是多少呢？习题一、1在下面的小方格内分别填入2∽10，使横行、竖行中的五个数的和相等。

2、把1、4、7、10、13、16、19这七个数填入下图中的7方框里，使每条直线上的三个数的和相等。

3、把6、8、10、12、14、16、18这七个数填在下图的小圆圈中，使每条直线上的三个数及大圆圈上的三个数的和都是32例题2、把数字1∽8分别填入右图的小圆圈内，使每个五边形上的五个数的和都等于20。

习题二、1、将数字1∽6分别填入下图的小圆圈内，使每个大圆圈上的四个数的和都是15.2、把5、6、7、8、9、10这六个数填入下图三角形三条边的小圆圈内，使每条边上的三个数的和都是21.3、把1∽8这8个数字分别填入下图的各个小方格里，使每一横行、每一竖行的三个数的和都是13.例题3、用5∽13这九个数补全右图的方格，使每行、每列及对角线上的三个数之和相等。

习题三、1、将1∽9这9个数字填在下面的方格内，使横行、竖行及对角线上的三个数的和都是15.2、将1∽16这16个数字分别填入下图的16个方格内，使每行、每列及两条对角线上的四个数的和都相等。

3、将1∽11这11个数分别填入下面的“王”字格中，使每行、每一列的数之和都等于18.例题4、将数字1、2、3、4、5、6、7、填入下图的小圆圈中，使大、小圆环上的三个数字之和以及每条直线上的三个数字之和都相等。

第7讲：填数游戏专题分析：小朋友都喜爱做游戏，填数游戏不但非常有趣，而且能促使你积极地思考问题、分析问题、但做填数游戏也有一定的难度，不过只要你掌握了方法，填起来就很轻松了。

填数时要仔细观察图形，确实图形中关键位置应填几，关键位置一般是图形的顶点或中间位置。

另外要将所填的空与所提供的数联系起来，一般要先计算所填数的总和与所提供的总和之差，进而确定关键位置应填几。

关键位置的数确定好了，其他问题就迎刃而解了。

例题1、在右图的小圆圈中他分别填入数字1∽9，使两条直线上的五个数的和相等，这五个数的和是多少呢？习题一、1在下面的小方格内分别填入2∽10，使横行、竖行中的五个数的和相等。

2、把1、4、7、10、13、16、19这七个数填入下图中的7方框里，使每条直线上的三个数的和相等。

3、把6、8、10、12、14、16、18这七个数填在下图的小圆圈中，使每条直线上的三个数及大圆圈上的三个数的和都是32例题2、把数字1∽8分别填入右图的小圆圈内，使每个五边形上的五个数的和都等于20。

习题二、1、将数字1∽6分别填入下图的小圆圈内，使每个大圆圈上的四个数的和都是15.2、把5、6、7、8、9、10这六个数填入下图三角形三条边的小圆圈内，使每条边上的三个数的和都是21.3、把1∽8这8个数字分别填入下图的各个小方格里，使每一横行、每一竖行的三个数的和都是13.例题3、用5∽13这九个数补全右图的方格，使每行、每列及对角线上的三个数之和相等。

习题三、1、将1∽9这9个数字填在下面的方格内，使横行、竖行及对角线上的三个数的和都是15.2、将1∽16这16个数字分别填入下图的16个方格内，使每行、每列及两条对角线上的四个数的和都相等。

3、将1∽11这11个数分别填入下面的“王”字格中，使每行、每一列的数之和都等于18.例题4、将数字1、2、3、4、5、6、7、填入下图的小圆圈中，使大、小圆环上的三个数字之和以及每条直线上的三个数字之和都相等。

三年级奥数培训资料填数游戏一、知识要点小朋友都喜爱做游戏。

填数游戏不但非常有趣，而且能促使你积极地思考问题、分析问题、发展能力。

但有时也有一定的难度，不过，只要你掌握了填写方法，填起来就很轻松了。

填数时，要仔细观察图形，确定图形中关键的位置应填几，一般是图形的顶点及中间位置。

另外，要将所填的空与所提供的数字联系起来，一般要先计算所填数的总和与所提供数字的和之差，从而确定关键位置应填几。

关键位置的数确定好了，其他问题就迎刃而解了。

二、精讲精练【例题1】在下图中分别填入1——9，使两条直线上五个数的和相等，和是多少呢？【思路导航】我们可以这样想，把1——9中间的5填到中心的○内，剩下八个数，一大一小，搭配成和都是10的四组，这样两条直线上五个数的和都是5＋10×2=25。

如果把1填在中心的○内，这样剩下的八个数可以一大一小搭配成和都是11的四组，这时两条直线上五个数的和是1＋11×2=23。

想想：两条直线上五个数的和还可以是多少？练习1：1.在下图（左下）中填入2——10，使横行、竖行中的五个数的和相同。

和是多少呢？2.把1、4、7、10、13、16、19七个数填入图（中上图）中7朵花里，使每条直线上三个数的和相等。

3.把6、8、10、12、14、16、18七个数填在右上图的○中，使每排三个数及外圆上三个数的和都是32。

【例题2】把数字1——8分别填入下图的小圆圈内，使每个五边形上5个数的和都等于20。

【思路导航】题目中所给8个数字的和是1＋2＋3＋4＋5＋6＋7＋8=36，题中要使每个五边形上五个数的和等于20，那么两个五边形上数字的总和是20×2=40。

两个五边形上的数字总和比8个数的和多40－36=4，多4的原因是图中中间两个圆圈的数字算了两次，多算了一次。

1——8中只有1和3的和为4，所以先确定关键的中间两个圆圈中，一个填1.一个填3。

20－（1＋3）=16，16可以分成2＋6＋8和4＋5＋7，所以本题应该这样填：练习2：1.将数字1——6填入下图（左下）中的小圆圈内，使每个大圆上4个数的和都是15。

欢迎阅读三年级奥数培训资料填数游戏一、知识要点小朋友都喜爱做游戏。

填数游戏不但非常有趣，而且能促使你积极地思考问题、分析问题、发展能力。

但有时也有一定的难度，不过，只要你掌握了填1.在下图（左下）中填入2——10，使横行、竖行中的五个数的和相同。

和是多少呢？2.把1、4、7、10、13、16、19七个数填入图（中上图）中7朵花里，使每条直线上三个数的和相等。

3.把6、8、10、12、14、16、18七个数填在右上图的○中，使每排三个数及外圆上三个数的和都是32。

【例题2】把数字1——8分别填入下图的小圆圈内，使每个五边形上5个数的和都等于20。

【思路导航】题目中所给8个数字的和是1＋2＋3＋4＋5＋6＋7＋8=36，题中要使每个五边形上五个数的和等于20，那么＋7＋4＋2=16填入4个顶点。

??想一想，有没有其他填法？练习3：1.把1——8填入下图（下左）中，使每边3个数的和等于13。

2.将1——9这九个数填入中上图中，使三角形每条边上四个数的和等于19，且有一个顶点的数字为1。

3.把1——10这十个数填入右上图中，使每个正方形顶点圆圈内四个数之和都相等，而且最大。

这个和是多少？【例题4】把1——8填入下图○内，使每边上三个数的和最大。

求最大的和是多少？【思路导航】这题的关键是找出中间部分填什么，因为所给的3个数都是双数，恰好每个圆内有两个双数，它们的和也是双数，再填入两个数后，使每个圆的4个数的和是21.21是单数，也就是每个圆内填入的两个数的和为单数，而3、5、7、8中3、5、7都是单数，要使和为单数，8要填入中间部分，如右上图。

练习5：1.在图（左下图）中各圆的空余部分分别填上1、2、4、6，使每个圆中4个数的和是15。

2.在图（中上图）中各圆空余部分分别填上4、5、7、9，使每个圆中4个数的和是27。

3.在图（右上图）中各圆空余部分分别填上6、8、10、11.使每个圆中4个数的和是33。

第07讲填数游戏教学目标经历填数游戏活动，初步提高分析推理能力。

在探索、尝试、交流等活动中，体会填数游戏的乐趣，激发学习兴趣。

知识梳理本讲有两部分主要内容：1、幻方的概念和性质，简单幻方的编制；2、把一些数字按照一定要求排列成相应的图形，叫做数阵图。

大致分为三类：(1)封闭型数阵图(2)辐射型数阵图(3)复合型数阵图幻方的概念：所谓幻方是指在正方形方格表的每个方格内填入数，使得每行、每列和两条对角线上的各数之和相等；而阶数是指每行、每列所包含的方格数。

幻方题可以粗略的分为两种(1)限制了所填入的数字，或者给出了需要填入的各个数字，或者已经填入一个或几个数字；(2)另一种是对填入的数字没有任何限制，填对即可。

幻方问题主要方法：(1)累加法：利用累加的方法可以求出“幻和”和关键位置上的数字。

通常将若干个“幻和”累加在一起，再计算每一个位置上的重数，从而求出“幻和”和关键位置上的数字。

(2)求出“幻和”和关键位置上的数字后，结合枚举法完成数阵图的填写，在填写数阵图的过程中注意从特殊的数字和位置入手。

(3)比较法：利用比较的方法可以直接填出某些位置的数字。

注意观察数阵图中相关联的“幻和”之间的关系，注意它们之间共同的部分，去比较不同的部分本讲还有一部分内容是数阵图拓展，也就是在三年级数阵图初步的基础上继续学习数阵图问题的解题方法。

数阵图问题方法多样且特殊，我们将在例题中详细讲解。

其实这些方法和幻方是一致的，大家可以在下面的学习中体会到这一点。

典例分析例1、在下图中分别填入1—9，使两条直线上五个数的和相等，和是多少呢？【解析】我们可以这样想，把1——9中间的5填到中心的○内，剩下八个数，一大一小，搭配成和都是10的四组，这样两条直线上五个数的和都是5＋10×2=25。

如果把1填在中心的○内，这样剩下的八个数可以一大一小搭配成和都是11的四组，这时两条直线上五个数的和是1＋11×2=23。

填数游戏专题简析：小朋友都喜爱做游戏。

填数游戏不但非常有趣，而且能促使你积极地思考问题、分析问题、发展能力。

但有时也有一定的难度，不过，只要你掌握了填写方法，填起来就很轻松了。

填数时，要仔细观察图形，确定图形中关键的位置应填几，一般是图形的顶点及中间位置。

另外，要将所填的空与所提供的数字联系起来，一般要先计算所填数的总和与所提供数字的和之差，从而确定关键位置应填几。

关键位置的数确定好了，其他问题就迎刃而解了。

【例题1】在下图中分别填入1——9，使两条直线上五个数的和相等，和是多少呢？【思路导航】我们可以这样想，把1——9中间的5填到中心的○内，剩下八个数，一大一小，搭配成和都是10的四组，这样两条直线上五个数的和都是5＋10×2=25。

如果把1填在中心的○内，这样剩下的八个数可以一大一小搭配成和都是11的四组，这时两条直线上五个数的和是1＋11×2=23。

想想：两条直线上五个数的和还可以是多少？9 18 2736410101010练习一1、在右图中填入2——10，使横行、竖行中的五个数的和相同。

和是多少呢？2、把1、4、7、10、13、16、19七个数填入图中7朵花里，使每条直线上三个数的和相等。

3、把6、8、10、12、14、16、18七个数三个数的和都是32。

【例题2】把数字1——8分别填入下图的小圆圈内，使每个五边形上5个数的和都等于20。

【思路导航】题目中所给8个数字的和是1＋2＋3＋4＋5＋6＋7＋8=36，题中要使每个五边形上五个数的和等于20，那么两个五边形上数字的总和是20×2=40。

两个五边形上的数字总和比8个数的和多40－36=4，多4的原因是图中中间两个圆圈的数字算了两次，多算了一次。

1——8中只有1和3的和为4，所以先确定关键的中间两个圆圈中，一个填1，一个填3。

20－（1＋3）=16，16可以分成2＋6＋8和4＋5＋7，所以本题应该这样填：练 习 二1、将数字1—6填入右图中的小圆圈内，使每个大圆上4个数的和都是15。

填数游戏专题简析：小朋友都喜爱做游戏。

填数游戏不但非常有趣，而且能促使你积极地思考问题、分析问题、发展能力。

但有时也有一定的难度，不过，只要你掌握了填写方法，填起来就很轻松了。

填数时，要仔细观察图形，确定图形中关键的位置应填几，一般是图形的顶点及中间位置。

另外，要将所填的空与所提供的数字联系起来，一般要先计算所填数的总和与所提供数字的和之差，从而确定关键位置应填几。

关键位置的数确定好了，其他问题就迎刃而解了。

【例题1】在下图中分别填入1——9，使两条直线上五个数的和相等，和是多少呢？【思路导航】我们可以这样想，把1——9中间的105填到中心的○，剩下八个数，一大一小，搭配成和都是10的四组，这样两条直线上五个数的和都是5＋10×2=25。

如果把1填在中心的○，这样剩下的八个数可以一大一小搭配成和都是11的四组，这时两条直线上五个数的和是1＋11×2=23。

想想：两条直线上五个数的和还可以是多少？练习一1、在右图中填入2——10，使横行、竖行中的五个数的和相同。

和是多少呢？2、把1、4、7、10、13、16、19七个数填入图中7朵花里，使每条直线上三个数的和相等。

3、把6、8、10、12、14、16、18七个数填在下图的○中，使每排三个数及外圆上三个数的和都是32。

形上5个数的和都等于20。

【思路导航】题目中所给8个数字的和是1＋2＋3＋4＋5＋6＋7＋8=36，题中要使每个五边形上五个数的和等于20，那么两个五边形上数字的总和是20×2=40。

两个五边形上的数字总和比8个数的和多40－36=4，多4的原因是图中中间两个圆圈的数字算了两次，多算了一次。

1——8中只有1和3的和为4，所以先确定关键的中间两个圆圈中，一个填1，一个填3。

20－（1＋3）=16，16可以分成2＋6＋8和4＋5＋7，所以本题应该这样填：练 习 二1、将数字1—6填入右图中的小圆圈，使每个大圆上4个数的和都是15。

第7讲巧添运算符号知识要点根据题目给定的条件和要求，添运算符号和括号，使等式成立，这是一种很有趣的游戏。

这种游戏需要动脑筋找规律，讲究方法，一旦掌握方法，就有取得成功的把握。

添运算符号问题，通常采用尝试探索法。

主要尝试方法有两种：1．如果题目中的数字比较简单，可以从等式的结果入手，推想哪些算式能得到这个结果，然后拼凑出所求的式子；2．如果题目中的数字多，结果也较大，可以考虑先用几个数字凑出比较接近于等式结果的数，然后再进行调整，使等式成立。

通常情况下，要根据题目的特点，选择方法，有时将以上两种方法组合起来使用，更有助于问题的解决。

精讲精练【例题1】在下列4个4中间，添上适当的运算符号＋、－、×、÷和（），组成3个不同的算式，使得数都是2。

4 4 4 4=24 4 4 4=24 4 4 4=2【例题2】给下列各算式添上＋、－、×、÷或（），使等式成立。

你能试一试吗？8 8 8 8 = 0 8 8 8 8 = 18 8 8 8 = 2 8 8 8 8 = 3【思路导航】这道题除了可以用倒推法来分析，还可以这样想：（1）等于0的思考方法：假设最后一步运算是减法，那么这四个数可以分成两组，这两组的和、差、积、商应该相等，有：8＋8－（8＋8）=0 8×8－8×8=0 8－8－（8－8）=0 8÷8－8÷8=0（2）等于1的思考方法：假设最后一步是除法，那么四个数分成两组，这两组的和、积、商分别相等，相同的数相除也可得到1，有：（8＋8）÷（8＋8）=1 8×8÷（8×8）=1 8÷8÷（8÷8）=1 8×8÷8÷8=1 8÷8×8÷8=1 8÷（8×8÷8）=1 （3）等于2的思考方法：假设最后一步是加法，那么两组数各为1，有：8÷8＋8÷8=2（4）等于3的思考方法：假设最后一步是除法，那么前三个数凑为3个8，有：（8＋8＋8）÷8=3【例题3】在下面算式适当的地方添上加号，使算式成立。

填数游戏举一反三.专题简析：小朋友都喜爱做游戏。

填数游戏不但非常有趣，而且能促使你积极地思考问题、分析问题、发展能力。

但有时也有一定的难度，不过，只要你掌握了填写方法，填起来就很轻松了。

填数时，要仔细观察图形，确定图形中关键的位置应填几，一般是图形的顶点及中间位置。

另外，要将所填的空与所提供的数字联系起来，一般要先计算所填数的总和与所提供数字的和之差，从而确定关键位置应填几。

关键位置的数确定好了，其他问题就迎刃而解了。

.例题1在下图中分别填入1——9，使两条直线上五个数的和相等，和是多少呢？思路导航：我们可以这样想，把1——9中间的5填到中心的○内，剩下八个数，一大一小，搭配成和都是10的四组，这样两条直线上五个数的和都是5＋10×2=25。

如果把1填在中心的○内，这样剩下的八个数可以一大一小搭配成和都是11的四组，这时两条直线上五个数的和是1＋11×2=23。

想想：两条直线上五个数的和还可以是多少？.练习一1，在下图中填入2——10，使横行、竖行中的五个数的和相同。

和是多少呢？答2，把1、4、7、10、13、16、19七个数填入图中7朵花里，使每条直线上三个数的和相等。

答3，把6、8、10、12、14、16、18七个数填在下图的○中，使每排三个数及外圆上三个数的和都是32。

答.例题2把数字1——8分别填入下图的小圆圈内，使每个五边形上5个数的和都等于20。

思路导航：题目中所给8个数字的和是1＋2＋3＋4＋5＋6＋7＋8=36，题中要使每个五边形上五个数的和等于20，那么两个五边形上数字的总和是20×2=40。

两个五边形上的数字总和比8个数的和多40－36=4，多4的原因是图中中间两个圆圈的数字算了两次，多算了一次。

1——8中只有1和3的和为4，所以先确定关键的中间两个圆圈中，一个填1，一个填3。

20－（1＋3）=16，16可以分成2＋6＋8和4＋5＋7，所以本题应该这样填：.练习二1，将数字1——6填入下图中的小圆圈内，使每个大圆上4个数的和都是15。

小学三年级奥数讲解及练习题：填数游戏
【例题2】把数字1——8分别填入下图的小圆圈内，使每个五边形上5个数的和都等于20。

【思路导航】题目中所给8个数字的和是1＋2＋3＋4＋5＋6＋7＋8=36，题中要使每个五边形上五个数的和等于20，那么两个五边形上数字的总和是20×2=40。

两个五边形上的数字总和比8个数的和多40－36=4，多4的原因是图中中间两个圆圈的数字算了两次，多算了一次。

1——8中只有1和3的和为4，所以先确定关键的中间两个圆圈中，一个填1.一个填3。

20－（1＋3）=16，16可以分成2＋6＋8和4＋5＋7，所以本题应该这样填：
练习2：
1.将数字1——6填入下图（左下）中的小圆圈内，使每个大圆上4个数的和都是15。

2.把5、6、7、8、9、10这六个数填入右上图三角形三条边的○内，使得每条边上的三个数的和是21。

3.把1——8这八个数，分别填入下图的各个□内，使得每一横行、每一竖行的三个数的和是13。

<<<1234>>>。

填数游戏专题简析:小朋友都喜爱做游戏。

填数游戏不但非常有趣,而且能促使您积极地思考问题、分析问题、发展能力。

但有时也有一定的难度,不过,只要您掌握了填写方法,填起来就很轻松了。

填数时,要仔细观察图形,确定图形中关键的位置应填几,一般就是图形的顶点及中间位置。

另外,要将所填的空与所提供的数字联系起来,一般要先计算所填数的总与与所提供数字的与之差,从而确定关键位置应填几。

关键位置的数确定好了,其她问题就迎刃而解了。

【例题1】在下图中分别填入1——9,使两条直线上五个数的与相等,与就是多少呢？【思路导航】我们可以这样想,把1——9中间的5填到中心的○内,剩下八个数,一大一小,搭配成与都就是10的四组,这样两条直线上五个数的与都就是5＋10×2=25。

如果把1填在中心的○内,这样剩下的八个数可以一大一小搭配成与都就是11的四组,这时两条直线上五个数的与就是1＋11×2=23。

想想:两条直线上五个数的与还可以就是多少？918 2736410101010练习一1、在右图中填入2——10,使横行、竖行中的五个数的与相同。

与就是多少呢？2、把1、4、7、10、13、16、19七个数填入图中7朵花里,使每条直线上三个数的与相等。

3、把6、8、10、12、14、16、18七个数填在下图的○中,使每排三个数及外圆上三个数的与都就是32。

【例题2】把数字1——8分别填入下图的小圆圈内,使每个五边形上5个数的与都等于20。

【思路导航】题目中所给8个数字的与就是1＋2＋3＋4＋5＋6＋7＋8=36,题中要使每个五边形上五个数的与等于20,那么两个五边形上数字的总与就是20×2=40。

两个五边形上的数字总与比8个数的与多40－36=4,多4的原因就是图中中间两个圆圈的数字算了两次,多算了一次。

1——8中只有1与3的与为4,所以先确定关键的中间两个圆圈中,一个填1,一个填3。

20－(1＋3)=16,16可以分成2＋6＋8与4＋5＋7,所以本题应该这样填:练 习 二1、将数字1—6填入右图中的小圆圈内,使每个大圆上4个数的与都就是15。

第07讲填数游戏教学目标经历填数游戏活动，初步提高分析推理能力.在探索、尝试、交流等活动中，体会填数游戏的乐趣，激发学习兴趣.知识梳理本讲有两部分主要内容：1、幻方的概念和性质，简单幻方的编制；2、把一些数字按照一定要求排列成相应的图形，叫做数阵图.大致分为三类：(1)封闭型数阵图(2)辐射型数阵图(3)复合型数阵图幻方的概念：所谓幻方是指在正方形方格表的每个方格内填入数，使得每行、每列和两条对角线上的各数之和相等；而阶数是指每行、每列所包含的方格数.幻方题可以粗略的分为两种(1)限制了所填入的数字，或者给出了需要填入的各个数字，或者已经填入一个或几个数字；(2)另一种是对填入的数字没有任何限制，填对即可.幻方问题主要方法：(1)累加法：利用累加的方法可以求出“幻和”和关键位置上的数字.通常将若干个“幻和”累加在一起，再计算每一个位置上的重数，从而求出“幻和”和关键位置上的数字.(2)求出“幻和”和关键位置上的数字后，结合枚举法完成数阵图的填写，在填写数阵图的过程中注意从特殊的数字和位置入手.(3)比较法：利用比较的方法可以直接填出某些位置的数字.注意观察数阵图中相关联的“幻和”之间的关系，注意它们之间共同的部分，去比较不同的部分本讲还有一部分内容是数阵图拓展，也就是在三年级数阵图初步的基础上继续学习数阵图问题的解题方法.数阵图问题方法多样且特殊，我们将在例题中详细讲解.其实这些方法和幻方是一致的，大家可以在下面的学习中体会到这一点.典例分析例1、在下图中分别填入1—9，使两条直线上五个数的和相等，和是多少呢？【解析】我们可以这样想，把1——9中间的5填到中心的○内，剩下八个数，一大一小，搭配成和都是10的四组，这样两条直线上五个数的和都是5＋10×2=25. 如果把1填在中心的○内，这样剩下的八个数可以一大一小搭配成和都是11的四组，这时两条直线上五个数的和是1＋11×2=23.想想：两条直线上五个数的和还可以是多少？例2、把数字1——8分别填入下图的小圆圈内，使每个五边形上5个数的和都等于20.【解析】题目中所给8个数字的和是1＋2＋3＋4＋5＋6＋7＋8=36，题中要使每个五边形上五个数的和等于20，那么两个五边形上数字的总和是20×2=40.两个五边形上的数字总和比8个数的和多40－36=4，多4的原因是图中中间两个圆圈的数字算了两次，多算了一次.1—8中只有1和3的和为4，所以先确定关键的中间两个圆圈中，一个填1.一个填3.20－(1＋3)=16，16可以分成2＋6＋8和4＋5＋7，所以本题应该这样填：例3、在图中填入2——9，使每边3个数的和等于15.【解析】解这题的关键是填出图中的4个顶点，因为求和时这4个顶点各算了两次，多算了一次，所以4边数的和是15×4=60，所给的数的和是2＋3＋4＋5＋6＋7＋8＋9=44，所以4个顶点数的和是60－44=16.我们可选出3＋7＋4＋2=16填入4个顶点.想一想，有没有其他填法？ .例4、把1—8填入下图○内，使每边上三个数的和最大.求最大的和是多少？【解析】要使每边上三个数之和最大，容易想到把8、7、6、5填在四角，因为四个角上的数在求和时各用了两次，其他数各用了一次.由此我们可以列出求和的算式为：[(8＋7＋6＋5)×2＋4＋3＋2＋1]÷4=62÷4 和不是整数，说明四条边上的总和要减少2才行，这只要将填在角上的5换成3即可.所以，最大的和为：(62－2)÷4=15 .例5、在下图各圆空余部分填上3、5、7、8，使每个圆的4个数的和都是21.【解析】这题的关键是找出中间部分填什么，因为所给的3个数都是双数，恰好每个圆内有两个双数，它们的和也是双数，再填入两个数后，使每个圆的4个数的和是21.21是单数，也就是每个圆内填入的两个数的和为单数，而3、5、7、8中3、5、7都是单数，要使和为单数，8要填入中间部分，如右图.例6、将3、4、5三个数分别填在图形的方格种，使每行每列每条对角线上三个数的和相等.【解析】可以这样想，如果每行的三个数是3、4、5，每列的三个数也分别是3、4、5，那么，每行、每列三个数的和是相等的.如果要满足对角线三个数的和与每行、每列三个数的和相等，一组可用3、4、5，另一组三个数必定都是4.例7、把2、3、4、5分别填入○内，使每条线上三个数的和都等于10.【解析】可以这样想，右边一条线上出现了1和6，最上面的圆中可填10－6－1＝3；左边下面两个圆中数的和是10－3＝7(7可以分成2和5).可下边另两个数的和是10－1＝9(9可以分成4和5)，那么5是左边和下边两条边上的公用数，5应填在左下角的圆内，2和4分别填在左边和下边的中间圆内.例8、将2、4、5、7分别填入下列图中，使每条线上三个数的和等于13.【解析】要使每条线上的三个数相加的和等于13，可以从有两个数的那一边入手，左下角可填13－8－3＝2；在上边8和1的中间可填13－8－1＝4；右下角可以填13－2－6＝5；右边1和5的中间应填13－1－5＝7.例9、将1、2、3、4、5、6、7分别填入图中，使每行、每列、每条对角线上三个数的和都等于15.【解析】先从中间横行入手，15－9－5＝1，8的下面填1；第一竖行15－8－1＝6，最下一格填6；两个对角分别填15－8－5＝2和15－6－5＝4；第一横行和第三横行中间数应填15－8－4＝3，15－6－2＝7.➢课堂狙击1.将6、8、9、10、11、12六个数分别填在小圆圈里，使每个大圆圈上五个数的和等于40.【解析】从图中可以看出，在5～12八个数中，7和5是两个大圆中的公用数.那么大圆中另三个数的和应是40－7－5＝28.可以推导出左边大圆中的另三个数可以为12、10和6；右边大圆中另三个数可以为11、9和8，反之亦可.2. 把2、3、4、6四个数分别填在灯笼里，使每个圆圈上四个灯笼里的数加起来，和都等于14.实战演练【解析】上方圆圈里已有两个灯笼填好5和1，要使四个灯笼内的数加起来和是14，另外两个灯笼里的数加起来的和应是8.在2、3、4、6这四个数中，只有2＋6＝8，所以把2和6分别填入这两个灯笼里，再把剩下的3和4填在另外两个相应的灯笼里.4.将1、2、3、4、5、6、7这七个数分别填入圆圈内，使每条线上的三个数的和都相等.【解析】“4”这个数是中间数，先填入图形中央，再将其余六个数分成三组，因为1＋2＋3＋5＋6＋7＝24，24÷3＝8，所以有1＋7＝8，2＋6＝8，3+5=8，分别把这六个数填入圆圈内就行了.5.将1、2、3、4、5、6、7这七个数分别填入圆圈内，使每条线上三个数的和都是10.【解析】关键是要确定中间的圆圈里填几.可以这样想：先分别求出七个数的和与三条线上的九个数的和，并作比较，30－28＝2，这多出的2，是由于中间圆圈内的数重复计算了2次，所以中间圆圈里应填2÷2＝1，然后将其余的六个数分成三组，每一组的和为9：2＋7＝9，3＋6＝9，4＋5＝9，同一组的数，填到同一条线上.6. 将1、2、3、4、5、6填入图中的小圆圈内，使每个大圆上4个数的和都是16.【解析】所给的六个数之和是1＋2＋3＋4＋5＋6＝21，题中要求每个大圆上数之和为16，那么两个大圆上数的总和是16×2＝32.两个大圆上数总和比六个数的和多32－21＝11，怎么多了？因为图中间两圆圈里的数算了两次，多算了一次就多了11.1～6中只有5 和6合起来是11，所以先确定中间的两个圆圈中一个填5、一个填6，确定了这两个关键的数，其余圆圈里的数就不难确定了.用16－(5＋6)＝5，5＝4＋1＝3＋2，两个大圆中另外两个小圆里分别填4、1和2、3➢课后反击1、如图：在空格中填入不同的数，使每一横行、竖行、斜行的三个数的和等于15.64 2【解析】2、下图中三个圆圈两两相交形成七个部分，分别填上1—7七个自然数，在一些部分中，自然数3，5，7三个数已填好，请填上其余各数，使每个圆圈中四个数的和都是15.5 73【解析】3、用数字1，2来填数，使正方形每条边的和为5，四条边的和为13.【解析】1 2 22 12 1 24．将2，3，5填入右图六个圆圈里，使每个三角形三个顶点上的数的和相等.【解析】先把2、3、5写在一个上面三角形的三个顶点上，然后再根据组成其它三角形的各个顶点都是用2、3、5这三个数进行求解即可．(答案不唯一)5．将1，2，3，4，5，6，7，8，9九个数字分别填入图中的小圆圈中，使三角形每边上四个数的和是17.【解析】1+2+3+4+5+6+7+8+9=45，而每条边上四个数字之和是17，则有三条边总和是17×3=51，而不是45.这是因为每个角的数字同属于两条边，故被重复计算了一次，由此可见三个角上的三个数字之和是51-45=6，九个数字中只有1+2+3=6，所以三个角上的数字应是1、2、3.6．把3，6，9，12，15五个数填在下面的O里，使每条线上三个数的和与正方形四个角上四个数的和相等.【解析】因为三条边的总和为：17×3=51，而1～9这九个数的和为45，那么三个顶点上的数字和为51-45=6，只有1+2+3=6，所以三个顶点数字为1、2、3，其他圆圈内数字再通过四个数字之和是17进行调整.每条线上的三个数字的和是：3+15+12=306+15+9=303+6+9+12=30正方形四个角上四个数字的和是：答案如图：名师点拨幻方问题主要方法：(1)累加法：利用累加的方法可以求出“幻和”和关键位置上的数字.通常将若干个“幻和”累加在一起，再计算每一个位置上的重数，从而求出“幻和”和关键位置上的数字.(2)求出“幻和”和关键位置上的数字后，结合枚举法完成数阵图的填写，在填写数阵图的过程中注意从特殊的数字和位置入手.(3)比较法：利用比较的方法可以直接填出某些位置的数字.注意观察数阵图中相关联的“幻和”之间的关系，注意它们之间共同的部分，去比较不同的部分本讲还有一部分内容是数阵图拓展，也就是在三年级数阵图初步的基础上继续学习数阵图问题的解题方法.数阵图问题方法多样且特殊，我们将在例题中详细讲解.其实这些方法和幻方是一致的，大家可以在下面的学习中体会到这一点.学霸经验➢本节课我学到了➢我需要努力的地方是。