选修42选修42矩阵与变换

高中数学选修4-2：矩阵与变换矩阵是研究图形（向量）变换的基本工具，有着广泛的应用，许多数学模型都可以用矩阵来表示。

本专题将通过平面图形的变换讨论二阶方阵的乘法及性质、逆矩阵和矩阵的特征向量等概念，并以变换和映射的观点理解解线性方程组的意义，初步展示矩阵应用的广泛性。

一、内容与要求1．引入二阶矩阵2．二阶矩阵与平面向量（列向量）的乘法、平面图形的变换（1）以映射和变换的观点认识矩阵与向量乘法的意义。

（2）证明矩阵变换把平面上的直线变成直线，即证明A(λ1α+λ2β)=λ1Aα+λ2Aβ。

（3）通过大量具体的矩阵对平面上给定图形（如正方形）的变换，认识到矩阵可表示如下的线性变换：恒等、反射、伸压、旋转、切变、投影。

3．变换的复合--二阶方阵的乘法（1）通过变换的实例，了解矩阵与矩阵的乘法的意义。

（2）通过具体的几何图形变换，说明矩阵乘法不满足交换律。

（3）验证二阶方阵乘法满足结合律。

（4）通过具体的几何图形变换，说明乘法不满足消去律。

4．逆矩阵与二阶行列式（1）通过具体图形变换，理解逆矩阵的意义；通过具体的投影变换，说明逆矩阵可能不存在。

（2）会证明逆矩阵的唯一性和(AB)-1=B-1A-1 等简单性质，并了解其在变换中的意义。

（3）了解二阶行列式的定义，会用二阶行列式求逆矩阵。

5．二阶矩阵与二元一次方程组（1）能用变换与映射的观点认识解线性方程组的意义。

（2）会用系数矩阵的逆矩阵解方程组。

（3）会通过具体的系数矩阵，从几何上说明线性方程组解的存在性，唯一性。

6．变换的不变量（1）掌握矩阵特征值与特征向量的定义，能从几何变换的角度说明特征向量的意义。

（2）会求二阶方阵的特征值与特征向量（只要求特征值是两个不同实数的情形）。

7．矩阵的应用（1）利用矩阵A的特征值、特征向量给出Anα简单的表示，并能用它来解决问题。

（2）初步了解三阶或高阶矩阵。

（3）了解矩阵的应用。

8．完成一个学习总结报告。

报告应包括三方面的内容：（1）知识的总结。

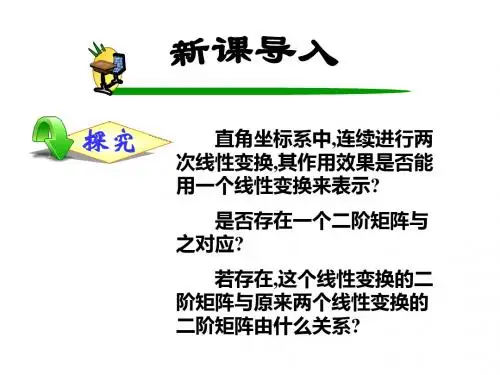
一般地,在线性变换下,是否仍然由平面上的直线变成直线,三角形变成三角形呢?教学目标知识与能力了解矩阵的概念掌握五类特殊的线性变换及其二阶矩阵过程与方法情感态度和价值观用代数方法表示几何变换,进而就可以从代数的角度研究几何变换体验在直角坐标系中线性变换与二阶矩阵之间的一一对应关系教学重难点重点1.二阶矩阵的概念2.线性变换及其对应的二阶矩阵难点线性变换与二阶矩阵之间的一一对应关系（一）几种特殊线性变换及其二阶矩阵旋转变换反射变换伸缩变换投影变换切变变换1.旋转变换探究将直角坐标系所有点绕原点沿逆时针方向旋转一个角度α.设平面内点P (x,y )经过旋转后变成点 ()y ,x P ′′′ 那么如何用P 的坐标(x,y )表示 的坐标 ?P ′()y ,x ′′得到：x ’=－x, y ’=－y.① ①称为旋转角为180°的旋转变换的表达式 P ’是P 在这个旋转变换的像. O 180°PP′ y x如图,在直角坐标系x o y 内,点P (x,y )绕原点O 按逆时针方向旋转180°,变成点 ().y ,x P ′′′例1 在直角坐标系x o y 内,将每个点绕原点O 按逆时针方向旋转30°的变换称为旋转角是30°的旋转变换.(1)求点A （1，0）在这个旋转变换下的像A ′;(2)写出这个旋转变化的表达式. A(1,0) O30° A ′y x 图1 图2 O yx (x,y ) P α30° ().y ,x P ′′′的横坐标和纵坐标为点解：如图A ,′123= 23×1= °30=cos OA x °30=sin OA y 21=21×1=)21,23(′(1,0)A A 为在这个旋转变换下的像点θ=θ=rsin y rcos x (2) 如图2,分别连接OP ,OP ’,设OP = OP′=r,.OP ,x 为终边的角以轴的正半轴为始边是以记θ∴()()°30+θ=′°30+θ=′sin r y cos r x即: yx y yx x 23+21=′2123=′－② 23212123－即得到正方形数表: 由两角和的三角函数公式得:,cos y sin x y ,sin y cos x x °30+°30=′°30°30=′－其中系数a,b,c,d 均为常数，则称③的几何变换为线性变换. ③式叫做这个线性变换的坐标变换公式.dycx y by ax x +=′+=′③线性变换③与dc b a 一一对应 在平面直角坐标系x O y 中,很多平面变换（平面内有点构成的集合）到它自身的映射都具有下列形式定义 由4个数a,b,c,d 排成的正方形数表 称为二阶矩阵dc b a 数a,b,c,d 称为矩阵的元素.零矩阵: 0000记为: 单位矩阵: 1001记为: 0E2.反射变换平面上的任意一点P 变成它关于直线l 的对称点P ’的线性变换叫做关于直线l 的反射. 例:在直角坐标系xOy 内,任意点P(x,y)关于直线y=x 的对称点为P ’(x ’,y ’).则相应 的坐标变换公式是: x ’=y,y ’=x.对应的二阶矩阵是 0113.伸缩变换在直角坐标系xOy内,将每个点的横坐标变为原来的k1倍,纵坐标变为原来的k2,其中k1 ,k2均为非零常数,称这样的几何变换为伸缩变换.定义伸缩变换的坐标变换公式为: x’=k1x,y’=k2y.对应的二阶矩阵:k k2 14.投影变换设l是一条给定的直线.对平面内任意一点P作直线l的垂线,垂足为P’,称点P’为点P在直线l上的投影.PlαP’定义平面上每一点P变成它在直线l上的投影P’,这个变换称为关与直线l的投影变换.在直角坐标系xOy 内,任意点P 关于x 轴的投影变换的坐标变换公式为: x ’=x,y ’=0.对应的二阶矩阵: 00015.切变变换如图,在直角坐标系xOy 内,将每一点P (x,y )沿与x 轴平行的方向平移ky 各单位变成P ’,其中k 为常数,称这类变换为平行于x 轴的切变变换. O y xP (x,y )P ’(x+ky ,y ) 定义平行与x轴的切变变换的坐标变换公式为:x’=x+ky,y’=y.1k对应的二阶矩阵:1抢答平行于y 轴的切变变换的坐标公式?x ’=x,y ’=kx +y.对应的二阶矩阵: 11k（二）变换、矩阵的相等2π3+2π3=′2π32π3=′cos y sin x y sin y cos x x－x ’=x,y ’=－x.旋转角为 的旋转变换的坐标变换公式 2π3即:2π32π32π32π3cos sin sincos －0110－对应的二阶矩阵:即:x ’=x,y ’=－x.）（－）（－）（－）－（－2π+2π=′2π2π=′cos y sin x y sin y cos x x 旋转角为 的旋转变换的坐标变换公式 2π－即:）（－）（－）（－－）（－2π2π2π2πcos sin sin cos 0110－即: 对应的二阶矩阵:观察1.旋转变换的坐标变换公式2.对应的二阶矩阵1.旋转角度定义设σ,ρ是同一直角坐标平面内的两个线性变换.若对平面内任意点P,都有σ（P）= ρ(P),则这两个线性变换相等,记为σ=ρ.设σ,ρ所对应的二阶矩阵分别为A = ,B = .若σ=ρ,则a 1=a 2,b 1=b 2,c 1=c 2,d 1=d 2.这时我们称二阶 矩阵A 与二阶矩阵B 相等.d c b a 2222d c b a 1111定义课堂练习.y ,x ,q ,p B A ,q p p q B ,x y x A ，求且－－例：设=2+=23+3=解:由矩阵定义: .x ,q p y ,p ,q x 2=+=23==+3－－.q ,p ,y x 1=3=2=2=－，－课堂小结1.几种特殊的线性变换:旋转变换、反射变换、伸缩变换、投影变换、切变变换(要求：理解并掌握各变换所对应的坐标变换公式及其对应的二阶矩阵.)课堂小结2.变换和矩阵的相等（1）变换相等:对应坐标变换公式和二阶矩阵相等（2）矩阵相等:对应系数相等注:两个线性变换相等当且仅当对应的二阶矩阵相等教材习题答案1.（1）坐标变换公式为:对应的二阶矩阵: .y x y ,y x x 22+22=′2222=′－22222222－（2）坐标变换公式为: .x y ,y x =′=′－对应的二阶矩阵: 10012.设P (x,y)是平面直角坐标系x O y 内的任意一点,则它关于原点O 的对称点 为 ∴坐标变换 公式为 对应的二阶矩阵为 ..y y ,x x －－=′=′1001－－(),y ,x P ′′′3.（1）点 在这个投影变换下的像为()；03′,A ()12,A（2）设P (x ,y )是平面直角坐标系xOy 内的任意一点，则它在这个变换下的像为P ’(x +y ,0),因此,坐标变换公式是 1001对应的二阶矩阵是 .y ,y x x 0=′+=′.Z k ,R R .k ∈其中2π32π3+π2=45.由X = Y ,得x = 3 , y =－9 , z = 0.6.设P (x 0 , y 0）是平面直角坐标系xOy 内的任意一点,它关于直线l :y =2x 的投影变换下的像为P ’（x ’,y ’). 易得:过点P （x 0,y 0)垂直于直线的斜率为k =－1/2.于是,直线方程为：().x x y y 0021=－－－(),x x y y ,x y 0021=2=－－－解方程组:得直线l :y =2x 与直线y －y 0=－1/2(x －x 0)的坐标(（x 0+2y 0)/5,（2x 0+4y 0)/5）.∵M 是线段PP ’的中点,所以,y y x y ,x y x x 00000054+2×2=′52+×2=′－－即: .y x y ,y x x 53+4=′54+3=′0000－∴坐标变换公式: .y x y ,yx x 53+4=′54+3=′－对应的二阶矩阵: 53545453－(2)对应的坐标变换公式: .y B A )B A (x B A AB y ,y B A ABx B A )A B (x 222222222222++2=′+2+=′－－－－－对应的二阶矩阵:B A )B A (B A AB B A AB B A A B 222222222222++2+2+－－－－－。

矩阵变换的性质-北师大版选修4-2 矩阵与变换教案矩阵变换是线性代数中一项重要的概念，它能够描述一个向量在变换后的位置。

在实际的计算机图形学、物理学、化学等领域中，矩阵变换都扮演着重要的角色。

本文将从矩阵变换的性质方面进行介绍。

矩阵变换的定义矩阵变换是一种将向量转换为另一个向量的数学运算，它通过给定一个矩阵A，将一个向量x变换为另一个向量y的过程。

矩阵变换的公式为：y=Ax其中，A为变换矩阵，x为原始向量，y为变换后的向量。

矩阵变换的性质1. 线性变换矩阵变换是一种线性变换，即它满足以下两个性质：•可加性：对于任意向量x1和x2，有A(x1+x2) = Ax1 + Ax2•齐次性：对于任意标量k和向量x，有A(kx) = k(Ax)这两个性质意味着，矩阵变换对向量加法和数乘保持线性。

这在实际计算中是非常有用的。

2. 逆变换矩阵变换是可逆的，即对于任意矩阵A，存在一个逆矩阵A-1，使得AA-1 = A^-1A= I。

其中，I为单位矩阵。

这意味着，任何矩阵变换都可以通过一个逆变换还原为原始向量。

3. 矩阵乘法的结合律矩阵乘法满足结合律，即对于任意矩阵A、B和C，有(AB)C = A(BC)。

这意味着，矩阵变换的顺序可以随意改变，不影响最终的结果。

4. 矩阵乘法的分配律矩阵乘法满足分配律，即对于任意矩阵A、B和C，有A(B+C) = AB + AC。

这意味着，对于一个向量，可以先将其进行某些变换，然后再将结果进行加法或减法运算，得到最终的结果。

5. 矩阵乘法的交换律矩阵乘法不满足交换律，即对于任意矩阵A和B，一般有AB ≠ BA。

这意味着，矩阵变换的顺序不能随意改变，需要根据具体的应用场景进行选择。

总结矩阵变换是线性代数中一项重要的概念，在计算机图形学、物理学、化学等领域都有广泛的应用。

本文从矩阵变换的性质方面进行了介绍，包括矩阵变换的线性性、可逆性、结合律、分配律和交换律。

这些性质都有极其重要的实际意义，能够帮助我们更好地理解和应用矩阵变换。

第二节矩阵的逆矩阵、特征值与特征向量［主匸離构］< O O Q <定义［距阵的逆矩阵、辐征值与特征向员». _________________________________________________匸杏征值与I怖向址1 .矩阵的逆矩阵(1)—般地，设p是一个线性变换，如果存在线性变换0,使得6严p齐I，则称变换p可逆，并且称O是p的逆变换.(2)设A是一个二阶矩阵，如果存在二阶矩阵B,使得BA= AB = E，则称矩阵A可逆,或称矩阵A是可逆矩阵，并且称B是A的逆矩阵.(3)(性质1)设A是一个二阶矩阵，如果A是可逆的，则A的逆矩阵是唯一的，A的逆矩阵记为A_I.-1 - 1 -(4)(性质2)设A，B是二阶矩阵，如果A，B都可逆，则AB也可逆，且(AB) = B A2.二阶行列式与方程组的解I—｛二阶行列式与方禅丽城i<⑸二阶矩阵A =, -d 可逆，当且仅当 det A= ad — bc^ 0时，A 1 = 工d」det A—edet A对于关于x ，y 的二元一次方程组ax+ by= m ， cx+ dy= n ，我们把称为二阶行列式，它的运算结果是一个数值，记为 det A =a b记为D ，m b 记为D x ，a m c dn dc n i=ad - be. de 若将方程组中行列式记为D y ，则当D 丰0时,D x x =D y y=3. 矩阵特征值、特征向量的相关概念宅 b"l(1) 定义：设矩阵A = J ，如果存在实数 入以及非零向量 匕使得A E=入,，则称入是jc d 」 矩阵A 的一个特征值，E 是矩阵A 的属于特征值 入的一个特征向量.(2) —般地，设E 是矩阵A 的属于特征值 入的一个特征向量，则对任意的非零常数 k, K E也是矩阵A 的属于特征值 入的特征向量.⑶一般地，属于矩阵的不同特征值的特征向量不共线=0为矩阵A 的特征方程.4. 特征向量的应用(1) 设A 是一个二阶矩阵，a 是矩阵A 的属于特征值 入的任意一个特征向量，则A na=fa n *€ N ).(2) 性质1设兀h 是二阶矩阵A 的两个不同特征值，&, &是矩阵A 的分别属于特征 值入，h 的特征向量，对于任意的非零平面向量 a,设a= b E i + t 2 ^2(其中t i , t 2为实数)，则对任意的正整数n,有A na=2jjj 2.加石测］＜ o o oo答案：152 1 - a 2解析：由题意|A | =2 2=2 x (a + 1) — 1 x (1 — a ) = a + 2a + 1 = 0 ,「a = — 1.h — a — bh — a — b A = ,称 f (h =为矩阵A 的特征多项式，方程£ d_ —c — d—c h — d(4)设矩阵2.若矩阵 3可逆，则k 的值不可能是k方程组的解为 1.矩阵—1的逆矩阵是 03.若矩阵A =可逆，则实数 a 的值为答案：—1x 3+ m 一4.对任意实数x,矩阵］总存在特征向量，则m的取值范围是___________2 — m 2k- x — 3 — m 解析：由条件得f( k=m— 2 — 2=(入一x)(入一2) — (m— 2)( — 3— m)2 » …一=入一(x+ 2) H 2x+ (m+ 3)(m— 2) = 0 有实数根，2 2所有A i= (x+ 2) — 4(2x + m + m— 6) > 0对任意实数 x恒成立,2所以A2= 16 + 4(4m + 4m — 28)<0,解得m的取值范围是一3< m W 2.答案：—3< m W 2.例1 求矩阵A= 3 2的逆矩阵.2 1【解析】法一：设矩阵A的逆矩阵为|x y\丄 W —5.已知矩阵M的特征值k= 8及对应的一个特征向量e i= £ l并有特征值k= 2及对应的一个特征向量e2= — 2则矩阵M =a解析：设M =JJDa +b =8, 故|c+ d = 8,a — 2b= 2,故|c— 2d=—788?'=.-1」-8」联立以上两个方程组解得 a = 6, b= 2, c= 4, d = 4,故M = f 2热点考向一求逆矩阵L— F ——― 1［求逆矩阵］公式3x+ 2z 3y+ 2w I 即 2x+ z 2y+ w 3x+ 2z= 1, 故2x+ z= 0,解得 x=— 1, z= 2, y = 2, w = — 3,【点评】 方法一是待定系数法；方法二是公式法.£变式训练1.已知变换矩阵 A 把平面上的点 P(2, — 1)、Q(— 1,2)分别变换成点 P i (3, — 4)、Q i (0,5).(1)求变换矩阵A ;—1(2)判断变换矩阵 A 是否可逆，如果可逆，求矩阵 A 的逆矩阵A理由.—1 —1 —23■ — 1 —1丿 f 1/- 3:A-1■— 1 21 卩1! 2 一=匸卜r 2a — b = 3,i< a= 2, 2c — d =— 4,b= 1,解得：j—a+ 2b = 0,c=—1,即a b c d-- y w3y+ 2w = 0,2y+ w = 1, 从而矩阵A 的逆矩阵A —1=■— 1 -23 2= •A法,.°det A = — 1.:如不可逆，请说明I I，依题意，可得l a£X z2 13N ►Hu贝_2 1-所以所求的变换矩阵2] ⑵'.det A = 2X 2- (— 1) X 1 = 5, ••A 可逆—11、 1551 |5—5A -1=1 = 1— u — n2 I 1 255丿‘5 5丿热点考向二 利用矩阵解二兀一次方程组步骤-求|a 1 b订的逆矩阵-求方程组的解 ---- 卫2 b 2」 -----------[例2 （1）求矩阵A = f J 的逆矩阵; （2）利用逆矩阵知识,2x+ 3y — 1 = 0, x+ 2y — 3= 0.【解析】 （1）法一：设矩阵A 的逆矩阵为A -1= r b 1,x d 」2a + 3c= 1,a = 2,b =— 3, c=— 1, d = 2.知 2b + 3d = 0， a+ 2c= 0, b+ 2d =1. ••|A |= 4— 3 = 1 ,解方程组:】=I ：解之得2 Z3|1 1 | f 3- 3【I-1 2-1 2-1 1 -二 31⑵二元一次方程组的系数矩阵为 A = I c，-1 2」由(1)知A- J 2 - 3]二 1 2一[2x+ 3y= 1,因此方程[x+ 2y= 3有唯一解即x=-7,|y= 5.有无数解或无解.2x+ y= 8,2.用矩阵方法求解二元一次方程组4x- 5y= 2.解析：原方程组可以写成『==I8 ',4- 5」®」-2」3 1记M = ,114 — 5a1x+ b1y= C1【点评】二兀一次方程组(a1, b1不同时为零,a2x+ b2y= C2(a1 b[系数矩阵为A= |42 b2，只有当|A|工0时，方程组有唯一解A-1|C1a2, b2不同时为零)的，若A l= 0,则方程组|x L A-1=2 X (— 5) — 1 X 4 =— 14工 0,(1)求A 的特征值4 ⑵求A B .【解析】 (1)设A 的一个特征值为 入由题意知: "X — 1 — 2~\=0,即(入一 2)( X — 3) = 0,解得 X= 2, X= 3,44 44一故 A B = A ( a+ a )= (2 a )+ (3 a )= 16 a+ 81 a =【点评】 求矩阵的特征值及对应的特征向量是矩阵与变换的重点和难点,题首先要利用行列式求出特征 徝，然后求出相应的特征向量. 请注意每一个特征值对应无数 个特征向量，选择坐标为整数的解就能使后面计算〔一11豊.'M —1=1 14r =M -11 '=! i 4，，即方程组的解为‘=3,■1X= 2时，由厂1I X L 2j，得A 属于特征值2的特征向量a 1= I 2E=3f，得A 属于特征值3的特征向量(2)由于 B = 13 L ?!711=a 1 + a .其行列式例3 给定矩阵 A = I入，h 及对应特征向量 a, a;[113 ^97解决此类问简单、方便.ion一、填空题71 3_11•已知A = | 可逆，则实数a 的取值范围是 _________________a 6」 解析：矩阵A 可逆当且仅当det(A)丰0,•'a 的取值范围为(一a, 2) L(2 ,+s ). 答案：(一a, 2) U (2 ,+a )_3，则矩阵M 的特征向量可以是- 23.已知矩阵A =3,若矩阵A 属于特征值6的一个特征向量为 d属于特征值1的一个特征向量，求矩阵A ,并写出A 的逆矩阵.解析：由矩阵A 属于特征值6的一个特征向量为=I ：可得, 一仁即 c + d= 6;-3] 由矩阵A 属于特征值1的一个特征向量a= 2 ,解得* 2,d = 4P 31 ，即 A = 2 4 .2•设矩阵 可得P即 3c — 2d= — 2,A 的逆矩阵是解析：矩阵M的特征多项式由于f （为=0得矩阵M 的特征值为 入=1 , ?2=— 1.经计算可得，矩阵M属于特征值x=1的一个特征向量为^3的一个特征向量为1（空3答案：「厂I —;3「ac 3,ab+ 3a = 1答案：2 —2 3丄 2 _2x — 2y =— 1， 解析：因为方程组---的矩阵形式是2x+ 2 y= 1,3 •设可逆矩阵A =J|a 3的逆矩阵A -1-4 5」解析：由AA - 1= E 得 ab + 3a ac — 3I71占b+ 5a 4c —5，而属于特征值匕-1 4b+ 5a= 0, 即4c — 5 =解方程组得a= 2, b= — 2 c= 3 2.承―韵=—1,4.已知二元一次方程组 ,呼x+%= 1 ,从线性变换的角度求解时应把向量—1_ 1绕原点作顺时针旋转的旋转变换.方程组就是把向量：1［绕原点作顺时针旋转沪旋转变换答案：n1+、321- .3 2答案:6. 现用矩阵对信息进行加密后传递，规定英文字母数字化为:解析：因为A =『4，所以det A = I14= 2工0,42->0 2对应信息为good”.n 变换得到—1，所以解4一i一1 - 2〕所以A -1=1，而密码矩阵为 ? 1 一B = I 67J3031 8_1 故明码矩阵X= A - 1B =-21 1 2 -31] 7 15]=I , 8」-15 4」[1 - 15A = _0，则 A -11解析：A =_01- 3 •41='X 1-丄X 區1工02 2 2 •4 11, b T 2,…，Z T 26,双方约定的矩阵为1 4，发送方传递的密码为67,30,31,8,此组密码所发信息为—P2答案：good--1 5[7. 矩阵M = 5 __________________________ 的特征值与特征向量分别为勺3一5 2=(入+ 1)( X — 3) — (— 2)( — -)= f — 2 - 8 = 0，得矩阵值为 X = 4, X = — 2.&= — 2的一个特征向量.答案: &已知矩阵A = f — 1, B =『—1，,则满足方程AX = B 的二阶矩阵X =_— 4 3 _— 3 1年-11解析：・.A =「4 3 一2 — 1.•|A |== 2 X 3 — (— 1) X (— 4) = 2 工 0.—4 3 3 1 1•■A — 1=2 2:：AX = B ,.・・X = A —1B ,5 1 -解析:M 的特征设属于特征值 ,则它满足方程(X+ 1)x+ (— 2)y= 0, 即卩 5x — 2y =0•故可取属于特征值 4的一个特征向量.设属于特征值 h= — 2的特征向量为x+ 2y = 0•故可取 -2为属于特征值量为综上所述，矩阵a-灯 属于■— 1 2〔有两个特征值 ?2=— 2的一个特征向量为 ?1= 4, ?2=— 2,属于入=4的一个特征向X = 4的特征向量为02\ = 4, a = || ■和 &=—2, J 5」而 A - 1AXB-B - 1= EXBB -1因为A - 1=- 3_2所以 X = A - 1CB「2 - 3110.已知矩阵A =6 2(1) 求矩阵A 的特征值及对应的特征向量; (2) 计算矩阵A n.当f= 8时，A 属于f 的特征向量为9一25-11AS2 ]7 317A = J ，B =,C =I- 2 -3」】12- 〕1C , 所以 1(A - A )XB B -1=A -1CB -19.已知矩阵 解析：AXB = 1，求满足AXB = C 的矩阵X . 0=X ( BB -1) = X , 所以 X = A - 1CB -1B -1=2 -31解析: (1)矩阵A 的特征方程为入一6=(—6)( — 4) — 8 = f - 10 入 + 16 = 0.得矩阵 A 的特征值为 f = 8, f= 2.当?2= 2时，A属于h的特征向量为⑵设A n =n n n nA a i = 8 a i, A a= 2 a,(1)求证：M和N互为逆矩阵；⑵求证：向量a同时是M和N的特征向量；(3)指出矩阵M和N的一个公共特征值.-2 — 1-j,3 — 3,2 们；1 0]解析：(1)证明：因MN = J = J ,.1 2〜2」J 1」-—3 2na + b= 8c+ d= 8n即a — 2b= 2nc-2d=— 2 2n解得a=n ^n2X 8 + 2n8 —2n8n+ 2n+i2 X 8n—2n+1c=故A n=2 X 8n+ 2n 8n—2nI 3 32 X 8n—2n+18n+ 2n+ 13 311.给定矩阵21，向量02 =且 NM = I 2所以M 和N 互为逆矩阵.(2)证明：因为M%因为故1是矩阵M 和N 的一个公共特征值. ① 若a= 2, b= 3，求M 的逆矩阵② 若曲线C: x 2+ y 2= 1，在矩阵M 所对应的线性变换作用下得到曲线2C'： x+ y 2= 1,求 a, b 的值.4•'2x 1= 1,2y 1= 0,3x 2= 0,3y 2= 1. 1 1即 x = 2，y 1 = 0, X 2= 0, y 2 = 3ax= x' by= y'-0 1J所以 a 是N 的特征向量.所以 a 是N 的特征向量.-1 |⑶由⑵知，M对应于特征向量―的特征值为1, N 对应于特征向量|彳 一 1的特征值也12. (2011年福建)设矩阵M =打0( b*其中 a>0, b>0) M T ；解析：①设M -1= -| y1.X2 y2则 MM -1= I 1-0 0'又 M =[1 - J) 3JO0：y 1 y 2-0 1②设C 上任一点P(x, y)，在M 作用下得点P' (x' , y')2 2即亍+ b 2y~ 1为曲线C 的方程.|a= 2,又a>0, b>0,所以[b= 1.卫答案：「1又点P'（X’，y'）在C'上，所以2・+ y' 2= 1.又C 的方程为x 2+ y 2= 1,a 2= 4,b 2= 1._1X= 3时，由.1• -1 =。

第 1 页共 21 页选修 4－ 2矩阵与变换第一节平面变换、变换的复合与矩阵的乘法1．二阶矩阵与平面向量(1) 矩阵的概念在数学中，把形如123134，1，20这样的矩形数字 (或字母 )阵列称为矩阵，其35－ 1中，同一横排中按原来次序排列的一行数(或字母 )叫做矩阵的行，同一竖排中按原来次序排列的一列数 (或字母 )叫做矩阵的列，而组成矩阵的每一个数(或字母 )称为矩阵的元素．(2)二阶矩阵与平面列向量的乘法① [a 11a12 ]b11＝ [ a11×b11＋ a 12×b 21 ] ；b21②a11a12x0＝a11× x0＋ a12× y0.a21a22 y0a21× x0＋ a22× y02．几种常见的平面变换10(1) 当 M ＝时，则对应的变换是恒等变换．01(2)k010由矩阵 M ＝或 M ＝(k>0) 确定的变换 T M称为 (垂直 )伸压变换．01k(3)反射变换是轴对称变换、中心对称变换的总称．cos θ － sin θ(4) 当 M ＝时，对应的变换叫旋转变换，即把平面图形(或点 )逆时针旋转sin θcos θθ角度．(5)将一个平面图投影到某条直线 (或某个点 )的变换称为投影变换．1k10 (6) 由矩阵 M ＝或 M ＝k 确定的变换称为切变变换．011 3．矩阵的乘法一般地，对于矩阵a11a12b11b12M ＝a22， N＝，规定乘法法则如下：a21b21b2211 12 11 12a bbb ba ab b11 11＋ a 12 21a 11 12＋ a 12 22MN ＝a 22b 21＝a 21b 11＋ a 22b 21.a 21 b22a 21b 12＋ a 22b 224．矩 乘法的几何意(1) 的复合：在数学中，一一 的平面几何 常可以看做是伸 、反射、旋 、切 的一次或多次复合，而伸 、反射、切 等 通常叫做初等 ； 的矩 叫做初等 矩 ．(2)MN 的几何意 ： 向量x 矩 乘法α＝ 施的两次几何 (先 T N 后 T M )y的复合 ．·(3) 当 向量 施 n ( n ＞ 1 且 n ∈ N * )次 T M ， 地我M n ＝ M ·M ·⋯ ·M .5．矩 乘法的运算性(1) 矩 乘法不 足交 律于二 矩A ，B 来 ，尽管 AB ， BA 均有意 ，但可能 AB ≠BA .(2) 矩 乘法 足 合律A ，B ，C 二 矩 ， 一定有(AB)C ＝ A(BC)．(3) 矩 乘法不 足消去律．A ，B ，C 二 矩 ，当 AB ＝ AC ，可能 B ≠C. [ 小 体 ]1 8 1 x1．已知矩 A ＝3，矩 B ＝.若 A ＝B ， x ＋ y ＝ ________.2y 3解析： 因 A ＝ B ，x ＝ 8， ＋ ＝10.所以y ＝ 2，x y答案： 102．已知x x ′2x ＋ 3y ， 它所 的 矩 ________．y→＝y ′x ＋ yxx ′ 2 3 x解析： 将它写成矩 的乘法形式→′ ＝1 ，所以它所 的 矩y1yy2 3 1 .12 3答案：111．矩 的乘法 着 的复合，而两个 的复合仍是一个 ，且两个 的复合 程是有序的，易 倒．2．矩阵乘法不满足交换律和消去律，但满足结合律．[ 小题纠偏 ]1 2 ， B ＝4 2 1．设 A ＝4k ，若 AB ＝ BA ，则实数 k 的值为 ________．37解析： AB ＝1 24 2 ＝4＋ 2k163 4k 7，12＋ 4k 3442 1 21016BA ＝ k7 34 ＝ ＋＋ 28，k 21 2k 因为 AB ＝ BA ，故 k ＝ 3.答案： 32．已知 A ＝1 0 ， B ＝－ 1 0－ 1 00 0 0 1， C ＝，计算 AB ， AC.0 － 1解： AB ＝1 0 － 1 0－ 1 00 1 ＝，1 0 － 10 － 1 0 . AC ＝0 0－ 1＝ 0 0 0考点一二阶矩阵的运算 基础送分型考点 —— 自主练透[ 题组练透 ]1 11 11．已知 A ＝2 2，计算 A 2， B 2.1 ， B ＝ － 1－ 1 1221 1 11 1 1 解： A 2＝2 2 2 2 2 2 . 1 1 1 ＝1 1 12 2222 21111B 2＝－ 1 － 1 － 1 ＝.－ 12．(2014 江·苏高考 )已知矩阵 A ＝－ 1 211 21 ，B ＝，向量 α＝ ，x ，y 为实数． 若x2－ 1 yA α＝B α，求 x ＋ y 的值．解： 由已知，得 A α＝ － 12 2 ＝ － 2＋ 2y ， α＝ 11 2 ＝ 2＋ y y2 － 1 y1 x 2＋ xy4－ y第 4 页共 21 页因为 A α＝ B α，所以 － 2＋ 2y2＋ y＝，2＋ xy 4－ y－ 2＋ 2y ＝ 2＋ y ，故2＋ xy ＝4－ y.x ＝－ 12，所以 x ＋ y ＝ 7 解得2.y ＝ 4.3．已知矩阵 A ＝1 0 － 4 3 31 ， B ＝ 4 － 2且 α＝ ，试判断 (AB)α与 A(B α)的关系．2 4解： 因为 AB ＝1 0－ 43 －4 31 2＝ ，4 － 2 4 － 1－ 43 3所以 (AB)α＝－ 1 4＝ ，48 因为 B α＝－433 ＝0 ，4 － 2441 0 0 0A(B α)＝24＝. 18所以 (AB)α＝ A(B α)．[ 谨记通法 ]1．矩阵的乘法规则两矩阵 M ， N 的乘积 C ＝ MN 是这样一个矩阵；(1) C 的行数与 M 的相同，列数与 N 的相同；(2) C 的第 i 行第 j 列的元素C ij 由 M 的第 i 行与 N 的第 j 列元素对应相乘求和得到． [ 提醒 ] 只有 M 的行数与 N 的列数相同时，才可以求MN ，否则无意义．2．矩阵的运算律(1) 结合律 (AB)C ＝ A(BC)；(2) 分配律 A(B ±C)＝ AB ±AC ， (B ±C)A ＝ BA ±CA ；(3) λ(AB)＝ (λA )B ＝ A( λB )．考点二平面变换的应用重点保分型考点 —— 师生共研[ 典例引领 ]2 － 2 2 2已知曲线 C ：xy ＝ 1，若矩阵 M ＝对应的变换将曲线C 变为曲线 C ′，求2 222曲线 C ′的方程．解： 设曲线 C 上一点 (x ′ ， y ′ )对应于曲线 C ′ 上一点 (x ，y)，2 － 222x ′x所以＝y，22 ′y222 222′＝所以x ＋ y y － x所以 ′ － ′ ＝ ， ′ ＋′ ＝ ，y ′ ＝ ，所以 x ′ y ′＝2 x2 yx2x2 yy.x22x ＋ y y － x ＝ 1，×2 2所以曲线 C ′ 的方程为 y 2－ x 2＝ 2.[ 由题悟法 ]利用平面变换解决问题的类型及方法：(1) 已知曲线 C 与变换矩阵，求曲线C 在变换矩阵对应的变换作用下得到的曲线C ′的表达式，常先转化为点的对应变换再用代入法(相关点法 )求解．(2) 已知曲线 C ′是曲线 C 在平面变换作用下得到的，求与平面变换对应的变换矩阵， 常根据变换前后曲线方程的特点设出变换矩阵，构建方程(组 )求解．[ 即时应用 ]a 022x ＋ y已知圆 C ：x 2＋ y 2＝ 1 在矩阵 A ＝(a>0，b>0) 对应的变换作用下变为椭圆＝0 b9 41，求 a ， b 的值．解：设 P(x ，y)为圆 C 上的任意一点， 在矩阵 A 对应的变换下变为另一个点 P ′ (x ′ ，y ′ )，x ′ a 0x x ′＝ ax ， 则 ＝，即y ′0 byy ′ ＝ by.2 2 2222xya xb y又因为点 P ′ (x ′ ， y ′ )在椭圆 9 ＋ 4 ＝ 1 上，所以 9 ＋ 4 ＝ 1. 由已知条件可知，x 2＋ y 2＝1，所以 a 2 ＝ 9， b 2＝ 4.因为 a>0 ， b>0 ，所以 a ＝ 3， b ＝ 2.考点三 变换的复合与矩阵的乘法 重点保分型考点 —— 师生共研[ 典例引领 ]在平面直角坐标系xOy 中，已知点 A(0,0)，B(－ 2,0)，C(－ 2,1)．设 k 为非零实数，矩阵k 0 0 1A 1，B 1，C 1，M ＝1 ， N ＝，点 A ， B ， C 在矩阵 MN 对应的变换下得到点分别为1 0△ A 1B 1C 1 的面积是△ ABC 面积的 2 倍，求 k 的值．k 0 0 1 0 k解： 由题设得 MN ＝1 1＝，1 0 由 0k 0 0 0 k － 2，＝，＝1 00 01－ 20 k －2k，可知 A 1(0,0)，B 1(0，－ 2)， C 1(k ，－ 2)．1 0＝1－ 2计算得△ABC 的面积是1，△A 1 1 1 的面积是 |k|，B C则由题设知： |k|＝ 2× 1＝ 2.所以 k 的值为 2 或－ 2.[ 由题悟法 ]矩阵的乘法对应着变换的复合，而两个变换的复合仍是一个变换，且两个变换的复合过程是有序的，不能颠倒．二阶矩阵的运算关键是记熟运算法则．[ 即时应用 ]1 0已知圆 C ：x 2＋ y 2＝ 1，先将圆 C 作关于矩阵 P ＝的伸压变换，再将所得图形绕原0 2点逆时针旋转 90°，求所得曲线的方程．0 － 1解： 绕原点逆时针旋转 90° 的变换矩阵 Q ＝，1 0则 M ＝ QP ＝0 － 11 0 0 － 210 2＝.1设 A(x 0， y 0 为圆 C 上的任意一点，在T M 变换下变为另一点 A ′ (x 0′ ， y 0′ )，)′－x 0′ ＝－ 2y 0，2则＝，即y 0 ′ 10 y 0y 0′ ＝ x 0，x 0＝ y 0′ ，所以x 0′y 0＝－ 2 .又因为点 A(x 0， y 0) 在曲线 x 2＋ y 2＝ 1 上，2x 0′ 2所以 (y 0′ ) ＋ －＝ 1.2故所得曲线的方程为x4＋ y 2 ＝1.0 11， N ＝1 ，求 MN .1．设 M ＝00 120 11 0 0 112.解： MN ＝0 ＝1211 2 T 把曲2．(2016 南·京三模 )已知曲线 C ：x 2＋ 2xy ＋ 2y 2＝ 1，矩阵 A ＝所对应的变换1 0线 C 变成曲线 C 1，求曲线 C 1 的方程．1 2 解： 设曲线 C 上的任意一点 P(x ， y)， P 在矩阵 A ＝对应的变换下得到点 Q(x ′ ，1 0y ′ )．1 2 x x ′ x ＋ 2y ＝ x ′ ，则10 ＝， 即y′ x ＝ y ′ ，yx ′ －y ′所以 x ＝ y ′ ， y ＝ .2x ′ － y ′＋2x ′ － y ′2＝ 1，即 x ′ 2＋ y ′ 2＝ 2，代入 x 2＋ 2xy ＋2y 2＝ 1，得 y ′ 2 ＋2y ′ ·22所以曲线 C 1 的方程为 x 2＋ y 2＝ 2.3． (2016 南·通、扬州、泰州、淮安三调 )在平面直角坐标系xOy 中，直线 x ＋ y － 2＝ 0 在矩阵 A ＝1 ax ＋ y － b ＝ 0(a ， b ∈ R) ，求 a ＋ b 的值．1 对应的变换作用下得到直线2解： 设 P(x ， y)是直线 x ＋ y －2＝ 0 上任意一点，由 1a x ＝x ＋ ay ，得 (x ＋ ay)＋ (x ＋ 2y)－ b ＝ 0，即 x ＋ a ＋ 2 － b＝ 0.12 y x ＋ 2y2 y 2a ＋ 22 ＝ 1， a ＝ 0，所以 a ＋b ＝ 4.由条件得解得－b＝－ 2，b ＝ 4，2第 8 页共 21 页4．已知 M ＝1－ 22 － 12 ， W ＝－ 3，试求满足 MZ ＝ W 的二阶矩阵 Z .3 1a b解： 设 Z ＝d ，c则 MZ ＝ 1 － 2 a b a － 2cb －2d＝.23 c d 2a ＋ 3c 2b ＋3d又因为 MZ ＝ W ，且 W ＝2 － 1，－ 31a － 2cb － 2d 2 － 1所以＋ ＝ － 3 1 ， ＋3c3d2a 2ba ＝ 0，a － 2c ＝ 2，1b ＝－b － 2d ＝－ 1，7，所以解得2a ＋ 3c ＝－ 3， c ＝－ 1，2b ＋ 3d ＝ 1.d ＝ 37.0 1 － 7故 Z ＝.－ 1371 15． (2016 苏·锡常镇一调 )设矩阵 M ＝y ＝ sin x 在矩阵， N ＝ 2，试求曲线21MN 变换下得到的曲线方程．11解： 由题意得 MN ＝ 1 0 2 0＝ 20 . 0 20 1 0 2设曲线 y ＝ sin x 上任意一点 P(x ， y)在矩阵 MN 变换下得到点 P ′ (x ′， y ′ )，x ′1x则2，＝yy21x ＝ 2x ′ ， 即 x ′ ＝ 2x ，得1y ′ ＝ 2y ，y ＝2y ′ .因为 y ＝ sin x ，所以 1 ′ ＝′ ，即 ′ ＝ ′2ysin 2xy2sin 2x .因此所求的曲线方程为 y ＝ 2sin 2x.6．(2017 苏·锡常镇调研 )已知变换 T 把平面上的点 (3，－ 4)，(5,0)分别变换成 (2，－ 1)，(－1,2)，试求变换 T 对应的矩阵 M .a b a b3 2 a b 5 ＝－ 1解： 设 M ＝，由题意，得＝ ， ，c dc d－ 4 － 1 c d 0 213a － 4b ＝ 2， a ＝－ 5，13，3c － 4d ＝－ 1，b ＝－20所以解得2 5a ＝－ 1，c ＝5，5c ＝ 2.11d ＝ 20.113－5－20即 M ＝.2 11 5207．(2016 ·通、扬州、淮安、宿迁、泰州二调南 )在平面直角坐标系xOy 中，设点 A(－ 1,2)－ 1 0 在矩阵 M ＝对应的变换作用下得到点 A ′，将点 B(3,4)绕点 A ′逆时针旋转90°得0 1到点 B ′，求点 B ′的坐标．解： 设 B ′(x ， y)，－ 1 0－ 11 依题意，由0 1＝，得 A ′ (1,2) ．22―→ ―→则 A ′ B ＝ (2,2) ， A ′ B ＝ (x － 1， y － 2)．0 － 1记旋转矩阵 N ＝，1 00 － 1 2x － 1 － 2x － 1 则＝，即＝，10 2－ 2－ 2y 2y 解得x ＝－ 1，y ＝ 4，所以点 B ′ 的坐标为 (－ 1,4)．1 0 1 02x 2－ 2xy ＋ 1＝ 0 在矩阵 MN 对应的变换作8．已知 M ＝， N ＝，求曲线0 2－ 1 1用下得到的曲线方程．1 0 1 01 0解： MN ＝2 － 11＝，－ 22设 P(x ′ ， y ′ )是曲线 2x 2－ 2xy ＋ 1＝ 0 上任意一点，点 P 在矩阵 MN 对应的变换下变为点 P ′ ( x ， y)，x1 0 x ′x ′则有＝2 ′＝，y－ 2－ ′ ＋ ′y2x 2yx ＝ x ′ ，即y ＝－ 2x ′ ＋ 2y ′ ，x ′ ＝x ，于是yy ′ ＝x ＋ 2.代入 2x 2－ 2xy ＋ 1＝ 0 得 xy ＝ 1，所以曲线 2x 2－ 2xy ＋ 1＝0 在 MN 对应的变换作用下得到的曲线方程为xy ＝ 1.第二节逆变换与逆矩阵、矩阵的特征值与特征向量1．逆变换与逆矩阵(1) 对于二阶矩阵 A ， B ，若有 AB ＝ BA ＝ E ，则称 A 是可逆的， B 称为 A 的逆矩阵．(2) 若二阶矩阵 A ，B 均存在逆矩阵，则 － 1－ 1 － 1AB 也存在逆矩阵，且 (AB) ＝ B A .(3) 利用行列式解二元一次方程组．2．逆矩阵的求法一般地，对于二阶矩阵a b － 1A ＝，当 ad － bc ≠ 0 时，矩阵 A 可逆，且它的逆矩阵 Ac dd－ b ad － bc ad － bc＝.－ c aad － bcad － bc3.特征值与特征向量的定义设 A 是一个二阶矩阵，如果对于实数 λ，存在一个非零向量 α，使得 A α＝ λα，那么 λ称为 A 的一个特征值，而α称为 A 的属于特征值 λ的一个特征向量．4．特征多项式的定义a b是一个二阶矩阵， λ∈ R ，我们把行列式f(λ)＝λ－ a － b 2设 A ＝d － c＝ λ－ (a ＋ d)λcλ－ d＋ ad － bc 称为 A 的特征多项式．5．特征值与特征向量的计算设 λ是二阶矩阵a bλ与 α的步骤为：A ＝的特征值， α为 λ的特征向量，求c d第一步：令矩阵λ－ a － b2A 的特征多项式 f(λ)＝λ－ d ＝ λ－ (a ＋ d)λ＋ ad － bc ＝ 0，求出 λ－ c的值．第二步： 将 λ的值代入二元一次方程组λ－ a x － by ＝ 0，得到一组非零解 x 0 ，于是－ cx ＋ λ－ d y ＝ 0，y非零向量 x 0即为矩阵 A 的属于特征值 λ的一个特征向量．y 06．A n α(n ∈ N * )的简单表示(1) 设二阶矩阵 A ＝a b ， α是矩阵 A 的属于特征值 λ的任意一个特征向量，则A n α＝cdn *)．λα(n ∈ N， λ是二阶矩阵 A 的两个不同特征值，α， β是矩阵 A 的分别属于特征值 λ， λ(2) 设 λ1 212的特征向量，对于平面上任意一个非零向量γ，设 γ＝ t 1 α＋ t 2β(其中 t 1， t 2 为实数 )，则 A n γ＝n n* ．1λ1α＋ t 2λ2β(n ∈ N)t[ 小题体验 ]1 61．矩阵 M ＝ － 2－ 6 的特征值为 __________ ．解析： 矩阵 M 的特征多项式为 f(λ)＝ λ－ 1 － 6λ＋2)( λ＋ 3) ，令 λ＝ ，得 M 的特(f( ) 02 λ＋ 6征值为 λ＝－1 2， λ＝－2 3.答案： － 2 或－ 32．设2 a 2 a 的值为 ________．3是矩阵 M ＝ 的一个特征向量，则实数322解析： 设是矩阵 M 属于特征值 λ的一个特征向量，3a 2 2 2则2 ＝ λ ， 33 32a ＋ 6＝2λ， λ＝ 4，故解得12＝ 3λ a ＝ 1.答案： 11．不是每个二阶矩阵都可逆， 只有当ab中 ad － bc ≠ 0 时，才可逆， 如当 A ＝10 ， c d0 01 0因为 1× 0－ 0× 0＝ 0，找不到二阶矩阵 B ，使得 BA ＝ AB ＝E 成立，故 A ＝ 不可逆．0 2．如果向量 α是属于 λ的特征向量，将它乘非零实数t 后所得的新向量t α与向量 α共线，故 t α也是属于 λ的特征向量，因此，一个特征值对应多个特征向量，显然，只要有了特征值的一个特征向量，就可以表示出属于这个特征值的共线的所有特征向量了．[ 小题纠偏 ]1．矩阵 A ＝2 35的逆矩阵为 ____________． 6x y 解析：法一： 设矩阵 A 的逆矩阵 A－1＝，z w2 3 x y1 0 则6 z w＝ ， 512x ＋ 3z 2y ＋ 3w 1 0即＝0 1 ， 5x ＋ 6z 5y ＋ 6w2x ＋ 3z ＝ 1，x ＝－ 2，2y ＋ 3w ＝ 0，y ＝ 1，所以解得55x ＋ 6z ＝ 0， z ＝ 3，5y ＋ 6w ＝ 1，2w ＝－ 3.A －1＝－21故所求的逆矩阵5－ 2 .3 3法二： 注意到 2× 6－ 3×5＝－ 3≠0，故 A 存在逆矩阵 A－1，6 － 3－ 3－ 3－ 21且 A －1＝＝52 .－ 5 2－3 3－ 3 － 3－ 2 1 答案：5 － 2331 222．已知矩阵 A ＝－ 4 的一个特征值为 λ，向量 α＝ 是矩阵 A 的属于 λ的一个特a－ 3 征向量，则 a ＋ λ＝ _____.解析： 因为 A α＝ λα，所以2－ 6＝ 2λ， 即解得2a ＋ 12＝－ 3λ，所以 a ＋ λ＝－ 3－ 2＝－ 5.答案： － 51 2 2 2a－ 4 － 3 ＝ λ ，－ 3a ＝－ 3，λ＝－ 2，考点一求逆矩阵与逆变换重点保分型考点 —— 师生共研[ 典例引领 ]－ 1 01 2 A －1已知矩阵 A ＝2， B ＝，求矩阵 B.6 解： 设矩阵 A 的逆矩阵为a bc，d－ 1 0 a b1 0，即 － a － b 1 0则＝＝ ，2 c d12c 2d 0 11故 a ＝－ 1， b ＝ 0， c ＝ 0， d ＝2.所以矩阵 A 的逆矩阵为 A －1＝－ 11 .2所以 A－ 1 0 1 2－ 1－ 2－1B ＝1＝.0 632[ 由题悟法 ]求一个矩阵 A 的逆矩阵或证明一个矩阵不可逆时，常用两种解法．法一： 待定矩阵法：先设出其逆矩阵，根据逆矩阵的定义 AB ＝ BA ＝ E ，应用矩阵相等的定义列方程组求解，若方程组有解，即可求出其逆矩阵，若方程组无解，则说明此矩阵不可逆，此种方法称为待定矩阵法．a b法二： 利用逆矩阵公式，对矩阵A ＝ ：c d①若 ad － bc ＝ 0，则 A 的逆矩阵不存在．d－ b ②若 ad － bc ≠ 0，则－ 1ad － bc ad － bc.A ＝－ caad － bc ad － bc[ 即时应用 ]11 1已知 A ＝ 1， B ＝，求矩阵 AB 的逆矩阵．1 021 0 1－ ＝ 1≠ 0， 解：法一： 因为 A ＝1 ，且 1 ×2 02 0212 －111 0所以 A－1＝22 ＝，20 1－ 1 12 2 1－ 1.同理 B－1＝0 1因此 (AB)－1＝ B－1A －1＝1－ 1 1 0 1 － 20 2 ＝.0 1 0 211 1法二： 因为 A ＝10 ， B ＝，20 1所以1 0 1 1 ＝ 11 ，且× 1－ × ＝ 1≠ 0，AB＝11 10 0 120 1222第 15 页 共 21 页1 － 1 21 11 － 2所以 (AB)－1＝22.＝20 1 01 12 2考点二特征值与特征向量的计算及应用重点保分型考点 —— 师生共研[ 典例引领 ]2 a已知矩阵 M ＝，其中 a ∈ R ，若点 P(1，－ 2)在矩阵 M 的变换下得到点 P ′(－ 4,0)．2 1(1) 求实数 a 的值；(2) 求矩阵 M 的特征值及其对应的特征向量．解： (1) 由 2 a1－ 4 ，得 － ＝－＝＝3.2 1 －22 2a4? a2 3λ－ 2 － 3(2) 由 (1)知 M ＝，则矩阵 M 的特征多项式为 f (λ)＝ ＝( λ－ 2)( λ－ 1)－ 621－ 2 λ－ 12＝ λ－ 3λ－4.令 f(λ)＝ 0，得矩阵 M 的特征值为－ 1 与 4.λ－ 2 x － 3y ＝ 0，把 λ＝－ 1 代入二元一次方程组－ 2x ＋ λ－ 1 y ＝0，得 x ＋ y ＝ 0，1所以矩阵 M 的属于特征值－ 1 的一个特征向量为；－1λ－ 2 x － 3y ＝ 0，把 λ＝ 4 代入二元一次方程组－ 2x ＋ λ－ 1 y ＝ 0，得 2x － 3y ＝ 0.所以矩阵 M 的属于特征值4 的一个特征向量为3.2[ 由题悟法 ](1) 求矩阵 A 的特征值与特征向量的一般思路为：先确定其特征多项式 f(λ)，再由 f(λ)＝ 0求 出 该 矩 阵 的 特 征 值 ， 然 后 把 特 征 值 代 入 矩 阵 A所 确 定 的 二 元 一 次 方 程 组λ－ a x － by ＝ 0， 即可求出特征向量．－ cx ＋ λ－ d y ＝ 0，(2) 根据矩阵 A 的特征值与特征向量求矩阵A 的一般思路：设 A ＝a b c ，根据 A α＝λαd构建 a ， b ， c ， d 的方程求解．[ 即时应用 ]1x 1 的属于特征值 － 21． (2015 江·苏高考 )已知 x ， y ∈ R ，向量 a ＝ 是矩阵 A ＝y 0 － 1的一个特征向量，求矩阵A 以及它的另一个特征值．解： 由已知，得 Aa ＝－ 2a ，x 11－ － 2即＝x 1＝，y0 － 1y2x － 1＝－ 2， x ＝－ 1， 则即y ＝ 2，y ＝ 2，－11 所以矩阵 A ＝2.从而矩阵 A 的特征多项式f (λ)＝ (λ＋ 2)( λ－ 1)，所以矩阵 A 的另一个特征值为1.1 2．已知二阶矩阵 M 有特征值 λ＝ 3 及对应的一个特征向量 α1＝，并且矩阵 M 对应的1变换将点 (－1,2)变换成 (9,15) ，求矩阵 M .解： 设 M ＝ a b ，则a b 1 1 3 a ＋ b ＝ 3，＝ 3＝，故c dc d 113c ＋d ＝ 3.a b － 1 9－a ＋ 2b ＝ 9，又＝ ，故c d215－ c ＋ 2d ＝ 15.联立以上两方程组解得a ＝－ 1，b ＝ 4，c ＝－ 3，d ＝ 6，－ 1 4故 M ＝.－ 3 6考点三根据 A ， α计算 A n αn ∈ N *重点保分型考点 —— 师生共研[ 典例引领 ]1 23给定的矩阵 A ＝ ， B ＝ .－ 1 4 2 (1) ， λ及对应的特征向量 α， α；求 A 的特征值 λ1 2 12(2) 求 A 4B.解： (1) 设 A 的一个特征值为 λ，由题意知：λ－ 1 － 2＝ 0，即 (λ－ 2)(λ－ 3)＝ 0，所以 λ1＝ 2， λ2＝ 3.1λ－ 4当 λ1＝ 2 时，由1 2 xx2 的特征向量 α1＝24 ＝ 2，得 A 属于特征值；－ 1 yy1当 λ2＝ 3 时，由1 2 xx 3 的特征向量 α2＝14 ＝ 3，得 A 属于特征值.－ 1 y y1(2) 由于 B ＝32 1＝ α＋ α，＝ ＋ 2 1 1 1 2故 A 4＝4 α＋ α ＝ 4α＋ 34α＝ 16α＋ 81α＝ 32 81＝ 1132 ＋ .16 8197[ 由题悟法 ]已知矩阵 A 和向量 α，求 A n α(n ∈ N * )，其步骤为：(1) 求出矩阵， λ和对应的特征向量 α， αA 的特征值 λ1 2 12. (2) 把 α用特征向量的组合来表示：α＝ s α1＋ t α2.nnn表示 A n(3) 应用 A α＝ s λα11 ＋ t λα.2α2[ 即时应用 ]已知 M ＝ 1 2 ， β＝ 1 ，计算 M 5β21 7.λ－ 1 － 2解： 矩阵 M 的特征多项式为f( λ)＝2＝ λ－ 2λ－ 3.－ 2 λ－ 1令 f(λ)＝ 0，解得 λ＝1 3，λ＝－2 1，12 xx，得x ＋ 2y ＝ 3x ，令＝ 32 1 y y2x ＋ y ＝ 3y ，从而求得 λ1＝3 的一个特征向量为1α1＝，11同理得对应λ2＝－1的一个特征向量为α2＝－ 1.令β＝ mα1＋ nα2，则 m＝4， n＝－ 3.55α－ 3α555551－ 3× (－ 1)51β＝＝α－＝－＝×＝M M (44(M3(Mα4(λα3(λα312)1)2) 1 1)22)41－ 1975.9691．(2016 无·锡期末 )已知矩阵 A＝1012－1对应的变换把直线 l 0， B＝，若矩阵 AB21变为直线 l′： x＋ y－ 2＝ 0，求直线 l 的方程．解：由题意得 B－1＝1－ 2，01101－ 21－ 2所以 AB－1＝＝，020102设直线 l 上任意一点 (x， y)在矩阵 AB－1对应的变换下为点 (x′， y′ )，则1－ 2x＝02yx′x′＝ x－ 2y，，所以y′y′＝ 2y，将 x′， y′代入 l′的方程，得 (x－ 2y)＋ 2y－2＝ 0，化简后得 l： x＝ 2.12－ 11－12． (2016 江·苏高考 )已知矩阵 A＝0－2，矩阵 B 的逆矩阵 B＝2，求矩阵02AB.解：设 B＝ab，c d－11－1a b10则 B2＝，＝B c d010 2即错误 ! ＝错误 ! ，1a ＝ 1， a － 2c ＝ 1，1，11b ＝ 1b － 2d ＝ 0，4所以 B ＝4故解得.2c ＝ 0，c ＝ 0，121d ＝2d ＝ 1，2，1 1 1 51424因此， AB ＝ 0－ 2＝.1 0－123． (2016 南·京、盐城、连云港、徐州二模)已知 a ， b 是实数，如果矩阵 3 aA ＝所b － 2对应的变换 T 把点 (2,3) 变成 (3,4)．(1) 求 a ， b 的值；(2) 若矩阵 A 的逆矩阵为 B ，求 B 2.3 a23解： (1) 由题意得＝，b － 2 34所以 6＋ 3a ＝ 3,2b － 6＝ 4，所以 a ＝－ 1， b ＝ 5.3 － 1(2) 由 (1)得 A ＝.5 － 22 － 1由矩阵的逆矩阵公式得B ＝.5 － 32 － 1 2 － 1－ 1 1所以 B 2＝＝. 5 － 3 5 － 3 － 544． (2016 常·州期末 )已知矩阵 M ＝a 2 8 的一个特征向量是e ＝14的属于特征值 ，点b1P(－ 1,2)在 M 对应的变换作用下得到点Q ，求 Q 的坐标．a 2 1 1 解： 由题意知4 b ＝ 8×，11a ＋ 2＝ 8，a ＝ 6，故解得4＋ b ＝ 8，b ＝ 4，6 2 － 1 ＝－ 2所以42，所以点 Q 的坐标为 (－2,4)．4 4－ 1 45． (2016 苏·州暑假测试 )求矩阵 M ＝2 的特征值和特征向量．6λ＋ 1 － 42解： 特征多项式f(λ)＝＝ λ＋1)( λ－6)＝ λ－7)( λ＋ 2) ，－ ＝ λ－ λ－(85 14(－ 2 λ－ 6由 f(λ)＝ 0，解得 λ1＝ 7，λ2＝－ 2.8x － 4y ＝ 0，1 将 λ＝ 7 代入特征方程组，得即 y ＝ 2x ，可取为属于特征值 λ＝ 7 的11－ 2x ＋ y ＝ 0，2一个特征向量．－ － ＝ ，4x 4y 0同理， λ＝－2 2 时，特征方程组是即 x ＝－ 4y ，所以可取为属于－ 2x － 8y ＝ 0，－ 1特征值 λ2＝－ 2 的一个特征向量．M ＝ － 1 4λ1＝ 7， λ2＝－ 2.属于 λ1＝7 的一个特征向量综上所述，矩阵2 有两个特征值61，属于 λ2＝－ 2 的一个特征向量为4为－ 1. 23 6λ＝ 8 的一个特征向量e ＝ 6，及属于特征值 λ＝－ 36．矩阵 M ＝有属于特征值255的一个特征向量 e ＝13 ，计算 M3α2－ 1 .对向量 α＝ 8.解： 令 α＝ me ＋ ne ，将具体数据代入，有m ＝ 1，n ＝－ 3，所以 α＝e － 3e 所以M 3α 1212 .3333 3 3 6 1 3 153＝ M － 3e ＝ － 3M － 3× (－3) 3 ＝(e 1＝ λ － 3λ ＝ 8.5－ 1 2 479－ 1 27． (2016 泰·州期末 )已知矩阵 M ＝5x 的一个特征值为－ 2，求 M 2.2λ＋ 1－ 22解： 把 λ＝－ 2 代入－λ－ ＋ ＝ ，得＝ ，＝ λ－5λ－ x(x1)(x 5)x 3－2第 21 页共 21 页－ 124所以矩阵 M ＝65，所以 M 2＝.351428．已知二阶矩阵 M 有特征值 λ＝ 8 及对应的一个特征向量 e 1＝1 ，并且矩阵 M 对应的1变换将点 (－1,2)变换成 (－ 2,4). 求：(1) 矩阵 M;(2) 矩阵 M 的另一个特征值，及对应的一个特征向量e 2 的坐标之间的关系；(3) 直线 l ： x －y ＋ 1＝ 0 在矩阵 M 的作用下的直线 l ′的方程．a ba b 1 18解： (1) 设 M ＝，则c d 1 ＝ 8 ＝ ，c d1 8a ＋ ＝ ，b－1－2－a ＋ 2b ＝－ 2，b8a＝ ，故故c d＋ ＝8.24－c ＋ 2d ＝ 4.c da ＝ 6，b ＝ 2，62 联立以上两方程组，解得故 M ＝.c ＝ 4，44d ＝ 4，2(2) 由 (1) 知，矩阵 M 的特征多项式为f (λ)＝ (λ－ 6)( λ－ 4)－ 8＝λ－ 10λ＋ 16，故其另一个特征值为λ＝ 2.设矩阵 M 的另一个特征向量是e 2＝x ，y则 Me 2＝6x ＋ 2yx ，解得 2x ＋ y ＝0.＝ 2y4x ＋ 4y(3) 设点 (x ，y)是直线 l 上的任意一点， 其在矩阵 M 的变换下对应的点的坐标为 (x ′ ，y ′ )，则 6 2 x ＝x ′，即 x ＝ 1 ′ －1 ′ ， ＝－1′ ＋3′ ，代入直线l 的方程后并化简，4 4 y′4x8yy4x8yy得 x ′ － y ′ ＋ 2＝0，即 x －y ＋ 2＝ 0.。