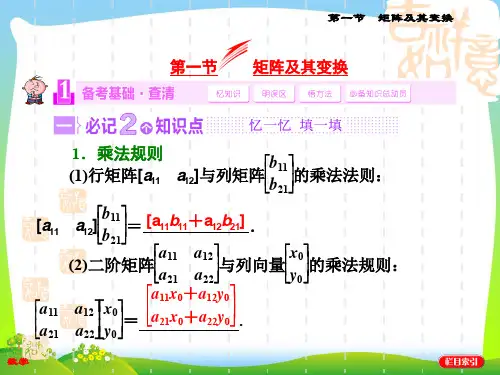
平面上的点( x,
y)左乘矩阵
2 0
0 1
后变成一个新的点
2x
y
.
一般地,对于平面上的任意一点(向量)
(x, y),若按照对应法则T,总能对应唯一的一个 平面点(向量)(x, y),则称T为一个变换,简记 为
T:(x, y) (x, y), 或
T: xy
对应位置上的元素不一样,这两个矩阵就不相等,如12
4 3
≠12 -43.两个不同行(或者不同列)的矩阵一定是不相等的,
如以零矩阵为例:[0,0]和00 00,尽管两个矩阵的元素均为 0,
但两者不相等.
用矩阵表示图形
用矩阵表示如图中的直角△ABC,其中 A(- 4,0),B(0,2),C(1,0)
表示 点(x,y) ,也可以表示以 O(0,0)为起点、以 P(x,y)
x
为终点的向量 y
区别.
,在不引起混淆的情况下,对它们不加以
1.矩阵(a23)与矩阵(a32)一样吗? 【提示】 不一样,因为矩阵(a23)表示 2 行 3 列矩阵,
而矩阵(a32)表示 3 行 2 列矩阵. 2.对于 m×n 矩阵,由多少个元素组成?
矩阵,并用 希腊字母α,β,…
来表示.
2.矩阵的相等
对于两个矩阵 A,B,只有当 A,B 的 行数 与 列数 分别 相等 ,并且 对应位置 的元素也分别 相等 时,A 和 B 才
相等,此时记作 A=B.
3.矩阵与平面向量的关系
由于点 P(x,y)―一―一―对―应→平面向量O→P,因此,xy既可以
0.6 0.6
86 75.
规定:
行矩阵 a11
a12