当前位置：文档之家 › 高阶系统的时域分析

高阶系统的时域分析

  • 格式：doc
  • 大小：345.50 KB
  • 文档页数：18

下载文档原格式

  / 18

合集下载

自动控制第三章s讲解

自动控制第三章s讲解

trtp ts
稳态误差
t
振荡系统定义为从零第一次上升到终值所需时间。
峰值时间tp：响应到达第一个峰值所需时间。 调节时间ts：到达并保持在终值 5％误差带内所需的最短时间 超调量%：最大偏离量c(tp)与终值c(∞)之差的百分比，即
% c(t p ) c() 100 %
c()
❖稳态性能：由稳态误差ess描述。
跟踪误差：e(t)=r(t)-c(t)=Tt-T2(1-e-t/T)随时间推 移而增长，直至无穷。因此一阶系统 不能跟踪加速度函数。
线性定常系统的特性
单位脉冲信号 r(t) (t) R(s) 1
单位阶跃信号 r(t) 1 单位斜坡信号 r(t) t
R(s) 1 s
R(s)
1 s2
单位加速度信号 r (t ) t 2 2 R(s) 1 s3
3.1 时间响应性能指标
3.1.1 典型输入信号
典型输入信号
单位阶跃信号、单位斜坡信号、单位脉冲信号、 单位加速度信号、正弦信号。
对应的输出分别被称为 单位阶跃响应 、单位斜坡响应 、单位脉冲响应 、 单位加速度响应。
一．阶跃函数
r(t)
A
0 r(t) A
t0 t0
R(s) A s
o
t
A=1时称为单位阶跃函数, 其数学表达式为
k Ts+1
输入R(s)
1 s2
输出速度 dc(t) 1 et T
dt
位置误差随时间增
单
大,最后为常值T
位
斜
T
坡
响
应
0T
3.2.5 一阶系统的单位加速度响应
无零点的一阶系统 Φ(s) =
k Ts+1

自动控制理论稳态误差

自动控制理论稳态误差
稳
3
3.5 线性系统的稳定性分析
线性定常系统稳定的充分必要条件
jω
s平面
稳定区域 稳定区域
不稳定区域
σ
不稳定区域
临界稳定 /临界不稳定 不稳定
根在复平面的位置
4
上节课要点复习
3.5 线性系统的稳定性分析
劳斯(Routh)稳定判据
S控制系统稳定的必要条件是：控制系统特征方程式的 所有系数符号相同且不为零（不缺项）。
K
−
K
+1 t
(1 − e T )
K +1
ess
=1−
K K +1
=
1 K +1
开环、闭环传递函数？！！ 17
3.3 二阶系统的时域分析(例子)
二阶系统的单位阶跃响应
R(s)
E(s)
ω
2 n
Y (s)
R(s)
ω
2 n
Y (s)
s(s + 2ζωn )
s2
+
2ζω n s
+
ω
2 n
a)
b)
G(s)H (s) =
E(s)
K
Ts
Y (s)
R(s)
K Y(s)
Ts + K
a)
b)
Ⅰ型系统 K p = ∞
−Kt
y(t) = 1− e T
R(s)
E(s)
K
Y (s)
R(s)
K
Y (s)
Ts +1
Ts + K +1
K P = limG(s)H (s) s→0
ess
=1 1+ Kp

高阶系统时域分析

高阶系统时域分析
阶系统的单位阶跃响应取决于闭环系统的零、极点分布。
[定性分析]： 对于闭环极点全部位于s左半平面的高阶系统（否则系统不稳 定），极点为实数（指数衰减项）和共轭复数（衰减正弦项）的 衰减快慢取决于极点离虚轴的距离。远，衰减的快；近，衰减的 慢。所以，近极点对瞬态响应影响大。
线性系统的时域分析法>>高阶系统的时域分析
线性系统的时域分析法>>高阶系统的时域分析
c(t) a0 n1 a je p jt j 1
n2
n2
e lnlt l
c os nl
1l2t
e lnlt
l
sin nl
1l2t
l 1
l 1
可见，c(t)不仅与 p j , l ,nl （闭环极点）有关，而且与系数
a j , l , l有关（这些系数都与闭环零、极点有关）。所以，高
系数 a j , l , l 取决于零、极点分布。有以下几种情况： 若极点远离原点，则系数小； 极点靠近一个零点，远离其他极点和零点，系数小； 极点远离零点，又接近原点或其他极点，系数大。
衰减慢且系数大的项在瞬态过程中起主导作用。
[主导极点]：满足下列条件的极点称为主导极点。 存在一对离虚轴最近的共轭极点； 附近无零点； 其他极点距虚轴的距离是它的5倍以上。
p3
离虚轴
远， p1, p2 离虚轴近，系统的瞬态特性主要由 p1, p2 决定，
呈二阶系统的特性。反之，当 1 时，表示
p1, p2 离虚轴远，系统的瞬态特性主要由
p3p决3 离定虚，轴呈近一，阶
系统的特性。第二个因素是阻尼系数 ，同前。如下图所示：
c(t)
1 0
图中， 表示无 p3 极点，由图 可见，加入极点 p3 后，当 不变 时，超调量下降了，但调节时间增

自动控制原理-第3章-时域分析法

自动控制原理-第3章-时域分析法
系统响应达到峰值所需要的时间。
调节时间
系统响应从峰值回到稳态值所需的时间。
振荡频率
系统阻尼振荡的频率，反映系统的动态性能。
系统的阶跃响应与脉冲响应
阶跃响应
系统对阶跃输入信号的响应，反映系 统的动态性能和稳态性能。
脉冲响应
系统对脉冲输入信号的响应，用于衡 量系统的冲激响应能力和动态性能。
03
一阶系统时域分析
01
单位阶跃响应是指系统在单位阶跃函数作为输入时的
输出响应。
计算方法
02 通过将单位阶跃函数作为输入，代入一阶系统的传递
函数中，求出系统的输出。
特点
03
一阶系统的单位阶跃响应是等值振荡的，其最大值为1，
达到最大值的时间为T，且在时间T后逐渐趋于0。
一阶系统的单位脉冲响应
定义
单位脉冲响应是指系统在单 位脉冲函数作为输入时的输
无法揭示系统结构特性
时域分析法主要关注系统的动态行为和响应，难以揭示系统的结构特 性和稳定性。
对初值条件敏感
时域分析法的结果对系统的初值条件较为敏感，初值条件的微小变化 可能导致计算结果的较大偏差。
感谢您的观看
THANKS
计算简便
时域分析法通常采用数值积分方法进 行计算，计算过程相对简单，易于实 现。
时域分析法的缺点
数值稳定性问题
对于某些系统，时域分析法可能存在数值稳定性问题，例如数值积分 方法的误差累积可能导致计算结果失真。
计算量大
对于高阶系统和复杂系统，时域分析法需要进行大量的数值积分计算， 计算量较大，效率较低。
自动控制原理-第3章-时域 分析法
目录
• 时域分析法概述 • 时域分析的基本概念 • 一阶系统时域分析 • 二阶系统时域分析 • 高阶系统时域分析 • 时域分析法的优缺点

3-4高阶系统的时域分析

3-4高阶系统的时域分析

h(t ) = 1 -
1
e - sot
bz 2(b - 2) + 1
-
e - zwn t
[bz 2(b -
bz 2(b - 2) + 1
2) cos wn
1- z 2t
bz (z 2(b - 2) + 1)
+
1- z2
sin wn
1- z2t]
由于
b 2 ( b 2 ) 1 2 ( b 1 ) 2 ( 1 2 ) 0 , b S 0 /w n
2、 超调量的计算
n
m
si
s% i3 n
s1 zi
i1
estp 10% 0
m
s1 si
zi
i3
i1
结论： （1）闭环零点会减小系统阻尼。 （2）闭环非主导极点会增大系统阻尼。 （3）若系统不存在闭环零点和非主导极点，则
s%e/ 12 10% 0
3、 调节时间的计算
s i为 D ( s ) 0 的 根 ， 称 为 闭 环 极 点 。
当输入为单位阶跃函数时，
m
K (szi)
C (s)q
i 1 r
(ssj) (s22k
ksk 2)1 sA s0jq 1s A jsjkr 1s2 B 2 ksk k C skk 2

ts 1n ln2
n
si
i2 n
s1 si

m
s1 zi
i1 m
zi

i2
i1

结论：
（1）闭环零点越接近虚轴，峰值时间越小，超调量 和调节时间越大；

自动控制原理-第3章

自动控制原理-第3章

响应曲线如图3-2所示。图中
为输出的稳态值。
第三章 线性系统的时域分析 法
图 3-2 动态性能指标
第三章 线性系统的时域分析 法
动态性能指标通常有以下几种:
延迟时间td: 指响应曲线第一次达到稳态值的一半所需的时间
上升时间tr: 若阶跃响应不超过稳态值, 上升时间指响应曲线从 稳态值的10%上升到90%所需的时间; 对于有振荡的系统, 上升时 间定义为响应从零第一次上升到稳态值所需的时间。上升时间越 短, 响应速度越快。
可由下式确定: (3.8)
振荡次数N: 在0≤t≤ts内, 阶跃响应曲线穿越稳态值c(∞)次 一半称为振荡次数。
上述动态性能指标中, 常用的指标有tr、ts和σp。上升时间tr 价系统的响应速度; σp评价系统的运行平稳性或阻尼程度; ts是同
时反映响应速度和阻尼程度的综合性指标。 应当指出, 除简单的一 、二阶系统外, 要精确给出这些指标的解析表达式是很困难的。
中可以看出, 随着阻尼比ζ的减小, 阶跃响应的振荡程度加剧。 ζ =0时是等幅振荡, ζ≥1时是无振荡的单调上升曲线, 其中临界阻尼 对应的过渡过程时间最短。 在欠阻尼的状态下, 当0.4＜ζ＜0.8时过
渡过程时间比临界阻尼时更短, 而且振荡也不严重。 因此在 控制工程中, 除了那些不允许产生超调和振荡的情况外, 通常都希
第三章 线性系统的时域分析法 4. 脉冲函数 脉冲函数(见图3-1(d))的时域表达式为
(3.4)
式中,h称为脉冲宽度, 脉冲的面积为1。若对脉冲的宽度取趋于 零的极限, 则有
(3.5) 及
(3.6)
称此函数为理想脉冲函数, 又称δ函数(见图3-1(e))。
第三章 线性系统的时域分析 法

第3章_时域瞬态响应分析_3.5高阶系统的瞬态响应

第3章_时域瞬态响应分析_3.5高阶系统的瞬态响应

×
1
偶极子 -1
0
s2×
相距很近的一对零点和极点叫作偶极子。 相距很近的一对零点和极点叫作偶极子。 一对靠得很近的零点和极点，在输出中， 一对靠得很近的零点和极点，在输出中，与该极 点相对应的分量可以忽略， 点相对应的分量可以忽略，也即这一对靠得很近的零 点和极点可以一起消掉，这种情况称为偶极子相消。 点和极点可以一起消掉，这种情况称为偶极子相消。 经验指出， 经验指出，如果闭环零点和极点之间的距离比它 们本身的模值小一个数量级时， 们本身的模值小一个数量级时，则这一对零点和极点 就构成了偶极子。 就构成了偶极子。 偶极子的概念对控制系统的综合设计是很有用的， 偶极子的概念对控制系统的综合设计是很有用的， 有时可以有目的地在系统中加入适当的零点， 有时可以有目的地在系统中加入适当的零点，以抵消 对动态性能影响较大的不利的极点， 对动态性能影响较大的不利的极点，使系统的性能得 到改善。 到改善。
m m −1 m m −1 X o ( s ) K ( s + b1s + L + bm −1s + bm ) K ( s + b1s + L + bm−1s + bm ) = q = n n −1 r Xi (s) s + a1s + L + an −1s + an ( s + pi ) ∏ ( s 2 + 2ξ jω j s + ω 2j ) ∏ i =1 j =1
《控制工程基础》 控制工程基础》
第3章 时域瞬态响应分析 章 3.5 高阶系统的瞬态响应
3.5.1 高阶系统的单位阶跃响应
一般的高阶机电系统可以分解成若干一阶惯 性环节和二阶振荡环节的叠加。 性环节和二阶振荡环节的叠加。其瞬态响应即是由 这些一阶惯性环节和二阶振荡环节的响应函数叠加 组成。对于一般单输入、单输出的线性定常系统， 组成。对于一般单输入、单输出的线性定常系统， 其传递函数可表示为

3.3高阶系统的时域分析

3.3高阶系统的时域分析

j 1
k 1
式中，q+2r=n, q为实数极点的个数；r为共轭复数极点的对数。
部分分式展开，并设0＜ζk＜1,取拉氏反变换，并整理
q
r
h(t) A0
Ajesjt
B e kkt k
c os ( k
1


2 k
)t
j 1
k 1

r k 1
Ck
k
Bk kk
3、 调节时间的计算


ts

1
n
ln
2
n
si
m s1 zi
i2 n
i1 m

s1 si
zi
i2
i 1

结论：
（1）闭环零点越接近虚轴，峰值时间越小，超调量 和调节时间越大；
（2）闭环非主导极点的作用是增大峰值时间，但可 减小系统的超调量和调节时间。
高阶系统的增益常常调整到使系统具有一对闭环共轭 主导极点，这时可以用二阶系统的动态性能指标来估 算高阶系统的动态性能。
设单位反馈高阶系统具有一对共轭复数闭环主导极点: 系统单位阶跃响应的近似表达式：
s1,2 s jd , 0 1
C(s) M (s) 1 N(s) s
1


2 k
e kk t
s in( k
表明
1


2 k
)t,
t

0
（1）响应由一阶系统和二阶系统的时间响应函数项组成。当所 有闭环极点都位于左半s开平面时，系统是稳定的。
（2）零极点对系统性能的影响。
三、闭环主导极点

高阶系统的单位阶跃响应

高阶系统的单位阶跃响应

自动控制原理
第三章 时域分析法
一、典型输入信号 1．阶跃函数
其表达式为
a t ≥ 0 r (t ) 0 0 t
当a=1时，称为单位阶跃函数，记作1(t)，则有
1 t ≥ 0 1(t ) 0 0 t 单位阶跃函数的拉氏变换为 1 R( s ) L [1( t )] s
稳：即稳定性，在响应曲线上的反应是有界输入产生 有界输出。 它是系统固有性质，由系统的结构和参数决定，与外 界因素无关。
自动控制原理 第三章 时域分析法 由单位阶跃响应曲线判定系统的稳定性
自动控制原理
第三章 时域分析法
过渡过程性能指标：描述快速性和平稳性。 稳态性能指标：描述准确性。
①延迟时间td
单位脉冲函数δ (t)，其数学描述为
t 0 (t ) 且 0t 0



(t )dt 1
单位脉冲函数的拉氏变换为
R( s ) L [ ( t )] 1
自动控制原理
第三章 时域分析法
r(t)
5．正弦函数 其表达式为
o
a sin tt ≥ 0 r (t ) t 0 0
自动控制原理
第三章 时域分析法
2．速度函数（斜坡函数）
其表达式为
at t ≥ 0，a为常量 r (t ) 0 0 t
当a=1时，r(t)=t，称为单位速度函数，其拉氏变 换为
1 R( s ) L [t 1( t )] 2 s
自动控制原理
第三章 时域分析法
3．加速度函数（抛物线函数） 其表达式为
%
h( tp ) h() h() 100%
②上升时间tr ③峰值时间tp ④超调量% ⑤调节时间ts

自动控制原理

自动控制原理

k ( t ) Ai e
i 1
i t
t
0
系统稳定的充要条件：系统所有闭环特征根均具有负的实部，
或所有闭环特征根均位于左半s平面。
系统稳定：充要条件 闭环特征方程的所有根均具有负实部 或系统闭环极点都位于S的左半平面 不稳定系统： 有一个或一个以上的正实部根。 临界稳定： 有一对纯虚根，而其余的特种根都有负 实部。 无阻尼系统 ＝0 。 12 工程上，临界稳定（线性系统不存在）为不稳定系统。
c1
b1a3 a1b2 b1 b a a1b3 c2 1 5 b1 b a a1b4 c3 1 7 b1
劳斯表第一列元素均大于零时系统稳定，否则系统不稳定 且第一列元素符号改变的次数就是特征方程中正实部根的个数
劳斯稳定判据
系统特征方程： a0 s
n
a1s an1s an 0
4
517 2.3 104

0 0
该表第一列系数符号不全为正，因而系统是不稳定的；且符 号变化了两次(+到－，－到＋)，所以该方程中有二个根在 S的右半平面。
18
例3.2 已知某调速系统的特征方程式为
S 3 41.5S 2 517S 1670 (1 K ) 0
求该系统稳定的K值范围。 解：列劳斯表
t
k ( t ) A1e
t
i t
A2 e
n i 1
2 t
i t
An e
0
n t
Ai e i t
i 1
n
limk ( t ) lim Ai e
t
i 0
i 1, 2, , n
n
充分性：

自动控制原理第三章2高阶系统

自动控制原理第三章2高阶系统

PID控制器的优化设计
通过优化算法，对PID控制器进行优 化设计。
高阶系统的状态反馈设计
状态反馈的设计原则
根据高阶系统的状态变量，设计状态反馈控 制器。
状态反馈的极点配置
通过配置状态反馈控制器的极点，实现系统 性能的优化。
状态反馈的鲁棒性分析
分析状态反馈控制器对系统参数变化的鲁棒 性。
状态反馈的优化设计
高阶系统的优化设计
通过优化算法，如遗传算法、粒子群算法等 ，对高阶系统进行优化设计。
高阶系统的PID控制设计
PID控制器的参数整定
根据高阶系统的特性，整定PID控制 器的比例、积分和微分参数。
PID控制器的稳定性分析
通过分析PID控制器的极点和零点， 判断系统的稳定性。
PID控制器的抗干扰能力
考虑PID控制器对外部干扰的抑制能 力，提高系统的鲁棒性。
通过研究高阶系统的 特性，可以提高对复 杂系统的理解和控制 能力。
高阶系统在飞行器控 制、机器人导航等领 域有重要应用。
高阶系统在自动控制中的应用
在复杂工业过程中， 高阶系统是常见的被 控对象，如多变量控 制系统。
通过研究高阶系统的 特性，可以提高对复 杂系统的理解和控制 能力。
高阶系统在飞行器控 制、机器人导航等领 域有重要应用。
缺点
对于高阶系统，根轨迹分析可能比较复杂，计算量大。
高阶系统的状态空间分析
状态空间分析是在状态空间中对系统进行分析的方法 ，通过建立系统的状态方程和输出方程来描述系统的
动态行为。
输入 标题
描述
状态空间分析通过求解状态方程和输出方程来得到系 统的状态响应和输出响应，可以全面了解系统的动态 性能和稳定性。
CATALOGUE

高阶系统的时域分析

高阶系统的时域分析

5n
n
c( t ) 1 Ai e
i 1
q
si t
Dk e si nk t cos( nk t 1 k2 k )
k 1
rn i 1
m
j
) ( s si ) s s
i
s ( s s i )
二．高阶系统单位阶跃响应的近似分析
C (s) ( s s i ) ( s 2 2 nk s nk )
2 j 1 k 1 q

1 s
r Bk ( s k nk ) C k nk 1 2 k 1 q Ai 2 s i 1 s s i k 1 s 2 2 k nk nk
§3-4 高阶系统的时域分析
一．闭环主导极点的概念
在高阶系统的诸多闭环极点中，把无闭环零点靠近，且其它闭环极点与虚轴的 距离都在该复数极点与虚轴距离的五倍以上，则称其为闭环主导极点。
| ReS3 | 5 S1,2 j d
K (s - z j )
j 1 m
n
s3 s1 s2 Im Re
k
k
由此可见高阶系统的暂态响应是一阶和二阶系统。
暂态响应分量的合成则有如下结论：
（1）各分量衰减的快慢由指数衰减系数 S i 及 k nk 决定。系统的极点在s平面左半部距虚轴愈远，相应的 暂态分量衰减愈快。 （2）系数 Ai 和 Dk 不仅与s平面中的极点位置有关， 并且与零点有关。
Ai 越小，对 c( t ) a.零极点相互靠近，且离虚轴较远， 影响越小；
b.零极点很靠近，对c(t ) 几乎没影响；
c.零极点重合（偶极子）， 对 c(t ) 无任何影响；

3.4高阶系统

3.4高阶系统

进行拉氏反变换：
A0 L ( ) A0 s q q q A A p jt j j 1 1 L ( ) L ( ) Aj e s pj j 1 s p j j 1 j 1
1
08:47
Bk s Ck L [ 2 ] 2 s 2 kk s k
1
08:47
c(t ) L1[C ( s )] A0 Aj e
j 1 q p jt
Ak e k k t sin dk t k
k 1
r
结论4：响应曲线的形状和闭环极点和零点有关。
对于稳定的系统，闭环极点负实部的绝对值越大 (极 点距虚轴愈远 ) ，则其对应的响应分量 ( 模态 ) 衰减的越 迅速，否则，衰减的越慢。(和极点有关) 在留数的计算过程中，要用到C(s),而C(s)中包含有 闭环的零点，因此不可避免地要影响到留数的值，而留 数的数值实际上就是指数项的系数。(和零点有关)
System: untitled1 Settling Time (sec): 3.91 System: untitled2 Settling Time (sec): 4.02
Amplitude
0.5 0.4 0.3 0.2 0.1 0
1 G1 ( s ) s 1
10 G2 ( s) ( s 1)( s 10)
08:47
运动的模态
按照一阶和二阶暂态响应指数的衰减系数的正 负值，将暂态响应的运动形式分为5个模态：

一阶模态 e p t pj<0 一阶收敛模态 pj>0 一阶发散模态
j

二阶模态 e t sin(bt ) n 0 二阶收敛模态 n 0 二阶等幅振荡模态 n 0 二阶发散模态

第三章 控制系统的时域分析—3高阶系统时域分析

第三章 控制系统的时域分析—3高阶系统时域分析

(s
5(s 2)(s 3) 4)(s2 2s 2)
s3 4
s1,2 1 j
c(t) 1 15 e4t 10 2et cos(t 3520 )
4
结论： 高阶系统的响应，是由一阶系统和二阶系统的
时间响应函数项叠加而成。只有所有闭环极点都具有负
实部，即所有极点均位于左半S平面，系统才是稳定的。 闭环极点负实部的绝对值越大，其对应的响应分量衰减
i 5 0
且s1,
远离零点
2
zk
,
衰减慢。
C(s) (s)R(s) N (s) 1 （首1） D(s) s
s1,2 0 j0
二阶主导极点
1 s
N (s)
•
D(s)
1 s
s
s1
1 s s1
N (s)
•
D(s)
1 s
s
s2
1 s s2
16
C(s)
1 s
N (s)
•
首先讨论典型三阶系统的瞬态响应，然后进行更具一般形式 的高阶系统的瞬态响应分析。从下面的讨论中，可以看到:
高阶系统的瞬态响应是由若干个一阶系统和二阶系 统的瞬态响应线性叠加而成。
1
1.三阶系统的单位阶跃响应
典型三阶系统的闭环传函可表示成：
(s)
C(s) R(s)
(s
P)(s2
Pn 2 2ns
n2 )
15 4 1 4 1 4(7 j) 1 4(7 j)
s s 4 s 1 j
s 1 j
c(t ) L1[C(s)] 1 [15 e4t (7 j)e(1 j)t (7 j)e(1 j)t )] 4
1 15 e4t 10 2et cos(t 3520 ) 4 14

系统动力学第9讲

系统动力学第9讲

1. 改变积分性质
用反馈
包围积分环节或者包围电动机的
X2 s
X2 s X1 s
K0 X1 s s K0 K H

Km Tm s 1 s K m K H
2.引入比例－微分控制
在原系统的前向通路中引入比例－微分控制。
H0 s
H s

s 2 Tm s 1 K s 1
2 1 1 4 2 5 s 6 1
0


0

s
0
5
结论：系统不稳定；系统特征方程有两个正实部的根。
劳斯表判据的特殊情况
在劳斯表的某一行中，第一列项为零。 在劳斯表的某一行中，所有元素均为零。 在这两种情况下，都要进行一些数学处理， 原则是不影响劳斯判据的结果。

例2
设系统的特征方程为：
高阶系统的时域分析
定义：用高阶微分方程描述的系统称为高阶系 统。
由于求高阶系统的时间响应很是困难，所以通常总 是将多数高阶系统化为一、二阶系统加以分析。 通常对于高阶系统来说，离虚轴最近的一个或两个 闭环极点在时间响应中起主导作用，而其他离虚轴 较远的极点，他们在时间响应中相应的分量衰减较 快，只起次要作用，可以忽略。
K s 1
其闭环特征方程为：
Tm s 3 s 2 Ks K 0
由稳定的充分必要条件：
ai 0则Tm , K , 均大于零； D2 0, D2 a1a2 a0 a3,故K KTm 0 Tm
引入比例－微分控制后，补上了特征方程中s的 一次项系数。只要适当匹配参数，满足上述条件， 系统就可以稳定。

例1
设系统特征方程如下：

自动控制原理(第二版)(赵四化)章 (3)

自动控制原理(第二版)(赵四化)章 (3)

(s) C(s) 1
R(s) Ts 1
(3-13)
第3章 时域分析法 图3-5 一阶系统的动态结构图
第3章 时域分析法
3.2.1 一阶系统的单位阶跃响应
设输入
R(s) 1 s
则输出量的拉氏变换为
C(s) (s) 1 1 1 1 1
s Ts 1 s s s 1/T
单位阶跃响应为
1t
C(s)
(s)R(s)
s2
n2 2ns
n2
1 s
其中, 由
s2 2 ns n2 0
可求得两个特征根
s1,2 n n 2 1
(3-22)
第3章 时域分析法
1) ξ>1, 过阻尼
ξ>1
时
, 2 1 s1,2=-ξωn±ωn
为两个不相等的负实数根， 即有
C(s)
n2
A1 A2 A3
(s)
C(s) R(s)
s2
n2 2ns
n2
(3-21)
其中， ξ为阻尼比， ωn为无阻尼自然振荡频率， 它们 均为系统参数。
第3章 时域分析法
由式(3-21)可以看出， 二阶系统的动态特性 可以用ξ和ωn这两个参数的形式加以描述。 如果0<ξ<1， 则闭环极点为共轭复数， 并且位于左半s平面， 这时系统 叫做欠阻尼系统， 其瞬态响应是振荡的。 如果ξ=1， 那 么就叫做临界阻尼系统。 而当ξ>1时， 就叫做过阻尼系 统。 临界阻尼系统和过阻尼系统的瞬态响应都不振荡。 如果ξ=0， 那么瞬态响应变为等幅振荡。
此时系统输出响应的拉氏变换为
C(s)
1 Ts 1
1 s2
1 s2
T s
T2 Ts 1
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

课程设计任务书学生姓名： 专业班级： 自动化1002班 指导教师： 肖纯 工作单位： 自动化学院 题 目: 高阶系统的时域分析 初始条件：设单位系统的开环传递函数为))(105()()(2a s s s s b s K s G ++++=要求完成的主要任务: （包括课程设计工作量及其技术要求，以及说明书撰写等具体要求）（1） 当K=10,a=1,b=5时用劳斯判据判断系统的稳定性。

（2） 如稳定，则求取系统的单位阶跃响应、单位斜坡响应和单位加速度响应，用Matlab 绘制相应的曲线，并计算单位阶跃响应的动态性能指标和稳态性能指标，计算单位斜坡响应和单位加速度响应的稳态性能指标。

（3） 如不稳定，则计算系统稳定时K 、a 和b 的取值范围，在稳定范围内任取一值重复第2个要求。

（4） 绘制稳定时系统的根轨迹（在稳定范围内任取a 、b 值）。

分析K 变化对系统性能的影响。

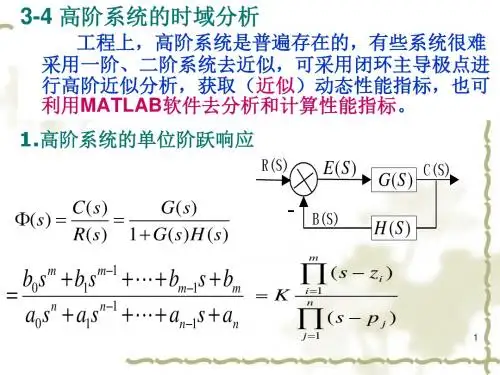
时间安排：指导教师签名： 年 月 日系主任（或责任教师）签名： 年 月 日目录1 高阶系统的数学模型 (1)2 系统稳定性分析 (2)3 高阶系统的时域分析 (5)3.1 单位阶跃响应 (5)3.1.1 单位阶跃响应 (5)3.1.2 单位阶跃响应动态性能 (7)3.1.3 单位阶跃响应稳态性能 (8)3.2 单位斜坡响应 (9)3.2.1 单位斜坡响应 (9)3.2.2 单位斜坡响应稳态性能 (10)3.3 单位加速度响应 (11)3.3.1 单位加速度响应 (11)3.3.2 单位加速度响应稳态性能 (12)4 系统根轨迹 (13)5 设计心得体会 (14)参考文献 (14)高阶系统的时域分析1 高阶系统的数学模型一个高阶系统的闭环传递函数的一般形式为：10111011()(),()m m m mn n n nb s b s b s b C s s m n R s a s a s a a ----++++Φ==≤++++ 对分子、分母进行因式分解，得到零极点形式：11()()()()()mi i njj K s z C s s R s s p ==-Φ==-∏∏ (1)式(1)中，K=b 0/a 0；z i ,p j 分别为系统闭环零、极点。

本设计给定的单位反馈系统的开环传递函数为)a s )(10s 5s (s b)s ()s (2++++=K G P (2)则其闭环传递函数为（假设为负反馈）：)3()10()510()5()()())(105()()(2342Kbs K a s a s a s b s K b s K a s s s s b s K s ++++++++=++++++=φ2 系统稳定性分析任何系统在扰动作用下都会偏离原平衡状态，产生初始偏差。

所谓稳定性， 是指系统在扰动消失之后，由初始偏差状态恢复到原平衡状态的性能。

线性系统 的稳定性仅取决于系统自身的固有特性，而与外界条件无关。

线性系统稳定的充 分必要条件是：闭环系统特征方程的所有根均具有负实部；或者说，闭环传递函 数的极点均位于 S 左半平面。

若求出闭环系统特征方程的所有根，就可判定系统的稳定性。

但对于高阶系统来说，求特征方程根很困难，并且不易对参数进行分析。

现使用一种不用求解特征根来判别系统稳定性的方法—劳斯稳定判据。

设系统的特征方程为10110()0,0n n n n D s a s a s a s a a --=++++=>，则可列出劳斯表如表1所示。

表1 劳斯表按照劳斯稳定判据，系统稳定的充分必要条件为：劳斯表中第一列各值均为正。

否则系统不稳定，且第一列各系数符号改变次数即为特征方程正实部根的数目。

当K=10，a=1，b=5时，代入式(3)得到系统闭环传递函数50201565010)(234+++++=s s s s s s φ则系统的闭环特征方程为：D(s)=s 4+6s 3+15s 2+20s+50=0. 按劳斯判据可列出如下劳斯表：由于劳斯表第一列数值符号有两次变化，故系统不稳定，且存在2个正实部根。

用 MATLAB 求出全部特征根如下：>> y=roots([1 6 15 20 50]) y =-3.1534 + 1.7836i-3.1534 - 1.7836i 0.1534 + 1.9458i 0.1534 - 1.9458i现继续用劳斯稳定判据求原给定系统稳定时K ，a ，b 的取值范围。

原给定系统的闭环特征方程为：D(s)=s 4+(5+a)s 3+(10+5a)s 2+(10a+K)s+Kb=0，按劳斯判据可列出如下劳斯表：根据劳斯稳定判据，令劳斯表中第一列各元素为正，即：⎪⎪⎪⎩⎪⎪⎪⎨⎧>>+-+++-++-++>++-++>+00)10()510)(5()5()10)](10()510)(5[(05)10()510)(5(052Kb K a a a a Kb K a K a a a a K a a a a (4) 即K 、a 和b 必须满足：⎪⎪⎩⎪⎪⎨⎧>>--+-++-++>-++>+002550)1015500()5250(50050255052232Kb K Kb K a Kb K a Kb K a K a a a (5) 系统才稳定。

3 高阶系统的时域分析取K=12，a=b=3时，此时系统由四阶变为三阶，系统开环传递函数为 )10s 5s (s 12)a s )(10s 5s (s b)s ()s (22++=++++=K G P (6)系统闭环传递函数为1210512)())(105()()(232+++=++++++=s s s b s K a s s s s b s K s φ (7) 经分析可知，此时 K 、a 、b 的值满足要求，系统稳定。

3.1 单位阶跃响应 3.1.1 单位阶跃响应单位阶跃响指的是系统在单位阶跃信号 r(t)=1(t)作用下的响应。

取其拉氏变换即 R(s)=1/s 。

此时，系统输出为:12105121)())(105()(1)()()(232+++=++++++==s s s s b s K a s s s s b s K s s s R s C φ对上式进行部分分式展开：425714.24286.035714.01)(2+++-+-=s s s s s s C 对部分分式进行拉普拉斯反变换，并设初始条件全部为零，得系统的单位阶跃响 应:)7321.1sin(2371.1)7321.1cos(4286.05714.01)]([)(31t e t e e s C L t c t t t -------==(8)对于一般的高阶系统来说，用这种方法来求取单位阶跃响应都比较麻烦，有时候甚至很难完成。

但利用 MATLAB 软件则可以很方便的得到响应，并绘制出响应曲线。

MATLAB 中tf2zp()函数能将传递函数模型转化为零极点模型，residue()函数可以直接求出传递函数部分分式展开，由这些结果可以直接写出系统的输出解析解。

另外，利用step()函数还能准确绘制系统单位阶跃响应曲线。

式(7)所表示系统可以用下面的MATLAB语句求解系统单位阶跃响应。

>> num=[12 36];den=[1 8 25 42 36] %描述闭环系统传递函数的分子、分母多项式sys=tf(num,den); %高阶系统建模[z,p,k]=tf2zp(num,den); %对传递函数进行因式分解zpk(z,p,k) %给出闭环传递函数的零极点形式[r,p,k]=residue(num,[den,0]) %对C(s)部分分式展开%在分母多项式后补零相当于乘以s step(sys) %绘制高阶系统的单位阶跃响应曲线grid %添加栅格title(‘单位阶跃响应’); %标注标题xlabel(‘t’); ylabel(‘c(t)’); %标注横、纵坐标轴绘制的单位阶跃响应曲线如图1所示。

图1 单位阶跃响应曲线由(8)式单位阶跃响应时域表达式可知系统闭环稳定时，单位阶跃响应的指数项和阻尼正弦余弦项均趋近于零，稳态输出为常数项1，这与用MATLAB绘制的响应曲线相符。

3.1.2 单位阶跃响应动态性能动态性能指标是指稳定的系统在单位阶跃函数作用下，动态过程随时间t的变化状况的指标，体现系统动态过程特征。

用解析法求解高阶系统的动态性能指标很困难，这里用MATLAB编程求解。

调用单位阶跃响应函数step()，获得系统的单位阶跃响应，当采用[y,t]=step(sys)的调用格式时，将返回值y及相应的时间t，通过对y和t进行计算，可以得到高阶系统各项动态性能指标。

利用MATLAB编程求取系统动态性能指标程序如下：sys=tf([12 36],[1 8 25 42 36])%系统建模%计算峰值时间tp和对应最大超调量MpC=dcgain(sys) %取系统终值[y,t]=step(sys); %求取单位阶跃响应，返回变量输出y和时间t[Y,k]=max(y); %求输出响应的最大值Y（即峰值）和位置ktp=t(k) %取峰值时间Mp=(Y-C)/C %计算最大超调量%计算上升时间trn=1;while y(n)<C %循环求取第一次到达终值时的时间n=n+1;endtr=t(n)%计算调节时间(误差带取2%)i=length(t); %求取仿真时间t序列的长度while(y(i)>0.98*C)&(y(i)<1.02*C)i=i-1;endts=t(i)输出结果为： C =1 tp =2.2557 Mp = 0.1216 tr =1.6787 ts =3.2000即上升时间为 1.6787s ，峰值时间为 2.2557s ，最大超调量为12.16%，并且系统在3.2000s 后进入稳态。

3.1.3 单位阶跃响应稳态性能稳态性能是系统在典型输入作用下，当时间t 趋于无穷大时，系统输出量的最终复现输入量的程度。

稳态性能分析主要是指稳态误差的计算。

稳态误差是系统控制精度或抗干扰能力的一种度量。

现采用静态误差系数法计算单位阶跃响应稳态误差。

将K=12，a=3，b=3代入（2）式，得待分析系统的开环传递函数为:)105(12)(2++=s s s s G p 其静态位置误差系数为：∞=++==→→)105(12lim)(lim 2s s s s G K s p s p 所以单位阶跃输入作用下系统的稳态误差为：1()01ss pe K ∞==+3.2 单位斜坡响应3.2.1 单位斜坡响应单位斜坡输入21(),()r t t R s s==，此时 )42)(3(12)()()(22+++=Φ⋅=s s s s s s R s C 展开为部分分式：428571.06429.031905.08333.01)(22++++++-=s s s s s s s C对部分分式进行拉普拉斯反变换，并设初始条件全部为零，得系统的单位斜坡响应：)7321.1sin(1237.0)7321.1cos(6429.01905.08333.0)(3t e t e e t t c t t t ---++-= (9)利用 MATLAB 软件绘制该系统在单位斜坡响应曲线。