二阶系统时域分析

二阶系统的时域分析二阶系统的数学模型二阶系统指的是系统的动态特性可以由一个二阶微分方程描述的系统。

在控制工程中，二阶系统的时域分析主要包括对系统阶跃响应、脉冲响应、频率响应等进行分析。

下面将详细介绍二阶系统的数学模型以及各种时域分析方法。

二阶系统可以由一个二阶微分方程进行描述。

一般而言，二阶系统的数学模型可以写成如下形式：\[a_2\frac{{d^2y(t)}}{{dt^2}} + a_1\frac{{dy(t)}}{{dt}} +a_0y(t) = b_2\frac{{d^2u(t)}}{{dt^2}} + b_1\frac{{du(t)}}{{dt}}+ b_0u(t)\]其中，y(t)为系统的输出，u(t)为系统的输入，a_0、a_1、a_2以及b_0、b_1、b_2分别为系统的系数。

这个方程也可以写成常用的形式：\[\frac{{d^2y(t)}}{{dt^2}} + 2ζω_n\frac{{dy(t)}}{{dt}} +ω_n^2y(t) = K_p\frac{{d^2u(t)}}{{dt^2}} +T_i\frac{{du(t)}}{{dt}} + K_cu(t)\]其中，ζ为阻尼比，ω_n为自然频率，K_p为比例增益，T_i为积分时间常数，K_c为控制器增益。

2.二阶系统的阶跃响应阶跃响应是指系统在接受一个单位阶跃信号作为输入时的响应。

通过对二阶系统的数学模型应用拉普拉斯变换，可以得到系统的传递函数。

对于一个传递函数为G(s)的系统，其阶跃响应可以通过下面的公式得到：\[y(t) = A(1 - e^{-ζω_nt}\cos(ω_d t + ϕ))\]其中，A为阶跃响应的幅度，ω_d为阻尼振荡角频率，ϕ为相位角。

3.二阶系统的脉冲响应脉冲响应是指系统在接受一个单位脉冲信号作为输入时的响应。

与阶跃响应类似，通过对二阶系统的数学模型进行拉普拉斯变换，可以得到系统的传递函数。

对于一个传递函数为G(s)的系统，其脉冲响应可以通过下面的公式得到：\[y(t) = \frac{{A(1 - e^{-ζω_nt}\cos(ω_d t + ϕ))}}{{\sqrt{1-ζ^2}}}\]其中，A为单位脉冲信号的幅度。

实验三 二阶系统的时域分析一、实验目的１、通过考察系统的过渡过程指标，研究二阶系统的特征参数—阻尼比和自然频率对系统特性的影响，以及系统特征根的位置与过渡过程的关系。

２、学习自己设计实验，安排适当的实验参数，达到以上实验目标。

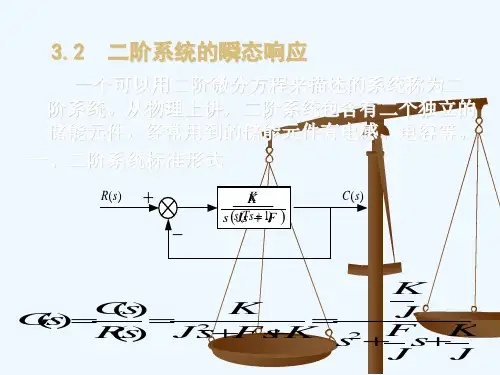
二、实验内容根据传递函数2222)(nn ns s s G ωζωω++=的单位阶跃响应，求取过渡过程的质量指标。

按表1的形式整理实验数据，分析实验结果，完成实验报告。

此时，系统的特征根为j j s n n βαζωζω±=-±-=22,11。

1、令ζ＝，取三种不同的n ω，观察根在根平面上的位置，求其过渡过程和它的质量指标，进行比较。

说明当ζ相同时，过渡过程的哪些指标是相同的00.20.40.60.811.21.4ωn 改变，ζ=0.5不变Tim e (sec)A m p l i t u d e2、固定n ω，取ζ＝０、、 、、1，观察根在根平面上的位置，求其过渡过程和它的质量指标。

总结当ζ不同时，质量指标有哪些变化00.20.40.60.811.21.41.61.82Time (sec)A m p l i t u d e通过上面两图形与表格总结可以得出：n ω影响二阶系统过渡过程中的峰值时间，过渡时间（在ζ不变的情况下，峰值时间随n ω增大而减小，过渡时间随n ω的增大而减小）ζ影响几乎全部过渡过程指标，其中超调量，衰减比仅与ζ有关（超调量随着ζ的增大而减小，衰减比随着ζ的增大而增大；在n ω不变的情况下，峰值时间随ζ增大而增大，过渡时间随ζ的增大而减小。

）n ω，ζ对系统的稳态误差均没有影响，且均为0.3、选三组实部（α）为负值且相等的复根，观察根在根平面上的位置，求其过渡过程和它的质量指标，进行比较，说明不同虚部（β）对过渡过程和质量指标有哪些影响。

00.20.40.60.811.21.41.6α=2,β分别取2，6，10Time (sec)A m p l i t u d e通过上图和表格中的数据可以得不同虚部对系统过渡过程的影响：在实部不变的情况下随虚部绝对值的增加，超调量增加，衰减比减少，峰值时间减小，调节时间不变，上升时间减小，稳态误差始终为0.。

二阶系统的时域分析二阶系统的数学模型二阶系统是指由两个一阶系统级联或并联组成的动态系统。

它的数学模型可以表示为如下形式：$$s^2Y(s) + 2ξω_nsY(s) + ω_n^2Y(s) = X(s)$$其中，$s$是复频域变量，$Y(s)$和$X(s)$分别是系统的输出和输入拉普拉斯变换形式；$ξ$是阻尼比，$ω_n$是自然频率。

为了进行时域分析，我们需要将模型转换为时域表示。

我们可以通过拉普拉斯逆变换对模型进行求解。

首先，我们可以将拉普拉斯变换模型转换为分母为二次方程的形式：$$s^2 + 2ξω_ns + ω_n^2 = 0$$这是一个特征方程，也称为二阶系统的特征方程。

根据特征方程的解，我们可以获得系统的阻尼比和自然频率。

特别地，当阻尼比$ξ$小于1时，系统被称为欠阻尼；当阻尼比$ξ$等于1时，系统被称为临界阻尼；当阻尼比$ξ$大于1时，系统被称为过阻尼。

根据不同的阻尼比，我们可以对系统的时域响应进行分类：1.欠阻尼情况下，系统的时域响应会产生振荡。

振荡的频率为阻尼比与自然频率的乘积。

2.临界阻尼情况下，系统的时域响应会趋于稳定，但不会产生振荡。

3.过阻尼情况下，系统的时域响应会趋于稳定，没有振荡，并且速度较快。

在实际应用中，我们经常需要对二阶系统的时域响应进行分析和设计。

常见的时域响应指标包括步响应、阶跃响应和频率响应。

这些响应可以通过对特征方程进行求解来获得。

对于步响应，我们可以通过求解特征方程的根来获得系统的过渡时间、最大超调量和静态误差等信息。

通过调整控制器和系统参数，我们可以改变这些指标，以满足系统设计的要求。

对于阶跃响应，我们可以通过求解特征方程的根来获得系统的上升时间、峰值时间和调节时间等信息。

同样，通过调整控制器和系统参数，我们可以改变这些指标，以满足系统设计的要求。

对于频率响应，我们可以通过将特征方程转换为复频域变量来获得系统的频率响应函数。

频率响应函数可以帮助我们分析系统在不同频率下的增益和相位变化。

二阶系统的时域分析二阶系统是指系统的传递函数为二次多项式的系统。

在控制工程中，常常会遇到这样一类系统，例如惯性系统、机械系统等。

对于这些二阶系统，我们不仅可以通过频域分析来研究其特性，还可以通过时域分析来了解其动态特性。

在进行二阶系统的时域分析时，可分为稳态分析和暂态分析两个方面。

稳态分析主要关注系统的稳定性、稳定偏差以及稳态响应等问题。

稳定性是指系统在输入信号恒定时是否能够收敛到一些有限的值。

对于二阶系统来说，稳定性分为两种情况：一是欠阻尼情况下的稳定性，二是过阻尼情况下的稳定性。

在欠阻尼情况下，系统的特征根是共轭复根，且位于单位圆内。

此时，系统的稳定性与初始条件无关，即系统总是能够收敛到稳态。

而且系统的稳态响应的振幅会发生一定的振荡，并随着时间逐渐减小。

该振荡的周期与系统的倍率有关，即与特征根的幅值有关。

在过阻尼情况下，系统的特征根是两个实根，分别对应着减震时间常数的倒数，且位于负实轴上。

此时，系统的稳态响应不会有振荡的情况发生，而是指数衰减的趋势。

稳态响应的衰减速率与特征根的位置有关，即与特征根的实部大小有关。

对于稳态偏差问题，我们可以通过查表法或直接计算法来求解。

稳态偏差是指系统在输入信号恒定时的输出值与预期值之间的差距。

通过分析系统的传递函数，我们可以得到系统的静态增益，从而计算出稳态偏差。

在暂态分析中，我们主要关注系统的动态响应，即系统在输入信号改变时的响应情况。

对于二阶系统来说，主要有两种典型的暂态响应情况：一是阻尼振荡响应，二是临界阻尼响应。

阻尼振荡响应是指系统在欠阻尼情况下的响应。

在这种情况下，系统会产生一定幅值的振荡，振荡的周期与系统的阻尼比有关，即与特征根的实部大小有关。

临界阻尼响应是指系统在特征根位于负实轴上时的响应。

此时，系统的响应既没有振荡也没有超调现象，而是以较快的速度趋近于稳态响应。

在实际工程中，我们可以通过使用MATLAB等软件工具来进行二阶系统的时域分析。

通过绘制系统的单位阶跃响应曲线、脉冲响应曲线以及动态响应曲线，并结合特征根分析法，可以对系统的动态特性进行深入研究。

二阶系统的时域分析二阶系统是指具有两个自由度的线性时不变系统，可以用二阶常微分方程来描述。

在时域分析中，我们可以通过研究系统的时间响应来了解系统的动态性能。

$$\frac{{d^2y(t)}}{{dt^2}}+2\zeta\omega_n\frac{{dy(t)}}{{dt}}+\omega_n^2y(t) = f(t)$$其中，$y(t)$是系统的输出，$f(t)$是系统的输入，$\zeta$是系统的阻尼比，$\omega_n$是系统的自然频率。

为了进行时域分析，我们通常关注以下几个方面的内容：零状态响应、零输入响应、阶跃响应和冲激响应。

首先，零状态响应是指当系统在其中一初始状态下，没有外部输入时的响应。

在二阶系统中，零状态响应可以表示为：$$\frac{{d^2y(t)}}{{dt^2}}+2\zeta\omega_n\frac{{dy(t)}}{{dt}}+\omega_n^2y(t) = 0$$通过求解这个方程可以得到系统的零状态响应。

其次，零输入响应是指当系统没有外部输入时的响应，也就是当$f(t)=0$时的响应。

在二阶系统中，可以通过设定初始条件（对应于零状态）来求解零输入响应。

接下来，阶跃响应是指当系统输入为单位阶跃信号时的响应。

单位阶跃信号可以用$\delta(t)$来表示，其傅里叶变换为$U(j\omega)=\frac{1}{{j\omega}}+\pi\delta(\omega)$。

阶跃响应可以通过将单位阶跃信号的傅里叶变换代入系统的传递函数来求解。

最后，冲激响应是指当系统输入为单位冲激信号时的响应。

单位冲激信号可以用$\delta(t)$表示，其傅里叶变换为$U(j\omega)=1$。

冲激响应可以通过将单位冲激信号的傅里叶变换代入系统的传递函数来求解。

在进行二阶系统的时域分析时，我们还可以研究系统的阻尼比对系统响应的影响。

当阻尼比$\zeta=1$时，系统处于临界阻尼状态，此时系统响应最快且无振荡；当阻尼比$\zeta<1$时，系统过阻尼，响应较慢且无振荡；当阻尼比$\zeta>1$时，系统欠阻尼，响应较快且有振荡。