3-3二阶系统的时域分析

实验报告册学年学期课程名称：学院：专业：班级：学号：学生姓名：河南工学院实验报告实验项目二阶系统的时域分析实验日期班级姓名指导教师综合成绩一、预习内容1）实验目的和要求1.验证二阶系统的特征参数阻尼比ζ和无阻尼自然频率ωn对系统动态性能的影响2.定量分析ζ和ωn与最大超调量σ%和调节时间ts之间的关系。

3.学习用MATLAB仿真软件对实验内容中的电路进行仿真。

2）实验内容和原理3）实验所用主要仪器设备（或实验环境）计算机MATLAB7.0二、实验数据（现象）记录及结果处理三、实验结果分析与讨论（对实验结果进行具体分析，并对实验中出现的问题或错误原因分析，以及改进的办法与建议）1. 阻尼比越小，超调量越大，上升时间越短。

2. Ωn 越大，响应速度越快。

3. 在过阻尼的状态下，由图像可知其阶跃响应实际上是两个一阶系统响应的叠加。

随着ζ的不断增加，一一个极点不断靠近原点，另一个不断远离。

4. 当两个极点相距较近时，对阶跃响应产生的影响都不能忽略。

ζ的增大使不断远离原点的极点所产生的影响越来越小，最后趋近于零。

教师评阅意见（1）实验预习 (30分)成绩：□预习认真、熟练掌握方法与步骤(30～28) □有预习、基本掌握方法与步骤(27～22)□有预习、但未能掌握方法与步骤(21～18) □没有预习，不能完成实验(17～0)（2）操作过程 (40分)成绩：□遵规守纪、操作熟练、团结协作 (40～37) □遵规守纪、操作正确、有协作 (36～29) □遵规守纪、操作基本正确、无协作 (28～24) □不能遵规守纪、操作不正确、无协作(17～0)（3）结果分析 (30分)成绩：□结果详实、结论清晰、讨论合理(30～28) □结果正确、讨论适当(27～22)□结果正确、没有分析讨论(21～18) □结果不正确、没有分析讨论(17～0)其它意见：教师签名：年月日。

第三章二阶系统响应与时域性能指标解析在控制系统中，二阶系统是指具有二阶传递函数的系统。

二阶系统在工程实践中非常常见，例如机械系统、电子电路系统等。

了解二阶系统的响应和时域性能指标对于设计和分析控制系统非常重要。

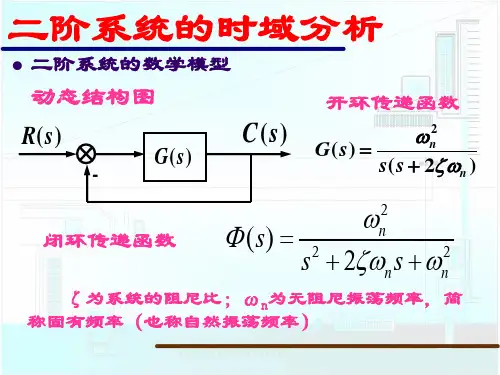
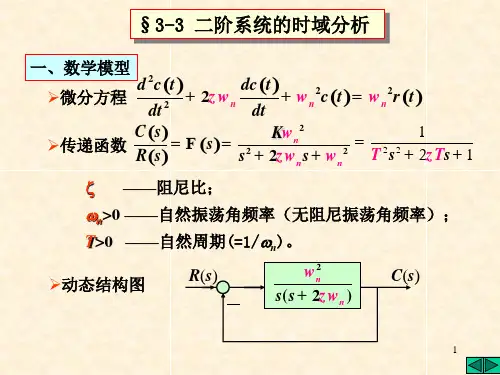
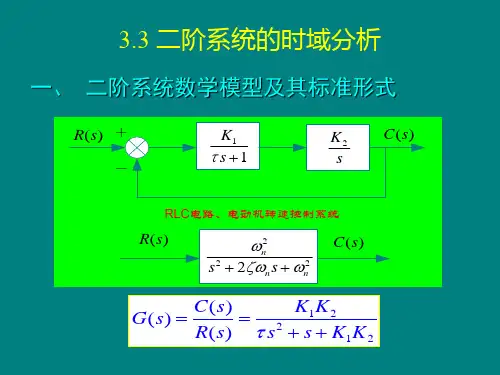
二阶系统的传递函数可以表示为$G(s)=\frac{\omega_n^2}{{s^2+2\zeta\omega_ns+\omega_n^2}}$，其中$\omega_n$是系统的自然频率，$\zeta$是系统的阻尼比。

首先我们从系统的阶跃响应来分析二阶系统的时域性能指标。

阶跃响应是系统对阶跃信号输入的响应。

通过对传递函数分母进行因式分解，我们可以将传递函数改写为$G(s)=\frac{\omega_n^2}{(s+s_1)(s+s_2)}$，其中$s_1 = (-\zeta+\sqrt{\zeta^2-1})\omega_n$，$s_2 = (-\zeta-\sqrt{\zeta^2-1})\omega_n$。

1. 峰值超调量（Percent Overshoot）：峰值超调量是指系统过渡过程中输出信号的最大超调量与步变幅度之比。

通过阶跃响应曲线可以直观地看出系统的峰值超调量。

2. 调节时间（Settling Time）：调节时间是指系统从初始状态到稳定状态所需的时间。

在阶跃响应曲线中，调节时间可以定义为系统的输出信号在峰值超调之后首次进入指定误差范围内所需的时间。

一般来说，稳定误差范围可以选择输出信号与目标信号之差小于目标值的一些百分比，例如5%。

3. 峰值时间（Peak Time）：峰值时间是指系统输出信号首次达到峰值超调量的时间。

在阶跃响应曲线中，峰值时间可以直接读取。

4. 上升时间（Rise Time）：上升时间是指系统输出信号从初始状态到达峰值的时间。

在阶跃响应曲线中，上升时间可以定义为系统输出信号从0.1倍峰值超调量到0.9倍峰值超调量之间所需的时间。

二阶系统的阶跃响应曲线具有不同的形态，取决于系统的阻尼比$\zeta$。

二阶系统的时域分析二阶系统是指系统的传递函数为二次多项式的系统。

在控制工程中，常常会遇到这样一类系统，例如惯性系统、机械系统等。

对于这些二阶系统，我们不仅可以通过频域分析来研究其特性，还可以通过时域分析来了解其动态特性。

在进行二阶系统的时域分析时，可分为稳态分析和暂态分析两个方面。

稳态分析主要关注系统的稳定性、稳定偏差以及稳态响应等问题。

稳定性是指系统在输入信号恒定时是否能够收敛到一些有限的值。

对于二阶系统来说，稳定性分为两种情况：一是欠阻尼情况下的稳定性，二是过阻尼情况下的稳定性。

在欠阻尼情况下，系统的特征根是共轭复根，且位于单位圆内。

此时，系统的稳定性与初始条件无关，即系统总是能够收敛到稳态。

而且系统的稳态响应的振幅会发生一定的振荡，并随着时间逐渐减小。

该振荡的周期与系统的倍率有关，即与特征根的幅值有关。

在过阻尼情况下，系统的特征根是两个实根，分别对应着减震时间常数的倒数，且位于负实轴上。

此时，系统的稳态响应不会有振荡的情况发生，而是指数衰减的趋势。

稳态响应的衰减速率与特征根的位置有关，即与特征根的实部大小有关。

对于稳态偏差问题，我们可以通过查表法或直接计算法来求解。

稳态偏差是指系统在输入信号恒定时的输出值与预期值之间的差距。

通过分析系统的传递函数，我们可以得到系统的静态增益，从而计算出稳态偏差。

在暂态分析中，我们主要关注系统的动态响应，即系统在输入信号改变时的响应情况。

对于二阶系统来说，主要有两种典型的暂态响应情况：一是阻尼振荡响应，二是临界阻尼响应。

阻尼振荡响应是指系统在欠阻尼情况下的响应。

在这种情况下，系统会产生一定幅值的振荡，振荡的周期与系统的阻尼比有关，即与特征根的实部大小有关。

临界阻尼响应是指系统在特征根位于负实轴上时的响应。

此时，系统的响应既没有振荡也没有超调现象，而是以较快的速度趋近于稳态响应。

在实际工程中，我们可以通过使用MATLAB等软件工具来进行二阶系统的时域分析。

通过绘制系统的单位阶跃响应曲线、脉冲响应曲线以及动态响应曲线，并结合特征根分析法，可以对系统的动态特性进行深入研究。

二阶系统的时域分析二阶系统是指具有两个自由度的线性时不变系统，可以用二阶常微分方程来描述。

在时域分析中，我们可以通过研究系统的时间响应来了解系统的动态性能。

$$\frac{{d^2y(t)}}{{dt^2}}+2\zeta\omega_n\frac{{dy(t)}}{{dt}}+\omega_n^2y(t) = f(t)$$其中，$y(t)$是系统的输出，$f(t)$是系统的输入，$\zeta$是系统的阻尼比，$\omega_n$是系统的自然频率。

为了进行时域分析，我们通常关注以下几个方面的内容：零状态响应、零输入响应、阶跃响应和冲激响应。

首先，零状态响应是指当系统在其中一初始状态下，没有外部输入时的响应。

在二阶系统中，零状态响应可以表示为：$$\frac{{d^2y(t)}}{{dt^2}}+2\zeta\omega_n\frac{{dy(t)}}{{dt}}+\omega_n^2y(t) = 0$$通过求解这个方程可以得到系统的零状态响应。

其次，零输入响应是指当系统没有外部输入时的响应，也就是当$f(t)=0$时的响应。

在二阶系统中，可以通过设定初始条件（对应于零状态）来求解零输入响应。

接下来，阶跃响应是指当系统输入为单位阶跃信号时的响应。

单位阶跃信号可以用$\delta(t)$来表示，其傅里叶变换为$U(j\omega)=\frac{1}{{j\omega}}+\pi\delta(\omega)$。

阶跃响应可以通过将单位阶跃信号的傅里叶变换代入系统的传递函数来求解。

最后，冲激响应是指当系统输入为单位冲激信号时的响应。

单位冲激信号可以用$\delta(t)$表示，其傅里叶变换为$U(j\omega)=1$。

冲激响应可以通过将单位冲激信号的傅里叶变换代入系统的传递函数来求解。

在进行二阶系统的时域分析时，我们还可以研究系统的阻尼比对系统响应的影响。

当阻尼比$\zeta=1$时，系统处于临界阻尼状态，此时系统响应最快且无振荡；当阻尼比$\zeta<1$时，系统过阻尼，响应较慢且无振荡；当阻尼比$\zeta>1$时，系统欠阻尼，响应较快且有振荡。

实验三——二阶系统的时域响应及性能分析实验三主要研究了二阶系统的时域响应及其性能分析，通过实验得到不同二阶系统的单位阶跃响应和单位脉冲响应，并对其进行分析和性能评估。

首先，实验中使用的二阶系统是由两个一阶系统串联而成，可以通过两个一阶系统的参数来确定二阶系统的性能。

实验中设置了不同的参数组合来得到不同的二阶系统，并测量了这些系统的单位阶跃响应和单位脉冲响应。

实验中，单位阶跃响应是通过给系统输入一个单位阶跃信号，观察系统的输出得到的。

单位脉冲响应是通过给系统输入一个单位脉冲信号，观察系统的输出得到的。

通过测量这两个响应，可以了解二阶系统在时域的性能。

对于单位阶跃响应，实验中测量了系统的超调量、调整时间和稳态误差。

超调量是指单位阶跃响应中最高峰值与稳态值之差与稳态值的比值，可用来评估系统的动态性能。

调整时间是指从单位阶跃信号开始输入到响应达到其稳态值所需要的时间，反映了系统调整过程的快慢。

稳态误差是指系统最终的输出值与期望值之差，用来评估系统的稳态准确性。

对于单位脉冲响应，实验中测量了系统的峰值和时间常数，用来评估系统的动态特性。

峰值是指单位脉冲响应中的最高值，与系统的阻尼比有关。

时间常数是指单位脉冲响应中曲线从0到达其最大值所需要的时间，与系统的阻尼比和自然频率有关。

通过实验数据的测量和分析，可以得到不同参数组合下的二阶系统的性能指标，进而对系统进行评估。

如果超调量小、调整时间短、稳态误差小，表示系统的动态特性优秀，能够快速、准确地响应输入信号；如果峰值小、时间常数短，表示系统的动态特性好，有较快的响应速度和较小的振荡现象。

综上所述，实验三通过对二阶系统的时域响应进行测量和分析，并对性能指标进行评估，可以得到不同二阶系统的动态特性和稳态准确性信息。

这些信息对于系统设计和参数调整具有重要的参考价值。

通过实验的学习，可以更深入地理解掌握二阶系统的性能分析方法，为系统控制和优化提供理论和实践基础。

实验三 二阶系统的动态响应分析实验指导书一、实验目的1．学习和掌握二阶系统动态性能指标的测试方法。

2．研究典型二阶系统参数对系统动态性能和稳定性的影响。

二、实验内容1．根据二阶系统的工作原理框图(动态结构方框图)建立matlab/simulink 仿真模型； 2．观测二阶系统的阶跃响应，测出其超调量和调节时间，并研究其参数变化对动态性能和稳定性的影响。

三、实验步骤1．建立由一个积分环节和一个惯性环节组成的二阶闭环系统的模型； 2．观测该二阶系统模拟电路的阶跃特性，并测出其超调量和调节时间； 3．改变该二阶系统模拟电路的参数，观测参数对系统动态性能的影响。

4．分析实验结果，完成实验报告。

四、附录1．典型二阶系统典型二阶系统的动态结构方框图如图3.1所示：其开环传递函数为1()(1)KG S S T S =+，10K K T =图3.1图3.2其闭环传递函数为11112111111121222111111()1(1)11212o o o o o o nn n o n n K T s T s K K s K T s T s K T T s T s K T s T s K T T w K s w s w s s T T T w w T ϕξξ+===++++++==++++===自然角频率阻尼比，其中n ω=ξ=取二阶系统的模拟电路如图3.2所示：（1） 比例环节1200()2100G S == （2） 比例积分环节121111()200o o C S G S R R C S s===（3）比例惯性环节 22312111()(1)100(1)x x x x x x R C s R R R C s G s R R C s R R s +===++（4）比例环节4()1R GS R==前向通道传递函数：123442()()()()()12200100(1)11010000(1)x x xx xG s G s G s G s G s R s R s R ss R s s R ==+==++系统的传递函数：4242424110()()11()1011010x xxss R G S s G S ss R s s R φ--+==+++=++210n w -==211502210n x x w R R ξ-===当ξ=1 ，系统为临界阻尼； 当ξ>1,系统为过阻尼； 当0<ξ<1,系统为欠阻尼； 当ξ=0，系统为无阻尼改变元件参数Rx大小，研究不同参数特征下的时域响应。