《余角和补角》公开课
- 格式:ppt
- 大小:1.88 MB
- 文档页数:37





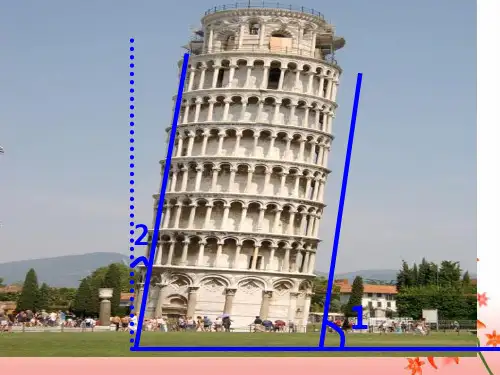


补角和余角教学目标1、使学生掌握两个角互为余角和互为补角的概念,2、使学生理解互余与互补的角的性质3、培养学生分析问题和解决问题的能力,以及运算能力。
教学重点重点:余角和补角的概念及其性质教学难点难点:⑴互余、互补角的正确判断⑵用代数方法计算角的度数设计亮点在引出概念时充分发挥了学生的自主性一学生为主体的体现教学过程备注一、新课引入右边合作学习让学生说出自己的方法:可以测量,也可以剪下来拼等等,学生的方法只要合理就应鼓励。
教师用多媒体演示∠1+∠2与Rt∠AOB重合,再移动一角,问∠1+∠2与Rt∠AOB相等吗?同样∠α+∠β与∠AOB重合,再移动一角,问∠α+∠β与∠AOB相等吗?通过上面的演示,我们看到有时两个角的和是90°,有时两个角的和是180°。
二、新课教学1.余角和补角的定义:①互为余角定义:如果两个锐角的和是一个直角,那么这两个角互为余角.简称互余.②互为补角定义:如果两个角的和是一个平角,那么这两个角互为补角.简称互补.注意:要特别向学生指出:互余与互补角是研究两个角的关系,单独一个角不能说是余角或补角,就像称呼两兄弟一样,而且不会随位置的改变。
2. 余角和补角的性质:问:①从中发现了什么?(进行小组讨论)师生共同总结出:同角的余角相等.同理可推出:同角的补角相等②如果两个角相等,那么它们的余角和补角有什么关系?由此得到补角和余角的性质:同角或等角的余角相等.同角或等角的补角相等.3.例题设计:例1:P169 例1学生回答时注意强调同角的余角。
例2:已知一个角的补角是这个角的余角的4倍,求这个角的度数。
自主探索引出概念理解概念通过计算引出性质分析:本题用直接列算式的方法比较困难,因此考虑用设未知数列方程的方法解。
本题有两种设法:①直接设这个角为x°,则它的余角为(90-x)°,它的补角为(180-x)°.得方程 180 – x = 4( 90 – x ) ,②也可以设这个角的余角为x°,它的补角为(90+x)°,列出方程为:90 + x = 4x小结:(1)这例题是利用代数方法解决几何问题,关键是正确设出未知数,正确列出方程,求出未知数的值.在设未知数的过程中,可以有不只一种设法.(2)注意题目中的隐含条件,若一个角为x时,它的余角为90-x,它的补角为180-x.(3)在设未知数的过程中,要注意写单位,但在列方程时,可以不带单位.三、课堂小结1、小结互余和互补的定义和性质。
