当前位置：文档之家 › 第八章 边界层方程的数值解

第八章 边界层方程的数值解

  • 格式：pdf
  • 大小：219.62 KB
  • 文档页数：19

下载文档原格式

  / 19

合集下载

边界层动量积分方程

边界层动量积分方程

边界层动量积分方程
边界层动量积分方程（Boundary Layer Momentum Integral Equation，BLMIE）是一种分析和解决边界层问题的有效方法。

它是将神经网络
中抽象的边界现象抽象化为数学形式，从而利用数值计算方法进行解析。

一、 BLMIE原理
边界层动量积分方程的基本原理是利用数值计算方法对边界层的运动
模式进行分析。

它指定了边界层中各个物理量在每个时刻的变化情况，也就是物理量的变化率和变化后的位置。

它使得实验者可以更为清晰
和直观地了解边界层的变化过程，从而更好地控制和优化边界层。

而且，它可以消除实验者对边界层运动模式分析的误差，提高结果的可
靠性和准确性。

二、 BLMIE求解方法
1、牛顿法：牛顿法可以独立求解边界层动量积分方程，其基本方法是
通过迭代法来求解，具体步骤为：根据边界层动量积分方程得到离散
系数方程，通过不断改变系数方程的解；在每次迭代中，根据当前变
量得出系数方程的新解；之后，根据其新解求得该变量的新值，以及
新的系数方程，重复如此迭代，直至系数方程达到解析解。

2、二分法：二分法是一种可以求解边界层动量积分方程的有效算法，
其原理是将求解的范围缩小成一定的步骤，使其距离最佳解越来越近，直到求得最佳解。

首先，根据边界层动量积分方程预先设定求解范围；然后，将该范围缩小成二分，求得两个最近的解；之后，针对这两个解，继续将其范围缩小成二分；重复该步骤，直至求得最佳解。

数值天气预报第八章_边界层模式及其参数化

数值天气预报第八章_边界层模式及其参数化

∂w ∂w ∂w ∂w ∂p′ +u +v +w = −α 0 ∂t ∂x ∂y ∂z ∂z
α′ 1 ⎡ ∂ ρ w′′u ′′ ∂ ρ w′′v′′ ∂ ρ w′′w′′ ⎤ + g− ⎢ + + ⎥ α0 ∂ ∂ ∂ x y z ρ⎣ ⎦
这就是中尺度数值模式中常采用的垂直运动方程的一种形式。
兰州大学大气科学学院 11
兰州大学大气科学学院 13
为了具体的给出参数化的公式，先把平均运动方程组中含有次网格尺度 通量项的方程改写如下：
du 1 ∂p 1 =− + f v+ dt ρ ∂x ρ
⎡ ∂τ xx ∂τ yx ∂τ xx ⎤ + + ⎢ ⎥ x ∂ ∂ y ∂ z ⎣ ⎦ 1 ∂p 1 ⎡ ∂τ xy ∂τ yy ∂τ zy ⎤ dv =− − fu+ ⎢ + + ⎥ ρ ∂y dt ∂ x ∂ y ∂ z ρ⎣ ⎦ 1 ∂p 1 ⎡ ∂τ xz ∂τ yz ∂τ zz ⎤ dw =− −g+ ⎢ + + ⎥ dt ∂y ∂z ⎦ ρ ∂z ρ ⎣ ∂x 1 ⎡ ∂H x ∂H y ∂H z ⎤ dθ θ = + + Q+ ⎢ ⎥ ∂y ∂z ⎦ dt c p T ρ ⎣ ∂x
9.1 平均运动方程及平均次网格尺度项
由于以下原因：
• 大气运动的湍流性，空气微团作极不规则的运动，虽满足瞬时运动方 程组，但其毫无意义 • 观测值是一定空间范围和一定时间间隔内的平均值
故应当研究物理量的平均值的变化规律。
以Φ 代表任一气象要素，在( x , y , z , t )坐标系中，其平均值 Φ 定义为

流体力学边界层理论

流体力学边界层理论

于是
τ 0 = 0.332
μρU 2 x
上式可看出平板层流边界层局部摩擦切应力与ｘ坐标的平方根成反比的规
律随着ｘ的增加而减小。
现计算整个平板上总摩擦阻力。设板长为Ｌ，板宽为ｂ，则平板单面总摩擦
阻力是：
∫ ∫ Rf =
Lτ
0
0bdx
=b
L
0.332
0
μρU 3 dx = 0.664 x
μρ LU 3
总摩擦阻力系数 C f 由下式确定：
2
则：
vx
(
x,
y)
=
U
⋅
1 2
ϕ ′(η )
设 U=25 km/h，ν=0.15cm2/s, x=3m,ｙ=5mm，
求：Vx＝？
解：U=25×1000/3600=6.95m/s, ν=0.0015m2/s,
x=3m, y=0.005m,
代入η中得：
η = 1 × 5×10−3 × 2
6.95 0.15 ×10−4
（11-14）式应采取如下形式：
ϕ(x, y) = xϕ( y ) x
（11-16）
返回为有量纲解时，不出现Ｌ，即 ：
ϕ = ν U x ϕ (η )
η=1y U 2 νx
（11-18）
通过以上分析，来求解下列形式的ψ。
⎡y⎤
ϕ=
νUL
x
⎢ ⎢
L⎢
⎢ ⎣
νL ⎥
U ⎥=
x⎥
L
⎥ ⎦
⎡ νUxϕ ⎢ y
Ｕ（起参数作用），ν和Ｕ不同时，同一空间点上ψ的值不同。
现设法将方程和边界条件中各个物理量无量纲化，不再出现ν和Ｕ。
选特征量：
Ｌ：ｘ的比例尺

第八章 边界层方程的数值解

第八章 边界层方程的数值解
i−2, j i−1, j i,j
对节点 (i, j) 处的速度 ui, j 和 vi, j 分别用泰勒级数展
开，可得：
ui−1, j
=
ui, j
−
Δx(
∂u ∂x
)i,
j
+
(Δx)2 2!
(
∂2u ∂x 2
)i,
j
− O(Δx)3
i−2, j−1 i−1, j−1 i, j−1
x
图 8－1 层流边界层的有限差分网点
定义网格点令i?1i分别表示在一给定值时的上游点和下游点节点i?1j?1i?1j1i?1j12ij12i?1jijij?12控制体i?1j?12i?1j?1ij?1此线上值已知沿此线值待定i?1j1ij?1ij1分别表示与节点ij相邻的网点如图84两条虚线表示j图84内部区域网格的划分11和j?它们与i?1和22i线构成了一个控制
采用轴对称坐标，仍避免不了矩形网格的缺点，为此需采用轴对称的流线坐标系。
引进流函数ψ 作为横流向的自变量，顺流向的坐标用 ζ ，ζ ≡ x 。这样，以 ( x , y )
表示的轴对称坐标系就变成了以 (ψ , ζ ) 表示的轴对称流线坐标系了。这种坐标变换称为
冯·米塞兹变换。
由于引入了流函数ψ ，则 ρur = ∂ψ ， ρvr = − ∂ψ 。显然，流函数能自动满足连续
Bj
=
3 2
(2ui−1,
j
− ui−2, j ) + 2ν
Δx (Δy)2
Cj
=
−
Δx 2Δy
(2vi−1, j
− vi−2, j ) −ν
Δx (Δy)2
Fj
=
1 2
(2ui−1, j

流体力学教案第8章边界层理论

流体力学教案第8章边界层理论

第八章 边界层理论§8-1 边界层的基本概念实际流体和理想流体的本质区别就是前者具有粘性。

对层流而言，单位面积摩擦力的大小yud d μτ=，可以看出，对于确定的流体的等温流场，摩擦力的大小与速度梯度有关，其比例函数即动力粘度。

速度梯度yud d 大，粘性力也大，此时的流场称为粘性流场。

若速度梯度yud d 很小，则粘性力可以忽略，称为非粘性流场。

对于非粘性流场，则可按理想流体来处理。

则N-S 方程可由欧拉方程代替，从而使问题大为简化。

Vlv l lV v A y u V l tVl t u mρρμρρ======2223d d d d 粘性力惯性力当空气、蒸汽，水等小粘度的流体与其它物体作高速相对运动时，一般雷诺数很大。

由vVl==粘性力惯性力Re ，则在这些流动中，惯性力>>粘性力，所以可略去粘性力。

但在紧靠物体壁面存在一流体薄层，粘性力却与惯性力为同一数量级。

所以，在这一薄层中，两者均不能略去。

这一薄层就叫边界层，或叫速度边界层，由普朗特在1904年发现。

a ．流体流过固体壁面，紧贴壁面处速度从零迅速增至主流速度，这一流体薄层，就叫边界层或速度边界层。

b ．整个流场分为两部分 层外，0=∂∂yu，粘性忽略，无旋流动。

层内，粘性流，主要速度降在此，有旋流动。

c ．由边界层外边界上∞=V u %99，来定义δ，δ为边界层厚度。

d ．按流动状态，边界层又分为层流边界层和紊流边界层。

由于在边界层内，流体在物体表面法线方向(即yu∂∂)速度梯度很大，所以，边界层内的流体具有相当大的旋涡强度；而在层外，由于速度梯度很小。

所以，即使对于粘度很大的流体，粘性力也很小，故可忽略不计，所以可认为，图8-2空气沿平板边界层速度分布外部区域边界层边界层外的流动是无旋的势流。

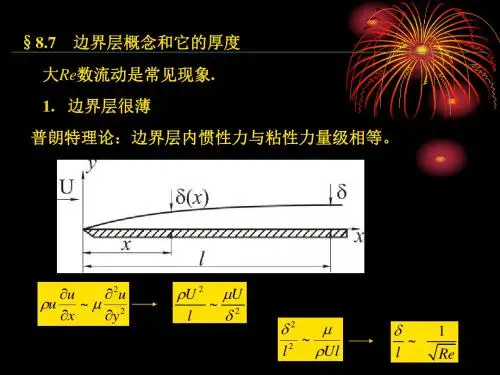
边界层的基本特征有： (1)1<<Lδ⇒薄层性质，其中L 为物体的长度；沿流方向↑↑→δx 。

(2) 层内yu∂∂很大， 边界层内存在层流和紊流两种流态。

流体力学第八章答案

流体力学第八章答案

流体力学第八章答案【篇一：流体力学第8、10、11章课后习题】>一、主要内容（一）边界层的基本概念与特征1、基本概念：绕物体流动时物体壁面附近存在一个薄层，其内部存在着很大的速度梯度和漩涡，粘性影响不能忽略，我们把这一薄层称为边界层。

2、基本特征：（1）与物体的长度相比，边界层的厚度很小；（2）边界层内沿边界层厚度方向的速度变化非常急剧，即速度梯度很大；（3）边界层沿着流体流动的方向逐渐增厚；（4）由于边界层很薄，因而可以近似地认为边界层中各截面上压强等于同一截面上边界层外边界上的压强；（5）在边界层内粘性力和惯性力是同一数量级；（6）边界层内流体的流动与管内流动一样，也可以有层流和紊流2种状态。

（二）层流边界层的微分方程（普朗特边界层方程）??v?vy?2v1?p?vy?????vx?x?y??x?y2????p??0?y???v?vy???0?x?y??其边界条件为：在y?0处，vx?vy?0 在y??处，vx?v(x)（三）边界层的厚度从平板表面沿外法线到流速为主流99%的距离，称为边界层的厚度，以?表示。

边界层的厚度?顺流逐渐加厚，因为边界的影响是随着边界的长度逐渐向流区内延伸的。

图8-1 平板边界层的厚度1、位移厚度或排挤厚度?1?1?2、动量损失厚度?2?vx1?(v?v)dy?(1?)dy x??00vv?2?1?v2???vx(v?vx)dy???vxv(1?x)dy vv（四）边界层的动量积分关系式??2???p?vdy?v?vdy?????wdx xx??00?x?x?x对于平板上的层流边界层，在整个边界层内每一点的压强都是相同的，即p?常数。

这样，边界层的动量积分关系式变为?wd?2d?vdy?vvdy?? x?x??00dxdx?二、本章难点（一）平板层流边界层的近似计算根据三个关系式：（1）平板层流边界层的动量积分关系式；（2）层流边界层内的速度分布关系式；（3）切向应力关系式。

边界层


dp = 0则整个流场压力处处相等。 dx 边界层微分方程虽然是在平壁的情况下导出的，但对曲率不太大的
dU e = ，， 0 dx
曲线壁面仍然适用。此时，x轴沿壁面方向，y轴沿壁面法线方向。
§8—3 边界层动量积分方程
一、边界层动量积分方程
由卡门在1921年提出。
推导前提：二元定常，忽略质量力，且u>>υ(由边界 层微分方程的数量级比较可看出)，所以只考虑x方向 的动量变化，不引入y方向的流速υ。
+ = 0 ，u~1， 并且边界层内，由u≥υ，故认为或由连续方程 ∂x ∂y υ~△ ∵x~1并且我们认为u~1，而y~△，必然是υ~△，这样才能满足连续方 1 ∆ 程，∂ u ∂ υ + =1 + =0 ，1 ∆ 。 ∂x ∂y dy ∆y = lim 注意：导数又称为微商，例如 dx ∆x→0 ∆x ，类似地在进行数量级比较 时，我们可以写成 ∂ u ~ 1 ，即 ∂y 是1的数量级。
1 ∂p ∂υ ∂υ ∂ 2υ ∂ 2υ u +υ =− + v( 2 + 2 ) ∂x ∂y ∂x ∂y ρ ∂y ∆ ∆ ∆ ∆ 1 ∆ ∆2 2 1 ∆ 1 ∆
∂u ∂u ∂ 2u 1 ∂p +v =− +ν u ∂x ∂y ∂y 2 ρ ∂x
∂p =0 ∂y
∂u ∂ υ + =0 ∂x ∂ y
方程第二项积分的物理意义为：
∫
δ
0
ρu (U e − u )dy 表示了因粘性影响而产生的流体动量的减少量。
ρδ 2 ⋅1⋅U e 2 = ρ ∫ u (U e − u )dy
0
令
δ
δ2 =
1 Ue

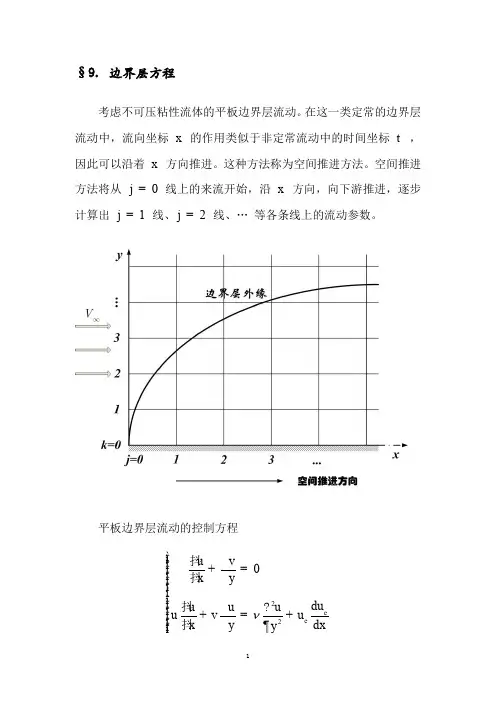
6-边界层方程

§9. 边界层方程考虑不可压粘性流体的平板边界层流动。

在这一类定常的边界层流动中，流向坐标 x 的作用类似于非定常流动中的时间坐标 t ，因此可以沿着 x 方向推进。

这种方法称为空间推进方法。

空间推进方法将从 0j = 线上的来流开始，沿 x 方向，向下游推进，逐步计算出 1j = 线、2j = 线、… 等各条线上的流动参数。

平板边界层流动的控制方程220e euvx ydu u u uu v u x y dx yìï抖ï+=ïï抖ïïíïï抖 ï+=+ïï抖¶ïî这里 ()e e u u x = 是边界层外缘处的速度分布。

通过求解边界层外的无粘流动，可事先求得 e u 。

因此在边界层流动的求解中，ee du u dx这一项是已知的。

边界层流动控制方程的初始条件是在平板前缘（0j = 线），给定来流速度 u V ¥= ，0v = 而边界条件是沿壁面（0k = 线），速度 0u = ，0v =取特征速度 V ¥ 和特征长度 1L = ，将方程无量纲化，平板边界层流动的控制方程成为2201Re e e u v x y du u u u u v u x y dx y ìï抖ï+=ïï抖ïïíïï抖 ï+=+ïï抖¶ïî方程中u u V ¥=、 v v V ¥= 、 e e u u V ¥= ， x x L = 、 y y L =而Re V L¥=是（来流）雷诺数。

下面为了简洁起见，省略所有无量纲量上方的横杠。

按照空间推进的观点，流向坐标 x 是类时间坐标。

边界层分析求解


5
对于管内的流动运 动，取临界雷诺数 2300
粘性底层：在紊流边界层内，由于紧贴壁面处那一层薄层内
粘滞力甚大，流体仍具有层流的特征。 紊流支层：粘性底层上方称为紊流支层，在该层内粘滞力较 小，流体具有紊流的特点。 边界层厚度=粘性底层+紊流支层
底 =29.4 x w
9
9 1 10

m
t∞ u
流体流过固体壁面的流场就 人为地分成两个不同的区域。
δ 0
t
δ
tw x
其一是边界层流动区，这里流体的黏性力与流体的惯性力共 同作用，引起流体速度发生显著变化；其二是势流区，这里 流体黏性力的作用非常微弱，可视为无黏性的理想流体流动， 也就是势流流动。
2）边界层的厚度
当速度变化达到 u u 0.99 时的空间位置为速度边界层的 外边缘，那么从这一点到壁面的距离就是边界层的厚度 x
0
x
x x 5.0 w x
1
2
5.0 Re
1
2
要使边界层的厚度远小于流动方向上的尺度(即 x x 1 )， 也就是所说的边界层是一个薄层，这就要求雷诺数必须足够 Re 1 的大,即
因此，对于流体流过平板，满足边界层假设的条件就是雷 诺数足够大。由此也就知道，当速度很小、黏性很大时或 在平板的前沿，边界层是难以满足薄层性条件。
3) 临界雷诺数
随着x的增大，δ（x）也逐步增大，同时黏性力对流 场的控制作用也逐步减弱，从而使边界层内的流动变得紊乱。 把边界层从层流过渡到紊流的x值称为临界值，记为xc， 其所对应的雷诺数称为临界雷诺数，即 Re c u xc
流体平行流过平板的 临界雷诺数大约是

二维不可压缩定常流动(平板)边界层方程

二维不可压缩定常流动(平板)边界层方程下载温馨提示：该文档是我店铺精心编制而成，希望大家下载以后，能够帮助大家解决实际的问题。

文档下载后可定制随意修改，请根据实际需要进行相应的调整和使用，谢谢!并且，本店铺为大家提供各种各样类型的实用资料，如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等，如想了解不同资料格式和写法，敬请关注!Download tips: This document is carefully compiled by the editor. I hope that after you download them, they can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!In addition, our shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!二维不可压缩定常流动(平板)边界层方程引言在流体力学领域，研究流体在固体表面附近的行为至关重要。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

u
∂C
* j
∂x
+
v
∂C
* j
∂y
=
D
∂
2C
* j
∂y 2
（ C 为质量浓度， D 为质扩散系数）。进行变换，也是变成抛物
型的偏微分方程，也能用该数值计算程序来求解，如下式：
∂C
* j
=
∂
(ρur 2 μeff
∂C
* j
+
Rj
)
∂ζ ∂ψ
Seeff ∂ψ ρu
（8－15）
其中， R j 为由于化学反应等原因组份 j 的产生率， Seeff 为有效斯密特数。
ui−2, j
= ui, j
−
2Δx(
∂u ∂x
)i
,
j
+
(2Δx)2 2!
(
∂2u ∂x 2
)i
,
j
− O(Δx)3
由此可得， ui, j = 2ui−1, j − ui−2, j + O(Δx)2 类 似 地 ， 对 于 vi, j ， 可 得
vi, j = 2vi−1, j − vi−2, j + O(Δx)2
(ρur 2μeff
∂u ∂ψ
)−
1 ρu
dp dζ
（8－13）
这就是以轴对称流线坐标系表示的动量方程。
同样，可将能量方程 ρc p (u
∂t ∂x
+ v ∂t ) ∂y
=
λ
∂2t ∂y 2
+
μ( ∂u )2 也改写成轴对称流线坐标系 ∂y
中的形式：
∂h~ ∂ζ
=∂ ∂ψ
⎪⎧ ⎨ ⎪⎩
ρur
2
⎡ ⎢ ⎢⎣
在对边界层微分方程进行数值计算时， 为了使边界层的有限差分网格会自动增长 或收敛，与定义的边界层外缘相一致，这里
特定义一个无量纲流函数η ，
等η线
yη ,ψη ,η x,ζ
E边界，η=1 I边界，η=0
η ≡ ψ −ψ I ψ E −ψ I
φ
r r1
对称轴
图 8－2 无量纲的流线坐标系
5
其中，ψ I 和ψ E 分别为所考虑的内边界 I 和外边界 E 处的流函数，通常ψ I 和ψ E 是 ζ 的函 数。这样，顺流向的变量为 ζ ，而横流向的变量则为η ，等η 线与等 ζ 正交。边界层位于
y = 0，u = 0，v = 0
（8－6）
y = δ ， u = u∞ x 和 y 分别是顺流向和横流向的坐标，u 和 v 分别是顺流向和横流向的分速度。如用矩
形网格，则层流边界层的有限差分网点如图 8－1 所示。其中， Δx 和 Δy 分别是顺流向和横
流向的步长，均取为常数。
y
i−2, j+1 i−1, j+1 i, j+1
=
lk
ρK
1 2
（8－3）
其中，lk
是距壁面距离的函数，K
是流体脉动的平均动能
(K
=
1 2
ρu′2
+
1 2
ρv′2
+
1 2
ρw′2 )
。
由于式（8－3）中包含有紊流动能 K ，因此必须联立求解紊流的能量方程和动量方程，因
此，布腊德晓（Bradshaw）等提出了一个将紊流的能量方程和动量方程联Leabharlann 求解的数值解程一、网格的划分
用数值法计算边界层内的动量、热量和质量交换情况时，必须把计算区域划分成网格，
并沿横流向解有限差分方程。网点之间的距离，亦即网格的尺寸应根据边界层内的速度或焓、
对 y 的导数用中心差分公式，对 x 的导数用向后差分公式，则得：
2
∂u ( ∂x )i, j
=
3ui, j
− 4ui−1, j 2Δx
+ ui−2, j
− O(Δx)2
∂u ( ∂y )i, j
=
ui, j+1 − ui, j−1 2Δy
+ O(Δy)2
及
(
∂2u ∂y 2
)i,
j
=
ui, j+1
μeff Preff
∂h~ ∂ψ
+ (μeff
− μeff Preff
)∂ ∂ψ
(
1 2
u
2
⎤ )⎥ ⎥⎦
⎪⎫ ⎬ ⎪⎭
（8－14）
其中， h~ ≡ CpT
+ 1 u 2 称为全焓 2
， Preff
为有效普朗特数。
经过这样的变换后，边界层的动量方程和能量方程具有相同的形式，即同为抛物型的
偏微分方程，因此能用相同的数值计算程序来求解。事实上，若对质量扩散方程
采用轴对称坐标，仍避免不了矩形网格的缺点，为此需采用轴对称的流线坐标系。
引进流函数ψ 作为横流向的自变量，顺流向的坐标用 ζ ，ζ ≡ x 。这样，以 ( x , y )
表示的轴对称坐标系就变成了以 (ψ , ζ ) 表示的轴对称流线坐标系了。这种坐标变换称为
冯·米塞兹变换。
由于引入了流函数ψ ，则 ρur = ∂ψ ， ρvr = − ∂ψ 。显然，流函数能自动满足连续
∂y
∂x
方程，同时可在边界层动量方程中除去横流向的速度 v ，使之简化。
由于坐标的变换，则式（8－12）中的 ∂u 、 ∂u 等项成为： ∂x ∂y
∂u = ∂u ∂ψ + ∂u ∂ζ = −ρvr ∂u + ∂u
∂x ∂ψ ∂x ∂ζ ∂x
∂ψ ∂ζ
∂u = ∂u ∂ψ + ∂u ∂ζ = ρur ∂u
∂u ∂y
（8－1）
其中， μeff 称为有效动力粘度，
μeff = μ + ρεt
（8－2）
层流时，εt = 0 ；紊流时，必须由半经验关系式给出 μeff ，不同的模型给出的半经验关系式
也不同，因而也有不同的数值解法。
布腊德晓（Bradshaw）等提出了将有效粘度与紊流动能 K 相联系的模型：
μeff
ui, j 值的变化，来试出边界层的外缘，因此在计算时间和储存方面都是不经济的。更好的办
法是用一个随着边界层增长而增长的坐标系。
8—2 流线坐标系
对于流体沿着平板的流动，如喷嘴或扩压器内流体的流动、沿对称物体的流动、圆管 和扁管内的流动以及各种自由射流均可建立轴对称极坐标系，使问题简化。
对于稳态、可压缩流体的流动，用轴对称极坐标系时，其连续方程和动量方程（忽略 体积力）为：
ui, j ( j = 2,3,L, N −1) 的线性代数方程组。因系数 Aj 、 B j 、 C j 、 Fj 中只包含已知量（即
预先算出的或初始的
u
和
v
值，以及已规定的
dp dx
值），ui,
j
的各未知值即可由形成的矩阵式
计算得出，边界条件为 ui,1 = 0 ， ui,N = u∞ 。得出 ui, j 后，可由连续方程求 vi, j ，
∂y ∂ψ ∂y ∂ζ ∂y
∂ψ
4
dp = dp （忽略横流向压力变化，即忽略 dp ）
dx dζ
dψ
1 r
∂(rτ ∂y
)
=
ρu
∂(rτ ∂ψ
)
经过转换，式（8－12）就成为：
∂u = ∂(rτ ) − 1 dp ∂ζ ∂ψ ρu dζ
当把τ
=
μ eff
∂u 代入后，即得： ∂y
∂u ∂ζ
=
∂ ∂ψ
∂(ρur) + ∂(ρvr) = 0
∂x
∂y
（8－11）
ρ(u ∂u + v ∂u ) = − dp + 1 ∂(rτ ) ∂x ∂y dx r ∂y
（8－12）
其中， x 和 y 仍分别是顺流向和横流向的距离， u 和 v 仍分别是顺流向和横流向的分速度。 r 为离对称轴的半径， r = 1时，上式即简化为笛卡尔坐标系的方程。
第八章 边界层方程的数值解
对于边界层，第五章中给出了其微分方程和积分方程。这两类方程均可用数值解法求解。 在高速数字计算机尚未普遍地得到应用之前，常采用积分方程的数值解。为了更准确地预测 边界层内的计算结果，以及在电子计算机的速度和储存量都大大增加的有利情况下，对于边 界层的微分方程也完全有能力进行数值计算。
表 8－1 和 Φ 相应的σ eff 和称为源项的 d 值
他变量 Φ
σ eff
d
u
1
1− 1 dp ρu dζ
h~
Preff
∂ ∂η
⎡ ρur 2
⎢ ⎢⎣
(ψ
E
−ψ
I
)2
(μeff
−
μeff Preff
)∂ ∂η
(
1
u
2
⎤ )⎥
2 ⎥⎦
C
* j
Seeff
Rj ρu
8—3 边界层方程的有限差分形式
6
将基本的偏微分方程用式（8－16）的形式表示后，需将转换成有限差分方程，以便求 出数值解。
Bj
=
3 2
(2ui−1,
j
− ui−2, j ) + 2ν
Δx (Δy)2
Cj
=
−
Δx 2Δy
(2vi−1, j
− vi−2, j ) −ν
Δx (Δy)2
Fj
=
1 2
(2ui−1, j
− ui−2, j )(4ui−1, j
− ui−2, j ) −
Δx ρ
dp ( dx )i
对于横贯边界层的 N 个网络点（y 方向除 y=0 和 y=δ以外）而言，就有 (N − 2) 个