下载文档原格式
第五章边界层的积分方程对于几乎任何种类的边界条件，边界层微分方程的特解总是可以得到。
某些类型的问题，已经得到精确的解析解。
对于更一般的问题，数值解常常是必要的。
值得寻求近似解法，例如积分解。
边界层的积分方程提供了许多近似解法赖以建立的基础，但它们本身是精确的，至少是在边界层近似的范畴内是这样。
特别注意本章中的排量厚度、动量厚度和焓厚度之定义所涉及的控制体，必须满足以下条件，① 控制体的左端取自物体与流体发生作用的地方，右端止于流动充分发展处；下端为物体表面，上端至少为势流与粘流交界处。
② 控制体置于层流区，而非湍流区。
§5.1排量厚度和动量厚度图：P57-Fig.5-3 推导边界层排量厚度与动量厚度的控制体 关于质量：● 体积内：()()BC AB ⋅∂∂θρ● 流过控制体表面的质量：⏹ 左端：⎰∞∞=Y dy u AB 0ρ⏹ 右端：⎰=Yudy CD 0ρ⏹ 下端：0=AD ⏹ 上端：?=BC ● 应用控制体的质量守恒原理()()000=⎥⎦⎤⎢⎣⎡---⋅∂∂⎰⎰∞∞BC udy dy u BC AB Y Y ρρθρ在定常条件下：0=∂∂θρ，有， ⎰⎰⎰⎪⎪⎭⎫⎝⎛-=-=∞∞∞∞∞∞YYYdy u u u udy dy u BC 0001ρρρρρ 令∞→Y ，以使得整个边界层均包括在积分之内，定义排量厚度1δ，使得，⎰⎰∞∞∞∞∞∞∞∞∞∞⎪⎪⎭⎫⎝⎛-=⇒⎪⎪⎭⎫ ⎝⎛-=010111dy u u dy u u u u ρρδρρρρδ 物理解释：1δ是由于边界层的存在所引起的主流排量的度量。
注意，排量厚度1δ只是一种定义，并不能实际应用，因为：① 被积函数中的u ρ项无法知晓；② 关于“∞”的积分上限无法实现。
后面的动量厚度之定义也存在着同样的问题。
关于动量● 体积内：()()BC AB u⋅∂∂θρ ● 流过控制面的动量⏹ 左端：⎰∞∞=Y dy u AB 02ρ⏹ 右端：⎰=Ydy u CD 02ρ⏹ 下端：0=AD ⏹ 上端：⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-=⎰∞∞∞∞∞dy u u u u BC Y1ρρρ——Y 足够大，以至于∞→u u 。
第五章对流换热分析通过本章的学习，读者应熟练掌握对流换热的机理及其影响因素，边界层概念及其应用，以及在相似理论指导下的实验研究方法，进一步提出针对具体换热过程的强化传热措施。
5.1 内容提要及要求5.1.1 对流换热概述1．定义及特性对流换热指流体与固体壁直接接触时所发生的热量传递过程。
在对流换热过程中，流体内部的导热与对流同时起作用。
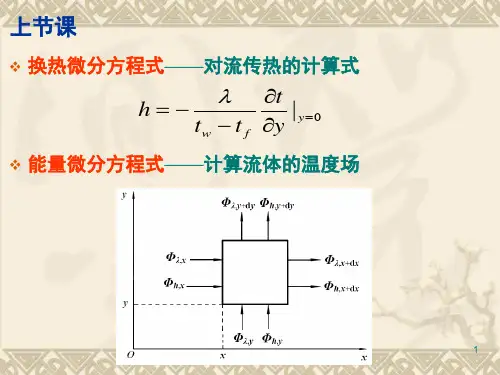
牛顿冷却公式q h(t w t f ) 是计算对流换热量的基本公式，但它仅仅是对流换热表面传热系数h 的定义式。
研究对流换热的目的是揭示表面传热系数与影响对流换热过程相关因素之间的内在关系，并能定量计算不同形式对流换热问题的表面传热系数及对流换热量。
2．影响对流换热的因素（1）流动的起因：流体因各部分温度不同而引起密度差异所产生的流动称为自然对流，而流体因外力作用所产生的流动称为受迫对流，通常其表面传热系数较高。
（2）流动的状态：流体在壁面上流动存在着层流和紊流两种流态。
（3）流体的热物理性质：流态的热物性主要指比热容、导热系数、密度、粘度等，它们因种类、温度、压力而变化。
（4）流体的相变：冷凝和沸腾是两种最常见的相变换热。
（5）换热表面几何因素：换热表面的形状、大小、相对位置及表面粗糙度直接影响着流体和壁面之间的对流换热。
综上所述，可知表面传热系数是如下参数的函数h f u, t w , t f , , c p , ,,, l这说明表征对流换热的表面传热系数是一个复杂的过程量，不同的换热过程可能千差万别。
3．分析求解对流换热问题分析求解对流换热问题的实质是获得流体内的温度分布和速度分布，尤其是近壁处流体内的温度分布和速度分布，因为在对流换热问题中“流动与换热是密不可分”的。
同时，分析求解的前提是给出正确地描述问题的数学模型。
在已知流体内的温度分布后，可按如下的对流换热微分方程获得壁面局部的表面传热系数由上式可有h xtt x yW/(m 2 K)w,x其中为过余温度，h xxyW/(m 2 K)w,x对流换热问题的边界条件有两类，第一类为壁温边界条件，即壁温分布为已知，待求的是流体的壁面法向温度梯度；第二类为热流边界条件，即已知壁面热流密度，待求的是壁温。
