选修专题与全国卷

专题60有机合成（选修）1．【2022年广东卷】基于生物质资源开发常见的化工原料，是绿色化学的重要研究方向。

以化合物I 为原料，可合成丙烯酸V 、丙醇VII 等化工产品，进而可制备聚丙烯酸丙酯类高分子材料。

（1）化合物I 的分子式为_______，其环上的取代基是_______(写名称)。

（2）已知化合物II 也能以II′的形式存在。

根据II′的结构特征，分析预测其可能的化学性质，参考①的示例，完成下表。

序号结构特征可反应的试剂反应形成的新结构反应类型①CH CH -=-2H 22CH CH ---加成反应②_____________________氧化反应③____________________________（3）化合物IV 能溶于水，其原因是_______。

（4）化合物IV 到化合物V 的反应是原子利用率100%的反应，且1mol IV 与1mol 化合物a反应得到2mol V ，则化合物a 为_______。

（5）化合物VI 有多种同分异构体，其中含结构的有_______种，核磁共振氢谱图上只有一组峰的结构简式为_______。

（6）选用含二个羧基的化合物作为唯一的含氧有机原料，参考上述信息，制备高分子化合物VIII 的单体。

写出VIII的单体的合成路线_______(不用注明反应条件)。

2．【2022年江苏卷】化合物G可用于药用多肽的结构修饰，其人工合成路线如下：（1）A分子中碳原子的杂化轨道类型为_______。

（2）B→C的反应类型为_______。

（3）D的一种同分异构体同时满足下列条件，写出该同分异构体的结构简式：_______。

①分子中含有4种不同化学环境的氢原子；②碱性条件水解，酸化后得2种产物，其中一种含苯环且有2种含氧官能团，2种产物均能被银氨溶液氧化。

C H NO，其结构简式为_______。

（4）F的分子式为12172（5）已知：(R和D'表示烃基或氢，R''表示烃基)；CH MgBr为原料制备的合成路线流程图(无机试剂和有写出以和3机溶剂任用，合成路线流程图示例见本题题干)_______。

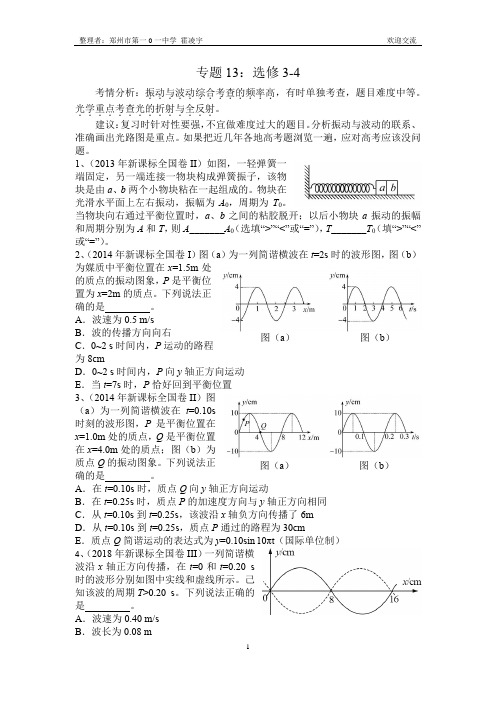
专题13：选修3-4考情分析：振动与波动综合考查的频率高．．．．．．．．．．．．．，有时单独考查，题目难度中等。

光学重点考查光的折射与全反射．．．．．．．．．．．．．．。

建议：复习时针对性要强，不宜做难度过大的题目。

分析振动与波动的联系、准确画出光路图是重点。

如果把近几年各地高考题浏览一遍，应对高考应该没问题。

1、（2013年新课标全国卷II ）如图，一轻弹簧一端固定，另一端连接一物块构成弹簧振子，该物块是由a 、b 两个小物块粘在一起组成的。

物块在光滑水平面上左右振动，振幅为A 0，周期为T 0。

当物块向右通过平衡位置时，a 、b 之间的粘胶脱开；以后小物块a 振动的振幅和周期分别为A 和T ，则A _______A 0（选填“>”“<”或“=”），T _______T 0（填“>”“<”或“=”）。

2、（2014年新课标全国卷I ）图（a ）为一列简谐横波在t =2s 时的波形图，图（b ）为媒质中平衡位置在x =1.5m 处的质点的振动图象，P 是平衡位置为x =2m 的质点。

下列说法正确的是 。

A ．波速为0.5 m/sB ．波的传播方向向右C ．0~2 s 时间内，P 运动的路程为8cmD ．0~2 s 时间内，P 向y 轴正方向运动E ．当t =7s 时，P 恰好回到平衡位置3、（2014年新课标全国卷II ）图（a ）为一列简谐横波在t =0.10s时刻的波形图，P 是平衡位置在x =1.0m 处的质点，Q 是平衡位置在x =4.0m 处的质点；图（b ）为质点Q 的振动图象。

下列说法正确的是 。

A ．在t =0.10s 时，质点Q 向y 轴正方向运动B ．在t =0.25s 时，质点P 的加速度方向与y 轴正方向相同C ．从t =0.10s 到t =0.25s ，该波沿x 轴负方向传播了6mD ．从t =0.10s 到t =0.25s ，质点P 通过的路程为30cmE ．质点Q 简谐运动的表达式为y =0.10sin 10πt （国际单位制）4、（2018年新课标全国卷III ）一列简谐横波沿x 轴正方向传播，在t =0和t =0.20 s时的波形分别如图中实线和虚线所示。

专题16 选修4-5不等式选讲【2021年】1．（2021年全国高考乙卷数学（文）试题）已知函数()3f x x a x =-++．（1）当1a =时，求不等式()6f x ≥的解集;（2）若()f x a >-，求a 的取值范围．2．（2021年全国高考甲卷数学（理）试题）已知函数()2,()2321f x x g x x x =-=+--．（1）画出()y f x =和()y g x =的图像；（2）若()()f x a g x +≥，求a 的取值范围．3．（2021年全国新高考Ⅰ卷数学试题）已知函数()()1ln f x x x =-.（1）讨论()f x 的单调性；（2）设a ，b 为两个不相等的正数，且ln ln b a a b a b -=-，证明：112e a b<+<.【2012年——2020年】1．（2020年全国统一高考数学试卷（文科）（新课标Ⅰ））已知函数()|31|2|1|f x x x =+--．（1）画出()y f x =的图像；（2）求不等式()(1)f x f x >+的解集．2．（2020年全国统一高考数学试卷（文科）（新课标Ⅰ））已知函数2()|21|f x x a x a =-+-+. （1）当2a =时，求不等式()4f x ≥的解集；（2）若()4f x ≥，求a 的取值范围.3．（2020年全国统一高考数学试卷（理科）（新课标Ⅰ））设a ，b ，c ∈R ，a +b +c =0，abc =1． （1）证明：ab +bc +ca <0；（2）用max{a ，b ，c }表示a ，b ，c 中的最大值，证明：max{a ，b ，c ．4．（2019年全国统一高考数学试卷（文科）（新课标Ⅰ））已知a ，b ，c 为正数，且满足abc =1．证明：（1）222111a b c a b c++≤++； （2）333()()()24a b b c c a +++≥++．5．（2019年全国统一高考数学试卷（理科）（新课标Ⅰ））已知()|||2|().f x x a x x x a =-+--（1）当1a =时，求不等式()0f x <的解集；（2）若(,1)x ∈-∞时，()0f x <，求a 的取值范围.6．（2019年全国统一高考数学试卷（文科）（新课标Ⅰ））设,,x y z ∈R ，且1x y z ++=.（1）求222(1)(1)(1)x y z -++++的最小值；（2）若2221(2)(1)()3x y z a -+-+-≥成立，证明：3a ≤-或1a ≥-. 7．（2018年全国普通高等学校招生统一考试文科数学（新课标I 卷））已知()11f x x ax =+--. （1）当1a =时，求不等式()1f x >的解集；（2）若()0,1x ∈时不等式()f x x >成立，求a 的取值范围.8．（2018年全国普通高等学校招生统一考试理数（全国卷II ））设函数()52f x x a x =-+--. （1）当1a =时，求不等式()0f x ≥的解集；（2）若()1f x ≤恒成立，求a 的取值范围.9．（2018年全国卷Ⅰ理数高考试题）设函数()211f x x x =++-．（1）画出()y f x =的图像；（2）当[)0x +∞∈，，()f x ax b ≤+，求+a b 的最小值．10．（2017年全国普通高等学校招生统一考试文科数学（新课标1卷））已知函数2()4f x x ax =-++，()|1||1|g x x x =++-．（1）当1a =时，求不等式()()f x g x ≥的解集；（2）若不等式()()f x g x ≥的解集包含[–1，1]，求a 的取值范围．11．（2017年全国普通高等学校招生统一考试理科数学（新课标2卷））已知0a >，0b >，332a b +=，证明：(1)()()554a b a b ++≥；(2)2a b +≤.12．（2017年全国普通高等学校招生统一考试文科数学（新课标3卷））已知函数()f x =│x +1│–│x –2│. （1）求不等式()f x ≥1的解集；（2）若不等式()f x ≥x 2–x +m 的解集非空，求实数m 的取值范围.13．（2016年全国普通高等学校招生统一考试文科数学（新课标1卷））（2016高考新课标Ⅰ，理24）选修4-5：不等式选讲已知函数f (x )=|x +1|−|2x −3|.（Ⅰ）画出y =f (x )的图象；（Ⅰ）求不等式|f (x )|>1的解集．14．（2016年全国普通高等学校招生统一考试文科数学（新课标2卷））选修4-5：不等式选讲已知函数11()22f x x x =-++，M 为不等式()2f x <的解集. （Ⅰ）求M ； （Ⅰ）证明：当a ，b M ∈时，1a b ab +<+.15．（2016年全国普通高等学校招生统一考试）已知函数()|2|f x x a a =-+.（1）当a=2时，求不等式()6f x ≤的解集；（2）设函数()|21|g x x =-.当x ∈R 时，()()3f x g x +≥，求a 的取值范围.16．（2015年全国普通高等学校招生统一考试理科数学（新课标））已知函数()|1|2||,0f x x x a a =+-->.（1）当1a =时，求不等式()1f x >的解集；（2）若()f x 的图象与x 轴围成的三角形面积大于6，求a 的取值范围.17．（2015年全国普通高等学校招生统一考试理科数学（新课标Ⅰ））选修4-5不等式选讲设a b c d ,,,均为正数，且a b c d +=+，证明：（Ⅰ）若ab cd >>；（Ⅰ>是a b c d -<-的充要条件．18．（2014年全国普通高等学校招生统一考试文科数学（新课标Ⅰ））若且 （I ）求的最小值； （II ）是否存在，使得？并说明理由.19．（2014年全国普通高等学校招生统一考试文科数学（全国Ⅰ卷））设函数1()|(0)f x x x a a a=++- （1）证明：()2f x ≥；（2）若(3)5f <，求a 的取值范围．20．（2013年全国普通高等学校招生统一考试理科数学（新课标1卷））选修4—5：不等式选讲 已知函数f （x ）＝|2x －1|＋|2x ＋a|，g （x ）＝x ＋3．（1）当a ＝－2时，求不等式f （x ）＜g （x ）的解集；（2）设a ＞－1，且当xⅠ1,22a ⎛⎫-⎪⎝⎭时，f （x ）≤g （x ），求a 的取值范围．21．（2013年全国普通高等学校招生统一考试文科数学（新课标2卷））设a ，b ，c 均为正数，且a+b+c=1，证明：（Ⅰ）ab+bc+ac ≤13； （Ⅰ）2221a b c b c a++≥.22．（2012年全国普通高等学校招生统一考试文科数学（课标卷））已知函数()f x =2x a x ++-. (Ⅰ)当3a =-时，求不等式()f x ≥3的解集；(Ⅰ) 若()f x ≤4x -的解集包含[1,2]，求a 的取值范围.（命题意图）本题主要考查含绝对值不等式的解法，是简单题.。

2017-2018全国卷I -Ⅲ高考真题数学不等式选修专题1.(2017全国卷I,文/理.23)（10分）[选修4—5：不等式选讲]（10分）已知函数f （x ）=–x 2+ax +4，g (x )=│x +1│+│x –1│.（1）当a =1时，求不等式f （x ）≥g （x ）的解集；（2）若不等式f （x ）≥g （x ）的解集包含[–1，1]，求a 的取值范围.【答案解析】解：（1）当1a =时，()24f x x x =-++，是开口向下，对称轴1x =的二次函数．()211121121x x g x x x x x >⎧⎪=++-=-⎨⎪-<-⎩，，≤x≤，，当(1,)x ∈+∞时，令242x x x -++=，解得12x =()g x 在()1+∞，上单调递增，()f x 在()1+∞，上单调递减∴此时()()f x g x ≥解集为112⎛⎤- ⎝⎦，．当[]11x ∈-，时，()2g x =，()()12f x f -=≥．当()1x ∈-∞-，时，()g x 单调递减，()f x 单调递增，且()()112g f -=-=．综上所述，()()f x g x ≥解集1⎡-⎢⎣⎦．（2）依题意得：242x ax -++≥在[]11-，恒成立．即220x ax --≤在[]11-，恒成立．则只须()()2211201120a a ⎧-⋅-⎪⎨----⎪⎩≤≤，解出：11a -≤≤．故a 取值范围是[]11-，．2.(2017全国卷Ⅱ,文/理.23)（10分）[选修4-5：不等式选讲]（10分）已知0a >，222ba b +==2.证明：（1）()22()4a b a b ++≥；（2）2a b +≤.【答案解析】3.(2017全国卷Ⅱ,文/理.23)（10分）[选修4—5：不等式选讲]（10分）已知函数f （x ）=│x +1│–│x –2│.（1）求不等式f （x ）≥1的解集；（2）若不等式f （x ）≥x 2–x +m 的解集非空，求m 的取值范围.【答案解析】解:(1)()|1||2|f x x x =+--可等价为()3,121,123,2--⎧⎪=--<<⎨⎪⎩x f x x x x ≤≥.由()1f x ≥可得：①当1-x ≤时显然不满足题意；②当12x -<<时，211-x ≥，解得1x ≥；③当2x ≥时，()31=f x ≥恒成立.综上，()1f x ≥的解集为{}|1x x ≥.(2)不等式()2-+f x x x m ≥等价为()2-+f x x x m ≥，令()()2g x f x x x =-+，则()g x m ≥解集非空只需要()max ⎡⎤⎣⎦g x m ≥.而()2223,131,123,2⎧-+--⎪=-+--<<⎨⎪-++⎩x x x g x x x x x x x ≤≥.①当1-x ≤时，()()max 13115g x g =-=---=-⎡⎤⎣⎦；②当12x -<<时，()2max 333531g x g ⎛⎫⎛⎫==-+⋅-=⎡⎤ ⎪ ⎪⎣⎦⎝⎭⎝⎭；③当2x ≥时，()()2max 22231g x g ==-++=⎡⎤⎣⎦.综上，()max 54g x =⎡⎤⎣⎦，故54m ≤.4.(2018全国卷I,文/理.23)（10分）[选修4—5：不等式选讲]（10分）已知()11f x x ax =+--．（1）当1a =时，求不等式()1f x >的解集；（2）若()01x ∈，时不等式()f x x >成立，求a 的取值范围．【答案解析】解：（1）当1a =时，()|1||1|f x x x =+--，即2,1,()2,11,2, 1.x f x x x x -≤-⎧⎪=-<<⎨⎪≥⎩故不等式()1f x >的解集为1{|}2x x >．（2）当(0,1)x ∈时|1||1|x ax x +-->成立等价于当(0,1)x ∈时|1|1ax -<成立．若0a ≤，则当(0,1)x ∈时|1|1ax -≥；若0a >，|1|1ax -<的解集为20x a <<，所以21a≥，故02a <≤．综上，a 的取值范围为(0,2]．5.(2018全国卷Ⅱ,文/理.23)（10分）[选修4－5：不等式选讲]（10分）设函数()5|||2|f x x a x =-+--．（1）当1a =时，求不等式()0f x ≥的解集；（2）若()1f x ≤，求a 的取值范围．【答案解析】解：（1）当1a =时，24,1,()2,12,26, 2.x x f x x x x +≤-⎧⎪=-<≤⎨⎪-+>⎩可得()0f x ≥的解集为{|23}x x -≤≤．（2）()1f x ≤等价于|||2|4x a x ++-≥．而|||2||2|x a x a ++-≥+，且当2x =时等号成立．故()1f x ≤等价于|2|4a +≥．由|2|4a +≥可得6a ≤-或2a ≥，所以a 的取值范围是(,6][2,)-∞-+∞ ．6.(2018全国卷Ⅲ,文/理.23)（10分）[选修4—5：不等式选讲]（10分）设函数()211f x xx =++-．（1）画出()y f x =的图像；（2）当[)0x +∞∈，，()f x ax b +≤，求a b +的最小值．【答案解析】解：（1）13,,21()2,1,23, 1.x x f x x x x x ⎧-<-⎪⎪⎪=+-≤<⎨⎪≥⎪⎪⎩()y f x =的图像如图所示．（2）由（1）知，()y f x =的图像与y 轴交点的纵坐标为2，且各部分所在直线斜率的最大值为3，故当且仅当3a ≥且2b ≥时，()f x ax b ≤+在[0,)+∞成立，因此a b +的最小值为5．。

坐标系与参数方程选做专题（2015-10-14）命题：靳建芳1．在直角坐标系x y O 中，以坐标原点O 为极点，以x 轴正半轴为极轴建立极坐标系．已知曲线1C :452x t y t=+⎧⎨=+⎩（t 为参数），曲线2C :26cos 10sin 90ρρθρθ--+=．（Ⅰ）将曲线1C 化成普通方程，将曲线2C 化成参数方程； （Ⅱ）判断曲线1C 和曲线2C 的位置关系．2．曲线1C 的参数方程为)(sin 22cos 2为参数ααα⎩⎨⎧+==y x ，M 是曲线1C 上的动点，且M 是线段OP 的中点，P 点的轨迹为曲线2C ，直线l的极坐标方程为sin()4πρθ+=直线l 与曲线2C 交于A ，B 两点。

（Ⅰ）求曲线2C 的普通方程； （Ⅱ）求线段AB 的长。

3．在直角坐标系xOy 中，曲线1C 的参数方程为1cos 2(1cos 2x y ααα=+⎧⎪⎨=⎪⎩为参数），在极坐标系中,曲线2C的极坐标方程为sin()4πρθ-=（1）求曲线2C 的普通方程；（2）设1C 与2C 相交于,A B 两点，求AB 的长．4．在直角坐标系xOy 中，以原点O 为极点，x 轴的正半轴为极轴建立极坐标系。

已知曲线C 1的极坐标方程为θρ22sin 12+=，直线l 的极坐标方程为θθρcos sin 24+=。

（Ⅰ）写出曲线C 1与直线l 的直角坐标方程；（Ⅱ）设Q 为曲线C 1上一动点，求Q 点到直线l 距离的最小值。

5．在直角坐标版权法xOy 吕，直线l 的参数方程为132(32x t t y t ⎧=+⎪⎪⎨⎪=⎪⎩为参数），以原点为极点，x 轴的正半轴为极轴建立极坐标系，的极坐标方程为23sin ρθ=.（Ⅰ）写出的直角坐标方程；（Ⅱ）P 为直线l 上一动点，当P 到圆心C 的距离最小时，求点P 的坐标.6．在直角坐标系xOy 中，直线1C :x =-2，圆2C ：()()22121x y -+-=,以坐标原点为极点， x 轴的正半轴为极轴建立极坐标系. （Ⅰ）求1C ，2C 的极坐标方程； （Ⅱ）若直线3C 的极坐标方程为()4R πθρ=∈，设2C 与3C 的交点为M ,N ,求2C MN ∆的面积.7．已知直线l ：352132x y t ⎧=+⎪⎪⎨⎪=⎪⎩（t 为参数）．以坐标原点为极点，x 轴的正半轴为极轴建立极坐标系，曲线C 的坐标方程为2cos ρθ=．（1）将曲线C 的极坐标方程化为直坐标方程；（2）设点M的直角坐标为，直线l 与曲线C 的交点为A ，B ，求|MA|•|MB|的值．8.在极坐标系中曲线C 的极坐标方程为2sin cos 0ρθθ-=，点(1,)2M π．以极点O 为原点，以极轴为x 轴正半轴建立直角坐标系．斜率为1-的直线l 过点M ，且与曲线C 交于,A B 两点．（Ⅰ）求出曲线C 的直角坐标方程和直线l 的参数方程； （Ⅱ）求点M 到两点,A B 的距离之积．9．在平面直角坐标系中，以坐标原点为极点，x 轴的正半轴为极轴建立极坐标系，已知曲线C 的极坐标方程为()2sincos 0a a ρθθ=>，过点()2,4P --的直线l 的参数方程为2242x y ⎧=-+⎪⎪⎨⎪=-+⎪⎩（t为参数），直线l 与曲线C 相交于,A B 两点． （Ⅰ）写出曲线C 的直角坐标方程和直线l 的普通方程；（Ⅱ）若2PA PB AB ⋅=，求a 的值．10．．(本小题满分12分)极坐标系的极点为直角坐标系xOy 的原点，极轴为x 轴的正半轴，两种坐标系中的长度单位相同．已知曲线C 的极坐标方程为()θθρsin cos 2+=，斜率为3的直线l 交y 轴与点()1,0E ． （1）求C 的直角坐标方程，l 的参数方程；（2）直线l 与曲线C 交于A 、B 两点，求EB EA +的值．11．在直角坐标系xOy中，圆C的参数方程1cos(sinxyϕϕϕ=+⎧⎨=⎩为参数）.以O为极点，x轴的非负半轴为极轴建立极坐标系.（Ⅰ）求曲线C的极坐标方程；（Ⅱ）设直线l极坐标方程是2sin()3πρθ+=射线:3OMπθ=与圆C的交点为O、P，与直线l的交点为Q，求线段PQ的长.12．选修４－４：坐标系与参数方程）已知极坐标系的极点与直角坐标系的原点重合,极轴与x轴的正半轴重合.若直线l的极坐标方程为sin()4πρθ-=(1)把直线l的极坐标方程化为直角坐标系方程;(2)已知P为椭圆22:139x yC+=上一点,求P到直线l的距离的最小值.坐标系与参数方程选做专题（2015-10-14）（参考答案）1．（Ⅰ） 1:C 23y x =-，2:C 35cos ,55sin .x y αα=+⎧⎨=+⎩（α为参数） ；（Ⅱ）相交.解析：（Ⅰ）∵4,52.x t y t =+⎧⎨=+⎩，∴4t x =-，代入52y t =+得，52(4)y x =+-，即23y x =-．∴曲线1C 的普通方程是23y x =-．将ρ=cos x ρθ=，sin y ρθ=代入曲线2C 的方程26cos 10sin 90ρρθρθ--+=，得2261090x y x y +--+=，即 22(3)(5)25x y -+-=．设35cos x α-=，55sin y α-=得曲线2C 的参数方程：35cos ,55sin .x y αα=+⎧⎨=+⎩（α为参数） （Ⅱ）由（Ⅰ）知，曲线1C 是经过点(4,5)P 的直线，曲线2C 是以(3,5)O '为圆心半径为5r =的圆．∵1PO r '=<，∴点(4,5)P 在曲线2C 内，∴曲线1C 和曲线2C 相交．2．（Ⅰ）16)4(22=-+y x（Ⅱ）解：（Ⅰ）设),(y x P ，则由条件知)2,2(y x M 。

（2024-全国卷2）[物理——选修3-4]（25分）(2)（5分）图(a)为一列简谐横波在t=0.20s 时的波形图，P 是平衡位置在x=2.0m 处的质点，Q 是平衡位置在x=4.0m 处的质点；图(b)为质点Q 的振动图形。

下列说法正确的是 。

（填正确答案标号。

选对2个得2分，选对2个得4分，选对3个得5分，每选错2个扣3分，最低得分为0分）A ．在t=0.20s 时，质点Q 向y 轴正方向运动B ．在t=0.25s 时，质点P 的加速度方向与y 轴正方向相问C ．从t=0. 20s 到t =0. 25s ，该波沿x 轴负方向传播了6mD ．从t=0. 20s 到t =0. 25s ，质点P 通过的路程为30cmE ．质点Q 简谐运动的表达式为0.10sin10y t π=（国际单位侧）【答案】BCE【解析】由Q 点的振动图线可知，t=0.20s 时质点Q 向y 轴负方向振动，A 错误；由波的图像可知，波向左传播，波的周期为T =0.2s ，t=0.20s 时质点P 向上振动，经过0.25s=3T/4时，即在t = 0.25s 时，质点振动到x 轴下方位置，且速度方向向上，加速度方向也沿y 轴正向，B 正确；波速8/40/0.2v m s m s T λ===，故从t = 0.20s 到t = 0.25s ，该波沿x 负方间传播的距离为：400.156x vt m m ==⨯=， C 正确；由于P 点不是在波峰或波谷或者平衡位置，故从t = 0.20s 到t=0.25的3/4周期内，通过的路程不等于3A = 30cm ，选项D 错误；质点Q 做简谐振动的表达式为：2sin()0.10sin10y A t t T ππ==（国际单位），选项E 正确。

(2) ( 20分）一厚度为h 的大平板玻瑞水平放置，共下表面贴有一半径为r 的圆形发光面。

在玻璃板上表面放置一半径为R 的圆纸片，圆纸片与圆形发光面的中心在同一竖直钱上。

专题15：选修3-3考情分析：（1）主要考查分子动理论知识；（2）重点考察气体三个实验定律。

建议：题目难度不大，考查点比较集中，应该有针对性地多做几道题目，如果把近几年全国各地高考题浏览一遍，应对高考应该没有问题。

1、（2018年新课标全国卷I ）如图，一定质量的理想气体从状态a 开始，经历过程①、②、③、④到达状态e 。

对此气体，下列说法正确的是A ．过程①中气体的压强逐渐减小B ．过程②中气体对外界做正功C ．过程④中气体从外界吸收了热量D ．状态c 、d 的内能相等E ．状态d 的压强比状态b 的压强小2、（2018年新课标全国卷I ）如图，容积为V 的汽缸由导热材料制成，面积为S 的活塞将汽缸分成容积相等的上下两部分，汽缸上部通过细管与装有某种液体的容器相连，细管上有一阀门K 。

开始时，K 关闭，汽缸内上下两部分气体的压强均为p 0。

现将K 打开，容器内的液体缓慢地流入汽缸，当流入的液体体积为V 8时，将K 关闭，活塞平衡时其下方气体的体积减小了V6。

不计活塞的质量和体积，外界温度保持不变，重力加速度大小为g 。

求流入汽缸内液体的质量。

3、（2018年新课标全国卷II ）对于实际的气体，下列说法正确的是______A ．气体的内能包括气体分子的重力势能B ．气体的内能包括分子之间相互作用的势能C ．气体的内能包括气体整体运动的动能D ．气体体积变化时，其内能可能不变E ．气体的内能包括气体分子热运动的动能4、（2018年新课标全国卷II ）如图，一竖直放置的气缸上端开口，气缸壁内有卡口a 和b ，a 、b 间距为h ，a 距缸底的高度为H ；活塞只能在a 、b 间移动，其下方密封有一定质量的理想气体。

已知活塞质量为m ，面积为S ，厚度可忽略；活塞和汽缸壁均绝热，不计他们之间的摩擦。

开始时活塞处于静止状态，上、下方气体压强均为p 0，温度均为T 0。

现用电热丝缓慢加热气缸中的气体，直至活塞刚好到达b 处。

2012-2017年新课标全国卷专题分类汇总——专题14：选修3-5编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（2012-2017年新课标全国卷专题分类汇总——专题14：选修3-5）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为2012-2017年新课标全国卷专题分类汇总——专题14：选修3-5的全部内容。

专题14：选修3—5考情分析：2017年首次变为必考部分，重要性大大增加。

原子物理主要考查光电效应和原子核相关问题。

动量主要考查利用动量守恒定律和能量关系解决物块的碰撞问题。

建议：除碰撞问题外，其它题目难度不大，要关注几个常考点。

碰撞问题的解题思路比较明确,注意机械能守恒定律的成立条件，有时还要用到动能定理。

如果把近几年各地高考题浏览一遍,应对高考应该没问题。

1、（2016年新课标全国卷I）现用某一光电管进行光电效应实验，当用某一频率的光入射时,有光电流产生。

下列说法正确的是_______。

A．保持入射光的频率不变，入射光的光强变大,饱和光电流变大B．入射光的频率变高,饱和光电流变大C．入射光的频率变高，光电子的最大初动能变大D．保持入射光的光强不变,不断减小入射光的频率，始终有光电流产生E．遏止电压的大小与入射光的频率有关，与入射光的光强无关2、（2015年新课标全国卷II)实物粒子和光都具有波粒二象性，下列事实中突出体现波动性的是_______。

A．电子束通过双缝实验后可以形成干涉图样B．β射线在云室中穿过会留下清晰的径迹C．人们利慢中子衍射来研究晶体的结构D．人们利用电子显微镜观测物质的微观结构E．光电效应实验中，光电子的最大初动能与入射光的频率有关，与入射光的强度无关3、（2014年新课标全国卷II）在人类对微观世界进行探索的过程中，科学实验起到了非常重要的作用.下列说法符合历史事实的是_______。

近三年全国Ⅰ卷地理选修试题分析之我见一、选做题《环境保护》考题分析（一）考题分类汇总（二）考情分析1、考题：背景与情境源于生活，源于某局部区域的客观存在；设问角度多是环境问题的危害及措施；答案语言脱离教材，源于生活和专业术语的概括。

2、考生：会联系生活和所学知识，但受生活经历和感知的局限，思考问题的角度多受限，且语言与所给答案差别较大。

3、变化（1）改变了“无图不成题”的惯例；（2）审题对语文素养的要求越来越高；（3）答案打破“校园和学科常规思维”，引导“社会和专业术语”（三）教学建议1、教学过程多设计学生活动2、教学内容与素材多关注“三生”3、增加课外实践，践行地理实践力，提升综合素养二、选做题《旅游地理》考题分析（一）考题分类汇总考点 图示类型 上级考点具体考点 旅游评价、旅游资源的开发与保护 村民生活在“传统古村落”中对促进当地旅游业健康发展的作用 景观照片 (实景图) 旅游评价 民宿旅游快速发展的原因 区域图 旅游安全 峡谷徒步旅游可能遭遇的风险 等高线地形图1、考题：通过景观照片或区域图，以某局部区域的客观存在为载体，；设问角度多是旅游评价或旅游安全；答案语言脱离教材，源于生活和专业术语的概括。

2、考生：会联系生活和所学知识，但受生活经历和感知的局限，思考问题的角度多受限，且语言与所给答案差别较大。

3、变化（1）通过实景图代替传统“地图”，越来越接近生活景观；（2）审题对语文素养的要求越来越高；（3）答案打破“校园和学科常规思维”，引导“社会和专业术语”（三）教学建议1、教学过程多设计学生活动2、教学内容与素材多关注“旅游前沿”问，大角度，小切口开展教学3、增加课外实践，践行地理实践力，提升综合素养三、选修模块高考试题的现状与建议（一）现状1、试题背景大部分脱离学生实际目前高考试题说是“生活”和“鲜活”，其实大部分是脱离学生生活的，而是部分大学教授就某一狭窄部分的研究区域，与“生活中的地理”和“有用的地理”相差很大。