种群增长曲线论文

高中生物种群的增长曲线与K值应用常卿在高中生物教材中，种群增长曲线是一个重要的知识点，并在近年的生物高考试卷中都有所体现。

但笔者在教学中发现，由于受到教材篇幅的限制，这一知识内容一上来起点就很高，学生一下子很难理解。

本文从理解的角度出发，对种群增长曲线进行释疑，同时释义其具体应用。

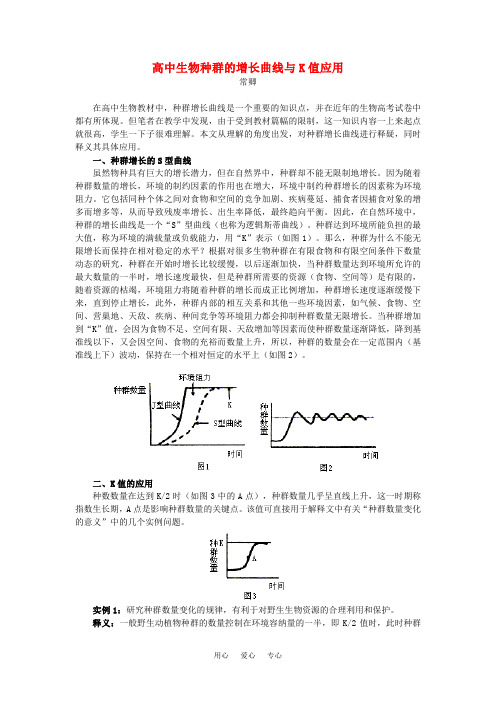
一、种群增长的S型曲线虽然物种具有巨大的增长潜力，但在自然界中，种群却不能无限制地增长。

因为随着种群数量的增长，环境的制约因素的作用也在增大，环境中制约种群增长的因素称为环境阻力。

它包括同种个体之间对食物和空间的竞争加剧、疾病蔓延、捕食者因捕食对象的增多而增多等，从而导致残废率增长、出生率降低，最终趋向平衡。

因此，在自然环境中，种群的增长曲线是一个“S”型曲线（也称为逻辑斯蒂曲线）。

种群达到环境所能负担的最大值，称为环境的满载量或负载能力，用“K”表示（如图1）。

那么，种群为什么不能无限增长而保持在相对稳定的水平？根据对很多生物种群在有限食物和有限空间条件下数量动态的研究，种群在开始时增长比较缓慢，以后逐渐加快，当种群数量达到环境所允许的最大数量的一半时，增长速度最快，但是种群所需要的资源（食物、空间等）是有限的，随着资源的枯竭，环境阻力将随着种群的增长而成正比例增加，种群增长速度逐渐缓慢下来，直到停止增长，此外，种群内部的相互关系和其他一些环境因素，如气候、食物、空间、营巢地、天敌、疾病、种间竞争等环境阻力都会抑制种群数量无限增长。

当种群增加到“K”值，会因为食物不足、空间有限、天敌增加等因素而使种群数量逐渐降低，降到基准线以下，又会因空间、食物的充裕而数量上升，所以，种群的数量会在一定范围内（基准线上下）波动，保持在一个相对恒定的水平上（如图2）。

二、K值的应用种数数量在达到K/2时（如图3中的A点），种群数量几乎呈直线上升，这一时期称指数生长期，A点是影响种群数量的关键点。

该值可直接用于解释文中有关“种群数量变化的意义”中的几个实例问题。

也谈种群增长曲线、增长率和增长速率的数学模型北京怀柔区育才中学（101400）吴昌贵吴昌贵（1978- ），男，大学本科，中学一级教师，E-mail:wcg78_0@关于种群增长率和增长速率的问题很多同行都有过精彩的论述，但是有一些基本的问题仍然令人困惑，例如J 型、S 型增长都有增长率与增长速率吗？如果有，它们之间是什么关系？我们讨论的种群增长率和增长速率与《普通生态学》中的周限增长率、每员增长率之间又是什么关系？逻辑斯蒂增长（即S 型增长）的增长速率与时间是什么关系？围绕以上几个问题，本文就常见的两种J 型曲线和一种S 型曲线的种群数量与时间的数学方程式、增长率和增长速率的数学方程式加以对比，以期抛砖引玉。

1、种群数量、增长率和增长速率的数学含义种群数量N 是关于时间t 的函数，记做N=f(t)，那么增长率f(t+t)-f(t)=f(t)∆ϕ（一般情况下按Δt=1考虑），代表的是种群增长量与起始数量的比值；而增长速率0f(t+t)-f(t)=lim tt dN dt ∆→∆∆，代表的是种群的瞬时增长量。

2、两种增长模型2.1 J 型增长模型2.1.1世代不连续的J 型增长模型模型假设：①食物和空间条件充裕、气候适宜、没有敌害等条件下（以下简称为理想条件下），种群数量以固定的倍数增长，不受种群密度的制约；②种群内生物世代不重叠，增长不连续；③不具年龄结构；④没有迁入和迁出。

种群数量N 与时间t 的数学方程式：0t N N =λ（N 0为种群起始数量，λ表示结束时种群数量与开始时的比值）。

种群增长率的方程式：=-1ϕλ（按Δt=1,即间隔一个时间单位计算，以下均如此计算）。

2.1.2世代连续的J 型增长模型模型假设：①理想条件下，种群有一个恒定的每员（单位）瞬时增长量，它与密度无关；②种群内生物世代重叠，连续增长；③具年龄结构；④没有迁入和迁出。

种群数量N 与时间t 的数学方程式：0e rt N N =（N 0为种群起始数量，e 为自然对数的底数，r 为种群的每员瞬时最大增长量）。

种群增长率与种群增长速率的辨析摘要：种群增长率、增长速率是生态学重点考查的内容，但是当今中学生物教材没有明确的解析，在平常的教学和练习中，经常混为一谈，错误百出，作者从不同层面进行了辨析。

关键词：种群增长率种群增长速率时间种群数差种群增长率与种群增长速率虽一字之差，但内涵完全不同，在练习题甚至高考题中没有很好地区分开。

在中学生物教材中处理较模糊，不少教辅资料的解读或解析都存在偏差。

对此，从以下几方面进行辨析，以期学生全面理解种群增长率和增长速率。

一、从概念上辨析1.增长率：增长率是指单位数量群体在单位时间内种群数量变化率，即种群在单位时间内净增加的个体数占个体总数的比率。

计算公式：增长率=出生率-死亡率=出生数-死亡数）/（单位时间×单位数量）*100%。

如某种群现有数量为a，一年后，该种群数为b，那么该种群在当年的增长率为（b-a）/a*100%。

2.增长速率：增长速率是指种群在单位时间内变化的数量，计算公式：增长速率=（出生数-死亡数）/单位时间，即增长速率=（现有个体数-原有个体数）/增长时间。

上述例子，增长速率为（b-a）/1年。

增长率是个百分率，没有”单位”，而增长速率有“单位”，“个（株）/年、个（株）/月”。

增长率和增长速率没有大小上的相关性。

二、从数学模型上辨析1.与密度无关的种群离散增长模型2.与密度无关的种群连续增长模型3.与密度有关的种群连续增长模型（逻辑斯谛增长）三、从种群增长曲线上辨析曲线斜率的含义是指的是单位时间内增加的数量，因此，“j”型和“s”型两种增长曲线图像中的斜率都可表示增长速率。

在“j”型增长曲线中，每年的增长率不变（如图5）；由于“j”型增长曲线的切线斜率是在不断增大，直至无穷，所以其增长速率也就不断增大（如图5）。

在“s”型增长曲线中，曲线的斜率变化规律是在最大值之前，种群增长速率逐渐增大，增大的过程遵循“慢→快→慢”的“s”型变化规律，在最大值之后，种群增长速率逐渐减小，减小的过程遵循“慢→快→慢”的反“s”型变化规律。

种群数量变化曲线中的种群增长率和增长速率
马彬
【期刊名称】《学苑教育》
【年(卷),期】2012(000)013
【摘要】在高中生物学的生态学部分中，种群数量变化是一个常见的考点。

而种群数量变化曲线的种群增长率和增长速率的代换是考试中常见的考查方式。

本文例析了种群数量变化的考题，用数学推导和推理的方法，归纳了种群数量的“J”型和“S”型变化的种群增长率和增长速率曲线。

【总页数】1页(P69-69)
【作者】马彬
【作者单位】四川省射洪中学校
【正文语种】中文
【中图分类】G633.91
【相关文献】
1.种群数量增长速率与增长率的辨析 [J], 黄建华
2.辨析种群增长率与种群增长速率一字之差 [J], 魏威
3.由种群增长率反向分析种群数量的变化 [J], 周泉
4.种群增长曲线中增长率和增长速率的辨析 [J], 刘松
5.种群增长曲线中增长率和增长速率的辨析 [J], 刘松
因版权原因，仅展示原文概要，查看原文内容请购买。

基于logistic数学模型的种群增长规律全文共四篇示例，供读者参考第一篇示例：种群增长是生物学中一个重要的研究课题，从古至今，人们一直致力于探索各种生物群体的增长规律。

logistic数学模型被广泛应用于种群增长的研究中。

logistic模型由数学家皮埃尔·弗朗索瓦·热涅提出，用来描述种群在资源有限的情况下的增长趋势。

通过logistic模型，我们可以更好地理解种群增长的规律，并预测未来的发展走势。

让我们来了解一下logistic模型的基本原理。

在logistic模型中，种群数量随着时间的推移呈现出S形曲线的增长趋势。

该模型的基本方程可以表示如下：dN/dt = rN(1 - N/K)dN/dt表示种群数量N随时间t的变化率，r是种群固有的增长速率，K是种群的环境容量。

在这个方程中，第一项rN表示种群的自然增长，第二项-rN^2/K表示种群数量受到环境资源限制的补偿性减少。

当种群数量接近环境容量K时，增长速率趋于零，种群数量稳定在一个平衡值。

通过logistic模型，我们可以得出一些关于种群增长的规律。

种群数量不会一直呈指数增长，而是会在某个阈值处趋于稳定。

这是因为种群在资源有限的情况下，无法无限地增长下去。

种群的增长速率取决于种群固有的增长速率r和环境容量K。

当种群数量接近环境容量时，增长速率会减缓，最终趋于零。

种群数量的波动会受到环境因素的影响，如自然灾害、疾病传播等，从而影响种群的增长走势。

在实际应用中，logistic模型可以帮助我们更好地管理和预测种群的增长情况。

通过对种群数量、环境容量和增长速率等参数的测算，我们可以预测未来种群数量的变化趋势，及时采取控制措施，保护种群的生存和发展。

logistic模型还可以用于研究不同因素对种群增长的影响，为生态环境保护和资源管理提供科学依据。

基于logistic数学模型的种群增长规律，为我们深入了解种群发展的机理提供了重要的理论支撑。

种群的增长速率曲线和增长率曲线再探讨浙江省绍兴县柯桥中学叶建伟摘要到目前为止，种群增长率曲线和增长速率曲线在中学生物教材和相应的教学辅导资料中还没有一个较为统一的说法，本文就种群增长率曲线和增长速率曲线进行了探讨。

关键词种群增长速率曲线增长率曲线探讨种群的增长方式包括指数增长（“J”型增长）和逻辑斯谛增长（“S”型增长），前者是在理想状态下，即资源无限、空间无限和不受其他生物制约的条件下产生的，后者是在现实状态下，即资源有限、空间有限和受其他生物制约的条件下产生的。

若以时间为横坐标，种群中个体数量为纵坐标，那么两种增长曲线如图1所示。

对于上述两种增长方式，需要区别种群增长率和增长速率的变化，但是到目前为止，对于种群增长率和增长速率曲线在中学生物教材和相应的教学辅导资料中还没有一个较为统一的说法，对此，笔者查阅相关资料，同时结合自己多年的教学实践，谈谈自己的看法。

1 种群增长速率和增长率的定义种群增长速率是指种群在单位时间内增加的个体数量，其计算公式为：增长速率 =（现有个体数－原有个体数）／增长时间，单位可以用“个/年”表示。

种群增长率指种群在单位时间内净增加的个体数占原个体总数的比率，其计算公式为：增长率 =（现有个体数－原有个体数）／（原有个体数·增长时间），单位可以用“个/个·年”表示。

种群的出生率减去死亡率就是种群的自然增长率[1]。

2 指数增长的增长速率和增长率种群在理想条件下呈指数增长，其增长曲线符合指数函数N t=N0λt或N t+1=N tλ（N为种群个体数，N 0为起始种群个体数，t为时间，λ为种群周限增长率，下同），其中λ具有开始和结束时间，它表示种群大小在开始和结束时的比率。

若以年为时间单位，指数增长种群的增长速率为：（N0λt+1－N0λt）个/年=N0λt（λ－1）个/年，所以指数增长种群的增长速率随时间变化呈等比数列，公比为λ，其通项公式为：= N0（λ－1）λt（表示种群增长速率）。

在有限环境中,种群增长的数学模型1.引言1.1 概述引言是一篇文章的开篇部分，用来介绍文章的主题和背景，并概述文章的结构和目的。

在这篇长文中，我们将讨论种群增长的数学模型在有限环境中的应用。

种群增长是动态生态学的重要研究领域之一，它关注的是在一定时间内，一个种群数量的变化规律及其驱动机制。

数学模型通过建立方程来描述和预测种群在不同环境条件下的变化趋势，对于生态学、保护生物学以及人口学等领域都具有重要的理论和应用价值。

然而，在有限环境中种群的增长受到了一系列限制，例如资源的有限性、生境的容纳能力、竞争关系以及捕食压力等因素的影响。

这些限制条件将对种群的增长速率、数量稳定性和种群结构产生重要影响，进而影响整个生态系统的稳定性和可持续性。

因此，本文将从数学模型的角度出发，重点探讨有限环境中种群增长的数学模型。

我们将首先介绍种群增长的基本原理和常用的数学模型，并针对有限环境下的种群增长问题进行深入研究。

通过建立精确的数学方程和参数估计方法，我们将探讨有限环境下种群增长的规律及其应对策略。

本文的目的在于提供一个全面而系统的框架，帮助读者理解和应用种群增长的数学模型。

通过研究有限环境下的种群增长，我们可以更好地了解和管理生态系统的动态变化，为保护和维护生物多样性提供科学依据和决策支持。

接下来，我们将在正文部分详细介绍种群增长的数学模型以及有限环境中的种群增长问题。

最后，我们将对结果进行总结，并展望未来在这一领域的研究方向和挑战。

让我们一起深入探索种群增长的奥秘，为可持续发展的生态系统贡献我们的智慧和力量。

1.2文章结构1.2 文章结构本文主要围绕在有限环境中种群增长的数学模型展开，共分为引言、正文和结论三个部分。

在引言部分，我们将对文章的主题进行概述，并介绍文章的结构和目的。

具体而言，在1.1小节中，我们将简要阐述种群增长的背景和重要性，以及数学模型在解释和预测种群增长中的作用。

在1.2小节中，我们将详细介绍文章的整体结构以及各个部分的内容和目的。