2019-2020年高三下学期数学周练一

2019-2020年高三下学期数学（文）周考测试题2016.4.16 含答案2016.4.16一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知全集{}1,2,3,4,5U =，集合{}{}1,2,3,3,4,5M N ==，则集合{}1,2可以表示为（ ） A ．M NB ．()UC M N C ．()U MC ND ．()()U U C M C N2.已知,a b R ∈，i 是虚数单位，若3a i bi +=-，则1a bii+=-（ ） A ．2i - B ．2i + C ．12i - D ．1i + 3.下列各组命题中，满足“‘p q ∨’为真、‘p q ∧’为假、‘q ⌝’为真”的是（ ） A ．:0;:0p q =∅∈∅B ．:2p x >是1x >成立的充分不必要条件；{}:1,1,0,210q x x ∀∈-+>C ．:(0,0);:p a b a b q +≥>>不等式x x >的解集是(,0)-∞D ．1:p y x=在定义域内是增函数；:()x xq f x e e -=+是偶函数 4.已知向量(,3),(1,4),(2,1)a k b e ===，且(2)a b c -⊥，则实数k =（ ） A ．152 B ．3 C ．92D ．0 5.已知等差数列的公差为2，若成等比数列，是的前n 项和，则9S 等于（ ）A. -8B. -6C. 10D. 0 6.已知2是函数2log (),2()2,2xx m x f x x +≥⎧=⎨<⎩的一个零点，则[](4)f f 的值是（ ） A ．3 B ．2 C ．1 D ．2log 37.已知x y 、满足101010x y x x y +-≥⎧⎪-≤⎨⎪-+≥⎩，目标函数2z y x =-的最大值为m ，则2sin()2y mx π=+的最小正击期是（ ）A ．3πB ．23πC ．πD ．2π8.阅读如图所示的程序框图，若输出的结果20152016S =，则整数m 的值为（ ）A ．2017B ．2016C ．2015D ．20149.如图所示是一个几何体的三视图，若该几何体的外接球的表面积是6π， 则正视图中三角形的高x 的值为（ ） A ．1 B ．2 CD10.已知函数()sin()(0,)2f x A x πωϕωϕ=+><的部分图象如图所示，则下列说法错误的是（ ） A ．(0)1f =- B ．()f x 关于直线6x π=-对称C ．()f x 在,2ππ⎡⎤⎢⎥⎣⎦上的值域为[]1,1-D ．()f x 的增区间为,,63k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦11.圆心在曲线2(0)y x x =>上，且与直线:210l x y ++=相切的面积最小的圆的方程为（ ）A ．22(2)(1)5x y -+-= B ．22(1)(2)5x y -+-= C ．22(1)(2)25x y -+-=D ．22(2)(1)25x y -+-=12.已知函数11,2()2(2),2x x f x f x x ⎧--<=⎨-≥⎩，12()2x g x -=，设方程()()f x g x =的根从小到大依次为*12,,,,n x x x n N ∈，则数列{}()f x 的前n 项和为（ ）A ．122n +- B ．21n -C ．2nD ．21n -第Ⅱ卷（共90分）二、填空题：本大题共4小题，每小题5分，共20分，把答案填在答题卡中对应题号后的横线上．13.如图是某学校一名篮球运动员在10场比赛中所得分数的茎叶图，若这10场比赛复仇的众数为16，则这10场比赛得分的中位数为 ________．14.函数3()2f x x x =-在点(1,(1))f 处的切线为l ，数列{}n a 的前n 项和为n S ，且点1(2,)n n S n ++ 在直线l 上，则数列{}n a 的通项n a =_________．15.若以双曲线2221(0)2x y b b-=>的左、右焦点12,F F和点M 为顶点的三角形为直角三角形，则24y bx =的焦点坐标为________．16.给定两个平面向量OA 和OB ，它们的夹角为120°，且OA OB =，点C 在以O 为圆心OA 为半径的圆弧AB 上，若OC xOA yOB =+（其中,x y R ∈），则满足x y +≥的概率为________．三、解答题 ：本大题共8小题，其中有3道选做题选做一道，共70分.解答应写出文字说明、证明过程或演算步骤.17.（本小题满分12分）在ABC ∆中，,,a b c 分别为内角,,A B C 的对边，且222b c a bc +-=． （1）求角A 的大小；（2）设函数2()sin 2cos ,2,()12x f x x a f B =+==时，求b ．18.（本小题满分12分）某组同学将高中学生课外阅读情况作为一个研究性课题，他们随机调查了100名同学，其中55个女同学，45个男同学，下图是根据调查结果绘制的周课外阅读时间的频率分布直方图，将周阅读时间不低于4小时的同学称为“阅读爱好者”，已知“阅读爱好者”中有10个女同学．0 5 8 61 2 4 x69269频率/组距（1）根据已知条件完成22⨯列联表，并据此资料你能否有95%的把握认为是否为“阅读爱好者”与性别有关？（2）将周阅读时间不低于5小时的同学称为“读书迷”，已知“读书迷”中有2名女同学，若从“读书迷”中任意选取2人，求至少有1名女同学的概率．附22()()()()()n ad bc K a b c d a c b d -=++++，19.（本小题满分12分）如图，平行四边形ABCD 中，0,,60AB BD DE BC A ⊥⊥∠=，将,ABD DCE ∆∆分别沿,BD DE 折起，使//AB CE ． （1）求证：AB BE ⊥；（2）若四棱锥D ABEC -求CE 长并求点C 到面ADE 的距离．20.（本小题满分12分）在圆221x y +=上任取一个动点P ，作PQ x ⊥轴于,Q M 满足2QM QP =，当P 在圆上运动时，M 的轨迹为曲线C ． （1）求曲线C 的方程；（2）曲线C 与x 轴正半轴、y 轴正半轴分别交于A 、B ，直线(0)y kx k =>与曲线C 交于E 、F ，当四边形AEBF 面积最大时，求k 的值．21.（本小题满分12分）已知定义在(0,)e 上的函数()ln x af x x x-=-． （1）求此函数的单调区间；（2）若过点(1,1)A -有且仅有一条直线与函数()y f x =的图象相切，求a 的取值范围．请考生在22、23、24三题中任选一题作答，如果多做，则按所做的第一题记分.22.（本小题满分10分）如图，AB 为圆的直径，过C 作ABC ∆的外接圆的切线,,CD BD CD BD ⊥与外接圆交于点E ．（1）求证：2BC AB BD =； （2）若2,3CD BE ==，求AB 长．23.（本小题满分10分）已知直线l 经过点(1,1)P ，倾斜角6πα=，圆2cos :2sin x C y θθ=⎧⎨=⎩（θ为参数）．（1）写出圆C 的普通方程和直线l 的参数方程；（2）设直线l 与圆C 相交于两点A 、B ，求点P 到A 、B 两点的距离之积．24.（本小题满分10分）设函数()f x x a =-．（1）当2a =时，解不等式()51f x x ≥-+； （2）若()1f x ≤的解集为[]0,2，11(0,0)2a m n m n+=>>，求证：24m n +≥．2016届高三文科数学周考测试题参考答案2016.4.161.C 【解析】1，2两个元素属于M ，故应取M 与其它集合的交集，又不属于N ，故其在N 的补集内，选C ．2.B 【解析】∵3a ibi +=-，∴3,1a b ==-，则3211a bi ii i i+-==+--，故选B ． 3．B 【解析】由题，应选p 为真、q 为假的选项．A 中p 、q 都为假；D 中p 为假、q 为真；C 中p 、q 都为真；B 中p 为真，q 为假，故选B ． 4．C 【解析】5．D 【解析】由题：2111(4)(6)a a a +=+ ，解得 ：19988,9(8)202a S ⨯=-=⨯-+⨯= ，选D ．6．A 【解析】由题2log (2)0m += ，∴1m =-；[]2log 32(4)(log 3)23f f f ===，选A ．7．B 【解析】题中不等式组表示的是一个三角形区域ABC ，其中(1,2),(0,1),(1,0)A B C ，目标函数2z y x =-在A 取得最大值，最大值为3，故2sin()2y mx π=+的最小正周期是23π，选B ．8．C 【解析】该框图为求和：1111111111223(1)22311n S n n n n n =+++=-+-++-=⨯⨯+++，结果为20152016，说明输出时S 中的2015n =，进入下一步运算后2016n =，故2015m =． 9．D，x ，其体对角线=外接球的表面积为22446S R πππ==⨯=，解得：x =，选D ．10．C【解析】由图，()2sin(2)6f x x π=-．11．A 【解析】设圆心2(,)x x，圆心到直线l 的距离为：15x x +≥=当2x =22(2)(1)5x y -+-=，选A ．12．B 【解析】函数11,2()2(2),2x x f x f x x ⎧--<=⎨-≥⎩的图象如图所示，1x =时，()1,3f x x ==时，()2,5f x x ==时，()4f x =，所以方程12()2x f x -=的根从小到大依次为1，3，5，…，数列{}()n f x 从小到大依次为1，2，4，…，组成以1为首项，2为公比的等比数列， 所以数列{}()n f x 的前n 项和为21n n S =-，故选B ．13．15 【解析】得分的众数为16，故6x =，中位数为1416152+=．14．21n- 【解析】函数3()2f x x x =-在点(1,(1))f 处的切线为:2l y x =-，∴1122,22n n n n S n S n +++=-=--，∴12(1)2n n S n -=---，∴1122(2(1)2)21(2),1n n n n n n a S S n n n n +-=-=------=-≥=时，2111212121a S ==--==-，∴*n N ∈时，21n n a =-．15．(1,0)【解析】显然点M1212F F c ==，∴1b =． 16．12【解析】不妨设1oA =，以O 为原点，OA 为x轴正半轴，建立直角坐标系，则1(1,0),(2A B -，设(cos ,sin )C θθ，则11(cos ,sin )(1,0)(()22x y x y y θθ=+-=-，所以cos x y θθθ⎧=⎪⎪⎨⎪⎪⎩，cos 2sin()6x y πθθθ+=+=+≥,62ππθ⎡⎤∈⎢⎥⎣⎦，故满足x y +≥的概率为126223πππ-=．17．【解析】（1）在ABC ∆中，因为222b c a bc +-=，由余弦定理可得2221cos 222b c a bc A bc bc +-===．．．3分 ∵0A π<< ∴3A π=．．．．．．．．．．．．．．．6分（2）2()sin 2cossin cos 1)124x f x x x x x π=+=++=++，())114f B B π=++=+，∴4B π=，．．．．．．9分 ∵sin sin a bA B=，即：002sin 60sin 45b =，∴b =．．．．．．．．．．12分 18．【解析】（1）由频率分布直方图可知，在抽取的100人中，“阅读爱好者”有25人，从而22⨯列联表如下： 非阅读爱好者 阅读爱好者 合计男 30 15 45 女 45 10 55 合计7525100．．．．．．．．．．． 3分由22⨯列联表中数据代入公式计算，得：222()100(30104515)100 3.030()()()()7525455533n ad bc K a b c d a c b d -⨯⨯-⨯===≈++++⨯⨯⨯因为3.030 3.841<，所以，没有95%的把握认为是否为“阅读爱好者”与性别有关．．．．．．．．6分（2）由频率分布直方图知：“读书迷”为5人，记他们为1，2，3，4，5，其中1，2为女同学， 从“读书迷”中任意选取2人，有以下10种情况：(1,2)、(1,3)、(1,4)、(1,5)、(2,3)、(2,4)、(2,5)、(3,4)、(3,5)、(4,5)．至少有1名女同学的情况数是7种，故至少有1名女同学的概率为710．．．．12分19．【解析】（1）证明：折叠前后都有：,AB BD CE DE ⊥⊥，因为：//AB CE ，∴AB DE ⊥，∴AB ⊥面BDE ，∴AB BE ⊥．．．．．．．．．．．．．．6分 （2）设ECx =，则2,,3AB DC x DE BE x ====，∵1(2)332D ABECx x x V -+⨯=⨯==，∴1x =故1CE =； ．．．．．．．．．．．．．．．．．9分∴2,3,AB DC DE BE AE =====∵C ADED AEC V V --=，即：1111133232h h ⨯=⨯⨯⨯=C 到面ADE 的距离．12分20．【解析】（1）设00(,),(,)M x y P x y ，则002x x y y =⎧⎨=⎩，得：0012x x y y=⎧⎪⎨=⎪⎩，而00(,)P x y 在圆221x y +=上，即2201x y +=，故：2214y x +=，此即曲线C 的方程．．．．．．．．6分 （2）设1122(,),(,)E x kx F x kx ，其中12x x <，将y kx =代入椭圆的方程2214y x +=整理得：22(4)4k x +=，故21x x =-=，① 又点,E F 到直线AB的距离分别为hh =，所以四边形AEBF的面积为122114(2)()5225(4)k S AB h h k +=+==+当24(0)k k =>，即当2k =时，上式取等号，所以当四边形AEBF 面积最大时，2k =．．．．．．12分21．【解析】（1）由题意2()x a f x x -'=．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．1分当a e ≥时，函数()f x 在(0,)e 上是减函数，当0a e <<时，此时函数()f x 在(0,)a 上是减函数，在(,)a e 上是增函数，当0a ≤时，函数()f x 在(0,)e 上是增函数．．．．．．．．．．．．．．．．．．．．．4分（2）设切点00020(,ln ),()x a x aT x x f x x x--'-=，∴切线的斜率000020ln 11AT x ax x ax k k x x --+-==-．．5分即：0000200()(1)ln 1x a x a x x x x ----+=，即：020021ln 10a ax x x ++--=， 所以过点(1,1)A -有且仅有一条直线与函数()y f x =的图象相切等价于方程020021ln 10a a x x x ++--=在定义域(0,)e 上有且只有一个解；．．．．．．．．．．．．．．．．．．．．．．．．．．．．．6分令221()ln 1a ag x x x x+=+--，则()g x 在(0,)e 上有且只有一个零点； 设231212()0a ag x x x x+'=-+=，得123(2)(1)0,1,2x a x x x a x --===．．．．．．．．．．．．．．．．．．．．．．．7分 ①当21e a >>时，min 2211(2)ln 21ln 20244a a g g a a a a a a +==+--=+>，而111()ln84161ln 830444g a a a =++--=-+<，由零点存在性原理，此时()g x 在(0,2)a 上有且只有一个零点，在[)2,a e 上没有零点，符合条件；同理，当2a e ≥时，符合条件；②当21a =时，23(1)()0x g x x -'=≥，()g x 在(0,)e 为增函数，1(1)02g a ==>，而111()ln 84161ln 830444g a a a =++--=-+<，（没有此处说明应扣1分）此时()g x 在(0,)e 上有且只有一个零点，符合条件；③当021a <<时，min (1)0g g a ==>，而242()ln 41ln 30222a a a g a a a =++--=-+<，（没有此处说明应扣1分）此时()g x 在(0,1)上有且只有一个零点，在[)1,e 上没有零点，符合条件；④当0a =时，1()ln 1g x x x =+-，令21()0x g x x -'==，min (1)0,()g g g x ==在(0,)e 上有且只有一个零点1，符合条件；⑤当0a <时，min 11(1)0,()ln83044g g a g a ==<=-+>， ()g x 在(0,1)上有且只有一个零点，而当2221(21)()ln 10a a e a eg e e eee+-+=+--=≤，即：21ea e ≤--时， ()g x 在(1,)e 上没有零点；此时()g x 在(0,)e 上有且只有一个零点，符合条件；当2(21)()0e a e g e e -+=>，即：021ea e -<<-时，()g x 在(0,1)和(1,)e 上各有一个零点；不符合条件；综上：0a ≥或21e a e ≤--．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．12分 22．【解析】（1）证明：∵AB 为圆的直径，∴090ACB ∠=，∵BD CD ⊥，∴090BDC BCA ∠==∠，∵CD 为切线，由弦切角定理，∴BCD A ∠=∠，∴BAC BCD ∆∆，∴AB BC BC BD=，∴2BC AB BD = 5分（2）解：∵CD 为切线，由切割线定理，∴2DC DE DB =，设DE x =，∴22(3)x x =+，解得：1x =，∴4,BD BC ==，∴25BC AB BD==．．．．．．．．．．．．．．．．．．．．．．．10分 23．【解析】（1）圆C 的普通方程为224x y +=，．．．2分直线l的参数方程是1112x y t ⎧=⎪⎪⎨⎪=+⎪⎩（t 是参数）．．5分（2）因为点,A B 都在直线l 上，所以可设它们对应的参数为1t 和2t ，则点,A B的坐标分别为112211(1,1),(1,1)22A tB t ++， 把直线l 的参数方程代入圆的方程224xy +=整理得到21)20t t +-=，① 因为1t 和2t 是方程①的解，从而122t t =-，所以1222PA PB t t ==-=．．．．．．．10分24．【解析】（1）当2a =时，不等式为215x x -++≥，不等式的解集为(][),23,-∞-+∞；．．．．．5分 （2）()1f x ≤即1x a -≤，解得11a x a -≤≤+，而()1f x ≤的解集是[]0,2， ∴1012a a -=⎧⎨+=⎩，解得1a =，所以111(0,0)2m n m n +=>>，所以112(2)()42m n m n m n +=++≥．．．10分。

2019-2020年高三数学下学期周练试题一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合A={x|x2﹣2x﹣3≤0}，B={x|y=ln（2﹣x）}，则A∩B=（）A．（1，3）B．（1，3] C．[﹣1，2）D．（﹣1，2）2．若复数z满足z（1+i）=4﹣2i（i为虚数单位），则|z|=（）A． B． C． D．3．若某几何体的三视图（单位：cm）如图所示，其中左视图是一个边长为2的正三角形，则这个几何体的体积是A．2cm2B．cm3C．3cm3D．3cm34．已知函数f（x）=sin（ωx+φ）（ω＞0，|φ|＜）的最小正周期为π，且其图象向左平移个单位后得到函数g（x）=cosωx的图象，则函数f（x）的图象（）A．关于直线x=对称B．关于直线x=对称C．关于点（，0）对称D．关于点（，0）对称5．在平面直角坐标系中，若不等式组表示的平面区域的面积为4，则实数t的值为（）A．1 B．2 C．3 D．46．命题“∀x∈[1，2]，x2﹣a≤0”为真命题的一个充分不必要条件是（）A．a≥4 B．a≤4 C．a≥5 D．a≤57.若实数满足10310x yx yy x-+≥⎧⎪+≥⎨⎪-+≥⎩，则的最大值是（）A． -3 B． C. D．8.已知是定义在上的奇函数，当时，（为常数），则的值为（）A．4 B． -4 C.6 D．-69.已知函数：①，②，则下列结论正确的是（）A．两个函数的图像均关于点成中心对称 B．两函数的图像均关于直线对称C.两个函数在区间上都是单调递增函数D．可以将函数②的图像向左平移个单位得到函数①的图像10. 已知是双曲线的上、下焦点，点关于渐近线的对称点恰好落在以为圆心，为半径的圆上，则双曲线的离心率为（）A ． 3B ． C. 2 D ． 11. 一个四面体的顶点都在球面上，它们的正视图、 侧视图、俯视图都是下图，图中圆内有一个以圆心为中心边长为1的正方形，则这个四面体的外接球的表面积是 A ． B ． C. D ．12.中国传统文化中很多内容体现了数学的对称美，如图所示的太极图是 由黑白两个鱼形纹组成的圆形图案，充分展现了相互转化、对称统一的形式美、和谐美，给出定义：能够将圆的周长和面积同时平分的函数称为这个圆的“优美函数”，给出下列命题：①对于任意一个圆，其“优美函数“有无数个”；②函数可以是某个圆的“优美函数”；③正弦函数可以同时是无数个圆的“优美函数”；④函数是“优美函数”的充要条件为函数的图象是中心对称图形． 其中正确的命题是：（ ） A ．①③ B ．①③④ C. ②③ D ．①④二、填空题（本大题共4小题，每小题5分，满分20分，将答案填在答题纸上） 13.已知向量，若，则 ． 14.在中，，则 ．15. 在中，角的对边分别为，且，若的面积为，则的最小值为 ．16.椭圆的上、下顶点分别为，点在上且直线斜率的取值范围是，那么直线斜率的取值范围是 ．三、解答题 （本题必作题5小题，共60分；选作题2小题，考生任作一题，共10分.） 17.已知，集合(){}|2,0M x f x x ==>，把中的元素从小到大依次排成一列，得到数列 ．（1）求数列的通项公式； （2）记，设数列的前项和为，求证：．18.某网站体育版块足球栏目组发起了“射手的上一场进连续进球有关系”的调查活动，在所有参与调查的人中，持“有关系”“无关系”“不知道”态度的人数如表所示：有关系 无关系 不知道 40岁以下 800 450 200 40岁以上（含40岁）100150300（Ⅰ）在所有参与调查的人中，用分层抽样的方法抽取n 个人，已知从持“有关系”态度的人中抽取45人，求n 的值；（Ⅱ）在持“不知道”态度的人中，用分层抽样的方法抽取5人看成一个总体，从这5人中任选取2人，求至少一人在40岁以下的概率；（Ⅲ）在接受调查的人中，有8人给这项活动打出分数如下：9.4、8.6、9.2、9.6、8，7、9.3、9.0、8.2，把这8个人打出的分数看做一个总体，从中任取1个数，求该数与总体平均数之差的绝对值超过0.6的概率．19.如图，边长为2的正方形中，点是的中点，点是的中点．将分别沿折起，使两点重合于点，连结．（1）求异面直线与所成角的大小；（2）求三棱锥的体积．20. 如图，抛物线的焦点为，抛物线上一定点． （1）求抛物线的方程及准线的方程；（2）过焦点的直线（不经过点）与抛物线交于两点，与准线交于点，记的斜率分别为，问是否存在常数，使得成立？若存在，求出的值；若不存在，说明理由．21.设函数()()21xa x ax a f x e --+=．（1）当时，求曲线在点处的切线方程；（2）当时，的最大值为，求的取值范围．请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分.22.选修4-4：坐标系与参数方程：在平面直角坐标系中，直线的参数方程为22x y ⎧=⎪⎪⎨⎪=⎪⎩（为参数），以为极点，轴的正半轴为极轴，取相同的单位长度建立极坐标系，曲线的极坐标方程为．（1）求曲线的直角坐标方程及直线的普通方程；（2）将曲线上的所有点的横坐标缩短为原来的，再将所得到的曲线向左平移1个单位，得到曲线，求曲线上的点到直线的距离的最小值．23.选修4-5：不等式选讲设．（1）求的解集；（2）若不等式对任意实数恒成立，求实数的取值范围．江西省樟树中学xx 届文科数学答题卡姓名： 班级： 成绩：一、选择题（本大题共10个小题，每小题5分，共50分）13． 14．15． 16．三、解答题：(本大题共6小题，共75分，解答写在对应框内。

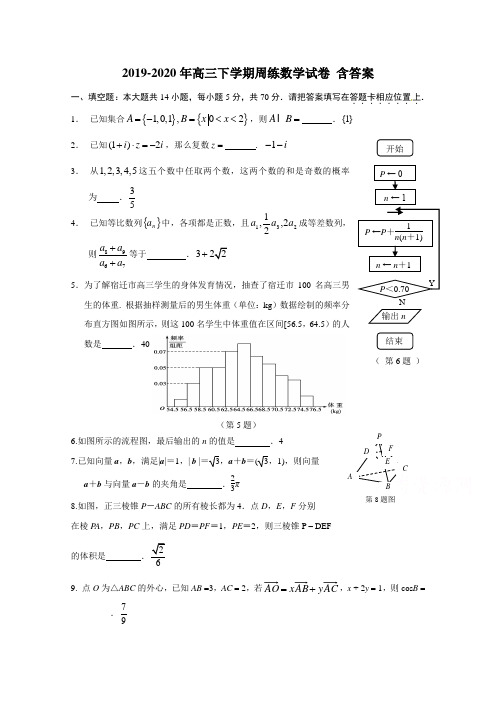
2019-2020年高三下学期周练数学试卷 含答案一、填空题：本大题共14小题，每小题5分，共70分．请把答案填写在答题卡相应位置．．．．．．．上．． 1． 已知集合{}{}1,0,1,02A B x x =-=<<，则AB = ．{1}2． 已知(1)2i z i +⋅=-，那么复数z = . 1i --3． 从1,2,3,4,5这五个数中任取两个数，这两个数的和是奇数的概率为 ．534． 已知等比数列{}n a 中，各项都是正数，且2312,21,a a a 成等差数列，则8967a a a a ++等于．3+5．为了解宿迁市高三学生的身体发育情况，抽查了宿迁市100名高三男生的体重. 根据抽样测量后的男生体重（单位：kg ）数据绘制的频率分布直方图如图所示，则这100名学生中体重值在区间[56.5，64.5）的人数是 ．406.如图所示的流程图，最后输出的n 的值是 ．47.已知向量a ，b ，满足|a |＝1，| b |＝3，a ＋b ＝(3，1)，则向量a ＋b 与向量a －b 的夹角是 ．23π8.如图，正三棱锥P －ABC 的所有棱长都为4．点D ，E ，F 分别 在棱P A ，PB ，PC 上，满足PD ＝PF ＝1，PE ＝2，则三棱锥P – DEF 的体积是．69. 点O 为△ABC 的外心，已知AB =3，AC = 2，若y x +=，x + 2y = 1，则cos B = _________．97 （第5题）（ 第6题 ）10.已知锐角A ，B 满足tan(A ＋B )＝2tan A ，则tan B 的最大值是 ．2411.如图，点F A ,分别是椭圆12222=+by a x )0(>>b a 的上顶点和右焦点，直线AF 与椭圆交于另一点B ，过中心O 作直AF的平行线交椭圆于D C ,两点，若CD AB =则椭圆的 离心率为 . 2112.已知圆O ：221x y +=，O 为坐标原点，若正方形ABCD 的一边AB 为圆O 的一条弦，则线段OC 长度的最大值是 .12+13. 已知函数111,[0,)22()12,[,2)2x x x f x x -⎧+∈⎪⎪=⎨⎪∈⎪⎩若存在12,x x ，当1202x x ≤<<时，12()()f x f x =，则12()x f x 的取值范围是 ．)21,422[- 14. 设0＜b ＜1＋a ，若关于x 的不等式(x －b )2＞(ax )2的解集中的整数恰好有3个，则实数a 的取值范围是________ 1＜a ＜3 二、解答题：15.（本小题满分14分）设△ABC 三个内角A 、B 、C 所对的边分别为a ，b ，c . 已知C ＝π3，a cos A =b cos B ．（1）求角A 的大小；（2）如图，在△ABC 的外角∠ACD 内取一点P ，使得PC ＝2．过点P 分别作直线CA 、CD 的垂线PM 、PN ，垂足分别是M 、N ．设∠PCA ＝α，求PM ＋PN 的最大值及此时α的取值．第11题图（第15题）ACMNPα解（1）由a cos A ＝b cos B 及正弦定理可得sin A cos A ＝sin B cos B ，即sin2A ＝sin2B ，又A ∈(0，π)，B ∈(0，π)，所以有A ＝B 或A ＋B ＝π2． ………………… 2分又因为C ＝π3，得A ＋B ＝2π3，与A ＋B ＝π2矛盾，所以A ＝B ，因此A ＝π3． …………………4分（2）由题设，得在Rt △PMC 中，PM ＝PC ·sin ∠PCM ＝2sin α；在Rt △PNC 中，PN ＝PC ·sin ∠PCN ＝ PC ·sin(π－∠PCB )＝2sin[π－(α＋π3)]＝2sin (α＋π3)，α∈(0，2π3).……………… 6分所以，PM ＋PN ＝2sin α＋2sin (α＋π3)＝3sin α＋3cos α＝23sin(α＋π6).……………… 10分因为α∈(0，2π3)，所以α＋π6∈(π6，5π6)，从而有sin(α＋π6)∈(12，1]，即23sin(α＋π6)∈(3，23]．于是，当α＋π6＝π2，即α＝π3时，PM ＋PN 取得最大值23．…………… 14分16.（本小题满分14分）在正三棱柱111ABC A B C -中，点D 是BC 的中点，1BC BB =． （1）求证：1A C ∥平面1AB D ； （2）试在棱1CC 上找一点M ，使1MB A B ⊥．C 11C60°αPNM CDBA（第15题）（1）证明：连接1A B ，交1AB 于点O , 连接OD . ∵O 、D 分别是1A B 、BC 的中点， ∴1A C ∥OD ． ………3分 ∵1AC ⊄平面1AB D ，OD ⊂平面1AB D ， ∴1A C ∥平面1AB D ． ………6分 （2）M 为1CC 的中点． ………7分 证明如下：∵在正三棱柱111ABC A B C -中，1BC BB =，∴四边形11BCC B 是正方形．∵M 为1CC 的中点，D 是BC 的中点，∴1B BD BCM ∆≅∆， ………9分 ∴1BB D CBM ∠=∠，1BDB CMB ∠=∠． 又∵112BB D BDB π∠+∠=，12CBM BDB π∠+∠=，∴1BM B D ⊥． ………11分∵ABC ∆是正三角形，D 是BC 的中点， ∴AD BC ⊥．∵平面ABC ⊥平面11BB C C , 平面ABC 平面11BB C C BC =，AD ⊂平面ABC ，∴AD ⊥平面11BB C C ． ∵BM ⊂平面11BB C C ，∴AD ⊥BM ． ………13分 ∵1ADB D D =，∴BM ⊥平面1AB D ． ∵1AB ⊂平面1AB D ，∴1MB AB ⊥． ………14分C 1B 1C17（本小题满分16分）在距A 城市45千米的B 地发现金属矿，过A 有一直线铁路AD ．欲运物资于A ，B 之间，拟在铁路线AD 间的某一点C 处筑一公路到B ．现测得BD =45BDA ∠=（如图）．已知公路运费是铁路运费的2倍，设铁路运费为每千米1个单位，总运费为y ．为了求总运费y 的最小值，现提供两种方案：方案一：设AC x =千米；方案二设BCD θ∠=． （1）试将y 分别表示为x 、θ的函数关系式()y f x =、()y g θ=；（2）请选择一种方案，求出总运费y 的最小值，并指出C 点的位置．解：(1)在ABD ∆中，由余弦定理解得AD=63 ………2分方案一：在ABC ∆中，222222227)36(7245cos 45245+-=-+=⋅-+=x x x A x x BC 2227)36(22)(+-+=+=∴x x BC AC x f ………5分方案二：在BCD ∆中，θθsin 2745sin sin 227==BC ，θθθθθsin )cos (sin 27)45sin(sin 227+=+= CD ， θθθθθθθsin cos 22736)sin cos sin sin 2(2763221)(-+=+-+=+-=⋅+⋅=BC CD AD BC AC g ………9分 (2)若用方案一，则8100)144(23)4572(4)(457222222222=+--+⇒+-=-⇒+-+=y x y x x x x y x x x y………11分 由0≥∆得327360891720)8100(3)144(222+≥⇒≥--⇒≥-+-y y y y y ………14分32736min +=∴y ，这时39363144-=-=yx ，C 距A 地)3936(-千米 ………16分若用方案二，则θθθθθ222sin cos 2127sin cos )cos 2(sin 27-=--='y ………11分 )(θg 在↓)3,0(π，在↑),3(ππ32736232122736min +=-+=∴y ………14分 这时3πθ=，C 距A 地)3936(-千米 ………16分18.（本小题满分16分）在平面直角坐标系xOy 中，椭圆C ： x 2a 2＋ y 2b 2＝1（a ＞b ＞0）的上顶点到焦点的距离为2，离心率为32． （1）求a ，b 的值．（2）设P 是椭圆C 长轴上的一个动点，过点P 作斜率为k 的直线l 交椭圆C 于A 、B 两点． （ⅰ）若k ＝1，求△OAB 面积的最大值；（ⅱ）若P A 2＋PB 2的值与点P 的位置无关，求k 的值． 解（1）由题设可知a ＝2，e ＝c a ＝32，所以c ＝3，故b ＝1．因此，a ＝2，b ＝1． ………………… 2分（2）由（1）可得，椭圆C 的方程为 x 24＋y 2＝1．设点P （m ，0）（－2≤m ≤2），点A （x 1，y 1），点B （x 2，y 2）． (ⅰ)若k ＝1，则直线l 的方程为y ＝x －m ．联立直线l 与椭圆C 的方程，即⎩⎪⎨⎪⎧y ＝x －m x 24＋y 2＝1．将y 消去，化简得 54x 2－2mx ＋m 2－1＝0．解之得x 1＝2(2m －1－m 2)5， x 2＝2(2m ＋1－m 2)5， 从而有，x 1＋x 2＝8m5， x 1· x 2＝4(m 2－1)5，而y 1＝x 1－m ，y 2＝x 2－m ，因此，∣AB |＝(x 1－x 2)2＋(y 1－y 2)2＝2(x 1－x 2)2＝2(x 1+x 2)2－4 x 1·x 2＝452·5－m 2， 点O 到直线l 的距离d ＝∣m ∣2，所以，S △OAB ＝12×|AB |×d ＝255－m 2×|m |，因此，S 2△OAB ＝425( 5－m 2)×m 2≤425·(5－m 2＋m 22)2＝1．………………… 6分又－2≤m ≤2，即m 2∈[0，4]．所以，当5－m 2＝m 2，即m 2＝52， m ＝±102时，S △OAB 取得最大值1．………………… 8分(ⅱ)设直线l 的方程为y ＝k (x －m ).将直线l 与椭圆C 的方程联立，即⎩⎪⎨⎪⎧y =k (x －m ) x 24＋y 2＝1． 将y 消去，化简得(1＋4k 2)x 2－8mk 2x ＋4(k 2m 2－1)＝0，解此方程，可得，x 1＋x 2＝8mk 21＋4k 2，x 1·x 2＝4(k 2m 2－1) 1＋4k 2．………………… 10分所以，P A 2＋PB 2＝(x 1－m )2＋y 12＋(x 2－m )2＋y 22＝34(x 12＋x 22)－2m (x 1＋x 2)＋2m 2＋2＝m 2·(－8k 4－6k 2＋2)＋(1＋4k 2)·(8k 2＋8) (1＋4k 2)2（*）. …………………14分因为P A 2＋PB 2的值与点P 的位置无关，即（*）式取值与m 无关， 所以有－8k 4－6k 2＋2＝0，解得k ＝±12．所以，k 的值为±12. …………………16分19. (本题满分16分)设函数()()2ln 1f x x b x =++.注：)11)1(n (l +=+'x x （1）若x =1时，函数()f x 取最小值，求实数b 的值；（2）若函数()f x 在定义域上是单调函数，求实数b 的取值范围；（3）若1b =-，证明对任意正整数n ，不等式33311 (312)11)1(n ＜k f nk ++++∑=都成立. 解:（1）由x + 1＞0得x ＞ – 1∴f(x)的定义域为( - 1，+ ∞),对x ∈ ( - 1，+ ∞),都有f(x)≥f(1)，∴f(1)是函数f(x)的最小值，故有f / (1) = 0,,022,12)(/=+∴++=bx b x x f 解得b= - 4. 经检验，列表（略），合题意； （2）∵,12212)(2/+++=++=x bx x x b x x f 又函数f(x)在定义域上是单调函数，∴f / (x) ≥0或f /(x)≤0在( - 1，+ ∞)上恒成立.若f / (x) ≥0，∵x + 1＞0，∴2x 2 +2x+b ≥0在( - 1，+ ∞)上恒成立, 即b ≥-2x 2 -2x = 21)21(22++-x 恒成立,由此得b ≥21;若f / (x) ≤0, ∵x + 1＞0, ∴2x 2 +2x+b ≤0,即b ≤- (2x 2+2x)恒成立，因-(2x 2+2x) 在( - 1，+ ∞)上没有最小值，∴不存在实数b 使f(x) ≤0恒成立.综上所述，实数b 的取值范围是⎪⎭⎫⎢⎣⎡+∞,21. （3）当b= - 1时，函数f(x) = x 2 - ln(x+1)，令函数h(x)=f(x) – x 3 = x 2 – ln(x+1) – x 3，则h /(x) = - 3x 2+2x - 1)1(31123+-+-=+x x x x ， ∴当[)+∞∈,0x 时，h /(x)＜0所以函数h(x)在[)+∞∈,0x 上是单调递减.又h(0)=0，∴当()+∞∈,0x 时，恒有h(x) ＜h(0)=0,[ 即x 2 – ln(x+1) ＜x 3恒成立. 故当()+∞∈,0x 时,有f(x) ＜x 3.. ∵()1,0,,k N k +∈∴∈+∞取,1k x =则有311(),f k k< ∴33311......31211)1(n ＜k f nk ++++∑=,故结论成立。

12019-2020南京一中高三数学周练一2020.2.191．限时训练120分钟＋30分钟．2．请同学们认真作答，不要上网查答案．写完后，根据答案的评分标准严格批改并上传． 一、填空题：本大题共14小题，每小题5分，计70分．请把答案写在答题纸的指定位置上． 1．已知集合{|02}A x x =<<，{|11}B x x =-<<，则A B =U ． 2．设复数z 满足i i z 46)32(+=-⋅（其中i 为虚数单位），则z 的模为 ．3．已知1234a a a a ，，，的方差为2，则123421212121a a a a ++++，，，的方差为 ．4．右图是一个算法的伪代码，其输出的结果为 ． 5．函数2()log 2f x x =-的定义域为 ．6．袋中有形状、大小都相同的5只球，其中2只白球，3只红球，从中一次随机摸出2只球，则这2只球颜色相同的概率为 ．7．在平面直角坐标系xOy 中，若双曲线)0,0(12222>>=-b a by a x 的一个焦点到一条渐近线的距离为a 2，则该双曲线的离心率为 ．8．若将函数f (x )的图象向右平移π6个单位后得到函数()π4sin 23y x =-的图象，则()π4f = ．9．已知等差数列{}n a 的前n 项和为n S ，298a a +=，55S =-，则15S 的值为 ．S ←0For i From 1 To 10 Step 1 S ←S ＋1i (i ＋1)（第4题）210．已知31)32sin(sin =+παα，则=+)3tan(πα ． 11．已知点A 、B 是圆O ：224x y +=上任意两点，且满足AB＝P 是圆C ：(x ＋4)2＋(y＋3)2＝4上任意一点，则PA PB +u u u r u u u r的取值范围是 ．12．若正实数x ，y 满足x yxy x y+=-，则实数x 的最小值为 ． 13．在平面直角坐标系xOy 中，A 为直线l ：y ＝2x 上在第一象限内的点，B (5，0)，以AB 为直径的圆C 与直线l 交于另一点D ．若AB ⊥CD ，则点A 的横坐标为 ．14．已知函数3()||f x x ax b =--，[1,1]x ∈-，a ，b ∈R ．若()f x M ≤恒成立，则当M 取得最小值时，a b +的值为 ．二、解答题：本大题共6小题，计90分．解答应写出必要的文字说明，证明过程或演算步骤，请把答案写在答题纸的指定区域内． 15．（本小题满分14分）已知向量a ＝(cos x ，sin x )，b ＝(3，－3)，x ∈[0，π]． （1）若a ⊥b ，求x 的值；（2）记f (x )＝a·b ，求f (x )的最大值和最小值以及对应的x 的值．316．（本小题满分14分）在三棱锥S —ABC 中，平面SAB ⊥平面SBC ，AB ⊥BC ，AS ＝AB ，过A 作AF ⊥SB ，垂足为F ，点E ，G 分别是棱SA ，SC 的中点．（1）求证：平面EFG ⊥平面ABC ． （2）求证：BC ⊥SA ．17．（本小题满分14分）如图，为方便市民游览市民中心附近的“网红桥”，现准备在河岸一侧建造一个观景台P ，已知射线AB ，AC 为两边夹角为120°的公路（长度均超过3千米），在两条公路AB ，AC 上分别设立游客上下点M ，N ，从观景台P 到M ，N 建造两条观光线路PM ，PN ，测得AM ＝3千米，AN ＝3千米．（1）求线段MN 的长度；（2）若⊥MPN ＝60°，求两条观光线路PM 与PN 之和的最大值．P CNA M B第17题图ABCFE S G第16题图418．（本小题满分16分）在平面直角坐标系xOy 中，已知椭圆C ：x 2a 2＋y 2b2＝1(a ＞b ＞0)的上顶点坐标为(0，2)，离心率为22．（1）求椭圆C 的标准方程；（2）若椭圆C 上的点P 的横坐标为2，且位于第一象限，点P 关于x 轴的对称点为点Q ，A ，B 是位于直线PQ 异侧的椭圆C 上的动点．⊥若直线AB 的斜率为12，求四边形APBQ 面积的最大值；⊥若动点A ，B 满足⊥APQ ＝⊥BPQ ，求证：直线AB 的斜率是为定值，并求出该定值．19．（本小题满分16分）已知各项都是正数的数列{a n }的前n 项和为S n ，且2S n ＝a n 2＋a n ，数列{b n }满足b 1＝12，12nn nnb b b a+=+． （1）求数列{a n }、{b n }的通项公式；（2）设数列{c n }满足2n n nb c S +=，求c 1＋c 2＋…＋c n 的和； （3）是否存在正整数p ，q ，r (p <q <r )，使得b p ，b q ，b r 成等差数列？若存在，求出所有满足要求的p ，q ，r ；若不存在，说明理由．520．（本小题满分16分）已知函数f (x )＝ln x －ax 在x ＝2处的切线l 与直线x ＋2y －3＝0平行． （1）求实数a 的值；（2）若关于x 的方程f (x )＋m ＝2x －x 2在[12，2]上恰有两个不相等的实数根，求实数m 的取值范围；（3）记函数g (x )＝f (x )＋12x 2－bx ，设x 1，x 2(x 1<x 2)是函数g (x )的两个极值点，若b ≥32，且g (x 1)－g (x 2)≥k 恒成立，求实数k 的最大值．6附加题21．【选做题】在A 、B 、C 三小题中只能选做2题，每小题10分，共计20分．请在答卷卡指定区域内作答．解答应写出文字说明、证明过程或演算步骤． A ．选修4—2：矩阵与变换已知矩阵3324A ⎡⎤=⎢⎥⎣⎦．（1）求A 2；（2）求矩阵A 的特征值和特征向量．B ．选修4—4：坐标系与参数方程在平面直角坐标系xOy 中，以O 为极点，x轴的正半轴为极轴建立极坐标系．直线sin()()4l m m R πθ-=∈，圆C 的参数方程为13cos 23sin x t y t=+⎧⎨=-+⎩（t 为参数）．当圆心C 到直线l时，求m 的值．7【必做题】第22题、第23题，每题10分，共计20分．请在答卷卡指定区域内作答．解答应写出文字说明、证明过程或演算步骤． 22．（本小题满分10分）箱中装有4个白球和m (m ∈N *)个黑球．规定取出一个白球得2分，取出一个黑球得1分，现从箱中任取3个球，假设每个球被取出的可能性都相等．记随机变量X 为取出的3个球所得分数之和．（1）若2(6)5P X ==，求m 的值； （2）当m =3时，求X 的分布列．23．（本小题满分10分）已知数列{a n }是等差数列，且a 1，a 2，a 3是1(1)2mx +展开式的前三项的系数． （1）求m 的值；（2）当n ≥2时，用数学归纳法证明：212111113n n n n a a a a ++++++>L ．8910111213141516。

2019-2020年高三下学期周考（3.20）数学（文）试题 含答案 本试卷共4页，分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分，考试时间120分钟.第Ⅰ卷（选择题，共50分）一、选择题：本大题共10个小题,每小题5分,共50分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知集合，，若，则实数的值是（ ）A ．0B ．0或2C ．2D ．0或1或22.已知为虚数单位，复数的虚部是（ ）A ．B ．C ．D ．3.已知函数是定义在上的奇函数，则的值为（ ）A ．B ．C ．1D ．无法确定4.若关于的不等式组02010x x y kx y ≤⎧⎪+≥⎨⎪-+≥⎩，表示的平面区域是直角三角形区域，则正数的值为（ ）A ．1B ．2C ．3D ．45.已知函数2ln ln ()()(1)1x x F x a a x x=+-+-，有三个不同的零点（其中），则222312123ln ln ln (1)(1)(1)x x x x x x ---的值为（ ） A ． B ． C ． D ．16. 0000sin80sin 40cos80cos 40-的值为（ ）A ．B ．C ．D ．7.已知数列5，6，1，-5，…，该数列的特点是从第二项起，每一项都等于它的前后两项之和，则这个数列的前16项之和等于（ ）A ．5B ．6C ．7D ．168.已知把函数的图像向右平移个单位，再把横坐标扩大到原来的2位，得到函数，则函数的一条对称轴为（ ）A． B． C． D．9.执行如图所示的程序框图，若输出，则输入的整数的最大值是（）A．18 B．50 C．78 D．10010.已知命题存在，曲线为双曲线；命题的解集是.给出下列结论中正确的有（）①命题“且”是真命题；②命题“且”是真命题；③命题“或”为真命题；④命题“或”是真命题.A．1个 B．2个 C．3个 D．4个第Ⅱ卷（非选择题共100分）二、填空题（本大题共5小题，每小题5分，共25分）11.观察下列各式：……设表示正整数，用关于的等式表示这个规律是_____.12.抛物线的焦点为，其准线与双曲线相交于两点，若为等边三角形，则_____.13.在中，角所对的边分别为，且，则的最大值为_____.14.已知抛物线的准线方程为，焦点为，为该抛物线上不同的三点，，，成等差数列，且点在轴下方，若，则直线的方程为_____.15.已知函数是定义在上的奇函数，在上单调递减，且，若，则的取值范围为_____.三、解答题16.（本小题满分12分）已知函数()2cos (cos )1f x x x x =-.（Ⅰ）求的最小值.（Ⅱ）在中，角的对边分别是，若且，求角.17. （本小题满分12分）十八届五中全会公报指出：努力促进人口均衡发展，坚持计划生育的基本国策，完善人口发展战略，全面实施一对夫妇可生育两个孩子的政策，提高生殖健康、妇幼保健、托幼等公共服务水平，为了解适龄公务员对放开生育二胎政策的态度，某部门随机调查了200位30到40岁的公务员，得到情况如下表：（1）是否有99%以上的把握认为“生二胎与性别有关”，并说明理由；（2）把以上频率当概率，若从社会上随机抽取甲、乙、丙3位30到40岁的男公务员，求这三人中至少有一人要生二胎的概率.附：22()()()()()n ad bc k a b c d a c b d -=++++18.（本题满分12分）已知直角梯形中，，，，，为的中点，将四边形沿折起使面面，过作，（1）若为的中点，求证：；（2）若，试求多面体体积.19.（本小题满分12分）若数列中存在三项，按一定次序排列构成等比数列，则称为“等比源数列”.（1）已知数列中，，.①求数列的通项公式；②试判断数列是否为“等比源数列”，并证明你的结论.（2）已知数列为等差数列，且，，求证：为“等比源数列”.20. （本小题满分13分）已知椭圆的离心率，过椭圆的左焦点且倾斜角为的直线与圆相交所得弦的长度为1. （1）求椭圆的方程；（2）若直线交椭圆于不同的两点，，设，，其中为坐标原点.当以线段为直径的圆恰好过点时，求证：的面积为定值，并求出该定值.请考生在21、22、23、24四题中任选一题作答，如果多做，则按所做的第一题记分.21.（本题满分10分）选修4-1：几何证明选讲.已知圆内接中，为上一点，且为正三角形，点为的延长线上一点，为圆的切线. （Ⅰ）求的度数；（Ⅱ）求证：22.（本题满分10分）选修4-4：坐标系与参数方程已知曲线的极坐标方程为，曲线：（为参数）. （1）求曲线的普通方程；（2）若点在曲线上运动，试求出到曲线的距离的范围.23（本小题满分10分）选修4—5：不等式选将已知函数，且关于的不等式的解集为.（1）求实数的取值范围；（2）求得最小值.24.（本题满分10分）选修4-5：不等式选讲.（Ⅰ）设函数.证明：；（Ⅱ）若实数满足，求证：.。

河北省衡水中学2019～2020届高三下学期第1周周测数学（理）试题第Ⅰ卷一、选择题（本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的）1、已知集合2{|160},{5,0,1}A x x B =-<=-，则A ．AB φ= B ．B A ⊆C ．{}0,1A B =D ．A B ⊆2、已知复数20162(1i z i i+=+为虚数单位），则复数z 的共轭复数在复平面内对应的点位于 A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限3、两曲线sin ,cos y x y x ==与两直线0,2x x π==所围成的平面区域的面积为A ．20(sin cos )x x dx π-⎰B ．40(sin cos )x x dx π-⎰C ．20(cos sin )x x dx π-⎰ D ．40(cos sin )x x dx π-⎰ 4、已知0,0a b >>，则“1ab >”是“2a b +>”的A ．充分不必要条件B ．必要不充分条件C ．充分条件D ．既不充分也不必要条件5、已知函数()sin()f x A x πϕ=+的部分图象如图所示，点,B C是该图象与x 轴的焦点，过点C 的直线与该图象交于,D E 两点，则()()BD BE BE CE +⋅-的值为A ．1-B ．12-C ．12D ．2 6、若6,4m n ==，按照如图所示的程序框图运行后，输出的结果是A ．1100B ．100C ．10D ．1 7、已知等比数列{}n a 中，284a a a =，等差数列{}n b 中，465b b a +=，则数列{}n b 的前9项和9S 等于A ．9B ．18C ．36D ．728、从装有若干个大小相同的红球、白球和黄球的袋中随机摸出1个球，摸到红球、白球和黄球的概率分别为111,,236，从袋中随机摸出一个球，记下颜色后放回，连续摸3次，则记下的颜色中有红有白，但没有黄的概率为A ．536B ．13C ．512D ．129、在平行四边形ABCD 中，220,240AC CB BC AC ⋅=+-=，若将其沿AC 折成直二面角D AC B --，则三棱锥D AC B --的外接球的表面积为A ．16πB ．8πC ．4πD ．2π10、过抛物线24y x =的焦点作两条垂直的弦,AB CD ，则11AB CD+=A ．2B ．4C ．12D ．1411、某四面体的三视图如图所示，正视图、俯视图都是腰长为2的等腰直角三角形，侧视图是边长为2的正方形，则此四面体中面积最大的为A ．．．4 D ．12、已知点P 为函数()ln f x x =的图象上任意一点，点Q 为 圆221[()]1x x e y e -++=上任意一点，则线段PQ 的长度的最小值为A D ．11e e+-第Ⅱ卷二、填空题：本大题共4小题，每小题5分，共20分，把答案填在答题卷的横线上..13、已知,x y 满足约束条件1000x y x y x +-≤⎧⎪-≤⎨⎪≥⎩，则2z x y =+的最大值为14、已知点,P Q 为圆22:25C x y +=上的任意两点，且6PQ <，若 PQ 中点组成的区域为M ，在圆C 内任取一点，则该点落在区域M 上的概率为15、5(15)x y --的展开式中不含x 的项的系数和为 16、已知函数()f x 是定义在(,0)(0,)-∞+∞上的偶函数，当0x >时，()121,021(2)22x x f x f x x -⎧-<<⎪=⎨->⎪⎩，则函数()()21g x f x =-的零点个数为 个三、解答题：本大题共6小题，满分70分，解答应写出文字说明、证明过程或演算步骤17、（本小题满分12分）设ABC ∆中的内角,,A B C 所对的边长分别为,,a b c ，且4cos ,25B b ==. （1）当53a =时，求角A 的度数； （2）求ABC ∆面积的最大值.18、（本小题满分12分）某大学志愿者协会有10名同学，成员构成如下表，其中表中部分数据不清楚，只知道从这10名同学中随机抽取一位，抽到该名同学为“数学专业”的概率为25.现从这10名同学中随机抽取3名同学参加社会公益活动（每位同学被选到的可能性相同）.（1）求,m n 的值；（2）求选出3名同学恰为专业互不相同的男生的概率；（3）设ξ为选出的3名同学中“女生或数学专业”的学生的人数，求随机变量ξ的分布列及其数学期望E ξ.19、（本小题满分12分）如图，四棱锥E ABCD -中，平面EAD ⊥平面,//,,ABCD DC AB BC CD EA ED ⊥⊥，且4,2AB BC CD EA ED =====.（1）求证：BD ⊥平面ADE ；（2）求直线BE 和平面CDE 所成角的正弦值.20、（本小题满分12分）已知椭圆222:1(0)3x y M a a +=>的一个焦点为(1,0)F -，左右顶点分别为,A B ，经过点F 的直线l 与椭圆M 交于,C D 两点.（1）求椭圆方程；（2）记ABD ∆与ABC ∆的面积分别为为1S 和2S ，求12S S -的最大值.21、（本小题满分12分）已知函数()2(sin 2)x f x e x ax a e =-+-，其中a R ∈， 2.7828e = 为自然对数的底数.（1）当0a =时，讨论函数()f x 的单调性；（2）当112a ≤≤时，求证：对任意的()[0,),0x f x ∈+∞<. （3）若1O 和2O 的半径之比为9:16，求DE DF的值.22、（本小题满分12分）已知直线l的参数方程2(2x t t y t ⎧=⎪⎪⎨⎪=+⎪⎩是参数）以原点为极点，x 轴的正半轴为极轴建立极坐标系，曲线C 的极坐标方程为4cos()4πρθ=+.（1）判断直线l 与曲线C 的位置关系； （2）过直线l 上的点作曲线C 的切线，求切线长的最小值.23、（本小题满分10分）已知关于x 的不等式21x m -≤的整数解有且仅有一个值为2.（1）求整数m 的值；（2）已知,,a b c R ∈，若444444a b c m ++=，求222a b c ++的最大值.24、附加题已知函数()22ln f x x x mx =-- （1）当0m =时，求函数()f x 的最大值；（2）函数()f x 与x 轴交于两点12(,0),(,0)A x B x 且220x x <<，证明：1212()033f x x +<.。

上海复旦附中2024学年高三年级第二学期数学试题周练一（含附加题）注意事项1．考试结束后，请将本试卷和答题卡一并交回．2．答题前，请务必将自己的姓名、准考证号用0．5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置． 3．请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符．4．作答选择题，必须用2B 铅笔将答题卡上对应选项的方框涂满、涂黑；如需改动，请用橡皮擦干净后，再选涂其他答案．作答非选择题，必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答，在其他位置作答一律无效． 5．如需作图，须用2B 铅笔绘、写清楚，线条、符号等须加黑、加粗．一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．如图所示，已知某几何体的三视图及其尺寸（单位：cm ），则该几何体的表面积为( )A ．15π2cmB ．21π2cmC ．24π2cmD ．33π2cm2．抛掷一枚质地均匀的硬币，每次正反面出现的概率相同，连续抛掷5次，至少连续出现3次正面朝上的概率是（ ） A ．14B ．13C ．532D ．3163．已知函数f (x )＝223,1ln ,1x x x x x ⎧--+≤⎨>⎩,若关于x 的方程f (x )＝kx －12恰有4个不相等的实数根，则实数k 的取值范围是( ) A ．1e 2⎛⎝ B ．12e ⎡⎢⎣C ．12e ⎛⎝⎦D ．12e ⎛⎝⎭4．已知函数()()sin f x A x =+ωϕ（其中0A >，0>ω，0ϕπ<<）的图象关于点5,012M π⎛⎫⎪⎝⎭成中心对称，且与点M 相邻的一个最低点为2,33N π⎛⎫- ⎪⎝⎭，则对于下列判断： ①直线2x π=是函数()f x 图象的一条对称轴；②点,012π⎛⎫-⎪⎝⎭是函数()f x 的一个对称中心； ③函数1y =与()351212y f x x ππ⎛⎫=-≤≤⎪⎝⎭的图象的所有交点的横坐标之和为7π. 其中正确的判断是（ ） A ．①②B ．①③C ．②③D ．①②③5．在ABC ∆中，a ，b ，c 分别为角A ，B ，C 的对边，若ABC ∆的面为S ，且()2243S a b c =+-，则sin 4C π⎛⎫+= ⎪⎝⎭（ ） A ．1B ．22C ．624- D ．624+ 6．中国古代数学著作《算法统宗》中有这样一个问题；“三百七十八里关，初行健步不为难，次后脚痛递减半，六朝才得到其关，要见每朝行里数，请公仔细算相还.”其意思为：“有一个人走了378里路，第一天健步走行，从第二天起脚痛每天走的路程是前一天的一半，走了6天后到达目的地，求该人每天走的路程.”由这个描述请算出这人第四天走的路程为（ ） A ．6里B ．12里C ．24里D ．48里7．已知函数()f x 的导函数为()f x '，记()()1f x f x '=，()()21f x f x '=，…，()()1n n f x f x +'=(n ∈N *). 若()sin f x x x =，则()()20192021f x f x += （ ）A ．2cos x -B ．2sin x -C ．2cos xD ．2sin x8．如图，在ABC ∆中，点Q 为线段AC 上靠近点A 的三等分点，点P 为线段BQ 上靠近点B 的三等分点，则PA PC +=（ ）A ．1233BA BC + B ．5799BA BC + C ．11099BA BC + D ．2799BA BC +9．明代数学家程大位（1533~1606年），有感于当时筹算方法的不便，用其毕生心血写出《算法统宗》，可谓集成计算的鼻祖．如图所示的程序框图的算法思路源于其著作中的“李白沽酒”问题．执行该程序框图，若输出的y 的值为2，则输入的x 的值为（ ）A ．74B ．5627C ．2D ．1648110．函数()5sin 20312f x x x ππ⎛⎫⎛⎫=+≤≤ ⎪⎪⎝⎭⎝⎭的值域为（ ） A ．1,12⎡⎤-⎢⎥⎣⎦B ．10,2⎡⎤⎢⎥⎣⎦C ．[]0,1D ．1,02⎡⎤-⎢⎥⎣⎦11．曲线24x y =在点()2,t 处的切线方程为（ ） A ．1y x =-B ．23y x =-C ．3y x =-+D ．25y x =-+12．若命题：从有2件正品和2件次品的产品中任选2件得到都是正品的概率为三分之一；命题：在边长为4的正方形内任取一点，则的概率为，则下列命题是真命题的是（ ）A ．B ．C ．D ．二、填空题：本题共4小题，每小题5分，共20分。

2019-2020年高三数学：第一次周练试卷 含答案一、选择题（36分）1．函数的部分图象大致是（ ）2．已知函数的图象关于直线对称,且当成立若a=(20.2)···,则a,b,c 的大小关系是（ ）A ．B ．C ．D ． 3．函数,若函数有三个零点,则实数的取值范围是（ ）A ．B ．C ．D ．4．对于函数,如果存在锐角使得的图象绕坐标原点逆时针旋转角,所得曲线仍是一函数,则称函数具备角的旋转性,下列函数具有角的旋转性的是（ ） A ． B ． C ． D ．5．已知定义在R 上的函数满足以下三个条件:①对于任意的,都有;②对于任意的121212,,02,()();x x R x x f x f x ∈≤<≤<且都有③函数的图象关于y 轴对称,则下列结论中正确的是（ ） A ． B ． C ． D ．6．已知定义在上的函数,对任意,都有成立,若函数的图象关于直线对称,则（ ）A ．B ．C ．D ．二、填空题（24分）7．函数的递增区间为_______________________.8．已知函数在实数集R 上具有下列性质:①直线是函数的一条对称轴;②; ③当时, 、、从大到小的顺序为_______.9．若函数8))1((,)0(3)0(lg )(02=⎪⎩⎪⎨⎧≤+>=⎰f f x dt t x x x x f a,则a 的值是__________.10．已知为上的偶函数,对任意都有且当, 时,有成立,给出四个命题:① ② 直线是函数的图像的一条对称轴 ③ 函数在上为增函数 ④ 函数在上有四个零点其中所有正确命题的序号为______________班级：姓名：座号：分数：一、选择题二、填空题7、8、9、10、三．解答题（40分）11．已知函数在点处取得极值.(1)求的值；(2)若有极大值28，求在[－3,3]上的最小值．（15分）12．已知函数(为常数)是实数集上的奇函数,函数是区间上的减函数。