理论力学论文
- 格式:docx
- 大小:870.90 KB
- 文档页数:5

2013理论力学小论文重心及其求法201X 级车辆工程2班 XXX 指导老师:张伟摘要:在工程中,物体重心的位置具有重要意义。
汽车、轮船、飞机的重心位置,对其行驶或飞行的稳定性有直接的影响;高速运转部件的重心如果不在轴线上,将引起机械的剧烈震动,因此必须了解重心的概念和重心位置的求法。
一、 重心的概念在地球表面附近的物体,它的每一部分都受到地球引力的作用,这些引力汇交于地球的中心,形成一个空间汇交力系,但由于我们所研究的物体其尺寸与地球的直径相比要小得多,因此可以近似地将物体上这部分力系看作是空间平行力系,这个平行力系的合力的大小即为物体的重量,合力的作用点即为物体的重心。
规则而密度均匀物体的重心就是它的几何中心。
不规则物体的重心,不一定在物体上,其求法也是多样的。
二、 物体重心坐标公式2.1平行力系的中心平行力系合力作用点的位置仅与各平行力系的大小和作用位置有关,而与各平行力的方向无关。
2.2 重心坐标的一般公式将物体分成许多微小部分n 份,各微小部分所受到的地球引力(重力)以G n G G F F F ∆⋅⋅⋅∆∆21表示,各微小部分作用点坐标为)()()(222111n n n z y x z y x z y x ⋅⋅⋅21r F r F + i iCi F r r F=∑∑则物体的重量为∑∑∆=∆==GinnGi G F F F 1重心的坐标用(xC ,yC ,zC )表示,根据空间力系的合力矩定理,对x 轴取矩,则i G i n G n G G G x y F y F y F y F F M ⨯∆=⨯∆+⋅⋅⋅+⨯∆+⨯∆=∆∑∑2211)(cG c G G x y F y F F M ⨯=⨯∆=∑)(因i G i c c y F y F ⨯∆=⨯∑则∑∑∑∆⨯∆=⨯∆=GiiGiGiGic FyF F y Fy同理∑∑∑∆⨯∆=⨯∆=Gii Gi GiGic F x F F x F x∑∑∑∆⨯∆=⨯∆=GiiGi GiGic Fz F F z Fz物体连同坐标轴转90度,而使坐标面oxz 成为水平面,由重心的概念知,此物体重心的位置不变,再对x 轴应用合力矩定理求Zc 。

台球运动与力学摘要:台球运动是一项智慧的运动,我想,掌握和了解其中的一些深层的原理必然会对水平的提高有不可忽视的作用。
作为一位狂热的台球爱好者,在打台球之余也会对一些现象有所思考,并尝试用理论的知识来解释。
本文主要结合所学的理论力学知识结合计算分析台球运动中一些比较常见的现象。
关键词:台球 ;力学;运动 ;碰撞随着台球运动的发展,我们在比赛中常会看到一些看似反物理原理的现象,例如;碰撞后球不作直线运动,而是作诡异的弧线运动;球碰撞后会加速前进等等。
下面仅就球的运动形式,两球的碰撞,滑杆现象作简要的分析和讨论。
一、台球运动的形式是什么使台球运动有如此快的发展?又是什么能使台球出现这么多美妙的运动现象?答案只有一个,那就是摩擦力,没有桌面的摩擦力,你看到的运动永远是单调的直线运动,,摩擦力是影响台球运动的关键因素。
谈到其运动形式,这绝对是典型的刚体运动,其在桌面上所作的各种运动,归根结底就是刚体小球的质心平动和绕质心的转动。
当台球受到的力通过球心时,它短时间内做平动;当台球受到的力不通过球心时,它在短时间内既转动又平动。
台球运动中所说的低杆、中杆、高杆就可以产生各自的运动效果。
下面作一一讨论:1、中杆:这是台球运动中使用最普遍的一种杆法,它要求击打球的中间部位(近似看作受力过球心)。
此种情况开始没有旋转,也就是一开始作平动,向前滑动一段距离后,因受台面的磨擦阻力f 作用,渐渐产生了逆时针方向的力矩,使球与台面接触点速度减慢,球的顶点速度不变,于是球便向前旋转起来。
2、高杆: 高杆要求击打球的上部。
在下图中,假设台球质量为m ,半径为R ,受到球杆沿水平方向击打的冲击力为F ,力的水平作用线距球心的距离为h ,质心运动速度为v ,转动角速度为ω。
我们分析台球的受力情况及运动状态。
mgFn f F动量P= mv (1)动量矩M=J ω…………………………………………….(2) ,式中J=2/5mR 2。


物理学生论文力学论文试论理论力学教学摘要:对于少学时的理论力学教学,存在教学时间少而教学内容多等问题。
笔者针对教学中出现的问题,阐述了一些观点。
关键词:理论力学普通物理力学习题课现代教学手段引言:《理论力学》课程作为理工科大学的一门重要的专业技术基础课,兼有基础理论和应用技术双重性质,它在基础课和专业课之间起承前启后的作用。
其主要以伽利略和牛顿总结的基本定律为基础,系统介绍静力学、运动学与动力学的基本概念、基本原理及分析问题、解决问题的基本方法。
课程的基本状况是概念多,定理多,公式多;前后联系紧密,题目灵活多变,解题技巧性强。
加之现时课程改革,理论力学课时较少,使很大一部分学生感到理论力学“理论难,解题难”,学习效果不甚理想。
那么如何在有限的学时里培养学生的学习兴趣,提高教学质量就成了力学教师的重要课题。
1.注意普通物理力学与理论力学课程的联系1.1教学内容的联系。
普通物理力学以下简称普物力学和理论力学同属经典力学。
普物力学和理论力学都以机械运动所遵循的基本规律及其推论和应用为研究对象,都包括运动学、动力学和静力学三个部分。
普物力学一般在大学入学的第一学年开设,而理论力学一般于第二学年开设,如何在同一内容的学习中注意二者的关系尤为重要。
在理论力学的教学中对普物力学中的概念就不再详细重复讲解,而是强调理论力学课程中的新概念,这样才能更有效地利用有限的课时,同时也能消除学生认为理论力学就是普物力学的认识误区。
1.2教学方法的联系。
普物力学主要是从物理现象出发,重视物理现象、物理过程,通过分析归纳的方法,由现象寻找规律,强调直观的物理图景,强调对基本物理概念和方法的理解和讨论,强调从感性到理性的认识过程。
理论力学则从物理学的几个逻辑框架出发,通过逻辑演绎的方法,推导出机械运动的性质、规律和图景。
研究的特点是强调概念的确切性和数学证明的严谨性,重点在于培养学生的理性思维能力。
对于数学知识的要求,理论力学除了要用到矢量运算和微分方程之外,还要求理解约束、自由度和广义坐标的概念,能根据实际情况正确选择广义坐标,熟练掌握和运用虚功原理,熟练掌握和运用拉格朗日方程,等等。

单自由度系统振动机设09-4班 田春宇摘要:单自由度系统的振动理论是振动理论的理论基础。
力学模型的简化方法。
振动特性的讨论。
扭转振动;计算系统固有频率的几种方法。
单自由度系统有阻尼自由振动。
简谐激振力引起的受迫振动。
关键词:振动 机械 系统 力学 理论 引言:单自由度系统的振动理论是振动理论的理论基础。
尽管实际的机械都是弹性体或多自由度系统,然而要掌握多自由度振动的基本规律,就必须先掌握单自由度系统的振动理论。
此外,许多工程技术上的具体振动系统在一定条件下,也可以简化为单自由度振动系统来研究。
例如:悬臂锤削镗杆;外圆磨床的砂轮主轴;安装在地上的床身等。
一、 力学模型的简化方法若忽略这些零部件中的镗杆、主轴和转轴的质量,只考虑它们的弹性。
忽略那些支承在弹性元件上的镗刀头、砂轮、床身等惯性元件的弹性,只考虑它们的惯性。
把它们看成是只有惯性而无弹性的集中质点。
于是,实际的机械系统近似地简化为单自由度线性振动系统的动力学模型。
在实际的振动系统中必然存在着各种阻尼,故模型中用一个阻尼器来表示。
阻尼器由一个油缸和活塞、油液组成。
汽车轮悬置系统等等。
二、单自由度振动系统——指用一个独立参量便可确定系统位置的振动系统。
所有的单自由度振动系统经过简化,都可以抽象成单振子,即将系统中全部起作用的质量都认为集中到质点上,这个质点的质量m 称为当量质量,所有的弹性都集中到弹簧中,这个弹簧刚度k 称为当量弹簧刚度。
以后讨论中,质量就是指当量质量,刚度就是指当量弹簧刚度。
在单自由度振动系统中,质量m 、弹簧刚度k 、阻尼系数C 是振动系统的三个基本要素。
有时在振动系统中还作用有一个持续作用的激振力P 。
应用牛顿运动定律,作用于一个质点上所有力的合力等于该质点的质量和该合力方向的加速度的乘积。
单自由度系统无阻尼自由振动无阻尼自由振动是指振动系统不受外力,也不受阻尼力影响时所作的振动。
三、振动特性的讨论 1.振动的类型无阻尼自由振动是简谐振动。

理论力学小论文理论力学小论文理论力学给人类提供了大量的物质财富,同时也提供了精神财富。
理论力学的高技术和强渗透性也使之成为社会发展的重要推动力。
今天我们就一起来欣赏理论力学小论文吧!理论力学小论文:浅析物理力学的产生及其发展摘要:物理力学主要是研究宏观力学的微观理论学科。
研究物理力学的主要目的是通过理解微观粒子性质的相互作用,找出介质的力学性质计算方法,进而使解决力学问题建立在微观分析的基础上。
本文主要探讨了物理力学的产生和发展,为有关物理力学问题的解决提供理论基础。
关键词:物理力学;产生;发展一、物理力学发展需要解决的问题分析在物理力学的发展过程中,我们需要解决两方面的问题,一个是关于物性的问题,另一个是有关运动规律的问题。
物理力学主要通过物性及其运动规律这两个方面的微观化而成为解决问题、建立微观分析的基础。
关于物性的参数主要表现为运动方程组中的系数,例如弹性系数、热导率、粘性系数、声速、比热等。
为了求解运动的方程组,需要知道它们相关的数值。
在传统力学中,物性参数的数值是需要试验测定的。
而在我们研究的物理力学中,是通过微观的分析以及对宏观数据分析相结合的方法计算参数的数值。
我们研究物理力学,不仅是为了能够找出物质性质的微观规律,而且还需要找能够预见新物质性质的方法。
针对物理力学发展中的相关问题,先了解一下有关激波结构问题的例子。
物态在激波前后会有很大的变化,在波阵面一定的厚度之内,物质是处在远离平衡的状态的。
这时,对于宏观物态的参数已经不适用了。
因此,我们需要从分子运用的这一个角度进行描述。
像从波尔兹曼方程的角度出发,进而直接进行求解。
在上世纪60年代,一对无内部自由度的'影响激波结构的问题得到了进一步发展。
其发展主要得力于计算机技术的发展,从而能够使波尔兹曼方程进而得到模型数学方程,求精确解。
另外,还能够实现激波管与稀薄气体风洞在较高区域的分辨率的相关方面的测量。
虽然对于这些问题的处理都是初步的,但是从物理力学微观运动规律上看,确是一个非常大的进步。

乒乓球加旋技术的分析摘要力学基本受力分析原理、动量定理、伯努力定理研究了乒乓球的旋转原因及从不同方向、不同力度下击球乒乓球的旋转特性发现以不同的方式、手法击乒乓球球将产生不同的旋转效果具备不同程度的杀伤力。
关键词受力分析旋转原理旋转分类加旋手法1 基本理论知识1.1动量定理物体动量的增量等于物体所受作用力对时间的累积作用即Ft=Δ mv.若质量不变力对物体的作用时间越长物体动量就越大即速度v越大.1.2摩擦力具有一定摩擦系数μ 的两物体相接触且产生压力若它们相对运动或有相对运动的趋势就会产生阻碍它们相对运动或相对运动趋势的作用力这个力就是摩擦力其大小F=μ FnFn 表示正压力大小。
1.3角动量定理对于质点角动量定理可表述为质点对固定点的角动量对时间的微商等于作用于该质点上的力对该点的力矩。
对于质点系由于其内各质点间相互作用的内力服从牛顿第三定律因而质点系的内力对任一点的力矩为零。
利用内力的这一特性即可导出质点系的角动量定理质点系对任一固定点O的角动量对时间的微商等于作用于该质点系的诸外力对O点的力矩的矢量和。
由此可见描述质点系整体转动特性的角动量只与作用于质点系的外力有关内力不能改变质点系的整体转动情况。
1。
4伯努力定理理想正压流体在有势彻体力作用下作定常运动时运动方程即欧拉方程沿流线积分而得到的表达运动流体机械能守恒的方程。
因D。
伯努利于1738年提出而得名.对于重力场中的不可压缩均质流体方程为p+ρ gz+1/2pv^=常量式中 p、ρ 、v 分别为流体的压强、密度和速度z 为铅垂高度g 为重力加速度. 上式各项分别表示单位体积流体的压力能 p、重力势能ρ g z 和动能1/2pv^在沿流线运动过程中总和保持不变即总能量守恒.但各流线之间总能量即上式中的常量值可能不同。
对于气体可忽略重力方程简化为p+1/2pV^常量(p0)各项分别称为静压、动压和总压。
显然流动中速度增大压强就减小速度减小压强就增大速度降为零压强就达到最大(理论上应等于总压).飞机机翼产生举力就在于下翼面速度低而压强大上翼面速度高而压强小因而合力向上。

理论力学论文
理论力学是研究力的本质、性质、特点和运动规律的科
学分支。
它通过建立力学的基本原理和公式来描述和解释物体的运动,是物理学中的重要组成部分。
本文将讨论理论力学的基本原理和常用方法,并探讨其在现代科学研究中的应用。
理论力学的基本原理包括牛顿力学、拉格朗日力学和哈
密顿力学。
牛顿力学描述了质点受力运动的规律,提出了力和加速度之间的关系,即力等于质量乘以加速度。
拉格朗日力学是一种优雅的力学方法,基于虚功原理,通过建立广义坐标和拉格朗日函数来描述系统的动力学行为。
哈密顿力学在拉格朗日力学的基础上引入广义动量和哈密顿函数,通过哈密顿方程描述系统的演化。
理论力学的常用方法包括动力学方程的求解和运动学分析。
动力学方程包括牛顿第二定律、拉格朗日方程和哈密顿方程,可通过数值求解或解析解法来得到系统的运动规律。
运动学分析涉及位置、速度和加速度等物理量的计算,可通过微分和积分等数学方法来求解。
理论力学在物理学、工程学和应用数学等领域都有重要
的应用。
在物理学中,理论力学的基本原理被广泛应用于解释和预测天体运动、分子动力学和量子力学等现象。
在工程学中,理论力学的方法被用于分析和设计建筑物、机械和电路等系统。
在应用数学中,理论力学的概念和方法为数学建模和计算机仿真提供了基础。
总之,理论力学是研究力学基本原理和运动规律的科学
分支,具有广泛的应用前景。
它不仅为我们理解和探索自然界提供了基础,还为解决实际问题提供了强有力的工具。
通过深入研究和应用理论力学,我们可以更好地理解物理世界的本质,并为人类社会的发展做出贡献。

理论力学论文在理论力学领域,有许多经典的论文对该领域的发展做出了重要的贡献。
以下列举了一些重要的理论力学论文:1. Isaac Newton的《自然哲学的数学原理》("Mathematical Principles of Natural Philosophy"),出版于1687年。
这部著作为经典物理学提供了坚实的数学基础,包括牛顿三定律和万有引力定律等。
2. Leonhard Euler的《振动理论》("Theories of Vibration"),出版于1747年。
该论文系统地研究了振动现象,并提出了振动方程和共振的理论。
3. Joseph-Louis Lagrange的《分析力学》("Analytical Mechanics"),出版于1788年。
这部著作引入了拉格朗日方程,极大地简化了力学问题的计算。
4. William Rowan Hamilton的《正则方程理论的应用》("Application of the Theory of Canonical Equations"),出版于1834年。
该论文提出了哈密尔顿力学的基本原理,包括哈密尔顿方程和正则变换等。
5. Carl Gustav Jacobi的《哈密尔顿原理》("The Hamiltonian Principle"),出版于1837年。
这篇论文将哈密尔顿力学用统一的方式表述,并强调了哈密尔顿原理的重要性。
6. Henri Poincaré的《三体问题的新方法》("New Methods ofCelestial Mechanics"),出版于1892年。
这篇论文提供了对于三体问题的新的数学方法,引入了混沌理论的概念。
7. Richard Feynman的《量子力学与路径积分》("Quantum Mechanics and Path Integrals"),出版于1948年。

自发电充电鞋班级:力学二班学号:1117030221 姓名:王翔设计原因:随着生活水平的提高,和手机行业的发展,以安卓为首的智能手机大行其道,智能手机有许多优点,同时为了实现这些优点,智能手机往往配备了大型触摸屏,强劲的处理器,虽然手机的性能大大加强,但是随之而来的一个重要问题就是手机的耗电量迅速增加。
虽然可以为手机而定制的电池的容量一增再增,但是仍然满足不了用户的需求。
你可能会为手机配备两块电池,但是一旦用完,那就没有办法充电了。
所以智能手机需要可靠的电力来源。
长期处于深山野地之中的地质工作者或野外探险爱好者,在野外生活中不可能携带大量的电池,因为既不方便也不环保。
因此他们需要一种简单,可靠的充电装置来为电器供电。
设计思路:如何寻找可靠而又持续的电力来源是个令人头疼的问题,看着道路上来来去去的行人,我突然想到何不用人行走是所必须的鞋来发电呢。
我们知道人在行走的时候,将内能转化为机械能,而发电机可以将机械能转化为电能,充电器则是将电能转化为化学能。
那么,如果将这三者合为一体呢?这就是我的发明-自发电充电鞋。
设计原理:自发电充电鞋事实上就是一种鞋。
它主要由如下6个部分组成:鞋,复原弹簧,小发电机,传动机构,变压器,电池盒。
如图所示,电池可以从鞋身前部的盒盖嵌入。
行走过程中,人在跨出一步时,脚跟着地,弹簧压缩,传动机构运作带动发电机产生电流,电流流经变压器,加大电压,从而为电池盒中的电池充电。
脚抬起后,复原弹簧复原,为下一次充电做准备。
电池盒可以为为一般电池充电用的电池盒,必要时也可换装手机电池盒以增加通用性。
可行性论证:这次关于自发电充电鞋的设计不仅可以用来为手机电池充电,如果需要,也可以为充电电池充电。
这款自发电充电鞋,结构简单:主体为鞋,小型变压器和发电机均可以很容易获得;有实际需求:不仅迎合手机达人需求,还可以供在山区工作的地质工作者实现自给自足;生产成本较低,所以完全可以实现大规模生产。
设计心得:此次设计来源于对生活的观察,通过对自己思路的整理,细化,最终得出此次设计。
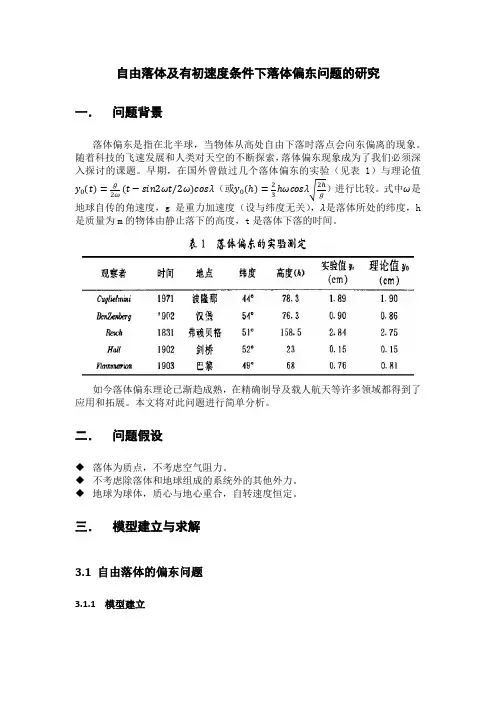
自由落体及有初速度条件下落体偏东问题的研究一.问题背景落体偏东是指在北半球,当物体从高处自由下落时落点会向东偏离的现象。
随着科技的飞速发展和人类对天空的不断探索,落体偏东现象成为了我们必须深入探讨的课题。
早期,在国外曾做过几个落体偏东的实验(见表1)与理论值y0(t)=g2ω(t−sin2ωt/2ω)cosλ(或y0(ℎ)=23ℎωcosλ√2ℎg)进行比较。
式中ω是地球自传的角速度,g是重力加速度(设与纬度无关),λ是落体所处的纬度,h 是质量为m的物体由静止落下的高度,t是落体下落的时间。
如今落体偏东理论已渐趋成熟,在精确制导及载人航天等许多领域都得到了应用和拓展。
本文将对此问题进行简单分析。
二.问题假设◆落体为质点,不考虑空气阻力。
◆不考虑除落体和地球组成的系统外的其他外力。
◆地球为球体,质心与地心重合,自转速度恒定。
三.模型建立与求解3.1 自由落体的偏东问题3.1.1模型建立地球自转速度为ω=0.72722×10−4rad/s地球的半径为R =6378164m质量为m 的物体位于地球赤道时的牵连惯性力F Ie 达到最大,即F Ie =m ×6378164×ω2=0.03373m与物体自重相比F Ie mg=0.00344 可见物体的牵连惯性力远小于其重力,且与运动无关。
故可忽略前因惯性力或将其合并入重力,而只考虑科氏惯性力。
以自由质点为例。
以质点初始位置为坐标原点,Oz 轴沿地球半径方向,Oy 轴沿纬线切线向东,Ox 轴沿经线切线向南。
如图:由质点相对运动微分方程r e c ma F ma ma =--设质点所在位置纬度为λ,则有cos sin ωωλωλ=-+i kr v x y z •••=++i j k 2Ic r F m v ω=-⋅⨯式(1)投影到x,y,z 轴2sin x y ωλ•••= (1)(2)c maG2(sin cos )y x z ωλλ•••⋅=-+2cos z g y ωλ•••=-+ 初始条件 0x y z ===0x y z •••===方程(4)中ω、y 的一阶导数均为小量,与g 相比,略去右端第二项 z g ••=-积分并考虑初始条件z =−12gt 2 方程(3)中x 的一阶导数相对z 的一阶导数为小量,可以略去。
理论力学案例分析论文引言理论力学是物理学的重要分支,并在众多应用领域发挥着重要作用。
本文将通过对一个具体案例的分析,探讨理论力学在实际问题中的应用。
本案例涉及一个弹簧振子系统,我们将基于牛顿力学的原理和公式,对该系统进行分析和求解,并给出相关的结论。
案例描述我们考虑一个简单的弹簧振子系统,如图所示。
这个系统由一个质量为m的物体通过一根劲度系数为k的弹簧悬挂而成。
在忽略空气阻力的情况下,我们将研究该系统在进行振动时的动力学特性。
分析方法我们将运用牛顿第二定律和弹簧的胡克定律,对该系统进行分析。
根据牛顿第二定律,该系统的运动方程可以表示为:m d2xdt2=−kx其中,m为物体的质量,x为物体的位移,t为时间。
为了解上述微分方程,可以采用常微分方程的求解方法。
将微分方程改写为标准形式:d2x dt2+kmx=0接下来,我们将通过求解上述方程,得到系统的解析解。
求解过程这是一个二阶常微分方程,我们将采用特征方程法求解。
首先,假设解具有形式:x(t)=Acos(ωt+φ),其中A为振幅,ω为角频率,φ为初相位。
代入方程,可以得到:mω2Acos(ωt+φ)+kAcos(ωt+φ)=0整理得:(mω2+k)Acos(ωt+φ)=0由于cos(ωt+φ)不为0,所以有:mω2+k=0解得:ω=√k m因此,系统的解析解为:x(t)=Acos(√kmt+φ)结论通过对弹簧振子系统的理论分析,我们得到了系统的解析解。
从中可以看出,系统的振动频率与弹簧的劲度系数和物体的质量有关,振幅和初相位则由初始条件决定。
理论力学在物理学中具有广泛的应用,不仅可以用于解决弹簧振子系统这样的简单问题,还可以用于研究更为复杂的物理现象。
通过理论分析,我们可以深入理解物体的运动规律,并为实际问题提供解决方案。
因此,理论力学在科学研究和工程技术中的应用不可忽视,对于进一步推动科学技术的发展和应用具有重要的意义。
参考文献[1] Marion, J. B., & Thornton, S. T. (2004). Classical dynamics of particles and systems. Brooks/Cole Publishing Company.。
纸飞机的原理土木21 2120702010 贾跃华摘要:本文是对我们童年的纸飞机做的一个研究性论文,其中包括对纸飞机受力的来源、其飞行的原理、怎样折出较好的纸飞机的方法以及现在纸飞机的发展等。
关键词:纸飞机、伯努利方程、纸飞机折叠方法、纸飞机的受力来源、纸飞机飞行原理1.引言据纸飞机研究者介绍,鉴于纸是中国人发明的,而且几百年前中国人就用纸放起了风筝,所以一般认为纸飞机起源于中国。
伦敦大学“纸飞机协会”也认同这一观点。
纸飞机的历史要追溯到第一张被抛掷到垃圾桶里的草纸说起。
第一次用纸制作飞行器的是在两千年前中国制造的风筝。
现在作为国际比赛项目,成为一种深受人们喜爱的全球性运动。
目前世界各地比赛繁多,一般国际性的纸飞机大赛比的是“距离最远”、“时间最长”以及“最有创意”几个项目。
2009年5月份,在奥地利的萨尔斯堡举行了世界纸飞机大赛总决赛,吸引了83个国家的253名选手参加。
如图1、2是现场的照片。
图1 各色各样的纸飞机图2 儿童在投掷纸飞机2.纸飞机飞行原理2.1 模型的建立图3如果两手各拿一张薄纸,使它们之间的距离大约4~6厘米。
然后用嘴向这两张纸中间吹气,如图3所示。
你会看到,这两张纸不但没有分开,反而相互靠近了,而且用最吹出的气体速度越大,两张纸就越靠近。
从这个现象可以看出,当两纸中间有空气流过时,压强变小了,纸外压强比纸内大,内外的压强差就把两纸往中间压去。
中间空气流动的速度越快,纸内外的压强差也就越大。
2.2 流体的连续性定理流体的连续性定理是指当流体连续不断而稳定地流过一个粗细不等的管道时,由于管道中任何一部分的流体都不能中断或挤压起来,因此在同一时间内,流进任一切面的流体的质量和从另一切面流出的流体质量是相等的。
连续性定理阐述了流体在流动中流速和管道切面之间的关系。
流体在流动中,不仅流速和管道切面相互联系,而且流速和压力之间也相互联系。
3.2 伯努利定律在纸飞机上的具体应用伯努利定律是空气动力最重要的公式,简单的说空气流动的速度越大,静压力越小,速度越小,静压力越大,设法使机翼上部空气流速较快,静压力则较小,机翼下部空气流速较慢,静压力较大,两边互相较力,于是机翼就被往上推去,然后纸飞机就飞起来了。
理论力学小论文 (北工大)关于木棍落地问题的研究段承阳 12044222指导教师:刘赵淼摘要:均质木棍以一定的倾斜角度自由下落,与地面会发生多次碰撞,直至能量全部耗尽。
求解与地面碰撞的次数以及影响次数的因素具有实际意义。
本文利用能量守恒原理及碰撞的有关知识,计算在理想条件下,各次碰撞的能量损失,使得n次碰撞的总的能量损失等于初始时的总能量来确定n的具体数值。
最后给出与地面碰撞次数n的计算公式,以及对影响因素的定性分析。
关键词:木棍落地,能量守恒,碰撞一、引言木棍落地反弹,从本质上讲属于一个碰撞问题。
根据百度百科,“碰撞”的定义为在两粒子或物体间极短的相互作用。
本文研究的就是木棍与地面的碰撞问题。
如今的碰撞理论比较完善,本文旨在利用现有的碰撞理论以及从能量守恒的观点出发,定量计算木棒以一定倾斜角度自由下落与地面碰撞次数及定性的研究木棍质量,木棍长度,下落高度,倾斜角度,恢复因数等对于碰撞次数的影响。
研究时要用到一些前人的研究成果。
牛顿在研究碰撞规律时[1]发现对于材料确定的物体,其恢复因数几乎是不变的。
碰撞过程的两个个基本定理,一是冲量定理即冲量矩等于[2]动量矩的改变量,二是能量守恒原理。
点运动学的基本知识如匀加速直线运动的基本规律也十分有用。
本文将先根据实际问题建立理想的力学模型,从理论上推导总共碰撞次数n的表达式,最后根据推导,定性分析各影响因素。
二、正文2.1 基本假设木棍为均质木棍(质心在几何中心),不考虑空气阻力即木棍开始时做自由落体。
第i次到第i+1次碰撞间,,u木棍所做运动为以质心轴为转轴的匀速转动(转动角速度为)与初速度为的匀加速直线运动的合成。
i,1ci2.2 理论计算设木棍长为L,质量为m,初始时木棍与水平夹角为θ1,当地重力加速度为g,木棍最低点离水平地面距离为h,v,木棍恢复因数为e,第i次碰撞前的瞬间木棍的质心速度大小为,绕质心轴转动的角速度为,碰撞后的瞬间质ciiu,,心的速度大小为,绕质心轴转动的角速度为,第i次碰撞瞬间木棍与水平夹角为,从第i次碰撞完成到第cii'itsi+1次碰撞开始经历的时间为,从第i次碰撞完成到第i+1次碰撞开始木棍质心下降的距离为,第一次碰撞前瞬ii间木棍质心处为势能零点,规定竖直向上为正方向.由基本假设易得(1) ,,,ii'1,图一如图一,对于第一次碰撞进行计算: 由冲量定理,碰撞时有(2) mumvI,,,()cc11由相对质心的冲量距定理,得L,,,,,cosJJI (3) cc211212JmL,其中,转动惯量 (4) c12碰撞前,A处的速度沿竖直方向的投影为L,,,,cosvv (5) ayc1112碰撞后,A处的速度沿竖直方向的投影为L,,,,cosuu (6) ayc1212由恢复系数定义uaye, (7) vay联立式(2)到(7)可解得26cos3cos6coseveLvL,,,,,,,,cc1111111 (8) ,,22LL,3cos,1 22coscos6cosevLeLv,,,,,,,,cc111111 (9) u,c1226cos,, 1122能量损失 (10) ,,,,EmghmuJ,cc11222为了方便计算及讨论,不妨设e=0.5 (11)从下落到碰撞木棍做平动,对于第一次碰撞,有(12) ,,01(13) vgh,2c1将(11)至(13)试代入(8)和(9)中,得92cosgh,1 (14) ,,22,(13cos)L,122(16cos)gh,,1 (15) u,c122(13cos),,1将试(14)(15)代入(10)中,得2,,9(121cos),,1 (16) ,,Emgh1,,22(13cos),,,,1图二第二次碰撞如图二所示t从第一次碰撞完成到第二次碰撞经历的时间为 1,,,12t, (17) 1,2由几何关系,LLs,,sinsin,, (18) 11222由牛顿运动定律12- (19) ,,,sutgtc11112联立(18)(19)得到关于的一个方程 ,2,,,,,,21212 (20) 2()(sinsin)0ugL,,,,,,c112,,22上试中只有未知,可以利用Matlab 求解上述方程。
摩擦角和自锁姓名:孙艳宁班级:2013 城市地下空间学号:201300206108摘要:自锁现象是力学中的一种特有现象,当自锁条件满足时,外力越大,物体保持静止的能力越强,这种现象在生产和生活中广泛存在,并根据自锁原理人们开发了大量的工具器械,广泛应用于工农业生产中,在日常生活中利用这一原理的现象也随处可见。
关键字:摩擦角、摩擦因数、自锁条件、自锁应用一、摩擦角当物体处于滑动的临界状态时,静摩擦力FS达到最大值Fmax,此时Fr与Fn 的夹角也最大,此时的φm 称为摩擦角。
由图可见:tanφm =Fmax/Fn = fFn /Fn= f (1)即:摩擦角的正切等于静摩擦因数。
可见,根据摩擦角可以来确定静摩擦因数。
当运动趋势方向(即主动力的方向)改变时,Fmax及支撑面的全反力Fr的方向也将改变。
当全反力Fr的作用线在空间连续改变时,将描出一空间锥面,称为摩擦锥。
如图所示。
图1常见的摩擦角有坡面滑行物体的摩擦角:在斜面上端A处有一个物体自静止起滑下,滑至水平面C点停止,若物体与斜面、平面间的摩擦因数均为μ,A与C之间水平距离为S,物体开始下滑的高度AD=h,滑动摩擦因数μ=h/S。
设斜面AB与水平面夹角为α,根据功能关系,物体克服摩擦力所做的功等于物体机械能的减少。
即mgh=F1•AB+F2•BC(2)F1、F2为摩擦力,分别等于μmgcosα和μmg,代入后可得mgh=μmgcosα•AB+μmg•BC (3)∵ABcosα=DB,上式可以写作h=μ(DB+BC) (4)式中DB+BC=S,∴μ=h/S。
有μ=tanθ(5)二、自锁我们都知道,由于静摩擦力不可能超过最大值,因此全约束力的作用线也不可能超出摩擦角以外,即全约束反力必在摩擦角之内。
由此可知:(1)如果作用于物块的全部主动力的合力的作用线在摩擦角之内,则无论这个力怎样大,物块必保持静止。
称这种现象为自锁现象。
因为在这种情况下,主动力的合力与法线间的夹角,因此,主动力的合力的作用线必在摩擦角之内,而全约束力的作用线也在此摩擦角之内,主动力的合力和全约束力必能满足二力平衡条件,如图所示,所以物块必静止。
讨论台球上的力学问题摘要:本文根据《理论力学》中的相关概念与知识,对台球桌上的力学问题进行分析,讨论。
我将从碰撞前后的状况,和台球的三种基本的击球方式进行论述,再对某些特殊打法进行简要分析。
其实在很久以前,我看过朋友们在打桌球时,他们能够很好的控制白球,想要击到目标时就停止、白球跟上、或者白球退回,他们都能够很好的表现出来,我对此很是惊奇,现在我将通过理论力学的知识来对此作出解释。
关键词:台球、碰撞、力学原理 引言:如今,台球运动,包括斯诺克,八球等已经成为了深受人们喜爱的运动。
当我们观赏台球比赛时,会看到高水平的运动员打出各种各样的旋转球,在碰撞后会“不规则”的运动,有时会反弹,有时碰撞后会突然加速,有的时候则会拐出一条曲线。
台球运动在我国有着广泛的群众基础。
从年龄上看有中小学生到年逾花甲的老年人。
从社会各阶层看有农民、工人、学生、教师、打工者、商人、官员以及职业运动员等等。
对于台球的运动过程中的力学原理我就此进行一些简要的分析。
1、台球碰撞前后的速度变化 在这里只解释正碰情况如图所示,球A 具有速度v ,和角速度w ,而球B 静止于桌面上,下面就w 的大小进行分类讨论 1.1w =0的情况: 这种情况是最简单的情况,我们假设两球的质量相等即A B m m =,则在碰撞过程中我们忽略摩擦力的作用,则两球碰撞可以看成是弹性碰撞,则这种情况下,就可以直接得出碰撞后,0A v =,B v v =。
1.20w ≠且w 的方向为从里向外:这种情况下,首先碰撞过程中忽略摩擦力的作用,所以由动量守恒定律得到:A B B A A m v m v m v =+在此碰撞过程中,由于时图1图2间短暂,且两球之间的摩擦系数较小,所以可以认为A 球给B 球的力AB F ,水平向右,而此时忽略了摩擦力,所以对于B 而言在碰撞过程中午力矩作用,所以0B w =,同样的A 球除了有摩擦力给它的力矩之外,就没有其他的力矩了,而此时摩擦力忽略掉,所以A 球也可以近似的看成力矩为0 。
不倒翁的力学思考沈安宁学号:1010101209 班级:B机制102任课教师:史有进不倒翁是一种历史悠久的玩具,特别受到各个年代儿童们的喜爱。
清代文人魏崧在《壹是纪始》写到:“不倒翁始于唐。
”他据《唐摭言》中的记载:“卢连举不第,赋《酒胡子》长篇以寓意,序日:‘巡觞之胡,旋转由人。
’今谓之不倒”,这便是不倒翁的最初模型。
而后渐渐流传至今,演变成为哄逗幼儿的玩具,给儿童乃至大人们增添了无穷乐趣。
那么,在我们学习了大学《理论力学》之后,便可以较为确切的从力学上来分析不倒翁的原理,并了解其在日常生活生产中的相关应用。
一、力学原理最常见的不倒翁是纸身、泥底,即用纸浆灌模或用废纸粘糊成形,再用泥土制成半圆形的底座,将二者粘合好之后,再在外表糊上净纸,施以彩绘而成;也有的用木头做底,底部中心固定上铁块和小石子;还有用小葫芦挖净内瓤,内部灌铅做成的“葫芦”;今天还有用鸡蛋壳、旧乒乓球做成的小不倒翁。
所有的这些不倒翁都有相同的特点:上半身为空心壳体、下半身是一个实心的半球体,底部为圆形。
这些特点使它们具有了一致的基本力学结构,都能达到“不倒”的效果。
1.不倒翁的形体结构不倒翁为空心壳体,重量很轻;下半身是一个实心的半球体,重量较大,不倒翁的重心就在半球体之内。
下面的半球体和支承面之间有一个接触点,这个半球体在支承面上滚动时,接触点的位置就要发生改变。
不倒翁始终用一个接触点站立在支承面上,它永远是一个独脚体。
2.不倒翁的平衡的稳定性不倒翁在受到外力的作用时,就要失去平衡,而在外力去除后,不倒翁能自行回复到平衡状态,这说明不倒翁具有一种抵抗外力干扰保持平衡的能力,这就是平衡的稳定性。
这种抵抗干扰保持平衡的能力的形成,应该从不倒翁的受力情况来看。
3.不倒翁的受力情况有三种第一,不倒翁平衡的受力情况。
不倒翁在桌面上,受到两个外力的作用:一个是重力G,地球对不倒翁的吸引力;另一个是支持力,桌面对牛球体的反作用力。
根据物体的平衡条件,只要这两个力大小相等、方向相反、作用在一条直线上,不倒翁就能够保持平衡的状态。
2013理论力学小论文
自锁
机械设计及其自动化 12级机制2班梁杰明张伟
图1
及支撑面的全反力Fr的方向也将改
F1、F2为摩擦力,分别等于μmgcos α和μmg ,代入后可得
mgh=μmgcos α•AB+μmg•BC
∵ABcos α=DB ,上式可以写作
h =μ(DB+BC)
式中DB+BC =S ,
∴μ=h/S 。
有 μ=tan θ
二、自锁
我们都知道,由于静摩擦力不可能超过最大值,因此全约束力的作用线也不可能超出摩擦角以外,即全约束反力必在摩擦角之内。
由此可知:
(1)如果作用于物块的全部主动力的合力的作用线在摩擦角 之内,则无论这个力怎样大,物块必保持静止。
称这种现象为自锁现象 。
因为在这种情况下,主动力的合力与法线间的夹角 ,因此,主动力的合力 的作用线必在摩擦角之内,而全约束力的作用线也在此摩擦角之内,主动力的合力和全约束力必能满足二力平衡条件,如图所示,所以物块必静止。
工程实际中常应用自锁原理设计一些机构或夹具,如千斤顶、压榨机、圆锥销等,使它们始终保持在平衡状态下工作。
(2)如果全部主动力的合力的作用线在摩擦角之外,则无论这个力怎样小,物块一定会滑动。
因为在这种情况下,全部主动力的合力的作用线已在摩擦角之外,全约束力的作用线不可能出现在摩擦角之外,不能满足二力平衡条件,如图所示,所以物块不会静止。
应用这个道理,可以设法避免发生自锁现象。
有上述分析可知自锁只与摩擦角有关,为什么呢?因为当φ<φf 时,随着主动力的不断增大,支撑面的反向法力和阻止物体滑动的摩擦力也会相应的增大,所以物体仍静止不动。
如图4紧靠在竖直墙壁上的物体,在适当大的外力作用下,可以保持静止。
当外力大到重力可以忽略,无论用斜向上的力,还是用斜向下的力,发生自锁的条件与水平面的情况是相同的。
如改用与竖直墙壁的夹角来表示,临界角α0可表达为
α0=arctan 1
与水平面不同的,只是保证物体静止的最小力条件有所不同。
当用斜
向上的力维持物体平衡时,不一定满足自锁条件,而若用斜向下的力使物
体平衡,一定首先满足自锁条件才可能发生。
而生产、生活中更多是发生
在竖直方向的自锁现象。
一、 自锁现象的应用
(1) 静摩擦因数的测定
如图所示。
把要测定的两种材料分别做成斜面和物块,把物块放在斜面上,并逐渐从零起增大斜面的倾角 θ ,直到物块刚开始下滑时为止。
记下斜面倾角 θ ,这时的 θ 角就是要测定的摩擦角 ,其正切就是要测定的摩擦因数。
理由如下:由于物块仅受重力和全约束力作用而平衡,所以重力与全约束力应等值、反向、共线,因此必沿铅直线,重力与斜面法线的夹角等于斜面倾角 θ 。
而当物块处于临界状态时,全约束力与法线间的夹角等于摩擦角 ,也即θ=φ。
所以摩擦因数为:μ=tan θ
x 2
图4
(2) 尼龙自锁螺母
尼龙自锁螺母是一种新型高抗振防松紧固零件,能应用于温度-50~100℃的各种机械、
电器产品中。
目前,宇航、航空、坦克、矿山机械、汽车运输机械、农业机械、纺织机械、电器产品以及各类机械对尼龙自锁螺母的需求量剧增,这是因为它的抗振防松性能大大高
于其他各种防松装置,而且振动寿命要高几倍甚至几十倍。
当前机械论坛设备的事故有80%以上是由于紧固件的松动而造成的,特别在矿山机械中尤为严重,而使用尼龙自锁螺母就可
以杜绝由于紧固件松脱所造成的重大事故。
(3) 劈
具有构成尖锐角度的两个平面形状的坚硬物体。
又称楔或尖劈。
属于斜面类简单机械。
两成尖锐角度的平面称为劈面,劈的尖端称为劈刃,宽端称为劈背。
i
我国周口店北京猿人遗址处发现的两面石器是尖劈的原始形式,距今约有40~50万年,新石器时代的石斧、石矛,商周时代的青铜器和兵器等,都说明尖劈是人类最早发明并广泛使用的一种简单工具。
尖劈可以用来卡紧物件。
如果尖劈的锐角足够小,它可以嵌入木头缝或墙缝里,这是由于摩擦力的作用使尖劈静止在木头缝中或墙缝里,称为摩擦自锁。
像木器家具中常在横接处打入木楔就是应用尖劈摩擦自锁的原理。
(4) 自锁在千斤顶中的应用
螺旋千斤顶是靠力推动手柄1,使丝杆2的方牙螺纹沿地座3的螺纹槽慢慢旋转而顶起重物4.承载时丝杆的螺纹和底座的螺纹槽之间产生一定的正压力和摩擦力。
由于螺纹相当于将一斜面卷到一圆柱体上的情形,所以,把它展开后,丝杆与螺母间的摩擦可简化为一物体放在斜面上的摩擦问题。
此时,承载的丝杆相当于物体,底座螺母相当于斜面,斜面倾角就是螺纹的升角θ。
螺旋千斤顶在使用过程中,要求顶起重物后丝杆不会自动下降,而在任意位置都保持平衡。
总结
自锁方面的运用很广阔,通过力学的分析,可以更好的利用自锁。
自锁对生活有重大意义,在了解自锁原理后,可以很好的使它为自己做的理想的状态。
自锁是由于物体之间的相互摩擦所导致的,在计算它们之间的相互作用后,可以知道自锁的相互摩擦达到最大值,自锁的作用越大。
参考文献
【1】郭映红、周志红.《理论力学》.清华大学出版社.
【2】李高斌、马辉. 力学中的自锁现象及应用.
【3】百度百科及参考文献.。