下载文档原格式
理论力学小论文理论力学小论文理论力学给人类提供了大量的物质财富,同时也提供了精神财富。
理论力学的高技术和强渗透性也使之成为社会发展的重要推动力。
今天我们就一起来欣赏理论力学小论文吧!理论力学小论文：浅析物理力学的产生及其发展摘要：物理力学主要是研究宏观力学的微观理论学科。
研究物理力学的主要目的是通过理解微观粒子性质的相互作用，找出介质的力学性质计算方法，进而使解决力学问题建立在微观分析的基础上。
本文主要探讨了物理力学的产生和发展，为有关物理力学问题的解决提供理论基础。
关键词：物理力学;产生;发展一、物理力学发展需要解决的问题分析在物理力学的发展过程中，我们需要解决两方面的问题，一个是关于物性的问题，另一个是有关运动规律的问题。
物理力学主要通过物性及其运动规律这两个方面的微观化而成为解决问题、建立微观分析的基础。
关于物性的参数主要表现为运动方程组中的系数，例如弹性系数、热导率、粘性系数、声速、比热等。
为了求解运动的方程组，需要知道它们相关的数值。
在传统力学中，物性参数的数值是需要试验测定的。
而在我们研究的物理力学中，是通过微观的分析以及对宏观数据分析相结合的方法计算参数的数值。
我们研究物理力学，不仅是为了能够找出物质性质的微观规律，而且还需要找能够预见新物质性质的方法。
针对物理力学发展中的相关问题，先了解一下有关激波结构问题的例子。
物态在激波前后会有很大的变化，在波阵面一定的厚度之内，物质是处在远离平衡的状态的。
这时，对于宏观物态的参数已经不适用了。
因此，我们需要从分子运用的这一个角度进行描述。
像从波尔兹曼方程的角度出发，进而直接进行求解。
在上世纪60年代，一对无内部自由度的'影响激波结构的问题得到了进一步发展。
其发展主要得力于计算机技术的发展，从而能够使波尔兹曼方程进而得到模型数学方程，求精确解。
另外，还能够实现激波管与稀薄气体风洞在较高区域的分辨率的相关方面的测量。
虽然对于这些问题的处理都是初步的，但是从物理力学微观运动规律上看，确是一个非常大的进步。
台球运动与力学摘要：台球运动是一项智慧的运动，我想，掌握和了解其中的一些深层的原理必然会对水平的提高有不可忽视的作用。
作为一位狂热的台球爱好者，在打台球之余也会对一些现象有所思考，并尝试用理论的知识来解释。
本文主要结合所学的理论力学知识结合计算分析台球运动中一些比较常见的现象。
关键词：台球 ；力学；运动 ；碰撞随着台球运动的发展，我们在比赛中常会看到一些看似反物理原理的现象，例如；碰撞后球不作直线运动，而是作诡异的弧线运动；球碰撞后会加速前进等等。
下面仅就球的运动形式，两球的碰撞，滑杆现象作简要的分析和讨论。
一、台球运动的形式是什么使台球运动有如此快的发展？又是什么能使台球出现这么多美妙的运动现象？答案只有一个，那就是摩擦力，没有桌面的摩擦力，你看到的运动永远是单调的直线运动，，摩擦力是影响台球运动的关键因素。
谈到其运动形式，这绝对是典型的刚体运动，其在桌面上所作的各种运动，归根结底就是刚体小球的质心平动和绕质心的转动。
当台球受到的力通过球心时，它短时间内做平动；当台球受到的力不通过球心时，它在短时间内既转动又平动。
台球运动中所说的低杆、中杆、高杆就可以产生各自的运动效果。
下面作一一讨论：1、中杆：这是台球运动中使用最普遍的一种杆法，它要求击打球的中间部位（近似看作受力过球心）。
此种情况开始没有旋转，也就是一开始作平动，向前滑动一段距离后，因受台面的磨擦阻力f 作用，渐渐产生了逆时针方向的力矩，使球与台面接触点速度减慢，球的顶点速度不变，于是球便向前旋转起来。
2、高杆： 高杆要求击打球的上部。
在下图中，假设台球质量为m ，半径为R ，受到球杆沿水平方向击打的冲击力为F ，力的水平作用线距球心的距离为h ，质心运动速度为v ，转动角速度为ω。
我们分析台球的受力情况及运动状态。
mgFn f F动量P= mv (1)动量矩M=J ω…………………………………………….(2) ，式中J=2/5mR 2。
质点系对任一动点的转动方程摘要：讨论了质点系对任一动点的转动方程以及在一些条件下的方程的简化。
假设A 是一个质点系，它由n 个质点组成，并且处在惯性坐标系Oxyz 中，O 为原点。
取其中的质点i ，则有i m 为质点i 的质量，i r为质点i 对固定点O 的矢径，e F为作用在质点i 上的外力。
由质点系动量矩定理可以得到：质点系对任一固定点动量矩的时间导数等于作用在质点系上的所有外力对同一点的力矩之和，所以有：e n i i i i n i i F r dt r d m r dt d ⨯=⨯∑∑==11 （1） 但是在实际的运用中，固定点的选取一般都比较困难，往往选取动点作为矩心。
这时有动坐标系ξηζ'O ，'O 为动坐标系原点，'i r 为质点i 对动点'O 的矢径。
先求质点系相对于动点转动的一般形式。
根据动量矩的定义，i m 动量矩为dt r d m r i i ni i '1'⨯∑=，对时间求导数，则 dt r d m r dt r d m r dt r d m dt r d dt r d m r dt d i i ni i i i i i i n i i i i n i i '21''2''1''1')( ⨯=⨯+⨯=⨯∑∑∑=== 其中dtr d i '2为质点i m 的相对加速度r a。
质点i m 的绝对加速度a a 等于相对加速度r a、牵连加速度e a 、科氏加速度c a 的矢量和，即：c e r a a a a a ++=，所以cn i i e n i i a n i i c e a i n i i i i n i i i i n i i F r F r F r a a a m r dt r d m r dt r d m r dt d ⨯+⨯+⨯=--⨯=⨯=⨯∑∑∑∑∑∑======1'1'1'1''21''1')(所以可以得到c ni i e n i i a n i i i i n i i F r F r F r dt r d m r dt d⨯+⨯+⨯=⨯∑∑∑∑====1'1'1''1' （2） a F 、e F 、c F分别为质点i m 受到的外力、牵连惯性力、科氏惯性力。
单自由度系统振动机设09-4班 田春宇摘要：单自由度系统的振动理论是振动理论的理论基础。
力学模型的简化方法。
振动特性的讨论。
扭转振动；计算系统固有频率的几种方法。
单自由度系统有阻尼自由振动。
简谐激振力引起的受迫振动。
关键词：振动 机械 系统 力学 理论 引言：单自由度系统的振动理论是振动理论的理论基础。
尽管实际的机械都是弹性体或多自由度系统，然而要掌握多自由度振动的基本规律，就必须先掌握单自由度系统的振动理论。
此外，许多工程技术上的具体振动系统在一定条件下，也可以简化为单自由度振动系统来研究。
例如：悬臂锤削镗杆；外圆磨床的砂轮主轴；安装在地上的床身等。
一、 力学模型的简化方法若忽略这些零部件中的镗杆、主轴和转轴的质量，只考虑它们的弹性。
忽略那些支承在弹性元件上的镗刀头、砂轮、床身等惯性元件的弹性，只考虑它们的惯性。
把它们看成是只有惯性而无弹性的集中质点。
于是，实际的机械系统近似地简化为单自由度线性振动系统的动力学模型。
在实际的振动系统中必然存在着各种阻尼，故模型中用一个阻尼器来表示。
阻尼器由一个油缸和活塞、油液组成。
汽车轮悬置系统等等。
二、单自由度振动系统——指用一个独立参量便可确定系统位置的振动系统。
所有的单自由度振动系统经过简化，都可以抽象成单振子，即将系统中全部起作用的质量都认为集中到质点上，这个质点的质量m 称为当量质量，所有的弹性都集中到弹簧中，这个弹簧刚度k 称为当量弹簧刚度。
以后讨论中，质量就是指当量质量，刚度就是指当量弹簧刚度。
在单自由度振动系统中，质量m 、弹簧刚度k 、阻尼系数C 是振动系统的三个基本要素。
有时在振动系统中还作用有一个持续作用的激振力P 。
应用牛顿运动定律，作用于一个质点上所有力的合力等于该质点的质量和该合力方向的加速度的乘积。
单自由度系统无阻尼自由振动无阻尼自由振动是指振动系统不受外力，也不受阻尼力影响时所作的振动。
三、振动特性的讨论 1．振动的类型无阻尼自由振动是简谐振动。
乒乓球加旋技术的分析摘要力学基本受力分析原理、动量定理、伯努力定理研究了乒乓球的旋转原因及从不同方向、不同力度下击球乒乓球的旋转特性发现以不同的方式、手法击乒乓球球将产生不同的旋转效果具备不同程度的杀伤力。
关键词受力分析旋转原理旋转分类加旋手法1 基本理论知识1.1动量定理物体动量的增量等于物体所受作用力对时间的累积作用即Ft=Δ mv.若质量不变力对物体的作用时间越长物体动量就越大即速度v越大.1.2摩擦力具有一定摩擦系数μ 的两物体相接触且产生压力若它们相对运动或有相对运动的趋势就会产生阻碍它们相对运动或相对运动趋势的作用力这个力就是摩擦力其大小F=μ FnFn 表示正压力大小。
1.3角动量定理对于质点角动量定理可表述为质点对固定点的角动量对时间的微商等于作用于该质点上的力对该点的力矩。
对于质点系由于其内各质点间相互作用的内力服从牛顿第三定律因而质点系的内力对任一点的力矩为零。
利用内力的这一特性即可导出质点系的角动量定理质点系对任一固定点O的角动量对时间的微商等于作用于该质点系的诸外力对O点的力矩的矢量和。
由此可见描述质点系整体转动特性的角动量只与作用于质点系的外力有关内力不能改变质点系的整体转动情况。
1。
4伯努力定理理想正压流体在有势彻体力作用下作定常运动时运动方程即欧拉方程沿流线积分而得到的表达运动流体机械能守恒的方程。
因D。
伯努利于1738年提出而得名.对于重力场中的不可压缩均质流体方程为p+ρ gz+1/2pv^=常量式中 p、ρ 、v 分别为流体的压强、密度和速度z 为铅垂高度g 为重力加速度. 上式各项分别表示单位体积流体的压力能 p、重力势能ρ g z 和动能1/2pv^在沿流线运动过程中总和保持不变即总能量守恒.但各流线之间总能量即上式中的常量值可能不同。
对于气体可忽略重力方程简化为p+1/2pV^常量(p0)各项分别称为静压、动压和总压。
显然流动中速度增大压强就减小速度减小压强就增大速度降为零压强就达到最大(理论上应等于总压）.飞机机翼产生举力就在于下翼面速度低而压强大上翼面速度高而压强小因而合力向上。
理论力学论文
理论力学是研究力的本质、性质、特点和运动规律的科
学分支。
它通过建立力学的基本原理和公式来描述和解释物体的运动，是物理学中的重要组成部分。
本文将讨论理论力学的基本原理和常用方法，并探讨其在现代科学研究中的应用。
理论力学的基本原理包括牛顿力学、拉格朗日力学和哈
密顿力学。
牛顿力学描述了质点受力运动的规律，提出了力和加速度之间的关系，即力等于质量乘以加速度。
拉格朗日力学是一种优雅的力学方法，基于虚功原理，通过建立广义坐标和拉格朗日函数来描述系统的动力学行为。
哈密顿力学在拉格朗日力学的基础上引入广义动量和哈密顿函数，通过哈密顿方程描述系统的演化。
理论力学的常用方法包括动力学方程的求解和运动学分析。
动力学方程包括牛顿第二定律、拉格朗日方程和哈密顿方程，可通过数值求解或解析解法来得到系统的运动规律。
运动学分析涉及位置、速度和加速度等物理量的计算，可通过微分和积分等数学方法来求解。
理论力学在物理学、工程学和应用数学等领域都有重要
的应用。
在物理学中，理论力学的基本原理被广泛应用于解释和预测天体运动、分子动力学和量子力学等现象。
在工程学中，理论力学的方法被用于分析和设计建筑物、机械和电路等系统。
在应用数学中，理论力学的概念和方法为数学建模和计算机仿真提供了基础。
总之，理论力学是研究力学基本原理和运动规律的科学
分支，具有广泛的应用前景。
它不仅为我们理解和探索自然界提供了基础，还为解决实际问题提供了强有力的工具。
通过深入研究和应用理论力学，我们可以更好地理解物理世界的本质，并为人类社会的发展做出贡献。
理论力学论文之力的平移1401011019 土木一班熊玉鹏力的平移定理作用于刚体上的力，可以平行移动至任一点，但必须在原力与新作用点所决定的平面内附加一个力偶，其力偶矩等于原力对新作用点之矩。
【说明】该定理是力系向一点简化的基础；在力的平移定理中，力的大小和方向都没有变化，变化的只是力的作用线；共面的一个力和一个力偶可以等效于一个合力；该定理只是适用于力对刚体的运动效应，当一个力平移后其变形和内力通常都要变化；在实际工程上常用近似力的平移定理得到相应的等效力系，使原来较为复杂的问题易于分析来分析解决，这将在以后的学习中逐步讨论。
5、平面任意力系向一点简化·主矢和主矩平面任意力系向作用面内任一点简化的结果一般是一个力和一个力偶。
这个力作用在简化中心，它的矢量称为原力系的主矢，等于这力系中各力的矢量和；这个力偶的力偶矩称为原力系对简化中心的主矩，等于这力系中各力对简化中心之矩的代数和。
【说明】①一般来说，主矢不是原力系的合力，主矩也不是原力系的合力偶，只有将作用在简化中心上大小和方向等于主矢的力和力偶矩为主矩的力偶综合作用才能与原力系等效。
②平面任意力系向一点的简化结果根据主矢和主矩是否为零可分为四种情况，但它简化的最终结果有三种：当主矢不为零时，不论主矩是不是零，最终结果都是一个力，这时可以称该力为原力系的合力；当主矢为零、主矩不为零时，最终结果是一个力偶，这时该力偶可称为原力系的合力偶；当主矢和主矩同时为零时，力系平衡。
【争议】主矢是不是力？主矩是不是力偶？关于这个问题国内多数相关教材上都没有明确提出来。
但从其表述中多数都说“主矢与简化中心无关，主矩一般与简化中心有关”，这就说明“主矢不是力，主矩不是力偶”。
关于这一点可以这样理解：力有大小、方向和作用点三个要素，由于不论选择哪一点作为简化中心，力系向一点简化后得到的主矢都相等，即主矢是一个自由矢量，与简化中心无关，所以主矢不是力；力偶对作用面内任一点的矩都等于力偶矩，其大小和转向都不变，而选择不同的点作为简化中心时，力系中各分力对简化中心的矩通常是不同的，其代数和即主矩一般也是不同的，所以主矩不具有力偶对平面内任一点的矩都不变的性质，因此主矩不是力偶。
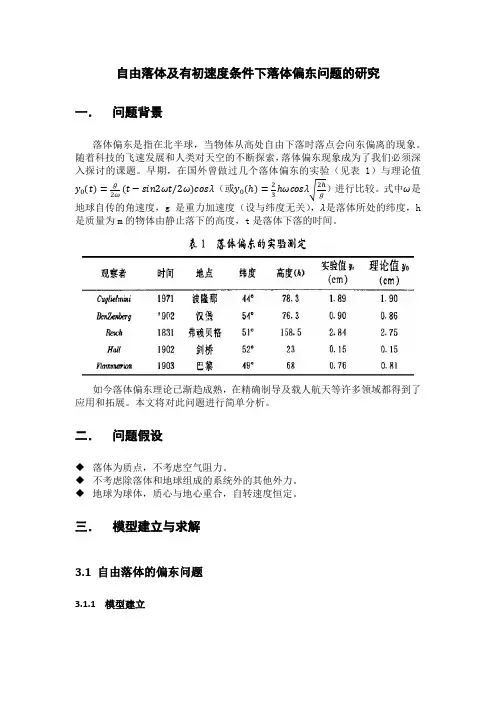
自由落体及有初速度条件下落体偏东问题的研究一．问题背景落体偏东是指在北半球，当物体从高处自由下落时落点会向东偏离的现象。
随着科技的飞速发展和人类对天空的不断探索，落体偏东现象成为了我们必须深入探讨的课题。
早期，在国外曾做过几个落体偏东的实验（见表1）与理论值y0(t)=g2ω(t−sin2ωt/2ω)cosλ（或y0(ℎ)=23ℎωcosλ√2ℎg）进行比较。
式中ω是地球自传的角速度，g是重力加速度（设与纬度无关），λ是落体所处的纬度，h 是质量为m的物体由静止落下的高度，t是落体下落的时间。
如今落体偏东理论已渐趋成熟，在精确制导及载人航天等许多领域都得到了应用和拓展。
本文将对此问题进行简单分析。
二．问题假设◆落体为质点，不考虑空气阻力。
◆不考虑除落体和地球组成的系统外的其他外力。
◆地球为球体，质心与地心重合，自转速度恒定。
三．模型建立与求解3.1 自由落体的偏东问题3.1.1模型建立地球自转速度为ω=0.72722×10−4rad/s地球的半径为R =6378164m质量为m 的物体位于地球赤道时的牵连惯性力F Ie 达到最大，即F Ie =m ×6378164×ω2=0.03373m与物体自重相比F Ie mg=0.00344 可见物体的牵连惯性力远小于其重力，且与运动无关。
故可忽略前因惯性力或将其合并入重力，而只考虑科氏惯性力。
以自由质点为例。
以质点初始位置为坐标原点，Oz 轴沿地球半径方向，Oy 轴沿纬线切线向东，Ox 轴沿经线切线向南。
如图：由质点相对运动微分方程r e c ma F ma ma =--设质点所在位置纬度为λ，则有cos sin ωωλωλ=-+i kr v x y z •••=++i j k 2Ic r F m v ω=-⋅⨯式(1)投影到x,y,z 轴2sin x y ωλ•••= (1)(2)c maG2(sin cos )y x z ωλλ•••⋅=-+2cos z g y ωλ•••=-+ 初始条件 0x y z ===0x y z •••===方程(4)中ω、y 的一阶导数均为小量，与g 相比，略去右端第二项 z g ••=-积分并考虑初始条件z =−12gt 2 方程(3)中x 的一阶导数相对z 的一阶导数为小量，可以略去。
理论力学案例分析论文引言理论力学是物理学的重要分支，并在众多应用领域发挥着重要作用。
本文将通过对一个具体案例的分析，探讨理论力学在实际问题中的应用。
本案例涉及一个弹簧振子系统，我们将基于牛顿力学的原理和公式，对该系统进行分析和求解，并给出相关的结论。
案例描述我们考虑一个简单的弹簧振子系统，如图所示。
这个系统由一个质量为m的物体通过一根劲度系数为k的弹簧悬挂而成。
在忽略空气阻力的情况下，我们将研究该系统在进行振动时的动力学特性。
分析方法我们将运用牛顿第二定律和弹簧的胡克定律，对该系统进行分析。
根据牛顿第二定律，该系统的运动方程可以表示为：m d2xdt2=−kx其中，m为物体的质量，x为物体的位移，t为时间。
为了解上述微分方程，可以采用常微分方程的求解方法。
将微分方程改写为标准形式：d2x dt2+kmx=0接下来，我们将通过求解上述方程，得到系统的解析解。
求解过程这是一个二阶常微分方程，我们将采用特征方程法求解。
首先，假设解具有形式：x(t)=Acos(ωt+φ)，其中A为振幅，ω为角频率，φ为初相位。
代入方程，可以得到：mω2Acos(ωt+φ)+kAcos(ωt+φ)=0整理得：(mω2+k)Acos(ωt+φ)=0由于cos(ωt+φ)不为0，所以有：mω2+k=0解得：ω=√k m因此，系统的解析解为：x(t)=Acos(√kmt+φ)结论通过对弹簧振子系统的理论分析，我们得到了系统的解析解。
从中可以看出，系统的振动频率与弹簧的劲度系数和物体的质量有关，振幅和初相位则由初始条件决定。
理论力学在物理学中具有广泛的应用，不仅可以用于解决弹簧振子系统这样的简单问题，还可以用于研究更为复杂的物理现象。
通过理论分析，我们可以深入理解物体的运动规律，并为实际问题提供解决方案。
因此，理论力学在科学研究和工程技术中的应用不可忽视，对于进一步推动科学技术的发展和应用具有重要的意义。
参考文献[1] Marion, J. B., & Thornton, S. T. (2004). Classical dynamics of particles and systems. Brooks/Cole Publishing Company.。
摩擦角和自锁姓名：孙艳宁班级：2013 城市地下空间学号：201300206108摘要：自锁现象是力学中的一种特有现象，当自锁条件满足时，外力越大，物体保持静止的能力越强，这种现象在生产和生活中广泛存在，并根据自锁原理人们开发了大量的工具器械，广泛应用于工农业生产中，在日常生活中利用这一原理的现象也随处可见。
关键字：摩擦角、摩擦因数、自锁条件、自锁应用一、摩擦角当物体处于滑动的临界状态时，静摩擦力FS达到最大值Fmax,此时Fr与Fn 的夹角也最大，此时的φm 称为摩擦角。
由图可见：tanφm =Fmax/Fn = fFn /Fn= f （1）即：摩擦角的正切等于静摩擦因数。
可见,根据摩擦角可以来确定静摩擦因数。
当运动趋势方向（即主动力的方向）改变时，Fmax及支撑面的全反力Fr的方向也将改变。
当全反力Fr的作用线在空间连续改变时，将描出一空间锥面，称为摩擦锥。
如图所示。
图1常见的摩擦角有坡面滑行物体的摩擦角：在斜面上端A处有一个物体自静止起滑下，滑至水平面C点停止，若物体与斜面、平面间的摩擦因数均为μ，A与C之间水平距离为S，物体开始下滑的高度AD＝h，滑动摩擦因数μ=h/S。
设斜面AB与水平面夹角为α，根据功能关系，物体克服摩擦力所做的功等于物体机械能的减少。
即mgh=F1•AB+F2•BC（2）F1、F2为摩擦力，分别等于μmgcosα和μmg，代入后可得mgh=μmgcosα•AB+μmg•BC （3）∵ABcosα＝DB，上式可以写作h＝μ(DB+BC) （4）式中DB+BC＝S，∴μ=h/S。
有μ＝tanθ(5)二、自锁我们都知道，由于静摩擦力不可能超过最大值，因此全约束力的作用线也不可能超出摩擦角以外，即全约束反力必在摩擦角之内。
由此可知：（1）如果作用于物块的全部主动力的合力的作用线在摩擦角之内，则无论这个力怎样大，物块必保持静止。
称这种现象为自锁现象。
因为在这种情况下，主动力的合力与法线间的夹角，因此，主动力的合力的作用线必在摩擦角之内，而全约束力的作用线也在此摩擦角之内，主动力的合力和全约束力必能满足二力平衡条件，如图所示，所以物块必静止。
工程实际中常应用自锁原理设计一些机构或夹具，如千斤顶、压榨机、圆锥销等，使它们始终保持在平衡状态下工作。
图2（2）如果全部主动力的合力的作用线在摩擦角之外，则无论这个力怎样小，物块一定会滑动。
因为在这种情况下，全部主动力的合力的作用线已在摩擦角之外，全约束力的作用线不可能出现在摩擦角之外，不能满足二力平衡条件，如图所示，所以物块不会静止。
应用这个道理，可以设法避免发生自锁现象。
有上述分析可知自锁只与摩擦角有关，为什么呢？因为当φ<φf时，随着主动力的不断增大，支撑面的反向法力和阻止物体滑动的摩擦力也会相应的增大，所以物体仍静止不动。
α0＝arctan 1(6) 与水平面不同的，只是保证物体静止的最小力条件有所不同。
当用斜向上的力维持物体平衡时，不一定满足自锁条件，而若用斜向下的力使物体平衡，一定首先满足自锁条件才可能发生。
而生产、生活中更多是发生在竖直方向的自锁现象。
三、自锁现象的应用1）登高脚扣在实际生活工作当中，人们有时需要登高，如电业工人要攀爬电线杆。
而登高杆对人来说是很困难的。
人们巧妙的运用自锁原理发明了高脚扣，它的发明方便了人们的工作生活。
一般脚扣是一对用机械强度较大的金属材制作，用于承受人体重量。
脚扣弯成略大于半圆形的弯扣，确保扣住电线杆，保证足够的接触面。
内侧面附有摩擦因数较大的材料，扣的一端安装脚踏板。
使用时，弯扣卡住电杆，当一侧着力向下踩时，形成两侧向里的挤压，接触 x 2图4面产生向上的摩擦力，且向下踩的力越大，压力也越大，满足自锁条件，因而不会沿杆滑下。
只需两脚交替上抬就可爬上电线杆。
2）螺纹副即螺母广泛存在与人们的生活当中，任何机械都或多或少有螺母的存在。
而自锁螺母能更好的工作，接下来分析螺母自锁的条件。
设螺母为矩形。
为了便于分析，假定作用在螺母上的轴向载荷F 集中作用于中径的圆上的一点。
给螺母加一水平力Ft 使螺母克服载荷F 作转动，这种转动可看成是一滑块 在水平力Ft 的推动下沿螺杆螺纹斜面等速旋转滑动。
将螺纹沿中径展开，则相当于滑块沿斜面等速向上滑动，斜面倾角λ称为螺纹升角。
作用于螺母的力有外载荷F 、水平力Ft 、螺杆斜面法向反力N 和摩擦力μN F m =（μ为摩擦系数），法向反力N 和摩擦力Fm 的合力R 称为螺杆对螺母的总反力，R 和N 的夹角为摩擦角，用ρ表示。
螺母受力如图（7）由几何关系可知 μμρ===N N N F m //tan 。
（7） F F m N R F t 图（7）螺母受力示意 图（6）矩形螺纹副剖面图 图5登高脚扣示意图外载荷F 与总反力R 的夹角为)(ρλ+ 。
显然，作用于螺母上的三个力F 、Ft 、R 是平衡的，即可构成力封闭三角形，如图(8）所示。
由此得)tan(ρλ+=F F t （8） Ft 相当于旋转螺母时必须在螺纹中径d2 处施加的圆周力，它对螺纹轴心线的力矩，即为旋转螺母（或拧紧螺母）所需克服螺纹副中的阻力矩2/)tan(2/22d F d F T t ρλ+== （9） 等速松退转动时，则相当于滑块在载荷F 作用下沿斜面等速下滑。
这时滑块上的摩擦力Fm 向上，总反力R 和力F 的夹角为）ρλ-(。
由力封闭三角形（9）可知)tan(ρλ-=F F t （10）3）劈 具有构成尖锐角度的两个平面形状的坚硬物体，称楔或尖劈。
属于斜面类简单机械。
两成尖锐角度的平面称为劈面，劈的尖端称为劈刃，宽端称为劈背。
我国周口店北京猿人遗址处发现的两面石器是尖劈的原始形式，距今约有40～50万年，新石器时代的石斧、石矛，商周时代的青铜器和兵器等，都说明尖劈是人类最早发明并广泛使用的一种简单工具。
尖劈可以用来卡紧物件。
如果尖劈的锐角足够小，它可以嵌入木头缝或墙缝里，这是由于摩擦力的作用使尖劈静止在木头缝中或墙缝里，称为摩擦自锁]10[。
像木器家具中常在横接处打入木楔就是应用尖劈摩擦自锁的原理。
图（8）角为)(ρλ+时 图（9）角为）ρλ-(时尖劈摩擦自锁力学分析假设楔子两面对称，受压力均为F 。
则可只分析一面。
楔子顶角为2α。
则压力F 分解如图（11）。
力F 和力N 的夹角为楔子顶角一半，即α。
则有αsin F R = （11）αcos F N = （12）摩擦力M 的分解如图(12)力O 和力M 的夹角为αμF M =有αcos M O = （13）当O R <即αμααcos cos sin F M O F R ==<= （14）化简得μα<tan当楔子满足μα<tan 时即能自锁。
4）螺旋千斤顶图（10）劈图（12）力M 的分解 图（11）力F 的分解螺旋千斤顶又称机械式千斤顶，是由人力通过螺旋副传动，螺杆或螺母套筒作为顶举件。
普通螺旋千斤顶靠螺纹自锁作用支持重物，构造简单，推动手柄，使丝杆的螺纹沿着底座螺纹槽慢慢旋进而顶起重物。
并在顶起重物后，重物和丝杆能保持状态，停在任何位置不自动下降。
即达到自锁状态。
螺旋千斤顶工作时螺旋可以看成是一个绕在圆柱体上的斜面]12[。
将其展开，这个斜面的倾角θ就是螺纹升角θ。
丝杆相当位于斜面上的物体。
千斤顶支撑的重物是加载于丝杆上的轴向载重。
这个载重相当于放在斜面上重为G 的物体。
为使丝杆螺纹在重物的重压下不会自动下旋，相当于物体不会沿斜面自动下滑，即物体在斜面上自锁。
要保证螺纹升角θ小于等于丝杆与底座螺纹槽之间的摩擦角。
即可自锁。
只要螺纹升角满足丝杆材料与底座材料之间的自锁条件，在材料强度的允许范围内，无论多种的物体它都能举起。
是名副其实的力举千金。
5）铁路路基常常可以看到工地上卡车卸下的沙石总是呈一个锥形，而且锥面与地面的夹角总是成一个常值。
当沙堆高度超过某个极限（或者锥角过大）时，沙石就会下滚，直到再次平衡。
这个极限角度α与沙堆的摩擦角m θ有着密切的联系。
在理论情况下，只有当m αθ≤时，沙堆才会处于平衡的静止状态。
铁路建设中路基斜坡与地面的夹角α的设计也与摩擦角β有着密切关系。
为了火车行车的安全，铁轨及其路基必须坚实，决不能让路基塌陷。
而摩擦自锁在这里便得到了很好的α≤，路基中的沙石摩擦自锁，则即使路基上作用再大的合力，应用，理想情况下，当β整个路基也能保持平衡而不变形塌陷。
参考文献[1] 漆安慎，杜婵英。
编著力学（第二版）[M]. 北京：高等教育出版社，2008：1-21[2] 周培源.理论力学[M].北京:人民教育出版社,1952：6-13[3] 曾田范宗[日].摩擦[M].北京:科学出版社,1978:78-85[4] 李俊峰.理论力学[M] .北京:清华大学出版社,2001:78-95[5] 贾书惠,李万琼.理论力学[M]. 北京高等教育出版社,2002:134-153[6] 范钦珊. 理论力学[M] 北京高等教育出版社,2000:67-83[7] 沈养中. 工程力学[M] . 北京: 高等教育出版社, 2003 :215-253[8] 蒋平编著工程力学基础[M]. 北京高等教育出版社,2003:168-183[9] 朱欣.有用的摩擦“自锁现象”.物理教学讨论，第22卷总第228期2008年第9期[10] 哈尔滨工业大学理论力学教研组编理论力学第六版北京高等教育出版社, 2002:234-251[11] 孙恒，陈作模，葛文杰.机械原理(第七版)[M].北京:高等教育出版社2009:210-243[12] 王奕. 摩擦角与螺旋千斤顶[J ] . 技术物理教学, 2004 (2)。
