人教版八年级下册数学 第17章 勾股定理 单元测试卷(含答案)

2017-2018学年八年级数学下册第17章勾股定理单元检测卷

姓名：__________ 班级：__________

题号 一 二 三 总分

评分

一、选择题（每小题3分；共33分）

1.下列各组数中，属于勾股数的是（ ）

A. 2.5，6，6.5 B. 5，7，10 C.

,, D. 6，8，10

2.已知一个Rt△的两边长分别为3和4，则第三边长的平方是( )

A. 25

B. 14 C. 7 D. 7或25

3.如图：一个长、宽、高分别为4cm、3cm、12cm的长方体盒子能容下的最长木棒长为（ ）

A. 11cm B. 12cm C. 13cm D. 14cm

4.如图，两正方形彼此相邻且内接于半圆，若小正方形的面积为16cm2 ， 则该半圆的半径为（ ）

A. (4+)cm B. 9cm C. 4cm D. 6cm

5.将下列长度的三根木棒首尾顺次连接，能组成直角三角形的是（ ）．

人教版八下数学勾股定理测试题及答案

一、选择题（共10小题；共30分）

1.三角形的三边长a，b，c满足a+b2−c2=2ab，则此三角形是()A.直角三角形B.锐角三角形C.钝角三角形D.等腰三角形

2.若直角三角形的三边长分别为2，4，x，则x的可能值有()

A.1个B.2个C.3个D.4个

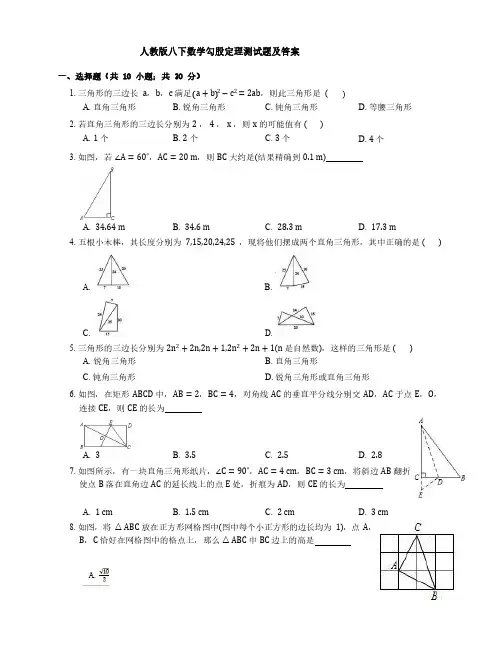
3.如图，若∠A=60∘，AC=20m，则BC大约是(结果精确到0.1m)

A.34.64mB.34.6mC.28.3mD.17.3m

4.五根小木棒，其长度分别为7,15,20,24,25，现将他们摆成两个直角三角形，其中正确的是()

A.

B.

C.

D.

5.三角形的三边长分别为2n2+2n,2n+1,2n2+2n+1(n是自然数)，这样的三角形是()A.锐角三角形B.直角三角形

C.钝角三角形D.锐角三角形或直角三角形

6.如图，在矩形ABCD中，AB=2，BC=4，对角线AC的垂直平分线分别交AD，AC于点E，O，

连接CE，则CE的长为

A.3B.3.5C.2.5D.2.8

7.如图所示，有一块直角三角形纸片，∠C=90∘，AC=4cm，BC=3cm，将斜边AB翻折

使点B落在直角边AC的延长线上的点E处，折痕为AD，则CE的长为

A.1cmB.1.5cmC.2cmD.3cm

8.如图，将△ABC放在正方形网格图中(图中每个小正方形的边长均为1)，点A，

B，C恰好在网格图中的格点上，那么△ABC中BC

边上的高是9.如图，将一个等腰直角三角形按图示方式依次翻折，若DE=a，则下列说法正确的个数有①DCʹ平分∠BDE；②BC长为BC的长．+2a；③△BCʹD是等腰三角形；④△CED的周长等于

A.1个B.2个C.3个D.4个

10.如图，等腰Rt△ABC中，∠ABC=90∘，O是△ABC内一点，OA=6，OB=42，OC=10，Oʹ

为△ABC外一点，且△CBO≌△ABOʹ，则四边形AOʹBO的面积为

A.10B.16C.40D.80

二、填空题（共6小题；共18分）

1 初中数学人教版八年级下册实用资料

勾股定理检测题

（总分：120分，时间：90分钟）

一、认真选一选，你一定很棒！（每题3分，共30分）

1，分别以下列五组数为一个三角形的边长：①6，8，10；②13，5，12 ③1，2，3；④9，40，41；⑤321，421，521.其中能构成直角三角形的有（ ）组

A.2 B.3 C.4

D.5

2，已知△ABC中，∠A＝12∠B＝13∠C，则它的三条边之比为（ ）

A.1∶1∶2 B.1∶3∶2 C.1∶2∶3 D.1∶4∶1

3，已知直角三角形一个锐角60°，斜边长为1，那么此直角三角形的周长是（ ）

A.52 B.3

C.3+2

D.332

4，如果梯子的底端离建筑物5米，13米长的梯子可以达到建筑物的高度是（ ）

A.12米 B.13米 C.14米 D.15米

5，放学以后，萍萍和晓晓从学校分手，分别沿东南方向和西南方向回家，若萍萍和晓晓行走的速度都是40米/分，萍萍用15分钟到家，晓晓用20分钟到家，萍萍家和晓晓家的距离为（ ）

A.600米 B.800米 C.1000米 D.不能确定

6，如图1所示，要在离地面5•米处引拉线固定电线杆，使拉线和地面成60°角，若要考虑既要符合设计要求，又要节省材料，则在库存的L1＝5.2米，L2＝6.2米，L3＝7.8米，L4＝10米四种备用拉线材料中，拉线AC最好选用（ ）

A.L1 B.L2 C.L3 D.L4

A

B C

图2 5mBCAD图1 BCAED图3

2 7，如图2，分别以直角△ABC的三边AB，BC，CA为直径向外作半圆.设直线AB左边阴影部分的面积为S1，右边阴影部分的面积和为S2，则（ ）

第 1 页 共 6 页 人教版八年级下册数学第十七章 勾股定理 单元测试卷

题号 一 二 三

总分

21 22

23 24 25 26 27

28

分数

一、选择题（每小题4分，共28分）

1. 下列各组数中,是勾股数的是( )

A. 14,36,39 B. 8,24,25 C. 8,15,17 D. 10,20,26

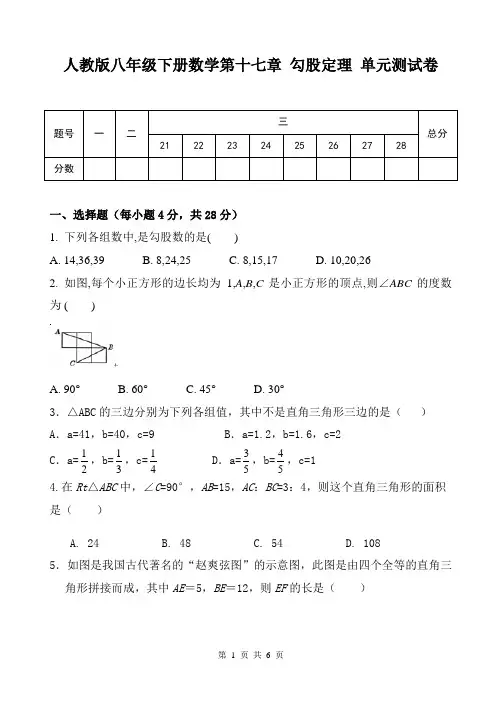
2. 如图,每个小正方形的边长均为1,A,B,C是小正方形的顶点,则∠ABC的度数为 ( )

A. 90° B. 60° C. 45° D. 30°

3．△ABC的三边分别为下列各组值，其中不是直角三角形三边的是（ ）

A．a=41，b=40，c=9 B．a=1.2，b=1.6，c=2

C．a=12，b=13，c=14 D．a=35，b=45，c=1

4.在Rt△ABC中，∠C=90°，AB=15，AC：BC=3：4，则这个直角三角形的面积是（ ）

A. 24 B. 48 C. 54 D. 108

5．如图是我国古代著名的“赵爽弦图”的示意图，此图是由四个全等的直角三角形拼接而成，其中AE＝5，BE＝12，则EF的长是（ ） 第 2 页 共 6 页

A．7 B．8 C．7 D．7

6．在下列各组数中，是勾股数的是（ ）

A．1、2、3 B．2、3、4 C．3、4、5 D．4、5、6

7．在同一平面上把三边BC＝3，AC＝4，AB＝5的三角形沿最长边AB翻折后得到△ABC′，则CC′的长等于（ ）

A． B． C． D．

二、填空题（每空4分，共28分）

8. 在直角三角形ABC中，∠ACB=90°，AC=6，BC=8，则斜边AB=

第1页共20页八年级下册 数学 第 17 章《勾股定理》单元测试题（含答案）

一、选择题(共10小题)1.下列各组数中，不是勾股数的是()

A.3，4，6B.7，24，25C.6，8，10D.9，12，15

2.在△ABC中，BC＝6，AC＝8，AB＝10，则该三角形为()

A.锐角三角形B.直角三角形

C.纯角三角形D.等腰直角三角形

3.如图，在边长为1个单位长度的小正方形网格中，点A、B都是格点(即网格线的交点)，

则线段AB的长度为()A.3B.5C.6D.44.我国汉代数学家赵爽为了证明勾股定理，创制了一副“弦图”，后人称其为“赵爽弦图如图，

由弦图变化得到，它是由八个全等的直角三角形拼接而成.记图中正方形ABCD，正方形EFGH，正方形MNKT的面积分别为S1，S2，S3，若S1+S2+S3＝21，则S2的值是()

第2页共20页A.9.5B.9C.7.5D.7

5.如图，是“赵爽弦图”，△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形，四边

形ABCD和EFGH都是正方形，如果EF＝4，AH＝12，那么AB等于()

A.30B.25C.20D.15

6.在我国古代数学著作《九章算术》“勾股”章有一题：“今有开门去阃(kǔn)一尺，不合二寸，

问门广几何.”大意是说：如图，推开双门(AD和BC)，门边缘D、C两点到门槛AB距离为1

尺(1尺＝10寸)，双门间的缝隙CD为2寸，那么门的宽度(两扇门的和)AB为()

A.100寸B.101寸C.102寸D.103寸

7.2019年10月1日，中华人民共和国70年华诞之际，王梓涵和学校国旗护卫队的其他同学

们赶到学校举行了简朴而降重的升旗仪式.倾听着雄壮的国歌声，目送着五星红旗级缓升起，

不禁心潮澎湃，爱国之情油然而生.爱动脑筋的王梓涵设计了一个方案来测量学校旗杆的高

度.将升旗的绳子拉直到末端刚好接触地面，测得此时绳子末端距旗杆底端2米，然后将绳

子末端拉直到距离旗杆5m处，测得此时绳子末端距离地面高度为1m，最后根据刚刚学习

《勾股定理》检测题

一、认真选一选，你一定很棒！（每题3分，共30分）

1，分别以下列五组数为一个三角形的边长：①6，8，10；②13，5，12 ③1，2，3；④9，40，41；⑤321，421，521.其中能构成直角三角形的有（ ）组

A.2 B.3 C.4 D.5

2，已知△ABC中，∠A＝12∠B＝13∠C，则它的三条边之比为（ ）

A.1∶1∶2 B.1∶3∶2 C.1∶2∶3 D.1∶4∶1

3，已知直角三角形一个锐角60°，斜边长为1，那么此直角三角形的周长是（ ）

A.52 B.3 C.3+2 D.332

4，如果梯子的底端离建筑物5米，13米长的梯子可以达到建筑物的高度是（ ）

A.12米 B.13米 C.14米

D.15米

5，放学以后，萍萍和晓晓从学校分手，分别沿东南方向和西南方向回家，若萍萍和晓晓行走的速度都是40米/分，萍萍用15分钟到家，晓晓用20分钟到家，萍萍家和晓晓家的距离为（ ）

A.600米 B.800米 C.1000米 D.不能确定

6，如图1所示，要在离地面5•米处引拉线固定电线杆，使拉线和地面成60°角，若要考虑既要符合设计要求，又要节省材料，则在库存的L1＝5.2米，L2＝6.2米，L3＝7.8米，L4＝10米四种备用拉线材料中，拉线AC最好选用（ ）

A.L1 B.L2 C.L3 D.L4

7，如图2，分别以直角△ABC的三边AB，BC，CA为直径向外作半圆.设直线AB左边阴影部分的面积为S1，右边阴影部分的面积和为S2，则（ ） A

B C

图2 5mBCAD图1 BCAED图3 A.S1＝S2 B.S1＜S2 C.S1＞S2 D.无法确定

勾股定理单元测试

（时间：100分钟总分：120分）姓名得分

一、相信你一定能选对！（每小题4分，共32分）

1.三角形的三边长分别为6,8,10，它的最短边上的高为()A.6B.4.5C.2.4D.8

2.下面几组数:①7,8,9；②12,9,15；③m2+n2,m2–n2,2mn（m，n均为正整数,mn）；④

2a,12a,22a.其中能组成直角三角形的三边长的是()

A.①②B.②③C.①③D.③④

3.三角形的三边为a、b、c，由下列条件不能判断它是直角三角形的是（）A．a:b:c=8∶16∶17B．a2-b2=c2

C．a2=(b+c)(b-c)D．a:b:c=13∶5∶12

4.三角形的三边长为abcba2)(22,则这个三角形是()

A.等边三角形B.钝角三角形C.直角三角形D.锐角三角形.

5．已知一个直角三角形的两边长分别为3和4，则第三边长是（）

A．5B．25C．7D．5或7

6．已知Rt△ABC中，∠C=90°，若a+b=14cm，c=10cm，则Rt△ABC的面积是（）A.24cm2B.36cm2C.48cm2D.60cm2

7．直角三角形中一直角边的长为9，另两边为连续自然数，则直角三角形的周长为（）

A．121B．120C．90D．不能确定

8.放学以后，小红和小颖从学校分手，分别沿东南方向和西南方向回家，若小红和小颖行走的速

度都是40米/分，小红用15分钟到家，小颖20分钟到家，小红和小颖家的直线距离为（）A．600米B.800米C.1000米D.不能确定

二、你能填得又快又对吗？（每小题4分，共32分）

9.在△ABC中，∠C=90°，AB＝5，则2AB+2AC+2BC=_______．10.如图，是2002年8月北京第24届国际数学家大会会标，由4个全等的直角三角形拼合而成.

如果图中大、小正方形的面积分别为52和4，那么一个直角三角形的两直角边的和等

于．

11．直角三角形两直角边长分别为5和12，则它斜边上的高为_______．

2017-2018学年八年级数学下册第17章勾股定理单元检测卷

姓名：__________ 班级：__________

题号 一 二 三 总分

评分

一、选择题（每小题3分；共33分）

1.下列各组数中，属于勾股数的是（ ）

A. 2.5，6，6.5 B. 5，7，10 C.

,, D. 6，8，10

2.已知一个Rt△的两边长分别为3和4，则第三边长的平方是( )

A. 25

B. 14 C. 7 D. 7或25

3.如图：一个长、宽、高分别为4cm、3cm、12cm的长方体盒子能容下的最长木棒长为（ ）

A. 11cm B. 12cm C. 13cm D. 14cm

4.如图，两正方形彼此相邻且内接于半圆，若小正方形的面积为16cm2 ， 则该半圆的半径为（ ）

A. (4+)cm B. 9cm C. 4cm D. 6cm

5.将下列长度的三根木棒首尾顺次连接，能组成直角三角形的是（ ）．

人教版八年级数学下册第17章《勾股定理》单元检测试题含答案

一、选择题

1.已知a、b、c是△ABC的三边长，且满足a3+ab2+bc2＝b3+a2b+ac2，则△ABC的形状是（ ）

A.等腰三角形 B.直角三角形

C.等腰三角形或直角三角形 D.等腰直角三角形

2.以下列各组数为边长，能组成直角三角形的是（ ）

A.8，15，17 B.4，5，6 C.5，8，10 D.8，39，40

3.如图所示为一个6×6的网格，在△ABC、△A′B′C′、△A″B″C″三个三角形中，直角三角形有（ ）

A.3个 B.2个 C.1个 D.以上都不对

4.如图，△ABC和△DCE都是边长为4的等边三角形，点B、C、E在同一条直线上，连接BD，则BD的长为（ ）

A.3 B.23 C.33 D.43

5.如果梯子的底端离建筑物5米，13米长的梯子可以达到建筑物的高度是（ ）

A.12米 B.13米 C.14米 D.15米

6.在△ABC中，∠C＝90°，周长为60，斜边与一直角边比是13∶5，则这个三角形三边长分别是（ ）

A.5，4，3 B.13，12，5 C.10，8，6 D.26，24，10

7.如图所示，如果将矩形纸沿虚线①对折后，沿虚线②剪开，剪出一个直角三角形，展开后得到一个等腰三角形.则展开后三角形的周长是（ ）

A.2+10 B.2+210 C.12 D.18

8.如图在长方形ABCD中，AB＝6，BC＝8，若将长方形折叠，使点B与点D重合，则折痕EF的长为（ ）

A.152 B.154 C.5 D.6

八下数学第17章《勾股定理》单元测试

一、选择题(共10小题)1.下列各组数中，不是勾股数的是()

A.3，4，6B.7，24，25C.6，8，10D.9，12，15

2.在△ABC中，BC＝6，AC＝8，AB＝10，则该三角形为()

A.锐角三角形B.直角三角形

C.纯角三角形D.等腰直角三角形

3.如图，在边长为1个单位长度的小正方形网格中，点A、B都是格点(即网格线的交点)，

则线段AB的长度为()A.3B.5C.6D.4

4.我国汉代数学家赵爽为了证明勾股定理，创制了一副“弦图”，后人称其为“赵爽弦图如图，由

弦图变化得到，它是由八个全等的直角三角形拼接而成.记图中正方形ABCD，正方形EFGH，正方形MNKT的面积分别为S1，S2，S3，若S1+S2+S3＝21，则S2的值是(

)

A.9.5B.9C.7.5D.7

5.如图，是“赵爽弦图”，△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形，四边

形ABCD和EFGH都是正方形，如果EF＝4，AH＝12，那么AB等于()

A.30B.25C.20D.15

6.在我国古代数学著作《九章算术》“勾股”章有一题：“今有开门去阃(kǔn)一尺，不合二寸，

问门广几何.”大意是说：如图，推开双门(AD和BC)，门边缘D、C两点到门槛AB距离为1

尺(1尺＝10寸)，双门间的缝隙CD为2寸，那么门的宽度(两扇门的和)AB为()

A.100寸B.101寸C.102寸D.103寸

7.2019年10月1日，中华人民共和国70年华诞之际，王梓涵和学校国旗护卫队的其他同学

们赶到学校举行了简朴而降重的升旗仪式.倾听着雄壮的国歌声，目送着五星红旗级缓升起，

不禁心潮澎湃，爱国之情油然而生.爱动脑筋的王梓涵设计了一个方案来测量学校旗杆的高

度.将升旗的绳子拉直到末端刚好接触地面，测得此时绳子末端距旗杆底端2米，然后将绳

子末端拉直到距离旗杆5m处，测得此时绳子末端距离地面高度为1m，最后根据刚刚学习

第17 章勾股定理

一、选择题

1.以下列各组数为边长，能构成直角三角形的是（ ）

A.5、6、7 B. 10、8、4 C. 7、24、25 D. 9、15、17

2.△ABC中，AB=13cm，AC=15cm，高AD=12，则BC的长为（ ）

A.14 B. 4 C. 14或4 D. 以上都不对

3.下列四组数中，其中有一组与其他三组规律不同，这一组是（ ）

A.3，4，5B.6，8，10C.5，12，13D.4，5，7

4.在△ABC中，若AC=15，BC=13，AB边上的高CD=12，则△ABC的周长为（ ）

A.32B.42C.32或42D.以上都不对

5.如图，正方形ABCD的边长为9．将正方形折叠．使顶点D落在BC边上的点E处，折痕为GH．

若BE：EC=2：1，则线段CH的长是( )

A.3 B. 4 C. 5 D. 6

6.如图，正方形小方格边长为1，则网格中的△ABC是（ ）

A.直角三角形B.锐角三角形C.钝角三角形D.以上答案都不对

7.给出下列长度的四组线段：①1，2，2；②5，12，13；③6，7，8；④3m，4m，5m（m＞0）.

其中能组成直角三角形的有（ ）A. ①② B. ②④ C. ②③ D. ③④

8.如图，一架25分米的梯子，斜立在一竖直的墙上，这时梯的底部距墙底端7分米，如果梯子的顶端沿墙

下滑4分米，那么梯的底部将平滑（ ）

A. 9分米 B. 15分米 C. 5分米 D. 8分米

9.下列各组数是三角形的三边，能组成直角三角形的一组数是（ ）

A. ，

， B. 2，3，4 C. 3，4，5 D. 6，8，12

10.Rt△ABC中，斜边BC=2，则AB2+AC2+BC2

的值为（ ） A. 8 B. 4 C. 6 D. 无法计算

11.在Rt△ABC中，∠ACB=90°，

AC= ，BC=2，则AB的长为（ ）

A.

B.

C. D. 6

12.已知△ABC的三边长分别为a，b，c，且满足（a﹣5）2+|b﹣

知识像烛光，能照亮一个人，也能照亮无数的人。--培根

1 / 5 第17章 勾股定理 综合测试题

一﹑填空题 (每小题2分, 共20分)

1. 如图，∠OAB=∠OBC=∠OCD=90°， AB=BC=CD=1，OA=2，则OD2=____________.

2. 如图， 等腰△ABC的底边BC为16, 底边上的高AD为6，则腰AB的长为____________.

3. 如图，某人欲横渡一条河，由于水流的影响，实际上岸地点C偏离欲到达点B200m，结

果他在水中实际游了520m，求该河流的宽度为____________________m.

4. 正方形的面积为18cm2, 则正方形对角线长为__________ cm.

5．在△ABC中，∠C=90°，若AB＝5，则2AB+2AC+2BC=__________.

6. 小华和小红都从同一点O出发，小华向北走了9米到A点，小红向东走了12米到了B点，则________=AB米．

7. 一个三角形三边满足(a+b)2－c2＝2ab, 则这个三角形是 三角形.

8. 木工做一个长方形桌面， 量得桌面的长为60cm， 宽为32cm， 对角线为68cm， 这个

桌面__________ (

填“合格”或“不合格”).

9. 直角三角形一直角边为12cm，斜边长为13cm，则它的面积为 ．

10. 有六根细木棒，它们的长分别是2，4，6，8，10，12（单位：cm），首尾连结能搭成直

角三角形的三根细木棒分别是

．

二﹑选择题(每小题3分, 共

30分

)

11. 一直角三角形的斜边长比一直角边长大2，另一直角边长为6，则斜边长为 （ ）

A. 4 B. 8 C. 10 D. 12

12. 小丰的妈妈买了一部29英寸(74cm)的电视机，下列对29英寸的说法中正确的是（ ）

A. 小丰认为指的是屏幕的长度

B. 小丰的妈妈认为指的是屏幕的宽度

C. 小丰的爸爸认为指的是屏幕的周长

人教版八年级下册第17章《勾股定理》单元测试卷

满分120分

一．选择题（共10小题,满分30分,每小题3分）

1．下列各组数中,是勾股数的一组是( )

A．6,7,8 B．5,12,13 C．0.6,0.8,1 D．2,4,5

2．下列线段a,b,c能组成直角三角形的是( )

A．2a,3b,4c B．4a,5b,6c C．1a,2b,3c D．7a,3b,6c

3．如图,在四边形ABCD中,90DABBCD,分别以四边形的四条边为边向外作四个正方形,若14135SS,349S,则2(S )

A．184 B．86 C．119 D．81

4．如图,在22的网格中,有一个格点ABC,若每个小正方形的边长为1,则ABC的边AB上的高为( )

A．22 B．55 C．510 D．1

5．如图,在高为3米,斜坡长为5米的楼梯台阶上铺地毯,则地毯的长度至少要( )

A．4米 B．5米 C．6米 D．7米 6．若直角三角形的两边长分别是5和12,则它的斜边长是( )

A．13 B．13或119 C．119 D．12或13

7．在《九章算术》中有一个问题（如图）：今有竹高一丈,末折抵地,去本三尺,问折者高几何？它的意思是：一根竹子原高一丈(10尺）,中部一处折断,竹梢触地面处离竹根3尺,试问折断处离地面( )尺．

A．4 B．3.6 C．4.5 D．4.55

8．如图,一轮船以12海里/时的速度从港口A出发向东北方向航行,另一轮船以5海里/时的速度同时从港口A出发向东南方向航行,离开港口2小时后两船相距( )

A．13海里 B．16海里 C．20海里 D．26海里

9．如图是一个圆柱形饮料罐,底面半径是5,高是12,上底面中心有一个小圆孔,则一条长16cm的直吸管露在罐外部分a的长度（罐壁的厚度和小圆孔的大小忽略不计）范围是( )

A．45a B．34a C．23a D．12a

人教版数学八年级下册第十七章测试卷

姓名： 分数：

一、选择题

1．适合下列条件的△ABC中，直角三角形的个数为（ ）

①a=，b=，c=②a=6，∠A=45°；③∠A=32°，∠B=58°；④a=7，b=24，c=25

⑤a=2，b=2，c=4．

A．2个 B．3个 C．4个 D．5个

2．在△ABC中，若a=n2﹣1，b=2n，c=n2+1，则△ABC是（ ）

A．锐角三角形 B．钝角三角形 C．等腰三角形 D．直角三角形

3．直角三角形斜边的平方等于两条直角边乘积的2倍，这个三角形有一个锐角是（ ）

A．15° B．30° C．45° D．60°

4．已知，如图长方形ABCD中，AB=3cm，AD=9cm，将此长方形折叠，使点B与点D重合，折痕为EF，则△ABE的面积为（ ）

A．3cm2 B．4cm2 C．6cm2 D．12cm2

5．分别以下列五组数为一个三角形的边长：①6，8，10 ②13，5，12 ③1，2，3 ④9，40，41 ⑤3，4，5．其中能构成直角三角形的有（ ）组．

A．2 B．3 C．4 D．5

6．已知△ABC中，∠A=∠B=∠C，则它的三条边之比为（ ）

A．1：1： B．1：：2 C．1：： D．1：4：1

7．已知直角三角形一个锐角60°，斜边长为1，那么此直角三角形的周长是（ ） A． B．3 C．+2 D．

8．如果梯子的底端离建筑物5米，13米长的梯子可以达到建筑物的高度是（ ）

A．12米 B．13米 C．14米 D．15米

9．如图所示，AB=BC=CD=DE=1，AB⊥BC，AC⊥CD，AD⊥DE，则AE=（ ）

A．1 B． C． D．2

10．直角三角形有一条直角边长为13，另外两条边长为连续自然数，则周长为（ ）

A．182 B．183 C．184 D．185

二、填空题

第十七章《勾股定理》单元测试卷

(共23题,满分120分,考试用时90分钟)

学校 班级 姓名 学号

一、选择题(共10小题,每小题3分,共30分)

1.如图,一根垂直于地面的旗杆在离地面5 m的B处撕裂折断,旗杆顶部落在离旗杆底部12 m的A处,则旗杆折断部分AB的高度是( )

A.5 m B.12 m C.13 m D.18 m

第1题图

第3题图

第5题图

2.下列各组数据中,不能作为直角三角形的三边长的是( )

A.3,4,6 B.7,24,25 C.6,8,10 D.9,12,15

3.如图,在Rt△ABC中,∠ACB=90°.若AB=10,则正方形ADEC和正方形BCFG的面积和为( )

A.100 B.120 C.140 D.160

4.若直角三角形的两条直角边长分别是3和4,则斜边长为( )

A.2.4 B.5 C.√7 D.7

5.如图,以数轴的单位长线段为边作一个正方形,数轴的原点为圆心,正方形对角线长为半径画弧,交数轴正半轴于点A,则点A表示的数是( )

A.1 B.1.4 C.√2 D.√3

6.在Rt△ABC中,a,b,c为三边长,则下列关系中正确的是( )

A.a2+b2=c2 B.a2+c2=b2 C.b2+c2=a2 D.以上都有可能

7.若一个直角三角形中,斜边的长为13,一条直角边长为5,则这个三角形的面积是( )

A.60 B.30 C.20 D.32

8.如图,将风筝放至高30 m,牵引线与水平面夹角约为45°的高空中,则牵引线AB的长约是( )

A.30 m B.45 m C.20√3 m D.30√2 m 第8题图

第9题图

第10题图

9.(跨学科融合)如图,在物理实验课上,小明将长为8 cm的橡皮筋放置在水平面上,固定两端A和B,然后把中点C垂直向上拉升3 cm至点D,则橡皮筋被拉长了( )

第17章 勾股定理

一．选择题（共7小题）

1．如图，直角三角形三边上的等边三角形的面积从小到大依次记为S1、S2、S3，则S1、S2、S3之间的关系是（ ）

A．S1+S2＞S3 B．S1+S2＜S3

C．S1+S2＝S3 D．S12+S22＞S32

2．在△ABC中，若∠ABC＝90°，则下列正确的是（ ）

A．BC＝AB+AC B．BC2＝AB2+AC2

C．AB2＝AC2+BC2 D．AC2＝AB2+BC2

3．Rt△ABC中，斜边BC＝2，则AB2+BC2+CA2＝（ ）

A．8 B．6 C．4 D．无法计算

4．如图所示，△ABC的顶点A、B、C在边长为1的正方形网格的格点上，BD⊥AC于点D，则BD的长为（ ）

A．3 B．2 C．4 D．

5．在△ABC中，AB＝AC＝10，BD是AC边上的高，DC＝2，则BD等于（ ）

A．2 B．4 C．6 D．8

6．已知一个Rt△的两边长分别为3和4，则第三边长的平方是（ ）

A．25 B．14 C．7 D．7或25

7．由下列条件不能判定△ABC为直角三角形的是（ ）

A．∠A+∠B＝∠C

B．∠A：∠B：∠C＝1：3：2

C．（b+c）（b﹣c）＝a2

D．a＝3+k，b＝4+k，c＝5+k（k＞0）

二．填空题（共6小题）

8．下列各组数据是勾股数的有

组．（填写数量即可）

（1）6，8，10 （2）1.5，2，2.5 （3）32，42，52（4）7，24，25 （5），，

9．如图，“赵爽弦图”由4个全等的直角三角形所围成，在Rt△ABC中，AC＝b，BC＝a，∠ACB＝90°，若图中大正方形的面积为42，小正方形的面积为5，则（a+b）2的值为 ．

10．如图，A在线段BG上，ABCD和DEFG都是正方形，面积分别为7平方厘米和11平方厘米，则△CDE的面积等于 平方厘米．