Bose-Einstein condensation in a rotating anisotropic TOP trap

2022年自考专业(英语)英语科技文选考试真题及答案一、阅读理解题Directions: Read through the following passages. Choose the best answer and put the letter in the bracket. (20%)1、 (A) With the recent award of the Nobel Prize in physics, the spectacular work on Bose-Einstein condensation in a dilute gas of atoms has been honored. In such a Bose-Einstein condensate, close to temperatures of absolute zero, the atoms lose their individuality and a wave-like state of matter is created that can be compared in many ways to laser light. Based on such a Bose-Einstein condensate researchers in Munich together with a colleague from the ETH Zurich have now been able to reach a new state of matter in atomic physics. In order to reach this new phase for ultracold atoms, the scientists store a Bose-Einstein condensate in a three-dimensional lattice of microscopic light traps. By increasing the strength of the lattice, the researchers are able to dramatically alter the properties of the gas of atoms and can induce a quantum phase transition from the superfluid phase of a Bose-Einsteincondensate to a Mott insulator phase. In this new state of matter it should now be possible to investigate fundamental problems of solid-state physics, quantum optics and atomic physics. For a weak optical lattice the atoms form a superfluid phase of a Bose-Einstein condensate. In this phase, each atom is spread out over the entire lattice in a wave-like manner as predicted by quantum mechanics. The gas of atoms may then move freely through the lattice. For a strong optical lattice the researchers observe a transition to an insulating phase, with an exact number of atoms at each lattice site. Now the movement of the atoms through the lattice is blocked due to therepulsive interactions between them. Some physicists have been able to show that it is possible to reversibly cross the phase transition between these two states of matter. The transition is called a quantum phase transition because it is driven by quantum fluctuations and can take place even at temperatures of absolute zero. These quantum fluctuations are a direct consequence of Heisenberg’s uncertainty relation. Normally phase transitions are driven by thermal fluctuations, which are absent at zero temperature. With their experiment, the researchers in Munich have been able to enter a new phase in the physics of ultracold atoms. In the Mott insulator state theatoms can no longer be described by the highly successful theories for Bose-Einstein condensates. Now theories are required that take into account the dominating interactions between the atoms and which are far less understood. Here the Mott insulator state may help in solving fundamental questions of strongly correlated systems, which are the basis for our understanding of superconductivity. Furthermore, the Mott insulator state opens many exciting perspectives for precision matter-wave interferometry and quantum computing.What does the passage mainly discuss?A.Bose-Einstein condensation.B.Quantum phase transitions.C.The Mott insulator state.D.Optical lattices.2、What will the scientists possibly do by reaching the new state of matter in atomic physics?A.Store a Bose-Einstein condensate in three-dimensional lattice of microscopic light traps.B.Increase the strength of the lattice.C.Alter the properties of the gas of atoms.D.Examine fundamental problems of atomic physics.3、Which of the following is NOT mentioned in relation to aweak optical lattice?A.The atoms form a superfluid phase of a Bose-Einstein condensate.B.Each atom is spread out over the entire lattice.C.The gas of atoms may move freely through the lattice.D.The superfluid phase changes into an insulating phase.4、What can be said about the quantum phase transition?A.It can take place at temperatures of absolute zero.B.It cannot take place above the temperatures of absolute zero.C.It is driven by thermal fluctuations.D.It is driven by the repulsive interactions between atoms.5、The author implies all the following about the Mott insulator state EXCEPT that______.A.the theory of Bose-Einstein condensation can’t possibly account for the atoms in the Mott insulator stateB.not much is known about the dominating interactions between the atoms in the Mott insulator stateC.it offers new approaches to exact quantum computingD.it forms a superfluid phase of a Bose-Einstein condensate6、 (B) Gene therapy and gene-based drugs are two ways we would benefit from our growing mastery of genetic science. But therewill be others as well. Here is one of the remarkable therapies on the cutting edge of genetic research that could make their way into mainstream medicine in the c oming years. While it’s true that just about every cell in the body has the instructions to make a complete human, most of those instructions are inactivated, and with good reason: the last thing you want for your brain cells is to start churning out stomach acid or your nose to turn into a kidney. The only time cells truly have the potential to turn into any and all body parts is very early in a pregnancy, when so-called stem cells haven’t begun to specialize. Most diseases involve the death of healthy cells—brain cells in Alzheimer’s, cardiac cells in heart disease, pancreatic cells in diabetes, to name a few; if doctors could isolate stem cells, then direct their growth, they might be able to furnish patients with healthy replacement tissue. It was incredibly difficult, but last fall scientists at the University of Wisconsin managed to isolate stem cells and get them to grow into neural, gut, muscle and bone cells. The process still can’t be controlled, and may have unforeseen limitations; but if efforts to understand and master stem-cell development prove successful, doctors will have a therapeutic tool of incredible power. The same applies to cloning, whichis really just the other side of the coin; true cloning, as first shown, with the sheep Dolly two years ago, involves taking a developed cell and reactivating the genome within, resenting its developmental instructions to a pristine state. Once that happens, the rejuvenated cell can develop into a full-fledged animal, genetically identical to its parent. For agriculture, in which purely physical characteristics like milk production in a cow or low fat in a hog have real market value, biological carbon copies could become routine within a few years. This past year scientists have done for mice and cows what Ian Wilmut did for Dolly, and other creatures are bound to join the cloned menagerie in the coming year. Human cloning, on the other hand, may be technically feasible but legally and emotionally more difficult. Still, one day it will happen. The ability to reset body cells to a pristine, undeveloped state could give doctors exactly the same advantages they would get from stem cells: the potential to make healthy body tissues of all sorts. And thus to cure disease.That could prove to be a true “miracle cu re”.What is the passage mainly about?A.Tomorrow’s tissue factory.B.A terrific boon to medicine.C.Human cloning.D.Genetic research.7、 According to the passage, it can be inferred that which of the following reflects the author’s opinion?A.There will inevitably be human cloning in the coming year.B.The potential to make healthy body tissues is undoubtedly a boon to human beings.C.It is illegal to clone any kind of creatures in the world.D.It is legal to clone any kind of creatures in the world except human.8、Which of the following is NOT true according to the passage?A.Nearly every cell in the human brain has the instructions to make a complete human.B.It is impossible for a cell in your nose to turn into a kidney.C.It is possible to turn out healthy replacement tissues with isolated stem cells.D.There will certainly appear some new kind of cloned animal in the near future.9、All of the following are steps involved in true cloning EXCEPT_______.A.selecting a stem cellB.taking a developed cellC.reactivating the genome within the developed cellD.resetting the developmental instructions in the cell to its original state10、The word “rejuvenated” in para. 5 is closest in meaning to_______.A.rescuedB.reactivatedC.recalledD.regulated参考答案：【一、阅读理解题】1~5CDDAD6~10DBBA。

a r X i v :c o n d -m a t /9810197v 1 [c o n d -m a t .s t a t -m e c h ] 16 O c t 1998Accepted to PHYSICAL REVIEW A for publicationBose-Einstein condensation in a one-dimensional interacting system due to power-lawtrapping potentialsM.Bayindir,B.Tanatar,and Z.GedikDepartment of Physics,Bilkent University,Bilkent,06533Ankara,TurkeyWe examine the possibility of Bose-Einstein condensation in one-dimensional interacting Bose gas subjected to confining potentials of the form V ext (x )=V 0(|x |/a )γ,in which γ<2,by solving the Gross-Pitaevskii equation within the semi-classical two-fluid model.The condensate fraction,chemical potential,ground state energy,and specific heat of the system are calculated for various values of interaction strengths.Our results show that a significant fraction of the particles is in the lowest energy state for finite number of particles at low temperature indicating a phase transition for weakly interacting systems.PACS numbers:03.75.Fi,05.30.Jp,67.40.Kh,64.60.-i,32.80.PjI.INTRODUCTIONThe recent observations of Bose-Einstein condensation (BEC)in trapped atomic gases [1–5]have renewed inter-est in bosonic systems [6,7].BEC is characterized by a macroscopic occupation of the ground state for T <T 0,where T 0depends on the system parameters.The success of experimental manipulation of externally applied trap potentials bring about the possibility of examining two or even one-dimensional Bose-Einstein condensates.Since the transition temperature T 0increases with decreasing system dimension,it was suggested that BEC may be achieved more favorably in low-dimensional systems [8].The possibility of BEC in one -(1D)and two-dimensional (2D)homogeneous Bose gases is ruled out by the Hohen-berg theorem [9].However,due to spatially varying po-tentials which break the translational invariance,BEC can occur in low-dimensional inhomogeneous systems.The existence of BEC is shown in a 1D noninteracting Bose gas in the presence of a gravitational field [10],an attractive-δimpurity [11],and power-law trapping po-tentials [12].Recently,many authors have discussed the possibility of BEC in 1D trapped Bose gases relevant to the magnetically trapped ultracold alkali-metal atoms [13–18].Pearson and his co-workers [19]studied the in-teracting Bose gas in 1D power-law potentials employing the path-integral Monte Carlo (PIMC)method.They have found that a macroscopically large number of atoms occupy the lowest single-particle state in a finite system of hard-core bosons at some critical temperature.It is important to note that the recent BEC experiments are carried out with finite number of atoms (ranging from several thousands to several millions),therefore the ther-modynamic limit argument in some theoretical studies [15]does not apply here [8].The aim of this paper is to study the two-body interac-tion effects on the BEC in 1D systems under power-law trap potentials.For ideal bosons in harmonic oscillator traps transition to a condensed state is prohibited.It is anticipated that the external potentials more confin-ing than the harmonic oscillator type would be possible experimentally.It was also argued [15]that in the ther-modynamic limit there can be no BEC phase transition for nonideal bosons in 1D.Since the realistic systems are weakly interacting and contain finite number of particles,we employ the mean-field theory [20,21]as applied to a two-fluid model.Such an approach has been shown to capture the essential physics in 3D systems [21].The 2D version [22]is also in qualitative agreement with the results of PIMC simulations on hard-core bosons [23].In the remaining sections we outline the two-fluid model and present our results for an interacting 1D Bose gas in power-law potentials.II.THEORYIn this paper we shall investigate the Bose-Einstein condensation phenomenon for 1D interacting Bose gas confined in a power-law potential:V ext (x )=V 0|x |κF (γ)G (γ)2γ/(2+γ),(2)andN 0/N =1−TF (γ)=1x 1/γ−1dx1−x,(4)and G (γ)=∞x 1/γ−1/2dxNk B T 0=Γ(1/γ+3/2)ζ(1/γ+3/2)T 01/γ+3/2.(6)Figure 1shows the variation of the critical temperature T 0as a function of the exponent γin the trapping po-tential.It should be noted that T 0vanishes for harmonic potential due to the divergence of the function G (γ=2).It appears that the maximum T 0is attained for γ≈0.5,and for a constant trap potential (i.e.V ext (x )=V 0)the BEC disappears consistent with the Hohenberg theorem.0.00.5 1.0 1.5 2.0γ0.00.20.40.6k B T 0 (A r . U n .)FIG.1.The variation of the critical temperature T 0withthe external potential exponent γ.We are interested in how the short-range interactioneffects modify the picture presented above.To this end,we employ the mean-field formalism and describe the col-lective dynamics of a Bose condensate by its macroscopictime-dependent wave function Υ(x,t )=Ψ(x )exp (−iµt ),where µis the chemical potential.The condensate wavefunction Ψ(x )satisfies the Gross-Pitaevskii (GP)equa-tion [24,25]−¯h 2dx 2+V ext (x )+2gn 1(x )+g Ψ2(x )Ψ(x )=µΨ(x ),(7)where g is the repulsive,short-range interaction strength,and n 1(x )is the average noncondensed particle distribu-tion function.We treat the interaction strength g as a phenomenological parameter without going into the de-tails of actually relating it to any microscopic descrip-tion [26].In the semi-classical two-fluid model [27,28]the noncondensed particles can be treated as bosons in an effective potential [21,29]V eff(x )=V ext (x )+2gn 1(x )+2g Ψ2(x ).(8)The density distribution function is given byn 1(x )=dpexp {[p 2/2m +V eff(x )−µ]/k B T }−1,(9)and the total number of particles N fixes the chemical potential through the relationN =N 0+ρ(E )dE2mgθ[µ−V ext (x )−2gn 1(x )],(12)where θ[x ]is the unit step function.More precisely,the Thomas-Fermi approximation [7,20,30]would be valid when the interaction energy ∼gN 0/Λ,far exceeds the kinetic energy ¯h 2/2m Λ2,where Λis the spatial extent of the condensate cloud.For a linear trap potential (i.e.γ=1),a variational estimate for Λis given by Λ= ¯h 2/2m (π/2)1/22a/V 0 1/3.We note that the Thomas-Fermi approximation would breakdown for tem-peratures close to T 0where N 0is expected to become very small.The above set of equations [Eqs.(9)-(12)]need to be solved self-consistently to obtain the various physical quantities such as the chemical potential µ(N,T ),the condensate fraction N 0/N ,and the effective potential V eff.In a 3D system,Minguzzi et al .[21]solved a simi-lar system of equations numerically and also introduced an approximate semi-analytical solution by treating the interaction effects perturbatively.Motivated by the suc-cess [21,22]of the perturbative approach we consider aweakly interacting system in1D.To zero-order in gn1(r), the effective potential becomesV eff(x)= V ext(x)ifµ<V ext(x)2µ−V ext(x)ifµ>V ext(x).(13) Figure2displays the typical form of the effective po-tential within our semi-analytic approximation scheme. The most noteworthy aspect is that the effective poten-tial as seen by the bosons acquire a double-well shape because of the interactions.We can explain this result by a simple argument.Let the number of particles in the left and right wells be N L and N R,respectively,so that N=N L+N R.The nonlinear or interaction term in the GP equation may be approximately regarded as V=N2L+N2R.Therefore,the problem reduces to the minimization of the interaction potential V,which is achieved for N L=N R.FIG.2.Effective potential V eff(x)in the presence of in-teraction(x0=(µ/V0)1/γa).Thick dotted line represents external potential V ext(x).The number of condensed atoms is calculated to beN0=2γa√ze x−1+ 2µ/k B Tµ/k B TH(γ,µ,xk B T)(2µ/k B T−x)1/γ−1/2dxexp[(E−µ)/k B T]−1=κ(k B T)1/γ+1/2J(γ,µ,T),(18) whereJ(γ,µ,T)= ∞2µ/k B T x1/γ+1/2dxze x−1.and Ecis the energy of the particles in the condensateE c=g(1+γ)(2γ+1)gV1/γ.(19)The kinetic energy of the condensed particles is neglected within our Thomas-Fermi approximation to the GP equa-tion.III.RESULTS AND DISCUSSIONUp to now we have based our formulation for arbitrary γ,but in the rest of this work we shall present our re-sults forγ=1.Our calculations show that the results for other values ofγare qualitatively similar.In Figs. 3and4we calculate the condensate fraction as a func-tion of temperature for various values of the interaction strengthη=g/V0a(at constant N=105)and different number of particles(at constantη=0.001),respectively. We observe that as the interaction strengthηis increased, the depletion of the condensate becomes more apprecia-ble(Fig.3).As shown in the correspondingfigures,a significant fraction of the particles occupies the ground state of the system for T<T0.The temperature depen-dence of the chemical potential is plotted in Figs.5and 6for various interaction strengths(constant N=105) and different number of particles(constantη=0.001) respectively.0.00.20.40.60.8 1.0T/T 00.00.20.40.60.81.0N 0/NN 0/N=1−(T/T 0)3/2η=10−5η=10−3η=10−1η=10FIG.3.The condensate fraction N 0/N versus temperature T /T 0for N =105and for various interaction strengths η.Effects of interactions on µ(N,T )are seen as large de-viations from the noninteracting behavior for T <T 0.In Fig.7we show the ground state energy of an interacting 1D system of bosons as a function of temperature for dif-ferent interaction strengths.For small η,and T <T 0, E is similar to that in a noninteracting system.As ηincreases,some differences start to become noticeable,and for η≈1we observe a small bump developing in E .This may indicate the breakdown of our approxi-mate scheme for large enough interaction strengths,as we can find no fundamental reason for such behavior.It is also possible that the Thomas-Fermi approximation em-ployed is violated as the transition to a condensed state is approached.0.00.20.40.60.8 1.0T/T 00.00.20.40.60.81.0N 0/NN 0/N=1−(T/T 0)3/2N=108N=105N=103N=101FIG.4.The condensed fraction N 0/N versus temperature T /T 0for η=0.001and for different number of particles N .0.00.20.40.60.8 1.0 1.2T/T 0−100100200300400µ/V 0η=1η=0.1η=0.001η=0.00001FIG.5.The temperature dependence of the chemical potential µ(N,T )for various interaction strength and for N =105particles.Although it is conceivable to imagine the full solution of the mean-field equations [Eq.(9)-(12)]may remedy the situation for larger values of η,the PIMC simulations [19]also seem to indicate that the condensation is inhibited for strongly interacting systems.The results for the spe-cific heat calculated from the total energy curves,i.e.C V =d E /dT ,are depicted in Fig.8.The sharp peak at T =T 0tends to be smoothed out with increasing in-teraction strength.It is known that the effects of finite number of particles are also responsible for such a be-havior [20].In our treatment these two effects are not disentangled.It was pointed out by Ingold and Lam-brecht [14]that the identification of the BEC should also be based on the behavior of C V around T ≈T 0.0.00.20.40.60.8 1.0 1.2T/T 0−5050100µ/V 0N=107N=105N=103N=101FIG.6.The temperature dependence of the chemical po-tential µ(N,T )for different number of particles N and for η=0.001.0.00.20.40.60.8 1.0 1.2T/T 00.00.20.40.60.8<E >/N k B T 0η=0η=0.001η=0.1η=1Maxwell−BoltzmannFIG.7.The temperature dependence of the total energy of 1D Bose gas for various interaction strengths ηand N =105particles.Our calculations indicate that the peak structure of C V remains even in the presence of weak interactions,thus we are led to conclude that a true transition to a Bose-Einstein condensed state is predicted within the present approach.0.00.20.40.60.81.01.2T/T 00.00.20.40.60.81.0C V /N k Bη=0η=0.001η=0.1Maxwell−BoltzmannFIG.8.The temperature dependence of the specific heat C V for various interaction strengths ηand N =105particles.IV.CONCLUDING REMARKSIn this work we have applied the mean-field,semi-classical two-fluid model to interacting bosons in 1D power-law trap potentials.We have found that for a range of interaction strengths the behavior of the thermo-dynamic quantities resembles to that of non-interactingbosons.Thus,BEC in the sense of macroscopic occu-pation of the ground state,occurs when the short-range interparticle interactions are not too strong.Our results are in qualitative agreement with the recent PIMC sim-ulations [19]of similar systems.Both 2D and 1D sim-ulation results [19,23]indicate a phase transition for a finite number system,in contrast to the situation in the thermodynamic limit.Since systems of much larger size can be studied within the present approach,our work complements the PIMC calculations.The possibility of studying the tunneling phenomenon of condensed bosons in spatially different regions sepa-rated by a barrier has recently attracted some attention [31–34].In particular,Dalfovo et al .[32]have shown that a Josephson-type tunneling current may exist for bosons under the influence of a double-well trap potential.Za-pata et al .[34]have estimated the Josephson coupling energy in terms of the condensate density.It is inter-esting to speculate on such a possibility in the present case,since the effective potential in our description is of the form of a double-well potential (cf.Fig.2).In our treatment,the interaction effects modify the single-well trap potential into one which exhibits two minima.Thus if we think of this effective potential as the one seen by the condensed bosons and according to the general ar-guments [31–34]based on two weakly connected systems we should have an oscillating flux of particles when the chemical potential in the two wells is different.Any con-figuration with N L =N R which is always the case for odd number of bosons will result in an oscillatory mo-tion.It would be interesting to explore these ideas in future work.ACKNOWLEDGMENTSThis work was supported by the Scientific and Techni-cal Research Council of Turkey (TUBITAK)under Grant No.TBAG-1736and TBAG-1662.We gratefully ac-knowledge useful discussions with Prof.C.Yalabık and E.Demirel.[5]D.J.Han,R.H.Wynar,Ph.Courteille,and D.J.Heinzen,Phys.Rev.A57,R4114(1998).[6]I.F.Silvera,in Bose-Einstein Condensation,Ed.by A.Griffin,D.W.Snoke,and S.Stringari(Cambridge Uni-versity Press,Cambridge,1995).[7]F.Dalfovo,S.Giorgini,L.P.Pitaevskii,and S.Stringari,preprint,cond-mat/9806038(to be published in Reviews of Modern Physics);A.S.Parkins and D.F.Walls,Phys.Rep.303,1(1998).[8]W.Ketterle and N.J.van Druten,Phys.Rev.A54,656(1996).[9]P.C.Hohenberg,Phys.Rev.158,383(1967).[10]A.Widom,Phys.Rev.176,254(1968).[11]L.C.Ioriatti,Jr.,S.G.Rosa,Jr.,and O.Hipolito,Am.J.Phys.44,744(1976).[12]V.Bagnato and D.Kleppner,Phys.Rev.A44,7439(1991).[13]T.Haugset and H.Haugerud,Phys.Rev.A57,3809(1998).[14]G.-L.Ingold and mbrecht,Eur.Phys.J.D1,29(1998).[15]W.J.Mullin,J.Low Temp.Phys.110,167(1998)[16]W.Deng and P.M.Hui,Solid State Commun.104,729(1997).[17]H.Monien,M.Linn,and N.Elstner,preprint,cond-mat/9711178.[18]F.Brosens,J.T.Devreese,and L.F.Lemmens,SolidState Commun.100,123(1996).[19]S.Pearson,T.Pang,and C.Chen,Phys.Rev.A58,1485(1998).[20]S.Giorgini,L.P.Pitaevskii,and S.Stringari,Phys.Rev.A,54,4633(1996);J.Low Temp.Phys.109,309(1997).[21]A.Minguzzi,S.Conti,and M.P.Tosi,J.Phys.Cond.Matter9,L33(1997).[22]M.Bayindir and B.Tanatar,Phys.Rev.A58,3134(1998).[23]S.Heinrichs and W.J.Mullin,preprint,cond-mat/9807331.[24]E.P.Gross,Nuovo Cimento20,454(1961).[25]L.P.Pitaevskii,Zh.Eksp.Teor.Fiz.40,646(1961)[Sov.Phys.JETP13,451(1961)].[26]M.Olshanii,Phys.Rev.Lett.81,938(1998).[27]R.J.Dodd,K.Burnett,M.Edwards,and C.W.Clark,Acta Phys.Pol.A93,45(1998).[28]M.Naraschewski and D.M.Stamper-Kurn,Phys.Rev.A58,2423(1998).[29]V.Bagnato,D.E.Pritchard,and D.Kleppner,Phys.Rev.A35,4354(1987).[30]G.Baym and C.J.Pethick,Phys.Rev.Lett.76,6(1996).[31]S.Grossmann and M.Holthaus,Z.Naturforsch.50a,323(1995).[32]F.Dalfovo,L.P.Pitaevskii,and S.Stringari,Phys.Rev.A54,4213(1996).[33]A.Smerzi,S.Fantoni,S.Giovanazzi,and S.R.Shenoy,Phys.Rev.Lett.79,4950(1997).[34]I.Zapata,F.Sols,and A.J.Leggett,Phys.Rev.A57,28(1998).。

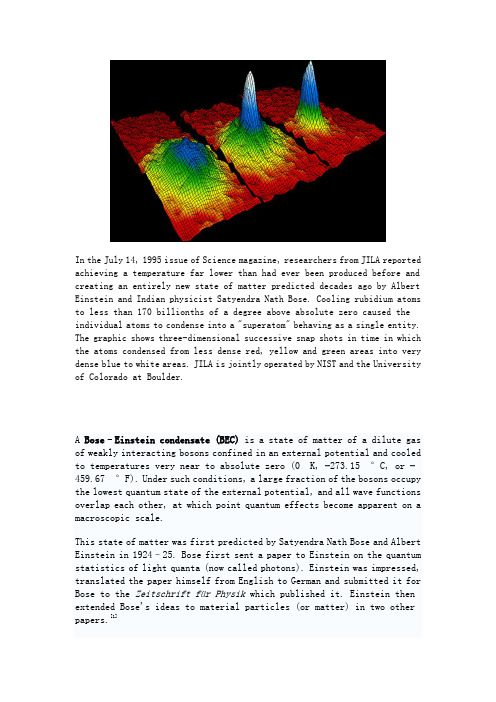
In the July 14, 1995 issue of Science magazine, researchers from JILA reported achieving a temperature far lower than had ever been produced before and creating an entirely new state of matter predicted decades ago by Albert Einstein and Indian physicist Satyendra Nath Bose. Cooling rubidium atoms to less than 170 billionths of a degree above absolute zero caused the individual atoms to condense into a "superatom" behaving as a single ent ity. The graphic shows three-dimensional successive snap shots in time in which the atoms condensed from less dense red, yellow and green areas into very dense blue to white areas. JILA is jointly operated by NIST and the University of Colorado at Boulder.A Bose–Einstein condensate (BEC) is a state of matter of a dilute gas of weakly interacting bosons confined in an external potential and cooled to temperatures very near to absolute zero (0 K, −273.15 °C, or −459.67 °F). Under such conditions, a large fraction of the bosons occupy the lowest quantum state of the external potential, and all wave functions overlap each other, at which point quantum effects become apparent on a macroscopic scale.This state of matter was first predicted by Satyendra Nath Bose and Albert Einstein in 1924–25. Bose first sent a paper to Einstein on the quantum statistics of light quanta (now called photons). Einstein was impressed, translated the paper himself from English to German and submitted it for Bose to the Zeitschrift für Physik which published it. Einstein then extended Bose's ideas to material particles (or matter) in two other papers.[1]Seventy years later, the first gaseous condensate was produced by Eric Cornell and Carl Wieman in 1995 at the University of Colorado at Boulder NIST-JILA lab, using a gas of rubidium atoms cooled to 170 nanokelvin (nK) [2](1.7×10−7 K). For their acheivments Cornell, Wieman, and Wolfgang Ketterle at MIT received the 2001 Nobel Prize in Physics. [3]TheoryThe slowing of atoms by use of cooling apparatus produces a singular quantum state known as a Bose condensate or Bose–Einstein condensate. This phenomenon was predicted in 1925 by generalizing Satyendra Nath Bose's work on the statistical mechanics of (massless) photons to (massive) atoms. (The Einstein manuscript, once believed to be lost, was found in a library at Leiden University in 2005.[4]) The result of the efforts of Bose and Einstein is the concept of a Bose gas, governed by Bose–Einstein statistics, which describes the statistical distribution of identical particles with integer spin, now known as bosons. Bosonic particles, which include the photon as well as atoms such as helium-4, are allowed to share quantum states with each other. Einstein demonstrated that cooling bosonic atoms to a very low temperature would cause them to fall (or "condense") into the lowest accessible quantum state, resulting in a new form of matter.This transition occurs below a critical temperature, which for a uniform three-dimensional gas consisting of non-interacting particles with no apparent internal degrees of freedom is given by:where:is t he critical temperature,is t he particle density,is t he mass per boson,is t he reduced Planck constant,is t he Boltzmann constant, andthe Riemann zeta function; (sequenceA078434 in OEIS)Einstein's argumentConsider a collection of N noninteracting particles which can each be in one of two quantum states, and . If the two states are equal in energy, each different configuration is equally likely.If we can tell which particle is which, there are 2N differentconfigurations, since each particle can be in or independently. In almost all the configurations, about half the particles are in and the other half in . The balance is a statistical effect, the number of configurations is largest when the particles are divided equally.If the particles are indistinguishable, however, there are only N+1 different configurations. If there are K particles in state , there are N-K particles in state . Whether any particular particle is in state or in state cannot be determined, so each value of K determines a unique quantum state for the whole system. If all these states are equally likely, there is no statistical spreading out; it is just as likely for all the particles to sit in as for the particles to be split half and half.Suppose now that the energy of state is slightly greater than the energy of state by an amount E. At temperature T, a particle will have a lesser probability to be in state by exp(-E/T). In the distinguishable case, the particle distribution will be biased slightly towards state and the distribution will be slightly different from half and half. But in the indistinguishable case, since there is no statistical pressure toward equal numbers, the most likely outcome is that most of the particles will collapse into state .In the distinguishable case, for large N, the fraction in state can be computed. It is the same as coin flipping with a coin which has probability p = exp(-E/T) to land tails. The fraction of heads is 1/(1+p), which is a smooth function of p, of the energy.In the indistinguishable case, each value of K is a single state, which has its own separate Boltzmann probability. So the probability distribution is exponential:For large N, the normalization constant C is (1-p). The expected total number of particles which are not in the lowest energy state, in the limitthat , is equal to . It doesn't grow when N islarge, it just approaches a constant. This will be a negligible fraction of the total number of particles. So a collection of enough bose particles in thermal equilibrium will mostly be in the ground state, with only a few in any excited state, no matter how small the energy difference.Consider now a gas of particles, which can be in different momentum states labelled . If the number of particles is less than the number of thermally accessible states, for high temperatures and low densities, the particles will all be in different states. In this limit the gas is classical. As the density increases or the temperature decreases, the number of accessible states per particle becomes smaller, and at some point more particles will be forced into a single state than the maximum allowed for that state by statistical weighting. From this point on, any extra particle added will go into the ground state.To calculate the transition temperature at any density, integrate over all momentum states the expression for maximum number of excited particles p/(1-p):When the integral is evaluated with the factors of k B and ℏ restored by dimensional analysis, it gives the critical temperature formula of the preceding section. Therefore, this integral defines the critical temperature and particle number corresponding to the conditions of zero chemical potential (μ = 0 in the Bose–Einstein statistics distribution).Gross–Pitaevskii equationMain article: Gross–Pitaevskii equationThe state of the BEC can be described by the wavefunction of the condensate . For a system of this nature, is interpreted as the particledensity, so the total number of atoms isProvided essentially all atoms are in the condensate (that is, have condensed to the ground state), and treating the bosons using mean fieldtheory, the energy (E) associated with the state is:Minimising this energy with respect to infinitesimal variations in ,and holding the number of atoms constant, yields the Gross-Pitaevski equation (GPE) (also a non-linear Schrödinger equation):where:is the mass of the bosons,is the external potential,is representative of the inter-particle interactions.The GPE provides a good description of the behavior of BEC's and is thus often applied for theoretical analysis.DiscoveryIn 1938, Pyotr Kapitsa, John Allen and Don Misener discovered that helium-4 became a new kind of fluid, now known as a superfluid, at temperatures less than 2.17 K (the lambda point). Superfluid helium has many unusual properties, including zero viscosity (the ability to flow without dissipating energy) and the existence of quantized vortices. It was quickly realized that the superfluidity was due to partialBose–Einstein condensation of the liquid. In fact, many of the properties of superfluid helium also appear in the gaseous Bose–Einstein condensates created by Cornell, Wieman and Ketterle (see below). Superfluid helium-4 is a liquid rather than a gas, which means that the interactions between the atoms are relatively strong; the original theory of Bose–Einstein condensation must be heavily modified in order to describe it. Bose–Einstein condensation remains, however, fundamental to the superfluid properties of helium-4. Note that helium-3, consisting of fermions instead of bosons, also enters a superfluid phase at lowtemperature, which can be explained by the formation of bosonic Cooper pairs of two atoms each (see also fermionic condensate).The first "pure" Bose–Einstein condensate was created by Eric Cornell, Carl Wieman, and co-workers at JILA on June 5, 1995. They did this by cooling a dilute vapor consisting of approximately two thousand rubidium-87 atoms to below 170 nK using a combination of laser cooling (a technique that won its inventors Steven Chu, Claude Cohen-Tannoudji, and William D. Phillips the 1997 Nobel Prize in Physics) and magnetic evaporative cooling. About four months later, an independent effort led by Wolfgang Ketterle at MIT created a condensate made of sodium-23. Ketterle's condensate had about a hundred times more atoms, allowing him to obtain several important results such as the observation of quantum mechanical interference between two different condensates. Cornell, Wieman and Ketterle won the 2001 Nobel Prize in Physics for their achievement.[5]The Bose–Einstein condensation also applies to quasiparticles in solids.A magnon in an antiferromagnet carries spin 1 and thus obeysBose–Einstein statistics. The density of magnons is controlled by an external magnetic field, which plays the role of the magnon chemical potential. This technique provides access to a wide range of boson densities from the limit of a dilute Bose gas to that of a strongly interacting Bose liquid. A magnetic ordering observed at the point of condensation is the analog of superfluidity. In 1999 Bose condensation of magnons was demonstrated in the antiferromagnet TlCuCl3.[6] The condensation was observed at temperatures as large as 14 K. Such a high transition temperature (relative to that of atomic gases) is due to the greater density achievable with magnons and the smaller mass (roughly equal to the mass of an electron). In 2006, condensation of magnons in ferromagnets was even shown at room temperature,[7]where the authors used pumping techniques.Velocity-distribution data graph（速度分布数据图）Velocity-distribution data of a gas of rubidium atoms, confirming the discovery of a new phase of matter, the Bose–Einstein condensate. Left: just before the appearance of a Bose–Einstein condensate. Center: just after the appearance of the condensate. Right: after further evaporation, leaving a sample of nearly pure condensate.In the image accompanying this article, the velocity-distribution data indicates the formation of a Bose–Einstein condensate out of a gas of rubidium atoms. The false colors indicate the number of atoms at each velocity, with red being the fewest and white being the most. The areas appearing white and light blue are at the lowest velocities. The peak is not infinitely narrow because of the Heisenberg uncertainty principle: since the atoms are trapped in a particular region of space, their velocity distribution necessarily possesses a certain minimum width. This width is given by the curvature of the magnetic trapping potential in the given direction. More tightly confined directions have bigger widths in the ballistic velocity distribution. This anisotropy of the peak on the right is a purely quantum-mechanical effect and does not exist in the thermal distribution on the left. This famous graph served as the cover-design for 1999 textbook Thermal Physics by Ralph Baierlein.[8]Vortices（涡旋）As in many other systems, vortices can exist in BECs. These can be created, for example, by 'stirring' the condensate with lasers, or rotating the confining trap. The vortex created will be a quantum vortex. Thesephenomena are allowed for by the non-linear term in the GPE. As the vortices must have quantised angular momentum, the wavefunction will be of the form where ρ,z and θ are as in thecylindrical coordinate system, and is the angular number. To determine φ(ρ,z), the energy of must be minimised, according to the constraint . This is usually done computationally, however in a uniform medium the analytic formwhere:is d ensity far from the vortex,is h ealing length of the condensate.demonstrates the correct behavior, and is a good approximation.A singly-charged vortex () is in the ground state, with its energy εv given bywhere:is t he farthest distance from the vortex considered.(To obtain an energy which is well defined it is necessary to include this boundary b.)For multiply-charged vortices () the energy is approximated bywhich is greater than that of singly-charged vortices, indicating that these multiply-charged vortices are unstable to decay. Research has,however, indicated they are metastable states, so may have relatively long lifetimes.Closely related to the creation of vortices in BECs is the generation of so-called dark solitons in one-dimensional BECs. These topological objects feature a phase gradient across their nodal plane, which stabilizes their shape even in propagation and interaction. Although solitons carry no charge and are thus prone to decay, relativelylong-lived dark solitons have been produced and studied extensively.[9] Unusual characteristicsFurther experimentation by the JILA team in 2000 uncovered a hitherto unknown property of Bose–Einstein condensates. Cornell, Wieman, and their coworkers originally used rubidium-87, an isotope whose atoms naturally repel each other, making a more stable condensate. The JILA team instrumentation now had better control over the condensate so experimentation was made on naturally attracting atoms of another rubidium isotope, rubidium-85 (having negative atom-atom scattering length). Through a process called Feshbach resonance involving a sweep of the magnetic field causing spin flip collisions, the JILA researchers lowered the characteristic, discrete energies at which the rubidium atoms bond into molecules, making their Rb-85 atoms repulsive and creating a stable condensate. The reversible flip from attraction to repulsion stems from quantum interference among condensate atoms which behave as waves.When the scientists raised the magnetic field strength still further, the condensate suddenly reverted back to attraction, imploded and shrank beyond detection, and then exploded, blowing off about two-thirds of its 10,000 or so atoms. About half of the atoms in the condensate seemed to have disappeared from the experiment altogether, not being seen either in the cold remnant or the expanding gas cloud.[10] Carl Wieman explained that under current atomic theory this characteristic of Bose–Einstein condensate could not be explained because the energy state of an atom near absolute zero should not be enough to cause an implosion; however, subsequent mean field theories have been proposed to explain it.Because supernova explosions are also preceded by an implosion, the explosion of a collapsing Bose–Einstein condensate was named "bosenova", a pun on the musical style bossa nova.The atoms that seem to have disappeared almost certainly still exist in some form, just not in a form that could be accounted for in that experiment. Most likely they formed molecules consisting of two bonded rubidium atoms.The energy gained by making this transition imparts a velocity sufficient for them to leave the trap without being detected.Current researchCompared to more commonly encountered states of matter, Bose–Einstein condensates are extremely fragile. The slightest interaction with the outside world can be enough to warm them past the condensation threshold, eliminating their interesting properties and forming a normal gas. It is likely to be some time before any practical applications are developed.Nevertheless, they have proven useful in exploring a wide range of questions in fundamental physics, and the years since the initial discoveries by the JILA and MIT groups have seen an explosion in experimental and theoretical activity. Examples include experiments that have demonstrated interference between condensates due to wave-particle duality,[11]the study of superfluidity and quantized vortices,[12]and the slowing of light pulses to very low speeds using electromagnetically induced transparency.[13]Vortices in Bose–Einstein condensates are also currently the subject of analogue gravity research, studying the possibility of modeling black holes and their related phenomena in such environments in the lab. Experimentalists have also realized "optical lattices", where the interference pattern from overlapping lasers provides a periodic potential for the condensate. These have been used to explore the transition between a superfluid and a Mott insulator,[14] and may be useful in studying Bose–Einstein condensation in fewer than three dimensions, for example the Tonks-Girardeau gas.Bose–Einstein condensates composed of a wide range of isotopes have been produced.[15]Related experiments in cooling fermions rather than bosons to extremely low temperatures have created degenerate gases, where the atoms do not congregate in a single state due to the Pauli exclusion principle. To exhibit Bose–Einstein condensation, the fermions must "pair up" to form compound particles (e.g. molecules or Cooper pairs) that are bosons. The first molecular Bose–Einstein condensates were created in November 2003 by the groups of Rudolf Grimm at the University of Innsbruck, Deborah S. Jin at the University of Colorado at Boulder and Wolfgang Ketterle at MIT. Jin quickly went on to create the first fermionic condensate composed of Cooper pairs.[16]In 1999, Danish physicist Lene Vestergaard Hau led a team from Harvard University which succeeded in slowing a beam of light to about 17 metresper second and, in 2001, was able to momentarily stop a beam. She was able to achieve this by using a superfluid. Hau and her associates at Harvard University have since successfully transformed light into matter and back into light using Bose–Einstein condensates: details of the experiment are discussed in an article in the journal Nature, 8 February 2007.[17]Subtleties(微妙之处)Up to 2004, using the above-mentioned "ultralow temperatures",Bose–Einstein condensates had been obtained for a multitude of isotopes involving mainly alkaline and alkaline earth atoms (7Li, 23Na, 41K, 52Cr,84St, 85Rb, 87Rb, 133Cs and 174Yb). Not astonishingly, condensation research was finally successful even with hydrogen, although with the aid of special methods. In contrast, the superfluid state of the bosonic 4He at temperatures below the temperature of 2.17 K is not a good example of Bose–Einstein condensation, because the interaction between the 4He bosons is simply too strong, so that at zero temperature, contrary to Bose–Einstein theory, only 8% rather than 100% of the atoms are in the ground state. Even the fact that the above-mentioned alkaline gases show bosonic, rather than fermionic behaviour, as solid state physicists or chemists would expect, is based on a subtle interplay of electronic and nuclear spins: at ultralow temperatures and corresponding excitation energies, the half-integer (in units of ) total spin of the electronic shell and the also half-integer total spin of the nucleus of the atom are coupled by the (very weak) hyperfine interaction to the integer (!) total spin of the atom. Only the fact that this last-mentioned total spin is integral causes the ultralow-temperature behaviour of the atom to be bosonic, whereas the "chemistry" of the systems at room temperature is determined by the electronic properties, i.e. is essentially fermionic, since at room temperature thermal excitations have typical energies which are much higher than the hyperfine values. (Here one should remember the spin-statistics theorem of Wolfgang Pauli, which states that half-integer spins lead to fermionic behaviour, e.g., the Pauli exclusion principle forbidding that more than two electrons possess the same energy, whereas integer spins lead to bosonic behaviour, e.g., condensation of identical bosonic particles in a common ground state.)The ultralow temperature requirement of Bose–Einstein condensates of alkali metals does not generalize to all types of Bose–Einstein condensates. In 2006, physicists under S. Demokritov in Münster, Germany,[18]found Bose–Einstein condensation of magnons (i.e. quantized spinwaves) at room temperature, admittedly by the application of pump processes。

Chapter19Bose-Einstein CondensationAbstract Bose-Einstein condensation(BEC)refers to a prediction of quantum sta-tistical mechanics(Bose[1],Einstein[2])where an ideal gas of identical bosons undergoes a phase transition when the thermal de Broglie wavelength exceeds the mean spacing between the particles.Under these conditions,bosons are stimulated by the presence of other bosons in the lowest energy state to occupy that state as well,resulting in a macroscopic occupation of a single quantum state.The con-densate that forms constitutes a macroscopic quantum-mechanical object.BEC was first observed in1995,seventy years after the initial predictions,and resulted in the award of2001Nobel Prize in Physics to Cornell,Ketterle and Weiman.The exper-imental observation of BEC was achieved in a dilute gas of alkali atoms in a mag-netic trap.Thefirst experiments used87Rb atoms[3],23Na[4],7Li[5],and H[6] more recently metastable He has been condensed[7].The list of BEC atoms now includes molecular systems such as Rb2[8],Li2[9]and Cs2[10].In order to cool the atoms to the required temperature(∼200nK)and densities(1013–1014cm−3) for the observation of BEC a combination of optical cooling and evaporative cooling were employed.Early experiments used magnetic traps but now optical dipole traps are also common.Condensates containing up to5×109atoms have been achieved for atoms with a positive scattering length(repulsive interaction),but small con-densates have also been achieved with only a few hundred atoms.In recent years Fermi degenerate gases have been produced[11],but we will not discuss these in this chapter.BECs are now routinely produced in dozens of laboratories around the world. They have provided a wonderful test bed for condensed matter physics with stunning experimental demonstrations of,among other things,interference between conden-sates,superfluidity and vortices.More recently they have been used to create opti-cally nonlinear media to demonstrate electromagnetically induced transparency and neutral atom arrays in an optical lattice via a Mott insulator transition.Many experiments on BECs are well described by a semiclassical theory dis-cussed below.Typically these involve condensates with a large number of atoms, and in some ways are analogous to describing a laser in terms of a semiclassi-cal meanfield.More recent experiments however have begun to probe quantum39739819Bose-Einstein Condensation properties of the condensate,and are related to the fundamental discreteness of the field and nonlinear quantum dynamics.In this chapter,we discuss some of these quantum properties of the condensate.We shall make use of“few mode”approxi-mations which treat only essential condensate modes and ignore all noncondensate modes.This enables us to use techniques developed for treating quantum optical systems described in earlier chapters of this book.19.1Hamiltonian:Binary Collision ModelThe effects of interparticle interactions are of fundamental importance in the study of dilute–gas Bose–Einstein condensates.Although the actual interaction potential between atoms is typically very complex,the regime of operation of current exper-iments is such that interactions can in fact be treated very accurately with a much–simplified model.In particular,at very low temperature the de Broglie wavelengths of the atoms are very large compared to the range of the interatomic potential.This, together with the fact that the density and energy of the atoms are so low that they rarely approach each other very closely,means that atom–atom interactions are ef-fectively weak and dominated by(elastic)s–wave scattering.It follows also that to a good approximation one need only consider binary collisions(i.e.,three–body processes can be neglected)in the theoretical model.The s–wave scattering is characterised by the s–wave scattering length,a,the sign of which depends sensitively on the precise details of the interatomic potential [a>0(a<0)for repulsive(attractive)interactions].Given the conditions described above,the interaction potential can be approximated byU(r−r )=U0δ(r−r ),(19.1) (i.e.,a hard sphere potential)with U0the interaction“strength,”given byU0=4π¯h2am,(19.2)and the Hamiltonian for the system of weakly interacting bosons in an external potential,V trap(r),can be written in the second quantised form asˆH=d3rˆΨ†(r)−¯h22m∇2+V trap(r)ˆΨ(r)+12d3rd3r ˆΨ†(r)ˆΨ†(r )U(r−r )ˆΨ(r )ˆΨ(r)(19.3)whereˆΨ(r)andˆΨ†(r)are the bosonfield operators that annihilate or create a par-ticle at the position r,respectively.19.2Mean–Field Theory —Gross-Pitaevskii Equation 399To put a quantitative estimate on the applicability of the model,if ρis the density of bosons,then a necessary condition is that a 3ρ 1(for a >0).This condition is indeed satisfied in the alkali gas BEC experiments [3,4],where achieved densities of the order of 1012−1013cm −3correspond to a 3ρ 10−5−10−6.19.2Mean–Field Theory —Gross-Pitaevskii EquationThe Heisenberg equation of motion for ˆΨ(r )is derived as i¯h ∂ˆΨ(r ,t )∂t = −¯h 22m ∇2+V trap (r ) ˆΨ(r ,t )+U 0ˆΨ†(r ,t )ˆΨ(r ,t )ˆΨ(r ,t ),(19.4)which cannot in general be solved.In the mean–field approach,however,the expec-tation value of (19.4)is taken and the field operator decomposed asˆΨ(r ,t )=Ψ(r ,t )+˜Ψ(r ,t ),(19.5)where Ψ(r ,t )= ˆΨ(r ,t ) is the “condensate wave function”and ˜Ψ(r )describes quantum and thermal fluctuations around this mean value.The quantity Ψ(r ,t )is in fact a classical field possessing a well–defined phase,reflecting a broken gauge sym-metry associated with the condensation process.The expectation value of ˜Ψ(r ,t )is zero and,in the mean–field theory,its effects are assumed to be small,amounting to the assumption of the thermodynamic limit,where the number of particles tends to infinity while the density is held fixed.For the effects of ˜Ψ(r )to be negligibly small in the equation for Ψ(r )also amounts to an assumption of zero temperature (i.e.,pure condensate).Given that this is so,and using the normalisationd 3r |Ψ(r ,t )|2=1,(19.6)one is lead to the nonlinear Schr¨o dinger equation,or “Gross–Pitaevskii equation”(GP equation),for the condensate wave function Ψ(r ,t )[13],i¯h ∂Ψ(r ,t )∂t = −¯h 22m ∇2+V trap (r )+NU 0|Ψ(r ,t )|2 Ψ(r ,t ),(19.7)where N is the mean number of particles in the condensate.The nonlinear interaction term (or mean–field pseudo–potential)is proportional to the number of atoms in the condensate and to the s –wave scattering length through the parameter U 0.A stationary solution forthe condensate wavefunction may be found by substi-tuting ψ(r ,t )=exp −i μt ¯h ψ(r )into (19.7)(where μis the chemical potential of the condensate).This yields the time independent equation,40019Bose-Einstein Condensation−¯h2 2m ∇2+V trap(r)+NU0|ψ(r)|2ψ(r)=μψ(r).(19.8)The GP equation has proved most successful in describing many of the meanfield properties of the condensate.The reader is referred to the review articles listed in further reading for a comprehensive list of references.In this chapter we shall focus on the quantum properties of the condensate and to facilitate our investigations we shall go to a single mode model.19.3Single Mode ApproximationThe study of the quantum statistical properties of the condensate(at T=0)can be reduced to a relatively simple model by using a mode expansion and subsequent truncation to just a single mode(the“condensate mode”).In particular,one writes the Heisenberg atomicfield annihilation operator as a mode expansion over single–particle states,ˆΨ(r,t)=∑αaα(t)ψα(r)exp−iμαt/¯h=a0(t)ψ0(r)exp−iμ0t/¯h+˜Ψ(r,t),(19.9) where[aα(t),a†β(t)]=δαβand{ψα(r)}are a complete orthonormal basis set and {μα}the corresponding eigenvalues.Thefirst term in the second line of(19.9)acts only on the condensate state vector,withψ0(r)chosen as a solution of the station-ary GP equation(19.8)(with chemical potentialμ0and mean number of condensate atoms N).The second term,˜Ψ(r,t),accounts for non–condensate atoms.Substitut-ing this mode expansion into the HamiltonianˆH=d3rˆΨ†(r)−¯h22m∇2+V trap(r)ˆΨ(r)+(U0/2)d3rˆΨ†(r)ˆΨ†(r)ˆΨ(r)ˆΨ(r),(19.10)and retaining only condensate terms,one arrives at the single–mode effective Hamil-tonianˆH=¯h˜ω0a †a0+¯hκa†0a†0a0a0,(19.11)where¯h˜ω0=d3rψ∗0(r)−¯h22m∇2+V trap(r)ψ0(r),(19.12)and¯hκ=U02d3r|ψ0(r)|4.(19.13)19.5Quantum Phase Diffusion:Collapses and Revivals of the Condensate Phase401 We have assumed that the state is prepared slowly,with damping and pumping rates vanishingly small compared to the trap frequencies and collision rates.This means that the condensate remains in thermodynamic equilibrium throughout its prepara-tion.Finally,the atom number distribution is assumed to be sufficiently narrow that the parameters˜ω0andκ,which of course depend on the atom number,can be re-garded as constants(evaluated at the mean atom number).In practice,this proves to be a very good approximation.19.4Quantum State of the CondensateA Bose-Einstein condensate(BEC)is often viewed as a coherent state of the atomic field with a definite phase.The Hamiltonian for the atomicfield is independent of the condensate phase(see Exercise19.1)so it is often convenient to invoke a symmetry breaking Bogoliubovfield to select a particular phase.In addition,a coherent state implies a superposition of number states,whereas in a single trap experiment there is afixed number of atoms in the trap(even if we are ignorant of that number)and the state of a simple trapped condensate must be a number state(or,more precisely, a mixture of number states as we do not know the number in the trap from one preparation to the next).These problems may be bypassed by considering a system of two condensates for which the total number of atoms N isfixed.Then,a general state of the system is a superposition of number difference states of the form,|ψ =N∑k=0c k|k,N−k (19.14)As we have a well defined superposition state,we can legitimately consider the relative phase of the two condensates which is a Hermitian observable.We describe in Sect.19.6how a particular relative phase is established due to the measurement process.The identification of the condensate state as a coherent state must be modified in the presence of collisions except in the case of very strong damping.19.5Quantum Phase Diffusion:Collapsesand Revivals of the Condensate PhaseThe macroscopic wavefunction for the condensate for a relatively strong number of atoms will exhibit collapses and revivals arising from the quantum evolution of an initial state with a spread in atom number[21].The initial collapse has been described as quantum phase diffusion[20].The origins of the collapses and revivals may be seen straightforwardly from the single–mode model.From the Hamiltonian40219Bose-Einstein CondensationˆH =¯h ˜ω0a †0a 0+¯h κa †0a †0a 0a 0,(19.15)the Heisenberg equation of motion for the condensate mode operator follows as˙a 0(t )=−i ¯h [a 0,H ]=−i ˜ω0a 0+2κa †0a 0a 0 ,(19.16)for which a solution can be written in the form a 0(t )=exp −i ˜ω0+2κa †0a 0 t a 0(0).(19.17)Writing the initial state of the condensate,|i ,as a superposition of number states,|i =∑n c n |n ,(19.18)the expectation value i |a 0(t )|i is given byi |a 0(t )|i =∑n c ∗n −1c n √n exp {−i [˜ω0+2κ(n −1)]t }=∑nc ∗n −1c n √n exp −i μt ¯h exp {−2i κ(n −N )t },(19.19)where the relationship μ=¯h ˜ω0+2¯h κ(N −1),(19.20)has been used [this expression for μuses the approximation n 2 =N 2+(Δn )2≈N 2].The factor exp (−i μt /¯h )describes the deterministic motion of the condensate mode in phase space and can be removed by transforming to a rotating frame of reference,allowing one to writei |a 0(t )|i =∑nc ∗n −1c n √n {cos [2κ(n −N )t ]−isin [2κ(n −N )t ]}.(19.21)This expression consists of a weighted sum of trigonometric functions with different frequencies.With time,these functions alternately “dephase”and “rephase,”giving rise to collapses and revivals,respectively,in analogy with the behaviour of the Jaynes–Cummings Model of the interaction of a two–level atom with a single elec-tromagnetic field mode described in Sect.10.2.The period of the revivals follows di-rectly from (19.21)as T =π/κ.The collapse time can be derived by considering the spread of frequencies for particle numbers between n =N +(Δn )and n =N −(Δn ),which yields (ΔΩ)=2κ(Δn );from this one estimates t coll 2π/(ΔΩ)=T /(Δn ),as before.From the expression t coll T /(Δn ),it follows that the time taken for collapse depends on the statistics of the condensate;in particular,on the “width”of the initial distribution.This dependence is illustrated in Fig.19.1,where the real part of a 0(t )19.5Quantum Phase Diffusion:Collapses and Revivals of the Condensate Phase403Fig.19.1The real part ofthe condensate amplitudeversus time,Re { a 0(t ) }for an amplitude–squeezed state,(a )and a coherent state (b )with the same mean numberof atoms,N =250.20.40.60.81-11234560b a is plotted as a function of time for two different initial states:(a)an amplitude–squeezed state,(b)a coherent state.The mean number of atoms is chosen in each case to be N =25.The timescales of the collapses show clear differences;the more strongly number–squeezed the state is,the longer its collapse time.The revival times,how-ever,are independent of the degree of number squeezing and depend only on the interaction parameter,κ.For example,a condensate of Rb 2,000atoms with the ω/2π=60Hz,has revival time of approximately 8s,which lies within the typical lifetime of the experimental condensate (10–20s).One can examine this phenomenon in the context of the interference between a pair of condensates and indeed one finds that the visibility of the interference pat-tern also exhibits collapses and revivals,offering an alternative means of detecting this effect.To see this,consider,as above,that atoms are released from two conden-sates with momenta k 1and k 2respectively.Collisions within each condensate are described by the Hamiltonian (neglecting cross–collisions)ˆH =¯h κ a †1a 1 2+ a †2a 22 ,(19.22)from which the intensity at the detector follows asI (x ,t )=I 0 [a †1(t )exp i k 1x +a †2(t )expi k 2x ][a 1(t )exp −i k 1x +a 2(t )exp −i k 2x ] =I 0 a †1a 1 + a †2a 2+ a †1exp 2i a †1a 1−a †2a 2 κt a 2 exp −i φ(x )+h .c . ,(19.23)where φ(x )=(k 2−k 1)x .If one assumes that each condensate is initially in a coherent state of amplitude |α|,with a relative phase φbetween the two condensates,i.e.,assuming that|ϕ(t =0) =|α |αe −i φ ,(19.24)40419Bose-Einstein Condensation then one obtains for the intensityI(x,t)=I0|α|221+exp2|α|2(cos(2κt)−1)cos[φ(x)−φ].(19.25)From this expression,it is clear that the visibility of the interference pattern under-goes collapses and revivals with a period equal toπ/κ.For short times t 1/2κ, this can be written asI(x,t)=I0|α|221+exp−|α|2κ2t2,(19.26)from which the collapse time can be identified as t coll=1/κ|α|.An experimental demonstration of the collapse and revival of a condensate was done by the group of Bloch in2002[12].In the experiment coherent states of87Rb atoms were prepared in a three dimensional optical lattice where the tunneling is larger than the on-site repulsion.The condensates in each well were phase coherent with constant relative phases between the sites,and the number distribution in each well is close to Poisonnian.As the optical dipole potential is increased the depth of the potential wells increases and the inter-well tunneling decreases producing a sub-Poisson number distribution in each well due to the repulsive interaction between the atoms.After preparing the states in each well,the well depth is rapidly increased to create isolated potential wells.The nonlinear interaction of(19.15)then determines the dynamics in each well.After some time interval,the hold time,the condensate is released from the trap and the resulting interference pattern is imaged.As the meanfield amplitude in each well undergoes a collapse the resulting interference pattern visibility decreases.However as the meanfield revives,the visibility of the interference pattern also revives.The experimental results are shown in Fig.19.2.Fig.19.2The interference pattern imaged from the released condensate after different hold times. In(d)the interference fringes have entirely vanished indicating a complete collapse of the am-plitude of the condensate.In(g),the wait time is now close to the complete revival time for the coherent amplitude and the fringe pattern is restored.From Fig.2of[12]19.6Interference of Two Bose–Einstein Condensates and Measurement–Induced Phase405 19.6Interference of Two Bose–Einstein Condensatesand Measurement–Induced PhaseThe standard approach to a Bose–Einstein condensate assumes that it exhibits a well–defined amplitude,which unavoidably introduces the condensate phase.Is this phase just a formal construct,not relevant to any real measurement,or can one ac-tually observe something in an experiment?Since one needs a phase reference to observe a phase,two options are available for investigation of the above question. One could compare the condensate phase to itself at a different time,thereby ex-amining the condensate phase dynamics,or one could compare the phases of two distinct condensates.This second option has been studied by a number of groups, pioneered by the work of Javanainen and Yoo[23]who consider a pair of statisti-cally independent,physically–separated condensates allowed to drop and,by virtue of their horizontal motion,overlap as they reach the surface of an atomic detec-tor.The essential result of the analysis is that,even though no phase information is initially present(the initial condensates may,for example,be in number states),an interference pattern may be formed and a relative phase established as a result of the measurement.This result may be regarded as a constructive example of sponta-neous symmetry breaking.Every particular measurement produces a certain relative phase between the condensates;however,this phase is random,so that the symme-try of the system,being broken in a single measurement,is restored if an ensemble of measurements is considered.The physical configuration we have just described and the predicted interference between two overlapping condensates was realised in a beautiful experiment per-formed by Andrews et al.[18]at MIT.The observed fringe pattern is shown in Fig.19.8.19.6.1Interference of Two Condensates Initially in Number States To outline this effect,we follow the working of Javanainen and Yoo[23]and consider two condensates made to overlap at the surface of an atom detector.The condensates each contain N/2(noninteracting)atoms of momenta k1and k2,respec-tively,and in the detection region the appropriatefield operator isˆψ(x)=1√2a1+a2exp iφ(x),(19.27)whereφ(x)=(k2−k1)x and a1and a2are the atom annihilation operators for the first and second condensate,respectively.For simplicity,the momenta are set to±π, so thatφ(x)=2πx.The initial state vector is represented simply by|ϕ(0) =|N/2,N/2 .(19.28)40619Bose-Einstein Condensation Assuming destructive measurement of atomic position,whereby none of the atoms interacts with the detector twice,a direct analogy can be drawn with the theory of absorptive photodetection and the joint counting rate R m for m atomic detections at positions {x 1,···,x m }and times {t 1,···,t m }can be defined as the normally–ordered averageR m (x 1,t 1,...,x m ,t m )=K m ˆψ†(x 1,t 1)···ˆψ†(x m ,t m )ˆψ(x m ,t m )···ˆψ(x 1,t 1) .(19.29)Here,K m is a constant that incorporates the sensitivity of the detectors,and R m =0if m >N ,i.e.,no more than N detections can occur.Further assuming that all atoms are in fact detected,the joint probability density for detecting m atoms at positions {x 1,···,x m }follows asp m (x 1,···,x m )=(N −m )!N ! ˆψ†(x 1)···ˆψ†(x m )ˆψ(x m )···ˆψ(x 1) (19.30)The conditional probability density ,which gives the probability of detecting an atom at the position x m given m −1previous detections at positions {x 1,···,x m −1},is defined as p (x m |x 1,···,x m −1)=p m (x 1,···,x m )p m −1(x 1,···,x m −1),(19.31)and offers a straightforward means of directly simulating a sequence of atom detections [23,24].This follows from the fact that,by virtue of the form for p m (x 1,···,x m ),the conditional probabilities can all be expressed in the simple formp (x m |x 1,···,x m −1)=1+βcos (2πx m +ϕ),(19.32)where βand ϕare parameters that depend on {x 1,···,x m −1}.The origin of this form can be seen from the action of each measurement on the previous result,ϕm |ˆψ†(x )ˆψ(x )|ϕm =(N −m )+2A cos [θ−φ(x )],(19.33)with A exp −i θ= ϕm |a †1a 2|ϕm .So,to simulate an experiment,one begins with the distribution p 1(x )=1,i.e.,one chooses the first random number (the position of the first atom detection),x 1,from a uniform distribution in the interval [0,1](obviously,before any measurements are made,there is no information about the phase or visibility of the interference).After this “measurement,”the state of the system is|ϕ1 =ˆψ(x 1)|ϕ0 = N /2 |(N /2)−1,N /2 +|N /2,(N /2)−1 expi φ(x 1) .(19.34)That is,one now has an entangled state containing phase information due to the fact that one does not know from which condensate the detected atom came.The corre-sponding conditional probability density for the second detection can be derived as19.6Interference of Two Bose–Einstein Condensates and Measurement–Induced Phase 407n u m b e r o f a t o m s n u m b e r o f a t o m s 8position Fig.19.3(a )Numerical simulation of 5,000atomic detections for N =10,000(circles).The solid curve is a least-squares fit using the function 1+βcos (2πx +ϕ).The free parameters are the visibility βand the phase ϕ.The detection positions are sorted into 50equally spaced bins.(b )Collisions included (κ=2γgiving a visibility of about one-half of the no collision case.From Wong et al.[24]40819Bose-Einstein Condensationp (x |x 1)=p 2(x 1,x )p 1(x 1)=1N −1 ˆψ†(x 1)ˆψ†(x )ˆψ(x )ˆψ(x 1) ˆψ†(x 1)ˆψ(x 1) (19.35)=12 1+N 2(N −1)cos [φ(x )−φ(x 1)] .(19.36)Hence,after just one measurement the visibility (for large N )is already close to 1/2,with the phase of the interference pattern dependent on the first measurement x 1.The second position,x 2,is chosen from the distribution (19.36).The conditional proba-bility p (x |x 1)has,of course,the form (19.32),with βand ϕtaking simple analytic forms.However,expressions for βand ϕbecome more complicated with increasing m ,and in practice the approach one takes is to simply calculate p (x |x 1,···,x m −1)numerically for two values of x [using the form (19.30)for p m (x 1,...,x m −1,x ),and noting that p m −1(x 1,...,x m −1)is simply a number already determined by the simu-lation]and then,using these values,solve for βand ϕ.This then defines exactly the distribution from which to choose x m .The results of simulations making use of the above procedure are shown in Figs 19.3–19.4.Figure 19.3shows a histogram of 5,000atom detections from condensates initially containing N /2=5,000atoms each with and without colli-sions.From a fit of the data to a function of the form 1+βcos (2πx +ϕ),the visibil-ity of the interference pattern,β,is calculated to be 1.The conditional probability distributions calculated before each detection contain what one can define as a con-000.10.20.30.40.50.60.70.80.91102030405060number of atoms decided 708090100x=0x=1x=2x=4x=6Fig.19.4Averaged conditional visibility as a function of the number of detected atoms.From Wong et al.[13]19.7Quantum Tunneling of a Two Component Condensate40900.51 1.520.500.5Θz ο00.51 1.520.500.5Θx ο(b)1,234elliptic saddle Fig.19.5Fixed point bifurcation diagram of the two mode semiclassical BEC dynamics.(a )z ∗,(b )x ∗.Solid line is stable while dashed line is unstable.ditional visibility .Following the value of this conditional visibility gives a quantita-tive measure of the buildup of the interference pattern as a function of the number of detections.The conditional visibility,averaged over many simulations,is shown as a function of the number of detections in Fig.19.4for N =200.One clearly sees the sudden increase to a value of approximately 0.5after the first detection,followed by a steady rise towards the value 1.0(in the absence of collisions)as each further detection provides more information about the phase of the interference pattern.One can also follow the evolution of the conditional phase contained within the conditional probability distribution.The final phase produced by each individual simulation is,of course,random but the trajectories are seen to stabilise about a particular value after approximately 50detections (for N =200).19.7Quantum Tunneling of a Two Component CondensateA two component condensate in a double well potential is a non trivial nonlinear dynamical model.Suppose the trapping potential in (19.3)is given byV (r )=b (x 2−q 20)2+12m ω2t (y 2+z 2)(19.37)where ωt is the trap frequency in the y –z plane.The potential has elliptic fixed points at r 1=+q 0x ,r 2=−q 0x near which the linearised motion is harmonic withfrequency ω0=q o (8b /m )1/2.For simplicity we set ωt =ω0and scale the length in units of r 0= ¯h /2m ω0,which is the position uncertainty in the harmonic oscillatorground state.The barrier height is B =(¯h ω/8)(q 0/r 0)2.We can justify a two mode expansion of the condensate field by assuming the potential parameters are chosen so that the two lowest single particle energy eigenstates are below the barrier,with41019Bose-Einstein Condensation the next highest energy eigenstate separated from the ground state doublet by a large gap.We will further assume that the interaction term is sufficiently weak that, near zero temperature,the condensate wave functions are well approximated by the single particle wave functions.The potential may be expanded around the two stablefixed points to quadratic orderV(r)=˜V(2)(r−r j)+...(19.38) where j=1,2and˜V(2)(r)=4bq2|r|2(19.39) We can now use as the local mode functions the single particle wave functions for harmonic oscillators ground states,with energy E0,localised in each well,u j(r)=−(−1)j(2πr20)3/4exp−14((x−q0)2+y2+z2)/r20(19.40)These states are almost orthogonal,with the deviation from orthogonality given by the overlap under the barrier,d3r u∗j(r)u k(r)=δj,k+(1−δj,k)ε(19.41) withε=e−12q20/r20.The localised states in(19.40)may be used to approximate the single particle energy(and parity)eigenstates asu±≈1√2[u1(r)±u2(r)](19.42)corresponding to the energy eigenvalues E±=E0±R withR=d3r u∗1(r)[V(r)−˜V(r−r1)]u2(r)(19.43)A localised state is thus an even or odd superposition of the two lowest energy eigenstates.Under time evolution the relative phase of the superposition can change sign after a time T=2π/Ω,the tunneling time,where the tunneling frequency is given byΩ=2R¯h=38ω0q20r2e−q20/2r20(19.44)We now make the two-mode approximation by expanding thefield operator asˆψ(r,t)=c1(t)u1(r)+c2(t)u2(r)(19.45) where。

a r X i v :c o n d -m a t /9906144v211J un1999Bose-Einstein condensates with vortices in rotating trapsY.Castin 1and R.Dum 1,21Laboratoire Kastler Brossel ∗,´Ecole normale sup´e rieure,24rue Lhomond,F-75231Paris Cedex 05,France2Institut d’optique,BP 147,F-91403Orsay Cedex,France (16March 1999)We investigate minimal energy solutions with vortices for an interacting Bose-Einstein condensate in a rotating trap.The atoms are strongly confined along the axis of rotation z ,leading to an effective 2D situation in the x −y plane.We first use a simple numerical algorithm converging to local minima of energy.Inspired by the numerical results we present a variational Ansatz in the regime where the interaction energy per particle is stronger than the quantum of vibration in the harmonic trap in the x −y plane,the so-called Thomas-Fermi regime.This Ansatz allows an easy calculation of the energy of the vortices as function of the rotation frequency of the trap;it gives a physical understanding of the stabilisation of vortices by rotation of the trap and of the spatial arrangement of vortex cores.We also present analytical results concerning the possibility of detecting vortices by a time-of-flight measurement or by interference effects.In the final section we give numerical results for a 3D configuration.I.INTRODUCTION After the achievement of Bose-Einstein condensates in trapped atomic gases [1]many properties of these systems have been studied experimentally and theoretically [2].However a striking feature of superfluid helium,quantized vortices [3],[4],has not yet been observed in trapped atomic gases.There is an abundant literature on vortices in helium II,an overview is given in [4].The atomic gases have interesting properties which justify efforts to generate vortices in these systems:the core size of the vortices is adjustable,as in contrast to helium the strength of the interaction can be adjusted through the density;the number of vortices in atomic gases can be in principle well controlled;for a small number of particles in the gas metastability of the vortices can be studied,that is one can watch spontaneous transitions between configurations with different number of vortices.Several ways to create vortices in atomic gases have been suggested.A method inspired from liquid helium consists in rotating the trap confining the atoms [5];at a large enough rotation frequency it becomes energetically favorable at low temperatures to produce vortices;two different paths could be in principle followed:(1)producing first a condensate then rotating the trap,or (2)cooling the gas directly in a rotating trap.It has been recently proposed in [6]to use quantum topological effects to obtain a vortex.Other methods that do not rely on thermal equilibrium have been suggested [7],[8].Here we study theoretically the minimal energy configurations of vortices in a rotating trap [9].The model is defined in section II;in sections III to VI we assume a strong confinement of the atoms along the rotation axis z so that we face an effective 2D problem in the transverse plane x −y .We present numerical results for solutions with vortices that are local minima of the Gross-Pitaevskii energy functional (section III).These solutions contain only vortices with a charge ±1,the vortices with a charge larger than or equal to 2are thermodynamically unstable (section IV).We discuss possibilities to get experimental evidence of vortices in atomic gases in section V.Finally,we concentrate on the regime where the interaction energy is much larger than the trap frequenciesωx,y ,the so-called Thomas-Fermi limit [2].This is complementary to the work of [10].We obtain inthis “strong interacting”regime analytical predictions based on a variational Ansatz that reproducesatisfactorily the numerical results (section VI).In section VII we present results for vortices in 3D,that is in a trap with a weak confinement along the rotation axis.II.MODEL CONSIDERED IN THIS PAPERThe atoms are trapped in a potential rotating at angular velocity Ω.In the laboratory frame theHamiltonian of the gas is therefore time dependent.To eliminate this time dependence we introducea rotating frame at the angular velocity Ωso that the trapping potential becomes time independent;this change of frame is achieved by the single-atom unitary transform:U(t)=e i Ω· Lt/¯h(1) where L is the angular momentum operator of a single atom.As the unitary transform is timedependent the Hamiltonian in the rotating frame contains an extra inertial term,given for eachatom byi¯h U†(t)dφ|φ +1φ|φ 2.(3)In this energy functional H0contains the kinetic energy and the trapping potential energy of theparticles:H0=−¯h22mω2αr2α.(5)Furthermore in all but in section VII we will assume that the trapping potential is much strongeralong the z axis than along the x,y axis,with an oscillation frequency much larger than the typicalinteraction energy Ng3D|φ|2per particle.This situation,although not realized experimentally yet,is not out of reach,in particular when one uses optical traps rather than magnetic traps[11].Inthis strong confining regime the motion of the particles along z is frozen in the ground state of thestrong harmonic potential:φ(x,y,z)≃ψ(x,y) mωz2¯hωz:E[ψ,ψ∗]= d2 rψ∗( r)[H⊥−ΩL z]ψ( r)2Ng|ψ|42m ∆x,y+12π¯h 1/2.(9)Most of the results of the paper are dealing with the2D energy functional;a numerical result for a local minimum of the full3D energy functional will be given in the section VII.We concentrate on the so-called Thomas-Fermi regime,where the interaction energy per particle is much larger than ¯hωx,y.The opposite regime has already been studied in[10].III.LOCAL MINIMA OF ENERGY WITH VORTICES In this section we briefly discuss the general problem of minimizing energy functionals of the type Eq.(7).We present the numerical algorithm that we have used and we give numerical results for the2D problem.A.A numerical algorithm tofind local minimaThe algorithm in our numerical calculations is commonly used in the literature to minize energy functionals E[ψ,ψ∗]of the form Eq.(7).The intuitive idea is to start from a randomψand move it opposite to the local gradient of E[ψ,ψ∗]that is along the local downhill slope of the energy. Numerically this is implemented by an evolution ofψparametrized by afictitious timeτ:−dδψ∗[ψ,ψ∗].(10)Assuming aψnormalized to unity we get the following equation of motion forψ:−ddτE[ψ,ψ∗]=−2 d2 r δE2mΩ2r2cannot exceed the trapping potential.Therefore E has to convergeto afinite value forτ→∞.Asymptotically dE/dτ=0andψsatisfiesδEωx=ω/(1+ǫ)(14)ωy=ω(1+ǫ).(15) In Fig.1we show different local minima configurations obtained forǫ=0.3and a rotation frequencyΩ=0.2ω;each configuration has been obtained for different random initialψ’s.The holes observedin the spatial density correspond to the vortex cores.We have always found that the phase ofψchanges by2πaround a vortex core;we have not found vortices with a charge±q,where the integerq is strictly larger than one;this fact will be explained in the next section.Furthermore the senseof circulation is the same for all vortices.To quantify the effect of the non-axisymmetry of the trap we have plotted in Fig.2the dependenceof energy of different vortex configurations onωx/ωy for afixedω;we measure the energies fromE iso,the energy of the zero-vortex solution in the axisymmetric caseǫ=0.The zero-vortex solutionexhibits a significant variation of energy withǫ;for a non-zeroǫthe wavefunctionψdevelops a phase proportional toΩfor weakΩ’s,which accounts for the energy change as explained in section VI B.The solutions with vortices experience quasi the same energy shift as function ofǫ.As only theenergy difference between the various local minima matters we will from now on only consider the axisymmetric caseǫ=0to identify the solution with the absolute minimal energy.Note that the solutionsψwith several vortices obtained in the limiting caseǫ=0are not eigen-vectors of L z;this reflects a general property of non-linear equations such as the Gross-Pitaevskiiequations to have symmetry broken solutions;it is explained in[10]how to reconcile this symmetrybreaking with the fact that eigenvectors of the full N-atom Hamiltonian are of well defined angular momentum.IV.STABILITY PROPERTIES OF VORTICESIn this section we recall that a(normalized)wavefunctionψsuch that E[ψ,ψ∗]has a local min-imum inψ,describes a condensate having all the desired properties of stability,that is dynamicaland thermodynamical stability.We then show that a vortex centered at r= 0with an angular mo-mentum strictly larger than¯h is not a local minimum of energy and is therefore thermodynamicallyunstable.A.Stability properties of local minimaLet us express the fact thatψcorresponds to a local minimum of the energy.Afirst condition isthat the energy functional is stationary forψ,that isψsolves the Gross-Pitaevskii equation Eq.(13).To get the second condition,we consider a small variation ofψ,ψ→ψ+δψ(16) preserving the normalization of the condensate wavefunction to unity:||ψ+δψ||2−||ψ||2=0= ψ|δψ + δψ|ψ + δψ|δψ .(17) We expand the energy functional E[ψ,ψ∗]in powers ofδψ,neglecting terms of orderδψ3or higher.Using Eq.(17)and Eq.(13)wefind that terms linear inδψvanish so that1δE=1.Dynamical stabilityConsiderfirst the problem of so-called“dynamical stability”:to be a physically acceptable con-densate wavefunction,ψhas to be a stable solution of the time dependent Gross-Pitaevskii equationi¯h∂tψ=H GPψ(21) otherwise any small perturbation ofψ,e.g.the effect of quantumfluctuations or experimental noise,may lead to an evolution ofψfar from its initial value.To determine the evolution of a smalldeviationδψas in Eq.(16)we linearize Eq.(21):i¯h∂t |δψ |δψ∗ =L |δψ |δψ∗ (22) where the operator L is related to L c byL c= 100−1 L.(23)Asψis time independent,so is L and dynamical stability is equivalent to the requirement that theeigenvalues of L have all a negative or vanishing imaginary part.As we now show the positivity ofL c leads to a purely real spectrum for L.Consider an eigenvector(u,v)of L with the eigenvalueε.Contracting Eq.(23)between the ket(|u ,|v )and the bra( u|, v|)we getε[ u|u − v|v ]=( u|, v|)L c |u |v .(24)Note that the matrix element of L c is real positive as L c is a positive hermitian operator.We nowface two possible cases for the real quantity u|u − v|v :• u|u − v|v =0.In this case L c has a vanishing expectation value in(|u ,|v );as L c is positive(|u ,|v )has to be an eigenvector of L c with the eigenvalue zero;from Eq.(23)and the fact that 100−1 is invertible wefind that(|u ,|v ) is also an eigenvalue of L with the eigenvalue0,so thatε=0is a real number.• u|u − v|v >0:we getεas the ratio of two real numbers,so thatεis real.2.Thermodynamical stabilityA second criterion of stability is the so-called“thermodynamical”stability.For zero temperature,this condition can be formulated in the Bogoliubov approach[2],where the particles out of thecondensate,which always exist because of the interactions,are described by a set of uncoupledharmonic oscillators with frequenciesεsign[ u|u − v|v ]/¯h,where(u,v)is an eigenvector of L withthe eigenvalueε.In order for a thermal equilibrium to exist for these oscillators,their frequenciesshould be strictly positive,which is the case here in virtue of Eq.(24)[13].If a mode with a negativefrequency were present thermalization by collisions would transfer particles from the condensateψto this mode,leading to a possible evolution of the system far from the initial stateψ[14].What happens for solutionsψof the Gross-Pitaevskii equations that are not local minima of energy?The operator L c has at least an eigenvector with a strictly negative eigenvalue.In thiscase one cannot have thermodynamical stability,that is one cannot haveε[ u|u − v|v ]>0forall modes[13].From the non-positivity of L c one cannot however distinguish between a simplethermodynamically instability or a more dramatic dynamical instability.B.Why not a vortex of angular momentum larger than¯h?For simplicity we consider only a single vortex in the center of an axi-symmetric trap.We show that vortices with a change of phase of2qπare not local minima of energy,that is are(at leastthermodynamically)unstable.We have found numerically a solution of the Gross-Pitaevskii equationEq.(13)by an evolution in complex time,starting from a wavefunctionψwith an angular momentumq¯h along z,as already done in[15];our solution of the Gross-Pitaevskii equation with imposedsymmetry is a local mimimum of energy in the subspace of functions with angular momentum q¯halong z,but not necessarily a local minimum in the whole functional space,as we will see for|q|>1.In the Thomas-Fermi regimeµ≫¯hωwefind that the solutions can be well reproduced bya variational Ansatz of the formψ(x,y)=e iqθ[tanhκq r]|q| ˜µ−1Ng 1/2(25) whereθis the polar angle in the x−y plane and where˜µ,the chemical potential in the lab frame˜µ=µ+q¯hΩ(26) does not depend onΩ.In this Ansatz the vortex core is accounted for by tanh|q|,a function thatvanishes as r|q|in zero as it should,and the condensate density outside the core coincides withthe Thomas-Fermi approximation commonly used for the zero-vortex solution[2].We calculate themean energy Eq.(7)of the variational Ansatz and we minimize it with respect to the variationalparameterκq;we getκq= ˜µmq2 +∞0du u tanh2|q|(u)−1 2(28) is a number(c1=0.7687,c2=0.5349,...).In order for the vortex of charge q to be a local minimum of energy,the operator L c of Eq.(19)has to be positive.This implies that the operator on thefirst line,first column of L c,the so-calledHartree-Fock Hamiltonian,be positive:H HF=H⊥+2Ng|ψ|2−˜µ+q¯hΩ−ΩL z≥0.(29) To show that this is not the case it is sufficient tofind a wavefunction f(x,y)leading to a negative expectation value for H HF.As the potential appearing in H HF has a dip at r=0we have taken fof a form localized around r=0:1f(x,y)=¯h2 1/2r (30) whereγis adjusted to minimize the expectation value.For e.g.q=2we takeγ=1leading tof|H HF|fsection the trap is axi-symmetry with a time dependent frequencyω(t).We consider the evolutionin the laboratory frame,as the detection is performed in this frame:i¯h∂tψlab= −¯h22mω2(t)r2+Ng|ψlab|2 ψlab.(32)As shown in[19,20]the effect of the time dependence ofω(t)can be absorbed by a scaling and gaugetransform of the wavefunction:1ψlab( r,t)=−ω2(t)λ(34)λ3with initial conditionsλ(0)=1,˙λ(0)=0;if the trap in the x−y plane is abruptly switched offatt=0+the scaling parameter is given byλ(t)==dτ(36)λ2(t)wefind that˜ψsolves the same equation asψlab with a constant trap frequency equal toω(0):i¯h∂τ˜ψ= −¯h22mω2(0)r2+Ng|˜ψ|2 ˜ψ.(37)Asψlab rotates in the trap at the frequencyΩin the lab frame,so does˜ψin terms of the renormalizedtimeτ.In the limit of t→∞,τtends to afinite valueτmax,so that˜ψis rotated by afinite angleduring the ballistic expansion:Ωτmax=Ω ∞0dt2ΩVI.INTUITIVE V ARIATIONAL CALCULATIONTo get a better understanding of the numerical results we now proceed to an intuitive Ansatzfor the wavefunction with several vortices.It coincides very well with the numerical results andallows an easy construction of the minimal energy configurations with vortices.It gives a physical understanding of the stability conditions and of the structure of the solutions:a set of n vortices isequivalent to a gas of interacting particles in presence of an external potential adjusted by the rota-tion frequency of the trap.We restrict to the case of an axi-symmetric trap,a good approximationfor weak(<10%)non-axisymmetries(see section III B).A.Ansatz for the densityTo construct the Ansatz we splitψin a modulus and a phase:ψ(x,y)=|ψ|e iS.(40) In the Thomas-Fermi regime,the modulus in presence of n vortices appears as a slowly varyingenvelope given by the Thomas-Fermi approximation used in the0-vortex case:ψslow= µ−1Ng 1/2(41)with narrow holes digged by the vortices with charge q=±1,represented by tanh functions ofadjustable widths and with zeros at adjustable positions:|ψ|=ψslow×nk=1tanh[κk| r− αk R|].(42)The positions of the vortex cores αk are expressed in units of the Thomas-Fermi radius R of the condensate:R= mω2.(43)From section IV B we expect as typical values for the inverse width of the vortex coresκk≃(mµ/¯h2)1/2.The chemical potential is not an independent variable but is expressed as a functionof the other parameters from the normalization condition ψ|ψ =1;neglecting overlap integralsbetween the holes we getµ=µ0 1+2n k=1(1−α2k)ln2(κR)4) (44)where1/(κR)4∼(¯hω/µ)4≪1and whereµ0is the Thomas-Fermi approximation for the condensatechemical potential without vortices:µ0= mω2Ngcentered on the vortex core and S 0is the single-valued part of the phase.The function S 0can in principle be determined from the modulus of ψfrom the continuity equation:div[|ψ|2 v ]=0.(47)The local velocity field v is related to the phase S byv =¯h ¯h [x∂y −y∂x ]|ψ|2=0.(49)This can be turned into an equation for the single-valued part S 0of the phase;because the density |ψ|2in a trap vanishes at the border of the condensate S 0is uniquely determined (up to a constant)by the resulting equation (see Appendix);this is to be contrasted to the case of superfluid helium in a container,where the flux,not the density,vanishes at the border,which requires a boundary condition on the gradient of the phase.Eq.(49)can be solved for a non-axisymmetric trap in the absence of vortices.The solution is given byS (x,y )=−m Ωω2x +ω2yxy (50)which leads to a change in the energy per particleδE =−1(ω2x +ω2y )ω2x ω2y(51)where µT F is the Thomas-Fermi approximation for the chemical potential for Ω=0,µT F =(mωx ωy Ng/π)1/2[23].As can be seen in Fig.2this prediction is in good agreement with our numerical results.In presence of vortices the equation for S is more difficult to solve analytically.From now on we consider the case of an axi-symmetric trap,as the energy ordering of the vortices solutions is not affected for weak (<10%)non-axisymmetries (see section III B).For a single vortex at the center of the trap one can see that S 0=0solves Eq.(49).From the spatial dependence of the phase obtained numerically (section III B)for a displaced vortex or several vortices we have identified the following heuristic Ansatz,obtained in setting ωx =ωy =ωin Eq.(50):S 0(x,y )≡0(52)that we will use in the remaining part of the section.C.Further approximations for the mean energyIn the calculation of the mean energy,we make some further approximations in the spirit of the Ansatz Eq.(42).The reader not interested by these more technical considerations can proceed to the next subsection.The kinetic energy involves an integral of the gradient squared of the wavefunction:| ∇ψ|2=|ψ|2 ( ∇ln |ψ|)2+( ∇S )2 .(53)For the gradient of the modulus of ψwe neglect the variation of the slow envelope ψslow :∇ln |ψ|≃nk =1κktanh ′of ψinvolves holes with a density varying as 1−tanh 2=sech 2.In the following we keep the sech 2for the vortex k only if it is multiplied by ( ∇θk )2,a quantity diverging in the center of the core;the other terms lead toconverging integrals smaller by a factor (µ/¯h ω)2,which is the inverse surface of a vortex core ( d 3 r |ψslow |2sech 2κr ∝1/(κR )2).This finally leads toE kin ≃¯h 22mω2r 2+13µ0+nk =1W ( αk ,κk )+1µ012ln(1−α2)−q ¯h Ω (1−α2)2 +µ0(κR )2(60)where C =0.495063.The lines inEq.(60)correspond successively to E kin ,E rot and E pot .This can be seen as an effective potential for the vortices.One can check that the part of W independent of Ωexpells the vortex core from the trap center,whereas the part proportional to Ωprovides a confinement of the vortex core (see the following subsection).The vortex interaction potential is given by12m q αq β d 2 r |ψslow |2 ∇θ αR · ∇θ βR .(61)This interaction term is equivalent to the one found in the homogeneous case and describes a repulsive interaction for vortices turning in the same direction (q αq β>0)and is attractive for vortices with opposite charges [9].An attractive interaction will lead to the coalescence and consequently annihilation of vortices with opposite charges.Therefore we find in stationary systems always vortices with equal charges.As the interaction potential V ( α, β)does not depend on the parameters κwe can optimize sepa-rately the self-energy part with respect to κand find(κR)2=ξ2(1−α2) µ03(4ln2−1) 1/2≃1.08707.By rewriting the above equation as¯h2κ22ξ2 µ−1µ0 13+lnνµ0¯hω2(1−α2) (64) whereν=0.49312.E.Case of a single vortex:critical frequenciesIn Fig.4we have plotted the self-energy of a vortex as a function of the displacement of the corefrom the trap center,for different values of the rotation frequencyΩ.The analytical predictioncoincides very well with the numerical value[24].ForΩ=0the position of the vortex at the trap center gives an energy maximum.ForΩ>0therotation of the trap provides an effective confinement of the vortex core at the center of the trap forpositive charges q(see the term proportional toΩin Eq.(64));from now one we therefore take allthe charges q k to be equal to+1.For a large enoughΩwe reach a situation where a vortex at thetrap center corresponds to a local energy minimum,by further increasingΩthe vortex state at thetrap center becomes a global minimum with energy less than the condensate without vortex.The above suggests that we have to distinguish two critical rotation frequencies:Thefirst onedefines the frequencyΩstab above which the vortex is a local minimum of energy.Above the frequencyΩc the single vortex solution has an energy lower than the condensate without vortex.We calculateΩstab from the condition d2W/dα2=0atα=0andΩc from the condition W=0atα=0:Ωc=¯hω2¯hω (65)Ωstab=¯hω2¯hω (66)where C′=e(2ln2+1)/3+1/2ν≃1.8011.As we are in the regimeµ0≫¯hωΩc is approximately twice Ωstab[25].Our prediction forΩc scale as(logµ0)/µ0as in[15],with a coefficient C′leading to better agreement with the numerics.F.Case of several vorticesBy integrating Eq.(61)we get an explicit form for the vortex interaction potential for vortices with equal charges:V( α, β)=(¯hω)2(1− α· β)+1| α− β|4 (67)At short distances between the two vortex cores the logarithmic term in the above expression dominates,leading to a repulsive potential∼−2(1− α· β)log| α− β|(¯hω)2/µ0.In Fig.5we plot the interaction energy between a vortex at the center of the trap and one of equal charge displaced by αR;the interaction is purely repulsive.A conclusion which essentially holds as well for arbitrary vortex positions.In Fig.6we show the total(interaction+self-energy)for two vortices symmetrically displaced from the trap center,as function of the displacement;the analytical prediction coincides again very well with the numerical results[24].To obtain the equilibrium distance between the two vortex cores one minimizes the total energy overαin Fig.6.To get the minimal energy configurations as function of the rotation frequency of the trap,we minimize our analytical prediction for the energy over the positions of the n=1,2,...vortex cores.The result is shown in Fig.7.Each curve corresponds to afixed value of n;it starts atΩ=Ωstab(n)(forΩ<Ωstab(n)there is no local minima of energy with n vortices);it becomes the global energyminimum forΩ=Ωc(n).We have plotted these two critical frequencies as function of n in Fig.8.We have also given numerical results(circles)in Fig.7.Even if there is good agreement between analytical and numerical results,we still need a numerical calculation to check the stability of thesolutions;our simple analytical Ansatz is indeed not sufficient to predict the destabilization of agiven vortex configuration at highΩ,a phenomenon studied with a numerical calculation of theBogoliubov spectrum for a single vortex in[26].For afixed value of the number of vortices n there may exist local minima of energy,in addition to the global minimum plotted in Fig.7,a situation known from superfluid helium[4].E.g.for n=6(see Fig.9)the global minimum of energy is given by a configuration with six vortex cores on acircle;there exists also a local minimum of energy with one vortex core at the center of the trap andfive vortex cores on a circle.The energy difference per particle between the two configurations isvery small,δE≃0.002¯hωfor the parameters of thefigure and probably beyond the accuracy of ourvariational Ansatz.For relatively large rotation frequenciesΩone canfind local minima of energyconfigurations with many vortices(see[4]for superfluid helium);we plot two configurations with18vortices in Fig.10,with an energy differenceδE=0.0034¯hω.In estimating the physical relevance of these energy differences one should keep in mind that NδE matters,rather thanδE,where N is the number of particles in the condensate: e.g.at afinite temperature T the ground energy configuration is statistically favored as compared to themetastable one when NδE≫k B T.VII.VORTICES IN A3D CONFIGURATIONWe have extended the numerical calculation to the case of a3D cigar-shaped trap,that is witha confinement weaker along the rotation axis than in the x−y plane.Even in this case rotationof the trap can stabilize the vortex.We show in Fig.11density cuts of a solution with5vortices;the vortex cores are almost straight lines in the considered Thomas-Fermi regime,except at vicinityof the borders of the condensate.As in section VI the core diameter is determined by the localchemical potential in the gas.This suggests that our2D Ansatz(section VI)can be generalized to3D situations,with αk and κk depending on z.VIII.CONCLUSION AND PERSPECTIVESWe have presented in this paper an efficient numerical algorithm and a heuristic variational Ansatz to determine the local minima energy configurations for a Bose-Einstein condensate stronglyconfined along z and subject to a rotating harmonic trap in the x−y plane.Our results can be used as afirst step towardsfinite temperature calculations.Interesting prob-lems are e.g.the critical temperature for the vortex formation and the Magnus forces induced bythe non-condensed particles on the vortex core[27].Acknowledgement:We acknowledge useful discussions with Sandro Stringari and Dan Rokhsar.We thank J.Dalibard for useful comments on the manuscript.We thank the ITP at Santa Barbarafor its hospitality and the NSF for support under grant No.PHY94-07194.This work was partiallysupported by the TMR Network“Coherent Matter Wave Interactions”,FMRX-CT96-0002.∗L.K.B.is an unit´e de recherche de l’Ecole Normale Sup´e rieure et de l’Universit´e Pierre et Marie Curie,associ´e e au CNRS.APPENDIX A:UNIQUENESS OF THE PHASE FROM THE CONTINUITY EQUATION IN A TRAPConsider two solutions S1and S2of the continuity equation:mΩdiv[|ψ|2 ∇S]=。

a r X i v :c o n d -m a t /0603590v 1 [c o n d -m a t .o t h e r ] 22 M a r 2006Adiabatic loading of a Bose-Einstein condensate in a 3D optical latticeT.Gericke,F.Gerbier,A.Widera,S.F¨o lling,O.Mandel,and I.BlochInstitut f¨u r Physik,Johannes Gutenberg-Universit¨a t,55099Mainz,Germany.(Dated:February 5,2008)We experimentally investigate the adiabatic loading of a Bose-Einstein condensate into an optical lattice potential.The generation of excitations during the ramp is detected by a corresponding decrease in the visibility of the interference pattern observed after free expansion of the cloud.We focus on the superfluid regime,where we show that the limiting time scale is related to the redistribution of atoms across the lattice by single-particle tunneling.PACS numbers:03.75.Lm,03.75.Hh,03.75.GgThe observation of the superfluid to Mott insulator (MI)transition [1]undergone by an ultracold Bose gas in an optical lattice has triggered a lot of experimen-tal and theoretical activities (see [2,3,4]).This sys-tem allows to experimentally produce strongly-correlated quantum systems in a well controlled environment,with applications ranging from the realization of novel quan-tum phases in multi-component systems (see,e.g.,[4]and references therein)to the implementation of collisional quantum gates [5,6,7].Most of these proposals rely on producing a system very close to its ground state.However,in experiments so far,the successful production of an ultracold gas in the optical lattice relies on adiabatic transfer.The conden-sate is first produced and evaporatively cooled in order to minimize the thermal fraction.The almost pure conden-sate is subsequently transferred into the lattice potential by ramping up the laser intensities as slow as possible in order to approach the adiabatic limit.For too fast a ramp,excitations are generated in the system,which eventually results in heating after the cloud has equili-brated at the final lattice depth.It is important in this respect to note the existence of two energy scales in this problem,related to the single-particle band structure on the one hand or to the many-body physics within the lowest Bloch band on the other hand.Adiabaticity with respect to the band structure is associated with the absence of interband transitions.The characteristic time scales are on the order of the inverse recoil frequency,typically hundreds of microsec-onds.Experimentally,adiabaticity with respect to the band structure is easily ensured,and can be checked by detecting atoms in the higher Bloch bands [8,9].Adia-baticity with respect to the many-body dynamics of the system involves considerably longer time scales (on the order of tens or even hundreds of milliseconds).Theoret-ical studies of the loading dynamics have been reported in [10,11,12,13,14,15].It is clear that non-adiabatic effects are more pronounced in the superfluid phase.The insulator phase is indeed expected to be quite insensitive to such effects,due to the presence of an energy gap.In this paper,we focus on the superfluid phase.Our goal is to to clarify experimentally how slowly the loading has toproceed to minimize unwanted excitations and heating.To this aim,we make use of long range phase prop-erties characteristic to a BEC.A key observable for ul-tracold Bose gases in optical lattices is the interference pattern observed after releasing the gas from the lat-tice and letting it expand for a certain time of flight [1,8,16,17,18,19].The contrast of this interference pattern is close to unity when most atoms belong to the condensate,but diminishes with the condensed fraction as the cloud temperature increases.Hence,the visibil-ity of this interference pattern can be used to investigate the dynamical loading of a condensate into the optical lattice.We focus here on a specific lattice depth in the superfluid regime.We find a characteristic time scale of ∼100ms above which the visibility of the interference pattern appears to be stationary.We show how it re-lates to the redistribution of atoms in the lattice through single-particle tunneling.In our experiment,a 87Rb Bose-Einstein condensate is loaded into an optical lattice created by three or-thogonal pairs of counter-propagating laser beams (see [1]for more details).The superposition of the lattice beams,derived from a common source at a wavelength λL =850nm,results in a simple cubic periodic poten-tial with a lattice spacing d =λL /2=425nm.The lattice depth V 0is controlled by the laser intensities,and is measured here in units of the single-photon recoil en-ergy,E r =h 2/2mλ2L ≈h ×3.2kHz.The optical lattice is ramped up in a time τramp ,using a smooth waveform that minimizes sudden changes at both ends of the ramp.The ramp form is calculated numerically.The program imposes that the lattice depth is initially zero and reaches its final value after a time τramp .In between (for times 0≤t ≤τramp ),it tries to match the functional formV 0(t )=V maxτramp,(1)with α=20,by a piecewise linear approximation.The function (1)has been proposed in [12]and is shown in Fig.1a.After this ramp,the cloud is held in the lattice potential for a variable hold time t hold (see Fig.1a),dur-ing which the system can re-thermalize.After switchingVmaxRamp timeHold timeL a t t i c e i n t e n s i t y0Lattice depth V max (E R )V i s i b i l i t y V 10.5051015202530FIG.1:(a )Sketch of the time profile used to ramp up the lattice depth to its maximum value V max .(b )Evolution of the visibility of the interference pattern as the lattice depth is increased.The set of data shown corresponds to ∼3×105atoms (grey circles).offthe optical and magnetic potentials simultaneously and allowing for typically t =10−22ms of free ex-pansion,standard absorption imaging of the atom cloud yields a two-dimensional map of the density distribution n (integrated along the probe line of sight).To extract quantitative information from time-of-flight pictures,we use the usual definition of the visibility of interference fringes,V =n max −n minfected by the ramping procedure,wefix the ramp time τramp and record how the interference pattern evolves as a function of hold timeτhold.Examples of such measure-ments are shown in Fig.2a-d.For the slowest ramp shown,τramp=160ms,the visi-bility decreases with a time constant∼500ms.In fact, a very similar behavior is observed as soon as the ramp time exceedsτramp>100ms.Since this behavior is es-sentially independent of the ramp speed,it points to the presence of heating mechanisms which significantly de-grade the visibility on a time scale of several hundred ms. The source of heating could be technical,due for instance to intensity or pointingfluctuations of the lattice beams, or intrinsic processes.An unavoidable process is for in-stance atomic spontaneous emission following excitations by one of the lattice beams.Here we attempt a crude es-timate of the effect of spontaneous emission on visibility as follows.The heating rateΓheat∼Γsp×(h2/2mλ20)is given by the rateΓsp at which such events happen due to all lattice beams,times the recoil energy h2/2mλ20, whereλ0≈780nm is the resonant wavelength of the D2 transition.To estimate the time scale T V over which the visibility vanishes,we compute the time over which the energy gain per particle,Γheat T V,is on the order of the critical temperature T c times Boltzmann’s constant k B. In a lattice potential with approximately one atom per site,we have k B T c∼zJ,where J is the tunneling ma-trix element and z=6the number of nearest neighbors in a three dimensional cubic lattice.This yields afinal estimatezJT V∼Γ−1sp4lattice,three energy scales appear:(i)the tunneling ma-trix element J defining the rate of hopping from site to site,(ii)the on-site interaction energy U and,(iii)the en-ergy associated to the“external”confinement potential usually present on top of the lattice.This potential V ext results from the combination of the magnetic trapping potential in which the condensate is initially produced, and of an additional confinement due to the Gaussian shape of the lasers producing the optical lattice.In prac-tice,V ext is nearly harmonic,with a trapping frequency Ω=ωext≈J2 .(5) For a given ramp,we require A≪1to ensure an adia-baticloading of the cloud into the lattice.In the inset of Fig.5,we show the quantity |˙J|/J2calculated for τramp=50ms.We have calculated this curve for afi-nal lattice depth of10E R using the lattice ramp given in Eq.(1),and the analytical estimate[2],J8V0/E r).(6)The sharp decrease for short times in the inset of Fig.5 follows from the inadequacy of the tight-binding approx-imation under which Eq.(6)is derived.We ignore this feature,and calculate A from the peak value occurring near t≈τramp/2,where the rate of change of the lattice depth is highest.We have repeated the calculation for several ramp times(see Fig.5).Wefind that the critical A=1corresponds to a ramp timeτramp≈80ms,close to the experimentalfindings.This suggests that for our experimental parameters,the loading is indeed limited by single-particle tunneling.In conclusion,we have studied how the visibility of the interference pattern was affected by the speed at which the lattice was ramped up.A time scale of∼100ms was found for adiabatic loading in the optical lattice. In this paper,we focused on the dynamics properties in the superfluid regime.Even more interesting is the dynamical evolution of the system as the superfluid-to-Mott-insulator transition is crossed.An important andAdiabaticityparameterRamp time(ms)FIG.5:Adiabaticity parameter(see text)plotted versus ramp time.In the calculation,we have used the actual ramp form as generated in the experiment to describe the lattice depth increase.In the inset,we show how the adiabaticity parame-ter changes in time as the lattice depth is ramped up.A ramp time ofτramp=50ms has been used for this plot.still open question is in particular how reversible this transition is.Experiments[1,16,17?]found that one could ramp up the lattice intensity and reach the regime where phase coherence is lost,then ramp down the lattice and regain it back.To what extent the ini-tial phase coherent state can be recovered,and what are the limiting mechanisms has however not been studied. Also,the recent availability of virtually exact methods for one-dimensional systems[12]could allow for a pre-cise comparison with the experimental data,in a strongly non-equilibrium regime where theory is still in progres-sion.Finally,new dynamical effects are predicted,such as oscillation of the order parameter and vortices-driven relaxation analog to the Kibble-Zurek mechanism[21]. Our work is supported by the Deutsche Forschungsge-meinschaft(SPP1116),AFOSR and the European Union under a Marie-Curie Excellence grant(OLAQUI).FG ac-knowledges support from a Marie-Curie Fellowship of the European Union.[1]M.Greiner,O.Mandel,T.Esslinger,T.W.H¨a nsch,andI.Bloch,Nature415,39(2002).[2]W.Zwerger,J.Opt.B:Quantum Semiclass.Opt.5,S9(2003).[3]I.Bloch,Nature Physics1,23(2005).[4]D.Jaksch and P.Zoller,Annals of physics315,52(2005).[5]D.Jaksch,H.J.Briegel,J.I.Cirac,C.W.Gardiner,andP.Zoller,Phys.Rev.Lett.82,1975(1999).[6]O.Mandel,M.Greiner, A.Widera,T.Rom,T.W.H¨a nsch,and I.Bloch,Phys.Rev.Lett.91,010407(2003).[7]O.Mandel,M.Greiner, A.Widera,T.Rom,T.W.H¨a nsch,and I.Bloch,Nature425,937(2003).[8]M.Greiner,I.Bloch,O.Mandel,T.W.H¨a nsch,and5T.Esslinger,Phys.Rev.Lett.87,160405(2001).[9]J.Hecker-Denschlag,J. E.Simsarian,H.Haeffner,C.McKenzie,A.Browaeys,D.Cho,K.Helmerson,S.L.Rolston,and W.D.Phillips,J.Phys.B:At.Mol.Opt.Phys.35,3095(2002).[10]S.E.Sklarz and D.J.Tannor,Phys.Rev.A66,053619(2002).[11]S.E.Sklarz,I.Friedler,,D.J.Tannor,Y.B.Band,andC.J.Williams,Phys.Rev.A66,053620(2002).[12]S.R.Clark and D.Jaksch,Phys.Rev.A70,043612(2004).[13]S.B.McKagan,D.L.Feder,and W.P.Reinhardt,cond-mat/0509666(2005).[14]J.Zakrewski,Phys.Rev.A72,043601(2005).[15]L.Isella and J.Ruostekoski,Phys.Rev.A72,011601(2005).[16]C.Orzel,A.K.Tuchman,M.L.Fenselau,M.Yasuda,and M.K.Kasevich,Science291,2386(2001).[17]T.St¨o ferle,H.Moritz, C.Schori,M.K¨o hl,andT.Esslinger,Phys.Rev.Lett.92,130403(2004). [18]F.Gerbier,A.Widera,S.F¨o lling,O.Mandel,T.Gericke,and I.Bloch,Phys.Rev.Lett.95,050404(2005). [19]F.Gerbier,A.Widera,S.F¨o lling,O.Mandel,T.Gericke,and I.Bloch,Phys.Rev.A72,053606(2005).[20]M.Greiner,Phd thesis,Ludwig Maximilians Universit¨a tM¨u nchen(2003).[21]E.Altman and A.Auerbach,Phys.Rev.Lett89,250404(2002).。

Bose-Einstein condensationShihao LiBJTU ID#:13276013;UW ID#:20548261School of Science,Beijing Jiaotong University,Beijing,100044,ChinaJune1,20151What is BEC?To answer this question,it has to begin with the fermions and bosons.As is known,matters consist of atoms,atoms are made of protons,neutrons and electrons, and protons and neutrons are made of quarks.Also,there are photons and gluons that works for transferring interaction.All of these particles are microscopic particles and can be classified to two families,the fermion and the boson.A fermion is any particle characterized by Fermi–Dirac statistics.Particles with half-integer spin are fermions,including all quarks,leptons and electrons,as well as any composite particle made of an odd number of these,such as all baryons and many atoms and nuclei.As a consequence of the Pauli exclusion principle,two or more identical fermions cannot occupy the same quantum state at any given time.Differing from fermions,bosons obey Bose-Einstein statistics.Particles with integer spin are bosons,such as photons,gluons,W and Z bosons,the Higgs boson, and the still-theoretical graviton of quantum gravity.It also includes the composite particle made of even number of fermions,such as the nuclei with even number ofnucleons.An important characteristic of bosons is that their statistics do not restrict the number of them that occupy the same quantum state.For a single particle,when the temperature is at the absolute zero,0K,the particle is in the state of lowest energy,the ground state.Supposing that there are many particle,if they are fermions,there will be exactly one of them in the ground state;if they are bosons,most of them will be in the ground state,where these bosons share the same quantum states,and this state is called Bose-Einstein condensate (BEC).Bose–Einstein condensation(BEC)—the macroscopic groundstate accumulation of particles of a dilute gas with integer spin(bosons)at high density and low temperature very close to absolute zero.According to the knowledge of quantum mechanics,all microscopic particles have the wave-particle duality.For an atom in space,it can be expressed as well as a wave function.As is shown in the figure1.1,it tells the distribution but never exact position of atoms.Each distribution corresponds to the de Broglie wavelength of each atom.Lower the temperature is,lower the kinetic energy is,and longer the de Broglie wavelength is.p=mv=h/λ(Eq.1.1)When the distance of atoms is less than the de Broglie wavelength,the distribution of atoms are overlapped,like figure1.2.For the atoms of the same category,the overlapped distribution leads to a integral quantum state.If those atoms are bosons,each member will tend to a particular quantum state,and the whole atomsystem will become the BEC.In BEC,the physical property of all atoms is totally identical,and they are indistinguishable and like one independent atom.Figure1.1Wave functionsFigure1.2Overlapped wave functionWhat should be stressed is that the Bose–Einstein condensate is based on bosons, and BEC is a macroscopic quantum state.The first time people obtained BEC of gaseous rubidium atoms at170nK in lab was1995.Up to now,physicists have found the BEC of eight elements,most of which are alkali metals,calcium,and helium-4 atom.Always,the BEC of atom has some amazing properties which plays a vital role in the application of chip technology,precision measurement,and nano technology. What’s more,as a macroscopic quantum state,Bose–Einstein condensate gives a brand new research approach and field.2Bose and Einstein's papers were published in1924.Why does it take so long before it can be observed experimentally in atoms in1995?The condition of obtaining the BEC is daunting in1924.On the one hand,the temperature has to approach the absolute zero indefinitely;on the other hand,the aimed sample atoms should have relatively high density with few interactions but still keep in gaseous state.However,most categories of atom will easily tend to combine with others and form gaseous molecules or liquid.At first,people focused on the BEC of hydrogen atom,but failed to in the end. Fortunately,after the research,the alkali metal atoms with one electron in the outer shell and odd number of nuclei spin,which can be seen as bosons,were found suitable to obtain BEC in1980s.This is the first reason why it takes so long before BEC can be observed.Then,here’s a problem of cooling atom.Cooling atom make the kinetic energy of atom less.The breakthrough appeared in1960s when the laser was invented.In1975, the idea of laser cooling was advanced by Hänsch and Shallow.Here’s a chart of the development of laser cooling:Year Technique Limit Temperature Contributors 1980～Laser cooling of the atomic beam～mK Phillips,etc. 19853-D Laser cooling～240μK S.Chu,etc. 1989Sisyphus cooling～0.1~1μK Dalibard,etc. 1995Evaporative cooling～100nK S.Chu,etc. 1995The first realization of BEC～20nK JILA group Until1995,people didn’t have the cooling technique which was not perfect enough,so that’s the other answer.By the way,the Nobel Prize in Physics1997wasawarded to Stephen Chu,Claude Cohen－Tannoudji,and William D.Phillips for the contribution on laser cooling and trapping of atoms.3Anything you can add to the BEC phenomena(recent developments,etc.)from your own Reading.Bose–Einstein condensation of photons in an optical microcavity BEC is the state of bosons at extremely low temperature.According to the traditional view,photon does not have static mass,which means lower the temperature is,less the number of photons will be.It's very difficult for scientists to get Bose Einstein condensation of photons.Several German scientists said they obtained the BEC of photon successfully in the journal Nature published on November24th,2011.Their experiment confines photons in a curved-mirror optical microresonator filled with a dye solution,in which photons are repeatedly absorbed and re-emitted by the dye molecules.Those photons could‘heat’the dye molecules and be gradually cooled.The small distance of3.5 optical wavelengths between the mirrors causes a large frequency spacing between adjacent longitudinal modes.By pumping the dye with an external laser we add to a reservoir of electronic excitations that exchanges particles with the photon gas,in the sense of a grand-canonical ensemble.The pumping is maintained throughout the measurement to compensate for losses due to coupling into unconfined optical modes, finite quantum efficiency and mirror losses until they reach a steady state and become a super photons.(Klaers,J.,Schmitt,J.,Vewinger, F.,&Weitz,M.(2010).Bose-einstein condensation of photons in an optical microcavity.Nature,468(7323), 545-548.)With the BEC of photons,a brand new light source is created,which gives a possible to generate laser with extremely short wavelength,such as UV laser and X-ray laser.What’s more,it shows the future of powerful computer chip.Figure3.1Scheme of the experimental setup.4ConclusionA Bose-Einstein condensation(BEC)is a state of matter of a dilute gas of bosons cooled to temperatures very close to absolute zero.Under such conditions,a large fraction of bosons occupy the lowest quantum state,at which point macroscopic quantum phenomena become apparent.This state was first predicted,generally,in1924-25by Satyendra Nath Bose and Albert Einstein.And after70years,the Nobel Prize in Physics2001was awarded jointly to Eric A.Cornell,Wolfgang Ketterle and Carl E.Wieman"for theachievement of Bose-Einstein condensation in dilute gases of alkali atoms,and for early fundamental studies of the properties of the condensates".This achievement is not only related to the BEC theory but also the revolution of atom-cooling technique.5References[1]Pethick,C.,&Smith,H.(2001).Bose-einstein condensation in dilute gases.Bose-Einstein Condensation in Dilute Gases,56(6),414.[2]Klaers J,Schmitt J,Vewinger F,et al.Bose-Einstein condensation of photons in anoptical microcavity[J].Nature,2010,468(7323):545-548.[3]陈徐宗,&陈帅.(2002).物质的新状态——玻色-爱因斯坦凝聚——2001年诺贝尔物理奖介绍.物理,31(3),141-145.[4]Boson(n.d.)In Wikipedia.Retrieved from:</wiki/Boson>[5]Fermion(n.d.)In Wikipedia.Retrieved from:</wiki/Fermion>[6]Bose-einstein condensate(n.d.)In Wikipedia.Retrieved from:</wiki/Bose%E2%80%93Einstein_condensate>[7]玻色-爱因斯坦凝聚态(n.d.)In Baidubaike.Retrieved from:</link?url=5NzWN5riyBWC-qgPhvZ1QBcD2rdd4Tenkcw EyoEcOBhjh7-ofFra6uydj2ChtL-JvkPK78twjkfIC2gG2m_ZdK>。

a r X i v :c o n d -m a t /0208385v 1 [c o n d -m a t .s o f t ] 20 A u g 2002Sodium Bose-Einstein Condensates in the F=2State in a Large-volume Optical TrapA.G¨o rlitz[*],T.L.Gustavson[†],A.E.Leanhardt,R.L¨o w[*],A.P.Chikkatur,S.Gupta,S.Inouye[‡],D.E.Pritchard and W.KetterleDepartment of Physics,MIT-Harvard Center for Ultracold Atoms,and Research Laboratory of Electronics,Massachusetts Institute of Technology,Cambridge,MA 02139(Dated:February 1,2008)We have investigated the properties of Bose-Einstein condensates of sodium atoms in the upper hyperfine ground state in a purely optical trap.Condensates in the high-field seeking |F=2,m F =-2 state were created from initially prepared |F=1,m F =-1 condensates using a one-photon microwave transition at 1.77GHz.The condensates were stored in a large-volume optical trap created by a single laser beam with an elliptical focus.We found condensates in the stretched state |F=2,m F =-2 to be stable for several seconds at densities in the range of 1014atoms/cm 3.In addition,we studied the clock transition |F=1,m F =0 →|F=2,m F =0 in a sodium Bose-Einstein condensate and determined a density-dependent frequency shift of (2.44±0.25)×10−12Hz cm 3.PACS numbers:03.75.Fi,32.70.JzSo far,Bose-Einstein condensation in dilute atomic gases [1,2,3,4,5]has been achieved in all stable bosonic alkali isotopes except 39K and 133Cs,as well as in atomic hydrogen [6]and metastable helium [7,8].The physics that can be explored with Bose-Einstein condensates (BEC)is to a large extent governed by the details of in-teratomic interactions.At ultra-low temperatures,these interactions not only vary significantly from one atomic species to another but can also change significantly for different internal states of a single species.While in 87Rb,only minor differences of the collisional properties are observed within the ground state manifolds,in 7Li,the magnitude of the scattering length differs by a factor of five between the upper and the lower hyperfine manifold and even the sign is inverted [9].The behavior of 23Na with a scattering length of 2.80nm in the |F=1,m F =±1 states and 3.31nm in the |F=2,m F =±2 states [10]is intermediate between these two extreme cases.Thus,sodium might provide a system in which the study of BEC mixtures of states with significantly differing scat-tering length is possible.Such a mixture would be a natural extension of earlier work on spinor condensates in 87Rb [11,12]and in the F=1manifold of 23Na [13,14].In this Letter,we report the realization of Bose-Einstein condensates of 23Na in the upper F=2hyperfine manifold in a large-volume optical trap [15].In 87Rb,condensates in both the F=1and F=2states had been achieved by loading atoms in either state into a magnetic trap and subsequent evaporative cooling.In contrast,sodium BECs have previously only been produced in the F=1state.Early attempts at MIT and NIST to evapo-ratively cool sodium in the F=2state were discontinued since the evaporative cooling scheme proved to be more robust for the F=1state.Instead of developing an opti-mized evaporation strategy for F=2atoms in a magnetic trap,we took advantage of an optical trap which traps atoms in arbitrary spin states [16].After producing F=1condensates and loading them into an optical trap,wetransferred the population into the F=2manifold using a single-photon microwave transition at 1.77GHz.We found that a BEC in the stretched |F=2,m F =-2 state is stable on timescales of seconds at densities of a few 1014atoms/cm 3.Simultaneous trapping of condensates in the |2,-2 and |1,-1 states for several seconds was also achieved.In contrast,at the same density,a condensate in the |2,0 state decays within milliseconds.Neverthe-less,we were able to observe the so-called clock transi-tion |1,0 →|2,0 in a BEC,which is to lowest order insensitive to stray magnetic fields.By taking spectra of this transition at various condensate densities,we were able to measure a density-dependent frequency shift of (2.44±0.25)×10−12Hz cm 3.The basic setup of our experiment is described in [17,18]and is briefly summarized here.We have pre-pared condensates of more than 4×10723Na atoms in a so-called ‘clover-leaf’magnetic trap with trapping fre-quencies of νx =16Hz and νy =νz =160Hz by ra-diofrequency evaporation for 20s.After preparation of the condensate in the |1,−1 state,the radial trapping frequencies were adiabatically lowered by a factor of 5to decompress the condensate.Subsequently,an optical trapping potential was superimposed on the condensate by slowly ramping up the light intensity.After turning offthe remaining magnetic fields,nearly all atoms were loaded into the large-volume optical dipole trap.The re-sulting peak density reached 5×1014atoms/cm 3,slightly higher than the density in the magnetic trap.The large-volume optical trap was realized by shaping the output of a Nd:YAG laser (typically 500mW at 1064nm)with cylindrical lenses leading to an elliptical focus with an aspect ratio of approximately 25.At the loca-tion of the condensate,the focal size was ≈20µm along the tight axis resulting in an optical trapping potential with typical trap frequencies of νx =13Hz axially and νy =36Hz and νz =850Hz transversely.The trap axis with the largest trapping frequency was oriented verti-2zx yg r a v i t yFIG.1:Sodium condensates in the |1,-1 and |2,-2 state,30ms after release from the trap.After preparation of the mixture the atoms were held in the optical trap for 1s.The horizontal separation of the spin states is due to application of a magnetic-field gradient during expansion.cally to counteract gravity.The pancake shape of the trap,which we had recently used to create (quasi-)2D condensates [18],provided a much larger trapping volume than our previous cigar-shaped optical traps [16,19]and thus significantly larger condensates could be stored.Optically trapped condensates were observed by absorption imaging on the closed |F=2,m F =-2 →|F ′=3,m ′F =-3 cycling transition at 589nm after sudden release from the trap,using light propagating parallel to the trap laser.The ballistic expansion time was typically 30ms,after which the vertical size of the condensate had increased by more than a factor of 100while the horizon-tal expansion was less than a factor of two.To make sure that atoms in both the F=1and the F=2manifold could be detected simultaneously,a short laser pulse resonant with the F=1→F ′=2transition was applied to pump all atoms into the F=2manifold.State-selective detection could be achieved by applying a magnetic field gradient of several G/cm during the free expansion of the atomic cloud,leading to a spatial separation of spin states which differ in the orientation of the magnetic moment (Fig.1).In order to test the intrinsic stability of the optical trap,we first investigated the lifetime of condensates in the |1,-1 state as shown in Fig.2a).Even after 70s of dwell time,more than 106atoms remained in the conden-sate.Generally,the decay of the number of atoms N in the condensate can be modelled by the rate equationdN3ing the solutions of Eq.1we deduce rate coeffi-cients for the atom loss,assuming that only one process is responsible for the loss.Thus,we obtain as upper bounds k2=(2.93±0.28±0.29)×10−15cm3s−1and k3=(1.53±0.13±0.32)×10−29cm6s−1.Both values are in reasonable agreement with theoretical predictions [21,22].Though,at typical densities,the decay rate in the F=2state is roughly an order of magnitude larger than in the F=1state,it should still be compatible with direct condensation in the F=2manifold,provided that the loss coefficients for the magnetically trapable|2,+2 state are similar to those for the|2,-2 state.By transferring only part of the atoms into the up-per hyperfine manifold we could also observe mixtures of condensates in the|1,-1 and|2,-2 states(see Fig.1). In the presence of small magneticfield gradients,we ob-served a rapid spatial separation of the two components in a time shorter than100ms due to the fact that the|1,-1 state is low-field seeking while the|2,-2 state is high-field seeking.During the separation,strong density modulations in both components were observed,which could be attributed to tunnelling processes playing a role in the separation process[23].Afterwards,the two com-ponents lived almost independently side by side in the trap and the individual lifetimes were not significantly affected.When we tried to compensate all stray mag-neticfield gradients,we still found that in steady state the two components tend to separate,i.e.we observed domains with only one component[14].This indicates that the two states are intrinsically not miscible.While we found23Na BECs in the|2,-2 state as well as mix-tures of|1,-1 and|2,-2 condensates to be stable for sev-eral seconds,non-stretched states in the F=2manifold as well as F=1,F=2mixtures with|m1+m2|=3de-cayed within several ms for typical condensate densities on the order of1014atoms/cm3.This fast decay is prob-ably due to(two-body)spin-relaxation which is strongly suppressed in87Rb but occurs with rate constants on the order of10−11cm3s−1in23Na[21].A particularly interesting transition within the elec-tronic ground state of alkali atoms is the magnetic-field insensitive transition|F,0 →|F+1,0 ,often referred to as clock transition since its equivalent in cesium is used as the primary time standard.Shortly after laser cooling had been realized,the benefits of using ultracold atoms for atomic clocks had become apparent[24]and today the most accurate atomic clocks are operated with laser-cooled atoms[25].Therefore,it seems natural to inves-tigate the use of a BEC with its significantly reduced kinetic energy for the study of the clock transition.To observe the clock transition,wefirst completely transferred an optically trapped|1,-1 condensate into the|1,0 state with a radiofrequency Landau-Zener sweep.Selective driving of the|1,-1 →|1,0 transi-tion was achieved by applying a3G offsetfield which provided a large enough quadratic Zeeman-shift to liftLineshift(Hz)Average density (1014 cm-3)FIG.3:Magnetic-field insensitive transition|1,0 →|2,0 in a BEC.(a)Spectrum in the trap at a mean density of1.6×1014atoms/cm3.(b)Spectrum after12.5ms time-of-flight at a mean density of4.3×1011atoms/cm3.The discrepancy between the center of the line andν=0is probably due to an error in the exact determination of the residual magneticfield. The solid lines are Gaussianfits.(c)Transition frequency as a function of density yielding a clock shift of(2.44±0.25)×10−12Hz cm3.the degeneracy with the|1,0 →|1,+1 transition.Sub-sequently,the magneticfield was reduced to a value of typically100mG which keeps the spins aligned and gives rise to a quadratic Zeeman shift of the clock transition of≈20Hz.The|1,0 →|2,0 transition was then ex-cited by using a microwave pulse at1.77GHz with a duration between2and5ms.The fraction of atoms transferred into the|2,0 state was kept below20%in order to ensure a practically constant density in the |1,0 state during the pulse.Immediately afterwards, the optical trap was turned offsuddenly and the num-ber of atoms which made the transition was detected by state-selective absorption imaging after15-30ms of bal-listic expansion.A typical spectrum showing the num-ber of transferred atoms as a function of microwave fre-quency(corrected for the calculated quadratic Zeeman shift)for a BEC with an average density of1.6×1014 atoms/cm3is shown in Fig.3a).The density was de-termined by measuring the release energy[18]of|1,-1 condensates without applying a microwave pulse.The release energy E rel is related to the chemical potential4µby E rel=(2/7)µ=(2/7)(h2a|1,−1 |1,−1 /πm)n o[26].Here,a|a |b is the scattering length between two23Naatoms in states|a and|b (a|1,−1 |1,−1 =2.80nm),mis the23Na mass,h is Planck’s constant and n0is thepeak density in the condensate related to the averagedensity by¯n=(4/7)n0.The spectrum in Fig.3a)issignificantly broadened compared to the one in Fig.3b),which is taken after ballistic expansion,and the transi-tion frequency is shifted with respect to the unperturbedfrequencyν0=1,771,626,129Hz[24].In the limit of weak excitation,the density-dependentshift of the clock-transition frequency is due to the differ-ence in mean-field potential that atoms in the|1,0 and|2,0 state experience within a|1,0 condensate.Takinginto account the inhomogeneous density distribution of atrapped BEC,this leads to a line shape given by[27]I(ν)=15h(ν−ν0)1−h(ν−ν0)πm(a|2,0 |1,0 −a|1,0 |1,0 ),(3)where the center of the line is atν0+2n0∆U/3h and the average frequency isν0+4n0∆U/7h.In our experiment, the line is additionally broadened and the asymmetry of Eq.2smeared out due to thefinite width of the mi-crowave pulse which was limited by rapid inelastic losses in the|2,0 state.Therefore,we have used a(symmetric) Gaussian tofit the resonances where we have identified thefitted center frequency as the average frequency of the line.By taking spectra of the clock-transition at different densities we have determined a density shift of (2.44±0.25)×10−12Hz cm3(Fig.3c).Here,the error is the statistical error from a linearfit to the data.Addi-tional systematic errors due tofitting of the line with a Gaussian and due to an uncertainty in the determination of the density are estimated to be smaller than20%.Us-ing Eq.3and a|1,0 |1,0 =2.71nm[10],we determine the scattering length a|2,0 |1,0 =3.15±0.05nm for collisions between two atoms in states|1,0 and|2,0 .In conclusion,we have prepared condensates in the up-per F=2hyperfine manifold of the sodium ground state in a large-volume optical trap and observed a stable con-densate in the high-field seeking stretched state|2,−2 . Since only the stretched state exhibits reasonable stabil-ity,experiments with more complex spinor condensates do not seem to be possible.Furthermore,we have for thefirst time observed the alkali clock-transition in a Bose-Einstein condensate and determined the value for the density-dependent mean-field shift.In present BEC experiments,the magnitude of the shift precludes the use of trapped condensates for precise atomic clocks.How-ever,under circumstances where the condensate density can be drastically reduced as may be feasible in space-based experiments,the extremely low velocity spread of BECs might help improve the accuracy of atomic clocks. This work was supported by NSF,ONR,ARO,NASA, and the David and Lucile Packard Foundation. A.E.L. acknowledges additional support from the NSF.[*]Current address:5th Phys.Inst.,University of Stuttgart, 70550Stuttgart,Germany[†]Current address:Finisar Corp.,Sunnyvale,CA94089 [‡]Current address:JILA,Boulder,CO80309[1]M.H.Anderson et al.,Science269,198(1995).[2]K.B.Davis et al.,Phys.Rev.Lett.75,3969(1995).[3]C.C.Bradley,C.A.Sackett,and R.G.Hulet,Phys.Rev.Lett.78,985(1997).[4]S.L.Cornish et al.,Phys.Rev.Lett.85,1795(2001).[5]G.Modugno et al.,Science294,1320(2001).[6]D.G.Fried et al.,Phys.Rev.Lett.81,3811(1998).[7]A.Robert et al.,Science292,461(2001).[8]F.Pereira Dos Santos et al.,Phys.Rev.Lett.86,3459(2001).[9]F.Schreck et al.,Phys.Rev.Lett.87,080403(2001).[10]C.Samuelis et al.,Phys.Rev.A63,012710(2000).[11]C.Myatt et al.,Phys.Rev.Lett.78,586(1997).[12]D.Hall et al.,Phys.Rev.Lett.81,4531(1998).[13]J.Stenger et al.,Nature396,345(1998).[14]H.-J.Miesner et al.,Phys.Rev.Lett.82,2228(1999).[15]Meanwhile,we have also realized a23Na BEC in the F=2state in a magnetic trap starting from an optical trap.(A.E.Leanhardt et al.,cond-mat0206303(2002)).[16]D.M.Stamper-Kurn et al.,Phys.Rev.Lett.80,2027(1998).[17]W.Ketterle,D.Durfee,and D.M.Stamper-Kurn(IOSPress,Amsterdam,1999),Proceedings of the Interna-tional School of Physics Enrico Fermi,Course CXL,p.67.[18]A.G¨o rlitz et al.,Phys.Rev.Lett.87,130402(2001).[19]T.L.Gustavson et al.,Phys.Rev.Lett.88,020401(2002).[20]H.M.J.M.Boesten,A.J.Moerdijk,and B.J.Verhaar,Phys.Rev.A54,R29(1996).[21]A.J.Moerdijk and B.J.Verhaar,Phys.Rev.A53,R19(1996).[22]A.J.Moerdijk,H.M.J.M.Boesten,and B.J.Verhaar,Phys.Rev.A53,916(1996).[23]D.M.Stamper-Kurn et al.,Phys.Rev.Lett.83,661(1999).[24]M.Kasevich et al.,Phys.Rev.Lett.63,612(1989).[25]G.Santarelli et al.,Phys.Rev.Lett.82,4619(1999).[26]F.Dalfovo et al.,Rev.Mod.Phys.71,463(1999).[27]J.Stenger et al.,Phys.Rev.Lett.82,4569(1999).。

High-temperature Bose-Einstein condensation of polaritons: realization under the intracavity laserpumping of matter conditionV.A. Averchenko1), A.P. Alodjants2*), S.M. Arakelian2), S.N. Bagayev3), E.A. Vinogradov4),V.S. Egorov1), A.I. Stolyarov1), I.A. Chekhonin1)1) St. Petersburg State University, Ul'yanovskaya ul. 1, 198504 St. Petersburg, Staryi Peterhof, Russia2) Vladimir State University, ul. Gor'kogo 87, 600000 Vladimir, Russia3) Insitute of Laser Physics, Russian Academy of Sciences, prosp. akad. Lavrent'eva 13/3, 630090Novosibirsk, Russia4) Institute of Spectroscopy, Russian Academy of Sciences, 142190 Troitsk, Moscow region, RussiaAbstract.A quantum model of Bose-Einstein condensation based on processes involvingpolaritons excited in an intracavity absorbing cell with resonance atoms, which is manifested inthe spectral characteristics of the system, is considered. It is shown that the spectral'condensation' appears which is directly related to the degeneracy of a weakly interacting gas ofpolaritons resulting in quasi-condensation at room temperature. The possibility of obtainingpolariton condensation as a new phase state by using the confinement of polaritons in an atomicoptical harmonic trap is discussed.Keywords: polaritons, quasi-condensation, Bose-Einstein condensation, polariton laser.1. IntroductionExperiments on the Bose-Einstein condensation (BEC) of macroscopic numbers of atoms (N ≥ 106 ) is one of the most spectacular recent advances, which have made a great influence on the development of various directions in modern quantum and laser physics and newest technologies (see, for example, [1]). In the case of BEC, when under conditions of the temperature phase transition a macroscopic number of atoms are in the ground (lower) quantum level, a new coherent state of matter is formed. This is manifested in the fact that, for example, at the limiting temperature T=0 an ensemble of condensate atoms, as each individual atom, is described by the common wave function corresponding to a coherent state. In this aspect, the BEC phenomenon is similar to lasing, for example, when strict phase locking of laser modes occurs in laser cavities [2, 3]. In addition, in the case of BEC, we can say about the realisation of a Bose laser (boser) emitting coherent ensembles of atoms [3, 4]. A remarkable feature of such macroscopic quantum states of matter is the possibility to use them for the development of new physical principles of quantum information processing and communication [5, 6].However, despite spectacular achievements in this direction, there exist a number of practical difficulties imposing principal restrictions on the possibility of real applications of the atomic BEC for these purposes. Thus, one of the basic problems is the necessity of maintaining extremely low temperatures (tens of nK) to realise such devices. In this connection the problem of obtaining macroscopic coherent (quantum) states of matter at high (room) temperatures becomes very important.One of the most attractive approaches to the solution of this problem is the preparation of a quasi-condensate of the two-dimensional Bose gas of weakly interacting polaritons (in atomic physics [7]) and _______________________________________________________*) Email: alodjants@vpti.vladimir.ruexcitons (in solid state physics [8-10] *)). Such collective states of the medium (quasi-particles) represent a superposition of photons and spin waves in the atomic medium and can be obtained, for example, within the framework of the Dicke model used to describe superradiance [12]. Although these states cannot be treated as a condensate in a strict thermodynamic sense due to the nonequilibrium state of the system as a whole, under certain conditions imposed on the type of atomic optical interactions in the system, polaritons do form a condensate, their distribution being described by the Bose-Einstein distribution function for an ideal gas of bosons [13].In this paper, we considered the interaction of a system of two-level atoms with an electromagnetic field in the cavity in the case of the so-called strong coupling, when the inequality1/220212c coh d n πωωτ⎛⎞=⎜⎟⎝⎠, (1) is fulfilled, where c ω is the cooperative frequency determining the collective interaction of atoms with the field; 0ω is the atomic transition frequency; d is the transition dipole moment; coh τ is the characteristic coherence time of the atomic medium; n is the atomic gas density; and is Planck's constant. In this case, the field itself is weak (in the number of photons).The so-called condensation of the spectrum occurs when inequality (1) is fulfilled [14, 15]. This effect consists in the fact that under some threshold conditions imposed on the concentration of absorbing atoms and pump intensity, radiation of a broadband laser with a narrowband absorbing intracavity cell is concentrated ('condensed') near the strongest absorption lines of matter.This phenomenon was observed experimentally and interpreted within the framework of a clear classical model of parametric excitation of two coupled oscillators (electromagnetic field and atoms of matter) upon coherent energy transfer between them. However, this model is one-dimensional and is not quantum one, which obviously restricts the field of its applications.In this paper, we propose a detailed quantum model of spectral condensation realised for polaritons excited in an intracavity absorbing cell [16]. We show that spectral condensation can be directly related to the condensation (quasi-condensation) of polaritons in the cavity if a strong coupling between the electromagnetic field and medium is provided. The latter statement is in itself of interest, and in this paper we substantiate for the first time the possibility of obtaining the true BEC in the polariton system at high (room) temperatures in the case of spectral condensation. In this respect, of interest are the experimental data [8, 9] obtained in semiconductor microcavities, which confirm the above assumption.2. Basic relationsConsider the interaction of two-level atoms (with levels a and b) with a quantum electromagnetic field, which is described by the photon annihilation (creation) operators ()k k f f + for the k-th mode. Within the framework of dipole approximation, such a system can be described by the Hamiltonian [13]12()()()()ph k k atk k k k k k k k k kH k E k f f E b b a a g f a b b a f ++++++=+−+−∑∑∑, (2) level a, and the inequality_______________________________________________________*) Here, we are dealing with the so-called Kosterlitz-Thouless phase transition to the superfluid state of two-dimensional Bose systems in which the true Bose-Einstein condensation (in the absence of confinement of gas particles in a trap) is impossible [11].k k k k b b a a ++ (3)is fulfilled. In this approximation, Hamiltonian (2) can be diagonalised by using the unitary transformation1,,k k k k k k Фf a b µν+=− 2,,k k k k k k Фf a b νµ+=+ (4)where the introduced annihilation operators ,j k Ф (j=1,2) characterise quasi-particles (polaritons) in the atomicmedium, corresponding to two types of elementary perturbations, which in approximation (3) satisfy the boson commutation relations,,;i k j k ij ФФδ+⎡⎤=⎣⎦, ,1,2i j =. (5)The transformation parameters k µand k v in expression (4) are real Hopfield coefficients satisfying the condition 221k k v µ+=, which determine the contributions of the photon and atomic (excited) components to a polariton, respectively:22221/2221/242(4)(4)k k k k g g g µδδδ=⎡⎤+++⎣⎦, 221/22221/2(4)2(4)k k k k g g δδνδ++=+ , (6a,b)where ()k at ph E E k δ=−is the phase mismatch determining the contributions of the photon and atomic components to expression (4) for polaritons. In particular, in the limiting case, when 2k g δ− , we have 21k µ→ (20k v →), which corresponds to the negligible contribution of the photon part to the polariton 2,k Ф. Inopposite limit, when 2k g δ , we have 20k µ→ (21kv →), which means that the photon contribution to the coherence of polaritons of this type increases. Expression (6) shows that the polariton is a half-matter and half-photon (221/2µν==) quasi-particle under the resonance condition 0k δ=.Taking expressions (4) and (6) into account, Hamiltonian (2) takes the form11,1,22,2,()()()k k k k k kH k E k ФФE k ФФ++=+∑∑, (7)where 1,2()E k determine the dispersion dependence of polaritons: {}1/2221,21()()()42at ph at ph E k E E k E E k g ⎧⎫⎡⎤=+±−+⎨⎬⎣⎦⎩⎭. (8) Figure la presents dispersion dependences 1,2()E k (8) of polaritons for the interaction of atoms with the quantum field in free space. One can see that the two allowed energy states, polaritons of the upper 1[()]E k and lower 2[()]E k branches, correspond to each value of the wave vector k .When the medium is placed into the resonator, the wave-vector component k ⊥ orthogonal to the mirrorsurface is quantised. At the same time, a continuum of modes exists in the direction parallel to the mirror surface due to the absence of boundary conditions. This means that in the single-mode (single-frequency for each value of k ⊥) regime, the dispersion of polaritons is determined only by the wave-vector component k parallel to the mirror surface. Then, under the condition k k ⊥ which corresponds physically to the paraxialapproximation in optics (see, for example, [17]), the dispersion relation for photons in the resonator has the form23221/22()()2ph k k E k c k k c k O k k ⊥⊥⊥⊥⎡⎤⎛⎞=+=++⎢⎥⎜⎟⎜⎟⎢⎥⎝⎠⎣⎦. (9)a bFigure 1. Dispersion dependences 1()E k (upper branch) and 2()E k (lower branch) of polaritons on the wave vector k in free space (a) and resonator (b). The wave vector is plotted on the abscissa in the units of the resonance wave vector k ⊥ on the ordinate the energy is plotted inthe units of the coupling coefficient g .Here /cav k m L π⊥=is the quantised component of the wave vector parallel to the resonator axis, which corre-sponds to the periodic boundary conditions in the standard field quantisation procedure; L cav is the effective resonator length; and the number m corresponds to the selected mode (frequency). In the case of strong coupling(1), the dispersion curves of a polariton are pushed apart, resulting in the appearance of the upper and lower polariton branches in the resonator (Fig. lb). The principal feature of these curves is the presence of the 'potential' well (for 0k =). The width of the lower polariton well can be found from the condition 2220E k ∂∂= . This condition determines the angular parameters of a polariton beam in the resonator. It is important to note that these effects, which are related to the transverse component of the wave vector of a polariton (k in our case), will not be suppressed due to light diffraction if the angular dimensions of the polariton beam exceed the diffraction-limited divergence ϕ of the light beam, which can be estimated from the expression cav d L ϕ≈ [d and cav L are the beam diameter and resonator (or absorbing cell) length, respectively].3. Spectral 'condensation' and condensation of polaritonsWithin the framework of our approach, the narrowing ('condensation') of the polariton spectrum, which was observed in experiments [14, 15], can be simply explained by BEC. In this connection, taking into account paraxial approximation (9), we represent Hamiltonian (7) in the formlong tr H H H =+, (10a)where''11,1,22,2,()()long k k k k k k H E k ФФE k ФФ⊥⊥⊥⊥⊥⊥++⊥⊥=+∑∑, (10b) ''1,1,1,2,2,2,()()tr tr k k tr k k k k H E k ФФE k ФФ++=+∑∑ (10c)The expression for long H describes polaritons formed along the resonator axis, ''1,21,20()()k E k E k ⊥=≡ determines their dispersion dependence [see (8)] for 0k = . The expression for tr H characterises polaritons produced in the two-dimensional plane perpendicular to the resonator axis. The dispersion of these polaritons is described by the expression '22(1,2)11,2,2/tr pol E k m = . Here,()(1,2)1/222214phpol m m g =∆∆+∓(11)is the mass of polaritons of the upper and lower branches; 20ph m k c E c ⊥=≈ is the effective photon mass inthe medium and 0E ck ⊥∆=− is the detuning of the resonator mode (frequency) from the atomic transitionfrequency.Thus, the BEC of polaritons in the resonator is related to the second term in the expression for the Hamiltonian H in (10a). This term leads in fact to the renormalisation of the photon mass in the medium [see(11)]. Quasi-particles (polaritons) appearing in this case can be treated as an ideal two-dimensional gas [see also (10b)]. Indeed, the possibility of BEC assumes the presence of a stable state with the minimal energy - a 'potential' well (at the point 0k = ), which, as shown in section 2, takes place for polaritons in the resonator (the2well expressed in energy units is of the order of the coupling coefficient222effk g m ∆≈ . (12)In this case, it is possible to introduce formally the effective temperature eff T of the two-dimensional Bose gas of polaritons, which is also of the order of the coupling coefficient within the polariton well [13], i.e., B eff K T g ≈, where B K is the Boltzmann constant.The approach discussed above determines the condensation (more exactly, quasi-condensation) of the two-dimensional gas by assuming that polaritons with large k efficiently relax to the bottom of the dispersion-curve well. In our case, unlike the case of semiconductor microcavities considered in [8, 9], the two-dimensional property of the polariton gas can be provided by the fact that an optically dense medium is excited, as a rule, by the wave packet of synchronised electromagnetic modes, which corresponds to the quasi-monochromatic interaction of the field with medium.The efficient relaxation of polaritons to the bottom of the 'dispersion' well can be related to the intense polariton-polariton interaction discussed in a number of papers (mainly concerning the problems with semiconductor micro-cavities [10, 18]).Consider now in more detail the quasi-condensation of a two-dimensional Bose gas of polaritons described by the last term in (10c). The chemical potential of such a gas is described by the expression [19]22ln 1exp()ln 1exp B T B d T K T n K T T µλ⎡⎤⎛⎞⎡⎤=−−≡−−⎢⎥⎜⎟⎣⎦⎢⎥⎝⎠⎣⎦, (13)where 222/()d eff B T n m K π= is the gas degeneracy temperature; 2n is the two-dimensional density of polaritonsin the plane perpendicular to the resonator axis; and 1/2/(2)T eff B m K T λ= is the thermal wavelength (de Broglie wavelength). The temperature T d in (13) is determined by the condition when the thermal wavelength T λ is of the order of the average distance 1/3V between particles (V is the system volume). Due to the interaction between polaritons (nonideal gas), the additional parameter a scat appears, which is the scattering length depending on the interaction potential. This parameter affects the energy spectrum, which becomes a phonon spectrum [9].It follows from (13) that, strictly speaking, the condensation of the two-dimensional polariton gas (0µ=) occurs at 0T →. At the same time, it is known (see, for example, [9]) that already at the temperature224sd KT eff B n T T m K π= (14)the Kosterlitz-Thouless phase transition to the superfluid state occurs in the two-dimensional weakly interacting Bose gas, when isolated condensate droplets with uncorrelated phases are formed on the two-dimensional surface [n s in (14) is the superfluid liquid density on the two-dimensional surface].For polaritons with the effective mass 33510eff m g −=×and density in a three-dimensional resonator 1133 3.510n cm −=×, the gas degeneracy can appear already at room temperature (T d = 300 K). Indeed, in this case the minimal two-dimensional density of the polariton gas estimated from (13) for d T T = gives the value 82230.310T n n cm λ−≈× [19] for the de Broglie wavelength 41.8410T cm λ−≈×. It is for this value of the atomic concentration 3n that spectral condensation was observed near the yellow doublet of sodium in experiments [14] (Fig. 2). For the upper spectrum (Fig. 2a), 103310n cm −<, and for the lower spectrum (Fig. 2c), 1133 3.510n cm −=×. The similar results obtained in [14] for the neon spectrum also demonstrated the spectralcondensation for polaritons.a bcFigure 2. Spectral condensation near the yellow doublet of sodium (see text) at the atomic concentration 10310n ≤(a), 1110 (b), and 1133.510cm −× (c).Let us find now the conditions under which the true (in thermodynamic sense) condensation of polaritons excited in the resonator can be obtained. It is known [19, 20] that, to obtain such condensation in a two-dimensional weakly interacting (ideal) gas, gas particles should be confined in a trap. For example, for a trap with the trapping potential described by the expression (harmonic potential)222020()2eff eff m r U r U r r Ω== (15)(eff Ω is the trapping (oscillation) frequency of particles, 0r is the transverse size of the trapping region, and r isthe transverse coordinate), the critical BEC temperature for a two-dimensional gas is (cf. [20])2221.645c eff Bn T m K π== , (16)where N is the total number of particles. We also took into account in the right-hand side of (16) that the number N 2 of particles trapped by the potential U(r) on the surface is described by the expression [20]2222B eff eff N n K T m π=Ω. In the absence of a trap (0eff Ω=), as should be, BEC does not occur: 0c T = in (16).(measurements of the first- and second-order coherence degree) is one of the main tools for diagnostics of polariton condensation (see [8, 9]). Because a polariton is a linear superposition of a photon and atomic excitation [see (4)], its coherent properties are caused by the coherence of the light field itself and of an ensemble of atoms with which the field interacts, as well as by their possible quantum interference caused by the condensation process. Within the framework of these experiments, when the condition of the exact resonance0∆= is fulfilled, we have 0k δ≈ and obtain 221/2k k v µ== from expressions (6) and (11), which means thatoptical and atomic parts make identical contributions to a polariton. In this case, the coherent properties of the polariton state can be simply caused by a high coherence of the optical field at the input to the atomic medium irrespective of BEC. However, the problem of measuring the coherence of atomic exitations caused by the interaction and of the intrinsic coherence of the polariton condensate (if it is produced in the system) remains open. In our opinion, this problem can be solved, in particular, by producing polariton BEC based on three-level atoms under conditions of electromagnetic induced transparency (EIT) (see below).Here we consider another possibility based on a small variation of the detuning ∆ [and, therefore, k δ, see (6)] in experiments as the parameter governing the contributions of photon and atomic parts to the resulting coherence of resonator polaritons. In this case, the effective mass of polaritons [see (11)] and, hence, the critical temperatures of degeneracy, condensation, and quasi-condensation in (13), (14), and (16) change. This specific property of a polariton gas means in fact that the formation of a Bose-Einstein condensate can be controlled in experiments.Note, however, that we do not consider in this paper the questions concerning the BEC of a photonic gas in the resonator or, more exactly, the condensation of polaritons of the upper branch of the dispersion curve (see Fig. lb) characterised by the first term in expression (10c). This problem is undoubtedly very important for the scope of questions considered in our paper although it was discussed only in connection with the quantum properties of light in media with cubic nonlinearity (see [3]).In addition, the formation of a photon condensate (or a condensate of polaritons of the upper branch), which is directly connected with lasing in the resonator (cf. [2]), upon varying the parameter ∆ also has an interesting feature. Indeed, for 0∆=, it follows from (11) that polaritons of both dispersion branches have equalmasses, i.e., (1)(2)pol pol eff m m m ==, which corresponds to the equal temperatures of their quasi-condensation [see(14)1. However, in the case of 0∆≠, we have from (11) that (1)(2)pol pol m m ≠ which means physically that thephase-transition temperatures (14) for polaritons of the upper (1)()KT T and lower (2)()KT T dispersion branches aredifferent. Thus, by introducing asymmetry with the help of a small change in the detuning ∆, it is possible to produce a very narrow temperature (energy) gap within which the coherent properties of polaritons of both branches should substantially change. These properties can be observed, for example, by measuring the function of their cross correlation or by using probe radiation under resonance conditions.Therefore, the study of this effect will give the answer to the principal question about the properties ofthe coherence of light, atomic system, and polaritons themselves in the case of BEC.4. ConclusionsWe have developed in the paper the quantum approach for solving the problems of formation of quasi-condensation and realisation of the true (in the thermodynamic sense) Bose - Einstein condensation of a two-dimensional gas of polaritons at room temperature. This approach has allowed us to explain some features of spectral condensation of broadband lasing near strong absorption lines in the laser resonator, which were observed in experiments (in particular, the so-called spectral condensation upon non-resonance pumping). In this aspect, BEC reduces the threshold pump power of parametric excitation of cooperative effects. Consider briefly some phenomena that are directly related to the problem studied in the paper.First, this is the condensation of polaritons, which is of interest in the presence of the EIT effect when alight pulse propagates in a resonance atomic medium without changing its shape in the absence of absorption (see, for example, [5, 21, 22]. A remarkable feature of this effect is the appearance of atomic coherence both for hot [21] and ultracold atoms [5, 22]. The EIT effect can be also explained in terms of bright and dark polaritons, which in the adiabatic approximation corresponding to condition (3) in our case, represent the coherent superposition of atoms in the two states of the hyperfine Zeeman structure and the external probe field maintained with the help of the external probe field at the optical frequency through the third (auxiliary) level (the so-called Λ- scheme [5, 6, 21]).Therefore, upon placing an atomic medium into the resonator to produce the BEC of polaritons, the EITeffect would become a tool for obtaining such a quantum state. In this case, the condensation process could be controlled more precisely by coupling directly two atomic levels with an external weak field, which would provide the ejection of 'hot' polaritons from a trap, as, for example, occurs for condensation of alkali atoms in a magneto-optical trap [1]. On the other hand, upon spectral condensation in the case of BEC, a 'bleaching' of the atomic medium in the resonator caused by a change in its refractive properties can be expected. In this case, the group velocity of a light pulse directed into an atomic medium after switching on probe radiation with the delay time del coh ττ< can decrease, in particular, due to polariton condensation. Indeed, it follows from expressions (10c) and (11) that the group velocities of such quasi-particles in the plane perpendicular to the resonator axis are determined by the expression1,2(1,2)(1,2)()tr gr polE k k m υ∂==∂ In the case of the exact atomic optical resonance (for 0∆=), we have from this that(1)(2)/2gr gr k c k υυ⊥= Therefore, in the paraxial approximation, when k k ⊥ the group velocity of condensedpolaritons is estimated as (1,2)gr c υ , which means in fact that the 'slow' light regime is observed for polaritons inthe resonator.Second, the high-temperature BEC of polaritons is of interest for quantum information, for example, forthe development of new physical principles of quantum memory and data storage. Indeed, as we have shown in[6], such macroscopic polariton states can be used in problems of cloning and quantum information storage.Acknowledgements. This work was partially supported by the Russian Foundation for Basic Research (Grants Nos 04-02-17359 and 05-02-16576) and the Ministry of Education and Science of the Russian Federation. A.P. Alodjants thanks the non-profit Dynasty Foundation for support.AppendixLet us discuss the problem of confinement of the BEC of intracavity polaritons in a trap. Consider a special atomic optical trap whose operation is based on the fact that polaritons represent a coherent superposition of a photon and atomic perturbation. Photons can be confined in the region of atomic-optical interaction in such a trap, where polaritons are produced, by focusing a light beam with a special gradient (cylindrical) lens (or inhomogeneous waveguide) with the refractive index varying along the transverse coordinate as2220()(1)n r n n r ′=−, (A.1)where 'n is the required gradient addition to the refractive index of the lens. The potential for trapping (focusing) photons of the light beam produced by such an optical system can be written in the form [17]222020()'()22opt n r n n r U r n −==,which exactly corresponds to the harmonic-trap potential (15) with the inhomogeneity parameter 2'eff eff n m =Ω.In addition, to trap atoms in the plane perpendicular to the resonator axis, we can use a two-dimensional magnetic trap with the oscillation frequency at Ω, which is widely applied in experiments with 'usual' atomic condensates [1].Thus, to confine polaritons in a trap, it is necessary to confine atoms by a standard method and focus simulta-neously the light beam into the region of atomic-optical interaction by selecting the appropriate parameters at Ωand 'n . This determines the value of eff Ω required in the experiment.References1. Ketterle V. Usp. Fiz. Nauk, 173, 1339 (2003).2. Oraevsky A.N. Kvantovaya Elektron., 24, 1127 (1997) [Quantum Electron., 27, 1094 (1997)].3. Chiao R., Boyce J. Phys. Rev. A, 60, 4114 (1999).4. Imamoglu A., Ram R.J., Pau S., Yamamoto Y. Phys. Rev. A, 53, 4250 (1996).5. Liu C, Dutton Z., Behroozi C.H., Hau L.N. Nature, 409, 490 (2001).6. Alodjants A.P, Arakelian S.M. Int. J. Mod. Phys. B, 20, 1593 (2006).7. Averchenko V.A., Bagayev S.N., et al. Abstract in Technical Digest o/ICONO'05 Conf. (Sankt-Petersburg, Russia, 2005).8. Deng H., Weihs G., Santori C, Bloch J., Yamamoto Y. Science, 298, 199 (2002).9. Kavokin A., Malpuech G., Laussy F.P. Phys. Lett. A, 306, 187 (2003); Richard M., Kasprzak J., Andre R., et al. Phys. Rev. B, 72, 201301(R) (2005).10. Gippius N.A., Tikhodeev S.G., Keldysh L.V., Kulakovskii V.D., Usp. Fiz. Nauk, 175, 327 (2005); Kulakovskii V.D., KrzhizhanovskiiD.N., et al. Usp. Fiz. Nauk, 175, 334 (2005).11. Kosterlitz J.M., Thouless D.J. J. Phys. B: Sol. State Phys., 6, 1181 (1973).12. Dicke R.H. Phys.Rev., 93, 99 (1954).13. Eastham P.R., Littlewood P.B. Phys. Rev. B, 64, 235101 (2001).14. Vasil'ev V.V., Egorov V.S., Fedorov A.N., Chekhonon LA. Opt. Spektr., 76, 146 (1994).15. Bagayev S.N., Egorov V.S., Moroshkin P.V., Fedorov A.N., Chekhonon LA. Opt. Spektr., 86, 912 (1999).16. Kocharovskii V.V., Kocharovskii Vl.V. Kvantovaya Elektron., 14, 2246 (1987) [Sov. J. Quantum Electron., 17, 1430 (1987)].17. Marte M.A., Stenholm S. Phys. Rev. A, 56, 2940 (1997).18. Savvidis P.G., Baumberg J.J., Stevenson P.M., et al. Phys. Rev. Lett., 84, 1547 (2000).19. Petrov D.S., Gangardt G.M., Shlyapnikov G.V. J. Phys. IV France, 116, 3 (2004).20. Bagnato V., Kleppner D.K. Phys. Rev. A, 44, 7439 (1991).21. Lukin M.D. Rev. Mod. Phys., 75, 457 (2003).22. Prokhorov A.V., Alodjants A.P., Arakelyan S.M. Pis'ma Zh. Eksp. Tear. Fiz., 80, 870 (2004).。