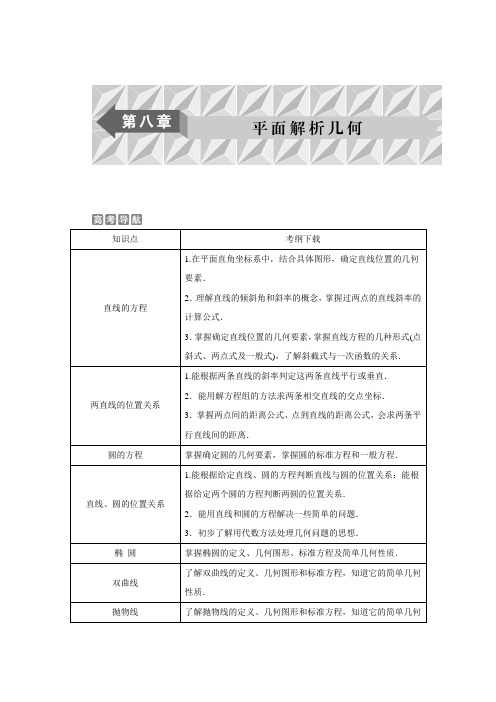
2013届高三人教A版文科数学一轮复习课时作业(45)直线的倾斜角与斜率、直线的方程

第1讲 直线的倾斜角与斜率、直线的方程1．直线的倾斜角(1)定义：x 轴正向与直线向上方向之间所成的角叫做这条直线的倾斜角．当直线与x 轴平行或重合时，规定它的倾斜角为0°．(2)倾斜角的范围为[0，π)． 2．直线的斜率(1)定义：一条直线的倾斜角α的正切值叫做这条直线的斜率，斜率常用小写字母k 表示，即k ＝tan α，倾斜角是90°的直线没有斜率．(2)过两点的直线的斜率公式经过两点P 1(x 1，y 1)，P 2(x 2，y 2)(x 1≠x 2)的直线的斜率公式为k ＝y 2－y 1x 2－x 1＝y 1－y 2x 1－x 2.3．直线的方程1．辨明四个易误点(1)求直线方程时要注意判断直线斜率是否存在；每条直线都有倾斜角，但不一定每条直线都存在斜率．(2)根据斜率求倾斜角，要注意倾斜角的范围．(3)直线的截距式中易忽视截距均不为0这一条件，当截距为0时可用点斜式． (4)由一般式Ax ＋By ＋C ＝0确定斜率k 时易忽视判断B 是否为0，当B ＝0时，k 不存在；当B ≠0时，k ＝－A B.2．求直线方程的一般方法(1)直接法：根据已知条件，选择适当的直线方程形式，直接写出直线方程，选择时，应注意各种形式的方程的适用范围，必要时要分类讨论．(2)待定系数法，具体步骤为： ①设所求直线方程的某种形式； ②由条件建立所求参数的方程(组)； ③解这个方程(组)求出参数； ④把参数的值代入所设直线方程．1.教材习题改编 经过两点A (m ，3)，B (1，2m )的直线的倾斜角为135°，则m 的值为( ) A ．－2 B ．2C ．4D ．－4B [解析] 由题意得2m －31－m ＝tan 135°＝－1，即2m －3＝m －1，所以m ＝2，故选B.2.教材习题改编 经过点P 0(2，－3)，倾斜角为45°的直线方程为( ) A ．x ＋y ＋1＝0 B ．x ＋y －1＝0 C ．x －y ＋5＝0D ．x －y －5＝0D [解析] 由点斜式得直线方程为 y －(－3)＝tan 45°(x －2)＝x －2， 即x －y －5＝0，故选D.3.教材习题改编 倾斜角为120°，在x 轴上的截距为－1的直线方程是( ) A ．3x －y ＋1＝0 B ．3x －y －3＝0 C ．3x ＋y －3＝0D ．3x ＋y ＋3＝0D [解析] 因为倾斜角为120°，所以斜率k ＝－ 3. 又因为直线过点(－1，0)，所以直线方程为y ＝－3(x ＋1)，即3x ＋y ＋3＝0.4．(2017·烟台模拟)如果AC ＜0，BC ＜0，那么直线Ax ＋By ＋C ＝0不通过( ) A ．第一象限 B ．第二象限 C ．第三象限D ．第四象限C [解析] 由题意知直线的斜率k ＝－A B ＜0，直线在y 轴上的截距b ＝－CB ＞0，故选C.5．直线l 过原点且平分▱ABCD 的面积，若平行四边形的两个顶点为B (1，4)，D (5，0)，则直线l 的方程为________．[解析] 直线l 平分平行四边形ABCD 的面积，则直线l 过BD 的中点(3，2)，则直线l ：y ＝23x . [答案] y ＝23x直线的倾斜角与斜率[学生用书P143][典例引领](1)直线2x cos α－y －3＝0⎝⎛⎭⎫α∈⎣⎡⎦⎤π6，π3的倾斜角的变化范围是( )A ．⎣⎡⎦⎤π6，π3B ．⎣⎡⎦⎤π4，π3C ．⎣⎡⎦⎤π4，π2D ．⎣⎡⎦⎤π4，2π3(2)已知线段PQ 两端点的坐标分别为P (－1，1)和Q (2，2)，若直线l ：x ＋my ＋m ＝0与线段PQ 有交点，则实数m 的取值范围是________．【解析】 (1)直线2x cos α－y －3＝0的斜率k ＝2cos α.由于α∈⎣⎡⎦⎤π6，π3，所以12≤cos α≤32，因此k ＝2cos α∈[1，3]．设直线的倾斜角为θ，则有tan θ∈[1，3]． 由于θ∈[0，π)，所以θ∈⎣⎡⎦⎤π4，π3，即倾斜角的变化范围是⎣⎡⎦⎤π4，π3.(2) 如图所示，直线l ：x ＋my ＋m ＝0过定点A (0，－1)，当m ≠0时，k QA ＝32，k P A ＝－2，k l ＝－1m.所以－1m ≤－2或－1m ≥32.解得0<m ≤12或－23≤m <0；当m ＝0时，直线l 的方程为x ＝0，与线段PQ 有交点． 所以实数m 的取值范围为－23≤m ≤12.【答案】 (1)B (2)⎣⎡⎦⎤－23，12(1)求倾斜角的取值范围的一般步骤 ①求出斜率k ＝tan α的取值范围．②利用三角函数的单调性，借助图象，确定倾斜角α的取值范围． 求倾斜角时要注意斜率是否存在． (2)斜率的求法①定义法：若已知直线的倾斜角α或α的某种三角函数值，一般根据k ＝tan α求斜率． ②公式法：若已知直线上两点A (x 1，y 1)，B (x 2，y 2)，一般根据斜率公式k ＝y 2－y 1x 2－x 1(x 1≠x 2)求斜率．[通关练习]1．直线x ＋3y ＋1＝0的倾斜角是( ) A ．π6B ．π3C ．2π3D ．5π6D [解析] 由直线的方程得直线的斜率为k ＝－33，设倾斜角为α，则tan α＝－33，又α∈[0，π)，所以α＝5π6.2．若点A (4，3)，B (5，a )，C (6，5)三点共线，则a 的值为________． [解析] 因为k AC ＝5－36－4＝1，k AB ＝a －35－4＝a －3.由于A ，B ，C 三点共线，所以a －3＝1，即a ＝4. [答案] 4求直线的方程(高频考点)[学生用书P144]直线方程是解析几何的一个基础内容，在高考中经常与其他知识结合考查，多以选择题、填空题的形式呈现，多为中、低档题目．高考中对直线方程的考查主要有以下两个命题角度： (1)已知两个独立条件，求直线方程；(2)已知直线方程及其他条件，求参数值或范围．[典例引领]根据下列条件，分别写出直线的方程： (1)经过点A (－3，2)，B (－3，5)； (2)斜率为32，在x 轴上的截距为－7； (3)经过点A (－1，－3)，倾斜角等于直线y ＝3x 的倾斜角的2倍．【解】 (1)显然A 、B 的横坐标相同，故直线AB 与y 轴平行，其方程为x ＝－3. (2)由题意，直线过点(－7，0)．代入直线的点斜式方程得y ＝32(x ＋7)， 即3x －2y ＋73＝0.(3)由已知，设直线y ＝3x 的倾斜角为α，则所求直线的倾斜角为2α. 因为tan α＝3，所以tan 2α＝2tan α1－tan 2α＝－34.又直线经过点(－1，－3)，因此所求直线方程为y ＋3＝－34(x ＋1)，即3x ＋4y ＋15＝0.与直线方程有关问题的解题策略(1)在求直线方程时，应先选择适当的直线方程的形式，并注意各种形式的适用条件，用斜截式及点斜式时，直线的斜率必须存在，而两点式不能表示与坐标轴垂直的直线，截距式不能表示与坐标轴垂直或经过原点的直线．(2)求参数值或范围．注意点在直线上，则点的坐标适合直线的方程，再结合函数的单调性或基本不等式求解．[题点通关]角度一 已知两个独立条件，求直线方程1．已知直线l 过圆x 2＋(y －3)2＝4的圆心，且与直线x ＋y ＋1＝0垂直，则l 的方程是( ) A ．x ＋y －2＝0 B ．x －y ＋2＝0C ．x ＋y －3＝0D ．x －y ＋3＝0D [解析] 已知圆x 2＋(y －3)2＝4的圆心为点(0，3)，又因为直线l 与直线x ＋y ＋1＝0垂直，所以直线l 的斜率k ＝1.由点斜式得直线l ：y －3＝x －0，化简得x －y ＋3＝0.角度二 已知直线方程及其他条件，求参数值或范围2．已知直线x ＋a 2y －a ＝0(a >0，a 是常数)，当此直线在x ，y 轴上的截距之和最小时，a 的值是( )A ．1B ．2C ．2D ．0A [解析] 直线方程可化为x a ＋y1a＝1，因为a >0，所以截距之和t ＝a ＋1a ≥2，当且仅当a ＝1a，即a ＝1时取等号．直线方程的综合问题[学生用书P144][典例引领]过点P (4，1)作直线l 分别交x ，y 轴正半轴于A ，B 两点． (1)当△AOB 面积最小时，求直线l 的方程； (2)当|OA |＋|OB |取最小值时，求直线l 的方程． 【解】 设直线l ：x a ＋yb ＝1(a >0，b >0)，因为直线l 经过点P (4，1)， 所以4a ＋1b ＝1.(1)4a ＋1b＝1≥24a ·1b ＝4ab， 所以ab ≥16，当且仅当a ＝8，b ＝2时等号成立，所以当a ＝8，b ＝2时，△AOB 的面积最小，此时直线l 的方程为x 8＋y2＝1，即x ＋4y －8＝0.(2)因为4a ＋1b ＝1，a >0，b >0，所以|OA |＋|OB |＝a ＋b＝(a ＋b )·⎝⎛⎭⎫4a ＋1b ＝5＋a b ＋4ba≥9，当且仅当a ＝6，b ＝3时等号成立， 所以当|OA |＋|OB |取最小值时， 直线l 的方程为x ＋2y －6＝0.直线方程的应用问题常见的类型及解法(1)与函数相结合命题：解决这类问题，一般是利用直线方程中x 、y 的关系，将问题转化成关于x 的某函数，借助函数性质来解决．(2)与方程、不等式相结合命题：一般是利用方程、不等式等知识来解决．已知直线l ：kx －y ＋1＋2k ＝0(k ∈R )．若直线l 交x 轴负半轴于A ，交y轴正半轴于B ，△AOB 的面积为S (O 为坐标原点)，求S 的最小值并求此时直线l 的方程．[解] 由l 的方程，得A ⎝⎛⎭⎫－1＋2k k ，0，B (0，1＋2k )．依题意得⎩⎪⎨⎪⎧－1＋2k k ＜0，1＋2k ＞0，解得k ＞0. 因为S ＝12·|OA |·|OB |＝12·⎪⎪⎪⎪1＋2k k ·|1＋2k |＝12·（1＋2k ）2k ＝12⎝⎛⎭⎫4k ＋1k ＋4 ≥12×(2×2＋4)＝4， “＝”成立的条件是k ＞0且4k ＝1k ，即k ＝12，所以S min ＝4，此时直线l 的方程为x －2y ＋4＝0., [学生用书P145])——分类讨论思想在求直线方程中的应用(2017·常州模拟)过点P (－2，3)且在两坐标轴上的截距相等的直线l 的方程为__________________．【解析】 (1)当截距不为0时，设所求直线方程为 x a ＋ya＝1，即x ＋y －a ＝0. 因为点P (－2，3)在直线l 上， 所以－2＋3－a ＝0，所以a ＝1， 所求直线l 的方程为x ＋y －1＝0.(2)当截距为0时，设所求直线方程为y ＝kx ， 则有3＝－2k ，即k ＝－32，此时直线l 的方程为y ＝－32x ，即3x ＋2y ＝0.综上，直线l 的方程为x ＋y －1＝0或3x ＋2y ＝0.【答案】 x ＋y －1＝0或3x ＋2y ＝0(1)在求与截距有关的直线方程时，注意对直线的截距是否为零进行分类讨论，防止忽视截距为零的情形，导致产生漏解．(2)常见的与截距问题有关的易误点有：“截距互为相反数”；“一截距是另一截距的几倍”等，解决此类问题时，要先考虑零截距情形，注意分类讨论思想的运用．(3)求直线方程时，还要断定直线是否具有斜率，应注意分类讨论，即应对斜率是否存在加以讨论．1.若直线过点P ⎝⎛⎭⎫－3，－32且被圆x 2＋y 2＝25截得的弦长是8，则该直线的方程为( )A ．3x ＋4y ＋15＝0B ．x ＝－3或y ＝－32C ．x ＝－3D ．x ＝－3或3x ＋4y ＋15＝0D [解析] 若直线的斜率不存在，则该直线的方程为x ＝－3，代入圆的方程解得y ＝±4，故该直线被圆截得的弦长为8，满足条件；若直线的斜率存在，不妨设直线的方程为y ＋32＝k (x ＋3)，即kx －y ＋3k －32＝0，因为该直线被圆截得的弦长为8，故半弦长为4.又圆的半径为5，则圆心(0，0)到直线的距离为52－42＝⎪⎪⎪⎪3k －32k 2＋1，解得k ＝－34，此时该直线的方程为3x ＋4y ＋15＝0.2．过点M (－3，5)且在两坐标轴上的截距互为相反数的直线方程为________． [解析] (1)当直线过原点时，直线方程为y ＝－53x ；(2)当直线不过原点时，设直线方程为x a ＋y－a ＝1，即x －y ＝a .代入点(－3，5)，得a ＝－8. 即直线方程为x －y ＋8＝0. [答案] y ＝－53x 或x －y ＋8＝0, [学生用书P275(独立成册)])1．倾斜角为135°，在y 轴上的截距为－1的直线方程是( ) A ．x －y ＋1＝0 B ．x －y －1＝0C ．x ＋y －1＝0D ．x ＋y ＋1＝0D [解析] 直线的斜率为k ＝tan 135°＝－1，所以直线方程为y ＝－x －1，即x ＋y ＋1＝0.2．已知直线l ：ax ＋y －2－a ＝0在x 轴和y 轴上的截距相等，则a 的值是( ) A ．1 B ．－1 C ．－2或－1D ．－2或1D [解析] 由题意可知a ≠0.当x ＝0时，y ＝a ＋2. 当y ＝0时，x ＝a ＋2a.所以a ＋2a＝a ＋2，解得a ＝－2或a ＝1.3．直线ax ＋by ＋c ＝0同时要经过第一、第二、第四象限，则a ，b ，c 应满足( ) A ．ab >0，bc <0 B ．ab >0，bc >0 C ．ab <0，bc >0D ．ab <0，bc <0A [解析] 由于直线ax ＋by ＋c ＝0经过第一、二、四象限，所以直线存在斜率，将方程变形为y ＝－a b x －c b .易知－a b <0且－cb>0，故ab >0，bc <0.4．两直线x m －y n ＝a 与x n －ym＝a (其中a 为不为零的常数)的图象可能是( )B [解析] 直线方程x m －y n ＝a 可化为y ＝n m x －na ，直线x n －y m ＝a 可化为y ＝mn x －ma ，由此可知两条直线的斜率同号．5．(2017·太原质检)若直线l 与直线y ＝1，x ＝7分别交于点P ，Q ，且线段PQ 的中点坐标为(1，－1)，则直线l 的斜率为( )A ．13B ．－13C ．－32D ．23B [解析] 依题意，设点P (a ，1)，Q (7，b )，则有⎩⎪⎨⎪⎧a ＋7＝2，b ＋1＝－2，解得a ＝－5，b ＝－3，从而可知直线l 的斜率为－3－17＋5＝－13.6．直线x －2y ＋b ＝0与两坐标轴所围成的三角形的面积不大于1，那么b 的取值范围是( )A ．[－2，2]B ．(－∞，－2]∪[2，＋∞)C ．[－2，0)∪(0，2]D ．(－∞，＋∞)C [解析] 令x ＝0，得y ＝b2，令y ＝0，得x ＝－b ，所以所求三角形的面积为12⎪⎪⎪⎪b 2|－b |＝14b 2，且b ≠0，14b 2≤1，所以b 2≤4，所以b 的取值范围是[－2，0)∪(0，2]．7．过点A (－1，－3)，斜率是直线y ＝3x 的斜率的－14的直线方程为________．[解析] 设所求直线的斜率为k ，依题意 k ＝－14×3＝－34.又直线经过点A (－1，－3)，因此所求直线方程为y ＋3＝－34(x ＋1)，即3x ＋4y ＋15＝0. [答案] 3x ＋4y ＋15＝08．直线l ：(a －2)x ＋(a ＋1)y ＋6＝0，则直线l 恒过定点________． [解析] 直线l 的方程变形为a (x ＋y )－2x ＋y ＋6＝0，由⎩⎪⎨⎪⎧x ＋y ＝0，－2x ＋y ＋6＝0，解得x ＝2，y ＝－2，所以直线l 恒过定点(2，－2)． [答案] (2，－2)9．设点A (－1，0)，B (1，0)，直线2x ＋y －b ＝0与线段AB 相交，则b 的取值范围是________．[解析] b 为直线y ＝－2x ＋b 在y 轴上的截距，如图，当直线y ＝－2x ＋b 过点A (－1，0)和点B (1，0)时，b 分别取得最小值和最大值． 所以b 的取值范围是[－2，2]． [答案] [－2，2]10．已知直线l 1：ax －2y ＝2a －4，l 2：2x ＋a 2y ＝2a 2＋4，当0＜a ＜2时，直线l 1，l 2与两坐标轴围成一个四边形，当四边形的面积最小时，a ＝________．[解析] 由题意知直线l 1，l 2恒过定点P (2，2)，直线l 1的纵截距为2－a ，直线l 2的横截距为a 2＋2，所以四边形的面积S ＝12×2×(2－a )＋12×2×(a 2＋2)＝a 2－a ＋4＝⎝⎛⎭⎫a －122＋154，当a ＝12时，面积最小．[答案] 1211．△ABC 的三个顶点分别为A (－3，0)，B (2，1)，C (－2，3)，求： (1)BC 边所在直线的方程；(2)BC 边上中线AD 所在直线的方程； (3)BC 边的垂直平分线DE 的方程．[解] (1)因为直线BC 经过B (2，1)和C (－2，3)两点， 由两点式得BC 的方程为y －13－1＝x －2－2－2，即x ＋2y －4＝0.(2)设BC 边的中点D 的坐标为(x ，y )， 则x ＝2－22＝0，y ＝1＋32＝2.BC 边的中线AD 过点A (－3，0)，D (0，2)两点， 由截距式得AD 所在直线的方程为x －3＋y2＝1，即2x －3y ＋6＝0.(3)由(1)知，直线BC 的斜率k 1＝－12，则BC 的垂直平分线DE 的斜率k 2＝2，由(2)知，点D 的坐标为(0，2)．由点斜式得直线DE 的方程为y －2＝2(x －0)， 即2x －y ＋2＝0.12．直线l 过点P (1，0)，且与以A (2，1)，B (0，3)为端点的线段有公共点，则直线l 斜率的取值范围为________．[解析] 如图，因为k AP ＝1－02－1＝1， k BP ＝3－00－1＝－3， 所以k ∈(－∞，－3]∪[1，＋∞)． [答案] (－∞，－3]∪[1，＋∞)13．设直线l 的方程为x ＋my －2m ＋6＝0，根据下列条件分别确定m 的值： (1)直线l 的斜率为1； (2)直线l 在x 轴上的截距为－3.[解] (1)因为直线l 的斜率存在，所以m ≠0， 于是直线l 的方程可化为y ＝－1m x ＋2m －6m .由题意得－1m ＝1，解得m ＝－1.(2)法一：令y ＝0，得x ＝2m －6. 由题意得2m －6＝－3，解得m ＝32.法二：直线l 的方程可化为x ＝－my ＋2m －6.由题意得2m －6＝－3，解得m ＝32.14. 如图，射线OA ，OB 分别与x 轴正半轴成45°和30°角，过点P (1，0)作直线AB 分别交OA ，OB 于A ，B 两点，当AB 的中点C 恰好落在直线y ＝12x 上时，求直线AB 的方程．[解] 由题意可得k OA ＝tan 45°＝1， k OB ＝tan(180°－30°)＝－33， 所以直线l OA ：y ＝x ，l OB ：y ＝－33x . 设A (m ，m )，B (－3n ，n )， 所以AB 的中点C ⎝⎛⎭⎪⎫m －3n 2，m ＋n 2，由点C 在直线y ＝12x 上，且A ，P ，B 三点共线得⎩⎪⎨⎪⎧m ＋n 2＝12·m －3n 2，m －0m －1＝n －0－3n －1，解得m ＝3，所以A (3，3)． 又P (1，0)，所以k AB ＝k AP ＝33－1＝3＋32，所以l AB ：y ＝3＋32(x －1)，即直线AB 的方程为(3＋3)x －2y －3－3＝0.。

课时规范练45直线的倾斜角、斜率与直线的方程基础巩固组1把直线x-y+√5-1=0绕点(1,√5)逆时针旋转15°后,所得直线/的方程是()A.>,=-V3ΛBJ=V5XC.x-V3y+2=OD.x+V3y-2=O答案:B解析:已知直线的斜率为1,则其倾斜角为45°,绕点(1,遮)逆时针旋转15°后,得到的直线/的倾斜角α=45°+15°=60°,直线/的斜率为tanα=tan600=√5,，直线/的方程为y-y/3=g(x-1),即y=y∕3x.2.(2023上海静安期中)设直线的斜率Z∈(∙8,-1]U[1,+oo),则该直线的倾斜角。

满足()A.--≤α≤-B.-≤α<-gg-<α≤—4 4 4 2 2 4TT.Ir r v TT .3TTC.-≤a<-D.-<a≤—4 2 2 4答案:B解析:因为A=tan0,所以当Ar≤-1时;<α≤邺,当左21时；≤α<A即直线的倾斜角a满足2 442-≤α<-或-<a≤郊.故选B.4 2 2 43.若经过两点44,2尹1)网2,-3)的直线的倾斜角为季则/等于()A.-1B.-3C.0D.2答案:B解析:由女=支竺二tan邳=-1,得-4-2y=2,所以y=-3.故选B.4.直线/经过点41,2),在/轴上的截距的取值范围是(-3,3),则其斜率的取值范围是()A.(-1,pB.(-∞,pU(1,+∞)C.(-∞,-1)U +8)D.(-oo,-1)∪(#8)答案:D解析:设直线的斜率为匕则直线方程为y-2=&(x-1),令尸0,得直线/在X轴上的截距为则-3<1]<3,解得左。

或%</.故选D.k25.(2023广东深圳调研)方程y=ax j fb和y=bx+a表示的直线可能是( )答案:D解析:根据题意,依次分析选项:对于A,对于y=αr+"图像经过第一、二、三象限,则4>0力>0J=H+。

第八章 解析几何与圆锥曲线 第一节 直线的倾斜角与斜率强化训练当堂巩固1.斜率为2的直线的倾斜角α所在的范围是… ( ) A.0 45α<< B.45 90α<< C.90 135α<< D.135 180α<< 答案:B解析:∵k=2>1,即tan 1α>,∴45 90α<< .2.过点M(-2,m),N(m,4)的直线的斜率等于1,则m 的值为( ) A.1 B.4 C.1或3 D.1或4 答案:A解析:由412m m-=,--得m=1.3.已知两条直线y=ax-2和y=(a+2)x+1互相垂直,则a 等于( ) A.2 B.1 C.0 D.-1 答案:D解析:由题意知22(2)121(1)0a a a a a +⨯=-⇒++=+=,∴a=-1.也可以代入检验. 4.已知直线1l 过点A(2,3)和B(-2,6),直线2l 过点C(6,6)和D(10,3).则1l 与2l 的位置关系为 . 答案:1l ∥2l解析:∵126336332246104l l k k --==-,==-,---∴12l l k k =.结合图知1l 与2l 不重合,∴1l ∥2l .5.点P(-1,3)在直线l 上的射影为点Q(1,-1),则直线l 的方程是 . 答案:x-2y-3=0解析:由题意知111312l k --,=-=,+∴直线l 的方程是11(1)2y x +=-,即x-2y-3=0.6.已知点M(2,5),N(1,1),在y 轴上找一点P,使90MPN ∠= ,求点P 的坐标. 解:设点P(0,y),根据题意,有PM PN ⊥,5121PM PN y yk k --=,=, 则51121PM PN y yk k --⨯=⨯=-,即2670y y -+=,解得3y =±即点P 的坐标为(03,.课后作业巩固提升题组一 直线的倾斜角1.若直线x=1的倾斜角为α,则α等于( ) A.0B.45C.90D.不存在答案:C2.已知直线l 过点P(3,4),它的倾斜角是直线y=x+1的两倍,则直线l 的方程为( )A.y-4=2(x-3)B.y-4=x-3C.y-4=0D.x-3=0 答案:D题组二 直线的斜率及应用 3.下列说法中正确的是( )A.平行的两条直线的斜率一定存在且相等B.平行的两条直线的倾斜角一定相等C.垂直的两直线的斜率之积为-1D.只有斜率相等的两条直线才一定平行 答案:B4.已知两点A(-1,-5),B(3,-2),若直线l 的倾斜角是直线AB 倾斜角的一半,则l 的斜率是 .答案:13解析:设直线AB 的倾斜角为2α,则直线l 的倾斜角为α,由于0 2180α≤< , ∴0 90α≤< .由tan 2α=2(5)33(1)4---=,--得tan 13α=,即直线l 的斜率为13.题组三 两条直线的平行与垂直5.若直线1l ,l 2的倾斜角分别为1α,2α,且12l l ⊥,则有( ) A.1290αα-= B.2190αα-= C.|21αα-|=90D.12180αα+=答案:C6.光线从点A(2,1)出发射到y 轴上的点Q,再经y 轴反射后过点B(4,3),则反射光线所在直线的斜率是 .答案:13解析:由物理中光的几何性质,可作A(2,1)关于y 轴的对称点A′(-2,1),并设入射点Q(0,b),则A′,Q,B 三点共线,∴ A Q BQ k k '=.∴130(2)40b b --=,---解得53b =.∴13BQ k =.7.已知直线ax-by-2=0与曲线y=3x 在点P(1,1)处的切线互相垂直,则a b为( )A.23B.23-C.13D.13-答案:D解析:曲线3y x =在点P(1,1)处的切线斜率为3, 所以13a b=-.8.若过点A(2,-2),B(5,0)的直线与过点P(2m,1),Q(-1,-m)的直线平行,则m= . 答案:1解析:201225321AB PQ m k k m --+==,=,-+因为直线AB 与PQ 平行,所以12321m m +=,+解得m=1.题组四 直线的倾斜角和斜率的综合问题9.若关于x 的方程|x-1|-kx=0有且只有一个正实数根,则实数k 的取值范围是 . 答案:1k ≥或k=0解析:数形结合.在同一坐标系内画出函数y=kx,y=|x-1|的图象如图所示,显然1k ≥或k=0时满足题意.10.已知点A(2,3),B(-5,2),若直线l 过点P(-1,6),且与线段AB 相交,则该直线倾斜角的取值范围是 .答案:3[]44ππ,解析:如图所示,63112PA k -==-,--∴直线PA 的倾斜角为34π.6211(5)PB k -==,---∴直线PB 的倾斜角为4π.从而直线l 的倾斜角的范围是3[]44ππ,.11.已知过原点O 的一条直线与函数y=log 8x 的图象交于A 、B 两点,分别过点A 、B 作y 轴的平行线与函数y=log 2x 的图象交于C 、D 两点.(1)证明点C 、D 和原点O 在同一直线上. (2)当BC 平行于x 轴时,求点A 的坐标.解:(1)证明:设A 、B 的横坐标分别为1x 、2x ,由题设知1x 211x >,>,点1(A x ,log 812)(x B x ,,log 82)x . 因为A 、B 在过点O 的直线上,所以128812x x log log x x =,又点C 、D 的坐标分别为1(x ,log 21)x 、2(x ,log 22)x . 由于log 213x =log 81x ,log 223x =log 82x , 则1212882211223x 3x x x log log log log OC OD k k x x x x ==,==.由此得OC OD k k =,即O 、C 、D 在同一直线上. (2)由BC 平行于x 轴,有log 21x =log 82x , 又log 213x =log 81x ,所以321x x =, 将其代入128812x x log log x x =得31x log 8113x x =log 81x ,由于11x >知log 810x ≠,故31113x x x =,=于是Alog .高考学习网－中国最大高考学习网站 | 我们负责传递知识！。

课时跟踪练(五十二) A 组 基础巩固 1．倾斜角为135°，在y 轴上的截距为－1的直线方程是()A ．x －y ＋1＝0B ．x －y －1＝0C ．x ＋y －1＝0D ．x ＋y ＋1＝0解析：直线的斜率为k ＝tan 135°＝－1，所以直线方程为y ＝－x －1，即x ＋y ＋1＝0.答案：D2．直线l ：x sin 30°＋y cos 150°＋1＝0的斜率是()A.33B. 3 C ．－3D ．－33 解析：设直线l 的斜率为k ，则k ＝－sin 30°cos 150°＝33. 答案：A3．(2019·海淀区模拟)过点(2，1)且倾斜角比直线y ＝－x －1的倾斜角小π4的直线方程是()A ．x ＝2B ．y ＝1C ．x ＝1D ．y ＝2解析：因为直线y ＝－x －1的斜率为－1，则倾斜角为3π4，依题意，所求直线的倾斜角为3π4－π4＝π2， 所以斜率不存在，所以过点(2，1)的直线方程为x ＝2.答案：A4．(2019·某某调研)在同一平面直角坐标系中，直线l 1：ax ＋y ＋b ＝0和直线l 2：bx ＋y ＋a ＝0有可能是()解析：当a >0，b >0时，－a <0，－b <0.选项B 符合．答案：B5.如图中的直线l 1，l 2，l 3的斜率分别为k 1，k 2，k 3，则()A ．k 1<k 2<k 3B ．k 3<k 1<k 2C ．k 3<k 2<k 1D ．k 1<k 3<k 2解析：直线l 1的倾斜角α1是钝角，故k 1<0，直线l 2与l 3的倾斜角α2与α3均为锐角且α2>α3，所以0<k 3<k 2，因此k 1<k 3<k 2，故选D.答案：D6．(2019·某某一模)已知直线l 的斜率为3，在y 轴上的截距为另一条直线x －2y －4＝0的斜率的倒数，则直线l 的方程为()A ．y ＝3x ＋2B ．y ＝3x －2C ．y ＝3x ＋12D ．y ＝－3x ＋2 解析：因为直线x －2y －4＝0的斜率为12，所以直线l 在y 轴上的截距为2，所以直线l 的方程为y ＝3x ＋2.故选A.答案：A7．设直线ax ＋by ＋c ＝0的倾斜角为α，且sin α＋cos α＝0，则a ，b 满足()A ．a ＋b ＝1B ．a －b ＝1C ．a ＋b ＝0D ．a －b ＝0解析：由sin α＋cos α＝0，得sin αcos α＝－1，即tan α＝－1. 又因为tan α＝－a b ，所以－a b＝－1，则a ＝b ，即a －b ＝0.答案：D8．直线x －2y ＋b ＝0与两坐标轴围成的三角形的面积不大于1，那么b 的取值X 围是()A ．[－2，2]B ．(－∞，－2]∪[2，＋∞)C ．[－2，0)∪(0，2]D ．(－∞，＋∞)解析：令x ＝0，得y ＝b 2，令y ＝0，得x ＝－b ，所以所围三角形的面积为12×⎪⎪⎪⎪⎪⎪b 2×|－b |＝14b 2，所以14b 2≤1，所以b 2≤4，又由题意知b ≠0，所以b ∈[－2，0)∪(0，2]．答案：C9．不论实数m 为何值，直线mx －y ＋2m ＋1＝0恒过定点________．解析：直线mx －y ＋2m ＋1＝0可化为m (x ＋2)＋(－y ＋1)＝0，因为m ∈R ，所以⎩⎪⎨⎪⎧x ＋2＝0，－y ＋1＝0，所以x ＝－2，y ＝1， 所以直线mx －y ＋2m ＋1＝0恒过定点(－2，1)．答案：(－2，1)10．已知三角形的三个顶点A (－5，0)，B (3，－3)，C (0，2)，则BC 边上中线所在的直线方程为________．解析：BC 边的中点坐标为⎝ ⎛⎭⎪⎫32，－12，所以BC 边上中线所在的直线方程为y －0－12－0＝x ＋532＋5，即x ＋13y ＋5＝0.答案：x ＋13y ＋5＝011．设点A (－1，0)，B (1，0)，直线2x ＋y －b ＝0与线段AB 相交，则b 的取值X 围是________．解析：b 为直线y ＝－2x ＋b 在y 轴上的截距，如图，当直线y ＝－2x ＋b 过点A (－1，0)和点B (1，0)时，b 分别取得最小值和最大值， 所以b 的取值X 围是[－2，2]．答案：[－2，2]12．若直线l 经过点A (1，2)，在x 轴上的截距的取值X 围是(－3，3)，则其斜率的取值X 围是________．解析：设直线l 的斜率为k ，则k ≠0，直线方程为y －2＝k (x －1)，在x 轴上的截距为1－2k.令－3<1－2k <3，解得k <－1或k >12. 答案：(－∞，－1)∪⎝ ⎛⎭⎪⎫12，＋∞ B 组 素养提升13．(2019·某某四地七校联考)已知函数f (x )＝a sin x －b cos x (a ≠0，b ≠0)，若f ⎝ ⎛⎭⎪⎫π4－x ＝f ⎝ ⎛⎭⎪⎫π4＋x ，则直线ax －by ＋c ＝0的倾斜角为() A.π4B.π3C.2π3D.3π4 解析：由f ⎝ ⎛⎭⎪⎫π4－x ＝f ⎝ ⎛⎭⎪⎫π4＋x 知函数f (x )的图象关于x ＝π4对称，所以f (0)＝f ⎝ ⎛⎭⎪⎫π2，所以a ＝－b ，由直线ax －by ＋c ＝0知其斜率为k ＝a b ＝－1，所以直线的倾斜角为3π4，故选D.答案：D14．(2019·某某一模)已知动直线l 0：ax ＋by ＋c －2＝0(a ＞0，c ＞0)恒过点P (1，m )，且Q (4，0)到动直线l 0的最大距离为3，则12a ＋2c的最小值为() A.92B.94C ．1D ．9 解析：动直线l 0：ax ＋by ＋c －2＝0(a ＞0，c ＞0)恒过点P (1，m )，所以a ＋bm ＋c －2＝0.又Q (4，0)到动直线l 0的最大距离为3， 所以（4－1）2＋（0－m ）2＝3，解得m ＝0.所以a ＋c ＝2.又a ＞0，c ＞0，所以12a ＋2c ＝12(a ＋c )⎝ ⎛⎭⎪⎫12a ＋2c ＝12(52＋c 2a ＋2a c)≥12⎝ ⎛⎭⎪⎫52＋2c 2a ·2a c ＝94， 当且仅当c ＝2a ＝43时取等号，故选B. 答案：B15．已知A (3，0)，B (0，4)，直线AB 上一动点P (x ，y )，则xy 的最大值是________．解析：直线AB 的方程为x 3＋y 4＝1. 因为动点P (x ，y )在直线AB 上，则x ＝3－34y ， 所以xy ＝3y －34y 2＝－34(y 2－4y )＝－34(y －2)2＋3≤3， 即当P 点坐标为⎝ ⎛⎭⎪⎫32，2时，xy 取最大值3. 答案：316．(2019·某某一中模拟)在平面直角坐标系中，如果x 与y 都是整数，就称点(x ，y )为整点，下列命题中正确的是________(写出所有正确命题的编号)．①存在这样的直线，既不与坐标轴平行又不经过任何整点；②若k 与b 都是无理数，则直线y ＝kx ＋b 不经过任何整点；③直线l 经过无穷多个整点，当且仅当l 经过两个不同的整点；④直线y ＝kx ＋b 经过无穷多个整点的充要条件是k 与b 都是有理数；⑤存在恰经过一个整点的直线．解析：对于①，比如直线y ＝2x ＋3，当x 取整数时，y 始终是一个无理数，即直线y ＝2x ＋3既不与坐标轴平行又不经过任何整点，①正确；对于②，直线y ＝2x －2中k 与b 都是无理数，但直线经过整点(1，0)，②错误；对于③，当直线经过两个整点时，它经过无数多个整点，③正确；对于④，当k ＝0，b ＝12时，直线y ＝12不经过任何整点，④错误；对于⑤，比如直线y ＝2x －2只经过一个整点(1，0)，⑤正确．故答案为①③⑤.答案：①③⑤。

第八章 第一节 直线的倾斜角与斜率、直线的方程一、选择题1．已知过点A (－2，m )和B (m,4)的直线与直线2x ＋y －1＝0平行，则m 的值为 ( ) A ．0 B ．－8 C ．2D ．10解析：由k ＝4－m m ＋2＝－2，得m ＝－8.答案：B2．(2012·宜宾模拟)直线x sin α＋y ＋2＝0的倾斜角的取值范围是 ( )A ．[0，π)B ．[0，π4]∪[3π4，π)C ．[0，π4]D ．[0，π4]∪(π2，π)解析：设题中直线的倾斜角为θ，则有tan θ＝－sin α，其中sin α∈[－1,1]．又θ∈[0，π)，所以0≤θ≤π4或3π4≤θ<π 答案：B3．直线2x －y －2＝0绕它与y 轴的交点逆时针旋转π2所得的直线方程是 ( )A ．x －2y ＋4＝0B ．x ＋2y －4＝0C ．x －2y －4＝0D ．x ＋2y ＋4＝0解析：直线2x －y －2＝0与y 轴的交点为A (0，－2)， 所求直线过A 且斜率为－12，∴所求直线方程：y ＋2＝－12(x －0)，即x ＋2y ＋4＝0.答案：D4．设点A (－2,3)，B (3,2)，若直线ax ＋y ＋2＝0与线段AB 没有交点，则a 的取值范围是( )A ．(－∞，－52]∪[43，＋∞)B ．(－43，52)C ．[－52，43]D ．(－∞，－43]∪[52，＋∞)解析：直线ax ＋y ＋2＝0恒过点M (0，－2)，且斜率为－a ， ∵k MA ＝3－－2－2－0＝－52，k MB ＝2－－23－0＝43，由图可知：－a >－52且－a <43，∴a ∈(－43，52)．答案：B5．(2012·皖南八校联考)已知直线a 2x ＋y ＋2＝0与直线bx －(a 2＋1)y －1＝0互相垂直，则|ab |的最小值为 ( )A ．5B ．4C ．2D ．1解析：由题意知，a 2b －(a 2＋1)＝0且a ≠0，∴a 2b ＝a 2＋1，∴ab ＝a 2＋1a ＝a ＋1a，∴|ab |＝|a ＋1a |＝|a |＋1|a |≥2.(当且仅当a ＝±1时取“＝”)．答案：C6．直线Ax ＋By －1＝0在y 轴上的截距是－1，而且它的倾斜角是直线3x －y ＝33的倾斜角的2倍，则 ( )A ．A ＝3，B ＝1B ．A ＝－3，B ＝－1C ．A ＝3，B ＝－1D ．A ＝－3，B ＝1解析：将直线Ax ＋By －1＝0化成斜截式y ＝－A Bx ＋1B.∵1B＝－1，∴B ＝－1，故排除A 、D.又直线3x －y ＝33的倾斜角α＝π3，∴直线Ax ＋By －1＝0的倾斜角为2α＝2π3，∴斜率－A B ＝tan 2π3＝－3，∴A ＝－ 3. 答案：B 二、填空题7．将一张坐标纸折叠一次，使得点(0,2)与点(4,0)重合，点(7,3)与点(m ，n )重合，则m ＋n ＝________.解析：由题可知纸的折痕应是点(0,2)与点(4,0)连线的中垂线，即直线y ＝2x －3，它也是点(7,3)与点(m ，n )连线的中垂线，于是⎩⎪⎨⎪⎧3＋n 2＝2×7＋m2－3n －3m －7＝－12，解得⎩⎪⎨⎪⎧m ＝35n ＝315.故m ＋n ＝345.答案：3458．(2012·长沙模拟)已知A (3,0)，B (0,4)，直线AB 上一动点P (x ，y )，则xy 的最大值是________．解析：直线AB 的方程为x 3＋y 4＝1，P (x ，y )，则x ＝3－34y ，∴xy ＝3y －34y 2＝34(－y 2＋4y )＝34[－(y －2)2＋4]≤3. 答案：39．与直线3x ＋4y ＋12＝0平行，且与坐标轴构成的三角形的面积是24的直线l 的方程是____________________．解析：先由“平行”这个条件设出直线方程为3x ＋4y ＋m ＝0，再用“面积”条件求m .因为直线l 交x 轴于A (－m 3，0)，交y 轴于B (0，－m 4)，由12·|－m 3|·|－m4|＝24，可得m ＝±24.所以，所求直线的方程为：3x ＋4y ±24＝0.答案：3x ＋4y ＋24＝0或3x ＋4y －24＝0 三、解答题10．在△ABC 中，已知A (5，－2)、B (7,3)，且AC 边的中点M 在y 轴上，BC 边的中点N 在x 轴上，求：(1)顶点C 的坐标； (2)直线MN 的方程．解：(1)设点C 的坐标为(x ，y )，则有x ＋52＝0，3＋y2＝0， ∴x ＝－5，y ＝－3.即点C 的坐标为(－5，－3)．(2)由题意知，M (0，－52)，N (1,0)，∴直线MN 的方程为x －y52＝1，即5x －2y －5＝0.11．已知两点A (－1,2)，B (m,3)． (1)求直线AB 的方程； (2)已知实数m ∈[－33－1，3－1]，求直线AB 的倾斜角α的取值范围． 解：(1)当m ＝－1时，直线AB 的方程为x ＝－1， 当m ≠－1时，直线AB 的方程为y －2＝1m ＋1(x ＋1)． (2)①当m ＝－1时，α＝π2；②当m ≠－1时，m ＋1∈[－33，0)∪(0，3]， ∴k ＝1m ＋1∈(－∞，－3]∪[33，＋∞)， ∴α∈[π6，π2)∪(π2，2π3]．综合①②知，直线AB 的倾斜角α的取值范围为[π6，23π]．12.为了绿化城市，拟在矩形区域ABCD 内建一个矩形草坪(如图所示)，另外，△AEF 内部有一文物保护区不能占用，经测量AB ＝100 m ，BC ＝80 m ，AE ＝30 m ，AF ＝20 m ，应如何设计才能使草坪面积最大？解：建立如图所示直角坐标系，则E (30,0)，F (0,20)，于是，线段EF 的方程是x 30＋y20＝1(0≤x ≤30)，在线段EF 上取点P (m ，n )，作PQ ⊥BC 于点Q ，PR ⊥CD 于点R ，设矩形PQCR 的面积为S ，则：S ＝|PQ |·|PR |＝(100－m )(80－n )，因为m 30＋n 20＝1，所以n ＝20(1－m30)，所以S ＝(100－m )(80－20＋23m )＝－23(m －5)2＋18 0503(0≤m ≤30)，于是，当m ＝5时，S 有最大值，这时|EP ||PF |＝51.答：当草坪矩形的两边在BC ，CD 上，一个顶点在线段EF 上，且这个顶点分EF 成5∶1时，草坪面积最大。

课时跟踪检测（四十六） 直线的倾斜角与斜率、直线的方程(二)重点高中适用作业A 级——保分题目巧做快做1．在同一平面直角坐标系中，直线l 1：ax ＋y ＋b ＝0和直线l 2：bx ＋y ＋a ＝0有可能是( )解析：选B 由题意l 1：y ＝－ax －b ，l 2：y ＝－bx －a ，当a ＞0，b ＞0时，－a ＜0，－b ＜0.选项B 符合．2．直线x ＋(a 2＋1)y ＋1＝0的倾斜角的取值范围是( )A.⎣⎢⎡⎦⎥⎤0，π4B.⎣⎢⎡⎭⎪⎫3π4，πC.⎣⎢⎡⎦⎥⎤0，π4∪⎝ ⎛⎭⎪⎫π2，π D.⎣⎢⎡⎭⎪⎫π4，π2∪⎣⎢⎡⎭⎪⎫3π4，π 解析：选B 由直线方程可得该直线的斜率为－1a 2＋1，又－1≤－1a 2＋1＜0，所以倾斜角的取值范围是⎣⎢⎡⎭⎪⎫3π4，π.3．直线l 经过点A (1,2)，在x 轴上的截距的取值范围是(－3,3)，则其斜率的取值范围是( )A.⎝⎛⎭⎪⎫－1，15 B.⎝⎛⎭⎪⎫－∞，12∪(1，＋∞)C.()－∞，－1∪⎝ ⎛⎭⎪⎫15，＋∞D ．(－∞，－1)∪⎝ ⎛⎭⎪⎫12，＋∞解析：选D 设直线方程为y －2＝k (x －1)，直线在x 轴上的截距为1－2k，令－3<1－2k<3，解不等式得k >12或k <－1.4．在等腰三角形MON 中，MO ＝MN ，点O (0,0)，M (－1,3)，点N 在x 轴的负半轴上，则直线MN 的方程为( )A ．3x －y －6＝0B ．3x ＋y ＋6＝0C ．3x －y ＋6＝0D ．3x ＋y －6＝0解析：选C 因为MO ＝MN ，所以直线MN 的斜率与直线MO 的斜率互为相反数，所以k MN＝－k MO ＝3，所以直线MN 的方程为y －3＝3(x ＋1)，即3x －y ＋6＝0，选C.5．若直线l 与直线y ＝1，x ＝7分别交于点P ，Q ，且线段PQ 的中点坐标为(1，－1)，则直线l 的斜率为( )A.13 B ．－13C ．－32D.23解析：选B 依题意，设点P (a,1)，Q (7，b )，则有⎩⎪⎨⎪⎧a ＋7＝2，b ＋1＝－2，解得a ＝－5，b ＝－3，从而可知直线l 的斜率为－3－17＋5＝－13.6．已知直线l 过点(1,0)，且倾斜角为直线l 0：x －2y －2＝0的倾斜角的2倍，则直线l 的方程为________．解析：由题意可设直线l 0，l 的倾斜角分别为α，2α， 因为直线l 0：x －2y －2＝0的斜率为12，则tan α＝12，所以直线l 的斜率k ＝tan 2α＝2tan α1－tan 2α＝2×121－⎝ ⎛⎭⎪⎫122＝43， 所以由点斜式可得直线l 的方程为y －0＝43(x －1)，即4x －3y －4＝0. 答案：4x －3y －4＝07．过点(2，－3)且在两坐标轴上的截距互为相反数的直线方程为________． 解析：若直线过原点，则直线方程为3x ＋2y ＝0；若直线不过原点，则斜率为1，方程为y ＋3＝x －2，即为x －y －5＝0，故所求直线方程为3x ＋2y ＝0或x －y －5＝0.答案：3x ＋2y ＝0或x －y －5＝08．设点A (－1,0)，B (1,0)，直线2x ＋y －b ＝0与线段AB 相交，则b 的取值范围是________．解析：b 为直线y ＝－2x ＋b 在y 轴上的截距，如图，当直线y ＝－2x ＋b 过点A (－1,0)和点B (1,0)时，b 分别取得最小值和最大值．∴b 的取值范围是[－2,2]．答案：[－2,2]9．已知直线l 与两坐标轴围成的三角形的面积为3，分别求满足下列条件的直线l 的方程：(1)过定点A (－3,4)； (2)斜率为16.解：(1)设直线l 的方程为y ＝k (x ＋3)＋4，它在x 轴，y 轴上的截距分别是－4k－3,3k＋4，由已知，得(3k ＋4)⎝ ⎛⎭⎪⎫4k＋3＝±6，解得k 1＝－23或k 2＝－83.故直线l 的方程为2x ＋3y －6＝0或8x ＋3y ＋12＝0. (2)设直线l 在y 轴上的截距为b ，则直线l 的方程为y ＝16x ＋b ，它在x 轴上的截距是－6b ，由已知，得|－6b ·b |＝6，∴b ＝±1.∴直线l 的方程为x －6y ＋6＝0或x －6y －6＝0.10.如图，射线OA ，OB 分别与x 轴正半轴成45°和30°角，过点P (1，0)的直线AB 分别交OA ，OB 于A ，B 两点，当AB 的中点C 恰好落在直线y ＝12x 上时，求直线AB 的方程．解：由题意可得k OA ＝tan 45°＝1，k OB ＝tan(180°－30°)＝－33， 所以直线l OA ：y ＝x ，l OB ：y ＝－33x . 设A (m ，m )，B (－3n ，n )， 所以AB 的中点C ⎝⎛⎭⎪⎫m －3n 2，m ＋n 2，由点C 在直线y ＝12x 上，且A ，P ，B 三点共线得⎩⎪⎨⎪⎧m ＋n 2＝12·m －3n2，m －0m －1＝n －0－3n －1，解得m ＝3，所以A (3，3)． 又P (1,0)，所以k AB ＝k AP ＝33－1＝3＋32，所以l AB ：y ＝3＋32(x －1)，即直线AB 的方程为(3＋3)x －2y －3－3＝0.B 级——拔高题目稳做准做1．(2018·南昌一模)已知A (1,2)，B (2,11)，若直线y ＝⎝⎛⎭⎪⎫m －6m x ＋1(m ≠0)与线段AB相交，则实数m 的取值范围是( )A ．[－2,0)∪[3，＋∞)B ．(－∞，－1]∪(0,6]C ．[－2，－1]∪[3,6]D ．[－2,0)∪(0,6]解析：选C 由题意得，A (1,2)，B (2,11)两点分布在直线y ＝⎝⎛⎭⎪⎫m －6m x ＋1(m ≠0)的两侧(或其中一点在直线上)，∴⎝⎛⎭⎪⎫m －6m－2＋1⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫m －6m －11＋1≤0，解得－2≤m ≤－1或3≤m ≤6，故选C.2．若a ，b ，p (a ≠0，b ≠0，p >0)分别表示同一直线的横截距、纵截距及原点到直线的距离，则下列关系式成立的是( )A.1a 2＋1b 2＝1p 2B.1a 2－1b 2＝1p2C.1a2＋1p2＝1b2D.1a 2p2＝1b2解析：选A 由题意设直线方程为x a ＋y b＝1，则p 2＝11a2＋1b2，∴1a 2＋1b 2＝1p2，故选A.3．已知点A (－1,0)，B (1,0)，C (0,1)，直线y ＝ax ＋b (a >0)将△ABC 分割为面积相等的两部分，则b 的取值范围是( )A ．(0,1)B.⎝ ⎛⎭⎪⎫1－22，12C.⎝ ⎛⎦⎥⎤1－22，13 D.⎣⎢⎡⎭⎪⎫13，12 解析：选B 法一：(1)当直线y ＝ax ＋b 与AB ，BC 相交时，如图①所示．易求得：x M ＝－b a，y N ＝a ＋b a ＋1.由已知条件得：⎝ ⎛⎭⎪⎫1＋b a ·a ＋b a ＋1＝1，∴a ＝b 21－2b.∵点M 在线段OA 上，∴－1<－ba<0，∴0<b <a .∵点N 在线段BC 上，∴0<a ＋ba ＋1<1，∴b <1.由⎩⎪⎨⎪⎧b 21－2b >b ，b21－2b >0，b >0，解得13<b <12.(2)当直线y ＝ax ＋b 与AC ，BC 相交时，如图②所示．设|MC |＝m ，|NC |＝n ，则S △MCN ＝12mn ＝12，∴mn ＝1.显然，0<n <2，∴m ＝1n >22.又0<m ≤2且m ≠n .∴22<m ≤2且m ≠1. 设D 到AC ，BC 的距离为t ，则t m ＝|DN ||MN |，t n ＝|DM ||MN |， ∴t m ＋t n ＝|DN ||MN |＋|DM ||MN |＝1. ∴t ＝mn m ＋n ，∴1t ＝1m ＋1n ＝1m＋m . 而f (m )＝m ＋1m ⎝ ⎛⎭⎪⎫22<m ≤2且m ≠1的值域为⎝ ⎛⎦⎥⎤2，322，即2<1t ≤322，∴23≤t ＜12.∵b ＝1－CD ＝1－2t ，∴1－22＜b ≤13. 综合(1)(2)可得b 的取值范围是⎝ ⎛⎭⎪⎫1－22，12. 法二：由⎩⎪⎨⎪⎧x ＋y ＝1，y ＝ax ＋b 消去x ，得y ＝a ＋ba ＋1，当a ＞0时，直线y ＝ax ＋b 与x 轴交于点⎝ ⎛⎭⎪⎫－b a ，0，结合图形知12×a ＋b a ＋1×⎝ ⎛⎭⎪⎫1＋b a ＝12，化简得(a ＋b )2＝a (a ＋1)，则a ＝b 21－2b .∵a ＞0，∴b 21－2b ＞0，解得b ＜12.考虑极限位置，即a ＝0，此时易得b ＝1－22，故答案为B. 4．已知点P 在直线x ＋3y －2＝0上，点Q 在直线x ＋3y ＋6＝0上，线段PQ 的中点为M (x 0，y 0)，且y 0<x 0＋2，则y 0x 0的取值范围是________．解析：依题意可得|x 0＋3y 0－2|10＝|x 0＋3y 0＋6|10，化简得x 0＋3y 0＋2＝0，又y 0<x 0＋2，k OM ＝y 0x 0，在坐标轴上作出两直线，如图，当点M 位于线段AB (不包括端点)上时，k OM >0，当点M 位于射线BN 上除B 点外时，k OM <－13.所以y 0x 0的取值范围是⎝⎛⎭⎪⎫－∞，－13∪(0，＋∞)．答案：⎝⎛⎭⎪⎫－∞，－13∪(0，＋∞)5.已知直线l 过点P (3,2)，且与x 轴、y 轴的正半轴分别交于A ，B 两点，如图所示，当△ABO 的面积取最小值时，求直线l 的方程．解：法一：设A (a,0)，B (0，b )(a >0，b >0)， 则直线l 的方程为x a ＋y b＝1. 因为l 过点P (3,2)，所以3a ＋2b＝1.因为1＝3a ＋2b ≥26ab，整理得ab ≥24，所以S △ABO ＝12ab ≥12，当且仅当3a ＝2b，即a ＝6，b ＝4时取等号．此时直线l 的方程是x 6＋y4＝1，即2x ＋3y －12＝0.法二：依题意知，直线l 的斜率k 存在且k <0， 可设直线l 的方程为y －2＝k (x －3)(k <0)，则A ⎝⎛⎭⎪⎫3－2k，0，B (0,2－3k )，S △ABO ＝12(2－3k )⎝ ⎛⎭⎪⎫3－2k＝12⎣⎢⎡⎦⎥⎤12＋－9k ＋4－k≥12⎣⎢⎡⎦⎥⎤12＋2 －9k ·4－k＝12×(12＋12)＝12， 当且仅当－9k ＝4－k ，即k ＝－23时，等号成立． 所以所求直线l 的方程为2x ＋3y －12＝0. 6．已知直线l ：kx －y ＋1＋2k ＝0(k ∈R)． (1)证明：直线l 过定点；(2)若直线l 不经过第四象限，求k 的取值范围；(3)若直线l 交x 轴负半轴于点A ，交y 轴正半轴于点B ，O 为坐标原点，设△AOB 的面积为S ，求S 的最小值及此时直线l 的方程．解：(1)证明：直线l 的方程可化为y ＝k (x ＋2)＋1，故无论k 取何值，直线l 总过定点(－2,1)．(2)直线l 的方程为y ＝kx ＋2k ＋1，则直线l 在y 轴上的截距为2k ＋1，要使直线l 不经过第四象限，则⎩⎪⎨⎪⎧k ≥0，1＋2k ≥0，解得k ≥0，故k 的取值范围是[)0，＋∞.(3)依题意，直线l 在x 轴上的截距为－1＋2kk，在y 轴上的截距为1＋2k ，∴A ⎝⎛⎭⎪⎫－1＋2k k，0，B (0,1＋2k )． 又－1＋2k k<0且1＋2k >0，∴k >0.故S ＝12|OA ||OB |＝12×1＋2k k ×(1＋2k )＝12⎝⎛⎭⎪⎫4k ＋1k ＋4≥12(4＋4)＝4，当且仅当4k ＝1k ，即k ＝12时，取等号．故S 的最小值为4，此时直线l 的方程为x －2y ＋4＝0.。

⾼考数学⼀轮复习第⼋章平⾯解析⼏何8.1直线的倾斜⾓与斜率、直线的⽅程课时提升作业理直线的倾斜⾓与斜率、直线的⽅程(25分钟50分)⼀、选择题(每⼩题5分,共35分)1.直线x+y+1=0的倾斜⾓是( )A. B. C. D.【解析】选D.由直线的⽅程得直线的斜率为k=-,设倾斜⾓为α,则tanα=-,⼜α∈[0,π),所以α=.2.设直线ax+by+c=0的倾斜⾓为α,且sinα+cosα=0,则a,b满⾜( )A.a+b=1B.a-b=1C.a+b=0D.a-b=0【解析】选D.由题意得sinα=-cosα,显然cosα≠0,则tanα=-1,所以-=-1,a=b,a-b=0.3.下列命题中,正确的是( )A.直线的斜率为tanα,则直线的倾斜⾓是αB.直线的倾斜⾓为α,则直线的斜率为tanαC.直线的倾斜⾓越⼤,则直线的斜率就越⼤D.直线的倾斜⾓α∈∪时,直线的斜率分别在这两个区间上单调递增【解析】选D.因为直线的斜率k=tanα,且α∈∪时,α才是直线的倾斜⾓,所以A不对; 因为任⼀直线的倾斜⾓α∈[0,π),⽽当α=时,直线的斜率不存在,所以B不对;当α∈时,斜率⼤于0;当α∈时,斜率⼩于0,C不对.4.倾斜⾓为120°,在x轴上的截距为-1的直线的⽅程是( )A.x-y+1=0B.x-y-=0C.x+y-=0D.x+y+=0【解析】选 D.由于倾斜⾓为120°,故斜率k=-.⼜直线过点(-1,0),所以⽅程为y=-(x+1),即x+y+=0.5.已知直线l:ax+y-2-a=0在x轴和y轴上的截距相等,则实数a的值是( )A.1B.-1C.-2或-1D.-2或1【解析】选D.显然a≠0,由题意得a+2=,解得a=-2或1.6.(2016·西安模拟)点A(1,1)到直线xcosθ+ysinθ-2=0的距离的最⼤值是( )A.2B.2-C.2+D.4【解析】选C.由点到直线的距离公式,得d==2-sin,⼜θ∈R,所以d max=2+.7.已知a,b均为正数,且直线ax+by-6=0与直线2x+(b-3)y+5=0互相平⾏,则2a+3b的最⼩值为( )A.5B.25C.13D.15【解析】选B.因为直线ax+by-6=0与直线2x+(b-3)y+5=0互相平⾏,所以a(b-3)-2b=0,且5a+12≠0,所以3a+2b=ab,即+=1,⼜a,b均为正数,则2a+3b=(2a+3b)=4+9++≥13+2=25.当且仅当a=b=5时上式等号成⽴.⼆、填空题(每⼩题5分,共15分)8.已知直线的倾斜⾓是60°,在y轴上的截距是5,则该直线的⽅程为.【解析】因为直线的倾斜⾓是60°,所以直线的斜率为k=tan60°=.⼜因为直线在y轴上的截距是5,由斜截式得直线的⽅程为y=x+5.即x-y+5=0.答案:x-y+5=0【加固训练】过点A(-1,-3),斜率是直线y=3x的斜率的-的直线的⽅程为. 【解析】设所求直线的斜率为k,依题意k=-×3=-.⼜直线经过点A(-1,-3),因此所求直线⽅程为y+3=-(x+1),即3x+4y+15=0.答案:3x+4y+15=09.已知A(3,5),B(4,7),C(-1,x)三点共线,则x= .【解析】因为k AB==2,k AC==-.⼜A,B,C三点共线,所以k AB=k AC,即-=2,解得x=-3.答案:-310.(2016·平顶⼭模拟)与直线x+y-1=0垂直的直线的倾斜⾓为.【解析】因为直线x+y-1=0的斜率为k1=-,所以与直线x+y-1=0垂直的直线的斜率为k2=-=.所以它的倾斜⾓为.答案:(20分钟40分)1.(5分)(2016·保定模拟)直线y=tan的倾斜⾓等于( )A. B. C. D.0【解析】选D.因为tan=,所以y=tan即y=,表⽰⼀条与x轴平⾏的直线,因此直线y=tan的倾斜⾓等于0.2.(5分)已知点A(-1,0),B(cosα,sinα),且|AB|=,则直线AB的⽅程为( )A.y=x+或y=-x-B.y=x+或y=-x-C.y=x+1或y=-x-1D.y=x+或y=-x-【解析】选B.|AB|===,所以cosα=,sinα=±,所以k AB=±,即直线AB的⽅程为y=±(x+1),所以直线AB的⽅程为y=x+或y=-x-.【加固训练】已知直线l过点(0,2),且其倾斜⾓的余弦值为,则直线l的⽅程为( )A.3x-4y-8=0B.3x+4y-8=0C.3x+4y+8=0D.3x-4y+8=0【解析】选D.因为cosα=,α∈[0,π),所以sinα=,k=tanα=,所以直线l的⽅程为y-2=x,即3x-4y+8=0.3.(5分)过点(1,3)作直线l,若经过点(a,0)和(0,b),且a∈N*,b∈N*,则可作出的直线l的条数为( )A.1B.2C.3D.4【解析】选B.由题意得+=1?(a-1)(b-3)=3.⼜a∈N*,b∈N*,故有两个解或4.(12分)已知直线l过点P(0,1),且与直线l1:x-3y+10=0和l2:2x+y-8=0分别交于点A,B(如图).若线段AB被点P平分,求直线l的⽅程.【解析】因为点B在直线l2:2x+y-8=0上,故可设点B的坐标为(a,8-2a).因为点P(0,1)是线段AB的中点,得点A的坐标为(-a,2a-6).⼜因为点A在直线l1:x-3y+10=0上,故将A(-a,2a-6)代⼊直线l1的⽅程,得-a-3(2a-6)+10=0,解得a=4.所以点B的坐标是(4,0).因此,过P(0,1),B(4,0)的直线l的⽅程为+=1,即x+4y-4=0.【加固训练】已知直线l经过A(cosθ,sin2θ)和B(0,1)不同的两点,求直线l倾斜⾓的取值范围.【解析】当cosθ=0时,sin2θ=1-cos2θ=1,此时A,B重合.所以cosθ≠0.所以k==-cosθ∈[-1,0)∪(0,1].因此倾斜⾓的取值范围是∪.5.(13分)已知直线l:kx-y+1+2k=0(k∈R).(1)证明:直线l过定点.(2)若直线l不经过第四象限,求k的取值范围.(3)若直线l交x轴负半轴于点A,交y轴正半轴于点B,O为坐标原点,设△AOB的⾯积为S,求S的最⼩值及此时直线l的⽅程.【解析】(1)⽅法⼀:直线l的⽅程可化为y=k(x+2)+1,故⽆论k取何值,直线l总过定点(-2,1). ⽅法⼆:设直线l过定点(x0,y0),则kx0-y0+1+2k=0对任意k∈R恒成⽴,即(x0+2)k-y0+1=0恒成⽴,所以x0+2=0,-y0+1=0,解得x0=-2,y0=1,故直线l总过定点(-2,1).(2)直线l的⽅程为y=kx+2k+1,则直线l在y轴上的截距为2k+1,要使直线l不经过第四象限,则解得k的取值范围是[0,+∞).(3)依题意,直线l在x轴上的截距为-,在y轴上的截距为1+2k,所以A,B(0,1+2k).⼜-<0且1+2k>0,所以k>0.故S=|OA||OB|=×(1+2k)=≥(4+4)=4,当且仅当4k=,即k=时,取等号.故S的最⼩值为4,此时直线l的⽅程为x-2y+4=0.。

直线的倾斜角与斜率、直线的方程基础练一、选择题1．直线l ：x sin30°＋y cos150°＋1＝0的斜率是( )A.33B. 3 C ．－3D ．－332．[2021·秦皇岛模拟]倾斜角为120°，在x 轴上的截距为－1的直线方程是( ) A.3x －y ＋1＝0B.3x －y －3＝0 C.3x ＋y －3＝0D.3x ＋y ＋3＝03．若经过两点A (4,2y ＋1)，B (2，－3)的直线的倾斜角为3π4，则y 等于( )A ．－1B ．－3C ．0D ．2 4．[2021·河南安阳模拟]若平面内三点A (1，－a )，B (2，a 2)，C (3，a 3)共线，则a ＝( )A ．1±2或0B.2－52或0C.2±52D.2＋52或05．[2021·湖南衡阳八中月考]已知直线l 的倾斜角为θ且过点(3，1)，其中sin ⎝⎛⎭⎫θ－π2＝12，则直线l 的方程为( )A.3x －y －2＝0B.3x ＋y －4＝0 C ．x －3y ＝0D.3x ＋3y －6＝0 6．[2021·安徽四校联考]直线l 经过点(1,3)且与两坐标轴的正半轴围成的三角形面积为6，则直线l 的方程是( )A ．3x ＋y －6＝0B ．3x －y ＝0C ．x ＋3y －10＝0D ．x －3y ＋8＝07．一次函数y ＝－m n x ＋1n的图象同时经过第一、三、四象限的必要不充分条件是( )A ．m >1，且n <1B ．mn <0C ．m >0，且n <0D ．m <0，且n <08．直线Ax ＋By －1＝0在y 轴上的截距是－1，而且它的倾斜角是直线3x －y ＝33的倾斜角的2倍，则( )A ．A ＝3，B ＝1B ．A ＝－3，B ＝－1C ．A ＝3，B ＝－1D ．A ＝－3，B ＝19．直线2x cos α－y －3＝0⎝⎛⎭⎫α∈⎣⎡⎦⎤π6，π3的倾斜角的变化范围是( ) A.⎣⎡⎦⎤π6，π3B.⎣⎡⎦⎤π4，π3 C.⎣⎡⎦⎤π4，π2D.⎣⎡⎦⎤π4，2π310．经过点(0，－1)且与直线2x ＋3y －4＝0平行的直线方程为( ) A ．2x ＋3y ＋3＝0B ．2x ＋3y －3＝0 C ．2x ＋3y ＋2＝0D ．3x －2y －2＝0二、填空题11．若三点A (2,3)，B (3,2)，C ⎝⎛⎭⎫12，m 共线，则实数m ＝________. 12．直线l 过点P (1,0)，且与以A (2,1)，B (0，3)为端点的线段有公共点，则直线l 斜率的取值范围为________．13．[2021·贵州遵义四中月考]过点(2,3)且在两坐标轴上的截距互为相反数的直线方程为________．14．一条直线经过点A (－2,2)，并且与两坐标轴围成的三角形的面积为1，则此直线的方程为________． 能力练15．[2021·湖北孝感调研]已知点A (2，－3)，B (－3，－2)，直线l 的方程为－kx ＋y ＋k －1＝0，且与线段AB 相交，则直线l 的斜率k 的取值范围为( )A ．k ≥34或k ≤－4 B.k ≥34或k ≤－14C ．－4≤k ≤34D.34≤k ≤416．[2021·山西大同重点中学模拟]数学家欧拉在1765年提出定理：三角形的外心、重心、垂心依次位于同一直线上，且重心到外心的距离是重心到垂心距离的一半，这条直线被后人称为三角形的欧拉线，已知△ABC 的顶点A (4,0)，B (0,2)，且AC ＝BC ，则△ABC 的欧拉线方程为( )A ．x －2y ＋3＝0B ．2x ＋y －3＝0C ．x －2y －3＝0D ．2x －y －3＝0 17．[2021·百所名校单元示范卷]直线l 经过A (2,1)，B (1，m 2)，m ∈R 两点，那么直线l 的倾斜角α的取值范围为________．参考答案：1．解析：设直线l 的斜率为k ，则k ＝－sin30°cos150°＝33.故选A.答案：A2．解析：由于倾斜角为120°，故斜率k ＝－ 3.又直线过点(－1,0)，所以直线方程为y ＝－3(x ＋1)，即3x ＋y ＋3＝0.故选D.答案：D3．解析：由k ＝－3－2y －12－4＝tan 3π4＝－1.得－4－2y ＝2，∴y ＝－3.故选B. 答案：B4．解析：∵平面内三点A (1，－a )，B (2，a 2)，C (3，a 3)共线， ∴k AB ＝k AC ， 即a 2＋a 2－1＝a 3＋a 3－1，即a (a 2－2a －1)＝0， 解得a ＝0或a ＝1±2.故选A. 答案：A5．解析：∵sin ⎝⎛⎭⎫θ－π2＝12，∴cos θ＝－12，θ＝2π3，则tan θ＝－3，直线的方程为y －1＝－3(x －3)，即3x ＋y －4＝0，故选B.答案：B6．解析：解法一 设直线l 的斜率为k (k <0)，则直线l 的方程为y －3＝k (x －1)．x ＝0时，y ＝3－k ；y ＝0时，x ＝1－3k .所以直线与坐标轴所围成的三角形的面积S ＝12×(3－k )⎝⎛⎭⎫1－3k ＝6，整理得k 2＋6k ＋9＝0，解得k ＝－3，所以直线l 的方程为y －3＝－3(x －1)，即3x ＋y －6＝0，故选A.解法二 依题意，设直线方程为x a ＋y b ＝1(a >0，b >0)，则可得1a ＋3b ＝1且ab ＝12，解得a＝2，b ＝6，则直线l 的方程为x 2＋y6＝1，即3x ＋y －6＝0，故选A.答案：A7．解析：因为y ＝－m n x ＋1n 的图象同时经过第一、三、四象限，故－m n >0，1n<0，即m >0，n <0，但此为充要条件，因此，其必要不充分条件为mn <0.故选B.答案：B8．解析：将直线Ax ＋By －1＝0化成斜截式y ＝－A B x ＋1B.∵1B＝－1，∴B ＝－1，故排除A ，D. 又直线3x －y ＝33的倾斜角α＝π3，∴直线Ax ＋By －1＝0的倾斜角为2α＝2π3，∴斜率－A B ＝tan 2π3＝－3，∴A ＝－3，故选B. 答案：B9．解析：直线2x cos α－y －3＝0的斜率k ＝2cos α.由于α∈⎣⎡⎦⎤π6，π3，所以12≤cos α≤32， 因此k ＝2cos α∈[1，3]．设直线的倾斜角为θ，则0≤θ<π，tan θ∈[1，3]．所以θ∈⎣⎡⎦⎤π4，π3， 即倾斜角的变化范围是⎣⎡⎦⎤π4，π3.故选B. 答案：B10．解析：∵直线2x ＋3y －4＝0的斜率为－23，与直线2x ＋3y －4＝0平行的直线的斜率也为－23，∴经过点(0，－1)且斜率为－23的直线，其斜截式方程为y ＝－23x －1，整理得2x ＋3y ＋3＝0，故选A.答案：A11．解析：由题意得k AB ＝2－33－2＝－1，k AC ＝m －312－2.∵A ，B ，C 三点共线，∴k AB ＝k AC ， ∴m －312－2＝－1，解得m ＝92. 答案：9212．解析：如图，因为k AP ＝1－02－1＝1， k BP ＝3－00－1＝－3， 所以k ∈(－∞，－3]∪[1，＋∞)． 答案：(－∞，－3]∪[1，＋∞)13．解析：当直线过原点时，直线斜率为3－02－0＝32，故直线方程为y ＝32x ，即3x －2y ＝0.当直线不过原点时，设直线方程为x a ＋y－a＝1，把(2,3)代入可得a ＝－1，故直线的方程为x －y＋1＝0.综上，所求直线方程为3x －2y ＝0或x －y ＋1＝0.答案：3x －2y ＝0或x －y ＋1＝014．解析：设所求直线的方程为x a ＋yb ＝1，∵A (－2,2)在直线上，∴－2a ＋2b＝1 ①又因为直线与坐标轴围成的面积为1， ∴12|a |·|b |＝1 ② 由①②得(1)⎩⎪⎨⎪⎧ a －b ＝1ab ＝2或(2)⎩⎪⎨⎪⎧a －b ＝－1ab ＝－2由(1)得⎩⎪⎨⎪⎧ a ＝2b ＝1或⎩⎪⎨⎪⎧a ＝－1b ＝－2，方程组(2)无解，故所求的直线方程为x 2＋y 1＝1或x －1＋y－2＝1，即x ＋2y －2＝0或2x ＋y ＋2＝0. 答案：x ＋2y －2＝0或2x ＋y ＋2＝0 15．解析：直线l 的方程－kx ＋y ＋k －1＝0可化为k (1－x )＋y －1＝0，∴直线l 过定点P (1,1)，且与线段AB 相交，如图所示．直线P A 的斜率k P A ＝－3－12－1＝－4，直线PB 的斜率k PB ＝－2－1－3－1＝34，则k ≤－4或k ≥34.故选A.答案：A16．解析：∵线段AB 的中点为M (2,1)，k AB ＝－12，∴线段AB 的垂直平分线方程为y －1＝2(x －2)，即2x －y －3＝0，∵AC ＝BC ，∴△ABC 的外心，重心，垂心都位于线段AB 的垂直平分线上，∴△ABC 的欧拉线方程为2x －y －3＝0，故选D.答案：D17．解析：直线l 的斜率存在且k l ＝m 2－11－2＝1－m 2≤1，又直线l 的倾斜角为α，则有tan α≤1，即tan α<0或0≤tan α≤1，根据正切函数在⎣⎡⎭⎫0，π2与⎝⎛⎭⎫π2，π上的图象，可得π2<α<π或0≤α≤π4，即倾斜角α的取值范围为⎣⎡⎦⎤0，π4∪⎝⎛⎭⎫π2，π. 答案：⎣⎡⎦⎤0，π4∪⎝⎛⎭⎫π2，π。

高考数学一轮复习：45 直线的倾斜角与斜率、直线的方程姓名:________ 班级:________ 成绩:________一、单选题 (共12题；共24分)1. （2分） (2019高一下·镇江期末) 已知点，则直线的倾斜角是（）A . 30°B . 45°C . 60°D . 120°2. （2分）直线l经过点和，则它的倾斜角是（）A .B .C .D .3. （2分）已知倾斜角为的直线l与直线x－2y＋2＝0平行，则的值为（）．A .B .C .D .4. （2分）设点，直线l过点P(1,1)且与线段AB相交，则l的斜率k的取值范围是（）A . 或B .C .D . 或5. （2分）已知直线上两点A，B的坐标分别为(3，5)，(a，2)，且直线与直线3x+4y-5=0平行，则|AB|的值为（）A .B .C .D . 56. （2分）已知经过A（2，1），B（1，m）两点的直线的倾斜角为锐角，则实数m的取值范围是（）A . m＜1B . m＞﹣1C . ﹣1＜m＜1D . m＞1，或m＜﹣17. （2分）设P为曲线上的点，且曲线C在点P处的切线的倾斜角的取值范围为，则点P的横坐标的取值范围为（）A .B .C .D .8. （2分）直线经过两点，那么直线的倾斜角的取值范围（）A .B .C .D .9. （2分）直线的倾斜角是（）A . 30°B . 120°C . 60°D . 150°10. （2分） (2019高二上·内蒙古月考) 若某直线的斜率，则该直线的倾斜角的取值范围是（）A .B .C .D .11. （2分）(2017·广西模拟) 直线y=x﹣1的斜率等于（）A . ﹣1B . 1C .D .12. （2分） (2018高二上·哈尔滨月考) 已知点，若直线过点与线段有公共点，则直线的斜率的取值范围是（）A .B .C .D .二、填空题 (共6题；共6分)13. （1分） (2017高一下·吉林期末) 直线的倾斜角的范围是________．14. （1分）过点（1，3）作直线l，若l经过点（a，0）和（0，b），且a，b∈N*，则可作出的l的个数为________ 条．15. （1分）直线l1 ， l2的斜率k1 ， k2是关于k的方程2k2-3k-b=0的两根，若l1⊥l2 ，则b=________；若l1∥l2 ，则b=________.16. （1分） (2019高一下·西城期末) 直线的倾斜角的大小是________．17. （1分） (2018高一上·阜城月考) 经过点作直线，若直线与连接，的线段相交，则直线的斜率的取值范围是________．18. （1分）直线2x﹣3y﹣12=0与坐标轴围成的三角形的面积为________三、解答题 (共3题；共25分)19. （10分）若实数x，y满足3x﹣2y﹣5=0（1≤x≤3），求的最大值和最小值．20. （5分）经过下列两点的直线的斜率是否存在？如果存在，求其斜率，并确定直线的倾斜角α.（1） A(2,3)，B(4,5)；（2） C(－2,3)，D(2，－1)；（3） P(－3,1)，Q(－3,10)．21. （10分）若经过点A(1－t,1＋t)和点B(3,2t)的直线的倾斜角α不是锐角，求实数t的取值范围．参考答案一、单选题 (共12题；共24分)1-1、2-1、3-1、答案：略4-1、答案：略5-1、6-1、7-1、8-1、答案：略9-1、答案：略10-1、11-1、答案：略12-1、二、填空题 (共6题；共6分)13-1、答案：略14-1、15-1、16-1、17-1、18-1、三、解答题 (共3题；共25分) 19-1、答案：略20-1、20-2、20-3、21-1、。