双代号网络图及管理计算题讲解

双代号网络计划图讲解：代号讲解计划网络双代号网络计划图es 双代号网络计划图计算双代号网络计划计算篇一：双代号网络图解析实例一、双代号网络图6个时间参数的计算方法（图上计算法）从左向右累加，多个紧前取大，计算最早开始结束；从右到左累减，多个紧后取小，计算最迟结束开始。

紧后左上-自己右下=自由时差。

上方之差或下方之差是总时差。

计算某工作总时差的简单方法：①找出关键线路，计算总工期；②找出经过该工作的所有线路，求出最长的时间③该工作总时差=总工期-②二、双代号时标网络图双代号时标网络计划是以时间坐标为尺度编制的网络计划，以实箭线表示工作，以虚箭线表示虚工作，以波形线表示工作的自由时差。

双代号时标网络图1、关键线路在时标双代号网络图上逆方向看，没有出现波形线的线路为关键线路（包括虚工作）。

如图中①→②→⑥→⑧2、时差计算1）自由时差双代号时标网络图自由时差的计算很简单，就是该工作箭线上波形线的长度。

如A工作的FF=0，B工作的FF=1但是有一种特殊情况，很容易忽略。

如上图，E工作的箭线上没有波形线，但是E工作与其紧后工作之间都有时间间隔，此时E工作的自由时差=E与其紧后工作时间间隔的最小值，即E的自由时差为1。

2）总时差。

总时差的简单计算方法：计算哪个工作的总时差，就以哪个工作为起点工作（一定要注意，即不是从头算，也不是从该工作的紧后算，而是从该工作开始算），寻找通过该工作的所有线路，然后计算各条线路的波形线的长度和，该工作的总时差=波形线长度和的最小值。

还是以上面的网络图为例，计算E工作的总时差：以E工作为起点工作，通过E工作的线路有EH和EJ，两条线路的波形线的和都是2，所以此时E的总时差就是2。

再比如，计算C工作的总时差：通过C工作的线路有三条，CEH，波形线的和为4；CEJ，波形线的和为4；CGJ，波形线的和为1，那么C的总时差就是1。

篇二：双代号网络计划图个人学习总结双代号网络计划图个人学习总结一．网络图要素1．节点：表示工作的开始、结束或连接关系，也称为事件。

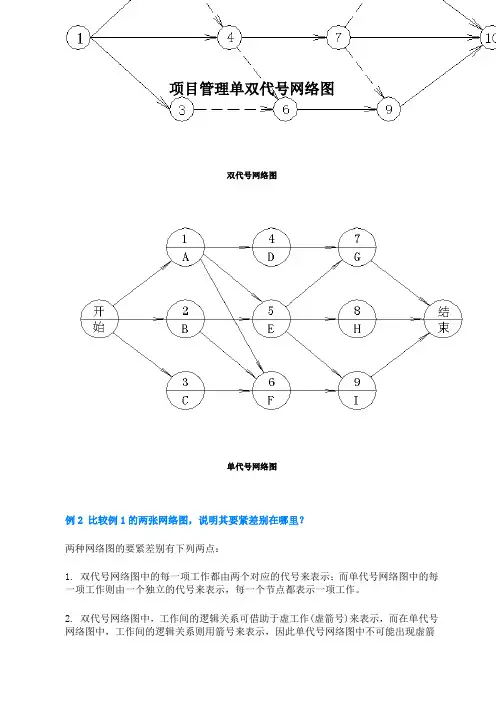
项目管理单双代号网络图双代号网络图单代号网络图例2 比较例1的两张网络图，说明其要紧差别在哪里？两种网络图的要紧差别有下列两点：1. 双代号网络图中的每一项工作都由两个对应的代号来表示；而单代号网络图中的每一项工作则由一个独立的代号来表示，每一个节点都表示一项工作。

2. 双代号网络图中，工作间的逻辑关系可借助于虚工作(虚箭号)来表示，而在单代号网络图中，工作间的逻辑关系则用箭号来表示，因此单代号网络图中不可能出现虚箭号。

一幅单代号网络图中，只会出现两个虚设的工作节点，那就是表示计划开始的虚工作节点与表示计划结束的虚工作节点。

例3 下图为一单号网络图，网络图各圆圈中横线上边的数字是工作代号，横线下边的数字是工作持续时间。

试用图上计算法计算各工作的最早可能开始时间ES i、最迟务必开始时间LS i、总时差TF i与局部时差FF i，标记出关键线路并确定总工期。

解：根据题意用图算法推算出的各工作时间参数，见上图，关键线路用粗箭号表示。

该网络图的计划总工期为11天。

例4 某工程的单代号网络如下图所示。

试用表上计算法求出网络图中各工作的ES i、EF、LS i、LF i、TF i、与FF i；确定关键工作并在图上说明关键线路；确定计划总工期(注：i下图中圆圈内横线上边为工作代号，横线下边为工作持续时间)。

解：用表算法推算了各工作的时间参数见下表。

该网络图的关键线路共有3条，它们分别为：计划总工期为19天。

一、网络计划技术基本概念二、网络图的绘制：知识点总结与归纳三、网络计划时间参数的计算（一）、网络计划时间参数的概念4．计算工作的总时差工作的总时差等于该工作最迟完成时间与最早完成时间之差，或者该工作最迟开始时间与最早开始时间之差。

5.计算工作的自由时差工作自由时差的计算应按下列两种情况分别考虑：(1)关于有紧后工作的工作，其自由时差等于本工作之紧后工作最早开始时间减本工作最早完成时间所得之差的最小值。

(2)关于无紧后工作的工作，也就是以网络计划终点节点为完成节点的工作，其自由时差等于计划工期与本工作最早完成时间之差。

关于计算双代号网络图的题目用图上计算法计算如图所示双代号网络图的各项时间参数（六时标注）确定关键路线、关键工作和总工期。

注：其中工作F的最迟完成时间为计算工期17 其自由时差为17-12=5（计算工期-F的最早完成时间，因F后没有紧后工作了；H后也没有紧后工作了）双代号网络图是应用较为普遍的一种网络计划形式。

它是以箭线及其两端节点的编号表示工作的网络图。

双代号网络图中的计算主要有六个时间参数：ES：最早开始时间，指各项工作紧前工作全部完成后，本工作最有可能开始的时刻；EF：最早完成时间，指各项紧前工作全部完成后，本工作有可能完成的最早时刻LF：最迟完成时间，不影响整个网络计划工期完成的前提下，本工作的最迟完成时间；LS：最迟开始时间，指不影响整个网络计划工期完成的前提下，本工作最迟开始时间；TF：总时差，指不影响计划工期的前提下，本工作可以利用的机动时间；FF：自由时差，不影响紧后工作最早开始的前提下，本工作可以利用的机动时间。

双代号网络图时间参数的计算一般采用图上计算法。

下面用例题进行讲解。

例题：试计算下面双代号网络图中，求工作C的总时差？早时间计算：ES，如果该工作与开始节点相连，最早开始时间为0，即A的最早开始时间ES=0；EF，最早结束时间等于该工作的最早开始+持续时间，即A的最早结束EF为0+5=5；如果工作有紧前工作的时候，最早开始等于紧前工作的最早结束取大值，即B的最早开始FS=5，同理最早结束EF为5+6=11，而E工作的最早开始ES为B、C工作最早结束（11、8）取大值为11。

迟时间计算：LF，如果该工作与结束节点相连，最迟结束时间为计算工期23，即F的最迟结束时间LF=23；LS，最迟开始时间等于最迟结束时间减去持续时间，即LS=LF-D；如果工作有紧后工作，最迟结束时间等于紧后工作最迟开始时间取小值。

时差计算： FF，自由时差=（紧后工作的ES-本工作的EF）；TF，总时差=（紧后工作的LS-本工作的ES）或者=（紧后工作的LF-本工作的EF）。

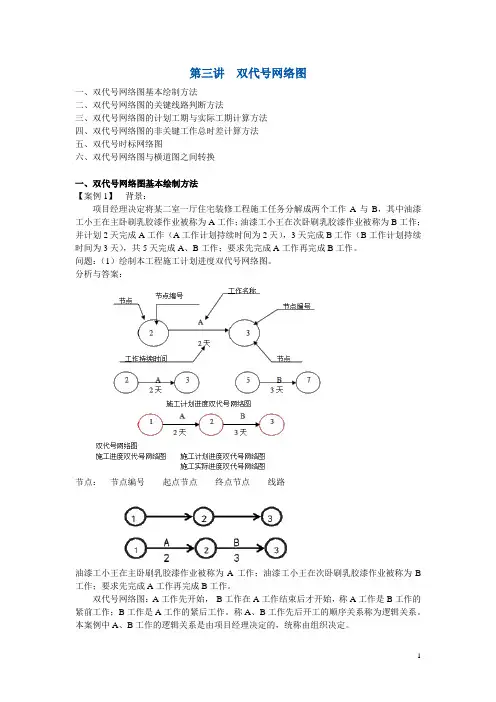
第三讲双代号网络图一、双代号网络图基本绘制方法二、双代号网络图的关键线路判断方法三、双代号网络图的计划工期与实际工期计算方法四、双代号网络图的非关键工作总时差计算方法五、双代号时标网络图六、双代号网络图与横道图之间转换一、双代号网络图基本绘制方法【案例1】背景：项目经理决定将某二室一厅住宅装修工程施工任务分解成两个工作A与B，其中油漆工小王在主卧刷乳胶漆作业被称为A工作；油漆工小王在次卧刷乳胶漆作业被称为B工作；并计划2天完成A工作（A工作计划持续时间为2天），3天完成B工作（B工作计划持续时间为3天），共5天完成A、B工作；要求先完成A工作再完成B工作。

问题：（1）绘制本工程施工计划进度双代号网络图。

分析与答案：节点：节点编号起点节点终点节点线路油漆工小王在主卧刷乳胶漆作业被称为A工作；油漆工小王在次卧刷乳胶漆作业被称为B 工作；要求先完成A工作再完成B工作。

双代号网络图：A工作先开始，B工作在A工作结束后才开始，称A工作是B工作的紧前工作；B工作是A工作的紧后工作。

称A、B工作先后开工的顺序关系称为逻辑关系。

本案例中A、B工作的逻辑关系是由项目经理决定的，统称由组织决定。

如需要表达A工作是B、C工作的紧前工作；B、C工作是A工作的紧后工作，则：如需要表达A、B工作是C工作的紧前工作；C工作是A 、B工作的紧后工作。

则：【案例2】背景项目经理决定将某二室一厅住宅装修工程施工任务分解成两个工作A与B，木工小李在主卧钉地龙骨施工作业被称为A工作；木工小李在主卧铺木地板施工作业被称为B工作，要求5天完成A、B工作，其中A工作计划持续时间是2天，B工作计划持续时间是3天。

问题:（1）绘制本工程施工计划进度双代号网络图。

分析与答案：A工作是B工作的紧前工作；B工作是A工作的紧后工作。

A、B工作先后开工的顺序关系称为逻辑关系。

本案例中A、B工作的逻辑关系是由工艺决定的。

根据案例1、案例2可以得出结论：A、B工作的逻辑关系，或者是由组织决定的；或者是由工艺决定的。

二建管理双代号网络图网络讲解（精选2篇）在日常学习、工作或生活中，大家总少不了接触作文或者范文吧，通过文章可以把我们那些零零散散的思想，聚集在一块。

范文书写有哪些要求呢？我们怎样才能写好一篇范文呢？这里我整理了一些优秀的范文，希望对大家有所帮助，为朋友们整理了2篇《二建管理双代号网络图网络讲解》，希望能对您的写作有一定的参考作用。

建管理双代号网络图网络讲解篇一『正确答案』c『答案解析』本题考查的是双代号网络计划。

a、b、c完成后d开始，说明a、b、c工作为d工作的紧前工作，选项a错误，d工作的紧前工作只有a工作；选项b错误，d工作的紧前工作只有a工作；选项d错误，d工作的紧前工作只有a、b工作。

参见教材p135。

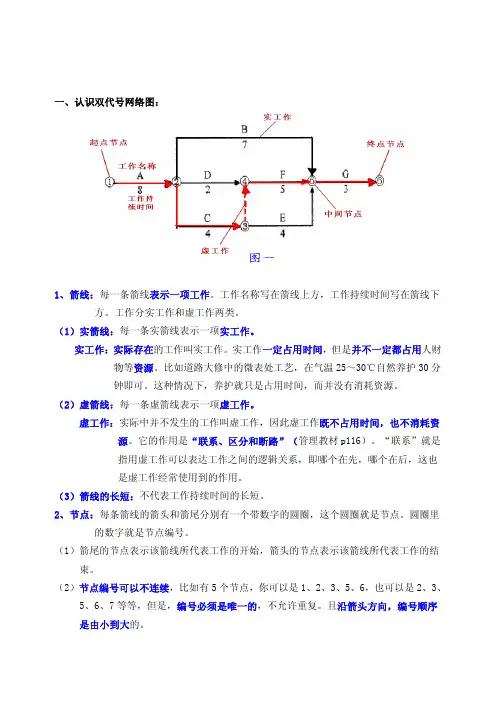
【例题】某双代号网络计划如下图所示，图中存在的绘图错误有()。

a.多个终点节点b.节点编号重复c.两项工作有相同的节点编号d.循环回路e.多个起点节点『正确答案』abc『答案解析』本题考查的是双代号网络计划。

图中存在多个终点节点⑨⑩;节点编号重复，两个⑦节点；两项工作有相同的节点编号⑦→⑨和⑧→⑨。

参见教材p134。

【例题】下列关于双代号网络计划绘图规则的说法，正确的有()。

a.网络图必须正确表达各工作间的逻辑关系b.网络图中可以出现循环回路c.网络图中一个节点只有一条箭线引出d.网络图中严禁出现没有箭头节点或没有箭尾节点的箭线e.单目标网络计划只有一个起点节点和一个终点节点『正确答案』ade『答案解析』本题考查的是双代号网络计划。

双代号网络计划的绘图规则包括：①双代号网络图必须正确表达已定的逻辑关系；②双代号网络图中，严禁出现循环回路；③双代号网络图中，在节点之间严禁出现带双向箭头或无箭头的连线；④双代号网络图中，严禁出现没有箭头节点或没有箭尾节点的箭线；⑤当双代号网络图的某些节点有多条外向箭线或多条内向箭线时，为使图形简洁，可使用母线法绘制(但应满足一项工作用一条箭线和相应的一对节点表示);⑥绘制网络图时，箭线不宜交叉。

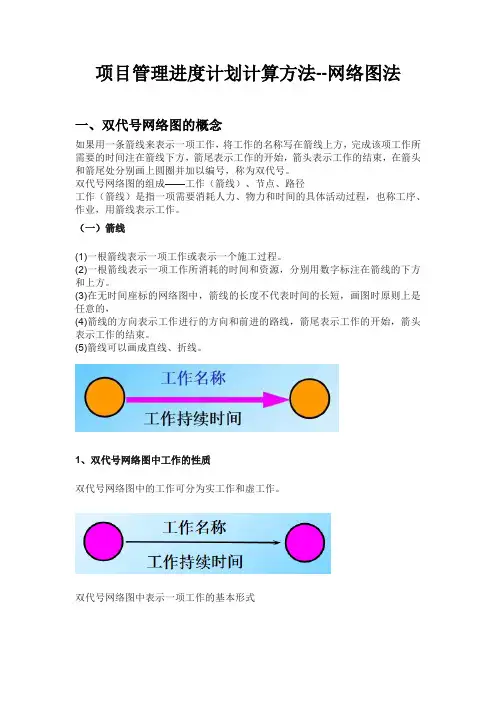
项目管理进度计划计算方法--网络图法一、双代号网络图的概念如果用一条箭线来表示一项工作，将工作的名称写在箭线上方，完成该项工作所需要的时间注在箭线下方，箭尾表示工作的开始，箭头表示工作的结束，在箭头和箭尾处分别画上圆圈并加以编号，称为双代号。

双代号网络图的组成——工作（箭线）、节点、路径工作（箭线）是指一项需要消耗人力、物力和时间的具体活动过程，也称工序、作业，用箭线表示工作。

（一）箭线(1)一根箭线表示一项工作或表示一个施工过程。

(2)一根箭线表示一项工作所消耗的时间和资源，分别用数字标注在箭线的下方和上方。

(3)在无时间座标的网络图中，箭线的长度不代表时间的长短，画图时原则上是任意的，(4)箭线的方向表示工作进行的方向和前进的路线，箭尾表示工作的开始，箭头表示工作的结束。

(5)箭线可以画成直线、折线。

1、双代号网络图中工作的性质双代号网络图中的工作可分为实工作和虚工作。

双代号网络图中表示一项工作的基本形式双代号网络图中虚工作的表达形式虚工作在双代号网络图中起着正确表达工序间逻辑关系的重要作用2.双代号网络图中工作间的关系双代号网络图中工作间有紧前工作、紧后工作和平行工作三种关系。

1. 紧前工作：紧排在本工作之前的工作称为本工作的紧前工作。

2. 紧后工作：紧排在本工作之后的工作称为本工作的紧后工作。

本工作和紧后工作之间可能有虚工作。

3. 平行工作：可与本工作同时进行称为本工作的平行工作。

（二）节点和编号在双代号网络图中，节点用圆圈“○” 表示。

它表示一项工作的开始时刻或结束时刻，是工作的连接点。

节点不需要消耗时间和资源。

1.节点的分类（圆圈）一项网络计划的第一个节点，称为该项网络计划的起始节点，它是整个项目计划的开始节点；一项网络计划的最后一个节点，称为终点节点，表示一项计划的结束。

其余节点称为中间节点。

2.节点编号（圆圈里的数字）为了便于网络图的检查和计算，需对网络图各节点进行编号。

节点编号的基本规则：(1) 节点编号必须满足二条基本规则：1.箭头节点编号大于箭尾节点编号，因此节点编号顺序是：箭尾节点编号在前，箭头节点编号在后，凡是箭尾节点没编号，箭头节点不能编号；2.在一个网络图中，所有节点不能出现重复编号，编号的号码按自然数顺序进行。

双代号网络图绘制例题详解双代号网络图是一种用于描述和分析复杂系统的工具，它可以帮助我们理清系统中各个因素之间的关系和影响，从而更好地进行规划和决策。

在本文中，我们将通过一个例题详细解释如何绘制双代号网络图，并对其进行分析和解释。

例题描述：某公司计划开展一个新产品的研发项目，该项目需要进行市场调研、技术开发、生产试验和市场推广等工作。

为了更好地组织和管理这个项目，公司决定使用双代号网络图来描述和分析项目的关键活动和其之间的关系。

现在，请你根据以下信息绘制该项目的双代号网络图，并分析关键路径和关键活动。

1. 市场调研需要2个月时间，完成后可以开始技术开发；2. 技术开发需要3个月时间，完成后可以进行生产试验；3. 生产试验需要1个月时间，完成后可以进行市场推广；4. 市场推广需要2个月时间，完成后项目结束。

解题步骤：1. 确定活动和活动之间的关系。

首先，我们需要确定该项目的关键活动和它们之间的先后关系。

根据题目描述，我们可以得出以下关键活动和其之间的关系：市场调研→技术开发。

技术开发→生产试验。

生产试验→市场推广。

市场推广→项目结束。

2. 绘制双代号网络图。

根据上述关键活动和其之间的关系，我们可以绘制出该项目的双代号网络图。

在双代号网络图中，活动用圆圈表示，活动之间的关系用箭头表示。

具体绘制过程如下：首先，在纸上绘制一个大圆圈，代表整个项目；然后，在大圆圈内部依次绘制代表各个活动的小圆圈，并用箭头连接它们，表示活动之间的关系；最后，在箭头上标注活动所需的时间。

3. 分析关键路径和关键活动。

在绘制完双代号网络图后，我们可以通过分析图中的路径和活动来确定项目的关键路径和关键活动。

关键路径是指项目中最长的路径，它决定了项目的最短完成时间；而关键活动是指在关键路径上的活动，它们的延误会直接影响整个项目的完成时间。

在该例题中，我们可以通过双代号网络图来确定关键路径和关键活动：首先，我们可以计算出各个路径的长度，从而确定最长的路径，即为关键路径；然后，我们可以找出关键路径上的活动，即为关键活动。

一、双代号网络图6个时间参数的计算方法（图上计算法）从左向右累加，多个紧前取大，计算最早开始结束；从右到左累减，多个紧后取小，计算最迟结束开始。

紧后左上-自己右下=自由时差。

上方之差或下方之差是总时差。

计算某工作总时差的简单方法：①找出关键线路，计算总工期；②找出经过该工作的所有线路，求出最长的时间③该工作总时差=总工期-②二、双代号时标网络图双代号时标网络计划是以时间坐标为尺度编制的网络计划，以实箭线表示工作，以虚箭线表示虚工作，以波形线表示工作的自由时差。

双代号时标网络图1、关键线路在时标双代号网络图上逆方向看，没有出现波形线的线路为关键线路（包括虚工作）。

如图中①→②→⑥→⑧2、时差计算1）自由时差双代号时标网络图自由时差的计算很简单，就是该工作箭线上波形线的长度。

如A工作的FF=0，B工作的FF=1但是有一种特殊情况，很容易忽略。

如上图，E工作的箭线上没有波形线，但是E工作与其紧后工作之间都有时间间隔，此时E工作的自由时差=E与其紧后工作时间间隔的最小值，即E的自由时差为1。

2）总时差。

总时差的简单计算方法：计算哪个工作的总时差，就以哪个工作为起点工作（一定要注意，即不是从头算，也不是从该工作的紧后算，而是从该工作开始算），寻找通过该工作的所有线路，然后计算各条线路的波形线的长度和，该工作的总时差=波形线长度和的最小值。

还是以上面的网络图为例，计算E工作的总时差：以E工作为起点工作，通过E工作的线路有EH和EJ，两条线路的波形线的和都是2，所以此时E的总时差就是2。

再比如，计算C工作的总时差：通过C工作的线路有三条，CEH，波形线的和为4；CEJ，波形线的和为4；CGJ，波形线的和为1，那么C的总时差就是1。

双代号网络图的绘制及时间参数计算图 （1）双代号网络图 1）绘制工作明细表（序号、工作、持续时间、逻辑关系（紧前或紧后关系） ） 2）依据逻辑关系绘制草图（按紧前关系为例） a.若某工作有且仅有一项紧前工作，则从其紧前工作的结束节点直接引出该工作； b.若某工作有多项紧前工作， 则从其紧前工作的结束节点各引出一项虚工作， 使得这些 虚工作交于一个节点，从该节点引出该工作。

3）草图整理，简化多余的虚工作 4）网络编号 （2）时间参数计算，采用图上作业法 （3）双代号网络图示例 时标图的应用 （1）有关要素的确定 1）时间参数 直接判读：ES，EF，FF 计算：TF，LS，LF。

2）关键线路 3）计算工期 （2）进度控制－前锋线法 1）进度实施现状 2）现状与计划对比、分析 3）措施 时标图的应用实例关键线路法 方法 1 补偿工期 索赔工期 奖罚工期补偿&索赔工期=调整后的合同工期-合同工期 奖罚工期=调整后的合同工期-实际工期 调整后的合同工期如何计算： 1、 首先找出原来的网络进度计划（调整的基础）； 2、 找出调整的要素（事件），梳理题目给出的事件类型，按发包人、承包人、不可抗力因 素分为三类（由设计人、监理人的原因造成的工期延误和逻辑关系变化归为发包人）； 3、 将发包人原因、不可抗力原因这两类导致的相应事件引起的工期延误和逻辑关系变化， 针对第一步找到的原有网络进度计划进行修正和调整。

注意： 实际工期是将三方原因引起的工期延误和逻辑关系变化， 均针对第一步找到的原有网 络进度计划进行修正和调整。

2.画草图工艺 组织 无一项二项及以上绘制草图的原则（依据工作的紧前关系从前往后画） ： 1） 没有紧前工作的直接从起点节点引出该工作； 2） 只有一项紧前工作的从其紧前工作的结束节点引出该工作； 3） 有二项紧前工作及其以上的从其紧前工作的结束节点分别引虚工作交于一个节点，从该 节点引出该工作。

双代号网络图经典例题引言双代号网络图是一种图形表示方法，用于描述一系列活动之间的关系。

通过双代号网络图，可以清晰地表示出活动的先后顺序、重要性以及活动之间的关系，从而有助于优化和管理项目进度。

本文将介绍双代号网络图的经典例题，并通过Markdown文本格式输出。

双代号网络图的基本概念在介绍双代号网络图的经典例题之前，我们先来了解一些基本概念。

活动（Activity）：指项目中的一项任务或工作。

活动可以是一个简单的任务，也可以是一个复杂的工作流程。

节点（Node）：用于表示活动的圆形图形，通常用字母来标识。

弧（Arc）：用于表示活动之间的关系，通常用箭头表示。

箭头的方向表示活动的先后顺序，箭头的长度表示活动的持续时间。

关键路径（Critical Path）：指项目中由一系列关键活动组成的路径，如果关键路径上的任何一个活动延迟，整个项目的进度都会受到影响。

经典例题下面我们将介绍一个经典的双代号网络图例题。

例题描述假设有一个软件开发项目，需要完成以下五个活动：A、B、C、D和E。

这些活动之间存在一些限制条件，它们之间的关系如下：1.活动A必须在活动B完成之前开始；2.活动B必须在活动C完成之前开始；3.活动C必须在活动D完成之前开始；4.活动D必须在活动E完成之前开始。

同时，给出了这些活动的预计持续时间（以天为单位）：A（3天）、B（4天）、C（2天）、D（5天）和E（3天）。

构建双代号网络图根据以上描述，我们可以构建双代号网络图来表示活动之间的关系和持续时间。

A(3) --> B(4) --> C(2) --> D(5) --> E(3)计算关键路径在双代号网络图中，关键路径表示项目中的关键活动，任何一个关键活动的延迟都会延迟整个项目的进度。

为了找到关键路径，我们需要计算每个活动的最早开始时间（ES）和最晚开始时间（LS），以及项目的最早完成时间（EF）和最晚完成时间（LF）。