当前位置：文档之家 › 震动测试第2章 信号分析基础.

震动测试第2章 信号分析基础.

  • 格式：pdf
  • 大小：918.77 KB
  • 文档页数：99

下载文档原格式

  / 99

合集下载

第2章 信号分析基础 题库-答案

第2章 信号分析基础 题库-答案

（1）傅里叶级数实数形式的幅值谱、相位谱；
（2）傅里叶级数复数形式的幅值谱、相位谱；
（3）幅值谱密度。
解：（1）实数形式
傅里叶级数三角形式的展开式：
x(t)
a0 2
n1
(an
cos n0t
bn
sin
n0t )
x(t)
2 2
Acos(0t)
2 2
A sin(0t )
得： a0
0 ， an
形脉冲。
x(t)
t
x1 (t )
x2 (t )
图2-31
解：矩形脉冲信号
x(t
)
E 0
| t | T1 的频谱密度 | t | T1 t
t
X ()
T1 T1
Ee
jt dt
2ET1
sinc(T1)
所以
X1
(
)
sinc(
1 2
)
，
X
2
(
)
3
sinc(
3 2
)
x(t)
1 2
x1 (t
2.5)
x2 (t
过程： T 0
A2
T 1 cos 2t dt
T0
2
A2 2
18.求正弦信号 xt Asin( t ) 的概率密度函数 p(x)。
解：
公式： p(x) lim P(x x(t) x x)
x0
x
过程：
在一个周期内Tx0 t1 t2 P[x x(t) x x] lim Tx Tx0
答：充分条件：绝对可积
充要条件：
（D） a X a f
6．判断对错：1、 随机信号的频域描述为功率谱。（ V ）

(3)第2章 信号分析基础

(3)第2章 信号分析基础

2.3 非周期信号与连续频谱
•
图2-5 非周期信号
2.3 非周期信号与连续频谱
• 2.3.1傅立叶变换
• 当周期T趋于无穷大时，相邻谱线的间隔 趋 近于无穷小，从而信号的频谱密集成为连续频谱 。同时，各频率分量的幅度也都趋近于无穷小， 不过，这些无穷小量之间仍保持一定的比例关系 。为了描述非周期信号的频谱特性，引入频谱密 度的概念。令
• 对于周期信号，在时域中求得的信号功率与在频域中求得 的信号功率相等。
2.3 非周期信号与连续频谱
• 2.3 非周期信号与连续频谱 • 非周期信号包括准周期信号和瞬态信号两种，其频谱
各有独自的特点：周期信号的频谱具有离散性，各谐波分 量的频率具有一个公约数——基频。但几个简谐具有离散 频谱的信号不一定是周期信号。只有各简谐成分的频率比 是有理数，它们才能在某个时间间隔后周而复始，合成的 信号才是周期信号。若各简谐信号的频率比不是有理数， 合成信号就不是周期信号，而是准周期信号。因此准周期 信号具有离散频谱，例如多个独立激振源激励起某对象的 振动往往是这类信号对于瞬态信号，不能直接用傅立叶级 数展开，而必须应用傅立叶变换的数学方法进行分解。
第2章 信号分析基础
2.1 信号的分类与描述
• 2.1 信号的分类与描述
• 2.1.1 信号的分类
• 信号是反映被测对象状态或特性的某种物理量。以信 号所具有的时间函数特性分类，信号主要分为确定性信号 与随机信号、连续信号与离散信号等。
• 1. 确定性信号与随机信号
• 确定性信号是指可以用精确的数学关系式来表达的信 号。确定性信号根据它的波形是否有规律地重复又可进一 步分为周期信号和非周期信号两种。
•
（2-21） F( j) lim Fn T 1 / T

第二章信号分析基础(频谱)

第二章信号分析基础(频谱)

（1）
A0 a0
An
an bn
2
2
bn n arctg an
周期信号的频谱分析
西安工业大学机电学院
复指数形式： 将三角函数形式中的正余弦用欧拉公式代换
e j e j cos 2
则：

e j e j sin 2j
带入并合并同类项
a0 an jbn jn0t an jbn jn0t f (t ) [ e e ] 2 n 1 2 2 a0 an jbn jn0t an jbn jn0t e e 2 n 1 2 2 n 1 an jbn jn0t e Cn e jn0t 2 n n
则：c1x1(t)+c2x2(t) ←→ c1X1(f)+c2X2(f)
例子：求下图波形的频谱
用线性叠加定理简化 X1(f)
+
X2(f)
2.4 傅立叶变换的性质 c.对称性
西安工业大学机电学院
若 x(t) ←→ X(f)，则 X(t) ←→ x(-f)
证明： 以－t替换t: 以f换t: 所以：
x(t )
∴当T0→∞时，Δω→0 上式变为：
T / 2
0
T0 / 2
f (t )e jn0t dt ]e jn0t
f (t )
＋

1 ＋ [ f (t )e jt dt ]e jt d 2
1 ＋ jt F e d 2
西安工业大学机电学院


X ( f )e j 2ft df X ( f )e j 2ft df
x(t )


x( f ) X (t )e j 2ft dt

非稳态振动信号分析(连载)2

非稳态振动信号分析(连载)2
""# """"""#
非稳态振动信号分析 （连载）
朱继梅
（上海理工大学）
可用数据长度本身就比较短， 这样， 谱的分辨率就变粗
第二讲
谐和变频信号的分析 （一）
了。 （:）所加的窗是固定的， 处理时窗的重叠程度也 不能随信号变化而调整。同时， 用于各时窗谱分析的 分析频段也是固定不变的， 当信号各时段的频率变化 较激烈时， 仍用同一分析频率是不合适的。 根据这些特点， 短时富氏变换主要用于变化较缓 慢的时变信号。对于变化激烈的信号， 所得到的瀑布 图其分析质量就变差了。
要获得准确的角度采样值的更直接方法是采用光 学编码器 （./01234 5627859） 来控制采样。将光学编码器 安装在转轴上， 随轴一起转动。利用光电转换装置， 编 码器每一转可以 发 出 一 定 数 量 的 电 脉 冲 （例 如 每 转 。把光学编码器所发出的脉冲作为采样 +,! 个脉冲） 的触发信号， 每发出一个脉冲， 作一次采样。这是真正 地将等时间间隔采样转化成等角度间隔采样， 达到角 域分析的目的。这种角域分析与上述的阶次跟踪分析 一样， 仅是在频率上将非稳态的变频信号转化成形式 上稳态的信号， 对于频率与幅值同时激烈变化的信号， 虽然经过 “频率” 稳态化， 但作富氏变换时仍会遇到一 定困难， 所以只适用于在某一段时间内幅值变化相对 不很激烈的信号。从理论上严格说， 仍属于部分地阶 段平稳假设这一类。 阶次跟踪分析与角域分析的一个弱点是采样的硬 件部分必须附加装置。光学编码器装置在有些机械上 可能会遇到不易安装的问题， 使用上受到一定限制。 短时富氏变换及阶次跟踪分析本质上都是以 ’’( 技术为基础的， 用以处理非稳态信号是采用了信号部 分地阶段平稳假设， 观察时间的长短限制了谱分辨率 的状况依然存在， 这是富氏变换方法固有的不足。对 于频率和幅值变化很激烈的信号， 其分析质量就变差。 它们是属于所谓 “频率滤波” 这一类。针对这些问题， 在 以下二节中， 我们将进而讨论 “时域滤波” 的分析方

3信号分析基础2(时域相关分析)

3信号分析基础2(时域相关分析)
因此，有

T
0
x (t )dt S x ( f )df
2
1 2 S x lim X f T T
信号的频域分析
自功率谱密度函数是偶函数,它的频率范围 (,) ， 又称双边自功率谱密度函数。它在频率范围 (,0) 的函数值是其在 (0, ) 频率范围函数值的对称映射， 因此 Gx ( f ) 2Sx ( f ) 。
x(t - τ)
自相关函数的性质 自相关函数为实偶函数
Rx ( ) Rx ( )
1 T 证明： Rx ( ) lim x(t ) x(t )dt T T 0 1 T lim x(t ) x(t )d (t ) T T 0 Rx ( )
波形变量相关的概念（相关函数 ）
如果所研究的变量x, y是与时间有关的函数， 即x(t)与y(t)：
x(t)
y(t)
2.4信号的时差域相关分析 这时可以引入一个与时间τ有关的量，称为 函数的相关系数，简称相关函数，并有：
x ( t ) y ( t ) dt xy ( ) 2 [ x ( t ) dt y 2 ( t ) dt ]1/ 2
2 2 x x

自相关函数的性质
周期函数的自相关函数仍为同频率的周期函数
1 Rx ( nT ) lim T T 1 lim T T

T 0 T 0
x(t nT ) x(t nT )d (t nT ) x(t ) x(t )d (t ) Rx ( )
相关函数反映了二个信号在时移中的相关性。
x(t) y(t) y(t) y(t) y(t)

2.2.2 自相关(self-correlation)分析

第二章 旋转机械振动分析基础汇总

第二章 旋转机械振动分析基础汇总

第二章 旋转机械振动分析基础振动在设备故障诊断中占了很大的比重，是影响设备安全、稳定运行的重要因素。

振动又是设备的“体温计”，直接反映了设备的健康情况，是设备安全评估的重要指标。

一台机组正常运行时，其振动值和振动变化值都应该比较小。

一旦机组振动值变大，或振动变的不稳定，都说明设备出现了一定程度的故障。

第一节 振动分析的基本概念振动是一个动态量。

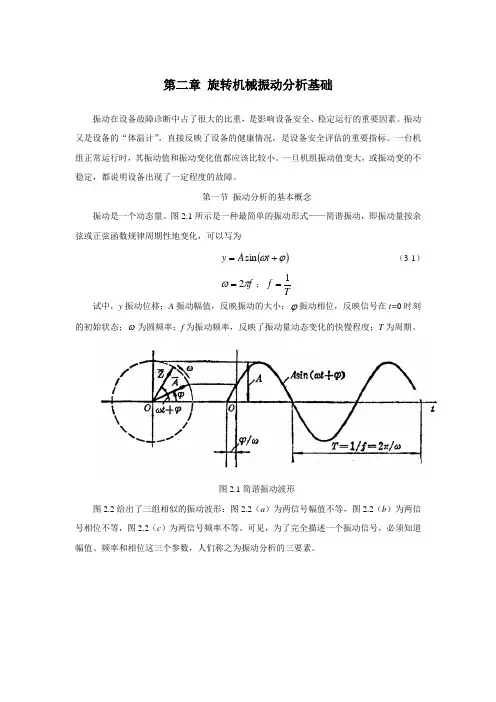
图2.1所示是一种最简单的振动形式——简谐振动，即振动量按余弦或正弦函数规律周期性地变化，可以写为()ϕω+=t A y sin （3-1）f πω2=；Tf 1= 试中，y 振动位移；A 振动幅值，反映振动的大小；ϕ振动相位，反映信号在t=0时刻的初始状态；ω为圆频率；f 为振动频率，反映了振动量动态变化的快慢程度；T 为周期。

图2.1简谐振动波形图2.2给出了三组相似的振动波形：图2.2（a ）为两信号幅值不等，图2.2（b ）为两信号相位不等，图2.2（c ）为两信号频率不等。

可见，为了完全描述一个振动信号，必须知道幅值、频率和相位这三个参数，人们称之为振动分析的三要素。

（a）幅值不等；（b）相位不等；（c）频率不等图2.2 三组相似的振动波型简谐振动时最简单的振动形式，实际发生的振动要比简谐振动复杂的多。

但是根据付立叶变换理论知道，不管振动信号多复杂，都可以将其分解为若干具有不同频率的简谐振动。

图2.3 付立叶变换图解旋转机械振动分析离不开转速，为了方便和直观起见，常以1x表示与转动频率相等的频率，又称为工（基）频，分别以0.5x、2x、3x等表示转动频率的0.5倍、2倍、3倍等相等的频率，又称为半频、二倍频、三倍频。

采用信号分析理论中的快速傅立叶变换可以很方便地求出复杂振动信号所含频率分量的幅值和相位。

目前频谱分析已成为振动故障诊断领域最基本的工具。

频谱分析所起的作用可以概括为以下两点：1）特定故障的频率特征具有必然性。

例如，转子不平衡的频率为工频，气流基振和油膜振荡等故障的频率为低频，电磁激振等故障为高频。

工程测试技术 第2章 信号分析基础-3


第二章、信号分析基础
Page 2 华中科技大学机械学院
2.5 信号的频域分析
信号频域分析是采用傅立叶变换将时域信号x(t)变换为 频域信号X(f)，从而帮助人们从另一个角度来了解信号的特 征。
傅里叶 变换
8563A
SPECTRUM ANALYZER 9 kHz - 26.5 GHz
第二章、信号分析基础
2.5 信号的频域分析
频域分析
Page 25 华中科技大学机械学院
吉布斯现象(Gibbs)
• 吉布斯现象是由于展开式在间断点邻域不能均匀收敛 引起的。
• 例：方波信号
x(t)
T
T
t
2.5 信号的频域分析
频域分析
Page 26 华中科技大学机械学院
N=1
2.5 信号的频域分析
Page 27 华中科技大学机械学院
用线性叠加定理简化
X1(f)
+Page 38 华中科技大学机械学院
5、频谱分析的应用
频谱分析主要用于识别信号中的周期分量，是信号分析 中最常用的一种手段。
在齿轮箱故障诊断中，可
以通过齿轮箱振动信号频谱分 析，确定最大频率分量，然后 根据机床转速和传动链，找出 故障齿轮。
2 T
T /2
T /2 x(t) sin n0tdt;
ω0―基波圆频率； f0 ―基频：f0= ω0/2π
An an2 bn2 ;
n
arctan bn an
;
2.5 信号的频域分析
傅里叶级数的复数表达形式：
x(t) Cne jn0t , (n 0,1,2,...) n
Page 9 华中科技大学机械学院
2.5 信号的频域分析

第二章信号分析基础随机信号和相关分析080327


2.6 随机信号
案例：自相关测转速
理想信号
实测信号
干扰信号
西安工业大学机电学院
自相关系数
从自相关图可以确定周期因素的 频率，从而得到转速大小。
性质4：可提取周期性转速成分。
2.6 随机信号
西安工业大学机电学院
案例：互相关分析对地下输油管道漏损位置的探测
x1,x2处放置传感器1，2，漏损处k视为向两侧传播声波的声源。因两 传感器位置离漏损处不等，其声波传到传感器就有时差，信号x1,x2 做相关分析，找出相关值最大时的τ ，即可确定漏损位置。 （在互相关图上， τ= τm处，Rx1x2(τ)的最大值τm就是时差）
T T
T x2 (t)dt
0
――信号的强度或平均功率
4．概率密度函数：
西安工业大学机电学院
x(t)的瞬时值落在某一个 (x, x x) 区间内的概率是
P[x x(t) x x] lim Tx T T
式中：T－观测时间
n
Tx ti i 1
表示信号幅值在T时间内落在 （x,x+△x）区间的总时间。
如果所研究的变量x, y是与时间有关的函数， 即x(t)与y(t)：
x(t)
y(t)
2.6 随机信号
西安工业大学机电学院
这时可以引入一个与时间τ有关的量，称为 函数的相关系数，简称相关函数，并有：
x(t ) y(t )dt
( ) xy
[ x2 (t )dt y2 (t )dt ]1/2
•集合平均：不是沿单个样本的时间轴进行，而是将集 合中所有样本函数对同一时刻ti的观测值取平均；（纵 向） •时间平均：单个样本的时间历程进行平均；（横向）
西安工业大学机电学院

工程测试技术基础 第二部分 信号分析基础

a)能量信号 在所分析的区间（-∞，∞），能量为有限值的信号称
为能量信号，满足条件：
x2 (t)dt
一般持续时间有限的瞬态信号是能量信号。
瞬态信号
2.1 信号的分类与描述
b)功率信号 在所分析的区间（-∞，∞），能量不是有限值．此时，
研究信号的平均功率更为合适。
T
lim

数学期望，称为相关性，表征了x、y之间其的中一关个联可程以度测。量的量
cxy xy x y
E[(xx )( y的 的y )变变] 化化来。表示另一个量
E[(xx )2 ]E[( y y )2 ]1/ 2
y
y
y
y
x
x
xy 1
xy 1
x
0 xy 1
b) sinc 函数
sin c(t) sin t , or, sint , ( t )
t
t
性质：
波形
偶函数；
闸门(或抽样)函数；
滤波函数；
内插函数。
2.1 信号的分类与描述
c) 复指数函数
est et e jt
t
et cost et sint ; s j
瞬态信号
瞬态信号:持续时间有限的信号，如 x(t)= e-Bt . Asin(2*pi*f*t)
2.1 信号的分类与描述
c)非确定性信号：不能用数学式描述，其幅值、相位变化 不可预知，所描述物理现象是一种随机过程。
噪声信号(平稳)
噪声信号(非平稳)
统计特性变异
2.1 信号的分类与描述 2 能量信号与功率信号
（3）卷积特性

f (t) * (t) f ( ) (t )d f (t)

工程测试技术 信号分析基础 掌握信号时域波形分析方法


2.2 信号的时域波形分析
实验：
12
2.2 信号的时域波形分析
5、波形分析的应用
信号类型识别
信号基本参数识别
Pp-p
超门限报警
2.2 信号的时域波形分析
案例：汽车速度测量:
T
14
2.2 信号的时域波形分析
案例：旅游索道钢缆检测
超门限报警
15
2.2 信号的时域波形分析 实验：声音信号有效值报警：
应用： （1）信号中的直流分量消除 （2）仪器的智能调零
2.3 信号的时域统计分析
2、均方值
信号的均方值E[x2(t)]，表达了信号的强度；其正平 方根值，又称为有效值(RMS)，也是信号平均能量的一种 表达。
2 x
E[x2 (t)]
lim
1 T
T x 2 (t)dt
0
T
工程测量中仪器的表头示值就是信号的有效值。 应用：局部异常信号识别（钢丝绳断丝检测）
2.4 信号的时差域相关分析
发火周期
1
0.5
Healthy #1 Misfire #1&2 Misfire
Correlation
0
-0.5
自相关分析的主要应用：
用来检测混肴在干扰信号中的确定 性周期信号成分。
-1
0
120
240
360
480
600
720
Crank Angle (degCA)
作一个循环内转速信号的的自相关函数，其周期为发火周期。
16
第二章、信号分析基础 2.3 信号的时域统计分析
1. 均值 2. 均方值 3. 方差 4. 概率密度函数 5. 概率分布函数 6. 直方图
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

自相关函数值的计算过程
将不同时差τ的计算值标在图上，然后在两点间连线， 就可以得到信号的相关函数曲线，如下图所示：
相关函数曲线的绘制
相关函数描述了两个信号或一个信号自身不同时刻 的相似程度，通过相关分析我们可以发现信号中许多有 规律的东西。
2.4.3 相关函数的性质
根据定义，相关函数有如下性质： (1).自相关函数是偶函数，即
频域有限信号
2.2.4.连续时间信号与离散时间信号 连续时间信号：在所讨论的时间间隔内，对于任意时间值(除若干个 第一类间断点外)都可给出确定的函数值，此类信号称为连续时间信号或 模拟信号。连续信号的幅值可以是连续的也可以是不连续的。
离散时间信号：离散时间信号在时间上是离散的．只是在某些不连 续的规定瞬时给出函数值，而在其他时间没有定义的信号。
2.4.4 相关分析的工程应用
相关函数描述了信号波形的相关性（或相似程度），揭示了信号波形的 结构特性．相关分析作为信号的时域分析方法之一，为工程应用提供了重要 信息，特别是对于在噪声背景下提取有用信息，更显示了它的实际应用价 值．下面列举一些工程应用实例． 1．机械加工表面粗糙度的自相关分析 下图表示用电感式轮廓仪测量工件表面粗糙度的示意图．金刚石触外将 工件表面的凸凹不平度，通过电感式传感器转换为时域（或空域）信号（图 中（a）），再经过相关分析得到自相关图形（图中（b））．可以看出，这 是一种随机信号中混杂着周期信号的波形，随机信号在原点处有较大相关 性，随τ值增大而减小，此后呈现出周期性，这显示出造成表面粗糙度的原 因中包含了某种周期因素．例如沿工件轴向，可能是走刀运动的周期性；沿 工件切向，则可能是由于主轴回转振动的周期性等．
2.4 信号的相关分析
2.4.1 相关的概念 相关是指客观事物变化量之间的相依关系，在统计学中是用相关系数来描 述两个变量x，y之间的相关性的，即：
式中 是两个随机变量波动量之积的数学期望，称之为协方差或相关性，表 征了x、y之间的关联程度； 、 分别为随机变量x、y的均方差，是随机变 量波动量平方的数学期望。 是一个无量纲的系数， 。 当| |＝１时，说明x、y两变 量是理想的线形相关； ＝０时，表示x、y两变量完全无关；0<| |<1时， 表示两变量之间有部分相关。下图分别表示了x、y两变量间的各种关系情况。
温度传感器
2.4.2 相关函数
如果所研究的随机变量x, y是与时间有关的函数，即x(t)与 y(t)，这时可以引入一个与时间 τ有关的量 ，称为相关系 数，并有：
式中假定x(t)、y(t)是不含直流分量(信号均值为零)的能量信号 。分母部分是一个常量，分子部分是时移τ的函数，反映了二 个信号在时移中的相关性，称为相关函数。因此相关函数定义 为： 或
4. 均方值 信号x(t)的均方值E[x2(t)]，或称为平均功率，其表达式为： 值表达了信号的强度，其正平方根值，又称为有效值，也是信号的平均能量 的一种表达。在工程信号测量中一般仪器的表头示值显示的就是信号的均方值。
5. 方差 信号x(t)的方差定义为： 称为均方差或标准差。 可以证明， 描述了信号的波动量； 描述了信号的静态量。 方差反映了信号绕均值的波动程度。
三种不同特征的信号
2.周期T 对周期信号来说，可以用时域分析来确定信号的周期，也就是计算相邻的 两个信号波峰的时间差。
信号周期测量
3.均值 均值E[x(t)]表示集合平均值或数学期望值．基于随机过程的各忘历经性，可 用时间间隔T内的幅值平均值表示，即 均值表达了信号变化的中心趋势，或称之为直流分量。
2.2.1 确定性信号与非确定性信号
a)确定性信号 可以用明确的数学关系式描述的信号称为确定性信号。它可以进一步分为周期 信号、非周期信号与准周期信号等，如下图所示。
信号的分类描述
周期信号是经过一定时间可以重复出现的信号，满足条件： x(t) = x ( t + nT )
式中，T——周期，T=2π/ω0；ω0——基频；n=0,±1, …。 例如，下面是一个50Hz正弦波信号10sin(2*3.14*50*t)的波形，信号周期为： 1/50=0.02秒:
信号的幅域、时域和频域
有量纲幅域诊断函数
量纲为一的幅域诊断函数
幅域参数对故障的敏感性和稳定 性比较
2.3 信号的时域分析
信号时域分析又称之为波形分析或时域统计分析，它是通过 信号的时域波形计算信号的均值、均方值、方差等统计参数。 信号的时域分析很简单，用示波器、万用表等普通仪器就可以 进行分析。 1.信号类型确定 信号时域分析(波形分析)的一个重要功能是根据信号的分类 和各类信号的特点 确定信号的类型。然后再根据信号类型选用 合适的信号分析方法。
b)功率信号 有许多信号，如周期信号、随机信号等，它们在区间（-∞，∞）内能量不是 有限值．在这种情况下，研究信号的平均功率更为合适． 在区间（t1，t2）内，信号的平均功率 若区间变为无穷大时，上式仍然大于零，那么信号具有有限的平均功率，称 之为功率信号．具体讲，功率信号满足条件： 对比上式，显而易见，一个能量信号具有零平均功率，而一个功率信号具有 无限大能量
2．地下输油管道漏损位置的探测 下图表示利用互相关分析方法，确定深埋在地下的输油管漏报位置的 示意图．在输油管表面沿轴向放置传感器（例如拾音器、加速度计或 AE 传感器等） 1和 2，油管漏损处 K可视为向两侧传播声波的声源，因放置 两传感器的位置距离漏损处不等，则油管漏油处的声波传至两传感器就有 时差，将两拾音器测得的音响信号X l（t）和X2（t）进行互相关分析，找 出互相关值最大处的延时cc，即可由τm确定油管漏报位置． S=vτm/2 式中，S——两传感器的中心至漏报处的距离； V——声波通过管道的传 播速度．
值得注意的是，互相关函数既不是偶函数，也不是奇函数，但 满足下式：
(2).当τ=0时，自相关函数具有最大值，此时对于能量信号 对于功率信号
(3).周期信号的自相关函数仍然时同频率的周期信号，但 不具有原信号的相位信息。如：正弦信号Asin(ωt+φ)的自相 关函数为：Rx( τ)=(A2cosωτ )/2 (4).两周期信号的互相关函数的仍然是同频率的周期信 号，但保留了原信号的相位信息。如正弦信号Asin( ωt) 与 Bsin(ωt -φ)的互相关函数 Rxy( τ) = ABcos(ωτ - φ ) (5).两个非同频率的周期信号互不相关。 (6).随机信号的自相关函数将随|τ|值增大而很快趋于零。
离散时间信号
2.2.5 物理可实现信号 物理可实现信号又称为单边信号，满足条件：t＜0时，x(t) = 0，即在时刻小于 零的一侧全为零，信号完全由时刻大于零的一侧确定。 在实际中出现的信号，大量的是物理可实现信号，因为这种信号反映了物理上 的因果律．实际中所能测得的信号，许多都是由一个激发脉冲作用于一个物理系统 之后所输出的信号．例如，切削过程，可以把机床、刀具、工件构成的工艺系统作 为一个物理系统，把工件上的硬质点或切削刀具上积屑瘤的突变等，作为振源脉 冲，仅仅在该脉冲作用于系统之后，振动传感器才有描述刀具振动的输出。
运算处理 中心设备 Operation Processing 频谱分析仪
显示、记录 Display, Plotting
后端设备
信号处理系统
A/D
• 模拟（Analog）
D/A
数字（Digital）
从模拟信号到数字信号
2.2 信号的分类与描述
为了深入了解信号的物理实质，将其进行 分类研究是非常必要的。以不同的角度来看 待信号，我们可以将信号分为 1. 确定性信号与非确定性信号 2. 能量信号与功率信号 3. 时限信号与频限信号 4. 连续时间信号与离散时间信号 5. 物理可实现信号
2.2.3.时限与频限信号
时域有限信号是在有限区间（t1，t2 ）内定义，而其外恒等于 零．例如，矩形脉冲、三角脉冲、余弦脉冲等。而周期信号、指数 衰减信号、随机过程等，则称为时城无限信号．
时域有限信号
频域有限信号是指信号经过傅里叶变换，在频域内占据一定带宽 （f1 ，f2），其外恒等于零．例如，正弦信号、sinc（t）函数、限带 白噪声等，为时城无限频域有限信号。白噪声、理想采样信号等，则 为频域无限信号． 时间有限信号的频谱，在频率轴上可以延伸至无限远。由时、频域对 称性可推论，一个具有有限带宽的信号，必然在时间轴上延伸至无限 远处。显然，一个信号不能够在时域和频域都是有限的
变量x、y间的不同相关情况
例如，玻璃管温度计液面高度(Y)与环境温度(x)的关系就是 近似理想的线形相关，在两个变量相关的情况下，我们可 以用其中一个可以测量的量的变化来表示另一个量的变 化。在后续章节中将要介绍的传感器部分中就应用了变量 中的这种相关性。 自然界中的事物变化规律的表现，总有互相关联的现 象，不一定是线形相关，也不一定是完全无关，如：人的 身高与体重，吸烟与寿命的关系。
加工过程中螺纹车床主轴受环境影响的振动信号波形
2.2.2 能量信号与功率信号
a)能量信号 在所分析的区间（-∞，∞），能量为有限值的信号称为能量信号，满足条 件： 关于信号的能量，可作如下解释：对于电信号，通常是电压或电流，电压在 已知区间（t1；，t2 ） 内消耗在电阻上的能量 对于电流，能量 在上面每一种情况下，能量都是正比于信号平方的积分．讨论消耗在IQ电阻 上的能量往往是很方便的，因为当R—IQ时，上述两式具有相同形式，采用这种 规定时，就称方程
50Hz正弦波信号波形
机械系统中，回转体不平衡引起的振动，往往也是一种周期性运动。例如，下图是某钢厂 减速机上测得的振动信号波形(测点3)，可以近似的看作为周期信号:
某钢厂减速机振动测点布置图
测点３振动信号波形
非周期信号是不会重复出现的信号。例如，锤子的敲击力；承载缆绳断裂时应力变 化；热电偶插入加热炉中温度的变化过程等，这些信号都属于瞬变非周期信号，并且 可用数学关系式描述。例如，下图是单自由度振动模型在脉冲力作用下的响应。