(完整版)第五章-点的运动学
- 格式:ppt
- 大小:1.34 MB
- 文档页数:31



第五章运动学基础一、是非题1.已知直角坐标描述的点的运动方程为X=f1(t),y=f2(t),z=f3(t),则任一瞬时点的速度、加速度即可确定。
()2.一动点如果在某瞬时的法向加速度等于零,而其切向加速度不等于零,尚不能决定该点是作直线运动还是作曲线运动。
()3.切向加速度只表示速度方向的变化率,而与速度的大小无关。
()4.由于加速度a永远位于轨迹上动点处的密切面内,故a在副法线上的投影恒等于零。
()5.在自然坐标系中,如果速度υ=常数,则加速度α=0。
()6.在刚体运动过程中,若其上有一条直线始终平行于它的初始位置,这种刚体的运动就是平动。
()7.刚体平动时,若刚体上任一点的运动已知,则其它各点的运动随之确定。
()8.若刚体内各点均作圆周运动,则此刚体的运动必是定轴转动。
()9.定轴转动刚体上点的速度可以用矢积表示为v=w×r,其中w是刚体的角速度矢量,r是从定轴上任一点引出的矢径。
()10、在任意初始条件下,刚体不受力的作用、则应保持静止或作等速直线平动。
()二、选择题1、已知某点的运动方程为S=a+bt2(S以米计,t以秒计,a、b为常数),则点的轨迹。
①是直线;②是曲线;③不能确定。
2、一动点作平面曲线运动,若其速率不变,则其速度矢量与加速度矢量。
①平行;②垂直;③夹角随时间变化。
3、刚体作定轴转动时,切向加速度为,法向加速度为。
①r×ε②ε×r③ω×v④v×ω4、杆OA绕固定轴O转动,某瞬时杆端A点的加速度α分别如图(a)、(b)、(c)所示。
则该瞬时的角速度为零,的角加速度为零。
①图(a)系统;②图(b)系统;③图(c)系统。
三、填空题1、点在运动过程中,在下列条件下,各作何种运动?①aτ=0,a n=0(答):;②aτ≠0,a n=0(答):;③aτ=0,a n≠0(答):;④aτ≠0,a n≠0(答):;2、杆O1B以匀角速ω绕O1轴转动,通过套筒A带动杆O2A绕O2轴转动,若O1O2=O2A=L,α=ωt,则用自然坐标表示(以O1为原点,顺时针转向为正向)的套筒A 的运动方程为s=。

理论力学运动学知识点总结第一篇:理论力学运动学知识点总结运动学重要知识点一、刚体的简单运动知识点总结1.刚体运动的最简单形式为平行移动和绕定轴转动。
2.刚体平行移动。
·刚体内任一直线段在运动过程中,始终与它的最初位置平行,此种运动称为刚体平行移动,或平移。
·刚体作平移时,刚体内各点的轨迹形状完全相同,各点的轨迹可能是直线,也可能是曲线。
·刚体作平移时,在同一瞬时刚体内各点的速度和加速度大小、方向都相同。
3.刚体绕定轴转动。
• 刚体运动时,其中有两点保持不动,此运动称为刚体绕定轴转动,或转动。
• 刚体的转动方程φ=f(t)表示刚体的位置随时间的变化规律。
• 角速度ω表示刚体转动快慢程度和转向,是代数量,以用矢量表示。
,当α与ω。
角速度也可• 角加速度表示角速度对时间的变化率,是代数量,同号时,刚体作匀加速转动;当α 与ω异号时,刚体作匀减速转动。
角加速度也可以用矢量表示。
• 绕定轴转动刚体上点的速度、加速度与角速度、角加速度的关系:。
速度、加速度的代数值为。
• 传动比。
一、点的运动合成知识点总结1.点的绝对运动为点的牵连运动和相对运动的合成结果。
• 绝对运动:动点相对于定参考系的运动;• 相对运动:动点相对于动参考系的运动;• 牵连运动:动参考系相对于定参考系的运动。
2.点的速度合成定理。
• 绝对速度:动点相对于定参考系运动的速度;• 相对速度:动点相对于动参考系运动的速度;• 牵连速度:动参考系上与动点相重合的那一点相对于定参考系运动的速度。
3.点的加速度合成定理。
• 绝对加速度:动点相对于定参考系运动的加速度;• 相对加速度:动点相对于动参考系运动的加速度;• 牵连加速度:动参考系上与动点相重合的那一点相对于定参考系运动的加速度;• 科氏加速度:牵连运动为转动时,牵连运动和相对运动相互影响而出现的一项附加的加速度。
• 当动参考系作平移或 = 0,或与平行时,= 0。




第5章 点的运动学习题1.是非题(对画√,错画×)5-1.某瞬时动点的速度为零,则动点的加速度必为零。
( ) 5-2.某瞬时动点的加速度为零,则动点的速度必为零。
( ) 5-3.切向加速度是表示动点速度的方向对时间的导数。
( ) 5-4.法向加速度是表示动点速度的大小对时间的导数。
( ) 5-5.点作曲线运动时,法向加速度是不等于零的。
( ) 5-6.点作运动时,法向加速度是等于零的。
( ) 5-7.点作直线运动时,切向加速度是等于零的。
( ) 5-8.轨迹曲线的曲率半径为无穷大时,点作直线运动。
( ) 5-9.点作匀变速运动时,切向加速度大小保持不变。
( ) 5-10.法向加速度的方向是恒指向轨迹曲线的曲率中心。
( ) 2.填空题(把正确的答案写在横线上)5-11.点作直线运动时,法向加速度等于 。
5-12.点作匀速曲线运动时,切向加速度等于 。
5-13.点运动方程t ωcos r x =、t sin ωr y =,点的轨迹方程 。
5-13.点运动方程222t cos x =、222t sin y =,当0=t 时点的速度=v ;点的加速度=a ;轨迹的曲率半径ρ= 。
5-14.点作曲线运动时,其点的加速度在 面内。
5-15.点的次法向加速度=b a 。
3.简答题5-16.点在下述情况下作何种运动 (1)0=τa ,0=n a ; (2)0≠τa ,0=n a ; (3)0=τa ,0≠n a ;(4)0≠τa ,0≠n a ;5-17.dt d v 与dtdv 的区别是什么?5-18.当点作曲线运动时,点的加速度是恒矢量,问点作匀速曲线运动吗?为什么? 5-19.写出描述动点直角坐标法和自然法的运动方程之间的关系。
5-20.若点沿已知的轨迹曲线运动时,其运动方程为242t s +=,t 为时间,则点作怎样的运动?4.计算题5-21.如图所示的平面机构中,曲柄OC 以角速度ω绕O 轴转动,图示瞬时与水平线夹角t ω=ϕ,A 、B 滑块分别在水平滑道和竖直滑道内运动,试求AB 中点M 的运动方程、速度和加速度。

理论力学Theoretical Mechanics2016年3月27日主讲教师:祝瑛转动惯量的概念综合实验楼508Tel 51682724定义2ii z r m J ∑=•转动惯量的概念(5.3)转动惯量(moment of inertia)也称惯性矩,表示刚体绕一轴或一点转动的惯性,是刚体转动惯性的度量ρ:回转半径⎰=m z dmr J 2kg ⋅m 22z z m J ρ=或mI z z =ρ转动惯量描述的是刚体绕转轴转动的惯性,其惯性主要取决于刚体质量的分布情况,质量分布离轴越远转动惯量值越大,越近越小;大型转轴一般将质量均匀地分布在边缘上,目的是增加转动惯量,储存动能,保持运转的稳定性;仪表盘指针一般将质量集中于转轴附近,目的是减小转动惯量,增加灵敏度。
刚体对质心最长轴的转动惯量值最小。
简单形状物体的转动惯量计算设杆长l ,质量m ,取微段d x==C z J J =zA J ⎰-⋅222l l dxlm x =132ml或1、均质细长杆2121ml =⎰⋅ldx lm x 02设平均半径r ,质量m ,取微弧段d s=O J ⎰⋅rds rm r ππ20222、均质细圆环2mr =O rd s d q3、均质圆盘设半径R ,质量m ,取细圆环=)(z O J ⎰⋅⋅Rrdr Rm r 0222ππ221mR =3、均质圆盘设半径R ,质量m⎰+=m z O my x J d )(22)(241mRr 2=x2+y2⎰⎰+=m m my m x d d 22OxOy J J +===Oy Ox J J21J J J z -=2222112121R m R m -=)(214241R R l J z -=ρπ21,,R R m 例:已知:,解:lR m 222ρπ=l R m 211ρπ=其中mR R l =-)(2221ρπ由)(212221R R m J z +=))((2122212221R R R R l +-=ρπz J 求。
点的运动学一,矢量法 矢径:22(),,d d d t dtdtdt====r v r r r v a ,方向为矢端曲线的切线二,直角坐标法()()(),,,x t y t z t =++r i j k i j k 为坐标轴的单位矢量 ,,,x y z d dx dy dz dx dy dz v v v dt dt dtdtdtdtdt==++===r v i j k22222222,,,y x z x y z dv dv dv d d x d y d z a a a dtdtdtdtdtdtdt==++===r a i j k ,由方向余弦来确定方向三,自然法利用点的运动轨迹建立弧坐标及自然轴系,并用它们来描述和分析点的运动 1,弧坐标 ()s f t =2,自然轴系 =⨯b τn ,切线,主法线和副法线,都是单位矢量 3,曲率曲线切线的转角对弧长一阶导数的绝对值,曲率的倒数为曲率半径,即01lims d sdsϕϕρ∆→∆==∆4,点的速度和加速度ds v dt==v ττ,2n d dv d dv d ds dv vvva a dtdtdtdtds dtdtτρ==+=+=+=+v ττa τττn τn直线运动情形 2001,2v v a t s s v t a tττ=+=++ 5,点的速度和加速度在柱坐标、极坐标、球坐标系中的表示方法刚体定轴转动1,定轴转动的运动方程22(),,d d d f t dtdtdtϕωϕϕωα====2各点的速度和加速度(R 为转动半径)s R ϕ=,ds d RR dt dtϕω===v τττ,()2222222,n R d s d va RR a R dtdtτωϕαωρρ======3,矢量表示角速度和角加速度,,,n d d d a a dtdtdtτωα===⨯==⨯+⨯=⨯+⨯=+v ωr ωk αk v ωr a r ωαr ωv τn。
哈尔滨工业大学理论力学教研室理论力学(I)第8版习题答案《理论力学(1 第8版)/“十二五”普通高等教育本科国家级规划教材》第1版至第7版受到广大教师和学生的欢迎。
第8版仍保持前7版理论严谨、逻辑清晰、由浅入深、宜于教学的风格体系,对部分内容进行了修改和修正,适当增加了综合性例题,并增删了一定数量的习题。
本书内容包括静力学(含静力学公理和物体的受力分析、平面力系、空间力系、摩擦),运动学(含点的运动学、刚体的简单运动、点的合成运动、刚体的平面运动),动力学(含质点动力学的基本方程、动量定理、动量矩定理、动能定理、达朗贝尔原理、虚位移原理)。
本书可作为高等学校工科机械、土建、水利、航空、航天等专业理论力学课程的教材,也可作为高职高理论力学(I)第8版哈尔滨工业大学理论力学教研室习题答案专、成人高校相应专业的自学和函授教材,亦可供有关工程技术人员参考。
本书配套的有《理论力学学习辅导》、《理论力学(I)第8版哈尔滨工业大学理论力学教研室习题答案理论力学思考题集》、《理论力学解题指导及习题集》(第3版)、《理论力学电子教案》、《理论力学网络课程》、《理论力学习题解答》、《理论力学网上作业与查询系统》等。
理论力学(I)第8版哈尔滨工业大学理论力学教研室课后答案前辅文静力学关注网页底部或者侧栏二维码回复理论力学(I)第8版答案免费获取答案引言第一章静力学公理哈尔滨工业大学理论力学教研室理论力学(I)第8版课后答案理论力学思考题集》、《理论力学解题指导及习题集》(第3版)、《理论力学电子教案》、《理论力学网络课程》、《理论力学习题解答》、《理论力学网上作业与查询系统》等。
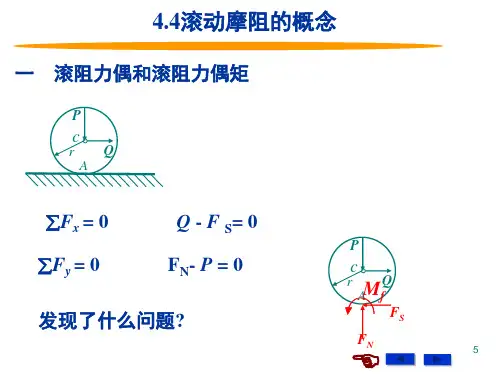
理论力学(I)第8版哈尔滨工业大学理论力学教研室课后答案前辅文静力学引言第一章静力学公理和物体的受力分析第二章平面力系第三章空间力系第四章摩擦理论力学(I)第8版哈尔滨工业大学理论力学教研室习题答案§4-4 滚动摩阻的概念运动学引言第五章点的运动学*§5-5 点的速度和加速度在球坐标中的投影思考题习题第六章刚体的简单运动§6-1 刚体的平行移动§6-2 刚体绕定轴的转动§6-3 转动刚体内各点的速度和加速度§6-4 轮系的传动比§6-5 以矢量表示角速度和角加速度·以矢积表示点的速度和加速度思考题习题第七章点的合成运动第八章刚体的平面运动动力学引言第九章质点动力学的基本方程第十章动量定理第十一章动量矩定理第十二章动能定理第十三章达朗贝尔原理第十四章虚位移原理参考文献习题答案索引Synopsis哈尔滨工业大学理论力学教研室理论力学(I)第8版课后答案第十四章虚位移原理。
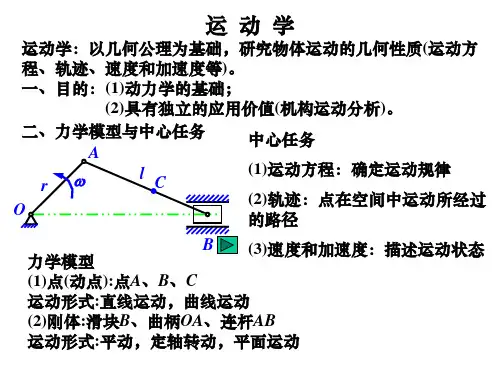
第五章点的运动学点的运动学是研究一般物体运动的基础,又具有独立应用意义。
本章将研究点的简单运动,研究点相对某一个参考系的几何位置随时间变动的规律,包括:点的运动方向运动轨迹速度和加速度等。
第五章点的运动学§5-1 矢量法§5-2 直角坐标法§5-3 自然法选取参考系上某确定点O为坐标原点, 自点O向动点M作矢量r ,称为点M相 对原点O的位置矢量,简称矢径。
)(t r r =上式称为矢量表示的点的运动方程 动点M在运动过程中,其矢径 r 的末端描绘出一条连续曲线, 称为矢端曲线。
矢径 r 的矢端曲线就是动点M的运动轨迹。
i j k xz Mr O 当动点M运动时,矢径 r 随时间而变化, 并且是时间的单值连续函数. §5-1 矢量法有缘学习更多+谓ygd3076考证资料或关注桃报:奉献教育(店铺)i j k x yz M r O 设点M 经过Δt 达到点M′ rM M ∆=′位移 M ′r ∆点的位移动点的速度 动点的速度等于它的矢径r 对时间的一阶导数,是矢量。
速度方向: 沿着矢径 r 的矢端曲线的切线,即沿动点运动轨迹的切线, 并 与此点运动的方向一致。
速度的大小: 即速度矢 v 的模,表明点运动 的快慢。
速度单位: 国际单位制中以 m/s 为 速度v 的 单位符号。
量纲: LT -1 i j k xz M r O 运动轨迹 v 0d d lim t r r v t t ∆→∆==∆动点的加速度矢等于该点的速度矢对时间的一阶导数, 或等于矢径对时间的二阶导数:也可以表示为: r v a r v ===加速度的大小: 即加速度矢 a 的模,表明点运动速度变化的快慢。
加速度单位: 国际单位制中以 m/s 2为加速度a 的单位符号。
量纲:LT -2点的加速度220lim dt r d dt v d t v a t ==∆∆=→∆是“矢量“,它表征了速度大小和方向的变化。