理论力学 第五章 点的运动学(合)

理论力学习题答案(总26页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--2第一章 静力学公理和物体的受力分析一、是非判断题在任何情况下，体内任意两点距离保持不变的物体称为刚体。

( ∨ ) 物体在两个力作用下平衡的必要与充分条件是这两个力大小相等、方向相反，沿同一直线。

( × ) 加减平衡力系公理不但适用于刚体，而且也适用于变形体。

( × ) 力的可传性只适用于刚体，不适用于变形体。

( ∨ ) 两点受力的构件都是二力杆。

( × ) 只要作用于刚体上的三个力汇交于一点，该刚体一定平衡。

( × ) 力的平行四边形法则只适用于刚体。

( × ) 凡矢量都可以应用平行四边形法则合成。

( ∨ ) 只要物体平衡，都能应用加减平衡力系公理。

( × ) 凡是平衡力系，它的作用效果都等于零。

( × ) 合力总是比分力大。

( × ) 只要两个力大小相等，方向相同，则它们对物体的作用效果相同。

( × )若物体相对于地面保持静止或匀速直线运动状态，则物体处于平衡。

( ∨ )当软绳受两个等值反向的压力时，可以平衡。

( × )静力学公理中，二力平衡公理和加减平衡力系公理适用于刚体。

( ∨ )静力学公理中，作用力与反作用力公理和力的平行四边形公理适用于任何物体。

( ∨ )凡是两端用铰链连接的直杆都是二力杆。

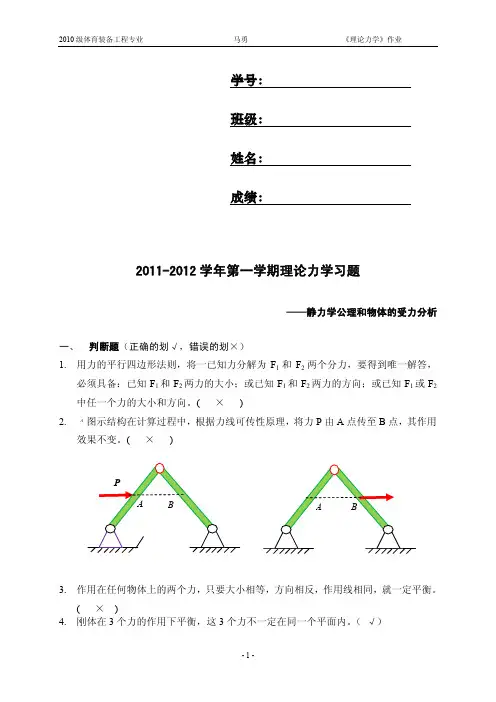
( × )如图所示三铰拱，受力F ，F 1作用，其中F 作用于铰C 的销子上，则AC 、BC 构件都不是二力构件。

( × )图3二、填空题力对物体的作用效应一般分为 外 效应和 内 效应。

对非自由体的运动所预加的限制条件称为 约束 ；约束力的方向总是与约束所能阻止的物体的运动趋势的方向 相反 ；约束力由 主动 力引起，且随 主动 力的改变而改变。

第五章 点的运动学5-1和 ， 和 是否相同？5-2点沿曲线运动，如图所示各点所给出的速度v和加速度a哪些是可能的？哪些是不可能的？5-3点M 沿螺线自外向内运动，如图所示。

它走过的弧长与时间的一次方成正比，问点的加速度是越来越大，还是越来越小?点M越跑越快，还是越跑越慢？5-4当点作曲线运动时，点的加速度a是恒矢量，如图所示。

问点是否作匀变速运动?5-5 作曲线运动的两个动点，初速度相同、运动轨迹相同、运动中两点的法向加速度也相同。

判断下述说法是否正确：（1）任一瞬时两动点的切向加速度必相同；（2）任一瞬时两动点的速度必相同；（3）两动点的运动方程必相同。

5-6 动点在平面内运动，已知其运动轨迹)(x f y 及其速度在x 轴方向的分量。

判断下述说法是否正确：（1）动点的速度可完全确定；（2）动点的加速度在x 轴方向的分量可完全确定；（3）当速度在x 轴方向的分量不为零时，一定能确定动点的速度、切向加速度、法向加速度及全加速度。

5-7 下述各种情况，动点的全加速度，切向加速度和法向加速度三个矢量之间有何关系？（1）点沿曲线作匀速运动；（2）点沿曲线运动，在该瞬时其速度为零；（3）点沿直线作变速运动；（4）点沿曲线作变速运动。

5-8 点作曲线运动时，下述说法是否正确：（1）若切向加速度为正，则点作加速运动；（2）若切向加速度与速度的符号相同，则点作加速运动；（3）若切向加速度为零，则速度为常矢量。

5-9 在极坐标系中，ρρ =v ，ρϕϕ =v 分别代表在极径方向与极径垂直方向（极角ϕ的方向）的速度。

但为什么沿这两个方向的加速度为2ϕρρρ -=a ϕρϕρϕ 2+=a 试分析ρa 中2ϕρρ -=a 和ϕa 中的ϕρ 出现的原因和它们的几何意义。

习 题5-1 如图5-13所示，偏心轮半径为R ，绕轴O 转动，转角t ωϕ=（ω为常量），偏心距e OC =，偏心轮带动顶杆AB 沿铅垂直线作往复运动。

试求顶杆的运动方程和速度。

图5-13)(cos )sin(222t e R t e y ωω-+=)(cos 2)2sin()[cos(222t e R t e t e yv ωωωω-+==5-2 梯子的一端A 放在水平地面上，另一端B 靠在竖直的墙上，如图5-14所示。

梯子保持在竖直平面内沿墙滑下。

已知点A 的速度为常值v 0，M 为梯子上的一点，设MA = l ，MB = h 。

试求当梯子与墙的夹角为θ时，试点M 速度和加速度的大小。

图5-14A M x hl hh x +==θsin θcos l y M = 0cos v h l h x h l h h xA M +=+== θθ 得 θθcos )(0h l v +=θθθθθt a n)(c o s )(s i n s i n 00h l lv h l v l l yM +-=+⨯-=-= 0=M xθθθθθ322002020cos )(cos )(sec )(sec )(h l lv h l v h l lv h l lv y M +-=+⨯+-=+-=θ3220cos )(h l lv a M+=5-3 已知杆OA 与铅直线夹角6/πt =ϕ（ 以 rad 计，t 以s 计），小环M 套在杆OA 、CD 上，如图5-15所示。

铰O至水平杆CD 的距离h =400 mm 。

试求t = 1 s 时，小环M 的速度和加速度。

图5-15ϕtan h x M = ϕϕϕ22sec 6π400sec ⨯== h xM ϕϕϕϕϕϕϕs i n s e c 9π200s i n s e c 6π3π400)s i n s e c 2(6π4003233=⨯⨯=⨯⨯= M x当s 1=t 时6π=ϕmm/s 3.2799π800346π400)6π(sec 6π4002==⨯==Mv 223232mm/s 8.168327π80021)32(9π200)6πsin()6π(sec 9π200==⨯⨯=⨯⨯=Ma5-4 点M 以匀速u 在直管OA 内运动，直管OA 又按t ωϕ=规律绕O 转动，如图5-16所示。

运动学重要知识点一、刚体的简单运动知识点总结1.刚体运动的最简单形式为平行移动和绕定轴转动。

2.刚体平行移动。

·刚体内任一直线段在运动过程中，始终与它的最初位置平行，此种运动称为刚体平行移动，或平移。

·刚体作平移时，刚体内各点的轨迹形状完全相同，各点的轨迹可能是直线，也可能是曲线。

·刚体作平移时，在同一瞬时刚体内各点的速度和加速度大小、方向都相同。

3.刚体绕定轴转动。

•刚体运动时，其中有两点保持不动，此运动称为刚体绕定轴转动，或转动。

•刚体的转动方程φ=f(t)表示刚体的位置随时间的变化规律。

•角速度ω表示刚体转动快慢程度和转向，是代数量，。

角速度也可以用矢量表示，。

•角加速度表示角速度对时间的变化率，是代数量，，当α与ω同号时，刚体作匀加速转动；当α与ω异号时，刚体作匀减速转动。

角加速度也可以用矢量表示，。

•绕定轴转动刚体上点的速度、加速度与角速度、角加速度的关系：。

速度、加速度的代数值为。

•传动比。

一、点的运动合成知识点总结1.点的绝对运动为点的牵连运动和相对运动的合成结果。

•绝对运动：动点相对于定参考系的运动；•相对运动：动点相对于动参考系的运动；• 牵连运动：动参考系相对于定参考系的运动。

2.点的速度合成定理。

•绝对速度：动点相对于定参考系运动的速度；•相对速度：动点相对于动参考系运动的速度；•牵连速度：动参考系上与动点相重合的那一点相对于定参考系运动的速度。

3.点的加速度合成定理。

•绝对加速度：动点相对于定参考系运动的加速度；•相对加速度：动点相对于动参考系运动的加速度；•牵连加速度：动参考系上与动点相重合的那一点相对于定参考系运动的加速度；•科氏加速度：牵连运动为转动时，牵连运动和相对运动相互影响而出现的一项附加的加速度。

•当动参考系作平移或= 0 ，或与平行时， = 0 。

该部分知识点常见问题有问题一牵连速度和牵连加速度的意义。

问题二应用速度合成定理时要画速度矢量图。

哈尔滨工业大学理论力学教研室理论力学（I）第8版习题答案《理论力学（1 第8版）/“十二五”普通高等教育本科国家级规划教材》第1版至第7版受到广大教师和学生的欢迎。

第8版仍保持前7版理论严谨、逻辑清晰、由浅入深、宜于教学的风格体系，对部分内容进行了修改和修正，适当增加了综合性例题，并增删了一定数量的习题。

本书内容包括静力学（含静力学公理和物体的受力分析、平面力系、空间力系、摩擦），运动学（含点的运动学、刚体的简单运动、点的合成运动、刚体的平面运动），动力学（含质点动力学的基本方程、动量定理、动量矩定理、动能定理、达朗贝尔原理、虚位移原理）。

本书可作为高等学校工科机械、土建、水利、航空、航天等专业理论力学课程的教材，也可作为高职高理论力学（I）第8版哈尔滨工业大学理论力学教研室习题答案专、成人高校相应专业的自学和函授教材，亦可供有关工程技术人员参考。

本书配套的有《理论力学学习辅导》、《理论力学（I）第8版哈尔滨工业大学理论力学教研室习题答案理论力学思考题集》、《理论力学解题指导及习题集》（第3版）、《理论力学电子教案》、《理论力学网络课程》、《理论力学习题解答》、《理论力学网上作业与查询系统》等。

理论力学（I）第8版哈尔滨工业大学理论力学教研室课后答案前辅文静力学关注网页底部或者侧栏二维码回复理论力学（I）第8版答案免费获取答案引言第一章静力学公理哈尔滨工业大学理论力学教研室理论力学（I）第8版课后答案理论力学思考题集》、《理论力学解题指导及习题集》（第3版）、《理论力学电子教案》、《理论力学网络课程》、《理论力学习题解答》、《理论力学网上作业与查询系统》等。

理论力学（I）第8版哈尔滨工业大学理论力学教研室课后答案前辅文静力学引言第一章静力学公理和物体的受力分析第二章平面力系第三章空间力系第四章摩擦理论力学（I）第8版哈尔滨工业大学理论力学教研室习题答案§4-4 滚动摩阻的概念运动学引言第五章点的运动学*§5-5 点的速度和加速度在球坐标中的投影思考题习题第六章刚体的简单运动§6-1 刚体的平行移动§6-2 刚体绕定轴的转动§6-3 转动刚体内各点的速度和加速度§6-4 轮系的传动比§6-5 以矢量表示角速度和角加速度·以矢积表示点的速度和加速度思考题习题第七章点的合成运动第八章刚体的平面运动动力学引言第九章质点动力学的基本方程第十章动量定理第十一章动量矩定理第十二章动能定理第十三章达朗贝尔原理第十四章虚位移原理参考文献习题答案索引Synopsis哈尔滨工业大学理论力学教研室理论力学（I）第8版课后答案第十四章虚位移原理。