当前位置：文档之家 › 点的运动学(滚动)

点的运动学(滚动)

  • 格式：ppt
  • 大小：1.37 MB
  • 文档页数：38

下载文档原格式

  / 38

合集下载

工程力学之点的运动学

工程力学之点的运动学

。
简谐振动
点在平衡位置附近作周期性往 复运动，加速度与位移成正比 、方向相反。
抛体运动
点在重力作用下沿抛物线轨迹 的运动，如平抛、斜抛等。
一般平面曲线运动
点在平面内沿任意曲线轨迹的 运动，加速度和速度方向可任
意变化。
05
工程应用实例分析
机械手臂的运动控制
运动学建模
01
通过D-H参数法或旋量理论建立机械手臂的运动学模型，描述
在航空航天工程中，点的运动学可用于分 析飞行器的飞行轨迹和姿态控制，为航空 航天技术的发展提供理论支持。
土木工程
生物医学工程
在土木工程中，点的运动学可用于研究结 构的动力响应和稳定性问题，为工程结构 的设计和施工提供科学依据。
在生物医学工程中，点的运动学可用于分 析人体运动系统的生物力学特性，为医疗 器械的设计和康复治疗提供理论指导。
曲线运动的合成与分解
运动的合成
将点的运动分解为沿不同坐标轴的分运动，通过矢量合成得到点 的实际运动。
运动的分解
根据实际需要，将点的曲线运动分解为多个简单的直线或圆周运动， 便于分析和计算。
运动的叠加原理
多个独立的分运动可以线性叠加，形成复杂的曲线运动。
曲线运动的特殊形式
匀速圆周运动
点绕固定中心以恒定速率作圆 周运动，加速度始终指向圆心
速直线运动。
特点
速度大小随时间均匀变化，加速度 大小和方向保持不变。
公式
s = v0t + 1/2at^2，其中s为位移， v0为初速度，a为加
已知分运动求合运动，其位移、速度、加速度遵 循平行四边形定则。
分解
已知合运动求分运动，可将合运动分解为两个简 单的分运动进行处理。
理论力学—点的运动学

理论力学—点的运动学

r v t

O
二.点的速度
⒈ 平均速度
⒉ t 时刻的速度 r dr v lim r t 0 t dt
1.1 矢量法
三.加速度
速度矢端 曲线---速度端图
v ⒈ 平均加速度 a t
*
a
⒉ t 时刻的加速度
v dv d r a lim r 2 t 0 t dt dt
v y r sin t
2 2
v v
2
x
v
2
y
cos( v, i )
vx t MB sin sin v 2 2 MD v t BD cos( v, j ) y cos cos v 2 2 MD
t r (1 cos t ) sin t 2r sin 2
大小
a a x a
2Leabharlann 2ya2
z
方向

d x d y d z dt 2 dt 2 dt 2
2 2 2
2
2
2
ay ax az cos(ai ) , cos(aj ) , cos(ak ) a a a
解：由点M的运动方程，得
8 cos 4t , ax 32 sin 4t vx x x
8 sin 4t , a y 32 cos 4t vy y y 0 vz j 4, a z
z
2 2 2 2 从而 v vx vy vz2 80m s , a ax ay az2 32m s 2
α
at v M
故在这瞬时飞机的总加速度 a 的大小和方向为
第6章例题-纯滚动圆盘

第6章例题-纯滚动圆盘

工 程 力 学 第 6 章 点 的 运 动 学
例 直线轨道上的纯滚动圆盘，C 点速度为常量。求 M 点的 轨迹、速度、加速度以及轨迹的曲率半径。 ϕ = vC t , ϕ = vC & r r y
r vC
C M O(M) A
r
Cr
ϕ
B P
x
解 (1) M 点运动方程
= ϕ r = vC t
ቤተ መጻሕፍቲ ባይዱ
xM = OP − MB = ϕ r − r sin ϕ yM = CP − BC = r − r cos ϕ
消去 ϕ 得轨迹方程：
版权所有 张强 钟艳玲
yM 2 ⇒ xM = r arccos 1 − − 2ryM − yM r
旋轮线 (摆线)
工 程 力 学 第 6 章 点 的 运 动 学
例 直线轨道上的纯滚动圆盘，C 点速度为常量。求 M 点的 轨迹、速度、加速度以及轨迹的曲率半径。 ϕ = vC t , ϕ = vC & r r y xM = ϕ r − r sin ϕ r yM = r − r cos ϕ v Cr
例 直线轨道上的纯滚动圆盘，C 点速度为常量。求 M 点的 轨迹、速度、加速度以及轨迹的曲率半径。
工 程 力 学 第 6 章 点 的 运 动 学
版权所有 张强 钟艳玲
C
ϕ
M O A
B P
x
解 (2) M 点速度-大小
vMx = vC (1 − cos ϕ ) = 2vC sin
2
ϕ
2 cos
vMy = vC sin ϕ
⇒ vM = v
2 Mx
= 2vC sin
2 My
ϕ
2
ϕ
(完整版)点的运动学

(完整版)点的运动学


dz dt
z
★点的速度矢量在直角坐标轴上的投影等于点的相应坐标对时间
的一阶导数。
点的运动学
速度的大小：
v (dx )2 (dy )2 (dz )2 dt dt dt
(vx )2 (v y )2 (vz )2
速度的方向余弦： cos(v, i )vx源自cos(v ,j)
v vy
v
cos(v ,
k)
vz
v
直角坐标法
z
vz
M
vy
rz
v
vx
a
k
O j
y
i
x
xy
点的运动学
3、点的加速度
设： a axi a y j azk
ax
dv x dt
d2 x dt 2
x
ay
dv y dt
d2 y dt 2
y
az
dvz dt
d2z dt 2
z
直角坐 标法
z
vz
M
vy
rz
v
vx
a
k
d2r dt 2
r
v(t )
v2 a
M a
r
M
v(t t)
a
加速度 — 描述点在 t 瞬时速度大小和方向变化O率的力学量。加速度
的方向为v的极限方向(指向与轨迹曲线的凹向一致) 加速度大小等
于矢量 a 的模。
点的运动学
§6-2 直角坐标法
直角坐标法
1、点的运动方程和轨迹方程
不受约束的点在空间有3个自由度，
r (t )
M
r (t )
末端将描绘出一条连续曲线，称为
矢径端图，它就是动点运动的轨迹。 O
理论力学(第7版)第五章 点的运动学

理论力学(第7版)第五章 点的运动学

a 4、匀速运动： v 常数， 0, s s0 vt
运 动 规 律
[例5-1 ] 已知点的运动方程为x=2sin 4t m，y=2cos 4t m， z=4t m。 求：点运动轨迹的曲率半径 。
解：
vx x 8 cos 4t , ax 32 sin 4t x
r r t
—以矢量表示的 点的运动方程
矢端曲线：动点M在运动过程中，矢 径r的末端绘出的一条连续曲线。 ——动点M的运动轨迹
3
二.点的速度
dr v r dt
方向：沿着矢径r的矢端曲线的切线 方向，且与此点的运动方向一致。
大小：速度矢的模，表明点运动的快慢。
三.加速度
dv d 2r a r 2 dt dt
dv v2 a a a n a a n n n dt
17
5-3 自然法 曲率(1 / ) ：
定义——曲线切线的转角对弧长 一阶导数的绝对值。表示曲线的 弯曲程度。
d lim| | t 0 S dS 1
由于a , an均在密切面内，全加速a必在密切面内。 度
— 与 弧 坐 标 的 正 向 一 致 n — 指 向 曲 线 内 凹 一 侧 b — 与 , n 构 成 右 手 系
b n
[注]：自然坐标系是沿曲 13 线而变动的游动坐标系。
(动画自然坐标轴的几何性质)
曲线在P点的密切面形成
5-3 自然法
二.点的速度
当t 0时，r MM' S
v y y 8 sin 4t , a y 32 cos 4t y
v z z 4, a z 0 z
2 2 2 2 v v x v 2 v z 80 m s , a a x a 2 a z 32m s 2 y y
(完整版)第五章-点的运动学

(完整版)第五章-点的运动学


解： 炸弹的运动方程
x vt cos45
y vt sin 45 gt2 / 2
炸弹的初速度
求炸弹落到地面的时间，由 1800 277.8t sin 45 gt2 / 2
得 t 7.688s
可求出炸弹与目标的水平距离，
40
45 40 5
得： 又： 比较两式得：
速度在各坐标轴上的投影等于动点的各对应坐标对时间的一阶导数。
Part two 运动学
运动学是研究 物体运动的几何性质的学科。
研究一个物体的机械运动，必须选取另一个物体作为 参考，这个参考的物体称为参考体。
运动学研究 点和刚体的运动。
点的运动学 是研究一般物体运动的基础，又 具有独立的应用意义.
研究点的简单运动，研究点相对某一个参考系的 几何位置随时间变动的规律。
(4)求点M速度矢、加速度矢的大小、方向。
x=asin=asinωt 轨迹方程： y=bcos=bcosωt
大小、方向均可求
例：如图，物体M自O点以速度v0 与水平成 角抛出，求M 点的运动规律及轨迹。
解：依题意，建坐标，有：
当t=0时： 得：
所以，有： V0 cos0t C3
V0 sin0t gt2 2 C4
连接各矢量端点构成矢量端点的连续曲线，称为速度
矢端曲线。
见flash
动点的加速度矢a 的方向与速度矢端曲线在相应点的切线相平行。
r1 r2 r3
v1 a
v2 v3
v1
v2
v v3
a
§5-2 直角坐标法
动点M的位置可以用r表示，也可 用坐标x、y、z来表示，如图所示。
矢径原点与坐标原点重合时，有：
当t=0时，有： x 0, y 0 得 C3 C4 0
理论力学 第一章 点的运动学

理论力学 第一章 点的运动学


已知速度的投影求速度
大小
v v v v
2 x 2 y
2 z
方向由方向余弦确定
cosv , i v x v cosv , j v y v cosv , k v z v
THEORETICAL MECHANICS
山东大学 土建与水利学院工程力学系
THEORETICAL MECHANICS
山东大学 土建与水利学院工程力学系
§ 1.1点的运动矢量分析方法
加
速
度
t 瞬时: 速度 v(t) t＋ t 瞬时:速度 v(t ＋ t ) 或v
t 时间间隔内速度的改变量
v ( t ) ＝ v ( t ＋ t ) － v( t )
点在 t 瞬时的加速度
§ 1.2 点的运动的直角坐标法
加速度
a ax i a y j az k
dv x d 2 x ax 2 dt dt dv y d 2 y ay 2 dt dt dv z d 2 z az 2 dt dt
dv y dv x dv z d2 y d2x d2z a i j k 2 i 2 j 2 k dt dt dt dt dt dt
方 cosa, i a x a, 向 cosa, j a y a, 余 弦 cosa, k a z a
THEORETICAL MECHANICS
山东大学 土建与水利学院工程力学系
§1.3 点的运动的自然坐标法
在点的运动轨迹已知的情况下，可建立弧
坐标和自然轴系来描述该点的运动，这种方
点的切线所组成的 平面，称为P点的密 切面。
P P
lim a1 a
理论力学第5章(点的运动)

理论力学第5章(点的运动)

包括几何静力学、分析静力学
(2) 运动学: 研究点与刚体运动的几何性质。
包括位移、轨迹、速度、加速度。 (与力无关、也是变形体运动基础)
A B
F
C
B
刚体运动
C
变形(包含刚体位移和相对位移)
(3) 动力学: 研究物体所受力与运动间的关系。
包括质点系、刚体，变形体的动力效应。
第五章 点的运动学
§5-1 运动学的基本概念
速度
已知： OC AC BC l , MC a , t。 求：运动方程、轨迹、速度和加速度。
x l a cost ax v x 2 a y vy y l a sin t
2
加速度
a a a
F ( x, y) 0
二、点的速度v
又
r = xi + yj + zk
式中 v x 所以得
dr dx dy dz v i j k dt dt dt dt v = vx i + vy j + vz k
、v y
、v z
vx
dx dt
v
表明：“动点的速度在坐标轴上的投影，等于动点对应的位置 坐标对时间 t 的一阶导数”。 则速度的大小和方向余弦为
弧坐标的运动方程sf切向加速度表示速度大小的变化三点的加速度法向加速度表示速度方向的变化匀速运动v常数常数常数匀变速直线运动匀速圆周运动匀速直线运动或静止直线运动匀速运动圆周运动匀速运动直线运动匀速曲线运动匀变速曲线运动点作曲线运动画出下列情况下点的加速度方向
(1) 静力学: 研究物体所受力系的简化、平衡规律及其应用。
△r称为在△t时间内动点M的位移。
间间隔△t内的平均速度。以 v*表示。则： Δr v Δt 平均速度表示动点在△t内平均运动的快慢和运动方向。
第6章 点的运动学

第6章 点的运动学

第二篇
运 动 学
机械电子工程学院
1/43
引言 运动学是研究物体机械运动的几何性 质。也就是从几何的观点研究物体的机械 运动，而不涉及运动的原因。 运动，而不涉及运动的原因。 运动学的内容包括：运动方程、轨迹、 运动学的内容包括：运动方程、轨迹、 速度和加速度。 速度和加速度。 学习运动学的意义： 学习运动学的意义：首先是为学习动 力学打下必要的基础； 力学打下必要的基础；其次运动学的理论 可以独立地应用到工程实际中。 可以独立地应用到工程实际中。 机械电子工程学院 2/43
x = x(t) y = y(t) z = z(t)
这就是直角坐标形式的点的运动方程。 这就是直角坐标形式的点的运动方程。 直角坐标形式的点的运动方程 直角坐标与矢径坐标之间的关系 r r r r r = x( t) i + y(t) j + z(t)k
机械电子工程学院 11/43
速度
r r r r r dr dx r dy r dz r v = = i + j + k = vxi +vy j +vzk dt dt dt dt
主法线
r τ r n
法面
r n
密切面
r r r b =τ ×n
副法线
r b
M
τ
r
切线
rr r 构成的坐标系称为自然轴 由三个方向的单位矢量 τ,n,b 构成的坐标系称为自然轴 r 它们的正向确定如下： 的正向指向弧坐标的正向； 正向确定如下 τ 系。它们的正向确定如下： 的正向指向弧坐标的正向；
r r r的方向将随动点在曲线上的位置变化 决定。 决定。自然轴系 τ,n,b 而变化，不是固定坐标系。 而变化，不是固定坐标系。
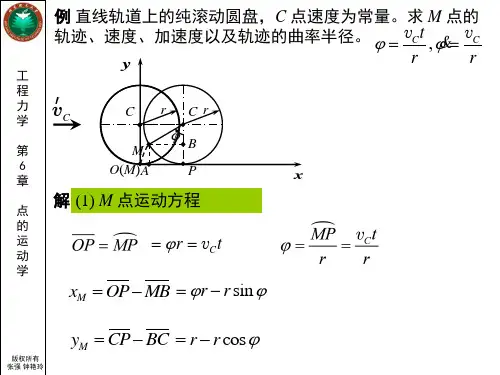
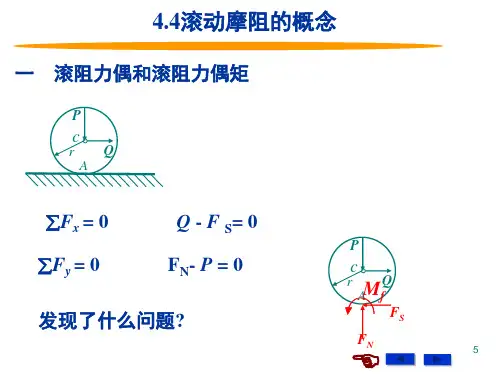
点的运动教案

点的运动教案

v 各点法向加速度的大小 与该点到轴心的距离
a 成正比 方向指向轴心
M
36
§6–3转动刚体内各点的速度和加速度
一 转动刚体内各点的速度和加速度的计算
2 加速度计算逆运算
at
dv dt
d dt
(R)
R
d
dt
R
an
v2
( R ) 2
R
R 2
A
加速转动的刚体，已知其上
一点A的切向加速度
O
判断 角加速度的转向 计算角加速度的大小
❖ 2 在车轮上观察得到的点的运动轨迹? P147例5-6
❖
运动的相对性
24
习题 P 153-154 5-4 注意：1 坐标原点选在固定的点
2 动点选在一般位置
25
§ 5-3 自然法
应用的场合以及如何应用？ 1 运动方程 ？速度如何计算？ 2 加速度如何计算？ 一 弧坐标
O (+)
s
M (-)
s f (t)
dt dt
d
dt
vA 各点速度的大小与该点
vD D
A 到轴心的距离成正比
vB 速度的方向垂直于该点到
O
轴心的连线，指向图形
B 转动的一方。
34
§7–3转动刚体内各点的速度和加速度
一 转动刚体内各点的速度和加速度的计算 速度计算的逆运算
v ds R d R
dt dt
vB OB
vB
8 刚体绕定轴转动时，其上各点的加速度大小 与点到轴心的距离成正比例关系。
A
B
O
66
判断题 9 平面直角折杆绕定轴转动，其中OA=L AB=a 则B点的速度与AB垂直 大小等于角速度与AB长 度的乘积
理论力学-点的运动学案例

理论力学-点的运动学案例

vy y (l a) cost v vx2 vy2 (l a)2 2 sin2 t (l a)2 2 cos2 t
l2 a2 2al cos 2t
cos(v, i ) vx
(l a) sin t
v
l 2 a2 2al cos 2t
cos(v, j ) vy
(l a) cost
2 l 2 a2 2al cos 2t
cos(a, i ) ax
(l a) cost
a
l 2 a2 2al cos 2t
cos(a, j ) ay
(l a) sin t
a
l 2 a2 2al cos 2t
例5-2
已知：正弦机构如图所示。曲柄OM长为r，绕O轴匀速转动，
B点的速度和加速度
vB xB r cost
aB xB r2 sin t 2xB
周期运动 x(t T ) xt
f 1 频率 T
例5-3 已知：如图所示，当液压减振器工作时，它的活塞在套
筒内作直线往复运动。设活塞的加速度 a kv
（ v为活塞的速度， 为k 比例常数)，初速度为 。v0
第五章 点的运动学
例 5-1
已知：椭圆规的曲柄OC 可绕定轴O 转动，其端点C 与规尺 AB 的中点以铰链相连接，而规尺A，B 两端分别在相互垂
直的滑槽中运动， OC AC BC l, MC a, ωt
求：① M 点的运动方程；
② 轨迹； ③ 速度； ④ 加速度。
解： 点M作曲线运动，取坐标系Oxy如图所示。 运动方程
求：活塞的运动规律。
解： 活塞作直线运动，取坐标轴Ox如图所示
由 a dv kv dt
得
v dv k

点的运动


● 1.3 自 然 法
利用点的运动轨迹建立弧坐标及自然轴系，并用它们 来描述和分析点的运动的方法称为自然法。
● 1.3.1 弧坐标形式的运动方程
设动点的轨迹为如图1.8所示的曲
线，则动点在轨迹上的位置可以这样确 定：在轨迹上任选一点O为参考点，并 设(1-1点3) O的某一侧为正向，动点M在轨迹 上的位置由弧长确定，视弧长s为代数 量，称它为动点M在轨迹上的弧坐标。 当动点M运动时，随着时间变化，它是 时间的单值连续函数，即
● 1.1 矢量法——描述点在空间运动的基本方法 ● 1.1.1 点的矢量形式的运动方程
为了描述动点M在某一时刻t相对于所选固定参考系 的位置，选取参考系上某确定点O为坐标原点，自点O向 动点M作矢量，如图1.1所示，称为点M相对原点O的位 置矢量，简称矢径。当动点M运动时，矢径随时间变化， 并且是时间的单值连续函数。
Δr r(t Δt) r(t)
由此可得动点在内点M的平均速度为
v r t
方向沿Δr方向，如图1.2所示。
r(t)
M
v

S
r
M
M’ v
r(t t)
O
当 Δt→0时，可得动点在t时刻的及时速度(简称速度)
v lim r dr t0 t dt
即动点的速度等于动点的矢径对时间的一阶导数。 动点的速度是矢量，动点速度方向为其轨迹曲线在M 点的切线方向并指向运动的一方。速度的单位为m/s。 将各不同时刻的速度，，…，如图1.3(a)所示，平行移 动到同一出发点O1 (任选)，以光滑曲线连接各速度端 点，，…。此曲线称为速度矢端曲线，简称速度端图，如 图1.3(b)所示。
z(t)

(1-5)

理论力学6—点的运动学

点的曲率半径。
2021/7/31
19
6.3 自然法
t
两个相关的计算 结果(当Δt→0)
△s M'
M △
O
t'
t"
△t
τ 2 τ sin
2
dτ lim τ lim n 1 n
ds s0 s s0 s
n为法线方向
2021/7/31
20
6.3 自然法
3 点的速度
r
S ds
v lim lim
at c
dv at dtv v0 att
s
s0
v0t
1 2
at
t
2
了解上述关系后，容易得到曲线运动的运
动规律。例如所谓匀速曲线运动，即动点速度
的代数值保持不变。 s s0 vt
2021/7/31
25
例3 已知点的运动方程为x＝2sin4t m, y＝2cos4t m, z＝4t m。求点的运动轨迹的曲率半径。
2021/7/31
8
r xi yj zk
6.2 直角坐标法
速度Байду номын сангаас
v r xi yj zk vxi vy j vzk
速度在各坐标轴上的投影等于动点的各对应坐 标对时间的一阶导数。
若已知速度在各个方向上的投影，则速度的大
小为:
v x2 y 2 z2
其方向余弦为
cos(v, i ) x , cos(v, j ) y , cos(v, k) z
4
4
由此可得滑块B的速度和加速度：
v dx rw(sinwt sin 2wt)
dt
2
a dv rw2 (coswt cos 2w)

第五章点的运动学

第5章
点的运动学
§5-1 矢量法 §5-2 直角坐标法 §5-3 自然法
运动学： 以几何观点(几何公理)研究物体的 运动(轨迹,速度和加速度), 不考虑物体运动的原 因. 固定参考系: 一般采用固连于地球上的坐标系为 参考系,称为固定参考系.
时间: 瞬时和时间间隔
本章将研究点的简单运动，研究点相对某一个 参考系的几何位置随时间变动的规律，包括点的 运动方程、运动轨迹、速度和加速度等。
OC M C r r t
问题：以M点的轨迹为弧坐标（摆线），求M点的运动方程？
M点的速度：
v x r (1 cos t ) v y r sin t
y
x r ( t sin t ) y r (1 cos t )

2
M
M点的速度大小为
2 2
cos( a , j)
ay a

( l a ) sin t l a 2 al cos 2 t
2 2
例 直杆AB两端分别沿两互相垂直的固定直线Ox和Oy运动， 如图所示。试确定杆上任一点M的运动方程和轨迹方程，已 知MA=a，MB=b，角= t。
y
A

x
a M b y
80 m s ,
a
a x a y a z 32 m s
2 2 2
2
而
a
故
dv dt
0,
v
2
a n a 32 m s
2
r
2 .5 m
an
例：半径为r的轮子沿着直线轨道无滑动的滚动，设轮子转角为
ψ=ωt。求用直角坐标和弧坐标表示轮缘上一点M的运动方程， 并求该点的速度、切向加速度和法向加速度。 解： 取点M与直线轨道的接触点O为原点.

轮子向前滚,轮上一点的运动运动学

轮子向前滚,轮上一点的运动运动学
本文将探讨轮子向前滚动时，轮子上一点的运动学。

轮子向前滚动时，轮子上一点的速度分为两个分量：切向速度和法向速度。

切向速度是轮子上一点沿着圆周方向的速度，大小等于该点所在圆周的半径乘以轮子的角速度。

法向速度是轮子上一点沿着轮子半径方向的速度，大小等于该点在轮子运动中沿轮子半径移动的距离乘以轮子的角速度。

当轮子向前滚动时，由于轮子的转动，轮子上一点的速度会不断变化。

具体来说，当该点沿圆周方向移动时，切向速度会不断增加；当该点沿轮子半径方向移动时，法向速度会不断减小。

当该点在轮子运动中离开圆心的距离越大时，该点的切向速度越大，法向速度越小。

此外，轮子上一点的运动学还与轮子的半径、角速度、线速度等因素有关。

例如，当轮子的半径增大时，轮子上一点的切向速度也会增大；当角速度增大时，切向速度和法向速度都会增大。

总之，轮子向前滚动时，轮子上一点的运动学是一个复杂而有趣的问题，需要结合几何、物理等多个学科进行深入探讨。

- 1 -。

理论力学 第七章 点的运动学



2
2 当t 0时,S 0,sin 2 2

2sin

| | 1于是 2
2sin sin d 1 2 2 lபைடு நூலகம்m | | lim lim ( ) S S dS t 0 S t 0 t 0
§7–5 自然坐标轴系
§7–6 速度与加速的自然坐标表示法
§7.1 运动学的基本概念
一. 运动学：运动学是从几何的角度研究物体运动的科学。 （即只研究物体运动的几何性质，不涉及改变运动的原因） 二．参考系：参考系就是固定在参考体上的坐标系。
如:静参考系（定系）就是固定在地球上或相对地球静止的物
体上的坐标系。
r 得 cos 1 ( ) 2 sin 2 l
r 2 2 于是B的运动方程为 x r cos l 1 ( ) sin l
r 2 于是B的运动方程为 x r cos l 1 ( ) sin 2 l
为使计算方便,令
r 2 2 1 r 2 2 cos 1 ( ) sin 1 ( ) sin l 2 l 1 r 2 1 r 2 1 ( ) ( ) cos 2 4 l 4 l
x = x(t) 点的运动方程为： y = y(t) z = z(t)
轨迹为F(x,y)=0
P
k j iO
r
a
y
x
三 矢径法 选取空间选一点O为原点，动 点的位置由矢径r表示 z
矢端曲线
P
P´ P
y
r r (t )
r r´ r
O
为点的矢径运动方程，且有
r xi y j z k
弧O1M R 2t

理论力学-点的运动学

详细描述
速度和加速度的矢量表示
04
CHAPTER
点的运动轨迹和运动参数
通过已知的初始位置和速度矢量，利用矢量合成法则确定点的运动轨迹。
直角坐标系
极坐标系
参数方程
利用极坐标表示点的位置，通过已知的初始位置和速度矢量，确定点的运动轨迹。
通过设定参数表示点的位置，根据初始条件和运动规律，确定参数方程，从而确定点的运动轨迹。
加速度与轨迹的关系
根据点的加速度矢量，可以判断点加速或减速的情况，进一步推断出其运动轨迹的变化趋势。
位移与轨迹的关系
根据点的位移矢量，可以确定点在平面或空间中的运动轨迹。
运动参数与轨迹的关系
05
CHAPTER
点的运动学应用
刚体的平动是指刚体在空间中的移动，其上任意两点之间的距离保持不变。
总结词
刚体的平动是刚体运动的一种基本形式，它描述了刚体在空间中的移动。在这种运动中，刚体的所有点都以相同的速度和方向移动，因此刚体上任意两点之间的距离保持不变。平动不会改变刚体的形状和大小。
点的速度和加速度
总结词
速度是描述物体运动快慢的物理量，其大小等于物体在单位时间内通过的位移。
详细描述
速度的大小可以用矢量表示，其大小等于物体在单位时间内通过的位移量，方向与物体运动方向相同。在直角坐标系中，速度矢量可以表示为位置矢量对时间的一阶导数。
速度的定义与计算
总结词
加速度是描述物体速度变化快慢的物理量，其大小等于物体在单位时间内速度的变化量。
详细描述
加速度的大小可以用矢量表示，其大小等于物体在单位时间内速度的变化量，方向与物体速度变化方向相同。在直角坐标系中，加速度矢量可以表示为速度矢量对时间的一阶导数。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

例：已知点的运动方程，求点任意时刻的速度、 加速度的大小和运动轨迹的曲率半径。
运动方程: x R ct o ,y R s st i ,z n ut
解：
vx vy
x
y
vz
z
v x 2y 2z 2 s R22u2const.
a x 2 y 2 z 2 R2
ax ay
x y
az
z
2
8
A
l
B
O
x
C
.
略去λ4以及更高阶项，并利用关系
sin2 t1cos2t
2
则
xrcostl 1rl2sin2 t
可表示为
xl142rcost4cos2t
滑块B的速度和加速度为
vd dx trsint2sin2t,
y A
O
C
ad d2 t2 xr2costcos2t
l
B
x
.
轨迹演示
.
•半径是 r 的车轮沿固定水平轨道滚动而不滑动（如图）。轮缘上一点M， 在初瞬时与轨道上的O点叠合；在瞬时t 半径MC与轨道的垂线HC 组成交角 φ=ωt，其中ω 是常量。试求M点的运动方程，速度和加速度。
an恒指向曲线凹侧
速度、加速度矢量在密切面内
.
运动演示
.
•销钉B可沿半径等于R 的固定圆弧滑道DE 和摆杆的直槽中滑动，
AO=R=0.1m。已知摆杆的转角 π sin2π t （时间以s计， φ以rad计），
8
试求销钉在t1=1/4 s 和 t2=1 s 时的加速度。
•选滑道上O‘点作为弧坐标的原点，
ax ay az
d 2x
dt 2 d 2y
dt 2 d 2z
dt 2
x y
z
a ax2ay2az2
.
曲柄连杆机构中曲柄OA和连杆AB的长度分别
为r和l。且l>r，角=ωt，其中ω是常量。滑块B可
沿轴Ox作往复运动，试求滑块B的运动方程，速度 和加速度。
y
A
l
B
O
x
C
.
运动演示 2/23.
并以O'D为正向。则B点在任一瞬时的弧坐标
D
C
+s
B
s R
ω
O
φ
θ
s
s2R π sin2πt
40
A
R
R
O' •这就是B点的自然形式的运动方程。
-s E
at
dvt dt
π3 sin2πt
10
教材题5-7P154
ds π2
vt
dt
cos2πt 20
an
v2
.
2π02 cos2πt2 0.1
π4 cos22πt 40
x
+ y
1、 弧坐标形式
的运动方程
ss(t)
.
曲线的几何性质 T”
M
T’
T M’ M' M s
•曲率(curvature) k lim
s0 s
•曲率半径(radius curvature)
1
k
MTT” 极限位置所在的平面称为 密切面(osculating plane)
.
以点M为坐标原点，并跟随点M一起运动的直角坐标系，称为
.
2
vxr(1cots) vy rsint
v 2rsin t
2
ax r 2sin t ay r2cos t a a2xa2y r2
当t = 2n时
vx 0
vy 0
a x 0 ay r 2
•这表示，当M点接触轨道时，它的速度等于零，而加速度垂直于轨道。 •这是轮子沿固定轨道滚而不滑的特征。
aat an
解: 考虑滑块 B 在任意位置，由几何关系得滑块 B 的坐标
x O C C B rco sl2 r2sin 2
将φ=ωt 代入上式得
xrcostl 1rl2sin2 t
令λ= r/l，将上式的根式展
开，有
y
1 2 s in 2 t 1 12 s in 2 t 14 s in 4 t
t
f(x,y,z)0
P138．点的速度
vdrdixdyjdk z dt dt dt dt
vx
dx dt
dy v y dt
vz
dz dt
x
y
z
.
v vx2vy2vz2
P138．点的加速度
aaxiayjazk dv d2r d2x d2y d2z
a i j k dtd2t d2t d2t d2t
• M点的切向加速度和法向加速度 •注意，尖点
由v2rsin t
2
at
dvr2cos
dt
t
2
.
an a2at2r2sin 2t
§5-3 自然坐标法
点的运动轨迹为已知曲线
•坐标原点O—在已知轨迹上任选一点。
•弧坐标s—沿轨迹从O到点M的弧长。
•坐标正方向—指定坐标原点O的某一侧为正向。
-0zsM来自r O（1）运动方程
x f1 (t) x(t) y f 2 (t) y(t) z f3 (t) z(t)
.
x f1 (t) x(t) y f 2 (t) y(t) z f3 (t) z(t)
书P137
•称为点 的运动轨迹的参数方程。
•消去式中的参数 t ，可得到点的轨迹方程 —空间曲线方程：
.
•第五章 点的运动 •研究任务：研究点在空间运动的几何性质，即点相对于某坐标系
运动的运动方程、运动轨迹、速度和加速度。
书137页 5- 2 直角坐标法 •当点的运动轨迹为已知直线或为未知时，
用直角坐标法描述点的运动规律。 1．点的运动方程和轨迹方程
z •取直角坐标系，点 在运动过程中，坐标 x，y ， 随时间而变化。
自然轴系。
主法线
en
密切面
2、速度与加速度
+s
速度 vset
法
面
M
eb
副法线
e t 切线
eteneb
et,en,eb 自然轴系
加速度 avd(set) dt 分解为两项
a s e t s e t a t a n
a t se t
an
s2
en
反映速度大小的变化 反映速度方向的变化
(trihedral axes on a curve)
什么是运动学？
• 运动学：研究物体运动的几何性质的科学。
• 点的运动学
– 点的运动方程（轨迹） – 点的速度 – 点的加速度 – 点的复合运动
• 刚体的运动学
– 刚体的平动（刚体上点的速度和加速度） – 刚体的定轴转动（刚体角速度和角加速度、其上点的速度和加速度） – 刚体的平面运动（刚体角速度和角加速度、其上点的速度和加速度） – 刚体的定点运动和一般运动（不讲）
解：考虑车轮在任意瞬时位置，因车轮滚动而不滑动，
故有OH=弧MH 。在图示瞬时动点M 的坐标为
y
x O r A rO si H nAH 弧 M H AH
D
xr(tsi n t)
C Mφ
yAM rrcos
yr(1cots)
OA
H
x
vxr(1cots)
vy rsint
v v 2 x v 2 y r ( 1 co t) 2 s2 itn 2 rsitn