超静定结构分析

用力法求解超静定结构概述超静定结构是指结构中的支座和约束条件多于结构自由度的情况。

用力法是一种经典的结构分析方法，常用于求解超静定结构。

本文将介绍用力法求解超静定结构的基本原理和步骤，并通过实例加以说明。

一、基本原理用力法的基本原理是根据平衡条件和变形约束，通过假设未知力的大小和方向，建立力的平衡方程和变形方程，解出未知力和结构的变形。

用力法适用于各种类型的结构，包括梁、柱、桁架等。

二、步骤用力法求解超静定结构的步骤如下：1. 选择合适的剖面根据结构的几何形状和约束条件，选择合适的剖面，将结构分割为若干个部分。

2. 假设未知力的方向和大小根据结构的特点和约束条件，假设未知力的方向和大小。

通常，未知力的方向可以根据结构的几何形状和外力的作用方向来确定，而未知力的大小则需要通过力的平衡方程来求解。

3. 建立力的平衡方程根据假设的未知力和结构的几何形状，建立力的平衡方程。

平衡方程包括力的平衡条件和力的矩平衡条件。

4. 建立变形方程根据结构的变形情况和约束条件，建立变形方程。

变形方程可以根据结构的刚度和约束条件来确定。

5. 解方程将力的平衡方程和变形方程联立，解方程组得到未知力和结构的变形。

6. 检验结果将求解得到的未知力和结构的变形代入原平衡方程和变形方程中，检验结果的准确性。

如果结果符合平衡和变形的要求，则求解成功；如果结果不符合要求，则需要重新假设未知力并重新求解。

三、实例分析为了更好地理解用力法求解超静定结构的步骤和原理，下面以一个简单的梁结构为例进行分析。

假设有一根悬臂梁，在梁的自重和外力作用下，需要求解支座反力和梁的变形。

1. 选择合适的剖面选择悬臂梁的剖面，将梁分割为两个部分：悬臂部分和支座部分。

2. 假设未知力的方向和大小假设支座反力的方向向上，大小为R。

3. 建立力的平衡方程根据力的平衡条件，可以得到悬臂部分的平衡方程：R - F = 0，其中F为梁的自重。

4. 建立变形方程根据梁的几何形状和约束条件，可以建立悬臂部分的变形方程，得到悬臂部分的弯矩和挠度。

超静定结构的受力分析及特性一、超静定结构的特征及超静定次数超静定结构的静力特征是仅由静力平衡条件不能唯一地确定全部未知反力和内力。

结构的多余约束数或用静力平衡条件计算全部未知反力和内力时所缺少的方程数称为结构的超静定次数。

通常采用去除多余约束的方法来确定结构的超静定次数。

即去除结构的全部多余约束，使之成为无多余约束的几何不变体系，这时所去除的约束数就是结构的超静定次数。

去除约束的方法有以下几种：(一)切断一根两端铰接的直杆(或支座链杆)，相当于去除一个约束。

(二)切断一根两端刚接的杆件，相当于去除三个约束。

(三)切断——个单铰(或支座固定铰)，相当于去除二个约束;切断一个复铰(连接n根杆件的铰)，相当于去除2(n—1)个约束。

(四)将单刚结点改为单铰节点，相当于去除一个约束;将连接n个杆件的复刚节点改为复铰节点，相当于去除n—1个约束。

去除一个超静定结构多余约束的方法可能有几种，但不管采用哪种方法，所得超静定次数一定相同。

去除图4—1a所示超静定结构的多余约束的方法之一如图4—1b所示，去除六个多余约束后，就成为静定结构，故为超静定六次。

再用其他去除多余约束的方案确定其超静定次数，结果是相同的。

二、力法的基本原理(一)力法基本结构和基本体系去除超静定结构的多余约束，代以相应的未知力Xi (i=1、2、…、n)，Xi 称为多余未知力或基本未知力，其方向可以任意假定。

去除多余约束后的结构称为力法基本结构。

力法基本结构在各多余未知力、外荷载(有时还有温度变化、支座位移等)共同作用下的体系称为力法基本体系，它是用力法计算超静定结构的基础。

选取力法基本结构应注意下面两点：1.基本结构一般为静定结构，即无多余约束的几何不变体系。

有时当简单超静定结构的解为已知时，也可以将它作为复杂超静定结构的基本结构，以简化计算。

2.选取的基本结构应使力法典型方程中的系数和自由项的计算尽可能简便，并尽量使较多的副系数和自由项等于零。

第4章超静定结构§4.1 超静定结构特性●由于多余约束的存在产生的影响1. 内力状态单由平衡条件不能惟一确定，必须同时考虑变形条件。

2. 具有较强的防护能力，抵抗突然破坏。

3. 内力分布范围广，分布较静定结构均匀，内力峰值也小。

4. 结构刚度和稳定性都有所提高。

●各杆刚度改变对内力的影响1. 荷载作用下内力分布与各杆刚度比值有关，与其绝对值无关。

2. 计算内力时，允许采用相对刚度。

3. 设计结构断面时，需要经过一个试算过程。

4. 可通过改变杆件刚度达到调整内力状态目的。

●温度和沉陷等变形因素的影响1. 在超静定结构中，支座移动、温度改变、材料收缩、制造误差等因素都可以引起内力，即在无荷载下产生自内力。

2. 由上述因素引起的自内力，一般与各杆刚度的绝对值成正比。

不应盲目增大结构截面尺寸，以期提高结构抵抗能力。

3. 预应力结构是主动利用自内力调节超静定结构内力的典型范例。

§4.2 力法原理●计算超静定结构的最基本方法超静定结构是具有多余联系（约束）的静定结构，其反力和内力（归根结底是内力）不能或不能全部根据静力平衡条件确定。

力法计算超静定结构的过程一般是在去掉多余联系的静定基本结构上进行，并选取多余力（也称赘余力）为基本未知量（其个数等于原结构的超静定次数）。

根据基本体系应与原结构变形相同的位移条件建立方程，求解多余力后，原结构就转化为在荷载和多余力共同作用下的静定基本结构的计算问题。

这里，基本体系起了从超静定到静定、从静定再到超静定的过渡作用，即把未知的超静定问题转换成已知的静定问题来解决。

●基本结构的选择（解题技巧）1. 通常选取静定结构；也可根据需要采用比原结构超静定次数低的、内力已知的超静定结构；甚至可取几何可变（但能维持平衡）的特殊基本结构。

2. 根据结构特点灵活选取，使力法方程中尽可能多的副系数δij = 0。

3. 应选易于绘制弯矩图或使弯矩图限于局部、并且便于图乘计算的基本结构。

超静定结构的超静定次数超静定结构是指在受力平衡条件下，由于约束条件数量大于自由度数量，使得结构不具有唯一的平衡位置。

超静定结构的超静定次数是指约束条件数量与自由度数量之差。

一、超静定结构的特点超静定结构具有以下特点：1. 约束条件数量大于自由度数量：超静定结构的约束条件数量大于自由度数量，使得结构不具有唯一的平衡位置。

这导致了结构的设计和分析变得更加困难。

2. 结构具有较高的刚度：由于超静定结构的约束条件数量较多，结构具有较高的刚度。

这使得超静定结构在承受荷载时能够更好地保持形状稳定性。

3. 结构能够承受更大的荷载：超静定结构由于具有较高的刚度，能够承受更大的荷载。

这使得超静定结构在工程实践中得到广泛应用。

二、超静定结构的应用超静定结构在工程实践中有着广泛的应用，主要包括以下几个方面：1. 桥梁工程：超静定结构在桥梁工程中得到了广泛应用。

由于桥梁需要承受大量的荷载，超静定结构能够提供更高的刚度和稳定性，保证桥梁在使用过程中不发生塌陷或变形。

2. 建筑结构：超静定结构在建筑结构中也有重要的应用。

例如，高层建筑的框架结构通常采用超静定结构设计，以提高结构的稳定性和抗震性能。

3. 机械设备：超静定结构在机械设备中也有广泛的应用。

例如，汽车的悬挂系统和起重机的支撑结构都是超静定结构，能够提供更高的稳定性和承载能力。

三、超静定结构的分析方法超静定结构的分析方法主要包括以下几个步骤：1. 定义自由度和约束条件：首先确定结构的自由度和约束条件。

自由度是指结构中可以独立变形的数量，约束条件是指结构中限制自由度的条件。

2. 建立平衡方程：根据结构的受力平衡条件，建立结构的平衡方程。

平衡方程是超静定结构分析的基础，通过平衡方程可以求解结构的受力状态。

3. 引入支座反力：由于超静定结构的约束条件数量大于自由度数量，结构中存在未知的支座反力。

通过引入支座反力，可以将超静定结构转化为静定结构进行分析。

4. 求解支座反力：利用平衡方程和约束条件，求解支座反力。

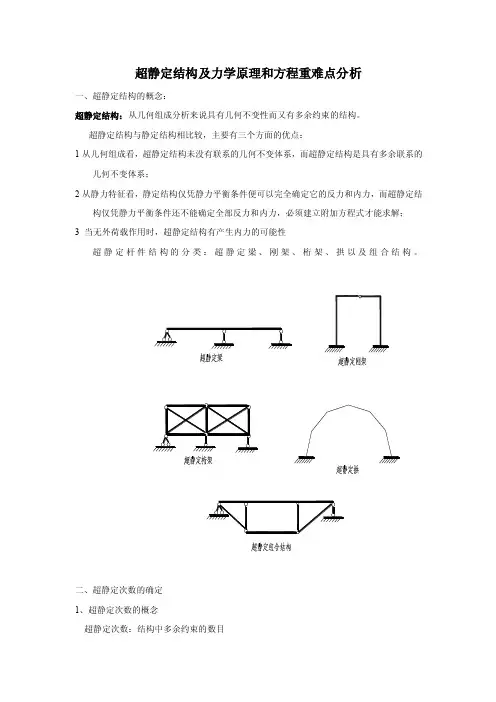
超静定结构及力学原理和方程重难点分析一、超静定结构的概念：超静定结构：从几何组成分析来说具有几何不变性而又有多余约束的结构。

超静定结构与静定结构相比较，主要有三个方面的优点：1从几何组成看，超静定结构未没有联系的几何不变体系，而超静定结构是具有多余联系的几何不变体系；2从静力特征看，静定结构仅凭静力平衡条件便可以完全确定它的反力和内力，而超静定结构仅凭静力平衡条件还不能确定全部反力和内力，必须建立附加方程式才能求解；3 当无外荷载作用时，超静定结构有产生内力的可能性超静定杆件结构的分类：超静定梁、刚架、桁架、拱以及组合结构。

二、超静定次数的确定1、超静定次数的概念超静定次数：结构中多余约束的数目2、方法去掉多余联系的常用方法如下：（1）去掉一根支杆或切断一根链杆，相当于去掉一个联系； （2）去掉一个单铰，相当于去掉二个约束；（3）切断一根弯杆或去掉一个固定支座，相当于去掉三个联系（4）将固定支座改成不动铰支座或将受弯杆切断改铰结，各相当去掉一个联系 3、举例例如图1所示的单跨静定梁，若去掉B 支座的支杆，代以多未知力B X ，则原梁变为静定的简支梁（即为基本结构），如图1（b ）所示;若将固定端A 支座加一个单铰,代以多余未知力A X ,则原梁变为静定的简支梁（即为基本结构），如图1（c ）所示,所有原结构一次超静定结构.同理,如图2所示的刚架,可将A 、B 两固定改成铰支座，代以多余力A X 、B X ，则得如图2（b ）所示的静定三铰刚架；或者去掉铰C ，代以多余力1X 、2X ，则得如图2（c ）所示的两各静定悬臂刚架；或者去掉铰C ，故原结构为二次超静定结构。

三、力法原理和力法方程1．力法的基本原理：将超静定结构转化为含多余力的静定结构 （一）一次超静定结构 （1）确定超静定次数：n=1次 （2）选基本结构⎩⎨⎧）几何不变体系（静定结构b a )(（3）位移条件： 01=∆ (a) 根据叠加原理 ：p1111∆+∆=∆ （b ）11111x δ=∆ (c)(4)力法方程（一次）：将（c ）代入（b ）式得：01111=∆+px δ…………(6-1)式中:--11δ系数(单位多余力1=X 作用时,B 点沿1x 方向的位移)--∆p1自由项(荷载单独作用时B 点沿1x 方向的位移)1x --基本未知量(多余未知力或多余力)系数(11δ) 和自由项(p1∆)都是基本结构(静定结构)在已知外力作用下的位移,可用上一章讲的单位荷载法或图乘法求得,代入(6-1)式后可求出多余未知力1x ,求得1x 之后其余的计算(支座反力和内力)同静定结构。

超静定混凝土结构内力分析1、前言目前在超静定混凝土结构设计中，结构的内力分析、构件截面设计是不相协调的，结构的内力分析仍采用传统的弹性理论，而结构的截面设计考虑了材料的塑性性能。

实际上，超静定混凝土在承载过程中，由于混凝土的非弹性变形、裂缝的出现和发展、钢筋的锚固滑移，以及塑性铰的形成和转动等因素的影响，结构构件的刚度在各受力阶段不断发生变化，从而使结构的实际内力与变形明显地不同于按刚度不变的弹性理论算得的结果。

所以在设计混凝土连续梁、板时，恰当地考虑结构的内力重分布，就能达到结构的内力分析和截面设计变形相协调的目的。

2、应力重分布及内力重分布的概念分析钢筋混凝土受弯构件破坏的过程分为三个阶段：弹性阶段、带裂缝工作阶段及破坏阶段。

在弹性阶段，应力沿截面高度的分布近似为直线，到了带裂缝阶段和破坏阶段，应力沿截面高度的分布就不再是直线了。

这种由于钢筋混凝土的非弹性性质，使截面上应力的分布不再是从线弹性分布规律的现象，这称之为应力重分布。

应力重分布是指截面上应力之间的非弹性关系，它是静定的和超静定的钢筋混凝土结构都具有的一种基本属性。

结构计算出静力平衡条件外，还需按照变形协调条件才能确定内力的结构是超静定结构。

超静定结构是具有多余约束的结构体系，它在弹性工作阶段各截面内力之间的关系是由各个构件弹性刚度决定的；到了带裂缝工作阶段，刚度就改变了，裂缝截面的刚度小于未开裂截面的；当内力最大的截面进入破坏阶段出现塑性铰后，结构的计算简图也改变了，致使各截面内力间的关系改变的更大。

这种由于超静定钢筋混凝土结构非弹性性质而引起的各截面内力之间不再遵循弹性关系的现象，称之为塑性内力重分布。

由此可见应力重分布和内力重分布概念是不同的，一个指截面上应力重分布，一个是指结构截面内力间的关系不再服从线弹性分布规律，超静定结构所特有的一种现象。

3、内力充分的过程超静定钢筋混凝土结构的内力重分布可概括为两个过程：第一过程发生在受拉混凝土开裂到第一个塑性铰形成之前，主要是由于结构各部分弯曲刚度比值的改变而引起的内力重分布；第二个过程发生于第一个塑性铰形成以后直到形成机构、结构破坏，由于结构计算简图的改变而引起的内力重分布。