5.1振幅调制的基本原理

实验四 振幅调制实验一、实验原理1、 振幅调制的一般概念调制，就是用调制信号（如声音、图像等低频或视频信号）去控制载波（其频率远高于调制信号频率，通常又称“射频”）某个参数的过程。

载波受调制后成为已调波。

振幅调制，就是用调制信号去控制载波信号的振幅，使载波的振幅按调制信号的规律变化。

设调制信号为()cos f fm f v t V t ω=载波信号为()cos c cm c v t V t ω=且c f ωω则根据振幅调制的定义，可以得到普通调幅波的表达为：()()1cos cos AM cm f c v t V m t t ωω=+ （5—1） 式中a fm cm cm cmK V V m V V ∆== （5—2） 称为调幅度（调制度），a K 为调制灵敏度。

为使已调波不失真，调制度m 应小于或等于1，当1m >时，称为过调制，此时产生严重失真，这是应该避免的。

不同调制度时的已调波波形如图5—1所示。

将式（5—1）用三角公式展开，可得到：()()()cos cos cos 22AM cm c cm c f cm c f m m v t V t V t V t ωωωωω=+++- （5—3） 由式（5—3）看出，单频调制的普通调幅波由三个高频正弦波叠加而成：载波分量，上边频分量，下边频分量。

在多频调制的情况下，各边频分量就组成了上下边带。

普通调幅波可用AM 表示。

在调制过程中，将载波抑制就形成了抑制载波双边带信号，简称双边带信号，用DSB 表示；如果DSB 信号经边带滤波器滤除一个边带或在调制过程中直接将一个边带抵消，就形成单边带信号，用SSB 表示。

单频调制时DSB 、SSB 信号波形如图5—2所示。

由以上讨论可以看出，若先将调制信号和一个直流电压相加，然后再与载波一起作用到乘法器上，则乘法器的输出将是一个普通调幅波；若调制信号直接与载波相乘，或在AM 调制的基础上抑制载波，即可实现DSB 调制；将DSB 信号滤掉一个边带，即可实现SSB 调制。

振幅调制（AM及DSB）摘要：信号调制可以将信号的频谱搬移到任意位置，从而有利于信号的传送，并且使频谱资源得到充分利用。

调制作用的实质就是使相同频率范围的信号分别依托于不同频率的载波上，接收机就可以分离出所需的频率信号，不致互相干扰。

这也是在同一信道中实现多路复用的基础。

而要还原出被调制的信号就需要解调电路。

所以现在调制与解调在高频通信领域有着更为广泛的应用。

关键词：振幅调制，单频信号引言：调制的作用是把消息置入消息载体，便于传输或处理。

在通信系统中为了适应不同的信道情况（如数字信道或模拟信道、单路信道或多路信道等）,常常要在发信端对原始信号进行调制,得到便于信道传输的信号，调制是各种通信系统的重要基础，也广泛用于广播、电视、雷达、测量仪等电子设备。

一．振幅调制的原理振幅调制常用于长波，中波，短波和超短无线电广播，通信，电视，雷达等系统。

这种调制方式是用传递的低频信号去控制作为传送媒体的高频震荡波的幅度，使已调波的幅度随调制信号的大小线性变化，而保持载波的角频率不变。

标准调幅（AM）就是其中一种。

标准振幅调制是一种相对便宜的质量不高的调制形式。

主要用于声频和视频的商业广播。

AM调制器是非线性设备，有2个输入端口和1个输出端口，一端输入振幅为常数的单频载波信号，另一端输入低频载波信息信号。

在调制器中，信息作用在载波上，就产生了振幅随调制信号瞬时值而变化的已调波。

通常已调波是能有效地通过天线发射，并在自由空间中传播的射频波。

二单频信号调制1.AM调幅波的数学表达式如果设单频调制信号为uI =UImcosΩt,设载波为u c=U cm cosωCt,那么调幅信号（已调波）就可以表示为：uAM =UAM(t) cosωCt, （1）在该式子中UAM(t)称为已调波的瞬时幅值（也称为调幅波的包络函数）。

由于调幅信号的瞬时振幅与调制信号成线性关系，则有：UAM (t)= U cm+kaUImcosΩt= U cm(1+ ka UImcosΩt/ U cm)= U cm(1+macosΩt) （2）式中ka 为比例常数，一般由调制电路的参数决定；ma= kaUIm/ U cm，为调制系数（或称调制深度）ma反映了调幅波振幅的改变量，常用百分比表示，将（2）式代入（1）式可得到单频信号调幅波的表达式如下：uAM = U cm(1+macosΩt) cosωCt基于以上原理，我们做的是单二极管开关状态调幅电路，图2.1单二极管调幅电路设负载Z L 为LC 选频回路，分析可知回路谐振时Z L =R L ，且流过负载回路的电流为：i d =Ld R r +1S(t)u d 式中u d = u I (t)+ u c (t); S(t)为开关函数，且有：S(t)=1，u c >0; S(t)=0, u c <0; S(t)为周期函数，其傅里叶级数为： S(t)=∙∙∙+-+t t c c ωπωπ3cos 32cos 221i d =L d R r +1⎥⎦⎤⎢⎣⎡∙∙∙+-+t t c c ωπωπ3cos 32cos 221 (U Im cos Ωt+ U cm cos ωC t) 如果LC 回路谐振在频率ωC 处，由谐振时负载阻抗Z L =R L ，则可得出回路的输出电压为：u L (t)=()()[]t t R U g t R U g c c L In d c L cm d Ω-+Ω++ωωπωcos cos 1cos 21 =t t U U R U g c cm InL cm d ωπcos cos 4121⎪⎪⎭⎫ ⎝⎛Ω+=()t t m U c Lm ωcos cos 1Ω+ 式中d g =Ld R r +1，m=cm In U U π4,Lm U =L cm d R U g 21;如果我们给定元件的参数，固定载波的振幅U cm 与频率ωC 不变，只改变调制信号的振幅U Im ，R L =900Ω，r d =100Ω, L=100H,C=0.01 μF;可知谐振频率为：LCc 1=ω=1000 rad/s ，载波信号给定为u c =6cos (200πt)当u I =43πcos(20πt )时, m=0.5. 在matlab 中编写代码实现AM 波的调幅，代码如下： 1）调制信号的程序代码： fs=1000;%设定采样频率 N=1024;%设定数据长度 i=0:N-1; t=i/fs;f=10;%设定信号频率 %生成正弦信号 x=(3*pi/4)*cos(2*pi*f*t); subplot(231);plot(t,x);%信号的时域波形 axis([0,0.3,-4,4]); xlabel('t'); ylabel('y');title('信号时域波形');grid;%进行FFT变换并做频谱图y=fft(x,N);%进行fft变换mag=abs(y);%求幅值f=(0:N-1)*fs/N;%横坐标频率的表达式为f=(0:M-1)*Fs/M; subplot(232);plot(f,mag);%做频谱图axis([0,200,0,2000]);xlabel('频率(Hz)');ylabel('幅值');title('信号幅频谱图')下面是调制信号的时域波形图与频谱图的截图：图2.22）载波信号的程序代码：fs=1000;%设定采样频率N=1024;%设定数据长度i=0:N-1;t=i/fs;f=100;%设定信号频率x=6*cos(2*pi*f*t); %生成余弦信号subplot(231);plot(t,x);%作信号的时域波形axis([0,0.05,-8,8]);xlabel('t');ylabel('y');title('载波信号时域波形');grid;%进行FFT变换并做频谱图y=fft(x,N);%进行fft变换mag=abs(y);%求幅值f=(0:N-1)*fs/N;%横坐标频率的表达式为f=(0:M-1)*Fs/M; subplot(232);plot(f,mag);%做频谱图axis([0,200,0,300]);xlabel('频率(Hz)');ylabel('幅值');title('信号幅频谱图')下面是载波信号的时域波形图与频谱图的截图：图2.33）两个信号叠加以后即为已调波，已调波代码如下fm=10; %调制信号频率fc=100; %载波信号频率t=0:0.000001:0.5;x=0:0.000001:2;m1=0.5;s_am1=6*(1+m1.*cos(2*pi*fm*t)).*cos(2*pi*fc*t); figure(2) %图2为ma=0.5时的已调波plot(t,s_am2); grid on;title('m=0.5时AM调制信号');xlabel('t'); ylabel('v');运行后其调幅波波形如下：图2.44）现在再来看m=0.5时已调波的频谱图，其代码如下：t=i/fs;fm=10; %调制信号频率Hzfc=100; %载波信号频率Hzma1=0.5;x=6*(1+ma1.*cos(2*pi*fm*t)).*cos(2*pi*fc*t);y=fft(x,N);%进行fft变换mag=abs(y);%求幅值f=(0:N-1)*fs/N;%横坐标频率的表达式为f=(0:M-1)*Fs/M; subplot(232);plot(f,mag);%做频谱图axis([0,200,0,1500]);xlabel('频率(Hz)');ylabel('幅值');title('已调波信号频谱图(m=0.5时)')下图是已调波的频谱图：图2.5由以上各图可知m=0.5时可以保证已调波的包络真实地反映出调制信号的变化规律当uI =23 cos(20πt)时, m=1.调制信号程序代码如下：fs=1000;%设定采样频率N=1024;%设定数据长度i=0:N-1;t=i/fs;f=10;%设定信号频率x=(3*pi/2)*cos(2*pi*f*t); %生成余弦信号subplot(231);plot(t,x);%信号的时域波形axis([0,0.3,-6,6]);xlabel('t');ylabel('y');title('调制信号时域波形');grid;%进行FFT变换并做频谱图y=fft(x,N);%进行fft变换mag=abs(y);%求幅值f=(0:N-1)*fs/N;%横坐标频率的表达式为f=(0:M-1)*Fs/M; subplot(232);plot(f,mag);%做频谱图axis([0,200,0,2000]);xlabel('频率(Hz)');ylabel('幅值');title('信号幅频谱图')下面是调制信号的时域波形图与频谱图：图2.6再来看已调波的波形图，程序的代码如下：fm=10; %调制信号频率fc=100; %载波信号频率t=0:0.000001:0.5;x=0:0.000001:2;m2=1;s_am2=6*(1+m2.*cos(2*pi*fm*t)).*cos(2*pi*fc*t); figure(2) %为m1=1时的已调波plot(t,s_am2); grid on;title('m=1时AM调制信号');xlabel('t'); ylabel('v');程序运行的结果如下：图2.7再来看m=1时已调波的频谱图，其代码如下：fs=1000;%设定采样频率N=1024;%设定数据长度i=0:N-1;t=i/fs;fm=10; %调制信号频率Hzfc=100; %载波信号频率Hzma2=1;x=6*(1+ma2.*cos(2*pi*fm*t)).*cos(2*pi*fc*t);y=fft(x,N);%进行fft变换mag=abs(y);%求幅值f=(0:N-1)*fs/N;%横坐标频率的表达式为f=(0:M-1)*Fs/M; subplot(232);plot(f,mag);%做频谱图axis([0,200,0,2500]);xlabel('频率(Hz)');ylabel('幅值');title('已调波信号频谱图(m=1时)')下图为程序运行后的结果图：图2.8由上图知m=1时，调制系数的百分比达到100%，此时包络振幅的最小值为0当uI =49 cos(20πt)时, m=1.5. 调制信号程序代码如下：fs=1000;%设定采样频率N=1024;%设定数据长度i=0:N-1;t=i/fs;f=10;%设定信号频率x=(9*pi/4)*cos(2*pi*f*t); %生成余弦信号subplot(231);plot(t,x);%作信号的时域波形axis([0,0.3,-8,8]);xlabel('t');ylabel('y');title('调制信号时域波形');grid;%进行FFT变换并做频谱图y=fft(x,N);%进行fft变换mag=abs(y);%求幅值f=(0:N-1)*fs/N;%横坐标频率的表达式为f=(0:M-1)*Fs/M; subplot(232);plot(f,mag);%做频谱图axis([0,200,0,2000]);xlabel('频率(Hz)');ylabel('幅值');title('信号幅频谱图')图2.9下面再来看已调波的波形图，程序的代码如下：fm=10; %调制信号频率fc=100; %载波信号频率t=0:0.000001:0.5;x=0:0.000001:2;m3=1.5;s_am2=6*(1+m3.*cos(2*pi*fm*t)).*cos(2*pi*fc*t); figure(2) %图2为ma=0.5时的已调波plot(t,s_am2); grid on;title('m=1.5时AM调制信号');xlabel('t'); ylabel('v');程序运行的结果如下：图2.10再来看m=1.5时已调波的频谱图，其代码如下：fs=1000;%设定采样频率N=1024;%设定数据长度i=0:N-1;t=i/fs;fm=10; %调制信号频率Hzfc=100; %载波信号频率Hzma3=1;x=6*(1+ma3.*cos(2*pi*fm*t)).*cos(2*pi*fc*t);y=fft(x,N);%进行fft变换mag=abs(y);%求幅值f=(0:N-1)*fs/N;%横坐标频率的表达式为f=(0:M-1)*Fs/M; subplot(232);plot(f,mag);%做频谱图axis([0,200,0,2500]);xlabel('频率(Hz)');ylabel('幅值');title('已调波信号频谱图(m=1.5时)')下图为程序运行后的结果图：图2.11由图知此时已调波的包络形状与调制信号不一样，产生了严重的包络失真，这种情况称为过量调幅，实际应用时应尽量避免。

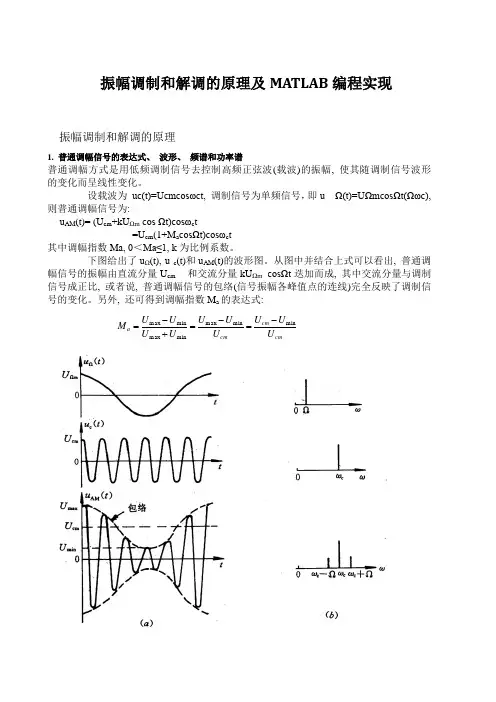
振幅调制和解调的原理及MATLAB 编程实现振幅调制和解调的原理1. 普通调幅信号的表达式、 波形、 频谱和功率谱普通调幅方式是用低频调制信号去控制高频正弦波(载波)的振幅, 使其随调制信号波形的变化而呈线性变化。

设载波为 uc(t)=Ucmcosωct, 调制信号为单频信号，即u Ω(t)=UΩmcosΩt(Ωωc), 则普通调幅信号为:u AM (t)= (U cm +kU Ωm cos Ωt)cosωc t=U cm (1+M a cosΩt)cosωc t 其中调幅指数Ma, 0＜Ma≤1, k 为比例系数。

下图给出了u Ω(t), u c (t)和u AM (t)的波形图。

从图中并结合上式可以看出, 普通调幅信号的振幅由直流分量U cm 和交流分量kU Ωm cosΩt 迭加而成, 其中交流分量与调制信号成正比, 或者说, 普通调幅信号的包络(信号振幅各峰值点的连线)完全反映了调制信号的变化。

另外, 还可得到调幅指数M a 的表达式:cmcm cm a U U U U U U U U U U M minmin max min max min max -=-=+-=调幅的波形与频谱显然, 当Ma ＞1时, 普通调幅波的包络变化与调制信号不再相同, 产生了失真, 称为过调制。

所以, 普通调幅要求Ma 必须不大于1。

上式又可以写成u AM (t)=U cm cosωc t+ ·［cos (ωc +Ω)t+cos (ωc -Ω)t ］可见, uAM(t)的频谱包括了三个频率分量：ωc (载波)、 ωc +Ω(上边频)和ωc -Ω(下边频)。

原调制信号的频带宽度是 Ω或（F= ） , 而普通调幅信号的频带宽度是2Ω(或2F), 是原调制信号的两倍。

普通调幅将调制信号频谱搬移到了载频的左右两旁,如下图所示还可以看到, 若此单频调幅信号加在负载R 上, 则载频分量产生的平均功率为:P c =两个边频分量产生的平均功率相同, 均为:PSB=调幅信号总平均功率为: P av =P c +2P SB =根据信号分析理论, 一般非周期调制信号u Ω(t)的频谱是一连续频谱, 假设其频率范围是Ωmin ～Ωmax , 如载频仍是ωc , 则这时的普通调幅信号可看成是调制信号中所有π2Ωca cm a p M U M R 2241)2(21=R U cm 221c n p M )211(2+2MaUcm频率分量分别与载频调制后的迭加, 各对上、下边频的迭加组成了上、 下边带。

振幅调制和解调的原理及MATLAB编程实现振幅调制和解调的原理及MATLAB 编程实现一、振幅调制和解调的原理：通常调制要传送的信号波形是比较复杂的，但无论多么复杂的信号都可用傅氏级数分解为若干正弦信号之和。

为了分析方便起见，我们一般把调制信号看成一简谐信号。

(a) 调制信过调制波形图(b) 由非正弦波调制所得到的调幅波形已调波形二、振幅调制：正交振幅调制是用两个独立的基带信号对两个相互正交的同频载波进行抑制载波的双边带调制，利用这种已调信号在同一带宽内频谱正交的性质来实现两路并行的数字信息传输。

正交振幅调制信号的一般表示式:式中，An 是基带信号幅度，g(t-nTs)是宽度为Ts 的单个基带信号波形。

上式还可以变换为正交表示形式:令Xn=An cos φnYn=Ansin φn 则v v )cos()()(n c S nnMQAMt w nT t g At S+-=∑)cos()()(n c S nnt t w nT t g ASMQAM+-∑=tw nT t g A t w nT t g A t Sc n S nn c n S nn MQAMsin ]sin )([cos ]cos )([)(??---=∑∑t w nT t g Y t w nT t g X t S c n S nn c n S n n MQAM sin ]sin )([cos ]cos )([)(??---=∑∑tw t y t w t X c c sin )(cos )(-=假设一调制信号ft=Am.cos(2πf m.t+Qm)，载波信号为ct=Ac.cos(2πfc.t+Qc)，则振幅调制（已调波信号为SAM=(AC+ft) .cos(2πfc.t+Qc) 。

二、振幅解调相干解调法如图将已调波SAM信号与解调载波相乘即spt=SAM.*cos(2*pi*fcP*t+QcP)得到含有二次高频和调制信号成分的spt波形和频谱。

振幅调制的基本原理用待传输的低频信号去转变高频载波振幅的过程，称为振幅调制，简称调幅，有一般调幅（AM）、抑制载波的双边带调幅（DSB）和抑制载波的单边带调幅（SSB）三种。

1、一般调幅(AM) 设调制信号为单频信号，即：载波信号为：则一般调幅信号的表达式为：其中，m 称为调幅系数，其值介于0与1之间。

当m1时，产生过调失真。

AM 调幅信号波的波形和频谱图分别如图11（a）、（b）所示。

图1 AM信号的波形和频谱由图1（b）可看出调幅波由三个频率重量组成，即载波重量ωc，上边频ωc+Ω，下边频ωc+Ω ，其带宽为：若调制信号是多频信号，设最高频率为，则带宽为：通常将调幅波电压加在电阻R端，电阻R消耗的各频率重量对应的功率表示为：载波平均功率为：两个边频重量产生的平均功率相等，为：调幅信号总平均功率为：故调幅波的输出功率随Ma的增大而增大。

当Ma=1时，包含信息的上下边频功率值之和只占总输出功率的1/3，其能量利用率很低。

2、抑制载波的双边带调幅信号（DSB）由于载波本身并不包含信息，而且还占有较大的功率，为了减小不必要的功率铺张，可以只放射边频，而不放射载波，称为抑制载波的双边带调幅信号，用DSB表示。

其数学表示式为。

DSB信号的波形和频谱图如图2（a）、（b）所示。

图2 DSB信号的时域波形以及频谱结构其带宽为：,由于DSB方式没有包含有载波，故其功率利用率为100%。

3、单边带调幅波（SSB）SSB是由DSB经过边带滤波器滤除一个边带或者在调制过程中直接将一个边带抵消而成的。

其波形和频谱图如图如图3（a）、（b）所示。

图3 SSB信号的时域波形、频谱结构其带宽为：；功率利用率为100%。

下面从占用信号带宽、功率利用率两方面对AM、DSB、SSB三种调制方式进行比较：AM方式：占用2倍调制信号最高频率带宽；功率利用率最高只能达到1/3；DSB方式：占用2倍调制信号最高频率带宽；功率利用率最高可达到100%；SSB方式：占用1倍调制信号最高频率带宽；功率利用率最高可达到100%。