乘除法的关系及运算律知识点整理

乘除法的关系和运算律乘除法的关系和运算律1、加法交换律：两数相加交换加数的位置，和不变。

2、加法结合律：三个数相加，先把前两个数相加，或先把后两个数相加，再同第三个数相加，和不变。

3、乘法交换律：两数相乘，交换因数的位置，积不变。

4、乘法结合律：三个数相乘，先把前两个数相乘，或先把后两个数相乘，再和第三个数相乘，它们的积不变。

5、乘法分配律：两个数的和同一个数相乘，可以把两个加数分别同这个数相乘，再把两个积相加，结果不变。

如：（2+4）×5＝2×5+4×56、除法的性质：在除法里，被除数和除数同时扩大（或缩小）相同的倍数，商不变。

O除以任何不是O的数都得O。

简便乘法：被乘数、乘数末尾有O的乘法，可以先把O前面的相乘，零不参加运算，有几个零都落下，添在积的末尾。

第一部分一、用简便方法计算。

21×2×522×8×526×4×5 630÷3÷7600÷5÷6280÷8÷5二、列式计算。

1.560除以28，再除以2得多少?2.1800除以45得多少?3.25乘128，积是多少?4.660除以15，再除以4得多少?第二部分：1．计算。

（1）直接写得数。

3800÷20＝8100÷30＝960÷60＝4200÷20＝360÷40＝1900÷10＝2．填空。

（1）3900÷100＝（）想：3900里面有（）个100。

8000÷400＝（）想：（）里面有（）个（）。

（2）下面的括号里最大能填几?200×（）<1210 800×（）<2100300×（）<2300 900×（）<4000第三部分一．计算下面各题。

483÷21= 475÷19= 35×13= 52×46=3200×33= 1080÷30= 480÷24=450÷18= 203×25= 304×65=三．选择答案。

乘法与除法的运算规律乘法和除法是数学中基本的运算符号，用于进行数字的乘法和除法操作。

乘法是将两个数相乘得到一个积的运算，而除法是将一个数除以另一个数得到一个商的运算。

在实际应用中，乘法和除法的运算规律十分重要，能够帮助我们更好地理解和应用数学知识。

一、乘法的运算规律乘法的运算规律包括乘法交换律、乘法结合律和乘法分配律。

1. 乘法交换律：对于任意的实数a和b，a乘以b的结果与b乘以a的结果相等。

即a×b = b×a。

例如，3乘以4等于4乘以3，即3×4 = 4×3。

2. 乘法结合律：对于任意的实数a、b和c，a乘以（b乘以c）的结果等于（a乘以b）乘以c的结果。

即a×（b×c）=（a×b）×c。

例如，2乘以（3乘以4）等于（2乘以3）乘以4，即2×（3×4）=（2×3）×4。

3. 乘法分配律：对于任意的实数a、b和c，a乘以（b加上c）的结果等于（a乘以b）加上（a乘以c）。

即a×（b+c）=（a×b）+（a×c）。

例如，2乘以（3加上4）等于（2乘以3）加上（2乘以4），即2×（3+4）=（2×3）+（2×4）。

二、除法的运算规律除法的运算规律包括除法的唯一性和分配率。

1. 除法的唯一性：对于任意的非零实数a和b，a除以b的结果是唯一确定的。

即对于a除以b等于c，如果a除以b等于d，则c等于d。

例如，6除以2等于3，如果6除以2等于2.5，则3等于2.5。

2. 除法的分配率：对于任意的实数a、b和非零实数c，a除以（b乘以c）的结果等于（a除以b）乘以c的结果。

即a÷（b×c）=（a÷b）×c。

例如，10除以（2乘以5）等于（10除以2）乘以5，即10÷（2×5）=（10÷2）×5。

数学知识点解析乘法和除法的关系乘法和除法是数学中基础的四则运算，它们之间存在着紧密的关系。

本文将通过解析数学知识点，详细探讨乘法和除法之间的关系。

一、乘法和除法的定义乘法是将两个或多个数相乘的运算，用符号“×”表示，例如2 × 3 = 6。

乘法的结果称为积。

除法是将一个数分为若干等分的运算，用符号“÷”表示，例如6 ÷ 3 = 2。

除法的结果称为商。

二、乘法和除法的运算规则1. 乘法运算规则乘法满足交换律和结合律。

具体来说，对于任意实数a、b和c，有以下运算规则：- 交换律：a × b = b × a- 结合律：(a × b) × c = a × (b × c)另外，乘法还满足分配律，即对于任意实数a、b和c，有以下运算规则：- 左分配律：a × (b + c) = (a × b) + (a × c)- 右分配律：(a + b) × c = (a × c) + (b × c)2. 除法运算规则除法的运算规则主要包括除数不为零和除法的求逆运算。

具体来说，对于任意非零实数a、b和c，有以下运算规则：- 除数不为零：a ÷ b，其中b ≠ 0- 除法的求逆运算：a ÷ b = a × (1/b)三、乘法和除法的关系乘法和除法有着密切的联系，它们之间可以通过互为逆运算来相互转化。

1. 乘法与除法的转化对于任意非零实数a和b，有以下乘法与除法的转化关系：- 乘法转除法：a × b = a ÷ (1/b)- 除法转乘法：a ÷ b = a × (1/b)通过这种转化，我们可以根据问题的特点选择使用乘法或除法进行计算，方便解决实际问题。

2. 乘法和除法在计算中的应用乘法和除法在数学计算中起着重要的作用。

乘法与除法的运算规则乘法和除法是数学中基本的运算方法，对于学习数学的人来说，掌握乘法与除法的运算规则是非常重要的。

下面本文将详细介绍乘法和除法的运算规则，帮助读者更好地理解和应用乘法和除法。

一、乘法运算规则乘法是一种加速计算的方法，其运算规则包括以下几点：1. 乘法交换律：对于任意两个数a和b，a与b的乘积等于b和a的乘积，即a × b = b × a。

这意味着乘法操作数的位置可以互换而不会改变结果。

2. 乘法结合律：对于任意三个数a、b和c，(a × b) × c = a × (b × c)。

这表示无论先乘以谁，最终结果都是相同的。

3. 乘法分配律：对于任意三个数a、b和c，a × (b + c) = (a × b) + (a× c)。

这表示乘法与加法之间存在分配关系。

二、除法运算规则除法是乘法的逆运算，其运算规则如下：1. 除法定义：对于任意两个数a和b，其中b不等于0，a除以b的商是唯一确定的数。

即a ÷ b = c，c是唯一满足条件的数。

2. 除法与乘法的关系：对于任意三个数a、b和c，如果a = b × c，那么a ÷ b = c。

这表示除法运算可以通过乘法运算来实现。

3. 除法的性质：除法运算满足以下性质：- 除数不为0：除数不能为0，否则运算无法进行。

- 被除数为0：任何数除以0都是无意义的，所以应避免除数为0的情况。

三、应用举例为了更好地理解乘法和除法的运算规则，下面给出一些具体的应用举例。

1. 乘法运算：- 例1：计算2 × 3 = 6。

根据乘法交换律，2 × 3的结果与3 × 2的结果相同，都等于6。

- 例2：计算5 × (4 + 3) = 35。

根据乘法分配律，5 × (4 + 3)等于(5 × 4) + (5 × 3)，即35。

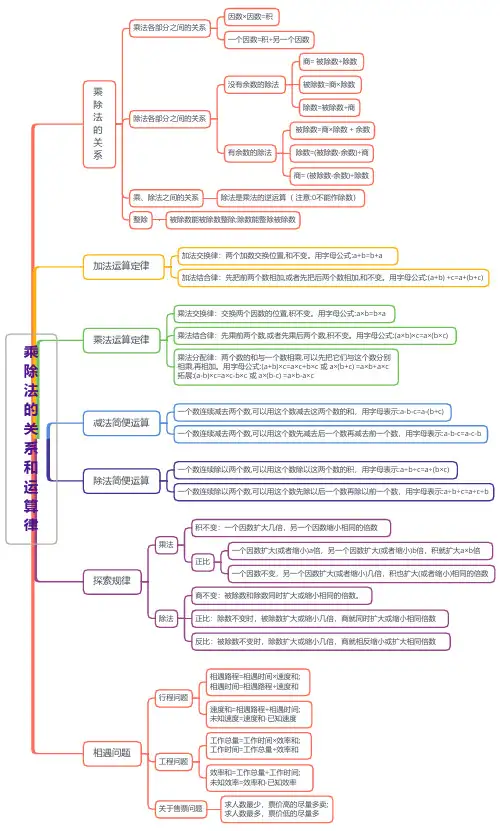
乘除法的关系和运算律乘除法的关系乘法各部分之间的关系因数×因数=积一个因数=积÷另一个因数除法各部分之间的关系没有余数的除法被除数=商×除数除数=被除数÷商有余数的除法被除数=商×除数 + 余数除数=(被除数-余数)÷商商= (被除数-余数)÷除数乘、除法之间的关系除法是乘法的逆运算（注意:0不能作除数）整除被除数能被除数整除;除数能整除被除数加法运算定律加法交换律：两个加数交换位置,和不变。

用字母公式:a+b=b+a加法结合律：先把前两个数相加,或者先把后两个数相加,和不变。

用字母公式:(a+b) +c=a+(b+c)乘法运算定律乘法交换律：交换两个因数的位置,积不变。

用字母公式:a×b=b×a乘法结合律：先乘前两个数,或者先乘后两个数,积不变。

用字母公式:(a×b)×c=a×(b×c)乘法分配律：两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加。

用字母公式:(a+b)×c=a×c+b×c 或 a×(b+c) =a×b+a×c拓展:(a-b)×c=a×c-b×c 或 a×(b-c) =a×b-a×c减法简便运算一个数连续减去两个数,可以用这个数减去这两个数的和，用字母表示:a-b-c=a-(b+c)一个数连续减去两个数,可以用这个数先减去后一个数再减去前一个数，用字母表示:a-b-c=a-c-b 除法简便运算一个数连续除以两个数,可以用这个数除以这两个数的积，用字母表示:a÷b÷c=a÷(b×c)一个数连续除以两个数,可以用这个数先除以后一个数再除以前一个数，用字母表示:a÷b÷c=a÷c÷b 探索规律乘法积不变：一个因数扩大几倍，另一个因数缩小相同的倍数正比一个因数扩大(或者缩小)a倍，另一个因数扩大(或者缩小)b倍，积就扩大a×b倍一个因数不变，另一个因数扩大(或者缩小)几倍，积也扩大(或者缩小)相同的倍数除法商不变：被除数和除数同时扩大或缩小相同的倍数。

六年级乘除法知识点六年级是学习乘除法的重要年级之一，在这个阶段，学生们需要掌握和运用乘除法的基本知识和技巧。

本文将介绍六年级乘除法的主要知识点，帮助学生们更好地理解和应用乘除法。

一、乘法基本概念和运算规则乘法是指将两个或多个数相乘得到一个积的运算。

在乘法运算中，我们可以通过横式计算或竖式计算来进行。

乘法的基本运算规则有以下几点：1. 乘法的交换律：改变乘法式子中数的顺序，积不变。

例如：2 ×3 = 3 × 2 = 6。

2. 乘法的结合律：改变乘法式子中数的位置，积不变。

例如：(2 × 3) × 4 = 2 × (3 × 4) = 24。

3. 分配律：乘法对于加法的分配律。

例如：2 × (3 + 4) = 2 × 3 + 2 × 4 = 14。

二、乘法口诀表掌握乘法口诀表是乘法运算的基础。

下面是六年级学生需要熟记的乘法口诀表：1 × 1 = 11 ×2 = 21 × 3 = 3...9 × 8 = 729 × 9 = 81通过反复背诵和运用乘法口诀表，可以提高乘法计算的速度和准确性。

三、除法基本概念和运算规则除法是将一个数分成若干等份的运算。

在除法运算中，我们需要掌握以下几个概念和规则：1. 被除数：被除数是需要被除以的数。

2. 除数：除数是用来除以被除数的数。

3. 商：商是表示除法的结果，即被除数除以除数得到的数。

4. 余数：余数是除法运算中未被除尽的部分。

例如：20 ÷ 7 = 2 余 6。

5. 整除：如果除法运算的结果没有余数，即余数为0，那么就称为整除。

四、乘法和除法之间的关系乘法和除法是相互关联的。

我们可以通过相反运算的方式来进行验证和应用。

1. 乘法验证除法：可以通过乘法来验证除法的结果是否正确。

例如：5 × 3 = 15，那么15除以5应该等于3。

小学数学五年级乘除法运算法则解释五年级是小学数学学习的关键年级，其中乘除法的运算法则是学生们必须掌握的重要内容。

本文将详细解释五年级乘除法运算法则，帮助阅读者理解并运用于实践中。

以下是对乘除法法则的详细解释：一、乘法法则：1. 乘法交换律：两个数相乘的结果不受因子的顺序影响。

例如：a ×b = b × a。

2. 乘法结合律：三个数相乘时，可以任意改变因子的顺序。

例如：a × (b × c) = (a × b) × c。

3. 乘法分配律：一个数乘以两个数的和等于它分别乘以这两个数后的和。

例如：a × (b + c) = a × b + a × c。

4. 乘以1和0：任何数乘以1都等于它自己，任何数乘以0都等于0。

例如：a × 1 = a，a × 0 = 0。

5. 乘法消去律：如果a和b相乘的结果等于0，那么a或b至少有一个是0。

例如：a × b = 0，则a = 0或b = 0。

二、除法法则：1. 除法定义：除法是乘法的逆运算。

即a ÷ b = c，等价于a = b × c。

2. 除法与乘法的关系：除法可以用乘法来表示，例如：a ÷ b = a ×(1/b)。

3. 除法的简便运算法则：当除数是10、100、1000等以10的幂为底的数时，可以通过移动小数点的位置来进行除法运算，简化计算。

4. 除法的余数：除法的余数为除数不能整除被除数所剩下的数。

例如：a ÷ b = c···d，其中d为余数。

5. 除法的整除性规则：如果一个数能被另一个数整除，则它们的商是整数，否则是小数。

总结：五年级的乘除法运算法则对学生们的数学学习和实际生活都有重要影响。

通过本文的解释，我们希望能够帮助阅读者更好地理解和运用乘除法法则。