薄壁杆件力学 主扇性坐标的求解
- 格式:pdf
- 大小:454.96 KB
- 文档页数:3

目录一.问题描述 (1)二.分析步骤 (2)1.前处理部分 (2)1.1 定义工作文件名 (2)1.2 定义单元类型 (2)1.3 定义材料性能参数 (2)1.4 生成几何模型 (2)1.5 网格划分前准备——分割模型 (3)1.6 划分网格 (4)2.求解问题 (5)2.1 选择PCG 迭代求解器: (5)2.2 施加载荷 (5)2.3 求解 (5)3.后处理部分——查看求解结果 (6)三.结论 (7)四.参考资料 (7)题目名称:有孔薄壁杆的受力分析(ANSYS建模)一.问题描述1.生活中有很多铝合金制造的薄壁杆,通常用于快速安装拆卸的简易用品,比如鞋架、或者衣柜等。
里面很多都是这样的薄壁杆组成。
三维模型如图1所示对该结构进行受力分析可以预测该结构容易受损部位。
2、杆的材料一般都为铝制品,则所有参数按照铝的规格设定。
弹性模量:E=7.3E+010;泊松比:NUXY=0.33杆的尺寸:外径:20mm;内径:15mm;长度:300mm;小孔直径:10mm;3、该杆为对称结构可以截取一半进行求取,这样可以使求解简单节省求解时间。
为了简化问题假设杆只受到上表面施加的力,设值为1000pa。
二.分析步骤1.前处理部分1.1 定义工作文件名选择Utility Menu→File→Change Jobname 出现Change Jobname对话框,在[/FILNAM] Enter new jobname 输入栏中输入工作名yuanningning-10074747并将New log and error file 设置为YES,单击[OK]按钮关闭对话框1.2 定义单元类型1)选择Main Menu→Preprocessor→Element Type→Add/Edit/Delete命令,出现Element Type对话框,单击[Add]按钮,出现Library of Element types对话框。
2)在Library of Element types复选框选择Structual、Solid、Brick 8node 45,单击[Apply],继续在复选框选择Solid、Brick 20node 95,单击[OK]按钮关闭该对话框。

均布扭矩作用下工字钢梁的应力计算张鹭超【摘要】论述工字钢梁扭转计算参数的基本原理,并给出了几何参数的计算方法,作为对即将出版的《钢结构设计规范》GB 50017-201X的一种补充,以便工程设计人员进行计算.特别指出:绝大多数工程设计人员在计算开口截面扭转时,均按自由扭转计算,然而即便在允许自由翘曲的支座条件下,工字梁的扭转应力也是属于约束扭转计算的一种.【期刊名称】《福建建筑》【年(卷),期】2015(000)009【总页数】5页(P101-105)【关键词】扇性面积;双力矩;翘曲;自由扭转;约束扭转;应力计算【作者】张鹭超【作者单位】现代建筑设计集团-上海建筑设计院研究院有限公司福建厦门361009【正文语种】中文【中图分类】TU391E-mail:*****************在即将出版的《钢结构设计规范》GB 50017—201X中即文献[1],提出了受扭构件的强度计算公式:1.1 受纯扭的实腹构件,其抗弯强度可按下式计算:式中B——构件截面的双力矩;ωn——为主扇性坐标;Iω——扇性惯性矩。
1.2 受纯扭的实腹构件,其抗剪强度可按下式计算:式中Tω——构件截面的约束扭转力矩; Tst——构件截面的自由扭转力矩;开口薄壁截面,不考虑这一项;Sω——扇性静矩;t——腹板厚度;A0——闭口截面中线所围的面积。
然而在传统的钢结构及力学相关课程中并没有详尽的介绍杆件在扭转下的应力计算。
许多工程设计人员只懂得文献[3]中关于自由扭转时杆件的应力计算方法。
再加上文献[2]、文献[3]对开口截面均提及自由扭转的计算方法,导致大部分工程技术人员认为开口截面杆件可以按自由扭转计算应力。
这是不正确的。
开口截面的自由扭转只是其扭转计算的一部分而已,只是一种理论计算,实际上开口截面的自由扭矩并不等于截面的总扭矩。
因此可以认为实际上绝大多数杆件为约束扭转(首先不是闭合的等直径圆杆)。
因此出现了以自由扭转下的杆件应力计算代替约束扭转下的杆件应力计算,而自由扭转只能用于圆形截面的等直径杆件计算,所以这是不正确的。

第六讲 薄壁杆件的约束扭转第一节 基本假定薄壁杆件的自由扭转是指杆件受扭时,截面的纵向翘曲位移不受约束,因而纵向翘曲应变和相应的正应力都不存在。
当截面的纵向翘曲位移受到约束时,便产生约束正应力和相应的附加剪应力,这便是约束扭转。
约束扭转的分析,可以从确定截面上纵向翘曲位移着手,进而利用弹性理论的几何方程确定纵向翘曲应变;利用物理方程确定翘曲正应力;最后利用微单元的平衡方程确定相应的翘曲剪应力。
薄壁杆件的约束扭转分析中,除沿用前两章的若干基本假定(包括平面假定、线性假定、小变形假定和周边投影不变形假定)外,补充的基本假定有:1、约束扭转产生的正应力和剪应力沿壁厚均匀分布(参见图5-7),并且杆件纵向纤维不存在正应力。
据此假定,由图3-2所示薄壁单元体s z d d 在z 轴方向的平衡条件,可得到截面正应力和剪应力间的微分关系,即式(3-19)0=∂∂+∂∂zt s q σ(6-1)(3-19) 2、在约束扭转分析中,杆件纵向翘曲位移w 采用自由扭转时的表达式。
根据弹性理论,参照图6-1,薄壁单元体s z d d 的剪切应变为:=γzs w ∂∂+∂∂ξ(6-2)由周边投影不变形假定有:ρφξ=。
这里,φ为扭转角,ρ为扭转中心S 到点P 切线的垂直距离c ρ(见图3-4),于是式(6-2)可写为:=γ+∂∂swφρ' 那么,纵向翘曲位移的一般表达式便可由此积分求得,即⎰⎰+'-=ssw s s w 0d d ρφγ (6-3)式中0w 为s =0处的翘曲位移值。
0)≠γa图6-10)=γb参照第三讲剪力中心推导中关于扇性坐标的定义有:⎰=ss d ρω (6-4)(3-30-1) 式中ω为自积分起点至扇性零点(s =0,)0=ω到s 点所包围的扇性面积的2倍。
于是,纵向翘曲位移的一般表达式(6-3)可写为:00d w s w s⎰+'-=ωφγ (6-5)对于开口薄壁杆件,其在中面上的自由扭转剪应变0=中γ,代入上式便得截面的纵向翘曲位移表达式0/w w +-=ωφ (6-6)对于闭口薄壁杆件,其在中面上的自由扭转剪应变0≠中γ,根据虎克定律Gτγ=,分别按单室或多室闭口截面确定剪应力τ剪应变γ。


大连理工大学专业硕士学位论文摘要随着世界航运业的发展与我国海军“从浅蓝走向深蓝”的战略部署,对于船舶航速的要求越来越高,对于商用船舶来说,船舶航速的提高就意味着更高的经济收益,而对于军用舰艇,更快的航行速度意味着更加强大、持久的战斗力与更加优秀的生存能力。
随着双体船、三体船及一些非对称高速船型的发展,船体横剖面的形状越来越趋于复杂。
对于现有的船舶工程计算领域来说,一般采用近似的铁木辛柯梁方法,以船体剖面在船宽、型深两个方向上的投影面积为剪切修正面积。
但是这种方法并没有考虑剪力滞后的影响,计算结果与实际相差较大。
本文将采用等效静矩方法来考虑剪力滞后的影响,从而精确计算剖面的剪切修正面积。
国内对于船体剖面剪切修正的精确计算仍然处于空白,若船舶需要对剪切流进行计算,就需要从DNV等船级社高价购买相关软件。
国内研究学者对于类似船体剖面的薄壁断面剪切流计算已经进行了比较充足的理论推导,本文就尝试利用C++语言来编写相关程序。
但是对于薄壁结构加筋剪切研究这一领域,已有的按照集中面积加筋方法存在着比较大的理论缺陷,在计算时忽略了加筋结构截面形状的影响。
作为本文的主要创新点,作者试图推导一种新的方法来进行薄壁加筋结构的剪切计算。
本文主要的研究目的有以下两个:一是利用编程语言对类船体剖面剪切特性进行精确数值计算,并与实际工程应用中的投影面积比较,确定相关的修正系数。
二是对加筋薄壁结构剪切计算进行相关理论推导与数值计算推导,并编写相关程序。
本文计算结果发现,对于未加筋船体剖面,某一方向上的剪切面积修正系数随着该方向的单元构件数增多而减小。
对于加筋船体剖面来说,本文推导的分汇流法与原有的集中面积法在计算中各有优劣,由计算结果可以看出加筋对于船体剖面剪切计算的影响不可以忽略。
关键词:薄壁结构;剪切;加筋;编程薄壁结构截面剪切特性计算与加筋研究目录摘要……………………………………………………………………………………………………………..IAbstract.....…………..…...…………..…….……....……….............……….…....….…….….…..….…...IIl绪论…………………………………………………………………………………………………………..1-1.1研究背景及意义…………………………………………………………一1.1.2国内外研究现状及发展趋势……………………………………………一2-1.2.1薄壁梁理论的发展…………………………………………………一2.1.2.2图论的介绍………………………………………………………….3.1.2.3加筋薄壁结构剪切特性的计算…………………………………….一4-1.3本文的主要研究内容………………………………………………………一4—2各类剪切应力概述……………………………………………………………….-5-2.1弯曲剪应力…………………………………………………………………..5-2.1.1开口薄壁梁断面弯曲剪应力计算…………………………………一5.2.1.2单闭室薄壁梁弯曲剪应力计算…………………………………….7-2。
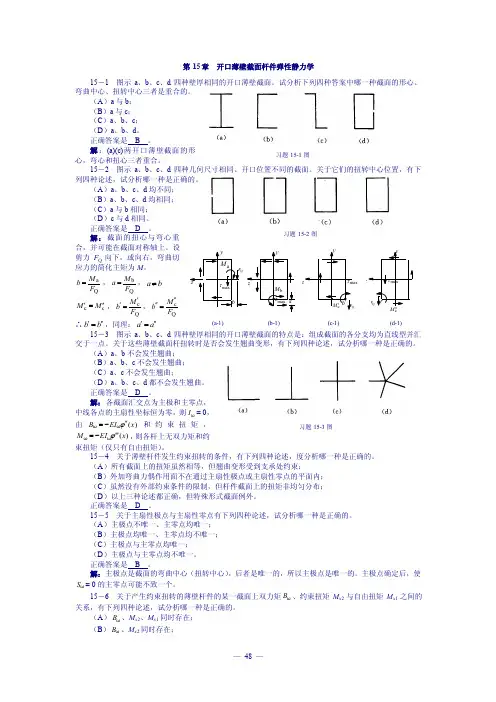
Z(a-1) (b-1) (c-1) (d-1) 习题15-1图习题15-2图习题15-3图第15章 开口薄壁截面杆件弹性静力学15-1 图示a 、b 、c 、d 四种壁厚相同的开口薄壁截面。
试分析下列四种答案中哪一种截面的形心、弯曲中心、扭转中心三者是重合的。
(A )a 与b ; (B )a 与c ; (C )a 、b 、c ; (D )a 、b 、d 。
正确答案是 B 。
解:(a)(c)两开口薄壁截面的形心,弯心和扭心三者重合。
15-2 图示a 、b 、c 、d 四种几何尺寸相同、开口位置不同的截面。
关于它们的扭转中心位置,有下列四种论述,试分析哪一种是正确的。
(A )a 、b 、c 、d 均不同; (B )a 、b 、c 、d 均相同; (C )a 与b 相同; (D )c 与d 相同。
正确答案是 D 。
解:截面的扭心与弯心重合,并可能在截面对称轴上。
设剪力F Q 向下,或向右,弯曲切应力的简化主矩为M 。
Q a F M b =,Q b F M a =,b a ≠ c cM M ''=',Q c F M b '=',Qc F M b ''='' ∴b b ''=',同理:a a ''='15-3 图示a 、b 、c 、d 四种壁厚相同的开口薄壁截面的特点是:组成截面的各分支均为直线型并汇交于一点。
关于这些薄壁截面杆扭转时是否会发生翘曲变形,有下列四种论述,试分析哪一种是正确的。
(A )a 、b 不会发生翘曲; (B )a 、b 、c 不会发生翘曲; (C )a 、c 不会发生翘曲;(D )a 、b 、c 、d 都不会发生翘曲。
正确答案是 D 。
解:各截面汇交点为主极和主零点,中线各点的主扇性坐标恒为零,则ωI = 0,由)(ωωx EI B ϕ''-=和约束扭矩,)(ωωx EI M ϕ'''-=,则各杆上无双力矩和约束扭矩(仅只有自由扭矩)。


高等桥梁结构理论课程作业参考答案(2014版)【作业1】如图1所示薄壁单箱断面,试分别计算:(1)该截面在竖向弯矩m kN M x ⋅=100作用下得正应力(注:平截面假定成立。
);(2)该截面在竖向剪力kN Q y 100=通过截面中心作用下得剪应力分布。
图1 薄壁单箱断面几何尺寸(单位:cm)【参考答案】由于该截面关于y 轴对称,故需要确定主轴ox 轴得位置,假定ox 轴距离上翼缘中心线为a,由0=x S ,得0)2(212)2(0.3212)5.20.35.2(22=-⨯--⨯-⨯+⋅++δδδδa a a a即04.01.04.03.06.01.08.022=+--+-+a a a a a0.15.1=a ,即m a 667.0=由ANSYS 计算截面几何特性参数,计算结果如图2所示。
具体几何特性计算结果为:竖向抗弯惯性矩为)(064.1)(10064.1448m cm I x =⨯=, 横向抗弯惯性矩为)(370.5)(10370.5448m cm I y =⨯=, 扭转常数为:)(470.1)(1047.1448m cm I y =⨯=,截面几何中心至顶板中心线距离为)(667.0m a =。
(1)截面在竖向弯矩m kN M x ⋅=100作用下,由初等梁理论可知,截面正应力分布由下式 计算,即y y y I M x x z 96.93984064.1000,100===σ(Pa) (m y m 667.0333.1≤≤-),具体截面正应力分布如图3所示。
XYO Sig1=62688PaSig2=125282Pa图2截面在竖向弯矩m kN M x⋅=100作用下正应力分布图(2)截面在竖向剪力kN Q y 100=作用下,闭口截面弯曲剪应力计算公式可知,截面剪应力为⎪⎪⎪⎪⎭⎫⎝⎛+-=⎰⎰δδds ds S S I Q q xx x y 划分薄壁断面各关键节点如图3(a)所示。
将截面在1点处切口,变为开口截面,求x S 、⎰δds与⎰ds S xδ。

薄壁型钢构件计算5 构件的计算5.1 轴心受拉构件5.1.1 轴心受拉构件的强度应按下式计算:式中σ——正应力;N——轴心力;A n——净截面面积;f——钢材的抗拉、抗压和抗弯强度设计值。
高强度螺栓摩擦型连接处的强度应按下列公式计算:式中n1——所计算截面(最外列螺栓)处的高强度螺栓数;n——在节点或拼接处,构件一端连接的高强度螺栓数;A——毛截面面积。
5.1.2 计算开口截面的轴心受拉构件的强度时,若轴心力不通过截面弯心(或不通过Z 形截面的扇性零点),则应考虑双力矩的影响。
注:本条规定也适用于轴心受压、拉弯、压弯构件。
5.2 轴心受压构件5.2.1 轴心受压构件的强度应按下式计算:式中:A en——有效净截面面积。
5.2.2 轴心受压构件的稳定性应按下式计算:式中——轴心受压构件的稳定系数,应按本规范表A.1.1-1或表A.1.1-2采用;A e——有效截面面积。
5.2.3 计算闭口截面、双轴对称的开口截面和截面全部有效的不卷边的等边单角钢轴心受压构件的稳定系数时,其长细比应取按下列公式算得的较大值:式中:λx、λy——构件对截面主轴x轴和y轴的长细比;l0x、l0y——构件在垂直于截面主轴x轴和y轴的平面内的计算长度;i x、i y——构件毛截面对其主轴x轴和y轴的回转半径。
5.2.4 计算单轴对称开口截面(如图5.2.4所示)轴心受压构件的稳定系数时,其长细比应取按公式5.2.3-2和下式算得的较大值:式中λω——弯扭屈曲的换算长细比;Iω——毛截面扇性惯性矩;I t——毛截面抗扭惯性矩;e0——毛截面的弯心在对称轴上的坐标;lω——扭转屈曲的计算长度,lω=β·l;l——无缀板时,为构件的几何长度;有缀板时,取两相邻缀板中心线的最大间距;α,β——约束系数,按表5.2.4采用。
表5.2.4 开口截面轴心受压和压弯构件的约束系数图5.2.4 单轴对称开口截面示意图5.2.5 有缀板的单轴对称开口截面轴心受压构件弯扭屈曲的换算长细比λω可按公式5.2.4-1计算,约束系数α、β可按表5.2.4采用,但扭转屈曲的计算长度lω=β·a,a 为缀板中心线的最大间距。
任意复杂薄壁截面自由扭转常数的数值计算方法康澜;张其林;王忠全;吴杰【摘要】针对任意复杂薄壁截面自由扭转常数的计算,提出一种便于计算机实现的建模方式和计算方法.采用一系列具有宽度的线段模拟薄壁截面,根据薄壁截面剪力流计算理论,编写相应计算程序,计算得到任意复杂薄壁截面的自由扭转常数.把本文的计算理论和计算方法运用到大型斜拉桥苏通大桥的截面计算中,并与Midas计算结果进行比较.计算结果表明:本文的建模方式实现了与CAD的无缝连接,方便工程应用;本文的计算方法对于不同剪力流指定方式得到相同的计算结果,克服了Midas 的计算缺陷,验证了本文计算方法的正确性和稳定性.%An effective algorithm and model building method for free torsion constant calculation of thin-walled bars with arbitrary complicated thin-walled cross sections was presented. Series of lines with given width were used to build the model of thin-walled cross section, corresponding calculation program was developed based on theory of shear flow,and free torsion constant for arbitrary complicated thin-walled cross section was obtained. The calculation theory and method were applied to the world's largest cable-stayed bridge i.e., Suzhou-Nantong Yangtze Road Bridge, and the results of this paper were compared with Midas. The results show that the model building method in this paper realizes the seamless connection with CAD, and is convenient to engineering application; the same results can be obtained by different given models of shear flow, this method overcomes the shortcomings of Midas, and the validity and stability of the method are verified.【期刊名称】《中南大学学报(自然科学版)》【年(卷),期】2011(042)005【总页数】5页(P1437-1441)【关键词】桥梁工程;薄壁截面;自由扭转常数;数值计算方法;剪力流【作者】康澜;张其林;王忠全;吴杰【作者单位】同济大学土木工程学院,上海,200092;中交四航工程研究院有限公司,广东广州,510230;同济大学土木工程学院,上海,200092;同济大学土木工程学院,上海,200092;同济大学土木工程学院,上海,200092【正文语种】中文【中图分类】TU448.213薄壁构件由于加劲肋的存在,断面形式越来越复杂,增加了截面特性的计算难度,尤其是其抗扭常数的计算。
异T形截面薄壁杆件解析解与数值解的比较研究关键词:薄壁杆件有限元解析解数值解取如图的异t形截面为例进行求解分析1.解析解求解1.2只有竖向力作用的分析在异t形截面中长翼缘板端加40kn竖向力,分析其应力。
可知:mx=-40000z,my=0则有:由此可知当z=4000mm(即固定端)的时候σz有最大值和最小值,得到。
对于水平翼缘板:,得到对于腹板:,得到。
所以得到了在竖向力荷载的作用下的弯曲正应力分布情况。
由于该图形的截面主扇性面积为零,所以忽略它的扭转正应力。
所以,在竖向力作用下的总正应力就约等于弯曲正应力。
对于弯曲剪应力的计算如下有效剪力为。
弯曲剪应力:由及形心的x、y图得到sy,sx。
即可得出其剪应力的分布。
由于该图形的截面主扇性面积为零,忽略它的扭转剪应力。
因此在竖向力作用下的总剪应力就约等于弯曲剪应力。
1.3只有竖向力作用的分析在异t形截面中长翼缘板端加40kn轴向力,应力分析如下:由截面中受力可知:mx=-4180000n,my=-5144000n则有:对于水平翼缘板:。
对于腹板:。
由于在只有轴向力的作用下时,不产生剪应力,所以。
2.数值解的求解利用ansys软件建模进行计算。
在只有竖向力作用的情况下,得出正应力最大的单元在短翼缘板边缘处,其中线附近的节点正应力为250.55mpa,最小正应力单元在腹板底部,其中线附近节点正应力为-210.44mpa。
最大剪应力单元在长翼缘板边缘,其中线附近的节点剪应力为126.15mpa。
最小剪应力单元在腹板底部,其中中线附近的节点剪应力为-145.81mpa。
在只有轴向力作用的情况下,得出正应力最大的单元在长翼缘板边缘处,其中线附近的节点正应力为37.732mpa,最小正应力单元中线附近节点正应力为-17.641mpa。
3.异t形截面的解析解和数值解的对比只有竖向力作用时,它们的正应力及剪应力分布情况大致相同。
最大最小正应力均相当吻合。
但最大最小剪应力有一定差异。