北师大版-数学-九年级上册-如何画位似图形
- 格式:doc
- 大小:202.00 KB
- 文档页数:2




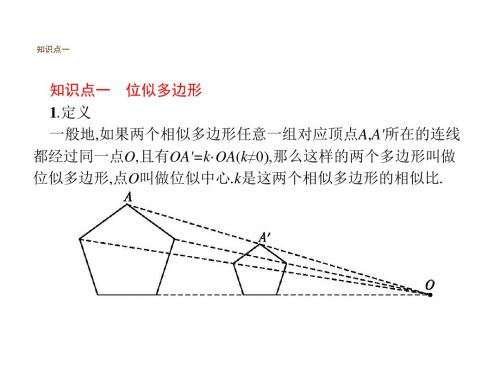
图形的位似--知识讲解【学习目标】1、了解位似多边形的概念,知道位似变换是特殊的相似变换,能利用位似的方法,将一个图形放大或缩小;2、能在同一坐标系中,感受图形放缩前后点的坐标的变化.【要点梳理】要点一、位似多边形1.位似多边形定义:如果两个相似多边形任意一组对应顶点所在的直线都经过同一个点O,且每组对应点与点O 点的距离之比都等于一个定值k,例如,如下图,OA′=k·OA(k≠0),那么这样的两个多边形叫做位似多边形,点O叫做位似中心.要点诠释:位似图形与相似图形的区别:位似图形是一种特殊的相似图形,而相似图形未必能构成位似图形.2.位似图形的性质:(1)位似图形的对应点相交于同一点,此点就是位似中心;(2) 位似图形的对应点到位似中心的距离之比等于相似比;(3)位似图形中不经过位似中心的对应线段平行.3.平移、轴对称、旋转和位似四种变换的异同:图形经过平移、旋转或轴对称的变换后,虽然对应位置改变了,但大小和形状没有改变,即两个图形是全等的;而位似变换之后图形是放大或缩小的,是相似的.4.作位似图形的步骤第一步:在原图上找若干个关键点,并任取一点作为位似中心;第二步:作位似中心与各关键点连线;第三步:在连线上取关键点的对应点,使之满足放缩比例;第四步:顺次连接各对应点.要点诠释:位似中心可以取在多边形外、多边形内,或多边形的一边上、或顶点,下面是位似中心不同的画法.要点二、坐标系中的位似图形在平面直角坐标系中,将一个多边形每个顶点的横坐标、纵坐标都乘同一个数k(k≠0),所对应的图形与原图形位似,位似中心是坐标原点,它们的相似比为|k|.要点诠释:在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标等于原来点的坐标乘以(或除以)k或-k.【典型例题】类型一、位似多边形1.下列每组的两个图形不是位似图形的是().A. B. C. D.【思路点拨】根据位似图形的概念对各选项逐一判断,即可得出答案.【答案】D【解析】解:对应顶点的连线相交于一点的两个相似多边形叫位似图形.据此可得A 、B 、C 三个图形中的两个图形都是位似图形;而D 的对应顶点的连线不能相交于一点,故不是位似图形.故选D .【总结升华】位似与相似既有联系又有区别,相似仅要求两个图形形状完全相同;而位似是在相似的基础上要求对应点的连线相交于一点.举一反三【变式】在小孔成像问题中, 根据如图4所示,若O 到AB 的距离是18cm ,O 到CD 的距离是6cm ,则像CD 的长是物AB 长的( ).A. 3倍B. 21 C. 31 D. 不知AB 的长度,无法判断 【答案】C2. 利用位似图形的方法把五边形ABCDE 放大1.5倍.【答案与解析】即是要画一个五边形A′B′C′D′E′,要与五边形ABCDE 相似且相似比为1.5.画法是: 1.在平面上任取一点O. 2.以O 为端点作射线OA 、OB 、OC 、OD 、OE. 3.在射线OA 、OB 、OC 、OD 、OE 上分别取点A′、B′、C′、D′、E′,使OA′:OA = OB′:OB =OC′:OC =OD′:OD =OE′:OE =1.5. 4.连结A′B′、B′C′、C′D′、D′E′、E′A′.这样:A′B′AB =B′C′BC =C′D′CD =D′E′DE =A′E′AE=1.5. 则五边形A′B′C′D′E′为所求. 另外一种情况,所画五边形跟原五边形分别在位似中心的两侧.【总结升华】由本题可知,利用位似的方法,可以把一个多边形放大或缩小.举一反三【变式】在已知三角形内求作内接正方形.【答案与解析】作法:(1)在AB 上任取一点G′,作G′D′⊥BC ;(2)以G′D′为边,在△ABC 内作一正方形D′E′F′G′;(3)连接BF′,延长交AC 于F ;(4)作FG ∥CB ,交AB 于G ,从F 、G 分别作BC 的垂线FE , GD ;∴四边形DEFG 即为所求.类型二、坐标系中的位似图形3. 如图,在10×10的正方形网格中,点A ,B ,C ,D 均在格点上,以点A 为位似中心画四边形AB′C′D′,使它与四边形ABCD 位似,且相似比为2.A 1B 1C 1D 1E 1 A B C D E(1)在图中画出四边形AB′C′D′;(2)填空:△AC′D′是三角形.【思路点拨】(1)延长AB到B′,使AB′=2AB,得到B的对应点B′,同样得到C、D的对应点C′,D′,再顺次连接即可;(2)利用勾股定理求出AC′2=42+82=80,AD′2=62+22=40,C′D′2=62+22=40,那么AD′=C′D′,AD′2+C′D′2=AC′2,即可判定△AC′D′是等腰直角三角形.【答案与解析】解:(1)如图所示:(2)∵AC′2=42+82=16+64=80,AD′2=62+22=36+4=40,C′D′2=62+22=36+4=40,∴AD′=C′D′,AD′2+C′D′2=AC′2,∴△AC′D′是等腰直角三角形.故答案为:等腰直角.【总结升华】本题考查了作图﹣位似变换.画位似图形的一般步骤为:①确定位似中心,②分别连接并延长位似中心和能代表原图的关键点;③根据相似比,确定能代表所作的位似图形的关键点;顺次连接上述各点,得到放大或缩小的图形.同时考查了勾股定理及其逆定理等知识.熟练掌握网格结构以及位似变换的定义是解题的关键.4. 如图△ABC的顶点坐标分别为A(1,1),B(2,3),C(3,0).(1)以点O为位似中心画△DEF,使它与△ABC位似,且相似比为2.(2)在(1)的条件下,若M(a,b)为△ABC边上的任意一点,则△DEF的边上与点M 对应的点M′的坐标为.【思路点拨】(1)把点A、B、C的横、纵坐标都乘以2可得到对应点D、E、F的坐标,再描点可得△DEF;把点A、B、C的横、纵坐标都乘以﹣2可得到对应点D′、E′、F′的坐标,然后描点可得△D′E′F′;(2)利用以原点为位似中心的位似变换的对应点的坐标特征求解.【答案与解析】解:(1)图略;(2)点M对应的点M′的坐标为(2a,2b)或(﹣2a,﹣2b).故答案为(2a,2b)或(﹣2a,﹣2b).【总结升华】本题考查了位似变换:如果两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行,那么这样的两个图形叫做位似图形,这个点叫做位似中心.在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或﹣k.举一反三:【变式】如图,将△AOB中各顶点的纵坐标,横坐标分别乘-1,•得到的图形与原图形相比有什么变化?作出所得的图形,这个过程可以看作是一个什么图形变换?【答案】解:图形的形状和大小都没有变化;可以看作是△AOB绕O•点按逆时针方向旋转180°得到的.。

如何画位似图形
位似变换是新课程标准中涉及的一个重要知识点,它是图形变换的一种,实际上它是相似变换的一种特殊情形,存在位似中心———即对应顶点连线的交点.其位似比就是相似比.作为一个新的知识点,越来越受到中考命题者的青睐.图形放大、缩小通常用位似变换的思想作图,位似中心的位置可在图形顶点处、图形边上、图形内部、图形外部.本文以一道中考题为例介绍几种常见画法,供同学们参考.
(辽宁省锦州中考题)如图1,己知四边形ABCD ,用尺规将它放大,使放大前后的图形对应线段的比为1:2.
画法一:
延长AD 到1D ,使1DD AD =,延长AC 到点1C ,使1CC AC =,延长AB 到点1B ,使1BB AB =,连接11D C ,11C B ,则四边形1111A B C D 即为所求(如图2).
说明:延长AD 得到1D 后,也可以过点1D 作11D C DC ∥,交AC 的延长线于1C ,再过点1C 作11B C BC ∥,交AC 的延长线于1B ,得到四边形1111A B C D .
画法二:
延长DA 到点1D ,使12AD AD =,延长CA 到点1C ,使12AC AC =,延长BA 到点1B ,使12AB AB =连接11B C ,11C D ,则四边形1111A B C D 即为所求(如图3).
画法三:
任取一点O ,连接OA 并延长到点1A ,使1AA OA =,连接OB 并延长到点1B ,使1BB OB =、连接OC 并延长到点1C ,使1CC OC =,连接OD 并延长到点1D ,使1DD OD =,顺次连接11A B ,11B C ,11C D ,11D A ,则四边形1111A B C D 即为所求(如图4). 运用这些作图方法可以解决不少数学问题.现举例说明:
例 如图5,在给定的锐角ABC △中,求作一个正方形DEFG ,使D E ,落在BC 上,F G ,分别落在AC AB ,边上,要求写出画法.
画法:
第一步:画一个有三个顶点落在ABC △两边上的正方形D E F G ''''(如图5);
第二步:连接BF '并延长交AC 于点F ;
第三步:过F 点作FE BC ⊥,垂足为点E ;
第四步:过F 作FG BC ∥交AB 于点G ;
第五步:过G 作GD BC ⊥,垂足为点D .
四边形DEFG 即为所求的正方形.(如图5)
想一想:为什么四边形DEFG 是正方形?请读者思考.。