向量三角拓展训练

三角形的思维拓展通过思维拓展训练提高解题能力三角形是初中数学中的一个基础概念，也是后续几何学习的重要基石。

在解题过程中，掌握一些思维拓展方法可以帮助我们更好地理解三角形的性质，提高解题能力。

本文将通过思维拓展的角度，探讨如何提高三角形解题的能力。

一、借助相似三角形拓展思维相似三角形是三角形学习中常见的重要概念，通过相似三角形的性质，可以拓展思维，解决一些复杂的三角形题目。

例如，当我们遇到无法直接应用几何定理解决的三角形问题时，可以通过构造相似三角形来解决。

例如，我们在解决附图1的题目时，原题给出了一个正三角形ABC 和线段DE，要求比较△EFG与△ABC的大小。

附图1:E----F\ /\ /G这时，我们可以构造相似三角形来找到答案。

首先，以线段EF为边界在△ABC内部构造一个正三角形E'FG，然后再连接E'G。

因为E'FG与ABC是相似三角形，所以我们可以得到两个比例关系：EG / AC = E'G / AE' 和 AG / AE = EG / E'G由于AE = AE'，所以可以推出EG = E'G，即△EFG与△E'FG的大小相等。

而根据正三角形的特性可知，△E'FG与△ABC的大小关系是EE'所在的线段上，所以可以得到△EFG与△ABC的大小关系。

通过构造相似三角形，我们在解决原问题时，引入了一个辅助三角形E'FG，借助相似三角形的知识，巧妙地解决了原问题。

二、角平分线的思维拓展角平分线是三角形中的重要性质之一，通过利用角平分线的性质，可以拓展思维，解决一些与角有关的三角形问题。

例如，我们在解决附图2的题目时，原题给出了△ABC中的点D，且∠BAD = ∠ACD。

要证明BD = CD。

附图2:A/ \/ \/ \B---D---C这时，我们可以利用角平分线的性质来解题。

根据题意，∠BAD =∠ACD，而BD是∠B的角平分线，CD是∠C的角平分线，根据角平分线的性质可知，∠BAD和∠DAC的平分线BD和CD相等。

向量与三角函数创新题型的解题技巧导言向量与三角函数是高中数学中重要的概念和工具。

在解题过程中，我们经常会遇到创新型的题目，需要我们运用向量和三角函数的知识来解决。

然而，这些题目往往较为复杂和难以直接套用常规的解题方法。

本文将介绍一些解题技巧，帮助读者更好地解答向量与三角函数创新题型。

技巧一：理解向量运算在解答向量与三角函数创新题型时，熟练掌握向量运算是非常重要的。

向量运算包括向量加法、向量减法和向量数乘。

首先，我们需要清楚地理解向量的几何意义，即向量是有方向和大小的量，并可以表示为一个有向线段。

在题目中，通常会涉及向量的平移、旋转以及投影等运算。

理解这些运算的几何意义可以帮助我们更好地理解问题，从而找到解题的关键。

技巧二：灵活运用平移与旋转许多向量与三角函数创新题型涉及到平移和旋转操作。

平移是指将向量的起点平移至其他位置，旋转是指将向量绕定点旋转一定的角度。

在解题过程中，我们可以通过平移和旋转来简化问题，使得解题更加容易。

例如，对于一个平面上的向量问题，我们可以通过平移将向量的起点设置为坐标原点，从而大大简化计算。

类似地，我们还可以通过旋转来使向量与坐标轴对齐，从而化简计算过程。

技巧三：利用三角函数的性质三角函数是向量与三角函数创新题型中经常会涉及到的概念。

在解答这类题目时，熟练掌握三角函数的性质是非常重要的。

首先，我们需要理解三角函数的定义和图像。

例如，正弦函数和余弦函数的图像是周期性的，周期为2π。

其次，我们还需要掌握三角函数的基本关系式，如正弦定理、余弦定理和正切函数的定义等。

利用这些性质和关系式，我们可以将问题转化为一些简单的代数方程或三角方程，然后再进行求解。

技巧四：巧用向量之间的关系在解决向量与三角函数创新题型时，我们经常会用到一些向量之间的关系。

例如，向量的数量积和叉积可以帮助我们求解角度和长度等问题。

在应用这些关系式时，我们需要注意向量的顺序和方向，以及向量之间的运算法则。

灵活运用这些关系式可以帮助我们简化计算，从而更快地解决问题。

习题课——三角恒等变换课后篇巩固提升基础巩固1.(多选)函数f (x )=sin x cos x+√32cos 2x 的最小正周期和振幅分别是() A .πB .2C .1D .2πf (x )=sin x cos x+√32cos2x=12sin2x+√32cos2x=sin (2x +π3), 得最小正周期为π,振幅为1.2.已知A (1,sinαsin (α+2β)),B (sinαsin (α-2β)-2,1),且OA ⃗⃗⃗⃗⃗ ·OB ⃗⃗⃗⃗⃗ =0,sin β≠0,sin α-k cos β=0,则k=()A .√2B .-√2C .√2或-√2D .以上都不对 由题意sinαsin (α-2β)-2+sinαsin (α+2β)=0,化简得sin α=±√2cos β,易知k=±√2,所以选C .3.若函数f (x )=sin x 3cos φ3+cos x 3sin φ3(φ∈[0,2π])是偶函数,则φ的值为()A .π2B .2π3C .3π2D .5π3(x )=sin x3cos φ3+cos x3sin φ3=sin (x3+φ3).由题意,知函数f (x )=sin (x3+φ3)(φ∈[0,2π])为偶函数,所以φ3=π2+k π,k ∈Z ,所以φ=3π2+3k π,k ∈Z .又φ∈[0,2π],故当k=0时,φ=3π2,选C .4.定义行列式运算|a 1 a 2a 3 a 4|=a 1a 4-a 2a 3.将函数f (x )=|√3 sinx 1 cosx|的图像向左平移n (n>0)个单位,所得图像对应的函数g (x )为奇函数,则n 的最小值为() A .π6B .π3C .5π6D .2π3 解析∵f (x )=√3cos x-sin x=2√32cos x-12sin x =2cos (x +π6),又平移后图像对应函数g (x )=2cos (x +n +π6)为奇函数,∴n+π6=k π+π2(k ∈Z ),即n=k π+π3(k ∈Z ),又n>0,∴n 的最小值为π3,故选B .5.(多选)已知函数f (x )=(sin x+cos x )cos x ,则下列说法错误的为() A .函数f (x )的最小正周期为2π B .f (x )的最大值为√2C .f (x )的图像关于直线x=-π8对称D .将f (x )的图像向右平移π8个单位,再向下平移12个单位后会得到一个奇函数的图像f (x )=(sin x+cos x )cos x ,得f (x )=√22sin (2x +π4)+12, 所以f (x )最小正周期为π,A 错; 所以f (x )的最大值为√22+12,B 错; f (x )的对称轴为x=π8+kπ2,k ∈Z ,所以x=-π8不是f (x )的对称轴,C 错;将f (x )的图像向右平移π8个单位得y=√22sin2x+12,再向下平移12个单位后会得到y=√22sin2x 为奇函数.6.若cos α=-45,α是第三象限的角,则1+tanα21-tanα2=.α是第三象限的角,∴k π+π2<α2<k π+3π4,k ∈Z , ∴tan α2<0. ∵cos α=-45,∴cos α=cos 2α2-sin 2α2=cos 2α2-sin 2α2cos 2α2+sin 2α2=1-tan 2α21+tan 2α2=-45,解得tan α2=-3,∴tan (α2+π4)=tan α2+tanπ41-tan α2tanπ4=-3+11+3=-12. -127.函数f (x )=√3sin 23x-2sin 213x (π2≤x ≤3π4)的最小值是.f (x )=√3sin 23x-2sin 213x=√3sin 23x+cos 23x-1=2sin (23x +π6)-1,又π2≤x ≤3π4,所以23x+π6∈[π2,2π3].所以当2x+π6=2π3时,f (x )取得最小值√3-1.√3-18.已知向量a =(cos α,sin α),b =(cos β,-sin β),α,β均为锐角,且|a -b |=√105, (1)求cos(α+β)的值; (2)若cos α=1213,求cos β的值.由题意可得a -b =(cos α-cos β,sin α+sin β),∵|a -b |=√105= √(cosα-cosβ)2+(sinα+sinβ)2=√2-2cos (α+β),∴cos(α+β)=45.(2)∵cos(α+β)=45,α,β均为锐角,∴α+β仍为锐角,sin(α+β)=√1-cos 2(α+β)=35.∵cos α=1213,∴sin α=√1-cos 2α=513,∴cos β=cos[(α+β)-α]=cos(α+β)cos α+sin(α+β)sin α=45×1213+35×513=6365.9.已知函数f (x )=sin 2ωx+√3sin ωx ·sin (ωx +π2)(ω>0)的最小正周期为π. (1)求ω的值;(2)求函数f (x )在区间[0,2π3]上的取值X 围.f (x )=1-cos2ωx2+√32sin2ωx=√32sin2ωx-12cos2ωx+12=sin (2ωx -π6)+12. 因为函数f (x )的最小正周期为π,且ω>0, 所以2π2ω=π,解得ω=1.(2)由(1)得f (x )=sin (2x -π6)+12, 因为0≤x ≤2π3,所以-π6≤2x-π6≤7π6,所以-12≤sin (2x -π6)≤1.因此0≤sin (2x -π6)+12≤32,所以f (x )的取值X 围是[0,32].能力提升1.设当x=θ时,函数f (x )=2sin x-cos x 取得最大值,则cos θ=() A .2√55B .-2√55C .√55D .-√55(x )=2sin x-cos x=√5sin(x-φ)=√5sin x ·cos φ-√5cos x sin φ;其中cos φ=√5,sin φ=√5;由题意得θ-φ=2k π+π2(k ∈Z ), 即θ=φ+2k π+π2(k ∈Z );所以cos θ=cos (φ+2kπ+π2)=cos (φ+π2)=-sin φ=-√5=-√55.2.若函数f (x )=sin ωx+√3cos ωx (x ∈R ),又f (α)=-2,f (β)=0,且|α-β|的最小值为3π4,则正数ω的值是() A .13B .32C .43D .23(x )=sin ωx+√3cos ωx=2sin (ωx +π3),又f (α)=-2,f (β)=0,从而当x=α时函数有最小值,x=β为平衡点,|α-β|的最小值是14T ,因此14×2πω=3π4,解得ω=23.3.已知函数f (x )=√3cos (π2+2x)+2sin 2(π2+x),x ∈[0,π2],则f (x )的最小值为() A .-1B .2C .3D .1-√3(x )=-√3sin2x+2cos 2x=-√3sin2x+1+cos2x=2cos (2x +π3)+1,因为0≤x ≤π2,所以π3≤2x+π3≤4π3,所以当2x+π3=π,即cos (2x +π3)=-1时,函数f (x )取最小值为-1.4.已知函数f (x )=cos x (sin x-√3cos x ),则() A .f (x )的周期为2π B .f (x )在区间[-π6,π6]上单调C .f (x )的图像关于直线x=-π12对称D .f (x )的图像关于点(π6,0)对称(x )=cos x sin x-√3cos 2x=12sin2x-√32·cos2x-√32=sin (2x -π3)−√32,所以T=2π2=π,排除A;令2k π-π2≤2x-π3≤2k π+π2(k ∈Z ),解得k π-π12≤x ≤k π+5π12(k ∈Z ),所以f (x )在区间[-π12,5π12]上单调,排除B;sin (-2π12-π3)=-1,所以f (x )的图像关于直线x=-π12对称,C 正确;f (π6)=sin (π3-π3)−√32≠0,所以f (x )的图像关于点(π6,0)不对称,排除D .5.已知向量a =(cos 2α,sin α),b =(1,2sin α-1),α∈(π2,π),若a ·b =25,则tan (α+π4)=() A .13B .27C .17D .23a ·b =25,得cos2α+sin α(2sin α-1)=25,求得sin α=35,又α∈(π2,π),则cos α=-45,所以tan α=-34,于是tan (α+π4)=tanα+tanπ41-tanαtanπ4=17.6.已知ω>0,a>0,f (x )=a sin ωx+√3a cos ωx ,g (x )=2cos (x +π6),h (x )=f (x )g (x ),这三个函数在同一直角坐标系中的部分图像如图所示,则函数g (x )+h (x )的图像的一条对称轴方程可以为()A .x=π6B .x=13π6C .x=-23π12D .x=-29π12f (x )=a sin ωx+√3a cos ωx=2a sin (ωx +π3),由题图可得2a=2,即a=1,f (x )=2sin (ωx +π3);而g (π3)=2cos (π3+π6)=0,h (x )=f (x )g (x )中,x ≠π3,所以{f (π3)=2sin (π3ω+π3)=0,f (0)=g (0);而ω>0,解得ω=2,即f (x )=2sin (2x +π3),所以F (x )=g (x )+h (x )=g (x )+f (x )g (x )=2cos (x +π6)+2sin(2x+π3)2cos(x+π6)=2cos (x +π6)+2sin (x +π6)=2√2sin (x +π6+π4)=2√2sin (x +5π12),而F (π6)≠±2√2,排除A;F (13π6)≠±2√2,排除B;F (-23π12)=2√2,即x=-23π12,即g (x )+h (x )的一条对称轴.7.(双空)已知向量a =(cos θ,sin θ),向量b =(√3,-1),则|2a -b |的最大值为,最小值为.2a -b =(2cos θ-3,2sin θ-1),则|2a -b |=√(2cosθ-√3)2+(2sinθ-1)2=√8-4√3cosθ-4sinθ=√8-8sin (θ+π3),当sin (θ+π3)=-1时,上式取最大值4,当sin (θ+π3)=1时,上式取最小值0.8.设f (x )=√3sin 3x+cos 3x ,若对任意实数x 都有m ≤f (x ),则实数m 的取值X 围是.(x )=√3sin3x+cos3x=2(√32sin3x +12cos3x)=2sin (3x +π6),所以f (x )min =-2,于是若对任意实数x 都有m ≤f (x ),则m ≤-2.-∞,-2]9.已知函数f (x )=sin (x -π6)+cos (x -π3),g (x )=2sin 2x2. (1)若α是第一象限角,且f (α)=3√35,求g (α)的值;(2)求使f (x )≥g (x )成立的x 的取值集合.(x )=sin (x -π6)+cos (x -π3)=√32sin x-12cos x+12cos x+√32sin x=√3sin x , g (x )=2sin 2x2=1-cos x , (1)由f (α)=3√35,得sin α=35,又α是第一象限角, 所以cos α>0.从而g (α)=1-cos α=1-√1-sin 2α=1-45=15. (2)f (x )≥g (x )等价于√3sin x ≥1-cos x , 即√3sin x+cos x ≥1.于是sin (x +π6)≥12. 从而2k π+π6≤x+π6≤2k π+5π6,k ∈Z ,即2k π≤x ≤2k π+2π3,k ∈Z ,故使f (x )≥g (x )成立的x 的取值集合为{x |2kπ≤x ≤2kπ+2π3,k ∈Z}.10.若函数f (x )=sin x+√3cos x+a 在(0,2π)内有两个不同的零点α,β. (1)某某数a 的取值X 围; (2)求tan(α+β)的值.由题意得sin x+√3cos x=212sin x+√32cos x =2sin (x +π3), ∵函数f (x )=sin x+√3cos x+a 在(0,2π)内有两个不同的零点, ∴关于x 的方程sin x+√3cos x+a=0在(0,2π)内有相异二解, ∴方程sin (x +π3)=-a2在(0,2π)内有相异二解. ∵0<x<2π,∴π3<x+π3<7π3.结合正弦函数的图像可得若方程有两个相异解, 则满足-1<-a2<1,且-a2≠√32, 解得-2<a<2,且a ≠-√3.∴实数a 的取值X 围是(-2,-√3)∪(-√3,2).(2)∵α,β是方程的相异解,∴sin α+√3cos α+a=0,① sin β+√3cos β+a=0,②①-②,得(sin α-sin β)+√3(cos α-cos β)=0, ∴2sinα-β2cosα+β2-2√3sinα+β2sinα-β2=0.又sinα+β2≠0, ∴tanα+β2=√33,α+β21-tan2α+β2=√3.∴tan(α+β)=2tan。

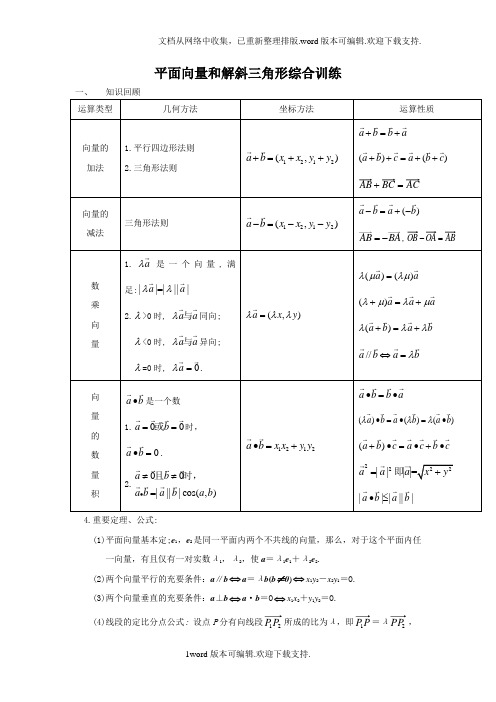
平面向量和解斜三角形综合训练运算类型几何方法坐标方法运算性质向量的 加法1.平行四边形法则2.三角形法则1212(,)a b x x y y +=++a b b a +=+()()a b c a b c ++=++AC BC AB =+向量的减法三角形法则1212(,)a b x x y y -=--()a b a b -=+-AB BA =-,AB OA OB =-数 乘 向 量1.a λ是一个向量,满足:||||||a a λλ=2.λ>0时, a a λ与同向;λ<0时, a a λ与异向;λ=0时, 0a λ=.(,)a x y λλλ=()()a a λμλμ=()a a a λμλμ+=+()a b a b λλλ+=+//a b a b λ⇔=向 量 的 数 量积a b •是一个数1.00a b ==或时，0a b •=.2.00||||cos(,)a b a b a b a b ≠≠=且时，1212a b x x y y •=+a b b a •=•()()()a b a b a b λλλ•=•=•()a b c a c b c +•=•+•2222||||=a a a x y =+即||||||a b a b •≤4.重要定理、公式:(1)平面向量基本定;e 1，e 2是同一平面内两个不共线的向量，那么，对于这个平面内任一向量，有且仅有一对实数λ1，λ2，使a ＝λ1e 1＋λ2e 2.(2)两个向量平行的充要条件：a ∥b ⇔a ＝λb (b ≠0)⇔x 1y 2－x 2y 1＝O. (3)两个向量垂直的充要条件：a ⊥b ⇔a ·b ＝O ⇔x 1x 2＋y 1y 2＝O.(4)线段的定比分点公式: 设点P 分有向线段21P P 所成的比为λ，即P P 1＝λ2PP ，则：⎪⎪⎩⎪⎪⎨⎧++=++=.1,12121λλλλy y y x x x (线段定比分点的坐标公式) 当λ＝1时，得中点公式：OP ＝21（1OP ＋2OP ）或⎪⎪⎩⎪⎪⎨⎧+=+=.2,22121y y y x x x（5）平行四边形对角线定理：对角线的平方和等于四边的平方和：)(22222b a b a b a +=-++5．解三角形：⑴正弦定理：.2sin sin sin R CcB b A a === ⑵余弦定理：a 2＝b 2＋c 2－2bc cos A ，b 2＝c 2＋a 2－2ca cos B ，c 2＝a 2＋b 2－2ab cosC . ⑶面积计算公式：高底⨯⨯=21S A bc B ac C ab S sin 21sin 21sin 21=== C B A R S sin sin sin 22= 其中R 为△ABC 外接圆半径R abcS 4=其中R 为△ABC 外接圆半径 2lrS = 其中l 为△ABC 周长，r 为其内切圆半径（4）△ABC 形状的判定：⇔+=222b a c △ABC 为直角△⇔∠A + ∠B =2π2c＜⇔+22b a △ABC 为钝角△⇔∠A + ∠B ＜2π如果要判断三角形是一个直角或者钝角三角形，则只需要判断其中一个角是直角或者钝角即可，如果要判断这个三角形是个锐角三角形，那么必须判断三个角都是锐角。

向量和三角函数的结合训练一．解答题（共40小题）1．在△ABC中，内角A，B，C所对的边分别为a，b，c，已知asin2B=bsinA．（1）求B；（2）已知cosA=，求sinC的值．2．在锐角△ABC中，a、b、c分别为角A、B、C所对的边，且=2csinA（1）确定角C的大小；（2）若c=，且△ABC的面积为，求a+b的值．3．△ABC的三个内角A、B、C所对的边分别为a、b、c，asinAsinB+bcos2A=a．（Ⅰ）求；（Ⅱ）若c2=b2+a2，求B．4．在△ABC中，角A，B，C的对边分别为a，b，c，C=，b=5，△ABC的面积为10．（1）求a，c的值；（2）求sin（A+）的值．5．在△ABC中，a，b，c分别是内角A，B，C所对的边，，若向量=（1，sinA），=（2，sinB），且∥．（Ⅰ）求b，c的值；（Ⅱ）求角A的大小及△ABC的面积．6．在锐角△ABC中，a、b、c分别为角A、B、C所对的边，且（Ⅰ）确定角C的大小；（Ⅱ）若c=，且△ABC的面积为，求a2+b2的值．7．在锐角△ABC中，cosA=，sinB=．（1）求角C；（2）设AB=，求△ABC的面积．8．已知a、b、c是△ABC中∠A、∠B、∠C的对边，S是△ABC的面积，若a=4，b=5，S=5，求c的长度．9．在△ABC中，BC=，AC=3，sinC=2sinA．（1）求AB的值；（2）求sinA的值．10．在△ABC中，a，b，c分别是角A、B、C的对边，且a2+b2=c2+ab．（1）求C；（2）若=，求A．11．已知a，b，c分别为△ABC的三个内角A，B，C的对边，，且．（Ⅰ）求角A的大小；（Ⅱ）若a=2，△ABC的面积为，求b，c．12．△ABC的面积是4，角A，B，C的对边分别是a，b，c，（1）求的值；（2）分别求c，a的值．13．在△ABC中，内角A，B，C的对边分别是a，b，c．（1）A=60°，a=4，b=4，求B；（2）已知a=3，c=2，B=150°，求边b的长．14．在△ABC中，已知A=30°，B=120°，b=5，解三角形．15．在△ABC中，角A，B，C所对的边分别为a，b，c，已知a=2，c=3，．（1）求b的值；（2）求sinA的值．16．在△ABC中，角A，B，C所对的边分别为a，b，c，且满足．（I）求角B的大小；（II）若b是a和c的等比中项，求△ABC的面积．17．在△ABC中，已知A=45°，．（Ⅰ）求sinC的值；（Ⅱ）若BC=10，求△ABC的面积．18．已知△ABC中，AB=6，∠A=30°，∠B=120°，解此三角形．19．在△ABC中，角A，B，C所对的边分别为a，b，c，满足，且△ABC的面积为2．（Ⅰ）求bc的值；（Ⅱ）若b+c=6，求a的值．20．在△ABC中，角A，B，C的对边分别为a，b，c．（1）若b=3，c=1，A=60°，求a；（2）若a=30，b=10，A=60°，求B，C，c．21．已知函数．（I）求f（x）的最小正周期及单调递减区间；（II）在△ABC中，a，b，c分别是角A，B，C的对边，若f（A）=2，b=1，△ABC 的面积为，求a的值．22．在△ABC中，A=30°，C=105°，a=10，求b，c．23．在△ABC中，已知，b=2，C为锐角，△ABC的面积S=，求第三边c．24．已知△ABC的面积为，且，向量和向量是共线向量．（1）求角C；（2）求△ABC的边长c．25．在△ABC中内角A，B，C的对边分别为a，b，c，已知（1）求sinC的值（2）求b边的长．26．已知△ABC的面积其中a，b，c分别为角A，B，C所对的边（1）求角A的大小．（2）若a=2，求的最大值．27．在△ABC中，角A，B，C的对边分别为a bc且．求：（Ⅰ）的值；（Ⅱ）b的值．28．已知：△ABC中角A、B、C所对的边分别为a、b、c且．（1）求角C的大小；（2）若sinA，sinC，sinB成等差数列，且，求c边的长．29．根据下列条件，解三角形．（Ⅰ）已知b=4，c=8，B=30°，求C，A，a；（Ⅱ）在△ABC中，B=45°，C=75°，b=2，求a，c，A．30．已知△ABC中，A=45°，C=30°，c=10cm，解三角形．31．在△ABC中，已知a=，b=1，∠B=45°，解此三角形．32．在△ABC中，a、b、c分别是角A、B、C的对边，已知，sinB=cosAsinC，（I）求边AC的长度；（II）若BC=4，求角B的大小．33．在△ABC中，角A、B、C的对边分别为a、b、c，若sin22C+sin2C•sinC+cos2C=1，且a+b=5，c=．（1）求角C的大小；（2）求△ABC的面积．34．（1）在△ABC中，a=3，c=2，B=60°求b（2）在△ABC中，A=60°，B=45°，a=2 求c．35．已知△ABC的周长为4（），且sinB+sinC=sinA．求边长a的值．36．在△ABC中，a=1，，B=45°，求角A、C及边c．37．在锐角△ABC中，已知，，BC=3．求△ABC的面积．38．在△ABC中，∠C=90°，CD是斜边AB上的高，已知CD=12，AD=5，求BD，AB，AC，BC的长．39．在△ABC中，a=5，B=45°，C=105°，解三角形．40．在△ABC中，A，B，C所对的边分别为a，b，c已知，c=1，B=45°，求a，A，C．参考答案与试题解析一．解答题（共40小题）1．（2016•天津）在△ABC中，内角A，B，C所对的边分别为a，b，c，已知asin2B=bsinA．（1）求B；（2）已知cosA=，求sinC的值．【分析】（1）利用正弦定理将边化角即可得出cosB；（2）求出sinA，利用两角和的正弦函数公式计算．【解答】解：（1）∵asin2B=bsinA，∴2sinAsinBcosB=sinBsinA，∴cosB=，∴B=．（2）∵cosA=，∴sinA=，∴sinC=sin（A+B）=sinAcosB+cosAsinB==．【点评】本题考查了正弦定理解三角形，两角和的正弦函数，属于基础题．2．（2015•郑州三模）在锐角△ABC中，a、b、c分别为角A、B、C所对的边，且=2csinA（1）确定角C的大小；（2）若c=，且△ABC的面积为，求a+b的值．【分析】（1）利用正弦定理把已知条件转化成角的正弦，整理可求得sinC，进而求得C．（2）利用三角形面积求得ab的值，利用余弦定理求得a2+b2的值，最后求得a+b 的值．【解答】解：（1）∵=2csinA∴正弦定理得，∵A锐角，∴sinA＞0，∴，又∵C锐角，∴（2）三角形ABC中，由余弦定理得c2=a2+b2﹣2abcosC即7=a2+b2﹣ab，又由△ABC的面积得．即ab=6，∴（a+b）2=a2+b2+2ab=25由于a+b为正，所以a+b=5．【点评】本题主要考查了正弦定理和余弦定理的运用．考查了学生对三角函数基础知识的综合运用．3．（2011•辽宁）△ABC的三个内角A、B、C所对的边分别为a、b、c，asinAsinB+bcos2A=a．（Ⅰ）求；（Ⅱ）若c2=b2+a2，求B．【分析】（Ⅰ）先由正弦定理把题设等式中边转化成角的正弦，化简整理求得sinB 和sinA的关系式，进而求得a和b的关系．（Ⅱ）把题设等式代入余弦定理中求得cosB的表达式，把（Ⅰ）中a和b的关系代入求得cosB的值，进而求得B．【解答】解：（Ⅰ）由正弦定理得，sin2AsinB+sinBcos2A=sinA，即sinB（sin2A+cos2A）=sinA∴sinB=sinA，=（Ⅱ）由余弦定理和C2=b2+a2，得cosB=由（Ⅰ）知b2=2a2，故c2=（2+）a2，可得cos2B=，又cosB＞0，故cosB=所以B=45°【点评】本题主要考查了正弦定理和余弦定理的应用．解题的过程主要是利用了正弦定理和余弦定理对边角问题进行了互化．4．（2015•苍梧县校级一模）在△ABC中，角A，B，C的对边分别为a，b，c，C=，b=5，△ABC的面积为10．（1）求a，c的值；（2）求sin（A+）的值．【分析】（Ⅰ）利用已知条件及三角形的面积公式求得a，进而利用余弦定理求得c．（Ⅱ）利用（Ⅰ）中求得的三边及余弦定理求得cosA的值，然后通过同角三角函数的基本关系求得sinA的值，最后利用正弦的两角和公式求得答案．【解答】解：（Ⅰ）由已知，，b=5，因为，即，解得a=8．由余弦定理可得：，所以c=7．（Ⅱ）由（Ⅰ）及余弦定理有，由于A是三角形的内角，易知，所以==．【点评】本题主要考查了解三角形及正弦定理和余弦定理的应用．考查了学生利用三角函数的基本性质处理边角问题的能力．5．（2014•漳州三模）在△ABC中，a，b，c分别是内角A，B，C所对的边，，若向量=（1，sinA），=（2，sinB），且∥．（Ⅰ）求b，c的值；（Ⅱ）求角A的大小及△ABC的面积．【分析】（Ⅰ）通过向量平行，求出A，B的关系式，利用正弦定理求出b的值，通过余弦定理求出c的值；（Ⅱ）直接利用正弦定理求出A的正弦函数值，然后求角A的大小，结合C的值确定A的值，利用三角形的面积公式直接求解△ABC的面积．【解答】解：（Ⅰ）∵=（1，sinA），=（2，sinB），，∴sinB﹣2sinA=0，由正弦定理可知b=2a=2，又∵c2=a2+b2﹣2abcosC，，所以c2=（）2+（2）2﹣2cos=9，∴c=3；（Ⅱ）由，得，∴sinA=，A=或，又C=，∴A=，所以△ABC的面积S===．【点评】本题是中档题，考查正弦定理与余弦定理的应用，注意向量的平行条件的应用，考查计算能力．6．（2014•蚌埠一模）在锐角△ABC中，a、b、c分别为角A、B、C所对的边，且（Ⅰ）确定角C的大小；（Ⅱ）若c=，且△ABC的面积为，求a2+b2的值．【分析】（Ⅰ）根据，利用正弦定理得，从而可求C 的大小；（Ⅱ）由面积公式得=，从而可得ab=6，由余弦定理，可得结论．【解答】解：（Ⅰ）∵，∴由正弦定理得…（2分）∴sinC=…（4分）∵△ABC是锐角三角形，∴C=…（6分）（Ⅱ）∵c=，C=，△ABC的面积为，∴由面积公式得=…（8分）∴ab=6 …（9分）由余弦定理得a2+b2﹣2abcos=7 …（11分）∴a2+b2=13 …（12分）【点评】本题考查正弦、余弦定理，考查学生的计算能力，属于基础题．7．（2016•广东模拟）在锐角△ABC中，cosA=，sinB=．（1）求角C；（2）设AB=，求△ABC的面积．【分析】（1）根据同角的三角函数关系，利用内角和定理即可求出sinC以及角C 的值；（2）由正弦定理和三角形的面积公式，即可求出△ABC的面积．【解答】解：（1）锐角△ABC中，cosA=，∴sinA==；又sinB=，∴cosB==；∴sinC=sin[π﹣（A+B）]=sin（A+B）=sinAcosB+cosAsinB=×+×=；又C∈（0，），∴C=；（2）△ABC中，由正弦定理得=，又AB=，∴AC===；∴△ABC的面积为S△ABC=•AB•AC•sinA=×××=．【点评】本题考查了同角的三角函数关系以及正弦定理的应用问题，是基础题目．8．（2001•上海）已知a、b、c是△ABC中∠A、∠B、∠C的对边，S是△ABC的面积，若a=4，b=5，S=5，求c的长度．【分析】由已知a=4，b=5，S=5及S=absinC可得sinC=，于是∠C=60°，或∠C=120°，然后利用余弦定理可求c【解答】解：∵S=absinC，∴sinC=，（4分）于是∠C=60°，或∠C=120°，（6分）又c2=a2+b2﹣2abcosC（8分）当∠C=60°时，c2=a2+b2﹣ab，c=（10分）当∠C=120°时，c2=a2+b2+ab，c=．（12分）【点评】本题主要考查了三角形面积公式，余弦定理等知识解三角形，属于基础试题．9．（2011春•万州区校级期中）在△ABC中，BC=，AC=3，sinC=2sinA．（1）求AB的值；（2）求sinA的值．【分析】（1）△ABC中，由正弦定理可得，再利用SinC=2SinA，求得AB值．（2）△ABC中，由余弦定理可求得cosA 的值，利用同角三角函数的基本关系，求得SinA．【解答】解：（1）△ABC中，由正弦定理可得，=2，∴AB=2×BC=2．（2）△ABC中，由余弦定理可得BC2=AB2+AC2﹣2AB•AC•cosA，5=20+9﹣12cosA，∴cosA=，∴SinA==．【点评】本题考查正弦定理、余弦定理的应用，同角三角函数的基本关系，利用这两个定理是解题的关键．10．（2013春•西区校级期中）在△ABC中，a，b，c分别是角A、B、C的对边，且a2+b2=c2+ab．（1）求C；（2）若=，求A．【分析】（1）利用题设等式整理代入余弦定理中求得cosC的值，进而求得C．（2）利用正弦定理把题设等式中变转化为角的正弦，利用二倍角和公式和两角和公式求得cosB的值，进而求得B，最后利用三角形内角和求得A．【解答】解：（1）∵a2+b2=c2+ab，∴=，∴cosC=，∴C=45°．（2）由正弦定理可得==，∴=∴sinBcosC=2sinAcosB﹣sinCcosB，∴sinBcosC+sinCcosB=2sinAcosB，∴sin（B+C）=2sinAcosB，∴sinA=2sinAcosB．∵sinA≠0，∴cosB=，∴B=60°，A=180°﹣45°﹣60°=75°．【点评】本题主要考查了解三角形问题．考查了对正弦定理和余弦定理的理解和应用．11．（2013秋•德州校级期中）已知a，b，c分别为△ABC的三个内角A，B，C 的对边，，且．（Ⅰ）求角A的大小；（Ⅱ）若a=2，△ABC的面积为，求b，c．【分析】（Ⅰ）通过向量的数量积直接得到A的正切值，即可求角A的大小；（II）通过△ABC的面积为，以及余弦定理推出b、c的关系，通过解方程即可求b，c【解答】解：（Ⅰ）因为，且，所以=cosA+sinA=0，所以tanA=，∵A∈（0，π），∴A=．=，且A=，（Ⅱ）∵S△ABC，故bc=4，…①又cosA=且a=2，∴，从而b2+c2=8…②，解①②得，b=c=2．【点评】本题考查向量的数量积以及三角形的面积公式，余弦定理的应用，考查计算能力．12．（2014秋•荔湾区校级期中）△ABC的面积是4，角A，B，C的对边分别是a，b，c，（1）求的值；（2）分别求c，a的值．【分析】（1）利用二倍角公式，化简代数式，代入计算即可求得结论；（2）利用面积公式求得c的值，再利用余弦定理，可求a的值．【解答】解：（1）==∵，∴=，∴=；（2）∵，∴∵△ABC的面积是4，b=2，∴，解得c=5由余弦定理可得a===．【点评】本题考查三角函数的化简，考查余弦定理的运用，考查学生的计算能力，属于基础题．13．（2016春•阿拉善左旗校级期末）在△ABC中，内角A，B，C的对边分别是a，b，c．（1）A=60°，a=4，b=4，求B；（2）已知a=3，c=2，B=150°，求边b的长．【分析】（1）由正弦定理可知=，求得sinB=，a＞b，可知A＞B，求得B=；（2）由余弦定理可知b2=a2+c2﹣2accosB，代入即可求得边b的长．【解答】解：（1）由正弦定理可知：=，∴=，解得：sinB=，由a＞b，∴A＞B，∴B=；（2）由余弦定理可知：b2=a2+c2﹣2accosB=27+4﹣2×3×2×（﹣）=49，∴b=7，边b的长7．【点评】本题考查解三角形的应用，考查正弦定理及余弦定理，考查计算能力，属于基础题．14．（2015秋•雷州市校级月考）在△ABC中，已知A=30°，B=120°，b=5，解三角形．【分析】由三角形的内角和可得C，可得等腰三角形，由正弦定理可得a和c．【解答】解：∵A=30°，B=120°，∴C=180°﹣（A+B）=30°．∴A=C，∴a=c．由正弦定理可得a===，综上可知，C=30°，a=c=【点评】本题考查解三角形，涉及正余弦定理的应用，属基础题．15．（2010•广州模拟）在△ABC中，角A，B，C所对的边分别为a，b，c，已知a=2，c=3，．（1）求b的值；（2）求sinA的值．【分析】（1）利用余弦定理，根据题设中的a=2，c=3，求得b．（2）根据三边长利用余弦定理求得cosA的值，进而利用三角函数基本关系求得sinA．【解答】解：（1）由余弦定理，b2=a2+c2﹣2accosB，得，∴b=3．（2）由余弦定理，得=，∵A是△ABC的内角，∴=．【点评】本题主要考查了解三角形的实际应用．解题的关键是利用正弦定理和余弦定理完成了边角问题的互化．16．（2011•绍兴一模）在△ABC中，角A，B，C所对的边分别为a，b，c，且满足．（I）求角B的大小；（II）若b是a和c的等比中项，求△ABC的面积．【分析】（I）题设利用两角和公式整理等式求得sin（B+）的值，进而求得B．（II）根据等比中项性质可求得b2=ac，代入余弦定理中求得a与c的值，进而可推断出三角形为正三角形，进而求得三角形的面积．【解答】解：（I）由，得，由B∈（0，π）得，故，得．（II）由b是a和c的等比中项得b2=ac又由余弦定理得b2=a2+c2﹣2ac•cosB=a2+c2﹣2ac•cos=a2+c2﹣ac，故ac=a2+c2﹣ac，得（a﹣c）2=0，得a=c=1，∴b==1故△ABC为正三角形故．【点评】本题主要考查了余弦定理的应用，两角和公式的化简求值．考查了学生对基础知识点综合运用．17．（2011•佛山一模）在△ABC中，已知A=45°，．（Ⅰ）求sinC的值；（Ⅱ）若BC=10，求△ABC的面积．【分析】（Ⅰ）由cosB的值和B的范围，利用同角三角函数间的基本关系求出sinB 的值，然后根据三角形的内角和定理得到所求式子中C等于180°﹣A﹣B，而A=45°，得到C=135°﹣B，把所求的式子利用两角差的正弦函数公式及特殊角的三角函数值化简后，把sinB和cosB的值代入即可求出值；（Ⅱ）根据正弦定理，由BC，sinA和（Ⅰ）中求得的sinC，即可求出AB的长度，然后利用三角形的面积公式，由sinB，AB和BC的值即可求出三角形ABC的面积．【解答】解：（Ⅰ）∵，且B∈（0°，180°），∴．sinC=sin（180°﹣A﹣B）=sin（135°﹣B）=；（Ⅱ）由正弦定理得，即，解得AB=14．则△ABC的面积．【点评】此题考查学生灵活运用同角三角函数间的基本关系、正弦定理及三角形的面积公式化简求值，是一道基础题．18．（2014秋•阿勒泰市校级期中）已知△ABC中，AB=6，∠A=30°，∠B=120°，解此三角形．【分析】利用条件，结合余弦定理，即可得出结论．【解答】解：∵AB=6，∠A=30°，∠B=120°，∴∠C=30°，BC=6，AC==6．【点评】本题考查解三角形，考查学生的计算能力，比较基础．19．（2010•南海区模拟）在△ABC中，角A，B，C所对的边分别为a，b，c，满足，且△ABC的面积为2．（Ⅰ）求bc的值；（Ⅱ）若b+c=6，求a的值．【分析】（Ⅰ）根据同角三角函数的基本关系利用sin的值求得cos的值，进而利用二倍角公式求得sinA的值，最后利用三角形面积公式求得bc的值．（Ⅱ）利用二倍角公式和sin的值求得cosA的值，进而把bc和b+c的值代入余弦定理求得a的值．【解答】解：（Ⅰ）∵，0＜A＜π∴．∴．∵，∴bc=5．（Ⅱ）∵，∴．∵bc=5，b+c=6，∴a2=b2+c2﹣2bccosA=（b+c）2﹣2bc（1+cosA）=20∴．【点评】本题主要考查了解三角形问题，余弦定理的应用，二倍角公式的化简求值．考查了学生综合运用所学知识和基本的运算能力．20．在△ABC中，角A，B，C的对边分别为a，b，c．（1）若b=3，c=1，A=60°，求a；（2）若a=30，b=10，A=60°，求B，C，c．【分析】（1）使用余弦定理解出；（2）使用正弦定理解出．【解答】解：（1）由余弦定理得a2=b2+c2﹣2bccosA=9+1﹣2×=7，∴a=．（2）由正弦定理得，即，解得sinB=，∴B=150°（舍）或B=30°．∴C=180°﹣A﹣B=90°．∴c==20．【点评】本题考查了正余弦定理在解三角形中的应用，属于基础题．21．（2011•安徽模拟）已知函数．（I）求f（x）的最小正周期及单调递减区间；（II）在△ABC中，a，b，c分别是角A，B，C的对边，若f（A）=2，b=1，△ABC 的面积为，求a的值．【分析】（I）利用两角和正弦公式化简f（x）=sin（2x+）+3，最小正周期T==π，令2kπ+≤2x+≤2kπ+，k∈z，解出x的范围，即得单调递减区间．（II）由f（A）=2 求出sin（2A+）=，由＜2A+＜，求得A 值，余弦定理求得a 值．【解答】解：（I）函数==sin （2x+）+．故最小正周期T==π，令2kπ+≤2x+≤2kπ+，k∈z，解得kπ+≤x≤kπ+，故函数的减区间为[kπ+，kπ+]，k∈z．（II）由f（A）=2，可得sin（2A+）+=2，∴sin（2A+）=，又0＜A＜π，∴＜2A+＜，∴2A+=，A=．∵b=1，△ABC的面积为=，∴c=2．又a2=b2+c2﹣2bc•cosA=3，∴a=．【点评】本题考查两角和正弦公式，正弦函数的单调性，奇偶性，根据三角函数的值求角，求出角A的值是解题的难点．22．（2014秋•清河区校级月考）在△ABC中，A=30°，C=105°，a=10，求b，c．【分析】由A与C的度数求出B的度数，再由正弦定理即可求出b，c的值．【解答】解：∵A=30°，C=105°，∴B=45°，∵，∴b==10，c==5+5．【点评】此题考查了正弦定理，以及特殊角的三角函数值，熟练掌握正弦定理是解本题的关键．23．（2014秋•思明区校级期中）在△ABC中，已知，b=2，C为锐角，△ABC的面积S=，求第三边c．【分析】根据三角形的面积公式，可求，结合C为锐角可求C，再由由余弦定理c2=a2+b2﹣2abcosC可求【解答】解：根据三角形的面积公式可得，∴∴∵C为锐角∴C=30°由余弦定理可得，c2=a2+b2﹣2abcosC=∴c=2【点评】本题主要考查了三角形的面积公式及正弦定理、余弦定理等公式在解题中的应用，属于基础试题．24．（2012•荆州模拟）已知△ABC的面积为，且，向量和向量是共线向量．（1）求角C；（2）求△ABC的边长c．【分析】（1）利用向量共线的条件，建立等式，再利用和角的正弦公式化简等式，即可求得角C；（2）由得：，进而利用△ABC的面积为，及余弦定理可求△ABC的边长c．【解答】解：（1）∵，∴（tanA+tanB）cosAcosB=sin2C，即sinAcosB+cosAsinB=sin2C，∴sin（A+B）=sin2C，∴sinC=2sinCcosC∵sinC≠0，∴，∵C∈（0，π）∴…（6分）（2）由得：，∴，∴，∴c2=a2+b2﹣2abcosC=54，∴…（12分）【点评】本题重点考查正弦、余弦定理的运用，考查向量知识的运用，解题的关键是正确运用正弦、余弦定理求出三角形的边．25．（2015秋•北京校级月考）在△ABC中内角A，B，C的对边分别为a，b，c，已知（1）求sinC的值（2）求b边的长．【分析】（1）利用正弦定理可得sinC；（2）由条件可得△ABC是等边三角形，即可求b边的长．【解答】解：（1）由正弦定理可得sinC==；（2）由条件可得△ABC是等边三角形，∴b=2．【点评】本题考查利用正弦定理解三角形，考查学生的计算能力，属于容易题．26．（2011秋•九江县校级月考）已知△ABC的面积其中a，b，c分别为角A，B，C所对的边（1）求角A的大小．（2）若a=2，求的最大值．【分析】（1）用三角形面积公式表示出S，利用题设等式建立等式，进而利用余弦定理求得2bccosA=b2+c2﹣a2，进而整理求得sinA和cosA的关系进而求得A．（2）由余弦定理可知2bccosA=b2+c2﹣a2，结合a=2，A=45°，及基本不等式可以求出bc的范围，结合=bc求出答案．【解答】解：（1）由三角形面积公式可知S=bcsinA，∵，∴bcsinA=由余弦定理可知2bccosA=b2+c2﹣a2∴sinA=cosA，即tana=1，又由A是三角形内角∴A=45°（2）∵由余弦定理可知2bccosA=b2+c2﹣a2，a=2，即bc=b2+c2﹣4≥2bc﹣4∴（2﹣）bc≤4∴bc≤=4+2∴=cosA=bc≤2+2故的最大值为2+2【点评】本题考查的知识点是解三角形，平面向量的综合题，本题的突破点是利用三角形的面积公式表示出S，与已知的S相等，化简得到tanC的值．要求学生熟练掌握三角形的面积公式以及余弦定理，牢记特殊角的三角函数值．27．（2012•迎泽区校级模拟）在△ABC中，角A，B，C的对边分别为a bc且．求：（Ⅰ）的值；（Ⅱ）b的值．【分析】（Ⅰ）由正弦定理可得，==2cosA，代入即可求解（Ⅱ）由a+c=10及可求a，c然后由余弦定理可知，cosA=即可求解b【解答】解：（Ⅰ）由正弦定理可得，==2cosA=（Ⅱ）由a+c=10及可得a=4，c=6由余弦定理可知，cosA==∴b2﹣9b+20=0∴b=4或b=5当b=4时，a=4，c=6，此时B=A，C=2A∴A=45°，与cosA=矛盾∴b=5【点评】本题主要考查了正弦定理及余弦定理在求解三角形中的应用，属于基础试题28．（2009秋•揭阳期末）已知：△ABC中角A、B、C所对的边分别为a、b、c且．（1）求角C的大小；（2）若sinA，sinC，sinB成等差数列，且，求c边的长．【分析】（1）利用两角和公式和诱导公式整理题设等式求得sin（A+B）=sin2C，进而整理求得cosC的值，进而求得C．（2）利用sinA，sinC，sinB成等差数列求得三者的关系式，利用正弦定理转化成边的关系式，利用求得ab的值，进而分别代入余弦定理求得c．【解答】解：（1）由cos（﹣A）•cosB+sinB•sin（+A）=sin（π﹣2C）得sinA•cosB+sinB•cosA=sin2C∴sin（A+B）=sin2C，∵A+B=π﹣C，∴sin（A+B）sinC∴sinC=sin2C=2sinCcosC，∵0＜C＜π∴sinC＞0∴cosC=∴C=（2）由sinA，sinC，sinB成等差数列，得2sinC=sinA+sinB，由正弦定理得2c=a+b∵，即abcosC=18，ab=36由余弦弦定理c2=a2+b2﹣2abcosC=（a+b）2﹣3ab，∴c2=4c2﹣3×36，c2=36，∴c=6【点评】本题主要考查了解三角形问题，三角函数恒等变换及化简求值．考查了考生分析问题的能力和基本的运算能力．29．（2016秋•兖州区校级期中）根据下列条件，解三角形．（Ⅰ）已知b=4，c=8，B=30°，求C，A，a；（Ⅱ）在△ABC中，B=45°，C=75°，b=2，求a，c，A．【分析】（Ⅰ）由条件利用正弦定理求得sinC的值，可得C为直角，求得A，再由勾股定理求得a的值．（Ⅱ）由条件利用三角形内角和公式求得A的值，再利用正弦定理求得a的值．【解答】解：（Ⅰ）已知△ABC中，∵已知b=4，c=8，B=30°，由正弦定理可，得sinC=1，可得C=90°，A=60°∴a=，（Ⅱ）∵已知△ABC中，B=45°，C=75°，b=2，由三角形内角和公式可得A=60°，由正弦定理可得=，得a=，c=【点评】本题主要考查了三角形内角和公式、正弦定理的应用，属于基础题．30．已知△ABC中，A=45°，C=30°，c=10cm，解三角形．【分析】由三角形内角和定理，直接计算可得B=180°﹣A﹣C=105°；根据三角形的三个角的大小和边c长，结合正弦定理加以计算即可得到a和b的大小．【解答】解：∵△ABC中，A=45°，C=30°，∴根据三角形内角和定理，得B=180°﹣A﹣C=105°；由正弦定理，得，解之得a=10cm，b=5（+）cm【点评】本题给出三角形的两个角和一条边，解此三角形．着重考查了三角形内角和定理、特殊角的三角函数和正弦定理等知识，属于基础题．31．在△ABC中，已知a=，b=1，∠B=45°，解此三角形．【分析】利用正弦定理，可求得A，从而由三角形的内角和定理可求得C，由三角形特点求c．【解答】解：由正弦定理得，即，所以sinA=1，所以A=90°，所以C=180°﹣A﹣B=45°，所以△ABC是等腰直角三角形，所以c=b=1．【点评】本题考查正弦定理的运用，考查运算能力．属于基础题．32．（2010春•沙坪坝区校级期末）在△ABC中，a、b、c分别是角A、B、C的对边，已知，sinB=cosAsinC，（I）求边AC的长度；（II）若BC=4，求角B的大小．【分析】（I）联立，sinB=cosAsinC，可知cbcosA=9，cosA•c=b，从而可求边AC的长度；（II）由（I），结合BC=4=a，b=3代入即得AB=5，从而三角形为直角三角形，由此可求角B的大小．【解答】解：（I），又sinB=cosAsinC⇒cosA•c=b代入得b=3，（II），将BC=4=a，b=3代入即得AB=5⇒【点评】本题以三角形为载体，考查向量的数量积，考查正余弦定理的运用，属于基础题．33．（2011•江西校级模拟）在△ABC中，角A、B、C的对边分别为a、b、c，若sin22C+sin2C•sinC+cos2C=1，且a+b=5，c=．（1）求角C的大小；（2）求△ABC的面积．【分析】（1）通过二倍角公式化简已知表达式，求出cosC的值，然后在三角形中求角C的大小；（2）结合（1）通过余弦定理，求出ab的值，然后直接求△ABC的面积．【解答】解：（1）因为sin22C+sin2C×sinC+cos2C=1，所以4sin2Ccos2C+2sin2CcosC+1﹣2sin2C=1，则2cos2C+cosC﹣1=0．得出cosC=所以C=60°…（6分）（2）由余弦定理可知：∴…（12分）【点评】本题是基础题，借助三角形考查二倍角公式的应用，余弦定理是解答（2）的关键，考查计算能力．34．（2016秋•陕西期中）（1）在△ABC中，a=3，c=2，B=60°求b（2）在△ABC中，A=60°，B=45°，a=2 求c．【分析】（1）利用余弦定理即可求出b的值；（2）利用三角形内角和求出C的值，再由正弦定理求出c的值．【解答】解：（1）在△ABC中，a=3，c=2，B=60°，由余弦定理可得b2=a2+c2﹣2accosB=32+22﹣2×3×2×cos60°=7，∴b=；（2）在△ABC中，A=60°，B=45°，∴C=75°，∴sin75°=sin（30°+45°）=sin30°cos45°+cos30°sin45°=；又a=2，由正弦定理得=，∴c=×sin75°=×=+．【点评】本题考查了正弦、余弦定理的应用问题，也考查了三角形内角和定理与三角恒等变换问题，是基础题．35．（2010•沈丘县校级模拟）已知△ABC的周长为4（），且sinB+sinC=sinA．求边长a的值．【分析】先根据正弦定理用角的正弦值和外接圆半径表示出边长，再由sinB+sinC=sinA可得到b+c=a，结合△ABC的周长为4（），可求得a 的值．【解答】解：设三角形的外接圆半径为R，根据正弦定理有a=2R×sinA，b=2R×sinB，c=2R×sinC因为sinB+sinC=sinA，两边同时乘以2R得：2R×sinB+2R×sinC=×2RsinA 即：b+c= a ①又由题意有：a+b+c=4（+1）②；解①②得：a=4即边长a的值为4．【点评】本题主要考查正弦定理的应用．正弦定理和余弦定理在解三角形中应用比较广泛，对于定理的内容一定要熟练掌握并能够熟练应用．36．（2013春•仙桃校级期中）在△ABC中，a=1，，B=45°，求角A、C及边c．【分析】由已知中a=1，，B=45°°，代入正弦定理可得A的正弦值，结合已知中a＜b，可得A值，进而根据内角和定理求出C，再由正弦定理求出c．【解答】解：由正弦定理∴sinA=，∵a＜b，∴A=30°，C=105°，∵=2，∴c=．【点评】本题考查的知识点是正弦定理，考查学生的计算能力，比较基础．37．在锐角△ABC中，已知，，BC=3．求△ABC的面积．【分析】先利用同角三角函数基本关系求得sinA和sinC的值，进而利用正弦定理求得AB，根据sinB=sin（A+C）利用两角和公式求得sinB的值，最后利用三角形面积公式求得答案．【解答】解：sinA==，sinC==由正弦定理可知=∴AB=×=2sinB=sin（A+C）=×+×=∴△ABC的面积为AB•BC•sinB=×2×3×=3【点评】本题主要考查了解三角形的实际应用．解题的关键是利用正弦定理完成边角问题的互化．38．在△ABC中，∠C=90°，CD是斜边AB上的高，已知CD=12，AD=5，求BD，AB，AC，BC的长．【分析】利用射影定理，即可求BD，AB，AC，BC的长．【解答】解：∵△ABC中，∠C=90°，CD是斜边AB上的高，∴CD2=AD•BD，∵CD=12，AD=5，∴BD=，∴AB=，∵AC2=AD•AB，BC2=BD•AB，∴AC=13，BC=．【点评】本题考查射影定理，考查学生的计算能力，正确运用射影定理是关键．39．（2016春•西秀区校级月考）在△ABC中，a=5，B=45°，C=105°，解三角形．【分析】由B与C的度数求出A的度数，利用正弦定理求出b与c的值即可．【解答】解：∵在△ABC中，a=5，B=45°，C=105°，∴A=30°，sinC=sin（45°+60°）=，由正弦定理得：b==5，c==．【点评】此题考查了正弦、余弦定理，两角和与差的正弦函数公式，以及特殊角的三角函数值，熟练掌握定理及公式是解本题的关键．40．（2015秋•邯郸校级月考）在△ABC中，A，B，C所对的边分别为a，b，c 已知，c=1，B=45°，求a，A，C．【分析】利用正弦定理，即可求解．【解答】解：由正弦定理可得，∴sinC=，∵c＜b，∴C＜B，∴C=30°，∴A=′180°﹣45°﹣35°=105°，∴，∴a=．【点评】本题考查正弦定理，考查学生的计算能力，比较基础．。

三角向量15分钟专题训练之三1、若函数()y f x =的图象按向量a 平移后，得到函数(1)2y f x =--的图象，则向量a =（C ）A ．(12)-，B ．(12)，C ．(12)-，D ．(12)-， 2、若π02x <<，则下列命题正确的是（ B ） Ａ．2sin πx x < Ｂ．2sin πx x > Ｃ．3sin πx x < Ｄ．3sin πx x > 3、设，a b 是非零向量，若函数()()()f x x x =+-a b a b 的图象是一条直线，则必有（ ）A ．⊥a bB ．∥a bC ．||||=a bD ．||||≠a b4、在△ABC 中，AB =1,B C =2,B =60°，则AC ＝。

5、已知1sin cos 5θθ+=，且324θππ≤≤，则cos2θ的值是 6.（本小题满分12分）如图，甲船以每小时当甲船位于1A 处时，乙船位于甲船的北偏西105方向的1B 处，此时两船相距20海里，当甲船航行20分钟到达2A 处时，乙船航行到甲船的北偏西120方向的2B 处，此时两船相距答案：CBA 3725- 1A 2A 120 1056、解：如图，连结12A B，22A B =122060A A =⨯=， 122A A B ∆是等边三角形，1121056045B A B ∠=︒-︒=︒， 在121A B B ∆中，由余弦定理得2221211121112222cos 4520220200B B A B A B A B A B =+-⋅︒=+-⨯⨯=，12B B =因此乙船的速度的大小为6020⨯=答：乙船每小时航行海里.。

解三角形： 1、正弦定理变形：A R a sin 2= R aA 2sin =C B A c b a sin :sin :sin ::= 2、余弦定理 变形： 3、△ABC 中,sin A>sin B ⇔ A>B4、△ABC 中，C B A -=+π，求取值范围时转化为函数用消元法（注意变量的取值范围）()()()C B A C B A C B A tan tan ,cos cos ,sin sin -=+-=+=+例：在ABC ∆中，已知C B A <<，B a cos =，A b cos =，C c sin =．（1）求ABC ∆的外接圆半径R 和角C 的值；（2）求c b a ++的取值范围5、判断三角形形状：（1）转化为边（2）转化为角 例：（1）已知B b A a cos cos =,判断三角形形状(等腰或直角三角形) （2）已知A b B a cos cos =,判断三角形形状（等腰三角形）6、△ABC 面积公式：A bc B ac C ab S sin 21sin 21sin 21===例：ABC ∆的三边分别为c b a ,,，面积22)(c b a S --=，则=2tanA____7、构成锐角三角形：构成三角形且最大角为锐角 构成钝角三角形：构成三角形且最大角为钝角 例：（1）锐角ABC ∆中，若1=a ，2=b ，则c 的取值范围是_________（2）已知1+k 、2+k 、3+k 为钝角三角形的三条边，且此三角形的最大角不超过 120，则实数k 的取值范围是8、△ABC 中，若A 为最大角，则018060<≤A ，若A 为最小角，则0600≤<A 9、已知锐角b a A ,,，三角形无解：A b a sin 0<<，一解：A b a sin =或b a ≥ 两解：b a A b <<sin已知钝角b a A ,,，三角形无解：b a ≤<0 一解：b a > 10、A 为锐角222c b a +<，A 为钝角222c b a +>R CB A cb a C B Ac b a C c B b A a 2sin sin sin sin sin sin sin sin sin =----=++++===C ab b a c Bac c a b A bc c b a cos 2cos 2cos 2222222222-+=-+=-+=2ab c b a cosC 2ac b c a cosB 2bcac b cosA222222222-+=-+=-+=11、在ABC ∆中，21sin =A 则030=A 或0150（一般求A cos ） 12、bc c b c b ,,-+与正余弦定理的结合例：ABC ∆中，15,8,2==+=+ac c a B C A ，求b向量知识点：1、a ∥b ⇔a ＝λb (0≠b )⇔x 1y 2－x 2y 1＝02、()()2211,,,y x B y x A 中点公式()y x M ,⎪⎪⎩⎪⎪⎨⎧+=+=.2,22121y y y x xx ()()212212y y x x -+-=()()()332211,,,,,y x C y x B y x A 的重心坐标⎪⎭⎫⎝⎛++++3,3321321y y y x x x G3、a ⊥b ⇔b a ⋅＝0⇔x 1x 2＋y 1y 2＝O （注意反过来时a 与b 为非零向量） 4、θb a =⋅（θ为a 与b 的夹角要共起点，001800≤≤θ）b a =θcos =222221212121y x y x y y x x +⋅++5、A 、B 、C 三点构成三角形：AB 与AC 不共线6、重视共线向量（夹角为0或32π） 例：同一平面上的向量c b a,,321====++b7、a 与b 夹角为锐角：0>⋅b a 且a 与b 不共线。

高中数学三角恒等变换【知识梳理】1．两角和与差的正弦公式：.=±)cos(βα .=±)tan(βα .1tan 1tan x x +=- .1tan 1tan xx-=+ .2．二倍角公式(升幂公式)：=α2sin .=α2cos ＝＝ . =α2tan . 3．倍角公式变形(降幂公式)：=ααcos sin .=α2sin .=α2cos .4．倍角公式变形（半角公式）1cos 2α+= ..1cos 2α-= ..1cos α+= ..1cos α-= .. 1sin 2α±= ..5．半角公式sin2α= .cos2α= .tan2α= ..6．辅助角公式sin cos a x b x += = .sin ϕ=其中 ，cos ϕ= .【典型例题】 考向一：求角问题例1．（1）已知,(0,)αβπ∈且11tan(),tan 27αββ-==-，求2αβ-的值； （2）已知120tancos 222πααβπβα<<<<,=,(-，求 β的值．变式1．【2014江苏】已知5sin 25παπα⎛⎫∈=⎪⎝⎭，，. （1）求sin()4πα+的值；（2）求5cos(2)6πα-的值．▲考向二：求值问题例2．（1）【2015课标】o o o o sin 20cos10cos160sin10=- ．（2）设当x θ=时，函数()sin 2cos f x x x =-取得最大值，则cos θ＝ ． 变式2：（1）【2015江苏】已知tan 2α=-，()1tan 7αβ+=，则tan β的值为 ． （2）【2013课标】设θ为第二象限角，若π1tan 42θ⎛⎫+= ⎪⎝⎭，则sin cos θθ+= ． （3）【2015四川】=+ 75sin 15sin ．考向三：三角恒等变形的综合应用例3 ．【2015广东】在平面直角坐标系中，已知向量，，． （1）若，求tan x 的值； （2）若与的夹角为，求的值．变式3．设向量()()3sin ,sin ,cos,sinx ,0,2a x x b x x π⎡⎤==∈⎢⎥⎣⎦．（1=x 的值；（2）设函数b a x f ⋅=)(，求)(x f 的最大值．例4．在△ABC 中，内角A ，B ，C 的对边分别是a，b ，c ，135=C ，设cos cos A B =， 2cos()cos()cos 5A B ααα++=，求tan α的值．变式4．【2014四川】已知函数()sin(3)4f x x π=+．若α是第二象限角4()cos()cos 2354f απαα=+，求cos sin αα-的值．例5．（1）已知()2tan 5αβ+=，π1tan 44β⎛⎫-= ⎪⎝⎭，求tan α的值； （2）已知α，β均为锐角，且()cos αβ+=，()sin αβ-=，求2β．期末复习专题四成都玉林中学高2020级期末复习 解三角形【知识梳理】1．正弦定理： （其中R 为ABC ∆外接圆的半径）.⇔ （边化角）⇔ （角化边）⇔ （边与角的关系）⇔ （等比性质）用途：⑴ ．⑵ ．2．余弦定理：（1） （2）变形：（角化边）用途：⑴ ．⑵ ． 做题中两个定理经常结合使用. 3．三角形面积公式：ABC S ∆= = = = ．4．三角形内角和定理：在ABC ∆中，有A B C π++=，则sin C = sin 2C⇔= ． 常用结论：（1）在ABC ∆中，①a b >⇔ ⇔ ．②若sin 2sin 2,A B =则 ．特别注意，在三角函数中，sin sin A B A B >⇔>不成立.（2）在△ABC 中，最小内角范围为 ，最大内角范围为 ． （3）若2b a c =+，则角B 的范围为 ． （4）若2b ac =，则角B 的范围为 ． （5）若,,A B C 成等差数列，则B = ．【典型例题】考向一：求解三角形中的角例1．（1）已知ABC ∆满足sin sin 2sin sin a A c C C b B +-=，则角B = ．（2）已知ABC ∆中2222sin ,3c b C a b c bc ==+-，则角C = ．变式1．在ABC ∆满足cos 20cos B a bC c c++=，则角C = ． ▲考向二：求解三角形的边与面积例2．（1）【2015福建】若锐角ABC ∆的面积为103，且5,8AB AC ==，则BC 等于 ．（2）【2014福建】在ABC ∆中，60,4,23A AC BC ===，则ABC ∆的面积等于 ．变式2．（1）【2014课标】在钝角ABC ∆中，3,1,30AB AC B ===，则ABC ∆的面积为 ．（2）【2015天津】在ABC ∆ 中，内角,,A B C 所对的边分别为,,a b c ，已知ABC ∆的面积为315 ，12,cos 4b c A -==-，则a 的值为 ．▲考向三：三角恒等变形在解三角形中的应用例3．已知,,a b c 分别是ABC ∆的三个内角,,A B C 的对边，2cos cos b c Ca A-=. （I ）求角A 的大小；（II ）求函数3sin 6y B C π⎛⎫=+- ⎪⎝⎭的值域．变式3．【2016课标】ABC ∆的内角,,A B C 所对的边分别为,,a b c ，已知2cos (cos cos ).C a B+b A c =（I ）求C ；（II ）若7,c ABC =∆33求ABC 的周长．考向四：向量在解三角形中的应用例4．在锐角ABC ∆中，,,a b c 分别是角,,A B C 的对边，2sin 3sin C A =，7tan 3A =． （I ）求cos ,cosBC 的值； （II ）若227BA BC ⋅=，求b 的值．变式4：【2013四川】在ABC ∆中，角A ，B ，C 的对边分别为a ，b ，c ，且232cos cos sin()sin cos()25A B B A B B A C ---++=-． （I ）求cos A 的值；（II ）若42a =，5b =，求向量BA 在BC 方向上的投影．考向五：正、余弦定理的实际应用例5．【2014湖南】如图5,在平面四边形ABCD 中,1,2,7AD CD AC ===.（I ）求cos CAD ∠的值；（II ）若7cos 14BAD ∠=-,21sin 6CBA ∠=,求BC 的长.变式5．（1）如图所示，为测量山高MN ，选择A 和另一座山的山顶C 为测量观测点．从A 点测得M 点的仰角∠MAN ＝60°，C 点的仰角∠CAB ＝45°，以及∠MAC ＝75°，从C 点测得∠MCA ＝60°.已知山高BC ＝100 m ，则山高MN ＝ m ．（2）【2015湖北】如图所示，一辆汽车在一条水平的公路上向正西行驶，到A 处时测得公路北侧一山顶D 在西偏北30°的方向上，行驶600 m 后到达B 处，测得此山顶在西偏北75°的方向上，仰角为30°，则此山的高度CD ＝ m ．期末复习专题五成都玉林中学高2020级期末复习 平面向量● 10个基本概念 1．向量与数量 2．向量的长度（或模） 3．向量的表示方法 4．零向量与单位向量 5．平行向量（或共线向量） 6．相等向量与相反向量 7．向量的加法与减法：三角形加法法则和平行四边形加法法则、 三角形减法法则.a b ≤+≤ . a b ≤-≤ . 8．向量的数乘：规定：实数λ与向量a 的积是一个向量，这种运算叫做 .记作： ，它的长度和方向规定如下：⑴a λ= .⑵当 时, a λ的方向与a 的方向相同；当时,a λ的方向与a 的方向相反.9．向量的数量积、夹角与投影：已知两个非零向量a 与b ，我们把数量 叫做a 与b 的数量积（或內积），记作： .其中θ是a 与b 的夹角， 叫做向量a 在b 方向上的投影， 叫做向量b 在a 方向上的投影. 注意： ||a b ⋅≤ . 10．基底与向量的坐标表示：a xi y j =+= . ● 两个定理：共线定理和平面向量的基本定理平面向量共线定理：向量()0≠a a 与b 共线，当且仅当有唯一一个实数λ，使 . 平面向量基本定理：如果21,e e 是同一平面内的两个不共线向量，那么对于这一平面内任一向量a ，有且只有一对实数21,λλ，使 .● 4个运算 ：加法、减法、数乘和数量积运算 ● 10个公式：1．已知()()2211,,,y x b y x a ==（1）a b += .（2）a b -= ，（3）a λ= ，（4）//a b ⇔ ⇔ . （5）a b ⊥⇔⇔ .（6）a b ⋅= = .（7）cos ,a b <>== .（8）2a ==⇔a = .2．设()()2211,,,y x B y x A ，则：（9）AB = .3．设()()()332211,,,,,y x C y x B y x A ，（10）.则①线段AB 中点坐标为 .②△ABC 的重心坐标为 .● 向量中一些常用的结论（1）PA PB PB PC PC PA ⋅=⋅=⋅⇔点P 为ABC ∆的 ； （2）0PA PB PC ++=⇔点P 为ABC ∆的 ； （3）向量()(0)||||AC AB AB AC λλ+≠所在直线过ABC ∆的 ；（4） PA PB PC 、、中三终点A B C 、、共线⇔存在实数αβ、使得 且 ； 【典型例题】考向一：平面向量的概念及其线性运算 例1：下列命题正确的是（ ） A ．若a b b c ⋅=⋅，则c a = B ．||||b a b a -=+，则0a b ⋅=C ．若a 与b 是共线向量，b 与c 是共线向量，则a 与c 是共线向量D ．若0a 与0b 是单位向量，则001a b ⋅=跟踪训练1：给出下列结论：①若0,0a a b ≠⋅=，则0b =；②若a b b c ⋅=⋅，则a c =；③()a b c ⋅⋅=()b c a ⋅⋅；④()()a a λμμλ=其中正确的结论有（ ）A ．1B ．2C ．3D ．4 考向二：平面向量的线性运算及其数量积运算（代数）例2：（1）【2015课标】设向量a ，b 不平行，向量a b λ+与2a b +平行，则实数λ=_________． （2）【2015陕西】对任意向量,a b ，下列关系式中不恒成立的是（ ） A ．||||||a b a b ⋅≤ B ．||||||||a b a b -≤-C ．22()||a b a b +=+ D ．22()()a b a b a b +-=-（3）【2015安徽】C ∆AB 是边长为2的等边三角形，已知向量a ，b 满足2a AB =，C 2a b A =+，则下列结论正确的是（ ）A ．1b =B ．a b ⊥C ．1a b ⋅=D ．()4C a b +⊥B（4）【2015课标】设D 为ABC ∆所在平面内一点3BC CD =，则（ ）A ．1433AD AB AC =-+ B ．1433AD AB AC =-C ．4133AD AB AC =+ D ．4133AD AB AC =- 跟踪训练2：（1）【2017山东】已知12,e e12-e 与12λ+e e 的夹角为60，则实数λ的值是 .（2）【2017天津】在ABC △中，60A =︒∠，3AB =，2AC =.若2BD DC =，()AE AC AB λλ∈=-R ，且4AD AE ⋅=-，则λ的值为 .（3）【2014天津，理8】已知菱形ABCD 的边长为2，120BAD ，点,E F 分别在边,BC DC 上，BEBC ，DF DC ．若1AE AF ，23CE CF，则 （ ） A ．12 B ．23 C ．56 D ．712考向三：平面向量的线性运算及其数量及运算（坐标）例3：（1）【2014福建】在下列向量组中，可以把向量()2,3=a 表示出来的是（ ）A ．)2,1(),0,0(21==e eB ．)2,5(),2,1(21-=-=e eC ．)10,6(),5,3(21==e eD ．)3,2(),3,2(21-=-=e e（2）设R y x ∈,，向量)1,(x a =，),1(y b =，)4,2(-=c ，且c a ⊥，c b //，则=+||b a （ ）A ．10B ．5C ．52D ．10跟踪训练3：（1） 【2014重庆】已知向量(,3),(1,4),(2,1)a k b c ===，且(23)a b c -⊥，则实数k =（ ）9.2A -.0B .C 3 D.152（2）【2014四川，理7】平面向量(1,2)a =，(4,2)b =，c ma b =+（m R ∈），且c 与a 的夹角等于c 与b 的夹角，则m =（ ）A ．2-B ．1-C ．1D ．2 （3）【2016课标】已知向量1(,22BA = ，31()22BC = ，则ABC ∠=（ ） A ．30︒ B ．45︒ C ．60︒ D ．120︒考向四：平面向量中坐标法的应用例4：（1）【2014江苏】如图在平行四边形ABCD 中，已知8,5AB AD ==，3,CP PD =2AP BP ⋅=则AB AD ⋅的值是 .AD C BP（2）【2017课标】已知ABC ∆是边长为2的等边三角形，P 为平面ABC 内一点，则()PA PB PC ⋅+的最小是（ ）A ．2-B ．32-C ．43- D ．1-跟踪训练4：（1）【2015北京】在ABC △中，点M ，N 满足2AM MC =，BN NC =．若MN xAB yAC =+，则x =；y = ．（2）【2015四川】设四边形ABCD 为平行四边形，6AB =，4AD =.若点M ，N 满足3BM MC =，2DN NC =，则AM NM ⋅=（ ）A ．20B ．15C ．9D ．6考向五：平面向量与三角函数综合问题例5：已知向量()()()cos ,sin ,cos ,sin ,sin 2sin ,cos 2cos a b x x c x x αααα===++，其中，0x απ<<<．（I ）若4πα=，求函数()f x b c =⋅的最小值及相应x 的值；（II ）若a 与b 的夹角为3π，且a c ⊥，求tan 2α的值．跟踪训练5：【2013江苏】已知a ＝(cos α，sin α)，b ＝(cos β，sin β)，0＜β＜α＜π． （I ）若|a －b |，求证：a ⊥b ； （II ）设c ＝(0,1)，若a b +＝c ，求α，β的值．期末复习专题六成都玉林中学高2020级期末复习 不等式知识点一 “三个二次”之间的关系所谓三个二次，指的是①二次函数图象及与x 轴的交点，②相应的一元二次方程的实根；③一元二次不等式的解集端点． 解决其中任何一个“二次”问题，要善于联想其余两个，并灵活转化． 知识点二 规划问题1．简述规划问题的求解步骤： ． 知识点三 基本不等式1．（非负性）2,a R a ∈ 0；2．（重要不等式）()20a b -≥⇔ ，当且仅当b a =时，等号成立．ab b a b a b a 222222≥≥+=+，当且仅当b a =时，等号成立．3．（均值不等式）当0,0>>b a 时，a b +≥ ⇔ ，当且仅当 时，等号成立．①注意使用均值不等式时要三步走：一正、二定、三相等②在利用均值不等式时要注意方法：（1）拆（2）凑（3）“1”的代换类型一“三个二次”之间的关系例1：设不等式x2－2ax＋a＋2≤0的解集为M，如果M⊆[1,4]，求实数a的取值范围.类型二规划问题例2：某人承揽一项业务，需做文字标牌4个，绘画标牌5个.现有两种规格的原料，甲种规格每张3 m2，可做文字标牌1个，绘画标牌2个；乙种规格每张2 m2，可做文字标牌2个，绘画标牌1个，求两种规格的原料各用多少张才能使得总用料面积最小．类型三利用基本不等式求最值例3：设f(x)＝50xx 2＋1．(1)求f(x)在[0，＋∞)上的最大值；(2)求f(x)在[2，＋∞)上的最大值．例4：某工厂要建造一个长方体无盖贮水池，其容积为4 800 m3，深为3 m，如果池底每1 m2的造价为150元，池壁每1 m2的造价为120元，问怎样设计水池才能使总造价最低？最低总造价是多少？练习：1．若关于x的不等式ax2－6x＋a2<0的解集是(1，m)，则m＝________．2．设x，y都是正数，且1x＋2y＝3，则2x＋y的最小值为________．3．设变量x，y满足约束条件⎩⎪⎨⎪⎧x＋y≤3，x－y≥－1，y≥1，则目标函数z＝4x＋2y的最大值为()A.12B.10C.8D.24．若不等式ax2＋bx－2>0的解集为{x|－2<x<－14}，则a＋b等于()A.－18B.8C.－13D.15．设a>b>0，则a2＋1ab＋1a a－b的最小值是()A.1B.2C.3D.46．已知变量x，y满足⎩⎪⎨⎪⎧x－4y≤－3，3x＋5y≤25，x≥1，则z＝2x＋y的最大值为，最小值．7．已知函数2()(8),f x ax b x a ab=+---不等式()0f x>的解集为{}32.x x-<<（1）求函数()y f x=的解析式．（2）当关于的x的不等式20ax bx c++≤的解集为R时，求c的取值范围．8．已知()()214f x a x x b =--+，若不等式()0f x >的解集是{}|31x x -<<．（1）求实数,a b 的值； （2）解关于x 的不等式()2212036ax c x bc +-->，c R ∈．9．解关于x 的不等式101ax x -<+（a R ∈）．10．已知定义在R 上的函数2()(3)2(1)f x x a x a =--+-(其中a R ∈). （1）解关于x 的不等式()0f x >；（2）若不等式()3f x x ≥-对任意2x >恒成立，求a 的取值范围．11．已知函数()()2,1ax bf x a b x -=∈-R . （1）若关于x 的不等式20ax b ->的解集为1,2⎛⎫+∞ ⎪⎝⎭，求()0f x <解集； （2）若12a =，解不等式()0f x >的解集.12．解不等式(2)1()1a x a x ->∈-R ．。

【引用】培训笔记——三角函数、向量、三角【引用】培训笔记——三角函数、向量、三角恒等变换2011年03月05日近期参加了新教材的培训，聆听了关于三角函数本质的解读，茅塞顿开，收获颇丰，下面是听课笔记，不一定全面，仅供参考。

改变习惯从理解内容开始——以三角函数为例一、强调“函数的角度”，强调刻画周期现象的数学模型。

三角函数与其他学科的练习与结合非常重要。

最重要的是它与振动和波动的联系。

“可以它几乎是全部高科技的基础之一”，这是当前数学教学的薄弱环节。

振动和波动都是周期现象，可以三角函数刻画，比如手机、电视机、网络、核磁共振、航天没有三角函数的不行的。

强化发挥单位圆的作用，强调利用向量方法，淡化三角恒等变形的技巧内容。

高考中恒等变换以前占的比例大，现在占的比例顶多是中下。

三角函数16课时，三角恒等变形8课时，解三角形8课时。

诱导公式2课时，比以前少。

教材编写顺序的变化：和差角独立成章，不是三角函数的核心环节。

解三角形不是任意角三角函数的应用。

任意角三角函数有它自己的应用。

如果要调整，要把向量调整到任意角三角函数之前，而不是调整到后面。

思考：为什么这样变化？三角函数与其他函数的不同点到底在哪里？为什么要强调单位圆的作用？二、强调单位圆作用的理由三角函数的本质。

过去对三角函数本质的理解是不到位的。

三角函数是匀速旋转这个最简单的圆周运动的本质表现。

用数学的模型表达出来就是三角函数。

这与三角函数的起源有关系：匀速旋转运动及其数学研究自古以来就是重大问题，三角学源自天文学。

正弦函数、余弦函数是一对起源于圆周运动、密切配合的周期函数；它们的基本性质则是圆的几何性质（主要是对称性）的直接反应。

——项武义圆有哪些几何性质，代数化以后就是三角函数的性质。

而且核心是对称性。

为什么？因为圆是中心对称图形，而且关于任意一条直径对称。

这是唯一的图形。

把这个对称性表达出来就是三角函数的性质。

你如果不注意单位圆的作用，你落后了。