切线与割线斜率关系的深度探析
- 格式:pdf
- 大小:155.90 KB
- 文档页数:3
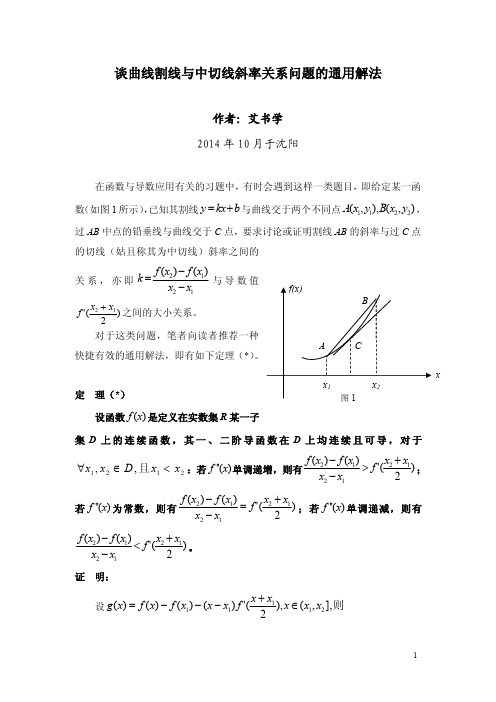


两条切线互相垂直斜率关系在数学领域中,我们经常会遇到两条直线相交的情况。
如果两条直线互相垂直,则它们会在交点处形成一个直角。
那么问题来了,我们如何确定两条切线互相垂直的情况呢?答案就是斜率关系。
什么是斜率?直线的斜率是这条直线在坐标系中形成一个角度,用于衡量直线的倾斜程度。
我们通常用k来表示。
现在我们来看两条切线相交的情况。
假设我们有两条曲线,f(x)和g(x),它们在某处相交。
我们定义点(A, f(A))为曲线f(x)在该点的一个坐标,同理,点(B, g(B))为曲线g(x)在该点的一个坐标。
在这两个点处,我们可以看到两个切线,分别是tang_f和tang_g。
我们需要分别确定这两条切线在交点处的斜率。
首先,我们来看切线tang_f的斜率。
根据微积分的定义,我们可以得出:f'(A) = lim((h->0) ((f(A+h) - f(A)))/h)f'(A)表示曲线f(x)在点A处的切线的斜率,lim表示h趋近于0的极限值。
我们可以将h=0代入方程,这样除数变成了0,但f(A+h) - f(A)不等于0。
所以,我们需要对分子和分母同时除以h。
这样,我们就可以得到:f'(A) = lim((h->0) (f(A+h) - f(A))/h) (*)同样,我们可以计算切线tang_g的斜率。
我们需要使用相同的方法,只不过需要将上式中的f变成g。
g'(B) = lim((h->0) (g(B+h) - g(B))/h)现在,我们来看两个斜率的乘积,即f'(A) * g'(B)。
如果它们相乘等于-1,则两条切线互相垂直。
因此,我们需要将这个等式的两边代入(*)式中,这样可以得到:f'(A) * g'(B) = -1如果你有数学基础,你可以自行证明这个等式成立。
如果你不确定它的正确性,可以自己尝试证明一下。
不难发现,这个等式和勾股定理非常相似,也是用来证明直角三角形的一个重要定理。


导数割线的斜率和切线的关系
关于导数割线的斜率与切线之间的关系,是工业工程的一个重要的概念。
从数学的角度来看,可以概括为:求得函数的唯一切线,其斜率等于该函数的导数。
理解这一关系,首先需要梳理清楚其中的基本概念:函数是由空间两点之间的关系图像表示的,斜率指的是空间中两点之间的对比,也就是定义域变量和值域变量之间的比值(可以理解为两点连线的倾斜程度);导数也是定义域变量与值域变量之间的变化率,它同样可以被用于表示两点之间对比的性质,但是它包含的信息比斜率多,它不仅包含了两点之间的对比性,而且包含了变化的加速度。
通过以上的解释,我们可以看出,斜率和导数之间的联系在于:斜率表体示两点之间的对比,而导数则则表明变化的加速度。
当定义域变量发生变化,函数的唯一切线的斜率便会对应发生变化,即变化率就等于函数的导数,这样一来,函数有唯一切线,其斜率则为该函数的导数。
在实际应用中,理解函数的导数割线与切线之间的关系,是工业工程的一个重要知识。
例如可以用于优化流程的能力,减少能量消耗;也可以将函数的导数割线实验,对新型加工器材等实施改进,从而取得最优化的生产效果。
据此,可以看出,函数的导数割线与切线之间的实质部分,是一种关系:斜率等于该函数的导数。
通过对这种关系的深入理解,可以为工业工程中节能,优化机械改进等应用提供指导意义。

切线方程和法线方程的斜率关系是一个比较经典的数学问题,它可以帮助我们理解曲线的特性,以及如何求解曲线上某一点的切线和法线方程。
首先,我们来看看曲线的切线方程和法线方程的定义。
切线方程是指曲线上某一点的切线方程,它可以用一般式来表示:y=kx+b。
其中k是切线的斜率,b是切点的y坐标。
而法线方程是指曲线上某一点的法线方程,它也可以用一般式来表示:y=m*x+n。
其中m是法线的斜率,n是法点的y坐标。
接下来,我们来看看切线方程和法线方程的斜率之间的关系。
我们知道,曲线上某一点的切线和法线是互相垂直的,因此它们的斜率也是互相垂直的。
这意味着,如果我们知道曲线上某一点的切线斜率,那么它的法线斜率就可以用下面的公式来计算:m=-1/k。
最后,我们来看看如何使用切线方程和法线方程的斜率关系来求解曲线上某一点的切线和法线方程。
首先,我们需要知道曲线上某一点的坐标,然后求出该点的切线斜率。
接着,根据切线斜率和法线斜率之间的关系,可以计算出法线斜率。
最后,根据切线斜率和法线斜率,以及曲线上某一点的坐标,就可以求出该点的切线方程和法线方程了。
总之,切线方程和法线方程的斜率关系是一个比较重要的数学问题,它可以帮助我们更好地理解曲线的特性,以及如何求解曲线上某一点的切线和法线方程。
斜率切线知识点斜率和切线是数学中的重要概念,特别在微积分中经常被使用。
在本文中,我们将逐步解释斜率和切线的概念以及它们在数学中的应用。
1.斜率的概念斜率是描述函数曲线的变化率的一个重要指标。
通常用字母m表示斜率。
对于一条直线来说,斜率表示该直线上任意两点之间的纵坐标变化量与横坐标变化量之比。
对于一条曲线来说,斜率表示曲线上某一点处的切线斜率。
2.切线的概念切线是曲线上某一点处与该点处曲线相切的直线。
切线与曲线在该点处有相同的斜率。
切线可以帮助我们研究曲线在某一点的性质,比如判断曲线是否上升或下降,以及在该点处的曲率等。
3.斜率和切线的计算对于一条直线来说,我们可以通过两点坐标来计算斜率。
假设直线上两点的坐标分别为(x1, y1)和(x2, y2),则斜率可以通过以下公式计算:m = (y2 - y1) / (x2 - x1)。
对于一条曲线来说,我们可以通过求导来计算曲线在某一点处的切线斜率。
假设曲线的方程为y = f(x),则切线斜率可以通过求f(x)的导数f’(x)来计算。
在某一点处,切线的方程可以表示为y - f(x0) = f’(x0)(x - x0),其中(x0, f(x0))是曲线上的某一点。
4.斜率和切线的应用斜率和切线在数学中的应用非常广泛。
它们可以帮助我们研究曲线的性质,比如凸性、拐点等。
此外,斜率和切线还可以用于求解最值问题,比如确定曲线上某一点处的最大值或最小值。
在物理学中,斜率和切线可以帮助我们研究物体的运动。
例如,通过计算物体的速度-时间图像的斜率,我们可以确定物体的加速度。
同样,通过计算位移-时间图像的斜率,我们可以确定物体的速度。
在经济学中,斜率和切线可以用于分析供需曲线。
供需曲线的交点处表示市场的均衡价格和数量。
通过计算供需曲线在交点处的斜率,我们可以了解价格和数量的变化关系。
总结起来,斜率和切线是数学中重要的概念,在微积分和其他领域中有着广泛的应用。
通过理解斜率和切线的概念以及计算方法,我们可以更好地理解曲线的性质,并在实际问题中应用这些知识点进行分析和求解。
两线相切斜率关系一、引言两线相切是初中数学中的一个重要概念,它在高中数学和大学数学中也有广泛的应用。
本文将从斜率的角度出发,探讨两线相切时斜率的关系。
二、什么是斜率?斜率是指直线在平面直角坐标系中与$x$轴正向夹角的正切值,也就是直线上任意两点纵坐标之差与横坐标之差的比值。
如果直线过点$(x_1,y_1)$和$(x_2,y_2)$,则它的斜率$k$可以表示为:$$k=\frac{y_2-y_1}{x_2-x_1}$$三、两条直线相交时斜率的关系当两条不平行直线相交时,它们一定有一个交点。
在交点处,这两条直线的斜率不同。
为了证明这个结论,我们可以采用反证法。
假设有两条不平行直线$L_1$和$L_2$,它们有一个公共点$(x,y)$且在该点处有相同的斜率$k$。
那么对于任意一点$(x+\Delta x,y+\Delta y)$(其中$\Delta x\neq0,\Delta y\neq0$),我们都可以得到:$$k=\frac{y+\Delta y-y}{x+\Delta x-x}=\frac{\Delta y}{\Delta x}$$即两条直线在该点处的斜率相同。
这意味着,$L_1$和$L_2$在该点处是平行的,与它们相交的假设矛盾。
因此,我们得出结论:两条不平行直线在交点处的斜率不同。
四、两条直线平行时斜率的关系当两条直线平行时,它们没有交点,也就是说它们在任何一点处的斜率都相同。
为了证明这个结论,我们可以采用反证法。
假设有两条平行直线$L_1$和$L_2$,它们在某一点$(x,y)$处有不同的斜率$k_1$和$k_2$。
那么对于任意一点$(x+\Delta x,y+\Deltay)$(其中$\Delta x\neq0,\Delta y\neq0$),我们都可以得到:$$k_1=\frac{y+\Delta y-y}{x+\Delta x-x}=\frac{\Delta y}{\Delta x}\quad k_2=\frac{y+\Delta y-y}{x+\Delta x-x}=\frac{\Deltay}{\Delta x}$$即两条直线在该点处的斜率相同。
切线与割线斜率关系的深度探析1.问题提出文【1】得出了如下的结论:设()y f x =是定义在(,)a b 上的可导函数,曲线:()C y f x =上任意两个不同点的连线(称为割线)斜率的取值区间为P ,曲线C 上任意一点处的切线斜率的取值范围为Q ,则P Q ⊆,而且Q 中元素比P 中元素至多多了区间P 的端点值. 并指出,求解1212()()f x f x x x -∨-的恒成立问题,可将1212()()f x f x x x --转化为()f x ',用导数法求解.设用导数法求得参数取值区间为D ,然后再检验区间D 的端点值是否符合题意. 例如,已知21()2ln (0)f x x x x xλ=++>,对于任意两个不等的正数12,x x ,恒有1212()()f x f x x x ''->-,求λ的取值范围(四川2006高考题变式). 【解】设21()()4g x f x x x x λ'==-+,322()4g x x xλ'=+-,依条件1212()()1g x g x x x ->-,由()1g x '>得32241x x λ+->,以1x 替换x ,则有32241x x λ-+>对任意0x >恒成立.①当0λ≤时,显然成立;②当0λ>时,令32()24(0)h x x x x λ=-+>,2()62h x x x λ'=-,令()03h x x λ'=⇒=.min ()()4327h x h λλ∴==-+. 若min ()0h x ≤,则m in ()0h x =,此时32241x xλ-+>对任意0x >不能恒成立,故必有min ()0h x >,此时3min min ()()427h x h x λ==-+,依条件有33412704027λλλ⎧-+>⎪⎪⇒<<⎨⎪-+>⎪⎩. 综上得λ<.下面检验端点λ=是否符合题意.当λ=时,1212()()f x f x x x ''->-12221241x x x x +⇔+>1212123x x x x x x +⇔+>或1212125x x x x x x ++<. 由于1212121212333x x x x x x x x x x ++>=≥(当12x x =时取等号),故λ=符合题意,因而λ=反思上述解法,总感到美中不足.因为在检验λ=验过程不轻松,且不容易想到.那么是否有一种融解答与检验为一体的导数解法呢?要回答这个问题,关键得弄清如下实质问题:何时曲线的割线斜率取值范围等于切线斜率的取值范围,即P Q =?何时P Q Ø,且Q 比P 多了区间P 的端点值?这些端点值究竟是何值?曲线上与这些端点值对应点的位置在哪里?2.结论构建定理 设()y f x =是定义在连通开区间()I I R ⊆上的二阶可导函数,其对应曲线C 上任意两点的连线斜率的取值集合为P ,曲线C 上任意一点处的切线斜率取值集合为Q ,则(1)P Q ⊆;(2)当曲线C 不存在拐点时,P Q =;(3)P Q ⇔Ø曲线上存在这样的拐点,使得平行于该拐点处切线的任意直线与曲线C 至多有一个交点;(4)在(3)的前提下,设所有这样的拐点处的切线斜率组成的集合为S ,则Q P S =ð. 引理1 函数()y f x =在(,)a b 内二阶可导,则曲线()y f x =在(,)a b 内上凸(或下凸)的(,)x a b ⇔∀∈,()0f x ''≤(或0≥),且在(,)a b 的任何子区间上()f x ''不恒为0.引理2 曲线的向上凸与向下凸部分的分界点称为该曲线的拐点.若()y f x =在一个连通开区间I 上二阶可导,则00(,())x f x 为曲线()y f x =拐点的必要条件是0()0f x ''=.下面给出定理的证明.(1)12,x x I ∀∈,设12x x <,由于()f x 在[]12,x x 上连续,在12(,)x x 内可导,由拉格朗日中值定理可得,在开区间(,)a b 内至少存在一点ξ,使1212()()()f x f x f x x ξ-'=-,故P Q ⊆. (2) 由于曲线C 不存在拐点,故曲线C 的凸性确定.不妨设下凸.设l 是曲线C 的任意一条切线,则C 必在l 的上方,将l 向上平移很小一段距离至直线m ,则m 必与C 交于两个不同的点,E F ,割线EF 的斜率等于l 的斜率,故Q P ⊆,但由(1)知P Q ⊆,故P Q =.(3)一方面,因曲线C 存在这样的拐点,使平行于该拐点处切线的任意直线与C 至多有一个交点,故曲线C 上任意两点的连线斜率都不等于该拐点处切线的斜率,P Q ∴Ø,充分性得证.另一方面,由于P Q Ø,故k Q ∃∈,但k P ∉,令曲线在点00(,())x f x 处的切线为l ,其斜率为k ,若00(,())x f x 不是拐点,则必存在开区间0I I ⊆,使 得00x I ∈,且曲线在0I 上凸性确定.由(2)的证明知,曲线在0I 上必存在某两点的割线斜率等于k ,故k P ∈与k P ∉矛盾,故00(,())x f x 一定是拐点,又k P ∉,故曲线C 不存在与l 平行的割线,也即平行于拐点00(,())x f x 处切线的任意直线与曲线至多有一个交点.必要性得证.(4)由(3) 的证明易知结论成立.由定理知,对于二阶可导曲线:()C y f x =,有①当且仅当曲线C 不存在拐点,或对曲线C 的每一个拐点,都存在平行于该拐点处切EF l E m线的直线与曲线C 至少有两个交点时,P Q =.②可导曲线C 的切线斜率的取值区间Q 至多比割线斜率的取值区间P 多了区间P 的端点值.这些端点值就是定理结论(3)条件中的拐点处切线的斜率.对于只有一个拐点的二阶可导函数,有如下的推论 当曲线C 只有一个拐点A 00(,())x f x 时,必有P Q Ø,而且{}0()Q P f x '=ð.证明:根据定理结论(3),只需要证明斜率为0()k f x '=的任意直线与曲线C 至多有一个交点即可.设斜率为0()k f x '=的任意一条直线为()g x kx b =+.考察方程()()0f x g x -=在I 上解的个数.令()()()()h x f x g x f x kx b =-=--,0()()()()h x f x k f x f x ''''=-=-.因为曲线C 只有一个拐点00(,())A x f x ,故在拐点的两侧曲线C 的凸性相反.不妨设左侧上凸,右侧下凸.则当0x x <时,()0f x ''<,故()f x ' ,0()()()0h x f x f x '''=->;当0x x >时,()0f x ''>,故()f x ' ,0()()()0h x f x f x '''=->.故()h x 在I 上 ,故()()0f x g x -=至多有一解,即直线()g x kx b =+与曲线C 的交点至多一个,根据定理(3)(4)推论得证.定理及推论反映了曲线切线斜率与割线斜率之间的具体关系,为借助切线斜率求解割线斜率范围问题提供了一种新方法.【例】已知曲线2:3()x x C y e e x R =-∈任意不同两点的连线斜率为k ,求k 的取值范围. 解 22399232()488xx x y e e e '=-=--≥-,又243(43)x x x x y e e e e ''=-=-. 当3ln 4x <时0y ''<,曲线上凸;当3ln 4x >时0y ''>,曲线下凸,故曲线在3ln 4x =处是一个拐点,而3498x y ='=-,根据推论,k 的取值范围为9(,)8-+∞. 曹军,《中学数学杂志》2010年11月.【附】文【1】主要结论1212()()f x f x x x -∨-定理 设()y f x =在(,)a b 内可导,连结其图象上任意两点,A B 的割线斜率为AB k ,图象上任意一点处的切线斜率为k ,则(1) 若k m >,则AB k m >;若k m ≥,则AB k m >或AB k m ≥.(2)若AB k m >,则k m >或k m ≥;若AB k m ≥,则k m ≥.证明:设11(,())A x f x ,22(,())B x f x 是曲线()y f x =图象上任意不同的两点.(1)不妨设12x x <,由拉格朗日中值定理可知,在12(,)x x 内至少存在一点ξ,使1212()()()f x f x f x x ξ-'=-. 由于k m >,故()f m ξ'>,故AB k m >.其余类似.(2)设21(0)x x x x =+∆∆≠,211121()()()()AB f x f x f x x f x k m x x x-+∆-==>-∆,则1100()()lim lim x x f x x f x m m x ∆→∆→+∆-≥=∆,即()f x m '≥.其余类似. A。