6 函数图象的割线斜率与切线斜率的关系

直线的斜率斜率一般以 m 表示，定義為 y 的改變除以 x 對應的改變，即 m 是改變的比例。

對於直角坐標系，若橫軸為 x 軸，縱軸是 y 軸，m 通常寫成：（表示變數的改變）。

和是直線上任意兩點的座標。

不論使用直線上哪兩點，其得出來的斜率都是一樣的。

切线设L为一条曲线，A,B为此曲线上的点，过此二点作曲线的割线，令B趋向A，如果割线的极限存在，则称此极限（一条直线）为曲线在A的切线。

圆的切线同一平面，与一个圆只有一个交点的直线，叫此圆的切线。

与半径互相垂直, 弦切角与交错弓形内角相等曲线相切处斜率相等，即导数相等。

例子：设曲线y=ax^(2)+bx+c在x=-1处取得极值,且与曲线f(x)=3x^2相切与点(1,3),试确定常数a,b,c用导数做y'=2ax+b因为在x=-1处取得极值，所以-2a+b=0, b=2a因为相切于点（1，3），所以3=a+b+c=3a+c, c=3-3a并且在点（1，3）处两曲线切线的斜率相等f'(x)=6x, f'(1)=6=2a+b=4a, a=3/2所以b=3，c=-3/2曲线斜率导数即表示函数在某一点的切线的斜率。

例如f(x)=x^2，在x=4时，f'(x)=8，在x=0时，f'(x)=0，所以在x=0时，f(x)=x^2的切线可看作与x轴平行。

研究某一函数的导数很重要，因为它的几何意义是该函数曲线在这一点上的切线斜率，而斜率直接关系到在某一个区间函数的增减性。

当对于任意x∈（a，b)都有f'(x)>0时，函数f(x)在（a，b）是增函数。

当对于任意x∈（a，b)都有f'(x)<0时，函数f(x)在（a，b）是减函数。

割线曲线的割线是指与它有2个公共点的直线.当这两个点不断靠近，并重合为一个点时，这条直线就变成了这条曲线的切线。

割线与正割函数的关系在原点处建立单位圆，在P(1,0)处画单位圆的切线。

函数图像的“切线斜率”的理解及在高中物理解题中的应用切线斜率即为图形在垂直方向变化量与水平方向变化量上的比值，这和数学概念当中的斜率存在一定的差异性。

此斜率并非倾角正切值。

在这一方面往往理解起来较为困难，由于过程相同，出于不同时刻的物理量便是明确的，但是每个人所画出的图像却不尽相同，相应的斜率也便有所不同。

因此就加强对函数图像中“切线斜率”的理解将具有十分重要的作用与价值，可在进行物理习题的解答时能够更好的应用“切线斜率”这一解题方法，提高对解题技巧的有效掌握。

一、理解函数图像“切线斜率”的意义要想促使学生能够对于函数图像当中某一切线位置的斜率做出准确的理解，首先便要能够理解函数的增量改变、平均变化率、变化率，同时还能够由函数的增量改变到函数平均变化率，直至函数在某一具体位置的变化率动态改变过程予以准确的理解，这些将会促进学生加强对于物理概念及规律的理解，并促使学生能够更加有效的解决物理难题，这将对于提升学生的解题技巧，促进物理学习效率的提升将具有极其重要的作用与价值。

二、物理图像“切线斜率”的物理意义三、无理函数图像“切线斜率”的具体应用在物理函数图像当中运用“切线斜率”之时，应先明确物理量会因为哪一个量的改变而产生出相应的函数图像，进而基于相应的物理量改变再进一步发展到平均变化率之时最终到达某一点的变化率予以动态化的了解，同时根据已经掌握的相关物理学概念、规律等内容来就其中所蕴含的内涵意义做到准确的理解。

依据图像“切线斜率”所具备的物理学概念内涵和切线斜率的改变规律来尽快获得相应的函数变化规律。

例题1，在某一空间当中其静电场电力势能？于x轴当中的分布情况如下图1所示，其中x轴于BC两点电场的强度于x位置上的分量依次为EBx与ECx，在以下选项当中正确的选项是（）A EBx的电场强度势能>ECxB EBx的分量方向为x轴正方向C O?c位置所存在的电荷强度在x轴方向当中的分量最大D x当中的负电荷在由B转移到C之时，电场力先做正功，后做负功。

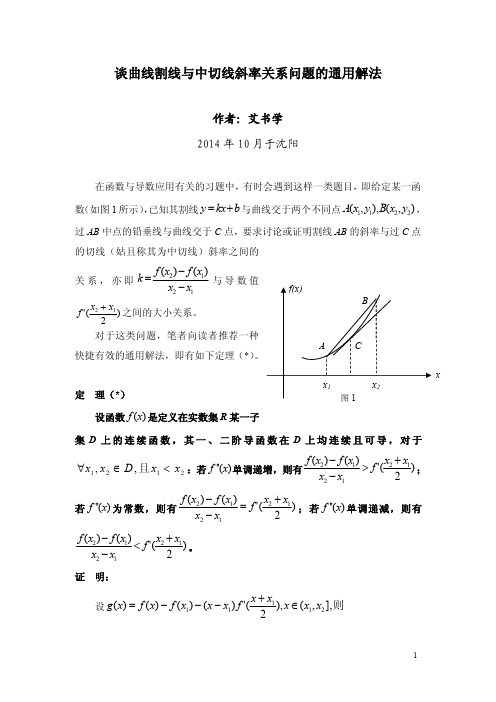
函数切线的知识点总结1. 切线的概念在数学中，给定曲线上一点P，通过这一点能够作出唯一的直线L，它与曲线相交于此点，并且在此点处与曲线的切线相切，这样的直线L称为曲线的切线，点P叫做切点。

任何一条曲线，在它的每一点上都存在切线。

2. 切线的定义设曲线L是可导的，点P(a,f(a))在L上，若直线L通过点P，且曲线L和直线L在点P处的切线重合，则直线L称为曲线L在点P处的切线。

3. 曲线的切线方程对于曲线y=f(x)，在点P(x0,y0)处的切线方程可以表示为：y - y0 = f'(x0)(x - x0)其中f'(x0)表示函数f(x)在x0处的导数。

4. 切线的斜率切线的斜率就是曲线在某一点的导数值，即切线的斜率等于曲线在该点处的导数值。

5. 切线的求解为了求得曲线在某一点的切线方程，我们需要进行以下步骤：a. 求出点(x0,y0)的横坐标和纵坐标；b. 求出函数f(x)在点x0处的导数f'(x0)；c. 将这些信息带入切线方程y - y0 = f'(x0)(x - x0)中，即可得到曲线在点(x0,y0)处的切线方程。

6. 切线的图像曲线的切线可以通过函数图像来形象地描述，当我们观察曲线上不同点处的切线时，可以得到这些切线的整体情况。

通过图像，我们可以看到切线在曲线上的变化情况，以及曲线在不同点处的斜率和变化趋势。

7. 切线的应用函数的切线在数学中有诸多应用，例如在微积分中的微分、函数极值点的判断、曲线的切线综合问题等。

在工程、物理、经济等领域，函数的切线也有广泛的应用，例如在物理中的速度、加速度的研究，经济学中的边际利润等。

8. 切线的性质曲线上任意一点的切线斜率恒等于函数在该点的导数。

通过切线方程可以得到曲线在某点处的局部变化情况，比如曲线在该点处的导数值、函数值等。

9. 切线和割线在数学中，除了切线外，还有一个相关的概念叫做割线。

割线是曲线上的两点A、B之间的直线，而切线则是曲线上的一点。

高考数学斜率知识点斜率是数学中一个重要的概念，它描述了函数曲线的变化率。

在高考数学中，斜率是一个常见的考点，掌握斜率的相关知识对解题非常有帮助。

本文将详细介绍高考数学中与斜率相关的知识点。

一、斜率的定义斜率描述了函数曲线在某一点的切线斜率，它表示函数的变化速率。

对于直线函数，斜率可以直接通过斜率公式计算得出；对于曲线函数，斜率可以通过求导函数得到。

以下是斜率的计算公式：1. 直线函数的斜率对于直线函数y = kx + b, 其中k为斜率。

斜率的计算公式为：k =(y₂ - y₁) / (x₂ - x₁)，其中(x₁, y₁)和(x₂, y₂)为直线上的两个点。

2. 曲线函数的斜率对于曲线函数y = f(x)，其斜率可以通过求导得到。

求导函数f'(x)表示了曲线在每个点的切线斜率。

二、斜率的性质了解斜率的性质对于高考数学题目的解答非常重要。

下面介绍几个斜率的性质：1. 斜率为正、负和零的含义当斜率大于0时，表示函数呈现递增趋势；当斜率小于0时，表示函数呈现递减趋势；当斜率等于0时，表示函数的值保持不变。

2. 平行线和垂线的斜率关系两条平行线的斜率相等；两条垂直线的斜率乘积为-1。

3. 斜率与角度的关系斜率为k的直线与x轴的夹角为θ，其中tanθ = k。

三、斜率在解题中的应用掌握斜率的应用方法对于高考数学题目的解答非常重要。

以下是一些常见的斜率应用：1. 判断直线的趋势通过计算斜率，可以判断直线是递增还是递减，也可以判断直线的陡峭程度。

2. 求平行线和垂线已知一条直线的斜率，可以通过斜率的性质求得与它平行或垂直的直线的斜率。

3. 求函数的切线已知曲线函数的斜率，可以通过斜率的定义求得函数曲线在某一点的切线方程。

4. 解决最优化问题最优化问题中经常需要求解某个函数的最大值或最小值，这可以通过斜率为0的点来实现。

四、总结斜率作为高考数学中的重要概念，对于解题非常有帮助。

本文详细介绍了斜率的定义、性质和应用，希望可以帮助到同学们在高考数学中顺利解题。

曲线切线的斜率怎么求
切线斜率等于切点所在的函数在切点处的导数（切线斜率必须存在）。

比如：点P(Xo，yo)在曲线y=f(x)上，f`(x)为函数y=f(x)导函数，k为过点P的切线的斜率，则k=f`(Xo)。

扩展资料
法线斜率和切线斜率的关系
法线斜率与切线斜率乘积为-1，即若法线斜率和切线斜率分别用α、β表示，则必有α*β=-1。

法线可以用一元一次方程来表示，即法线方程。

与导数有直接的转换关系。

用导数表示曲线y=f(x)在点M（x0,y0）处的切线方程为：y-f(x0)=f'(x0)(x-x0) 法线方程为：y-f(x0)=(-1/f'(x0))*(x-x0)。

通过方程求解可以免去逆向思考的`不易，直接正向列出含有欲求解的量的等式即可。

方程具有多种形式，如一元一次方程、二元一次方程、一元二次方程等等，还可组成方程组求解多个未知数。

方程一定是等式，但是等式可以有其他的，比如上面举的1+1=2，100×100=10000，都是等式，显然等式的范围大一点。

5.1.1变化率问题教学设计一、课时教学内容1. 通过求高台跳水运动员在具体时刻的瞬时速度，体会求瞬时速度的一般方法.2.通过求曲线处某点处切线斜率的过程，体会求切线斜率的一般方法.3.理解函数的平均变化率，瞬时变化率的概念．二、课时教学目标1.体会由平均速度过渡到瞬时速度的过程，理解平均速度、瞬时速度的区别和联系.2.掌握瞬时速度的概念，会求解瞬时速度的相关问题.3.掌握割线与切线的定义，会求其斜率.三、教学重点、难点1、教学重点瞬时速度的概念、割线与切线的定义及斜率求法.2、教学难点割线与切线的斜率.四、教学过程设计环节一创设情境，引入课题为了描述现实世界中的运动、变化现象，在数学中引入了函数．刻画静态现象的数与刻画动态现象的函数都是数学中非常重要的概念．在对函数的深入研究中，数学家创立了微积分，这是具有划时代意义的伟大创造，被誉为数学史上的里程碑．微积分的创立与处理四类科学问题直接相关．一是已知物体运动的路程作为时间的函数，求物体在任意时刻的速度与加速度，反之，已知物体的加速度作为时间的函数，求速度与路程；二是求曲线的切线；三是求函数的最大值与最小值；四是求长度、面积、体积和重心等，历史上科学家们对这些问题的兴趣和研究经久不衰，终于在17世纪中叶，牛顿和莱布尼茨在前人探索与研究的基础上，凭着他们敏锐的直觉和丰富的想象力，各自独立地创立了微积分．导数是微积分的核心内容之一，是现代数学的基本概念，蕴含着微积分的基本思想；导数定量地刻画了函数的局部变化，是研究函数增减、变化快慢、最大(小)值等性质的基本方法，因而也是解决诸如增长率、膨胀率、效率、密度、速度、加速度等实际问题的基本工具．在本章，我们将通过丰富的实际背景和具体实例，学习导数的概念和导数的基本运算，体会导数的内涵与思想，感悟极限的思想．通过具体实例感受导数在研究函数和解决实际问题中的作用，体会导数的意义．5.1导数的概念及其意义在必修第一册中，我们研究了函数的单调性，并利用函数单调性等知识定性地研究了一次函数、指数函数、对数函数增长速度的差异，知道“对数增长”是越来越慢的，“指数函数”比“直线上升”快得多．进一步地，能否精确定量地刻画变化速度的快慢呢？下面我们就来研究这个问题．5.1.1变化率问题问题1高台跳水运动员的速度探究:在一次高台跳水运动中，某运动员在运动过程中的重心相对于水面的高度h （单位：m ）与起跳后的时间t （单位：s ）存在函数关系2() 4.9 4.811h t t t =-++．如何描述运动员从起跳到入水的过程中运动的快慢程度呢？直觉告诉我们，运动员从起跳到入水的过程中，在上升阶段运动得越来越慢，在下降阶段运动得越来越快．我们可以把整个运动时间段分成许多小段，用运动员在每段时间内的平均速度v 近似地描述他的运动状态． 例如，在00.5t ≤≤这段时间里，(0.5)(0)2.35(m /s)0.50h h v -==-；在12t ≤≤这段时间里，(2)(1)9.9(m /s)21h h v -==--一般地，在12t t t ≤≤这段时间里，211221()()4.9() 4.8h t h t v t t t t -==-++-．环节二 观察分析，感知概念 思考:计算运动员在48049t ≤≤这段时间里的平均速度，你发现了什么？ 你认为用平均速度描述运动员的运动状态有什么问题吗？ 我们发现，运动员在049t ≤≤这段时间里的平均速度为0．显然，在这段时间内，运动员并不处于静止状态．因此，用平均速度不能准确反映运动员在这一时间段里的运动状态． 为了精确刻画运动员的运动状态，需要引入瞬时速度的概念．我们把物体在某一时刻的速度称为瞬时速度（instantaneous velocity ）．探究:瞬时速度与平均速度有什么关系？你能利用这种关系求运动员在1s t =s 时的瞬时速度吗？设运动员在0t 时刻附近某一时间段内的平均速度是v ，可以想象，如果不断缩短这一时间段的长度，那么v 将越来越趋近于运动员在0t 时刻的瞬时速度． 用运动变化的观点研究问题是微积分的重要思想．为了求运动员在1t =时的瞬时速度，我们在1t =之后或之前，任意取一个时刻1t +∆，t ∆是时间改变量，可以是正值，也可以是负值，但不为0．当0t ∆>时，1t +∆在1之后，当0t ∆<时，1t +∆在1之前．当0t ∆>时，把运动员在时间段[1,1]t +∆内近似看成做匀速直线运动，计算时间段[1,1]t +∆内的平均速度v ，用平均速度v 近似表示运动员在1t =时的瞬时速度．当0t ∆<时，在时间段[1,1]t +∆内可作类似处理．为了提高近似表示的精确度，我们不断缩短时间间隔，得到如下表格（表5.1-1）．表5.1-1当0t ∆<时，在时间段[1,1]t +∆内当0t ∆>时，在时间段[1,1]t +∆内t ∆2(1)(1)1(1)4.9()5 4.95h h t v t t tt t-+∆=-+∆∆+∆==-∆--∆t ∆2(1)(1)(1)14.9()5 4.95h t h v t t tt t+∆-=+∆--∆-∆==-∆-∆－0.01 －4.951 0.01 －5.049 －0.001 －4.9951 0.001 －5.0049 －0.0001 －4.99951 0.0001 －5.00049 －0.00001 －4.999951 0.00001 －5.000049 －0.000001－4.9999951 0.000001－5.0000049……观察:给出t ∆更多的值，利用计算工具计算对应的平均速度v 的值．当t ∆无限趋近于0时，平均速度v 有什么变化趋势？1时，平均速度v 都无限趋近于5-．事实上，由(1)(1)4.95(1)1h t h v t t +∆-==-∆-+∆-可以发现，当t ∆无限趋近于0时， 4.9t -∆也无限趋近于0，所以v 无限趋近于5-．这与前面得到的结论一致．数学中，我们把5-叫做“当t ∆无限趋近于0时，(1)(1)h t h v t+∆-=∆的极限”，记为0(1)(1)lim5t h t h t ∆→+∆-=-∆．从物理的角度看，当时间间隔t ∆无限趋近于0时，平均速度v 就无限趋近于1t =时的瞬时速度．因此，运动员在1s t =时的瞬时速度(1)5m /s v =-． 思考:（1）求运动员在2s t =时的瞬时速度；（2）如何求运动员从起跳到入水过程中在某一时刻0t 的瞬时速度？ 解：（1）运动员在2s t =时的瞬时速度2200(2)(2)[ 4.9(2) 4.8()11][ 4.92 4.8211](2)lim lim (2)2t t h t h t t t v t t ∆→∆→+∆--+∆++∆+--⨯+⨯+==+∆-∆lim( 4.914.8)14.8t t ∆→=-∆+=．（2）运动员从起跳到入水过程中在某一时刻0t 的瞬时速度2200000000000()()[ 4.9() 4.8()11][ 4.9 4.811]()lim lim()t t h t t h t t t t t t t v t t t t t∆→∆→+∆--+∆++∆+--++==+∆-∆000lim( 4.99.8 4.8)9.8 4.8t t t t ∆→=-∆-+=-+．1．求问题1中高台跳水运动员在0.5s t =时的瞬时速度．1．【解析】22(0.5)(0.5)[ 4.9(0.5) 4.8(0.5)11]( 4.90.5 4.80.511)h t h t t +∆-=-+∆++∆+--⨯+⨯+24.9()0.1t t =-∆-∆，所以，00(0.5)(0.5)(0.5)limlim(0.1 4.9)0.1(m /s)t t h t h v t t∆→∆→+∆-==--∆=-∆．所以，高台跳水运动员在0.5s t =时的瞬时速度为0.1m /s -． 2．火箭发射s t 后，其高度（单位：m ）为2()0.9h t t =，求： （1）在12t ≤≤这段时间里，火箭爬高的平均速度； （2）发射后第10s 时，火箭爬高的瞬时速度． 2．【解析】（1）因为22(2)(1)0.920.91 2.7(m /s)21h h v -==⨯-⨯=-，所以在12t ≤≤这段时间里，火箭爬高的平均速度为2.7m /s ；（2）因为222000(10)(10)0.9(10)0.9100.9()18lim lim lim (10)10t t t h t h t t t t t t ∆→∆→∆→+∆-⨯+∆-⨯∆+∆==+∆-∆∆ 0lim(0.11898)t t ∆→=∆+=．所以发射后第10s 时，火箭爬高的瞬时速度18m /s ．3．一个小球从5 m 的高处自由下落，其位移y （单位：m ）与时间t （单位：s ）之间的关系为2() 4.9y t t =-．求1s t =时小球的瞬时速度．3．【解析】由题意知：222000()() 4.9() 4.99.8 4.9()lim lim limt t t y t t y t t t t t t t t t t∆→∆→∆→+∆--+∆+-⋅∆-∆==∆∆∆ 0lim(9.8 4.9)9.8t t t t ∆→=--∆=-，当1s t =时，小球的瞬时速度为s 9.8m /-．环节四 辨析理解，深化概念 问题2抛物线的切线的斜率我们知道，如果一条直线与一个圆只有一个公共点，那么这条直线与这个圆相切．对于一般的曲线C ，如何定义它的切线呢？下面我们以抛物线2()f x x =为例进行研究． 探究：你认为应该如何定义抛物线2()f x x =在点0(1,1)P 处的切线？与研究瞬时速度类似，为了研究抛物线2()f x x =在点0(1,1)P 处的切线，我们通常在点0(1,1)P 的附近任取一点2(,)P x x ，考察抛物线2()f x x =的割线0P P 的变化情况．观察：如图5.1-1，当点2(,)P x x 沿着抛物线2()f x x =趋近于点0(1,1)P 时，割线0P P 有什么变化趋势？我们发现，当点P 无限趋近于点0P 时，割线0P P 无限趋近于一个确定的位置，这个确定位置的直线0P T 称为抛物线2()f x x =在点0(1,1)P 处的切线． 环节五 概念应用，巩固内化探究我们知道，斜率是确定直线的一个要素．如何求抛物线2()f x x =在点0(1,1)P 处的切线0P T 的斜率0k 呢？从上述切线的定义可见，抛物线2()f x x =在点0(1,1)P 处的切线0P T 的斜率与割线0P P 的斜率有内在联系．记1x x ∆=-①，则点P 的坐标是2(1,(1))x x +∆+∆．于是，割线0P P 的斜率2()(1)(1)121(1)1f x f x k x x x -+∆-===∆+-+∆-．①x ∆可以是正值，也可以是负值，但不为0．我们可以用割线0P P 的斜率k 近似地表示切线0P T 的斜率0k ，并且可以通过不断缩短横坐标间隔x ∆来提高近似表示的精确度，得到如下表格（表5.1-2）．表5.1-20x ∆< 0x ∆>x ∆ 2k x =∆+ x ∆ 2k x =∆+ －0.01 1.99 0.01 2.01 －0.001 1.999 0.001 2.001 －0.00011.99990.00012.0001OxyP 0PT2()f x x =－0.00001 1.99999 0.00001 2.00001 －0.0000011.9999990.0000012.000001……观察：利用计算工具计算更多割线0P P 的斜率k 的值，当x ∆无限趋近于0时，割线0P P 的斜率k 有什么变化趋势？近于1时，割线0P P 的斜率k 都无限趋近于2．事实上，由(1)(1)2f x f k x x+∆-==∆+∆可以直接看出，当x ∆无限趋近于0时，2x ∆+无限趋近于2．我们把2叫做“当x ∆无限趋近于0时，(1)(1)f x f k x+∆-=∆的极限”，记为(1)(1)lim2x f x f x∆→+∆-=∆．从几何图形上看，当横坐标间隔x ∆无限变小时，点P 无限趋近于点0P ，于是割线0P P 无限趋近于点0P 处的切线0P T ．这时，割线0P P 的斜率k 无限趋近于点0P 处的切线0P T 的斜率0k ．因此，切线0P T 的斜率02k =．思考：观察问题1中的函数2() 4.9 4.811h t t t =-++的图象（图5.1-2），平均速度(1)(1)(1)1h t h v t +∆-=+∆-的几何意义是什么？瞬时速度(1)v 呢？环节六 归纳总结,反思提升问题:请同学们回顾本节课的学习内容,并回答下列问题： 1. 本节课学习的概念有哪些？2() 4.9 4.811h t t t =-++(1,(1))h (1,(1))t h t +∆+∆图5.1-2(1) 平均速度、瞬时速度的概念及其关系。

两线相切斜率关系一、引言两线相切是初中数学中的一个重要概念，它在高中数学和大学数学中也有广泛的应用。

本文将从斜率的角度出发，探讨两线相切时斜率的关系。

二、什么是斜率？斜率是指直线在平面直角坐标系中与$x$轴正向夹角的正切值，也就是直线上任意两点纵坐标之差与横坐标之差的比值。

如果直线过点$(x_1,y_1)$和$(x_2,y_2)$，则它的斜率$k$可以表示为：$$k=\frac{y_2-y_1}{x_2-x_1}$$三、两条直线相交时斜率的关系当两条不平行直线相交时，它们一定有一个交点。

在交点处，这两条直线的斜率不同。

为了证明这个结论，我们可以采用反证法。

假设有两条不平行直线$L_1$和$L_2$，它们有一个公共点$(x,y)$且在该点处有相同的斜率$k$。

那么对于任意一点$(x+\Delta x,y+\Delta y)$（其中$\Delta x\neq0,\Delta y\neq0$），我们都可以得到：$$k=\frac{y+\Delta y-y}{x+\Delta x-x}=\frac{\Delta y}{\Delta x}$$即两条直线在该点处的斜率相同。

这意味着，$L_1$和$L_2$在该点处是平行的，与它们相交的假设矛盾。

因此，我们得出结论：两条不平行直线在交点处的斜率不同。

四、两条直线平行时斜率的关系当两条直线平行时，它们没有交点，也就是说它们在任何一点处的斜率都相同。

为了证明这个结论，我们可以采用反证法。

假设有两条平行直线$L_1$和$L_2$，它们在某一点$(x,y)$处有不同的斜率$k_1$和$k_2$。

那么对于任意一点$(x+\Delta x,y+\Deltay)$（其中$\Delta x\neq0,\Delta y\neq0$），我们都可以得到：$$k_1=\frac{y+\Delta y-y}{x+\Delta x-x}=\frac{\Delta y}{\Delta x}\quad k_2=\frac{y+\Delta y-y}{x+\Delta x-x}=\frac{\Deltay}{\Delta x}$$即两条直线在该点处的斜率相同。