11_真空中静电场习题课

⼤学物理第6章真空中的静电场课后习题及答案第6章真空中的静电场习题及答案1. 电荷为q +和q 2-的两个点电荷分别置于1=x m 和1-=x m 处。

⼀试验电荷置于x 轴上何处，它受到的合⼒等于零？解：根据两个点电荷对试验电荷的库仑⼒的⼤⼩及⽅向可以断定，只有试验电荷0q 位于点电荷q +的右侧，它受到的合⼒才可能为0，所以200200)1(π4)1(π42-=+x qq x qq εε故 223+=x2. 电量都是q 的三个点电荷，分别放在正三⾓形的三个顶点。

试问：(1)在这三⾓形的中⼼放⼀个什么样的电荷，就可以使这四个电荷都达到平衡(即每个电荷受其他三个电荷的库仑⼒之和都为零)?(2)这种平衡与三⾓形的边长有⽆关系?解：(1) 以A 处点电荷为研究对象，由⼒平衡知，q '为负电荷，所以2220)33(π4130cos π412a q q aq'=εε故 q q 3='(2)与三⾓形边长⽆关。

3. 如图所⽰，半径为R 、电荷线密度为1λ的⼀个均匀带电圆环，在其轴线上放⼀长为l 、电荷线密度为2λ的均匀带电直线段，该线段的⼀端处于圆环中⼼处。

求该直线段受到的电场⼒。

解：先求均匀带电圆环在其轴线上产⽣的场强。

在带电圆环上取dl dq 1λ=，dq 在带电圆环轴线上x 处产⽣的场强⼤⼩为)(4220R x dq dE +=πε根据电荷分布的对称性知，0==z y E E2322)(41 cos R x xdq dE dE x +==πεθ式中：θ为dq 到场点的连线与x 轴负向的夹⾓。

+=23220)(4dq R x xE x πε232210(24R x R x +?=πλπε232201)(2R x xR+=ελ下⾯求直线段受到的电场⼒。

在直线段上取dx dq 2λ=，dq 受到的电场⼒⼤⼩为dq E dF x =dx R x xR 232221)(2+=ελλ⽅向沿x 轴正⽅向。

真空静电场(一)一．选择题1. 一均匀带电球面，电荷面密度为σ，球面内电场强度处处为零，球面上面元dS 的一个带电量为dS σ的电荷元，在球面内各点产生的电场强度 [ ]（A ） 处处为零 （B ）不一定都为零 （C ）处处不为零 （D ）无法判断2. 设有一“无限大”均匀带负电荷的平面，取X 轴垂直带电平面，坐标原点位于带电平面上，则其周围空间各点的电场强度E 随距离平面的位置坐标X 变化的关系曲线为（规定场强方向沿X 轴方向为正，反之为负） []3. 下面列出的真空中静电场的场强公式，其中哪个是正确的？ [ ]（A ） 点电荷Q 的电场: 204QE r πε=（B ） 无限长均匀带电直线（线密度λ）的电场： 302E r rλπε= （C ） 无限大均匀带电平面（面密度σ）的电场：02E σε= （D ） 半径为R 的均匀带电球面（面密度σ）外的电场：230R E r r σε= 4. 将一个试验电荷Q （正电荷）放在带有负电荷的大导体附近P 点处，测得它所受的力为F 。

若考虑到电量Q 不是足够小，则 [ ](A) F/Q 比P 点处原先的场强数值大(B) F/Q 比P 点处原先的场强数值小(C) F/Q 与P 处原先的场强数值相等(D) F/Q 与P 处原先的场强数值关系无法确定。

5. 根据高斯定理的数学表达式0s q E dS ε=∑⎰可知下列各种说法中，正确的是 [ ] （A ） 闭合面内的电荷代数和为零时，闭合面上各点场强一定为零（B ） 闭合面内的电荷代数和不为零时，闭合面上各点场强一定处处不为零（C ） 闭合面内的电荷代数和为零时，闭合面上各点场强不一定处处为零（D ） 闭合面上各点场强均为零时，闭合面内一定处处无电荷6. 当带电球面上总的带电量不变，而电荷的分布作任意改变时，这些电荷在球心处产生的电场强度E 和电势U 将 [ ]（A ）E 不变，U 不变； （B ）E 不变，U 改变；（C ）E 改变，U 不变 （D ） E 改变，U 也改变7. 在匀强电场中，将一负电荷从A 移至B ，如图所示，则： [ ]（A ） 电场力作正功，负电荷的电势能减少（B ） 电场力作正功，负电荷的电势能增加（C ） 电场力作负功，负电荷的电势能减少（D ） 电场力作负功，负电荷的电势能增加8. 真空中平行放置两块大金属平板，板面积均为S ，板间距离为d ，（d 远小于板面线度），板上分别带电量＋Q 和－Q ，则两板间相互作用力为 [ ]（A ）2204Q d πε （B ）220Q S ε （C ）2205k Q S ε+ （D ）2202Q S ε 二．填空题1 带有N 个电子的一个油滴，其质量为m ，电子的电量的大小为e ，在重力场中由静止开始下落（重力加速度为g ），下落中穿越一均匀电场区域，欲使油滴在该区域中匀速下落，则电场的方向为________________，大小为____________________。

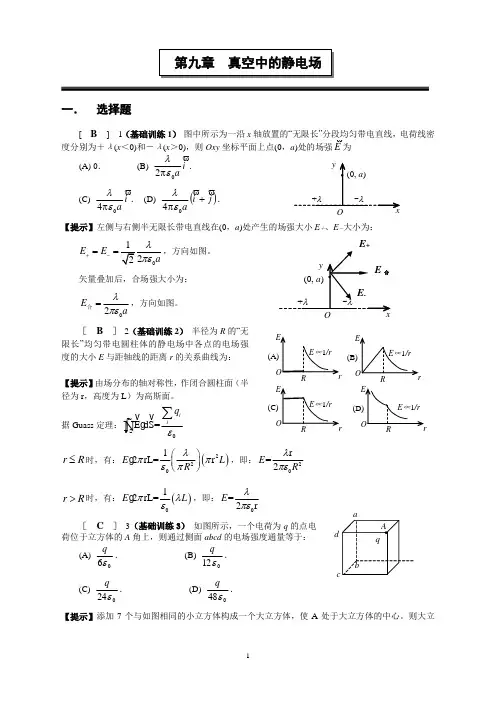
一． 选择题[ B ] 1（基础训练1） 图中所示为一沿x 轴放置的“无限长”分段均匀带电直线，电荷线密度分别为＋λ(x ＜0)和－λ(x ＞0)，则Oxy 坐标平面上点(0，a )处的场强E为(A) 0． (B) i a 02ελπ． (C) i a 04ελπ． (D)()j i a+π04ελ． 【提示】左侧与右侧半无限长带电直线在(0，a )处产生的场强大小E ＋、E －大小为：E E +-==矢量叠加后，合场强大小为：02E aλπε=合，方向如图。

［ B ］ 2（基础训练2） 半径为R 的“无限长”均匀带电圆柱体的静电场中各点的电场强度的大小E 与距轴线的距离r 的关系曲线为：【提示】由场分布的轴对称性，作闭合圆柱面（半径为r ，高度为L ）为高斯面。

据Guass 定理：SE dS=iiq ε∑⎰r R ≤时，有：()22012rL=r E L R λππεπ⎛⎫ ⎪⎝⎭，即：20r =2E R λπε r R >时，有：()012rL=E L πλε ，即：0=2rE λπε ［ C ］ 3（基础训练3） 如图所示，一个电荷为q 的点电荷位于立方体的A 角上，则通过侧面abcd 的电场强度通量等于： (A)06εq ． (B) 012εq． (C) 024εq ． (D) 048εq ．【提示】添加7个与如图相同的小立方体构成一个大立方体，使A 处于大立方体的中心。

则大立方体的外表面构成一个闭合的高斯面。

由Gauss 定理知，通过该高斯面的电通量为qε。

另一方面，该高斯面可看成由24个面积与侧面abcd 相等的面组成，且具有对称性。

所以，通过侧面abcd 的电场强度通量等于24εq ［ D ］ 4（基础训练6） 在点电荷+q 的电场中，若取图中P 点处为电势零点 ， 则M 点的电势为 (A) a q 04επ． (B) a q 08επ． (C) a q 04επ-． (D) a q 08επ-．【提示】200248P a M M aq qU E dl dr r a πεπε-===⎰⎰［ B ］ 5（自测提高6）如图所示，两个同心的均匀带电球面，内球面半径为R 1、带电荷Q 1，外球面半径为R 2、带有电荷Q 2．设无穷远处为电势零点，则在内球面之内、距离球心为r 处的P 点的电势U 为：(A)rQ Q 0214επ+． (B) 20210144R Q R Q εεπ+π． (C) 0． (D) 1014R Q επ． 【提示】根据带电球面在球内外所激发电势的公式，以及电势叠加原理即可知结果。

dq = ρ ⋅ 4π r 2 dr
5
第 6 页共 6 页
1 真空中的静电场习题详解
习题册-下-1
dq 在球心处产生的电势为
dU =
dq ρr d r = 4πε 0 r ε0
整个带电球层在球心处产生的电势为
U 0 = ∫ dU 0 =
ρ ε0
∫
R2
R1
rdr =
ρ
2ε 0
(R
2 2
− R12 )
3 a ，由点电荷的电势公式得 2
（D）
Q 。 12 πε 0 a
U=
Q Q = 4 πε 0 r 2 3 πε 0 a
二、填空题 1．真空中两平行的无限长均匀带电直线，电荷线密度分别为
+λ 2d
d d −λ
− λ 和 λ ，点P1和P2与两带电线共面，位置如图，取向右为坐
标正方向，则P1和P2两点的场强分别 为 答案： E1 = 和 。
a b r P
a b λ λ λ ln ； （B） E = ,U= ln ； 2πε 0 r 2πε 0 r 2πε 0 r b b λ λ λ ln ； （D） E = ,U= ln 。 2πε 0 a 2 πε 0 r 2πε 0 a
λ
λ ，则 P 点的电势为 2πε 0 r
U = ∫ Edr = ∫ 0dr + ∫
4πε 0 d ( L + d )
q
x O L
dq
(L+d-x) d
P dE
x
解：带电直杆的电荷线密度为 λ = q / L 。设坐标原点
O 在杆的左端，在 x 处取一电荷元 dq = λ dx = qdx / L ，它在 P 点的场强为

3 2 3 大小： 区：E i i i 2 0 2 0 2 0 2 0 2 区：E i i i 大小： 2 0 2 0 2 0 2 0 2、 E dS Q E 0 S a 0
大小： 2 0
i (i )
杆 0
EP dE
2
i
P
以无穷远处电势为零， P点电势为：
Ld x
U P dU
杆
L
0
(q / L)dx (q / L) L d ln 4 0 ( L d x) 4 0 d 1
2、一电荷面密度为σ 的“无限大”平面，在距离平面 a米远处一点的场强大小的一半是由平面上的一个半径 为R的圆面积范围内的电荷产生的。试求该圆半径的大 小。 解：圆盘在其轴线上P点场强：
根据电势叠加原理，P点处的电势也与电荷在环L上的 分布状况无关，为： dq
UP
4 0 r Nq 4 0 r
L

dq

4 r
0
1
L
R dq
L
r
P

dE
Z
9、C 空间各点处的总场强为：（方法与选择题第5小题 的方法相同）
0 (r R1 ) 2 E Eer er Q1 /(4 0 r ) ( R1 r R2 ) e (Q Q ) /(4 r 2 ) (r R2 ) 2 0 r 1
'
R
dl
R
Rd

d
y
dE
θ位置处的一窄条在轴线上的一点产生的场强为：
' ' dE i sin j cos 2 0 R 2 0 R d d i sin j cos 2 2 2 0 R 2 0 R

通过任一闭合曲面S的电场强度通量 e E dS
e ES cos
闭合曲面外法线方向(自内向外)为正
s
穿进闭合面的电场线对该闭合面提供负通量； 穿出闭合面的电场线对该闭合面提供正通量 C.有时利用高斯定理求电通量非常方便
利用高斯定理求电通量 例1: 点电荷ｑ位于正立方体中 q 心,则通过侧面ａｂｃｄ的电通量 e 6
4 0
(A)
0
(B)
(C)
(D)
8 0
2. 如图所示，两个“无限长”的共轴圆柱面， 半径分别为R1和R2，其上均匀带电，沿轴线 方向单位长度上所带电荷分别为1和2 ，则 在两圆柱面之间、距离轴线为r的P点处的场 ［ A ］ 强大小E为： 1 1 1 2 2 (A) 2 π r (B) (C) 2 R r (D) 2 0 r R1 0 2 2 0 r 0
UP
i
E
3、 先求 V,再求 E 。 E gradV
V V V gradV x i y j z k
4 0 r 带电体

dq
2
r
0
4 0 ri
dq 4 0 r
qi
U
带电体

先求 E 再求 U 。
pe q
q2 F q 2 0 2 0 s
Sd S
•电偶极子在均匀外电场中所受到的力和力矩 ＝ｐ ｅ ｅ Ｅ Ｆ＝０ Ｍ •力偶矩 力图使电偶极子的偶极矩 转到与外电场
一致方向上来
八、电势、电势差与电势能 零电势点 1. 电势： U E dl （ ＝ E dl ） ａ
底
2 E DS d DS / 0

5、给出电场强度的方向
xdq dE 2 2 3/ 2 4 0 ( r x )
哈尔滨工程大学理学院
静电场习题课
y
dl R r O x R x R x
y
r

O dE
r R sin ,
x R cos ,
dl Rd
E
/2
0
2R 3 sin cos d 3 4 0 40 R
哈尔滨工程大学理学院
静电场习题课 2. 一锥顶角为θ的圆台，上下底面半径分别为R1和R2 ， 在它的侧面上均匀带电，电荷面密度σ，求：顶角O的 电势。（以无穷远处电势为零点）

R1

R2
哈尔滨工程大学理学院
静电场习题课 1、判断带电体类型（均匀的连续面分布） 2、选坐标 3、找微元
dq ds
4 r q U 4 r
i 1 0
i
连续分布的带电体 场无对称性
U

dq 4 r
0
场有对称性
哈尔滨工程大学理学院
U P E dl
P
静电场习题课
F
定理
D ds q
0
qq ˆ r 4 r 1
1 2 2
i
有源场
s
静 电 学
方向沿x正方向
电荷元在球面电荷电场中具有电势能： dW = (qdx) / (40 x) 整个线电荷在电场中具有电势能：
q W 4 0
哈尔滨工程大学理学院

r0 l r0
r0 l dx q ln x 4 0 r0
静电场习题课 8.一电容器由两个很长的同轴薄圆筒组成，内、外圆筒半 径分别为R1 = 2 cm，R2 = 5 cm，其间充满相对介电常量 为r 的各向同性、均匀电介质．电容器接在电压U = 32 V 的电源上，(如图所示)，试求距离轴线R = 3.5 cm处的A点 的电场强度和A点与外筒间的电势差．

D） 电势不变的空间内，场强一定为零。
4、在静电场中，下列说法正确的是：[
D
]
A）带正电荷的导体，其电势一定是正值。 B）等势面上各点的场强一定相等。 C）场强为零处，电势也一定为零。
D）场强相等处，电势梯度矢量一定相等。
5、图中实线为某电场中的电场线，虚线表示等势面，由图
可看出：[
D
]
A) EA＞EB＞EC，UA＞UB＞UC． B) EA＜EB＜EC，UA＜UB＜UC． C) EA＞EB＞EC，UA＜UB＜UC．
环上均匀带正电，总电量为q，则圆心O 处的场强大小 qd 从O点指向缺口中心点 E = ————————，方向为 ——————————。 8 2 0 R 3
R
O
d
8、图中所示为静电场的等势线图，已知U1< U2< U3，在图上画 出a、b两点的电场强度的方向，比较它们的大小。Ea Eb
U3 U2 U1
C）若高斯面内有净电荷，则高斯面上 E 处处不为零。 D）若通过高斯面的电通量为零，则高斯面内的净电荷 一定为零。
3、以下各种说法正确的是： [ D ] A） 场强为零的地方，电势也一定为零。电势为零的地方， 场强也一定为零。 B） 电势较高的地方，场强一定较大。场强较小的地方， 电势也一定较低。 C） 场强相等的地方，电势相同。电势相等的地方，场强也 都相等。
E q er , 40 r 2 1 q U 40 r 1
2） 均匀带电无限长直线 E er , U lnr (U ( r 1) 0) 20 r 20 3） 均匀带电无限大平面 E er , 2 0 4 ）均匀带电球面 E0 在球内 q U 4 0 R
1）O′点的场强： EO E大球 E小球 E小球 0 EO E大球

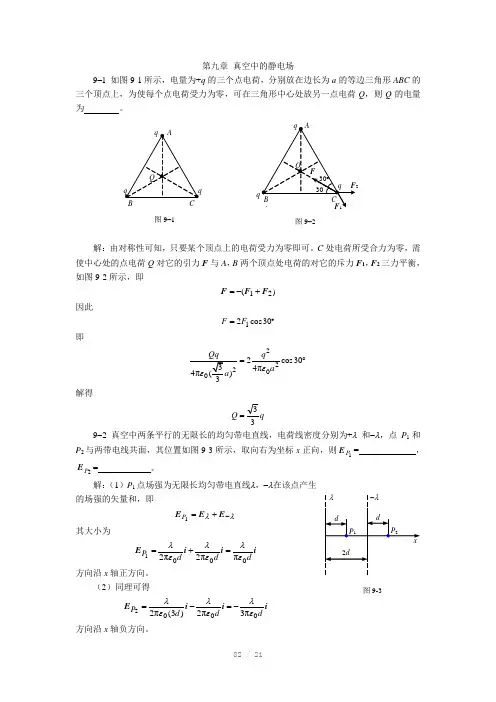
第九章 真空中的静电场9–1 如图9-1所示，电量为+q 的三个点电荷，分别放在边长为a 的等边三角形ABC 的三个顶点上，为使每个点电荷受力为零，可在三角形中心处放另一点电荷Q ，则Q 的电量为 。

解：由对称性可知，只要某个顶点上的电荷受力为零即可。

C 处电荷所受合力为零，需使中心处的点电荷Q 对它的引力F 与A ，B 两个顶点处电荷的对它的斥力F 1，F 2三力平衡，如图9-2所示，即)21(F F F +-=因此12cos30F F ︒=即2202cos304πq aε=︒解得q Q 33=9-2 真空中两条平行的无限长的均匀带电直线，电荷线密度分别为+λ 和-λ，点P 1和P 2与两带电线共面，其位置如图9-3所示，取向右为坐标x 正向，则1P E = ，2P E = 。

解：（1）P 1点场强为无限长均匀带电直线λ，-λ在该点产生的场强的矢量和，即λλ-+=E E E 1P其大小为i i i E dd d P 000ππ2π21ελελελ=+=方向沿x 轴正方向。

（2）同理可得i i i E dd d P 000π3π2)3(π22ελελελ-=-=方向沿x轴负方向。

图9–2图9-3C B图9–19-3 一个点电荷+q 位于一边长为L 的立方体的中心，如图9-4所示，则通过立方体一面的电通量为 。

如果该电荷移到立方体的一个顶角上，那么通过立方体每一面的电通量是 。

解：（1）点电荷+q 位于立方体的中心，则通过立方体的每一面的电通量相等，所以通过每一面的通量为总通量的1/6，根据高斯定理1d in Sq ε⋅=∑⎰⎰E S ，其中S 为立方体的各面所形成的闭合高斯面，所以，通过任一面的电通量为0d 6Sqε⋅=⎰⎰E S 。

（2）当电荷+q 移至立方体的一个顶角上，与+q 相连的三个侧面ABCD 、ABFE 、BCHF 上各点的E 均平行于各自的平面，故通过这三个平面的电通量为零，为了求另三个面上的电通量，可以以+q 为中心，补作另外7个大小相同的立方体，形成边长为2L 且与原边平行的大立方体，如图9–5所示，这个大立方体的每一个面的电通电都相等，且均等于6εq ，对原立方体而言，每个面的面积为大立方体一个面的面积的1/4，则每个面的电通量也为大立方体一个面的电通量的1/4，即此时通过立方体每一面的电通量为0111d 4624Sqε⋅⋅=⎰⎰E S 。

第八章 真空中的静电场 1、[D] 2、[C]要使p 点的电场强度为零，有两种可能：1、在p 点的右侧放正电荷；2、在p 点的左侧放负电荷。

根据题意为负电荷，根据点电荷强度的公式：204rQ E πε=。

其中r=1,负电荷产生的电场：2442120210=⇒=r rQ r Q πεπε，该点在原点的左边。

3、[D]1、粒子作曲线运动的条件必须存在向心力。

2、粒子从A 点出发经C 点运动到B 点是速率递增，存在和运动方向一致的切向力。

3、依据粒子带正电荷，作出作用在质点上的静电力后，符合上诉1、2条件的是[D]。

4、[C]5、[B]6、[D]1、点电荷的电场强度：r e rq E204πε=；2、无限长均匀带电直导线：r rq e rq E r20022πεπε==；3、无限大均匀带电平面：r e E2εσ=4、半径为R 的均匀带电球面外的电场强度：r r R r R r e rq E r302230204414εσσππεπε=⋅==7、[C]对高斯定理的理解。

E是高斯面上各处的电场强度，它是由曲面内外所有静止点和产生的。

∑=0q 并不能说明E有任何特定的性质。

8、[A]应用高斯定理有:⎰=⋅sS d E 0,即:⎰⎰⎰⎰=∆Φ+⋅=⋅+⋅=⋅∆ses s s S d E S d E S d E S d E 0⎰∆Φ-=⋅seS d E9、[B]10、[C]依据公式:R r rQ E ≥=,420πε已知:,4,22σπR Q R r ==代入上式可得:2024444εσπεσπ==RR E11、[D]先构建成一个边长为a 的立方体,表面为高斯面,应用高斯定理,一个侧面的磁通量为: 0661εq S d E S d E ss=⋅=⋅⎰⎰12、[D]13、[D]半径为R 的均匀带电球面:R r R Q U <=,40πεR r r Q U >=,40πε半径为R 的均匀带电球体: R r r Q U >=,40πεR r RQ r R RQ U <+-=,4)(802230πεπε正点电荷: ,40rQ U πε=负点电荷: ,40rQ U πε-=14、[C]分析:先求以无限远处为电势的零点.则半径为R 电量为Q 的球面的电势： 0)(,4)(0=∞=U RQ R U πε,4)()(0RQ R U U U R πε-=-∞=∞对15、[B]利用电势的叠加来解。

第六章 真空中的静电场1、电量为－5×10-9 C 的试验电荷放在电场中某点时，受到 20×10-9 N 的向下的力，求该点的电场强度大小和方向。

解：由q E F = 得C N q F E /4105/1020/99-=⨯-⨯==--方向向上2、一个带负电荷的质点，在电场力作用下从A 点 经C 点运动到B 点，其运动轨迹如图所示．已知质点运动的速率是递减的，试定性画出电场E的方向。

解：速率是递减→τa 为负→切向力与v相反做曲线运动→有n a →受合力方向如图→即电场E-的方向3、一均匀静电场，电场强度()j i E 600400+=V ·m -1，求点a (3,2)和点b (1,0)之间的电势差U ab ．(点的坐标x ,y 以米计) 解：⎰⋅=baab l d E U)()600400(⎰+⋅+=baj dy i dx j i +=⎰13400dx ⎰2400dy=－2×103 V4、如图所示，真空中一长为L 的均匀带电细直杆，总电荷为q ，试求在直杆延长线上距杆的一端距离为d 的P 点的电场强度．解：设杆的左端为坐标原点O ，x 轴沿直杆方向．带电直杆的电荷线密度为λ=q / L ，在x 处取一电荷元d q = λd x = q d x / L ，它在P 点的场强： ()204d d x d L qE -+π=ε()204d x d L L xq -+π=ε 2分总场强为 ⎰+π=Lx d L xL q E 02)(d 4－ε()d L d q +π=04ε 3分方向沿x 轴，即杆的延长线方向．-qEO5、A 、B 为真空中两个平行的“无限大”均匀带电平面，已知两平面间的电场强度大小为E 0，两平面外侧电场强度大小都为E 0/3，方向如图．求A 、B 两平面上的电荷面密度σA , σB ． 解：设电荷面密度为σA , σB由场强迭加原理，平面内、外侧电场强度由σA , σB 共同贡献： 外侧：32200E BA=+-εσεσ内侧：0022E BA=+εσεσ联立解得：3/200E Aεσ-= 3/400E Bεσ=6、半径为R 的半球面置于场强为E的均匀电场中，其对称轴与场强方向一致，如图所示．求通过该半球面的电场强度通量。

真空中的静电场一 选择题1．两个等量的正电荷相距为2a ，P 点在它们的中垂线上，r 为P 到垂足的距离。

当P 点电场强度大小具有最大值时，r 的大小是：[ ]（A ）42a r =（B ）32a r = （C ）22ar = （D ）a r 2= 2．如图5-1所示，两个点电荷的电量都是q +，相距为a 2，以左边点电荷所在处为球心，以a 为半径作一球形高斯面，在球面上取两块相等的小面积1S 和2S ，设通过1S 和2S 的电通量分别为1Φ和2Φ，通过整个球面的电通量为Φ，则[ ]（A ）021εq=ΦΦ>Φ,（B ）0212,εq=ΦΦ<Φ（C ）021εq=ΦΦ=Φ,（D ）021εq=ΦΦ<Φ,3．在静电场中，高斯定理告诉我们 [ ]（A ）高斯面内不包围电荷，则高斯面上各点E的量值处处相等；（B ）高斯面上各点E只与面内电荷有关，与面外电荷无关；（C ）穿过高斯面的E（D ）穿过高斯面的E 通量为零，则高斯面上各点的E必为零； 4．如图5-2所示，两个“无限长”的同轴圆柱面，半径分别为1R 和2R ，其上均匀带电，沿轴线方向单位长度上的带电量分别为1λ和2λ，则在两圆柱面之间、距轴线为r 的P 点处的场强大小为：[ ]（A ）r 012πελ （B ）r 0212πελλ+ （C ）()r R -2022πελ （D ）()1012R r -πελ5．电荷面密度为+σ和-σ的两块“无限大”均匀带电平行平板，放在与平面垂直的x2-5 图1 - 5 图轴上a +和a -位置，如图5-3所示。

设坐标圆点o 处电势为零，则在a x a +<<-区域的电势分布曲线为： （ ）6．真空中两个平行带电平板A 、B ，面积均为S ，相距为)(S d d <<2，分别带电量q +和q -，则两板间相互作用力的大小为：[ ]（A ）204d q πε （B ）Sq 0ε （C ）Sq 022ε （D ）不能确定7．静电场中，下列说法哪一个是正确的？[ ]（A ）正电荷的电势一定是正值； （B ）等势面上各点的场强一定相等；（C ）场强为零处，电势也一定为零； （D ）场强相等处，电势梯度矢量一定相等。

ro R r
(A)
(B)
(C)
(D)
(E)
[A]
大学物理学A
习题课
9.下面说法正确的是
第7章 真空中的静电场
(A)等势面上各点场强的大小一定相等； (B)在电势高处，电势能也一定高； (C)场强大处，电势一定高； (D)场强的方向总是从电势高处指向低处.
[D]
大学物理学A
习题课
第7章 真空中的静电场
例：.求无限长均匀带电直线的电势分布
场强分布 E 2 0r
由定义 V Edr
dr
P
r 2 0r
PQ
r
发散
R
选有限远为电势零点( Q )
R
R
VP r Edr 2 0r dr 2 0 ln r
讨 论
rR V 0 rR V0 rR V0
大学物理学A
习题课
第7章 真空中的静电场
12.如图所示，在X--Y平面内有与Y轴平行、位于
大学物理学A
习题课
本章内容要点：
静电场的场量 点电荷 电场叠加性
F
E
q0
q
E E
4
r2
0
r0
Ei
dE
第7章 真空中的静电场
E u 关系
VP E • dl
P
Va
Wa q0
E • dl
a
q V
4 0 r V
Vi
dV
E V
大学物理学A
习题课
场强的计算
叠加法 高斯定理法
E
④无限长均匀带电圆柱体 E
大学物理学A
第7章 真空中的静电场
E
0
rR
2 0r

E
任意曲面
dS
r n
θ
E
dS ⊥ θ
dS
d Φe = EdS ⊥ = EdS cos θ r r = E ⋅ dS
r r d Φ e = E ⋅ dS
v v E与dS同向，dΦe >0 ； v v E与dS反向，dΦe >0 。
S
闭合曲面上的电通量
Zhang Shihui
闭合曲面的电通量
Φe = ∫
B
l/2
习题课 例1
用矢量形式表示为
v P
Zhang Shihui
v v 1 P E=− 2 2 3/2 4πε 0 (d + l / 4)
−q
v l
+q
+
若 d >>l
vC E+
E
D v
v E−
v v 1 P E=− 4πε 0 d 3
α P
d
O
A −q
α
l/2
+ +q
B
l/2
习题课 例2上
Zhang Shihui
带电体场强的计算1
Zhang Shihui
线状带电体 线状带电体
面状带电体 面状带电体
体状带电体 体状带电体
v dq λ dl v E=∫ e 2 r 4πε 0 r
取一小段
v σdq dS v E=∫ e 2 r 4πε 0 r
取一小片
v ρdq dV v E=∫ e 2 r 4πε 0 r
取一小块
v v S v
v v S 与v的夹角为θ
dS
v E
θ
dS ⊥
θ
r n
v E

的电场 Ex
4 0a
(sin 2
sin 1 )
Ey
4 0a
(cos1
cos2 )
特例：无限长均匀带电(dài diàn)直线的
场强
E 20a
（2）一均匀带电圆环轴线上任一点 x处的电场
xq
E
4 0 (
x2
a2
3
)2
i
（3）无限大均匀带电平面的场强
精品文档
E 2 0
五、高斯定理可能应用(yìngyòng)的
搞清各种(ɡè zhǒnɡ) 方法的基本解题步 骤
4、q dV Ar 4r 2dr
精品文档
6.有一带电球壳，内、外半径分别为a和b，电荷体 密度r = A / r，在球心处有一点电荷Q，证明当A = Q / ( 2pa2 )时，球壳区域内的场强的大小(dàxiǎo) 与r无关．
证：用高斯定理求球壳内场强：
一、一个实验(shíyàn)定律：库仑定F律12
二、两个物理(wùlǐ)概念：场强、电势；
q1q2
4 0r122
e12
三、两个基本定理：高斯定理、环流定理
有源场
E
dS
1
0
qi
LE dl 0
（ qi 所有电荷代数和）
（与
VA VB
B
E
dl等价）
A
（保守场）
精品文档
四、电场(diàn c1h.ǎ点n电g)荷强的度电的场计(d算iàn
b
Wab qE dl q(Ua Ub ) qUab (Wb Wa )
a
3. 电势叠加原理
(1)点电荷的电势分布:
q
U P 4 0r
(2)点电荷系的电势分布:

dq=dx
Ex 40
l l x dx
1 l d l x2
0
(l
x)2 a2 3/2
4 0
( ) 2
0
(l
x)2 a2 3/2
8 0
l d[l x2 a2 ]
0 (l x)2 a2 3/2
l
[ l x 2 a2 ]1/2
[ l x 2 a2 ]1/2 l
a 4 0
2(
3 2
1)a 2
lx
l x2
a2
31 2
2 3 3 2
2( 3 1)a2 2
l
dx
0
l
x2
1
a
2
2
l
lx
l
q
4 0
a
lx
2
a
2
1/
2
0
4 0
a
l2 a2
1/2 4 0a
l2 a2
1/ 2
9.0
109
2.0 10-7 1 (22 12 )1/
1
0
(S)
qi
可得立方体内的电荷为： q 0 1.058.851012 9.291012 (C)
v 总 E 通量的三个无关：
(3) 当R>>L时，该点的场强为：
E y 2 0 R
2 0 R2
L 4R2 L2
L 42 (L / r)2
L
Q
4 0 R 4 0 R
可近似看做点电荷
dE θ
y
M
R
O dx
x
1-11、（附加）电荷以线密度λ均匀分布在长为L的直线段 上。求在棒的延长线，且离棒中心为r 处的电场强度。