实验1 卷积积分运算

一、实验目的1. 理解卷积的概念及其物理意义。

2. 掌握卷积运算的原理和方法。

3. 通过实验加深对卷积运算在实际应用中的理解。

二、实验原理1. 卷积的定义：卷积是一种线性运算，它描述了两个信号在时域上的相互作用。

对于两个连续时间信号f(t)和g(t)，它们的卷积定义为：F(t) = ∫f(τ)g(t-τ)dτ其中，F(t)是卷积结果，f(τ)是信号f(t)的任意时刻的值，g(t-τ)是信号g(t)在时刻t-τ的值。

2. 卷积的性质：卷积具有交换律、结合律和分配律等性质。

其中，交换律是指f(t)和g(t)的卷积与g(t)和f(t)的卷积相等；结合律是指三个信号f(t)、g(t)和h(t)的卷积可以分别进行两两卷积后再进行一次卷积；分配律是指一个信号与两个信号的卷积等于该信号分别与两个信号卷积后的和。

三、实验内容1. 实验一：连续时间信号卷积实验（1）选用信号：选取两个连续时间信号f(t)和g(t)，其中f(t)为矩形脉冲信号，g(t)为指数衰减信号。

（2）卷积计算：根据卷积的定义，计算f(t)和g(t)的卷积F(t)。

（3）结果分析：观察F(t)的波形，分析卷积结果的物理意义。

2. 实验二：离散时间信号卷积实验（1）选用信号：选取两个离散时间信号f[n]和g[n]，其中f[n]为单位阶跃信号，g[n]为矩形脉冲信号。

（2）卷积计算：根据离散时间信号卷积的定义，计算f[n]和g[n]的卷积F[n]。

（3）结果分析：观察F[n]的波形，分析卷积结果的物理意义。

3. 实验三：MATLAB仿真实验（1）选用信号：选取两个连续时间信号f(t)和g(t)，其中f(t)为正弦信号，g(t)为余弦信号。

（2）MATLAB编程：利用MATLAB的信号处理工具箱，编写程序实现f(t)和g(t)的卷积运算。

（3）结果分析：观察MATLAB仿真得到的卷积结果，分析其物理意义。

四、实验结果与分析1. 实验一：连续时间信号卷积实验（1）实验结果：通过计算得到f(t)和g(t)的卷积F(t)的波形。

信号与系统上机实验报告一连续时间系统卷积的数值计算140224 班张鑫学号 14071002 一、实验原理计算两个函数的卷积卷积积分的数值运算实际上可以用信号的分段求和来实现，即：如果我们只求当 t = n∆ t1 是r ( t )的值，则由上式可以得到：∆t足够小时，r(t2)就是e(t)和f(t)卷积积分的数值近似值由上面的公式可当1以得到卷积数值计算的方法如下：(1)将信号取值离散化，即以为周期，对信号取值，得到一系列宽度间隔为的矩形脉冲原信号的离散取值点，用所得离散取值点矩形脉冲来表示原来的连续时间信号；(2)将进行卷积的两个信号序列之一反转，与另一信号相乘，并求积分，所得为t=0时的卷积积分的值。

以为单位左右移动反转的信号，与另一信号相乘求积分，求的t<0和t>0时卷积积分的值；(3)将所得卷积积分值与对应的t标在图上，连成一条光滑的曲线，即为所求卷积积分的曲线。

1信号与系统上机实验报告一二、处理流程图三、C程序代码#include"stdafx.h"#include"stdio.h"//#include "stdilb.h"float u(float t){while (t>= 0) return(1);while (t<0) return(0);}float f1(float t){return(u(t+2)-u(t-2));}float f2(float t){return(t*(u(t)-u(t-2))+(4-t)*(u(t-2)-u(t-4)));}int_tmain(int argc, _TCHAR* argv[]){FILE *fp;fp=fopen("juanji.xls","w+");float t,i,j,result=0;for(i=-2;i<=6;i=i+0.1){result=0;for(j=0;j<=4;j=j+0.1)result+=f2(j)*f1(i-j)*0.1;printf("%.1f\t%.2f\t",i,result);fprintf(fp,"%.1f\t%.2f\n",i,result);}printf ("\n");return 0;}四、运行结果五、卷积曲线六、感想与总结卷积是信号与系统时域分析的基本手段，主要用于求解系统的零状态响应。

3
7) t≥7时,
y(t ) 0
注意：积分上下限应由被 积函数存在的时域范围的 上下限确定。
卷积积分在电路分析中的应用
例1、电路如图所示，uS=15e-0.25t(t)V。采用卷积计算uC。
解：以uC为响应，求单位阶跃响应
uC (0 ) uC (0 ) 0
uCf 40 1 0.5V 40 40
t t
t t
t 0
d dt t t
卷积积分上下限分析
t
0
r t h t f t f t h t
卷积符合交换律
δ t f t δ f t dτ τ τ
k 0
f (t ) f a (t )
f ( k ) ( t k ) ( t ( k 1) )
k 0 n 1

k 0 n 1
k 0
n 1
(t k ) (t (k 1) ) f (k )
例2、电路如图，R=10，L=1H，激励uS的波形如图 所示，求零状态响应i(t)。
解：以电流i 为响应，求单位阶跃响应为：
R t 1 g( t ) (1 e L ) ( t ) R 0.1(1 e 10 t ) ( t )
则单位冲激响应为：
dg( t ) h (t ) e 10 t ( t ) dt
40 40 RC 0.05 1s 40 40
uC ( t ) uCf (1 e ) ( t ) 0.5(1 e t ) ( t )V
t
单位阶跃响应为：
g(t ) 0.5(1 e t ) (t )

信号与系统实验实验一 信号的时域基本运算一、 实验目的1.掌握时域内信号的四则运算基本方法；2.掌握时域内信号的平移、反转、倒相、尺度变换等基本变换；3.注意连续信号与离散信号在尺度变换运算上区别。

二、 实验原理信号的时域基本运算包括信号的相加（减）和相乘（除）。

信号的时域基本变换包括信号的平移（移位）、反转、倒相以及尺度变换。

(1) 相加（减）: ()()()t x t x t x 21±= [][][]n x n x n x 21±= (2) 相乘: ()()()t x t x t x 21∙= [][][]n x n x n x 21∙=(3) 平移（移位）: ()()0t t x t x -→ 00>t 时右移，00<t 时左移[][]N n x n x -→ 0>N 时右移，0<N 时左移(4) 反转：()()t x t x -→ [][]n x n x -→ (5) 倒相：()()t x t x -→ [][]n x n x -→ (6) 尺度变换: ()()at x t x →1>a 时尺度压缩，1<a 时尺度拉伸，0<a 时还包含反转[][]mn x n x → m 取整数1>m 时只保留m 整数倍位置处的样值，1<m 时相邻两个样值间插入1-m 个0，0<m 时还包含反转三、实验结果1、连续时间信号时域的基本运算 （1） 相加减X1(t)=t+2 , x2(t)=cos(2*pi*t) , x(t)=x1(t)+x2(t).验证：由理论得x(t)=t+2+cos(2*pi*t)，而上图x（t）满足该表达式，故得证。

（2）相乘X1(t)=t+2 , x2(t)=cos(2*pi*t) , x(t)=x1(t)*x2(t).验证：由理论得x(t)=（t+2）*cos(2*pi*t)，而上图x（t）满足该表达式，故得证。

e
t T
t
e RC
ε(t)
➢卷积积分的图解
求f(t)与h(t)的卷积，实质上是求一个新函数
f()h(t)在 由0到t的区间内的定积分。根据定积分的 几何意义，函数在0到t区间内的定积分值，决定于被积 函数f()h(t)的曲线在该区间内与 轴之间所限定的面
积。
设 f (t) ε(t)
h(t ) etε(t )
计算。
解： 当 0<t <1 时
r(t ) te(t )ε(t )d 0 t e(t )d 1 et 0
当 t >1 时
r(t ) e1 (t )ε(t )d 0 1 e(t )d e(t1) et 0
注意：积分上下限应由被 积函数存在的时域范围的 上下限确定，用作图的方 法可方便地确定出积分上 下限。
δt
f
t
t
0
δ
f
t
d
0δ f 0
t d
f
t
δt f t f t
f tδt f t
δt
t0
f
t
t
0
δ
t 0
f
t
d
δ t0
t0
t0
f
t
d
f t t0
例1 求卷积 [e tε(t)] ε(t)
解： [e tε(t)] ε(t) t e ε( )ε(t )d 0
t ed 0
h(t)
1
t
e RC ε(t )
RC
零状态响应电压为
t
uC (t)
u( )h(t ) d
0
t 0
u0e T
ε(
)
1 RC

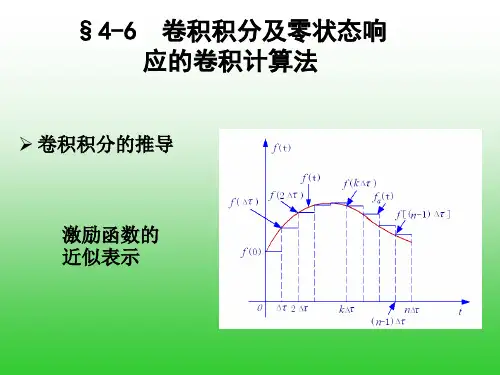
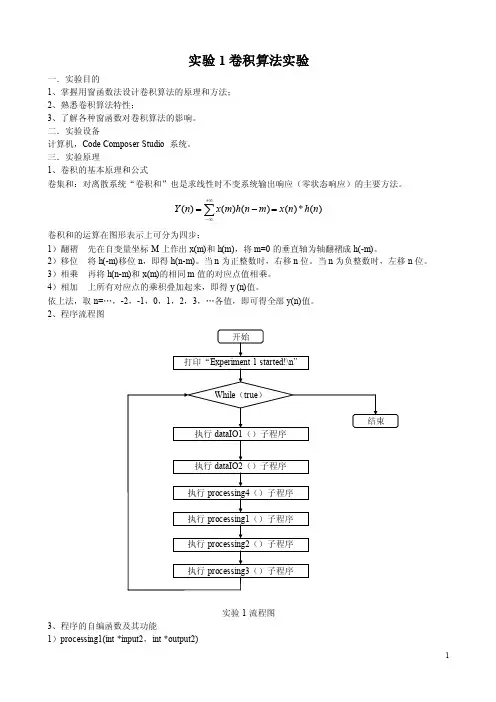
实验1卷积算法实验一．实验目的1、掌握用窗函数法设计卷积算法的原理和方法；2、熟悉卷积算法特性；3、了解各种窗函数对卷积算法的影响。

二．实验设备计算机，Code Composer Studio 系统。

三．实验原理1、卷积的基本原理和公式卷集和：对离散系统“卷积和”也是求线性时不变系统输出响应（零状态响应）的主要方法。

()()()()*()Y n x m h n m x n h n +∞-∞=-=∑卷积和的运算在图形表示上可分为四步：1）翻褶 先在自变量坐标M 上作出x(m)和h(m)，将m=0的垂直轴为轴翻褶成h(-m)。

2）移位 将h(-m)移位n ，即得h(n-m)。

当n 为正整数时，右移n 位。

当n 为负整数时，左移n 位。

3）相乘 再将h(n-m)和x(m)的相同m 值的对应点值相乘。

4）相加 上所有对应点的乘积叠加起来，即得y (n)值。

依上法，取n=…，-2，-1，0，1，2，3，…各值，即可得全部y(n)值。

2、程序流程图实验1流程图3、程序的自编函数及其功能1）processing1(int *input2，int *output2)调用形式：processing1(int *input2，int *output2)参数解释：intput2、output2为两个整型指针数组。

返回值解释：返回了一个“TRUN”，让主函数的while循环保持连续。

功能说明：对输入的input2buffer波形进行截取m点，再以零点的Y轴为对称轴进行翻褶，把生成的波形上的各点的值存入以OUTPUT2指针开始的一段地址空间中。

2）processing2(int *output2，int *output3)调用形式：processing2(int *output2，int *output3)参数解释：output2、output3为两个整型指针数组。

返回值解释：返回了一个“TREN”，让主函数的while循环保持连续。

实验报告实验名称：连续时间系统卷积的数值计算一、实验目的：1、加深对卷积概念及原理的理解；2、掌握借助计算机计算任意信号卷积的方法。

二、实验原理：卷积积分不仅可以通过直接积分或查表的方法来求解，还可以用积分的数值计算方法来求解。

在线性系统的分析过程中，有时会遇到复杂的激励信号，或者有时只是一组测试数据或曲线，冲激响应也可能出现同样的情况。

显然，此时直接计算积分或查表都有困难，而采用近似的数值计算方法可以解决这个问题，求得卷积积分。

1、卷积的定义卷积积分可以表示为2卷积计算的几何算法卷积积分的计算从几何上可以分为四个步骤：翻转→平移→相乘→叠加。

3卷积积分的应用卷积积分是信号与系统时域分析的基本手段，主要用于求系统零状态响应，它避开了经典分析方法中求解微分方程时需要求系统初始值的问题。

设一个线性零状态系统，已知系统的单位冲激响应为h(t)，当系统的激励信号为e(t)时，系统的零状态响应为由于计算机技术的发展，通过编程的方法来计算卷积积分已经不再是冗繁的工作，并可以获得足够的精度。

因此，信号的时域卷积分析法在系统分析中得到了广泛的应用。

卷积积分的数值运算实际上可以用信号的分段求和来实现，即：如果我们只求当t = nΔt （n为正整数,nΔt 记为t ）时r(t)的值，则由上式可以得到：当Δt 足够小时，r(t )就是e(t)和h(t)卷积积分的数值近似，由上面的公式可以得到卷积数值计算的方法如下：1 将信号取值离散化，即以 Ts 为周期，对信号取值，得到一系列宽度间隔为 Ts 的矩形脉冲原信号的离散取值点，用所得离散取值点矩形脉冲来表示原来的连续时间信号；2 将进行卷积的两个信号序列之一反转，与另一信号相乘，并求积分，所得为 t=0 时的卷积积分的值。

以 Ts 为单位左右移动反转的信号，与另一信号相乘求积分，求的t<0和t>0时卷积积分的值；3 将所得卷积积分值与对应的t 标在图上，连成一条光滑的曲线，即为所求卷积积分的曲线。

一、实验目的：
1.理解卷积的概念及物理意义；
2.通过实验的方法加深对卷积运算的图解方法及结果的理解。
二、实验内容：（请将实验的题目内容、实验及过程代码、实验结果（必要时可以进行拷屏）、实验体会等填写到此处。页面空间不够，可另附页或另附文件。
卷积积分的物理意义是将信号分解为冲激信号之和，借助系统的冲激响应，求解系统对任意激励信号的零状态响应。设系统的激励信号为 ，冲激响应为 ，则系统的零状态响应为 。
实验步骤：
（1）连接P04和P101；
（2）调节信号源，使P04输出f=1KHz，占空比为50%的脉冲信号，调节W701使信号幅度为4V；
（3）按下SW101按钮，使程序指示灯D3D2D1D0=0100，指示灯对应系统卷积；
(4)将示波器的CH1接于TP801，CH2接于TP802，分别观察系统冲击响应 波形与卷积后的输出信号 * 的波形；
信号 为矩形脉冲信号， 为锯齿波信号，如图9-2所示。根据卷积积分的运算方法得到 和 的卷积积分结果 ，如图9-2(c)所示。
图10-2矩形脉冲信号与锯齿脉冲信号的卷积积分的结果
3.本实验进行的卷积运算的实现方法
在本实验装置中采用了DSP数字信号处理芯片，因此在处理模拟信号的卷积积分运算时，是先通过A/D转换器把模拟信号转换为数字信号，利用所编写的相应程序控制DSP芯片实现数字信号的卷积运算，再把运算结果通过D/A转换为模拟信号输出。结果与模拟信号的直接运算结果是一致的。数字信号处理系统逐步和完全取代模拟信号处理系统是科学技术发展的必然趋势。图9-3为信号卷积的流程图。
(5)按下SS702，使频率表右侧t/T指示灯亮，之后旋转SS702，调节P04输出信号的占空比，改变激励信号的脉宽，观测卷积后波形，记录到表10-2中；

1引言信号的卷积是针对时域信号处理的一种分析方法，信号的卷积一般用于求取信号通过某系统后的响应。

在信号与系统中，我们通常求取某系统的单位冲激响应，所求得的h(k)可作为系统的时域表征。

任意系统的系统响应可用卷积的方法求得。

离散时间信号是时间上不连续的“序列”，因此，激励信号分解为脉冲序列的工作就很容易完成，对应每个样值激励，系统得到对此样值的响应。

每一响应也是一个离散时间序列，把这些序列叠加既得零状态响应。

因为离散量的叠加无需进行积分，因此，叠加过程表现为求“卷积和”。

LabVIEW是一种程序开发环境，由美国国家仪器（NI）公司研制开发的，类似于C和BASIC开发环境，但是LabVIEW与其他计算机语言的显著区别是：其他计算机语言都是采用基于文本的语言产生代码，而LabVIEW使用的是图形化编辑语言G编写程序，产生的程序是框图的形式。

本课程设计就是利用LabVIEW软件来实现方波序列卷积的过程，然后对方波序列移位过程进行演示，通过卷积过程演示和卷积和的波形图可以看出，方波序列的幅值大小不会影响卷积和的宽度而方波序列的宽度大小就会影响卷积序列相交部分的范围宽度即卷积宽度。

通过labview你能直观清晰地观察卷积的过程。

2虚拟仪器开发软件LabVIEW8.2入门2.1 LabVIEW介绍LabVIEW（Laboratory Virtual Instrument Engineering Workbench）是一种用图标代替文本行创建应用程序的图形化编程语言。

传统文本编程语言根据语句和指令的先后顺序决定程序执行顺序，LabVIEW 则采用数据流编程方式，程序框图中节点之间的数据流向决定VI及函数的执行顺序。

VI指虚拟仪器，是 LabVIEW]的程序模块。

LabVIEW 提供很多外观与传统仪器（如示波器、万用表）类似的控件，可用来方便地创建用户界面。

用户界面在 LabVIEW中被称为前面板。

使用图标和连线，可以通过编程对前面板上的对象进行控制。

§2.5 卷积积分的运算和图解
y(t) x(t) h(t) x( )h(t )d
1）将x(t)和h(t)中的自变量由t改为，成为函数的自 变量； 2）把其中一个信号翻转、平移；
h( ) 翻转h( ) 平移th(( t)) h(t )
3）将x() 与h(t )相乘；对乘积后的图形积分。
例11：画出下列系统的模拟图
y(t) 5 y(t) 3 y(t) 3x(t) x(t)
例：引入辅助函数q(t)
q(t) 5q(t) 3q(t) x(t) 利用微分特性法 y(t) 3q(t) q(t)
q(t) x(t) 5q(t) 3q(t)
例12：根据系统的模拟图写出其微分方程模型
et
d
r t
d
et
rt
et
rt
et
T rt
rt de(t)
dt
t
r(t) e(t)dt
rt et rt et T
例10：试用系统模拟图来表示下列方程所描述的LTI系统
a2 y(t) a1 y(t) a0 y(t) b2 x(t) b1 x(t) b0 x(t) a2 y(t) b2 x(t) b1 x(t) b0 x(t) a1 y(t) a0 y(t)
y(t )
1 a2
[b2 x(t )
b1 x(t )
b0 x(t )
a1
y(t)
a0
y(t )]
y(t )
1 a2
[b2 x(t )
b1 x(1) (t )
b0 x(2) (t ) a1 y(1) (t ) a0 y(2) (t )]
根据该式，可直接画出系统模拟图
y(t)

深圳大学实验报告课程名称：信号与系统实验项目名称：信号的卷积实验学院：专业：指导教师：报告人：学号：班级：实验时间：2019年5月20日星期一实验报告提交时间：2019年5月24日星期五教务部制1、掌握信号的卷积运算。

2、掌握系统的输入、单位冲激响应和输出间的卷积关系。

二、实验内容1、测量信号的卷积运算并与理论计算值比较。

三、实验仪器1、ELF-BOX 实验箱一台（主板）。

2、电脑一台。

3、线性系统综合实验模块一块。

4、导线若干条。

5、示波器RIGOL DS1102E 。

四、实验原理考察下图RC 积分电路：由电路分析可知，电容两端的电压为：⎰---+=tt RC c RCt c d e e RCV et V _0)(1)(1_)0()(τττ其中e (t )为系统的输入信号，V c (t)为系统的输出信号，V C (0-)为电容C 两端的起始电压，又称为系统的初始状态。

若V C (0-)=0，则上式为⎰--=tt RC c d e e RCt V 0)(1)(1)(τττ显然，上图电路系统等价于如下LTI 系统，其中，x (t )= e (t )u(t)，y (t )= V c (t)，11()t RCh t e RC-=为系统的单位冲激响应。

x (t ) y (t )其输入输出符合卷积运算：()()()y t x t h t =*。

tRC e RCt h 11)(-=1、把220V电源线插到插座上，给主板插上USB打印机线，完成后把ELF-BOX的电源开关打开，开关指示灯变成红色，同时箱子上的指示灯也变成红色，接着会看到ELF-BOX执行自检程序。

当自检完成后才能正常使用。

2、主板上有5个节点是专用的电源口，正面看从左到右分别为+12v、-12v、GND、-5v、+5v。

模块使用的是正负12V和地，模块的电源接口一一对应，把线性系统综合实验模块插在主板上。

按照孔位对准插入，两只手分别按下模块，直到端子和实验箱的孔完全接触。

卷积积分的步骤
卷积积分图解法的步骤依次为:1.换元；2.翻转；3.平移；4.相乘；5.积分。

卷积积分图示法的五个步骤：
1、公式如下：卷积积分公式是（f *g）∧（x）=(x)·(x)，卷积是分析数学中一种重要的运算。

2、设f（x），g（x）是R1上的两个可积函数，作积分，可以证明，关于几乎所有的x∈（－∞，∞），上述积分是存在的。

3、这样，随着x的不同取值，这个积分就定义了一个新函数h(x)，称为f与g的卷积，记为h（x）=（f *g）（x）。

4、容易验证，（f *g）（x）=（g *f）（x），并且（f *g）（x）仍为可积函数。

卷积与傅里叶变换有着密切的关系。

6、以(x) ，(x)表示L1（R）1中f和g的傅里叶变换，那么有如下的关系成立：（f *g）∧（x）=(x)·(x)，即两函数的傅里叶变换的乘积等于它们卷积后的傅里叶变换。

7、这个关系，使傅里叶分析中许多问题的处理得到简化。

8、由卷积得到的函数（f *g）（x），一般要比f，g都光滑。

9、特别当g为具有紧支集的光滑函数，f 为局部可积时，它们的卷积（f *g）（x）也是光滑函数。

10、利用这一性质，对于任意的可积函数，都可以简单地构造出一列逼近于f 的光滑函数列fs（x），这种方法称为函数的光滑化或正则化。

11、卷积的概念还可以推广到数列、测度以及广义函数上去。

(5) 利用剖析工具分析程序各段执行的时间 周期，为优化代码提供参考。
CCS还提供 剖析工具Profiler，分析代码所消耗的机器
16
北京交通大学 国家工科电工电子教学基地
DSP应用技术
三、实验内容
1.建立工程(test.pjt)，编写计算序列x[k]={1,2,3,4,5}与
序列h[k]={2,-2,3,5}的卷积和互相关的C源程序(test.c)。
2.工程的调试
2.利用CCS工具进行工程的调试
(4) 利用文件I/O实现外部数据和DSP存储区的交换(探针)
CCS还提供File I/O工具，将外部数据文件导入DSP物
理存储区，或将DSP物理存储区中的数据导入到外部文
件中。
15
北京交通大学 国家工科电工电子教学基地
DSP应用技术
2.工程的调试
2.利用CCS工具进行工程的调试
实验一 序列的卷积与相关运算
一、实验目的 二、实验原理 三、实验内容
四、实验思考题
1
北京交通大学 国家工科电工电子教学基地
DSP应用技术
一、实验目的
1．掌握利用CCS建立工程、编译与调试代码的基本过程
2．掌握序列线性卷积和相关的基本原理
3．掌握利用DSP实现序列线性卷积和相关运算
2
北京交通大学 国家工科电工电子教学基地
DSP应用技术
2.工程的调试
2.利用CCS工具进行工程的调试
(2) 观察数据的图形
CCS除了提供观察数据的窗口以外，还提供直观地以图
形的方式显示数据。
11
北京交通大学 国家工科电工电子教学基地
DSP应用技术
2.工程的调试
(2) 观察数据的图形

一、实验目的1. 理解卷积积分的概念及物理意义；2. 掌握卷积积分的计算方法；3. 通过实验验证卷积积分的性质；4. 培养学生运用数学工具解决实际问题的能力。

二、实验原理卷积积分是信号与系统中的一个重要概念，它描述了两个信号相互作用的过程。

设f(t)和g(t)是两个连续时间信号，它们的卷积积分定义为：(f g)(t) = ∫[f(τ)g(t - τ)]dτ其中，τ是积分变量。

卷积积分具有以下性质：1. 交换律：f g = g f2. 结合律：(f g) h = f (g h)3. 分配律：f (g + h) = f g + f h4. 平移不变性：f g(t - t0) = f g(t)g(t0)三、实验内容1. 准备实验器材：示波器、信号发生器、信号分析仪、计算机、实验软件等；2. 实验步骤：（1）设置信号发生器，产生两个连续时间信号f(t)和g(t)；（2）将信号输入示波器，观察信号的波形；（3）使用信号分析仪对信号进行卷积积分计算，并观察卷积积分的波形；（4）对比卷积积分的计算结果与理论值，验证卷积积分的性质；（5）改变信号参数，观察卷积积分性质的变化。

四、实验结果与分析1. 信号波形：实验中，我们分别设置了两个连续时间信号f(t)和g(t)，观察到了它们的波形。

通过对比理论波形与实验波形，可以验证信号波形的一致性。

2. 卷积积分计算：使用信号分析仪对信号进行卷积积分计算，得到了卷积积分的波形。

通过观察实验波形与理论波形，可以验证卷积积分的计算结果。

3. 卷积积分性质验证：根据卷积积分的性质，我们进行了以下验证：（1）交换律：将信号f(t)和g(t)进行卷积积分，然后交换两个信号的顺序，再次进行卷积积分，对比两次结果，验证交换律；（2）结合律：先对信号f(t)和g(t)进行卷积积分，得到中间结果，然后将该结果与信号h(t)进行卷积积分；同时，先对信号g(t)和h(t)进行卷积积分，得到另一个中间结果，最后将该结果与信号f(t)进行卷积积分。

实验一、卷积（Convovle ）算法实验一、实验目的1、 了解卷积算法的原理。

2、 掌握TMS320汇编程序在CCS 环境下的编译和调试方法。

二、实验设备计算机、DSP 硬件仿真机、 EXPII 实验箱，。

三、实验原理若LTI 系统)(n δ的响应为h(n)，h(n)称为系统的单位脉冲响应，则由时不变有，系统对)(k n -δ的响应为h(n-k)；又根据齐次性，系统对)()(k n k x -δ的响应为)()(k n h k x -；再由叠加性，系统对∑∞-∞=-k k n k x )()(δ的响应为∑∞-∞=-k k n h k x )()(，即离散时间LTI 系统对输入x(n)的响应为∑∞-∞=-=k k n h k x n y )()()(此式称为卷积和，通常记为)()()(n h n x n y *=四、实验步骤与内容1、 重新熟悉卷积的基本原理。

2、 阅读本实验所提供的样例子程序。

3、 运行CCS 软件，对样例程序进行跟踪、分析结果、记录必要的参数。

4、 填写实验报告。

A.实验前的准备 1）正确完成计算机、DSP 仿真器和实验箱的连接后，按键K10后：即仿真器连接右边的CPU 。

系统上电。

2）设置实验板上的拨码开关，其他开关缺省设置：S25: 输入信号选择 S26:输入信号选择B.实验启动CCS2.0,Project/Open 打开“Algorithm”目录中“exp04_cpu2”子目录下“Exp-CONV-AD.prj”工程文件，双击“Exp-CONV-AD.prj”及其“Source”可查看各源程序;编译程序，并加载“Exp-CONV-AD.out”（file-load problem-debug中）;在主程序中，在t++及flag=0处分别设置断点；单击“Run”运行程序，程序将运行至第一个断点处停止;用View/Graph/Time/Frequency打开图形观察窗口；设置图形窗口变量及参数；采用双综观察两路输入变量Input及Impulse的波形，波形长度为128，数值类型为32位浮点型。

1. 理解卷积的基本概念和原理；2. 掌握卷积的计算方法；3. 通过MATLAB软件实现卷积运算；4. 分析卷积运算在信号处理中的应用。

二、实验原理卷积是一种线性运算，它描述了两个信号之间的相互作用。

对于两个离散信号x[n]和h[n]，它们的卷积y[n]定义为：y[n] = Σx[k]h[n-k]其中，n和k为离散时间变量，Σ表示求和。

卷积运算具有以下性质：1. 交换律：x[n] h[n] = h[n] x[n]2. 结合律：(x[n] h[n]) g[n] = x[n] (h[n] g[n])3. 分配律：x[n] (h[n] + g[n]) = x[n] h[n] + x[n] g[n]卷积运算在信号处理中具有重要的应用，如信号滤波、系统分析、图像处理等。

三、实验内容1. 熟悉MATLAB软件环境；2. 编写MATLAB程序实现卷积运算；3. 分析卷积运算的结果，验证卷积性质；4. 应用卷积运算解决实际问题。

四、实验器材1. 计算机；2. MATLAB软件；3. 离散信号数据。

1. 创建离散信号数据：在MATLAB中创建两个离散信号x[n]和h[n]，分别代表输入信号和系统响应。

2. 编写卷积程序：使用MATLAB内置函数conv实现卷积运算，计算y[n] = x[n] h[n]。

3. 分析卷积结果：观察卷积运算的结果，验证卷积性质，如交换律、结合律、分配律等。

4. 应用卷积运算解决实际问题：选择一个实际问题，如信号滤波，使用卷积运算进行求解。

六、实验结果与分析1. 卷积运算结果：运行卷积程序，得到卷积运算结果y[n]。

观察y[n]的波形，分析卷积运算对信号的影响。

2. 验证卷积性质：通过比较x[n] h[n]和h[n] x[n]的卷积结果，验证交换律；通过比较(x[n] h[n]) g[n]和x[n] (h[n] g[n])的卷积结果，验证结合律；通过比较x[n] (h[n] + g[n])和x[n] h[n] + x[n] g[n]的卷积结果，验证分配律。

卷积和积分运算卷积和积分运算先看到卷积运算，知道了卷积就是把模版与图像对应点相乘再相加，把最后的结果代替模版中⼼点的值的⼀种运算。

但是，近来⼜看到了积分图像的定义，⽴马晕菜，于是整理⼀番，追根溯源⼀下吧。

1 卷积图像1.1 源头⾸先找到了⼀篇讲解特别好的博⽂，原⽂为：贴过正⽂来看：---------------------------------------------------------------------------------------------------------------信号处理中的⼀个重要运算是卷积.初学卷积的时候,往往是在连续的情形, 两个函数f(x),g(x)的卷积,是∫f(u)g(x-u)du 当然，证明卷积的⼀些性质并不困难，⽐如交换，结合等等，但是对于卷积运算的来处，初学者就不甚了了。

其实，从离散的情形看卷积，或许更加清楚， 对于两个序列f[n],g[n],⼀般可以将其卷积定义为s[x]= ∑f[k]g[x-k] 卷积的⼀个典型例⼦,其实就是初中就学过的多项式相乘的运算, ⽐如(x*x+3*x+2)(2*x+5) ⼀般计算顺序是这样, (x*x+3*x+2)(2*x+5) = (x*x+3*x+2)*2*x+(x*x+3*x+2)*5 = 2*x*x*x+3*2*x*x+2*2*x+ 5*x*x+3*5*x+10 然后合并同类项的系数, 2 x*x*x 3*2+1*5 x*x 2*2+3*5 x 2*5 ---------- 2*x*x*x+11*x*x+19*x+10 实际上,从线性代数可以知道,多项式构成⼀个向量空间,其基底可选为 {1,x,x*x,x*x*x,...} 如此,则任何多项式均可与⽆穷维空间中的⼀个坐标向量相对应, 如,(x*x+3*x+2)对应于 (1 3 2), (2*x+5)对应于 (2,5). 线性空间中没有定义两个向量间的卷积运算,⽽只有加法,数乘两种运算,⽽实际上,多项式的乘法,就⽆法在线性空间中说明.可见线性空间的理论多么局限了. 但如果按照我们上⾯对向量卷积的定义来处理坐标向量, (1 3 2)*(2 5) 则有 2 3 1 _ _ 2 5 -------- 2 2 3 1 _ 2 5 ----- 6+5=11 2 3 1 2 5 ----- 4+15 =19 _ 2 3 1 2 5 ------- 10 或者说, (1 3 2)*(2 5)=(2 11 19 10) 回到多项式的表⽰上来, (x*x+3*x+2)(2*x+5)= 2*x*x*x+11*x*x+19*x+10 似乎很神奇,结果跟我们⽤传统办法得到的是完全⼀样的. 换句话,多项式相乘,相当于系数向量的卷积. 其实,琢磨⼀下,道理也很简单, 卷积运算实际上是分别求 x*x*x ,x*x,x,1的系数，也就是说，他把加法和求和杂合在⼀起做了。