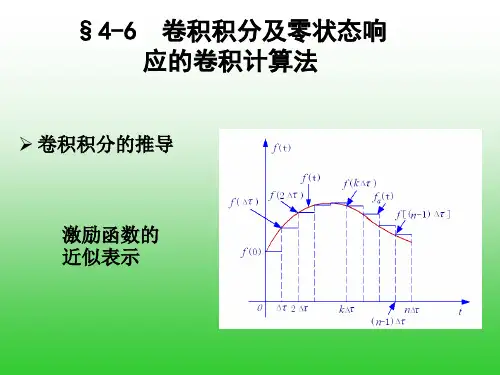
当前位置：文档之家 › 卷积积分及零状态响应的卷积计算法.

卷积积分及零状态响应的卷积计算法.

  • 格式：ppt
  • 大小：433.50 KB
  • 文档页数：15

下载文档原格式

  / 15

合集下载

信号与系统教学课件-§2.6 卷积及其性质和计算

信号与系统教学课件-§2.6 卷积及其性质和计算


r(t) e u h t u t d
0 t 0
0 t
rt0tehtd
X
二、卷积的性质
一、代数性质 • 分配律
对于函数f1t,f2t,f3t,存在 f 1 t f 2 t f 3 t f 1 t f 2 t f 1 t f 3 t
根据卷积的定义
推论
ft t ft d ftd
f t
1 . f( t) ( t t0 ) f( t t0 )
2 . f ( t t 1 ) ( t t 2 ) f ( t t 1 t 2 )
X
二、卷积的性质
三、δ(t)的卷积特性 • δ(t)的微分和积分特性
微分特性
f(t) (t) f'(t) (t)
f 1 t f 2 t f 3 t f 1 f 2 t f 3 t d
f 1 f 2 t d f 1 f 3 t d
f 1 t f 2 t f 1 t f 3 t
X
二、卷积的性质
一、代数性质 • 分配律
对于函数f1t,f2t,f3t,存在
信号与系统
§2.6 卷积及其性质和计算
北京航空航天大学电子信息学院 2020/4/19
一、卷积的定义
卷积运算的定义为，对于函数x(t)和y(t) ，则
st xytd
称为函数 x(t)和y(t)的卷积积分，简称卷积。
通常表示为
stxtyt
或
stxtyt
X
一、利用卷积计算系统零状态响应
对于激励信号e(t)，根据信号的时间轴分解，可得
f 1 t f 2 t f 3 t f 1 t f 2 t f 1 t f 3 t
h1 t
e(t )
h2 t
卷积计算(图解法)

卷积计算(图解法)

Байду номын сангаас
an4 a7
1 a
,
6 n 10
2021/3/11
0,
10 n 8
(4)相加：把所有的乘积累加起来，即得y(n)。
2021/3/11
1
计算卷积时，一般要分几个区间分别加以 考虑，下面举例说明。
例 已知x(n)和h(n)分别为：
1, 0 n 4 x(n) 0, 其它
an , 0 n 6
和 h(n)
0,
其它
a为常数，且1<a，试求x(n)和h(n)的卷积。
2021/3/11
5
x(m)
(3)在4<n≤6区间上
4
y(n) x(m)h(n m)
m0
m 04
h(n-m)
4
4
1 anm an am
m0
m0
m
n-6 0
46 n
an 1 a(14) an4 a1n
1 a1
1 a
2021/3/11
6
x(m)
(4)在6<n≤10区间上
n
y(n) x(m)h(n m)
2021/3/11
2
解 参看图，分段考虑如下：
x(m)
n 04
h(m)
n 06
h(n-m)
(1)对于n<0；
n-6 n
(2)对于0≤n≤4；
(3)对于n>4，且n-6≤0，即4<n≤6；
(4)对于n>6，且n-6≤4，即6<n≤10；
(5)对于(n-6)>4，即n>10。
2021/3/11
m
3
(1) n<0
卷积的几种计算方法以及程序实现FFT算法

卷积的几种计算方法以及程序实现FFT算法


e ( t 1) )u(t 2)
Made by 霏烟似雨
数字信号处理
ht 1
e

t 2
u (t ) u (t 2)
e t 1
e t u (t )
O
t
波形
O
2
t
2. 今有一输油管道，长 12 米，请用数字信号处理的方法探测管道内部的损伤，管道的损伤可能为焊 缝，腐蚀。叙述你的探测原理，方法与结果。 （不是很清楚） 探测原理：因为输油管道不是很长，可以考虑设计滤波器器通过信号测量来测试管道的损伤，当有 焊缝时，所接受的信号会有所损失，当管道式腐蚀时，由于管壁变得不再是平滑的时候，信号的频率 就会有所改变。
rk r ( k N / 2)
，则后半段的 DFT 值表达式：
X 1[
N N / 2 1 N / 2 1 r ( k ) N N rk k ] x1[r ]WN / 22 x1[r ]WN ， k ] X 2 [k ] （ k=0,1, … ,N/2-1 ） / 2 X 1[ k ] ，同样， X 2 [ 2 2 r 0 r 0
d it L Ri t et dt


t
t 2
u(t ) u(
i(t )
L 1H
2) 冲激响应为 h(t ) e u(t ) 3)
i(t ) e( ) h(t ) d

程序： function test x = rand(1 , 2 .^ 13) ; tic X1 = fft(x) ; toc tic X2 = dit2(x) ; toc tic X3 = dif2(x) ; toc tic X4 = real_fft(x) ; toc max(abs(X1 - X2)) max(abs(X1 - X3)) max(abs(X1 - X4)) return ; function X = dit2(x) N = length(x) ; if N == 1 X=x; else X1 = dit2(x(1:2:(N-1))) ; X2 = dit2(x(2:2:N)) ; W = exp(-1i * 2 * pi / N * (0:(N/2-1))) ; X = [X1 + W .* X2 , X1 - W .* X2] ; end return ;
《信号与系统教学课件》§2.6 卷积及其性质和计算

《信号与系统教学课件》§2.6 卷积及其性质和计算


将卷积的微分性质和积分性质加以推广，可以得到
s
t
nm
f (n) 1
t
f (m) 2
t
f (m) 1
t
f (n) 2
t
X
二、卷积的性质
注意函数的积分和微分并不是一个严格的可逆关系， 因为函数加上任意常数后的微分与原函数的微分是相 同的。因此，对于等式
f1 t
f2 t
f1' t
k
d
k
f
3
t
d
令w k
f1
k
f2
w f3
t
k
w d w d k
令st f2t f3t
f1 k s t k d k
f1 t st
f1 t
f2 t
f3 t
f 1
t f2 t
f3 t
X
二、卷积的性质
一、代数性质 • 结合律
对于函数f1 t , f2 t , f3 t ,存在
h2 t
r(t)
h1 t
图2.6.2 卷积交换律的系统意义
X
二、卷积的性质
一、代数性质
• 结合律
对于函数f1 t , f2 t , f3 t ,存在
f1 t f2 t f3 t f1 t f2 t f3 t
根据卷积的定义
f1 t
f2
t
f3
t
f1
k
f2
X
三、卷积的计算
根据卷积的定义，卷积计算是由若干基本的信号运算组成的， 对于
s
t
f1
f2
t
d
第一步 反褶：将 f1 t 反褶运算，得到 f1
信号第二章3卷积

信号第二章3卷积



若将此信号作用到冲激信号为h(t)的线性时不 变系统，则系统的响应为
r (t ) H [e(t )] H [ e( ) (t )d ]


e( ) H [ (t )]d


e( )h(t )d

零状态响应：rzs (t ) e( )h(t )d h(t ) e(t )
def
2.算子符号基本规则
(1)算子多项式可以进行因式分解 ( p 2)( p 3) p 2 5 p 6 例如： (2)等式两端的算子符合因式不能相消 ( p 2) r (t ) ( p 1) e(t ) ( p 2)( p 3) r (t ) ( p 2 4 p 3) e(t ) 不能简化为： (3)算子的乘除顺序不能随意颠倒
（3）结合律： f1(t) f2 (t) f3 (t) f1(t) f2 (t) f3 (t)
e(t)
h1(t)
h2(t)
r(t)
串联系统 r (t ) e(t ) h1 (t ) h2 (t )
2.卷积的微分与积分
d f1 (t ) f 2 (t ) df 2 (t ) （4）微分性： f1 (t ) dt dt df1 (t ) (适于高阶微分） f 2 (t ) dt

r (t ) e( )h(t )d


1 (a) t 2
e(t ) * h(t ) 0
h(t )
e( )
1
1 2
t 2
(b)
0
1 t 1 2
相乘
t
1
1 t 1 2 t 1 e(t ) * h(t ) 1 1 (t )d 2 2 t2 t 1 4 4 16 (b)
离散系统的零状态响应

离散系统的零状态响应


k
对比 : g (t ) h( )d

t
2. 已知g (k )求h(k ) :
(k ) (k ) (k 1) h(k ) g (k ) g (k 1)
X
例题（书P127例5－9）(自学，不要求)
求离散系统 y k 4 y k 1 3 y k 2 2 k y 1 1, y( 2) 1 的单位响应 (其中k 0)
(k ) (k j ) (k ) (k 1) (k j )

第 7 页
由于 (k ) h(k )根据LTI性质
g ( k ) h( k j )
j 0 i
j 0
i
(i)
k
h(i)
单位序列响应的初值h1 (0),1h1 (1), h(2)可由下式递推得到
h1 (k ) (k ) a1h1 (k 1) an 1h1 (k n 1) anh1 (k n)
h(k ) b0 h1 (k ) b1h1 (k－1) bm 1h (k m 1) bmh1 (k m)
ik 6 4
k i 0
i
k-6
k 0
y (k ) 0
k i a
3.k 4
k-6 k
k 6 0
k
4.k 6 0 k 6 4
4
i0
k-6
5.k 6 4即 : k 10
k-6
k
y(k) 0
X
1.k 0, y (k ) 0
2.0 k 4 y (k ) a
设系统激励仅在是δ(k) →h1(k),此时系统差分方程变为:
卷积积分介绍

卷积积分介绍


h(t)
(1) 1
O
(1) t
g(t)
1
O12 1
g(t)f(1)(t)h(1)(t)
t 3 2t
t 3
0t 1 1t 2 2t 3
3 t
注意
28
注意
当f1(t)
t df1(t)dt时, dt
f 1 ( t) f 2 ( t) f 1 ( t) f 2 ( 1 )( t)
例 sg t： n t
系统并联运算
3．结合律
f ( t ) f 1 ( t ) f 2 ( t ) f ( t ) [ f 1 ( t ) f 2 ( t )]
系统级联运算
22
系统并联
f 1 ( t ) [ f 2 ( t ) f 3 ( t ) f ] 1 ( t ) f 2 ( t ) f 1 ( t ) f 3 ( t ) 系统并联，框图表示：
一般数学表示： g(t) f1()f2(t)d 信号无起因时： g(t) f()h(t)d
(4)卷积是数学方法，也可运用于其他学科 。
(5)积分限由 f1(t),f2(t)存在的区间决定，即由
f1()f2(t)0的范围决定。
20
总结
求解响应的方法： 时域经典法： 完全解=齐次解 + 特解 双零法：
: 信号作用的时刻，积分变量
从因果关系看，必定有 t
(2)分析信号是手段，卷积中没有冲激形式，但有其内容；
f() 是h(t-)的加权，求和
即d f() 是h(t-)的加权，积分
(t-)的响应
19
(3)卷积是系统分析中的重要方法，通过冲激响应h(t)建 立了响应r(t)与激励e(t)之间的关系。
零输入响应：解齐次方程，用初（起）始条件求系数；
计算卷积的方法

计算卷积的方法

f (t1)
f(t1t1) f (0)
t1
t1
u(t) g(t) DaHlantrem gra
*.Duharmal integral
t
r(t) e(0)g(t) e' ( )g(t )d
0
d(g t)
r(t)e(t)h(t)e(t)
dt
de(t) *g(t)
dt
e(t)e(t)u(t)
f(t)
h1 (t ) y1(t)
f2 (t) h2 (t)
y(t)
解:1当 . 输入f(t) (t)时,子系统h1(t)的输出为
cost
y 1 ( t ) f ( t ) h 1 ( t ) ( t ) u ( t ) u ( t )
由图,子 可系 知 h2(统 t)的输入 f2 (t)为 y 1 (t)cto csto ( u t)s
*.表达式的推导
t t j
1.将被卷积的两个函数f(t)和 h(t)都表示成单位阶跃u(t)移
位加权之和. p
f(t) fi(t)u(tti)......1 .... i1 q
h(t) hj(t)u(ttj)....2 .. j1
其中fi(t)和hj(t)分别是f(t)的第i段和h(t)的第j段数学表达
式.ti和tj分别是fi(t)和hj(t)的起点.
2.将(1)和(2)代入卷积公式:
f h [ pfi( ) u ( t ti) ] qh [ j( t ) u ( t tj)d ]
i 1
j 1
p q
fi(t)h j(t)u [ ( ti)u (t tj)d ]
i 1j 1
2 .当系 f(统 t')(t)， 输子 入 h 1(t)的 系输 统出为
卷积积分法求零状态响应

卷积积分法求零状态响应

卷积积分法求零状态响应
卷积积分法是一种求解线性时不变系统零状态响应的方法。

零状态响应是指系统在没有初始状态（即零初始条件）下，仅由输入信号引起的响应。

以下是使用卷积积分法求解零状态响应的步骤：
确定系统的单位冲激响应h(t)。

单位冲激响应是系统对单位冲激信号（在时间t=0处为1，其他时间为0）的响应。

确定输入信号f(t)。

输入信号是系统接收到的外部信号，可以是任意信号。

计算卷积积分。

卷积积分是输入信号f(t)与系统单位冲激响应h(t)的卷积，表示为∫f(τ)h(t-τ)dτ。

这个积分表示了在时间t之前所有时刻τ的输入信号对系统响应的贡献之和。

将积分结果作为零状态响应。

计算出的卷积积分就是在没有初始条件下，由输入信号f(t)引起的系统响应，即零状态响应。

需要注意的是，卷积积分法只适用于线性时不变系统，并且需要知道系统的单位冲激响应。

此外，卷积积分法的计算过程可能比较复杂，需要使用数值计算或符号计算工具来辅助计算。

另外，也可以通过频域方法来求解零状态响应，将时域信号和系统转换为频域表示，然后进行乘积运算，最后再将结果转换回时域。

这种方法在某些情况下可能更为简便。

卷积公式

卷积公式

卷积公式卷积的物理意义是将输入信号用时移加权的单位冲激信号和（积分）表示，然后输出就是各个冲激信号作用系统后再求和，而时移量u（f(t-u)），再对u积分，就产生了反转。

卷积的物理意义(2009-11-30 09:25:54)卷积这个东东是“信号与系统”中论述系统对输入信号的响应而提出的。

因为是对模拟信号论述的，所以常常带有繁琐的算术推倒，很简单的问题的本质常常就被一大堆公式淹没了，那么卷积究竟物理意义怎么样呢？卷积表示为y(n) = x(n)*h(n)假设0时刻系统响应为y(0),若其在1时刻时，此种响应未改变，则1时刻的响应就变成了y(0)+y(1),叫序列的累加和（与序列的和不一样）。

但常常系统中不是这样的，因为0时刻的响应不太可能在1时刻仍旧未变化，那么怎么表述这种变化呢，就通过h(t)这个响应函数与x(0)相乘来表述，表述为x(m)×h(m-n)，具体表达式不用多管，只要记着有大概这种关系，引入这个函数h(t)就能够表述y(0)在1时刻究竟削弱了多少，然后削弱后的值才是y(0)在1时刻的真实值，再通过累加和运算，才得到真实的系统响应。

再拓展点，某时刻的系统响应往往不一定是由当前时刻和前一时刻这两个响应决定的，也可能是再加上前前时刻，前前前时刻，前前前前时刻，等等，那么怎么约束这个范围呢，就是通过对h(n)这个函数在表达式中变化后的h(m-n)中的m 的范围来约束的。

即说白了，就是当前时刻的系统响应与多少个之前时刻的响应的“残留影响”有关。

当考虑这些因素后，就可以描述成一个系统响应了，而这些因素通过一个表达式（卷积）即描述出来不得不说是数学的巧妙和迷人之处了。

对于非数学系学生来说，只要懂怎么用卷积就可以了，研究什么是卷积其实意义不大,它就是一种微元相乘累加的极限形式。

卷积本身不过就是一种数学运算而已。

就跟“蝶形运算”一样，怎么证明，这是数学系的人的工作。

在信号与系统里，f(t)的零状态响应y(t)可用f(t)与其单位冲激响应h(t) 的卷积积分求解得，即y(t)=f(t)*h(t)。

卷积积分及零状态响应的卷积计算法.

卷积积分及零状态响应的卷积计算法.


如按式
t
r(t)
f (t) h(t) 0
f ( )h(t ) d
计算。
如按式
t
r(t) 0 h( ) f (t ) d h(t) f (t)
计算。
例3 图示某电路的激励函数与冲激响应。求电路的零状态响应。
如按
t
r(t) f (t) h(t) 0 f ( )h(t ) d
δt
f
t
t
0
δ
f
t
d
0δ f 0
t d
f
t
δt f t f t
f tδt f t
δt
t0
f
t
t
0
δ
t 0
f
t
d
δ t0
t0
t0
f
t
d
f t t0
例1 求卷积 [e tε(t)] ε(t)
解： [e tε(t)] ε(t) t e ε( )ε(t )d 0
t ed 0
f ( )ε(t ) ε(t 2 )
f (2 )ε(t 2 ) ε(t 3 )
f (n 1) ε(t (n 1) ) ε(t n )
n1
f (k )ε(t k ) ε(t (k 1) ) k0
f (t) fa(t)
n1 k0
f
(k )ε(t
k )
1 e t
0
(t 0)
(t 0)
1 1 e t ε(t)
ቤተ መጻሕፍቲ ባይዱ
例2 设图示RC串联电路中电压源的电压
t
u(t) u0e T ε(t)
求零状态响应电压uC(t)。
解： 用卷积积分公式求uC(t)，应先求冲激响应

matlab用卷积求零状态响应

matlab用卷积求零状态响应在信号处理和控制系统中，卷积是一种常用的数学操作，用于描述线性系统的输入与输出之间的关系。

在Matlab中，我们可以使用conv函数来进行卷积运算。

卷积的一个常见应用是求解零状态响应。

零状态响应指的是系统在初始时刻没有任何输入时的输出。

通过计算零状态响应，我们可以了解系统对于不同输入信号的响应情况。

为了求解零状态响应，我们需要知道系统的冲激响应。

冲激响应是系统对于一个单位冲激信号的输出响应。

在Matlab中，我们可以使用impulse函数来获取系统的冲激响应。

假设我们有一个系统，其冲激响应为h(t)，输入信号为x(t)，输出信号为y(t)。

则系统的零状态响应可以通过卷积运算来计算： y(t) = conv(x(t), h(t))在Matlab中，我们可以按照以下步骤来求解零状态响应：1. 定义输入信号x(t)和系统的冲激响应h(t)。

可以使用符号或者数值的方式来表示这些信号。

2. 使用conv函数进行卷积运算，计算得到零状态响应y(t)。

下面是一个示例代码，演示了如何使用Matlab进行零状态响应的计算：```matlab% 定义输入信号和冲激响应x = [1, 2, 3]; % 输入信号h = [1, 1, 1]; % 冲激响应% 计算零状态响应y = conv(x, h);% 绘制输入信号、冲激响应和零状态响应 t_x = 0:length(x)-1;t_h = 0:length(h)-1;t_y = 0:length(y)-1;figure;subplot(3, 1, 1);stem(t_x, x);xlabel('Time');ylabel('x(t)');title('Input Signal');subplot(3, 1, 2);stem(t_h, h);xlabel('Time');ylabel('h(t)');title('Impulse Response');subplot(3, 1, 3);stem(t_y, y);xlabel('Time');ylabel('y(t)');title('Zero-State Response');```运行以上代码，将会得到输入信号、冲激响应和零状态响应的图形表示。

4-6卷积积分及零状态响应的卷积计算法


f (k ) (t k )
k 0
n 1
(t ) NzS h(t )
(t K ) NzS h(t k )
f (k ) (t k ) NzS f (k )h(t k )
f (k ) (t k )
e
0
t
( t )
d e ( t ) d
t
e
0 t
t
( t )
d e
e d e

0 t
t
t
(e 1) (1 e ) (t )
t t t ( t 1)
e d e (e e) (1 e ) (t 1) t ( t 1) rzS (t ) (1 e ) (t ) (1 e ) (t 1)
3 1 2 n t
1
f (t ) f a (t ) f (k ) (t k ) (t (k 1) )
(t k ) (t (k 1) ) f (k ) k 0
k 0 n 1
§4-6卷积积分及零状态响应的 卷积计算法 Convolution integral
一 卷积积分的导出
用n个矩形脉冲来近 似代替连续函数f(t) 用冲击函数来近似 代替矩形脉冲 用n个冲击函数分别 单独作用产生的rzS(t) 之和来近似代替f(t) 产生的rzS(t)
n 1
f a( t ) 第K+1个
k 0
n 1
NzS f (k ) h(t k )
k 0
n 1
f (t )
n 1 k 0 n 1
rzS (t )
f (t ) f (k ) (t k )

信号与系统连续时间LTI系统的几种响应求解方法及例题

1) 直接求解初始状态为零的微分方程。 2) 卷积法：
利用信号分解和线性时不变系统的特性求解。
卷积法求解系统零状态响应yf (t)的思路
1) 将任意信号分解为单位冲激信号的线性组合 2) 求出单位冲激信号作用在系统上的响应
—— 冲激响应 3) 利用线性时不变系统的特性，即可求出任意
信号f(t)激励下系统的零状态响应yf (t) 。
解：y f (t) f (t) h(t) f ( ) h(t )d = 3u( ) 2e3(t )u(t )d
= 0t 3 2e 3(t )d
0 2(1 e3t ) = 0 = 2(1 e3t )u(t)
初始条件y(0)=1, y '(0)=2, 输入信号f (t)=et u(t)，求 系统的完全响应y(t)。
解:
(3) 求方程的全解
y(t)

yh (t)
yp (t)
Ae 2t

Be 4t

1 et 3
y(0) A B 1 1
y' (0)

2A
3 4B

1

2
解得 A=5/2，B= 11/6
解得 K1= 6，K2= 5
yx (t) 6e2t 5e3t , t 0
[例2] 已知某线性时不变系统的动态方程式为:
y" (t)+4y ' (t) +4y (t) = 2f ' (t )+3f(t), t>0 系统的初始状态为y(0) = 2，y'(0) = 1， 求系统的零输入响应yx(t)。
系统的初始状态为y(0) = 1，y' (0) = 3， 求系统的零输入响应yx(t)。

离散时间系统的零状态响应

系统串连与子系统次序无关3分配率系统并联等效12卷积和的上下限ab上下限之和r1a1r1如果mna如果特征方程没有重根则
离散时间系统的零状态响应
重点：零输入响应；卷积和; 因果和稳定性
1）经典法:分通解和特解两部分分别求解。 2）时域卷积和法:类似与连续时间系统中的卷积积 分方法。 3）变换域法:Z.T. ，类似于L.T.
充分条件
n
h(k )
例4：h(k ) 14 (k ) (2k 1 12 5k 1 ) (k 1)
此系统为不稳定系统
七 离散系统的全响应 例4：已知一离散因果系统
y(k 2) 0.7 y(k 1) 0.1 y(k ) 7e(k 2) 2e(k 1)
r(0) =0
r(1) =A
r(1)= r(0)+ A(0)
r(k+1) - r(k)= 0 k>=1
r(k+1) = r(k)
k>=1
1 若H ( S ) ( S )2
h(k ) (k 1) k 2 (k 1)
bm S bm1S bm2 S ... b1S b0 H (S ) n n 1 n2 S an1S an2 S ... a1S a0
离散系统的描述与模拟
S y(k ) y(k 1)
e (t)
1/S
x ( n)
D
x(n 1)
∑ -a
e (k)

y(t) y'(t)＋ay(t)＝e(t)
∑ -a
D
y(k)
y(k+1)＋ay(k)＝e(k)
一、离散信号的时域分解
(k )

连续系统的零状态响应—卷积积分


f2(t)+f3(t) h(t)
yf(t)
f2(t)
h(t)
yf(t)
f3(t)
h(t)
h1 (t )
f(t)
yf(t)
h2 (t) h(t)
连续时间信号与系统的时域分析
说明：
a) 系统由f2 (t) f3(t) 共同作用产生的零状态响应是 f2 (t) 和 f3(t) 分别单独作用产生的零状态响应的叠加。
1、将 f1(t) 和 f2(t) 的自变量 t
2、反折，将 f2 ( )反折得 f2 ( )
3、时移，将 f2 ( )时移 t 得 f2 (t )
4、相乘，将时移后的 f2 (t )与 f1( )相乘得
f1( ) f2 (t )
连续时间信号与系统的时域分析
5、积分，对 积分。
6、由于时移量 t 是变量，当 t 变化时，积分不同，
源码
0 k
0 k
即
f (t)
f ( )h(t )d
2-28 源码
连续时间信号与系统的时域分析
f (t)作用下系统的零状态响应为
y f (t) f (t) h(t)
f ( )h(t )d
四、卷积积分的图解法
由卷积积分的定义：f1(t)
f2 (t)
f1 (
)
f2 (t
)d
可知：用图解法计算卷积积分按如下步骤进行：1 t 0
源码
f1(t) f2 (t)
1 t
0
0 t 1
t 1
1
2-30 源码
1
0
1 t
结论：（１）两个等宽的门信号卷积得到一个三角脉冲。 （２）两个不等宽的门信号卷积得到一个梯形脉冲。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

t
e RC
RCT
T RC t
e RCT 0
RC T RC
(t 0)
u0T T RC
e
t T
t
e RC
ε(t)
➢卷积积分的图解
求f(t)与h(t)的卷积，实质上是求一个新函数
f()h(t)在 由0到t的区间内的定积分。根据定积分的 几何意义，函数在0到t区间内的定积分值，决定于被积 函数f()h(t)的曲线在该区间内与 轴之间所限定的面
§4-6 卷积积分及零状态响 应的卷积计算法
➢ 卷积积分的推导
激励函数的 近似表示
f (t) fa (t) f (0)ε(t) ε(t )
f ( )ε(t ) ε(t 2 )
f (2 )ε(t 2 ) ε(t 3 )
f (n 1) ε(t (n 1) ) ε(t n )
解： [e tε(t)] ε(t) t e ε( )ε(t )d 0
t ed 0
1 e t
0
(t 0)
(t 0)
1 1 e t ε(t)
例2 设图示RC串联电路中电压源的电压
t
u(t) u0e T ε(t)
求零状态响应电压uC(t)。
解： 用卷积积分公式求uC(t)，应先求冲激响应
如按
t
r(t) h( ) f (t ) d h(t) f (t)
0
当 0<t <1 时
计算。
r(t ) te ε( )d t e d 1 et
0
0
当 t >1时
r(t ) t e ε( )d t 1
t e d e(t1) et t 1 返回
注意ቤተ መጻሕፍቲ ባይዱ分上、下限
r(t) f (t) h(t)
t
0
f
ht
d
rt ht f t
t
0
h
f
t
d
rt ht f t f tht
δt
f
t
t
0
δ
f
t
d
0δ f 0
t d
f
t
δt f t f t
f tδt f t
δt
t0
f
t
t
0
δ
t 0
f
t
d
δ t0
t0
t0
f
t
d
f t t0
例1 求卷积 [e tε(t)] ε(t)
因为
1
uC (0 ) C
0 1 δ(t )dt 1
0 R
RC
所以，冲激响应
h(t)
1
t
e RC ε(t )
RC
零状态响应电压为
t
uC (t)
u( )h(t ) d
0
t 0
u0e T
ε(
)
1 RC
t
e RC
ε(t
)
d
u0
t
e RC
t T RC
e RCT d
RC
0
(t 0)
u0
积。
设 f (t) ε(t)
h(t ) etε(t )
如按式
t
r(t)
f (t) h(t) 0
f ( )h(t ) d
计算。
如按式
t
r(t) 0 h( ) f (t ) d h(t) f (t)
计算。
例3 图示某电路的激励函数与冲激响应。求电路的零状态响应。
如按
t
r(t) f (t) h(t) 0 f ( )h(t ) d
n1
f (k )ε(t k ) ε(t (k 1) ) k0
f (t) fa(t)
n1 k0
f
(k )ε(t
k )
ε(t
(k
1)
)
n1
f (t) fa (t) f (k )δ(t k ) k0
零状态响应的近似解
n1
r(t) f (k ) h(t k ) k0
准确解 r(t) t f h(t )d 0
计算。
解： 当 0<t <1 时
r(t ) te(t )ε(t )d 0 t e(t )d 1 et 0
当 t >1 时
r(t ) e1 (t )ε(t )d 0 1 e(t )d e(t1) et 0
注意：积分上下限应由被 积函数存在的时域范围的 上下限确定，用作图的方 法可方便地确定出积分上 下限。