平行线复习2

2023年浙教版七下数学第一章平行线章节复习（教师版）一、知识梳理知识点1：平行线的定义1．定义：在同一平面内，不相交的两条直线叫做平行线，如果直线a与b平行，记作a ∥b．注意：(1)平行线的定义有三个特征：一是在同一个平面内；二是两条直线；三是不相交，三者缺一不可；(2)有时说两条射线平行或线段平行，实际是指它们所在的直线平行，两条线段不相交并不意味着它们就平行．(3)在同一平面内，两条直线的位置关系只有相交和平行两种．特别地，重合的直线视为一条直线，不属于上述任何一种位置关系．知识点2：同位角、内错角和同旁内角两条直线被第三条线所截，可得八个角，即“三线八角”，如图6所示。

（1）同位角：可以发现∠1与∠5都处于直线l的同一侧，直线a、b的同一方，这样位置的一对角就是同位角。

图中的同位角还有∠2与∠6，∠3与∠7，∠4与∠8。

（2）内错角：可以发现∠3与∠5都处于直线l的两旁，直线a、b的两方，这样位置的一对角就是内错角。

图中的内错角还有∠4与∠6。

（3）同旁内角：可以发现∠4与∠5都处于直线l的同一侧，直线a、b的两方，这样位置的一对角就是同旁内角。

图中的同旁内角还有∠3与∠6。

知识点3：平行公理及推论1．平行公理：经过直线外一点，有且只有一条直线与这条直线平行．2．推论：如果两条直线都与第三条直线平行，那么这两条直线也互相平行．记作：如果a∥b，a∥c，那么a∥c注意：(1)平行公理特别强调“经过直线外一点”，而非直线上的点，要区别于垂线的第一性质．（2）“平行公理的推论”也叫平行线的传递性知识点4：平行线判定判定方法（1）：两条直线被第三条直线所截，如果同位角相等，那么这两条直线平行简单说成：同位角相等，两直线平行。

几何语言：∵∠1＝∠2∴ AB∥CD（同位角相等，两直线平行）判定方法（2）：两条直线被第三条直线所截，如果内错角相等，那么这两条直线平行．简单说成：内错角相等，两直线平行。

相交线与平行线复习（2）班级----------- 姓名-----------学习目标：复习巩固相交线与平行线的有关概念和性质，使学生会用这些概念和性质进行简单的推理或计算；加深理解推理证明，提高学生分析问题解决问题能力。

学习方法：自主探索合作交流一、自主学习（第1题）（第2题）（第3题）1、如图所示，图中用数字标出的角中，同位角有______ ；内错角有______ ；同旁内角有______ ．2、如图，请分别依据所给出的条件，判定相应的哪两条直线平行?并写出推理的根据．(1)如果∠2＝∠3，那么____________．(____________ ，____________)(2)如果∠2＝∠5，那么____________．(____________，____________)(3)如果∠2＋∠1＝180°，那么____________．(____________，____________ )(4)如果∠5＝∠3，那么____________．(____________，____________)(5)如果∠4＋∠6＝180°，那么____________．(____________，____________)(6)如果∠6＝∠3，那么____________．(____________，____________)3、如图，请分别根据已知条件进行推理，得出结论，并在括号内注明理由．(1)如果AB∥EF，那么∠2＝______．理由是____________________________________．(2)如果AB∥DC，那么∠3＝______．理由是____________________________________ ．(3)如果AF∥B,那么∠1＋∠2＝______．理由是______________________________ ．(4)如果AF∥BE∠4＝120°那么∠5＝______．理由是_______________________ ．三、合作探究1、在下列四个图中，∠1与∠2是同位角的图是( )．图①图②图③图④(A)①②(B)①③C)②③(D)③④2、同一平面内的四条直线满足a⊥b，b⊥c，c⊥d，则下列式子成立的是（）A．a∥b B．b⊥d C．a⊥d D．b∥c3、在下列条件中：①∠1＝∠2；②∠BAD＝∠BCD；③∠ABC＝∠ADC且∠3＝∠4；④∠BAD＋∠ABC＝180°，能判定AB∥CD的有( )．（第3题）（第5题）(A)3个(B)2个(C)1个(D)0个4、以下五个条件中，能得到互相垂直关系的有( )．①对顶角的平分线②邻补角的平分线③平行线截得的一组同位角的平分线④平行线截得的一组内错角的平分线⑤平行线截得的一组同旁内角的平分线(A)1个(B)2个 (C)3个(D)4个5、把一张对边互相平行的纸条折成如图所示，EF是折痕，若∠EFB＝32°，则下列结论正确的有( )．(1)∠C′EF＝32° (2)∠AEC＝148°(3)∠BGE＝64°(4)∠BFD＝116°(A)1个B)2个(C)3个(D)4个6、把命题“对顶角相等”写成“如果…，那么…”的形式为：；7、把命题“等角的补角相等”写成“如果…，那么…”的形式为：；三、反馈检测1.已知：如图，CD⊥AB于D，DE∥BC，EF⊥AB于F，求证：∠FED＝∠BCD．2.已知：如图，∠ABC＝∠ADC，BF、DE分别平分∠ABC与∠ADC．且∠1＝∠3．求证：AB∥DC．3..试讨论下列各种情况下∠A、∠C、∠E三者之间的关系。

八年级上册期末考试考前复习高频考点专题练习一遍过：《平行线性质》（二）1．如图1，AB∥CD，G为AB、CD之间一点．（1）若GE平分∠AEF，GF平分∠EFC．求证：EG⊥FG；（2）如图2，若∠AEP＝∠AEF，∠CFP＝∠EFC，且FP的延长线交∠AEP的角平分线于点M，EP的延长线交∠CFP的角平分线于点N，猜想∠M+∠N的结果并且证明你的结论；（3）如图3，若点H是射线EB之间一动点，FG平分∠EFH，MF平分∠EFC，过点G作GQ ⊥FM于点Q，请猜想∠EHF与∠FGQ的关系，并证明你的结论．2．已知，AB∥CD．点M在AB上，点N在CD上．（1）如图1中，∠BME、∠E、∠END的数量关系为：；（不需要证明）如图2中，∠BMF、∠F、∠FND的数量关系为：；（不需要证明）（2）如图3中，NE平分∠FND，MB平分∠FME，且2∠E+∠F＝180°，求∠FME的度数；（3）如图4中，∠BME＝60°，EF平分∠MEN，NP平分∠END，且EQ∥NP，则∠FEQ的大小是否发生变化，若变化，请说明理由，若不变化，求出∠FEQ的度数．3．如图1，已知直线l 1∥l 2，且l 3和l 1、l 2分别相交于A 、B 两点，l 4和l 1、l 2分别交于C 、D 两点，∠ACP 记作∠1，∠BDP 记作∠2，∠CPD 记作∠3．点P 在线段AB 上．（1）若∠1＝20°，∠2＝30°，请你求出∠3的度数．（2）请你根据上述问题，请你找出图1中∠1、∠2、∠3之间的数量关系，并说明理由．（3）如果点P 在直线l 3上且在A 、B 两点外侧运动时，其他条件不变，试探究∠1、∠2、∠3之间的关系（点P 和A 、B 两点不重合），写出你的结论并说明理由．4．已知AM ∥CN ，点B 为平面内一点，AB ⊥BC 于B ．（1）如图1，过点B 作BD ⊥AM 于点D ，∠BAD 与∠C 有何数量关系，并说明理由；（2）如图2，在（1）问的条件下，点E ，F 在DM 上，连接BE ，BF ，CF ，若BF 平分∠DBC ，BE 平分∠ABD ，∠FCB +∠NCF ＝180°，∠BFC ＝5∠DBE ，求∠ABE 的度数．5．已知EM∥BN．（1）如图1，求∠E+∠A+∠B的大小，并说明理由．（2）如图2，∠AEM与∠ABN的角平分线相交于点F．①若∠A＝120°，∠AEM＝140°，则∠EFD＝．②试探究∠EFD与∠A的数量关系，并说明你的理由．（3）如图3，∠AEM与∠ABN的角平分线相交于点F，过点F作FG⊥BD交BN于点G，若4∠A＝3∠EFG，求∠EFB的度数．6．对于平面内的∠M和∠N，若存在一个常数k＞0，使得∠M+k∠N＝360°，则称∠N为∠M 的k系补周角．如若∠M＝90°，∠N＝45°，则∠N为∠M的6系补周角．（1）若∠H＝120°，则∠H的4系补周角的度数为°（2）在平面内AB∥CD，点E是平面内一点，连接BE，DE．①如图1，∠D＝60°，若∠B是∠E的3系补周角，求∠B的度数．②如图2，∠ABE和∠CDE均为钝角，点F在点E的右侧，且满足∠ABF＝n∠ABE，∠CDF＝n∠CDE（其中n为常数且n＞1），点P是∠ABE角平分线BG上的一个动点，在P点运动过程中，请你确定一个点P的位置，使得∠BPD是∠F的k系补周角，并直接写出此时的k值（用含n的式子表示）．7．如图把一个含有30°角的直角三角板的直角顶点A放在直线a上，a∥b，B、C两点在平面上移动，请根据如下条件解答：（1）如图1，若点C在直线b上，点B在直线b的下方，∠2＝20°，则∠1＝；（2）如图2，若点C在平行直线a，b内部，点B在直线b的下方，∠2＝n°，求∠1的度数．8．如图，AB∥CD，直线EF交直线AB、CD于点M、N，NP平分∠ENC交直线AB于点P，∠EMB ＝76°．（1）求∠PNC的度数；（2）若PQ将∠APN分成两部分，且∠APQ：∠QPN＝1：3，求∠PQD的度数．9．当光线经过镜面反射时，入射光线、反射光线与镜面所夹的角对应相等例如：在图①、图②中，都有∠1＝∠2，∠3＝∠4．设镜子AB与BC的夹角∠ABC＝α．（1）如图①，若α＝90°，判断入射光线EF与反射光线GH的位置关系，并说明理由．（2）如图②，若90°＜α＜180°，入射光线EF与反射光线GH的夹角∠FMH＝β．探索α与β的数量关系，并说明理由．（3）如图③，若α＝120°，设镜子CD与BC的夹角∠BCD＝γ（90°＜γ＜180°），入射光线EF与镜面AB的夹角∠1＝m（0°＜m＜90°），已知入射光线EF从镜面AB开始反射，经过n（n为正整数，且n≤3）次反射，当第n次反射光线与入射光线EF平行时，请直接写出γ的度数．（可用含有m的代数式表示）10．如图，AB∥CD，点E在直线CD上，射线EF经过点B，BG平分∠ABE交CD于点G．（1）求证：∠BGE＝∠GBE；（2）若∠DEF＝70°，求∠FBG的度数．参考答案1．解：（1）∵AB∥CD，∴∠AEF+∠CFE＝180°，∵GE平分∠AEF，GF平分∠EFC，∴∠AEG＝∠FEG＝∠AEF，∠CFG＝∠GFE＝∠CFE，∴∠FEG+∠GFE＝90°，即EG⊥FG；（2）∵分别过M，N作MG∥AB，NH∥AB，∵AB∥CD，∴AB∥MG∥NH∥CD，∴∠AEM＝∠EMG，∠GMF＝∠MFC，∠AEN＝∠ENH，∠HNF＝∠NFC，∴∠EMF＝∠AEM+∠MFC，∠ENF＝∠AEN+∠NFC，同理：∠EPF＝∠AEP+∠PFC，∴∠EMF+∠ENF＝∠AEM+∠MFC+∠AEN+∠NFC，∵EM平分∠AEN，FN平分∠MFC，∴∠AEM＝∠AEN，∠NFC＝∠MFC，∴∠EMF+∠ENF＝∠AEN+∠MFC+∠MFC+∠AEN＝（∠MFC+∠AEN），∵∠AEP＝∠AEF，∠CFP＝∠EFC，∴∠MFC+∠AEN＝（∠AEF+∠EFC）＝×180°＝72°，∴∠EMF+∠ENF＝（∠MFC+∠AEN）＝×72°＝108°；（3）∠FGQ＝∠EHF．证明：∵AB∥CD，∴∠EHF+∠CFH＝180°，∵GQ⊥MF，∴∠FGQ＝90°﹣∠GFQ，∵FG平分∠EFH，MF平分∠EFC，∴∠GFE＝∠EFH，∠QFE＝∠CFE，∴∠GFQ＝∠CFH＝（180°﹣∠EHF）＝90°﹣∠EHF，∴∠FGQ＝90°﹣（90°﹣∠EHF）＝∠EHF．2．解：（1）过E作EH∥AB，如图1，∴∠BME＝∠MEH，∵AB∥CD，∴HE∥CD，∴∠END＝∠HEN，∴∠MEN＝∠MEH+∠HEN＝∠BME+∠END，即∠BME＝∠MEN﹣∠END．如图2，过F作FH∥AB，∴∠BMF＝∠MFK，∵AB∥CD，∴FH∥CD，∴∠FND＝∠KFN，∴∠MFN＝∠MFK﹣∠KFN＝∠BMF﹣∠FND，即：∠BMF＝∠MFN+∠FND．故答案为∠BME＝∠MEN﹣∠END；∠BMF＝∠MFN+∠FND．（2）由（1）得∠BME＝∠MEN﹣∠END；∠BMF＝∠MFN+∠FND．∵NE平分∠FND，MB平分∠FME，∴∠FME＝∠BME+∠BMF，∠FND＝∠FNE+∠END，∵2∠MEN+∠MFN＝180°，∴2（∠BME+∠END）+∠BMF﹣∠FND＝180°，∴2∠BME+2∠END+∠BMF﹣∠FND＝180°，即2∠BMF+∠FND+∠BMF﹣∠FND＝180°，解得∠BMF＝60°，∴∠FME＝2∠BMF＝120°；（3）∠FEQ的大小没发生变化，∠FEQ＝30°．由（1）知：∠MEN＝∠BME+∠END，∵EF平分∠MEN，NP平分∠END，∴∠FEN＝∠MEN＝（∠BME+∠END），∠ENP＝∠END，∵EQ∥NP，∴∠NEQ＝∠ENP，∴∠FEQ＝∠FEN﹣∠NEQ＝（∠BME+∠END）﹣∠END＝∠BME，∵∠BME＝60°，∴∠FEQ＝×60°＝30°．3．解：（1）∵l1∥l2，∴∠1+∠PCD+∠PDC+∠2＝180°，在△PCD中，∠3+∠PCD+∠PDC＝180°，∴∠3＝∠1+∠2＝50°；（2）∠1+∠2＝∠3，理由：∵l 1∥l 2，∴∠1+∠PCD +∠PDC +∠2＝180°，在△PCD 中，∠3+∠PCD +∠PDC ＝180°，∴∠1+∠2＝∠3；（3）当P 点在A 的外侧时，如图2，过P 作PF ∥l 1，交l 4于F ，∴∠1＝∠FPC ，∵l 1∥l 4， ∴PF ∥l 2，∴∠2＝∠FPD ，∵∠3＝∠FPD ﹣∠FPC ，∴∠3＝∠2﹣∠1，当P 点在B 的外侧时，如图3，过P 作PG ∥l 2，交l 4于G ， ∴∠2＝∠GPD ，∵l 1∥l 2，∴PG ∥l 1，∴∠1＝∠CPG ，∵∠3＝∠CPG ﹣∠GPD ，∴∠3＝∠1﹣∠2．4．解：（1）如图1，过点B 作BG ∥DM ，∵BD ⊥AM ，∴∠ABD +∠BAD ＝90°，DB ⊥BG ，即∠ABD +∠ABG ＝90°， 又∵AB ⊥BC ，∴∠CBG +∠ABG ＝90°，∴∠ABD＝∠CBG，∵AM∥CN，BG∥AM，∴CN∥BG，∴∠C＝∠CBG，∴∠ABD＝∠C，∴∠C+∠BAD＝90°；（2）如图2，过点B作BG∥DM，∵BF平分∠DBC，BE平分∠ABD，∴∠DBF＝∠CBF，∠DBE＝∠ABE，由（1）可得∠ABD＝∠CBG，∴∠ABF＝∠GBF，设∠DBE＝α，∠ABF＝β，则∠ABE＝α，∠ABD＝2α＝∠CBG，∠GBF＝β＝∠AFB，∠BFC＝5∠DBE＝5α，∴∠AFC＝5α+β，∵∠AFC+∠NCF＝180°，∠FCB+∠NCF＝180°，∴∠FCB＝∠AFC＝5α+β，△BCF中，由∠CBF+∠BFC+∠BCF＝180°，可得（2α+β）+5α+（5α+β）＝180°，①由AB⊥BC，可得β+β+2α＝90°，②由①②联立方程组，解得α＝9°，∴∠ABE＝9°．5．解：（1）过A作AQ∥EM，∴∠E+∠EAQ＝180°，∵EM∥BN，∴AQ∥BN，∴∠QAB+∠B＝180°，∵∠EAB＝∠EAQ+∠QAB，∴∠E+∠EAB+∠B＝360°；（2）①由（1）知∠AEM+∠A+∠ABN＝360°，∵∠A＝120°，∠AEM＝140°，∴∠ABN＝100°，∵∠AEM与∠ABN的角平分线相交于点F，∴∠DEF＝70°，∠FBC＝50°，∵EM∥BN，∴∠EDF＝∠FBC＝50°，∴∠EFD＝180°﹣∠DEF﹣∠EDF＝180°﹣70°﹣50°＝60°，故答案为60°；②由（1）知∠AEM+∠A+∠ABN＝360°，∴∠ABN＝360°﹣∠AEM﹣∠A，∵∠AEM与∠ABN的角平分线相交于点F，∴∠DEF＝∠AEM，∠FBC＝∠ABN，∵EM∥BN，∴∠EDF＝∠FBC＝∠ABN，∴∠EFD＝180°﹣∠DEF﹣∠EDF＝180°﹣∠AEM﹣∠ABN＝180°﹣（360°﹣∠A）＝∠A，即∠A＝2∠EFD；（3）设∠EFD＝x，则∠A＝2x，由题意得4•2x＝3（90+x），解得x＝54°，答：∠EFB的度数为54°．6．解：（1）设∠H的4系补周角的度数为x°，根据新定义得，120+4x＝360，解得，x＝60，∠H的4系补周角的度数为60°，故答案为60；（2）①过E作EF∥AB，如图1，∴∠B＝∠BEF，∵AB∥CD，∴EF∥CD，∠D＝60°，∴∠D＝∠DEF＝60°，∵∠B+60°＝∠BEF+∠DEF，即∠B+60°＝∠BED，∵∠B是∠BED的3系补周角，∴∠BED＝360°﹣3∠B，∴∠B+60°＝360°﹣3∠B，∴∠B＝75°；②当BG上的动点P为∠CDE的角平分线与BG的交点时，满足∠BPD是∠F的k系补周角，此时k＝2n．7．解：由题意可知：∠BAC＝90°，∠B＝30°，则∠ACB＝60°．（1）如图1，∵a∥b，∴∠1＝∠3，∵∠2+∠3＝∠ACB＝60°，∠2＝20°，∴∠3＝40°，故答案为40°；（2）如图2，过C作c∥a，∴∠1＝∠4，∵a∥b，∴c∥b，∴∠2＝∠5，∵∠4+∠5＝∠ACB＝60°，∴∠1+∠2＝60°，∵∠2＝n°，∴∠1＝（60﹣n）°．8．解：（1）∵AB∥CD，∴∠END＝∠EMB＝76°，∴∠ENC＝180°﹣∠END＝104°，∵NP平分∠ENC，∴∠PNC＝ENC＝52°；（2）∵∠APQ：∠QPN＝1：3，∴∠QPN＝3∠APQ，∵AB∥CD，∴∠MPN＝∠PNC＝52°，∴∠APN＝180°﹣∠MPN＝128°，∴∠APQ+∠QPN＝128°，∴4∠APQ＝128°，∴∠APQ＝32°，∴∠PQD＝∠APQ＝32°．则∠PQD的度数为32°．9．解：（1）EF∥GH，理由如下：在△BEG中，∠2+∠3+α＝180°，α＝90°，∴∠2+∠3＝90°，∵∠1＝∠2，∠3＝∠4，∴∠1+∠2+∠3+∠4＝180°，∵∠1+∠2+∠FEG＝180°，∠3+∠4+∠EGH＝180°，∴∠FEG+∠EGH＝180°，∴EF∥GH；（2）β＝2α﹣180°，理由如下：在△BEG中，∠2+∠3+α＝180°，∴∠2+∠3＝180°﹣α，∵∠1＝∠2，∠1＝∠MEB，∴∠2＝∠MEB，∴∠MEG＝2∠2，同理可得，∠MGE＝2∠3，在△MEG中，∠MEG+∠MGE+β＝180°，∴β＝180°﹣（∠MEG+∠MGE）＝180°﹣（2∠2+2∠3）＝180°﹣2（∠2+∠3）＝180°﹣2（180°﹣α）＝2α﹣180°；（3）90°+m或150°．理由如下：①当n＝3时，如下图所示：∵∠BEG＝∠1＝m，∴∠BGE＝∠CGH＝60°﹣m，∴∠FEG＝180°﹣2∠1＝180°﹣2m，∠EGH＝180°﹣2∠BGE＝180°﹣2（60°﹣m），∵EF∥HK，∴∠FEG+∠EGH+∠GHK＝360°，则∠GHK＝120°，则∠GHC＝30°，由△GCH内角和，得γ＝90°+m．②当n＝2时，如果在BC边反射后与EF平行，则α＝90°，与题意不符；则只能在CD边反射后与EF平行，如下图所示：根据三角形外角定义，得∠G＝γ﹣60°，由EF∥HK，且由（1）的结论可得，∠G＝γ﹣60°＝90°，则γ＝150°．综上所述：γ的度数为：90°+m或150°．10．解：（1）证明：∵AB∥CD，∴∠ABG＝∠BGE，∵BG平分∠ABE，∴∠ABG＝∠GBE，∴∠BGE＝∠GBE；（2）∵AB∥CD，∴∠ABE＝∠DEF＝70°，∴∠ABF＝180°﹣∠ABE＝110°，∵BG平分∠ABE，∴∠ABG＝ABE＝35°，∴∠FBG＝∠ABF+∠ABG＝110°+35°＝145°．答：∠FBG的度数为145°．。

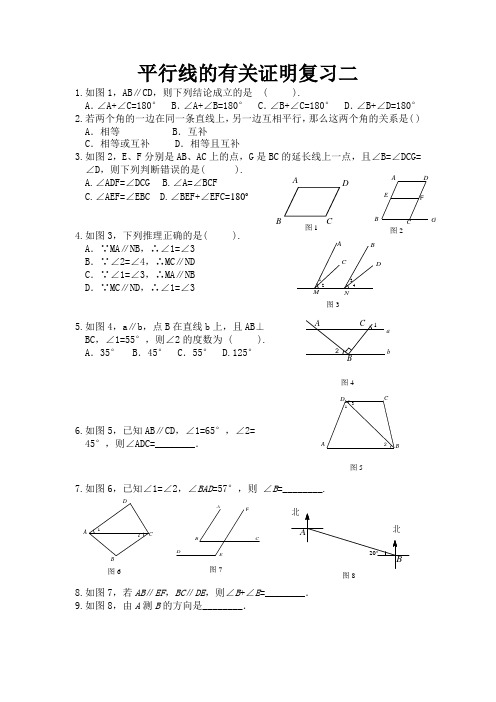
F A B C D EG 图2平行线的有关证明复习二1.如图1，AB∥CD，则下列结论成立的是 ( ). A ．∠A+∠C=180° B ．∠A+∠B=180° C ．∠B+∠C=180° D ．∠B+∠D=180°2.若两个角的一边在同一条直线上，另一边互相平行，那么这两个角的关系是( ) A ．相等 B ．互补 C ．相等或互补 D ．相等且互补3.如图2，E 、F 分别是AB 、AC 上的点，G 是BC 的延长线上一点，且∠B=∠DCG= ∠D，则下列判断错误的是( ).A.∠ADF=∠DCGB.∠A=∠BCFC.∠AEF=∠EBC D .∠BEF+∠EFC=1804.如图3，下列推理正确的是( ).A ．∵MA∥NB，∴∠1=∠3B ．∵∠2=∠4，∴MC∥NDC ．∵∠1=∠3，∴MA∥NBD ．∵MC∥ND，∴∠1=∠35.如图4，a∥b，点B 在直线b 上，且AB⊥ BC ，∠1=55°，则∠2的度数为 ( ).A ．35°B ．45° C．55° D.125°6.如图5，已知AB∥CD，∠1=65°，∠2=45°，则∠ADC=________．7.如图6，已知∠1=∠2，∠BAD =57°，则 ∠B =________.8.如图7，若AB ∥EF ，BC ∥DE ，则∠B +∠E =________． 9.如图8，由A 测B 的方向是________．A BC D4321M N 图3 21 A C ab 图4 231 A BC DA D 21A BC D FABC D E 图710.已知：如图，∠B =∠C.（1）若AD ∥BC,求证：AD 平分∠EAC;(2)若∠B+∠C+∠ABC=180°,AD 平分∠EAC,求证AD ∥BC.11.已知：如图，∠1=∠B ，∠A =32°.求：∠2的度数．12.如图，∠B+∠BCD+∠D=360， 求证：∠1=∠2．13.已知：如图，直线a 、b 被直线c 所截， 若∠1十∠2=180°，求证：a ∥b14. 如图14，已知AB ∥ED ，∠CAB=135°∠ACD=80°，求∠CDE 的度数B D1A BCD 2A BC DE1 32 415. 已知：如图15，AD ⊥BC 于D ，EG ⊥BC 于G ，∠E =∠3。

平行线综合复习及三角形全等基本判定一、知识梳理： （一）平行线1、平行线的判定方法：⑴平行线的定义：在同一平面内，不相交的两条直线叫做平行线； ⑵平行公理推论：平行于同一条直线的两条直线平行； ⑶在同一平面内，垂直于同一条直线的两条直线平行； ⑷ 同位角相等，两条直线平行； ⑸ 内错角相等，两条直线平行； ⑹ 同旁内角互补，两直线平行。

2、平行线的性质：⑴平行线不相交(根据定义)； ⑵两条直线平行，同位角相等； ⑶两条直线平行，内错角相等； ⑷两条直线平行，同旁内角互补。

（二）认识三角形：1. 三角形三边关系：三角形任意两边之和大于第三边，三角形任意两边之差小于第三边.判断三线段能否构成三角形方法：较短两段之和是否大于最长线段。

2. 三角形中的角的关系：(1)三角形的三个内角的和等于180°； （2）三角形的外角和等于360°；（3）三角形的一个外角等于不相邻的两内角之和； （4）三角形的一个外角大于不相邻的内角. 3. 三角形三线：（1）有三条角平分线，交于一点，在三角形的内部； （2）有三条中线，交于一点，在三角形内部；（3）有三条高线，交于一点，在锐角三角形的内部、在直角三角形的直角顶点处、在钝角三角形的外部.4. 三角形分类： Ⅰ、按角分类：（1）锐角三角形；（2）直角三角形；（3）钝角三角形. Ⅱ、按边分类：（1）不等边三角形；（2）等腰三角形；（3）等边三角形.（三）三角形全等的判定方法：1．全等图形定义：两个能够重合的图形称为全等图形． 2．全等图形的性质：（1）全等图形的形状和大小都相同，对应边相等，对应角相等 （2）全等图形的面积相等3．全等三角形：两个能够完全重合的三角形称为全等三角形（1）表示方法：两个三角形全等用符号“≌”来表示，读作“全等于” 如DEF ABC ∆∆与全等，记作ABC ∆≌DEF ∆（2）符号“≌”的含义：“∽”表示形状相同，“=”表示大小相等，合起来就是形状相同，大小也相等，这就是全等．的角叫做对应角．（4）证两个三角形全等时，通常把表示对应顶点的字母写在对应的位置上． 4．全等三角形的判定（一）：三边对应相等的两个三角形全等，简写成“边边边”或“SSS ”．如图，在ABC ∆和DEF ∆中⎪⎩⎪⎨⎧===DF AC EF BC DE ABABC ∆∴≌DEF ∆ 全等三角形的判定（二）：两边和它们的夹角对应相等的两个三角形全等，简写成“边角边”或“SAS”.几何表示：如图，在ABC ∆和DEF ∆中，ABC EF BC E B DEAB ∆∴⎪⎩⎪⎨⎧=∠=∠=≌)(SAS DEF ∆全等三角形的判定（三）：有两角和它们的夹边对应相等的两个三角形全等．简写成“角边角”或“ASA ” 如图，在ABC ∆与DEF ∆中EB DE AB DA ∠=∠=∠=∠∴)(ASA DEF ABC ∆≅∆ASA 公理推论（AAS 公理）：有两角和其中一角的对边对应相等的两个三角形全等．直角三角形全等的另外一种特殊判定方法：斜边和直角边对应相应的两直角三角形全等，简写成“斜边直角边”或“HL ”. 如图：在ABC ∆与DEF ∆中，∠C=∠E=90°AB DFAC DE=⎧⎨=⎩ 则Rt ABC ≌Rt DFE二、分类探究：（一）平行线综合巩固：例1、如图，已知AB ∥CD ∥EF ，GC ⊥CF ，∠B ＝60°，∠EFC ＝45°，求∠BCG 的度数. A B C DEFA BCED FD EFAB CA 2C F 3 ED 1 B例2、如图，已知∠1＝∠2，∠C ＝∠D ． 求证：∠A ＝∠F .例3、如图，已知，AB ∥CD .求证：∠α、∠β、∠γ、∠ψ之间的关系是∠α＋∠γ＋∠ψ－∠β＝180°例4、如图，已知AB ∥ MP ∥CD , MN 平分∠AMD ，∠A ＝20°，∠D ＝30°，求∠NMP 的度数.例5、如图，已知∠1＋∠2＝180°，∠3＝∠B ． 求证：∠AED ＝∠ACB.例6、如图将面积为a 2的小正方形和面积为b 2的大正方形放在一起，用添补法如何求出阴影部分面积？（二）认识三角形：例1、下列每组数分别是三根小木棒的长度，用它们能摆成三角形吗？为什么？（单位：cm ）（1） 1， 3， 3 （ ） （2） 3， 4， 7 （ ） （3） 5， 9， 13 （ ） （4） 11， 12， 22 （ ） （5） 14， 15， 30 （ ）例2、已知一个三角形的两边长分别是3cm 和4cm ，则第三边长x 的取值范围是 ；若x 是奇数，则x 的值是 ，这样的三角形有 个；若x 是偶数，则x 的值是 ；这样的三角形又有 个。

期末复习二平行线与相交线本章知识结构图1.如图，△DAF沿直线AD平移得到△CDE，CE，AF的延长线交于点B.若∠AFD=111°,则∠CED=（）【A】110°【B】111°【C】112°【D】113°2.如图，能判断AD//BC 的条件是（）【A】∠DAC=∠BCA 【B】∠DCB+∠ABC=180°【C】∠ABD=∠ADC 【D】∠BAC=∠ACD3.如图，直线1l ∥2l ,直线AB 交直线1l ,2l 于D,B 两点,AC⊥AB 交直线1l 于C. 若∠1=15°20′， 则∠2=___.4.如图，说法正确的是 （ ）【A 】∠A =∠1 是同位角 【B 】∠A =∠2 是内错角【C 】∠A =∠3 是同旁内角 【D 】∠A =∠B 是同旁内角5.如图，a ∥b ，设∠1＝（3m ＋10）°，∠4＝（7m －30）°，（ ）【A 】若∠2＝∠3，则∠2＝（3m －10）° 【B 】若∠1＝∠4，则∠3＝（m ＋30）°【C 】若∠1＝2∠2＝2∠3，则∠2＝（3m ）° 【D 】若∠1＝∠2＝∠3，∠2＝（5m －10）°6. 如图，△DAF 沿直线AD 平移得到△CDE ，CE ，AF 的延长线交于点B ．若∠AFD ＝111°，则∠CED ＝（ ）A ．110°B ．111°C ．112°D ．113°7.如图，在下列条件中，能判断AD ∥BC 的是（ ）A ．∠DAC ＝∠BCAB ．∠DCB +∠ABC ＝180°C ．∠ABD ＝∠BDCD ．∠BAC ＝∠ACD 8. 如图，∠3的同位角是（ ）A ．∠1B ．∠2C ．∠BD ．∠C 9. 如图，把一副三角板放在桌面上，若两直角顶点重合，两条斜边平行，则∠1与∠2的差是（ ）A ．45°B ．30°C ．25°D ．20°10.如图，直线AB 交∠DCE 的边CE 于点F ，则∠1和∠2是（ ）A 对顶角B 同旁内角C 同位角D 内错角11．如图，点E在AC的延长线上,给出四个条件：①∠1=∠2；②∠3=∠4；③∠A=∠DCE；④∠D+∠ABD=180°.其中能判断AB∥CD的有（）A ①②B ②③C ③④D ①④12、下列两个命题，①过一点有且只有一条直线和已知直线平行；②垂直于同一条直线的两条直线互相平行，其中判断正确的是( )【A】①②都对【B】①对②错【C】①②都错【D】①错②对13、如图，点C在射线BM上，CF是∠ACM的平分线，且CF∥AB，∠ACB＝50°，则∠B的度数为（）A．65°B．60°C．55°D．50°14、如图，将△ABC沿BC方向平移2cm得到△DEF，若△ABC的周长为16cm，则四边形ABFD的周长为（）A．16cm B．18cm C．20cm D．22cm15、如图，用直尺和三角尺画图：已知点P和直线a，经过点P作直线b，使b∥a，其画法的依据是（）A．同位角相等，两直线平行B．两直线平行，同位角相等C．过直线外一点有且只有一条直线与已知直线平行D．内错角相等，两直线平行16、如图，直线a，b被直线c所截，∠1＝62°，∠3＝80°，现逆时针转动直线a至a′位置，使a′∥b，则∠2的度数是（）A．8°B．10°C．18°D．28°二、填空题1.如图，直线l1∥l2，直线AB交l1，l2于D，B两点，AC⊥AB交直线l1于点C．若∠1＝15°20'，则∠2＝．2、如图，点E在AD的延长线上，下列四个条件：①. ∠1=∠2②. ∠C+∠ABC=180°③. ∠C+∠CDE④. ∠4=∠3.能判断AB∥CD的是（填序号）3. 如图，将△ABC沿BC方向平移4cm得到△DEF，如果四边形ABFD的周长是28cm，则△DEF 的周长是cm．4.如图，小聪把一块含有60°角的直角三角板的两个顶点分别放在长方形的一组的对边上，并测得∠1＝26°，则∠2的度数是．5. 已知直线m∥n，将一块含30°角的直角三角板ABC，按如图所示方式放置，其中A、B两点分别落在直线m、n上，若∠1=25°，则∠2的度数为。

第五章相交线与平行线单元复习巩固(2)班级姓名座号月日主要内容:掌握命题的概念及平行线的性质和判定的综合运用和利用平移设计图案一、课堂练习:1.已知命题:(1)对顶角的角平分线构成一条直线；(2)两条直线相交构成的两组对顶角的角平分线互相垂直；(3)邻补角的角平分线互相垂直；(4)如果两条直线平行,那么同位角的角平分线也互相平行.这四个命题中,真命题的个数是( )A.1个B.2个C.3个D.4个2.一个台球桌的桌面如图所示,一个球在桌面上的点A滚向桌边PQ,碰着PQ上的点B后便反弹而滚向桌边RS,碰着RS上的点C便反弹而滚向点D.如果PQ∥RS,AB、BC、CD都是直线,且∠ABC的平分线BN垂直于PQ,∠BCD的平分线CM垂直于RS,那么,球经过两次反弹后所滚的路径CD是否平行于原来的路径AB?C3.如图,MN ∥PQ ,∠M =∠P .试说明MQ ∥NP .(请用三种方法加以说明)4.在方格纸上,利用平移画出正方形ABCD 的立体图,其中点D '是D 的对应点.(要求在立体图中,看不到的线条用虚线表示)二、课后作业: 5.选择题(1)如图,点E 在AC 的延长线上,下列条件能判断AB ∥CD 的是( ) A.∠3=∠4 B.∠1=∠2 C.∠D =∠DCE D.∠D +∠ACD =180 (2)如图,∠1+∠2=180,∠3=108,则∠4的度数是( ) A.72 B.80 C.82 D.1086.图中所示为一组护网的示意图,它可看成由两组平行线组成,你能通过检验一些角的大小来判断它们是否平行吗?说出你的理由.ABCDE1342abcd1234ABCDD '7.指出下列命题的题设和结论,并判断它们是真命题还是假命题.如果是假命题,请举出一个反例.(1)两个角的和等于平角时,这两个角互为补角；(2)相等的角是对顶角；(3)两条平行线被第三条直线所截,内错角相等.8.如图,∠1+∠2=180,∠DAE=∠BCF,DA平分∠BDF.(1)AE与FC会平行吗?说明理由.(2)AD与BC的位置关系如何?为什么?(3)BC平分∠DBE吗?为什么?AB CDE F1 2参考答案一、课堂练习:1.已知命题:(1)对顶角的角平分线构成一条直线；(2)两条直线相交构成的两组对顶角的角平分线互相垂直；(3)邻补角的角平分线互相垂直；(4)如果两条直线平行,那么同位角的角平分线也互相平行.这四个命题中,真命题的个数是( D )A.1个B.2个C.3个D.4个 2.一个台球桌的桌面如图所示,一个球在桌面上的点A 滚向桌边PQ ,碰着PQ 上的点B 后便反弹而滚向桌边RS ,碰着RS 上的点C 便反弹而滚向点D .如果PQ ∥RS ,AB 、BC 、CD 都是直线,且∠ABC 的平分线BN 垂直于PQ ,∠BCD 的平分线CM 垂直于RS ,那么,球经过两次反弹后所滚的路径CD 是否平行于原来的路径AB ? 解:球经过两次反弹后所滚的路径CD 平行于原来的路径AB. 理由:∵CM ⊥RS∴∠2+∠5=90° 同理∠3+∠6=90° ∵PQ ∥RS∴∠5=∠6(两直线平行,内错角相等)∴∠2=∠3(等角的余角相等)∵BN 是∠ABC 的平分线∴∠ABC =2∠3 同理∠BCD =2∠2 ∴∠ABC =∠BCD∴CD ∥AB3.如图,MN ∥PQ ,∠M =∠P .试说明MQ ∥NP .(请用三种方法加以说明)C解法一:∵MN ∥PQ∴∠M +∠Q =180 ∵∠M =∠P∴∠P +∠Q =180 ∴MQ ∥NP解法二:延长MQ∵MN ∥PQ ∴∠M =∠1∵∠M =∠P ∴∠P =∠1 ∴MQ ∥NP解法三:连接MP ∵MN ∥PQ ∴∠1=∠2 ∵∠NMQ =∠NPQ ∴∠3=∠4∴MQ ∥NP4.在方格纸上,利用平移画出正方形ABCD 的立体图,其中点D '是D 的对应点.(要求在立体图中,看不到的线条用虚线表示)二、课后作业: 5.选择题(1)如图,点E 在AC 的延长线上,下列条件能判断AB ∥CD 的是( B ) A.∠3=∠4 B.∠1=∠2 C.∠D =∠DCE D.∠D +∠ACD =180(2)如图,∠1+∠2=180,∠3=108,则∠4的度数是( A ) A.72 B.80 C.82 D.1086.图中所示为一组护网的示意图,它可看成由两组平行线组成,你能通过检验一些角的大小来判断它们是否平行吗?说出你的理由.解:可检验它们的同旁内角是否互补,若同旁内角互补, 则两直线平行,否则两直线不平行.7.指出下列命题的题设和结论,并判断它们是真命题还是假命题.如果是假命题,请举出一个反例.(1)两个角的和等于平角时,这两个角互为补角； (2)相等的角是对顶角； (3)两条平行线被第三条直线所截,内错角相等.ABCDE1342abcd1234ABCDA 'C 'D 'B '答:(1)题设是两个角的和等于平角,结论是这两个角互为补角.这是真命题.(2)题设是两个角相等,结论是这两个角是对顶角.这是假命题.反例:长方形的邻角相等,但它们不是对顶角.(3)题设是两条平行线被第三条直线所截,结论是内错角相等.这是真命题.8.如图,∠1+∠2=180,∠DAE=∠BCF,DA平分∠BDF.(1)AE与FC会平行吗?说明理由.(2)AD与BC的位置关系如何?为什么?(3)BC平分∠DBE吗?为什么?解:(1)答:AE∥FC理由:∵∠1+∠2=180,∠2+∠CDB=180(邻补角定义) ∴∠1=∠CDB∴AE∥FC(同位角相等,两直线平行)(2)答: AD∥BC理由:∵AE∥CF∴∠C=∠CBE(两直线平行,内错角相等)又∵∠A=∠C∴∠A=∠CBE∴AD∥BC(同位角相等,两直线平行)(3)答:BC平分∠DBE理由:∵DA平分∠BDF∴∠FDA=∠ADB∵AE∥CF∴∠FDA=∠A∴∠A=∠ADB∵AD∥BC∴∠EBC=∠A,∠CBD=∠ADB∴∠EBC=∠CBD即BC平分∠DBE A BC DEF1 2。