七下第一章平行线复习

七年级数学下《平行线及其判定》笔记
一、平行线的定义
平行线是指在同一平面内，两条直线没有交点，或者说两条直线之间的距离处处相等。

二、平行线的判定定理
1.同位角相等：当两条直线被第三条直线所截，如果同位角相等，则这两条直线
平行。

2.内错角相等：当两条直线被第三条直线所截，如果内错角相等，则这两条直线
平行。

3.同旁内角互补：当两条直线被第三条直线所截，如果同旁内角互补（即角度和
为180°），则这两条直线平行。

三、应用实例
1.交通标志：在公路上，车道线通常都是平行的，这些线可以帮助驾驶员判断车
辆是否在正确的车道上行驶。

2.建筑设计：在建筑设计中，为了确保建筑物的稳定性，通常会使用平行线来构
建平行的梁和柱子。

3.机械制造：在机械制造中，为了确保机器的精确度，常常需要使用平行线来检
测和调整机器的部件。

四、注意事项
1.平行线必须在同一平面内定义。

2.平行线的判定定理必须同时满足，不能只满足其中一条。

3.在实际应用中，要结合具体情境判断两条线是否平行。

五、练习与巩固
1.判断题：给出一些线段的图片，判断它们是否平行。

2.选择题：给出一些关于平行线的描述，选择正确的判定定理。

3.应用题：结合实际问题，例如计算平行线的距离、判断两条线是否平行等。

浙教版七年级下册期末复习（第一章平行线）姓名 __________一：选择题1、如图，两只手的食指和拇指在同一个平面内，它们组成的一对角可当作是（）A、同位角B、内错角C、对顶角D、同旁内角2．如图，直线 a、b 被直线 c 所截，以下说法正确的选项是（）A．当∠ 1=∠2 时，必定有 a∥ b B．当 a∥b 时，必定有∠C．当 a∥b 时，必定有∠ 1＋∠ 2=180°D．当 a∥b 时，必定有∠1=∠21＋∠ 2=90°3、如图 3 所示，点 E 在 AC 的延伸线上，以下条件中能判断 AB ∥ CD 的是 ( ) A．∠3= ∠4 B ．∠ 1= ∠2 C．∠ D=∠DCED． D、∠ D+∠ACD=180°4．以下图形中，∠ 1 与∠ 2 不是同位角的是()5．一架飞机向北飞翔，两次改变方向后，行进的方向与本来的航行方向平行，已知第一次向左拐50°，那么第二次向右拐（）A、40°B、50°C、 130°D、150° 6、以以下图，在△ABC 中， D、E、F 分别在 AB 、 BC、 AC 上，且 EF∥ AB ，要使 DF ∥BC，只要知足以下条件中的（）A 、∠1=∠2B 、∠2=∠AFDC 、∠ 1=∠AFD D、∠1=∠DFE第7题图 D C 第6题图 213第8题图A B E7．如图，点A．∠ 1=∠2 E 在 AD 的延伸线上，以下条件中能判断BC∥ADB.∠2=∠3C.∠1=∠5D.∠3=∠4的是（）8、如图，已知∠A、AB∥CD1=∠2, 则有 ()B、AE∥DCC、AB∥CD 且 AE∥DCD、以上都不对9．给出以下说法：（1）两条直线被第三条直线所截，同位角相等；（2）平面内的一条直线和两条平行线中的一条订交，则它与另一条也订交；（3）内错角相等正确的有（）个。

A ． 0 B.1 C.2 D.310．如图，给出了过直线外一点画已知直线的平行线的方法，其依照是（）A ．同位角相等，两直线平行B．内错角相等，两直线平行C．同旁内角互补，两直线平行D．两直线平行，同位角相等二：填空题11、如图，一个合格的弯形管道，经过两次拐弯后保持平行（即 AB∥ DC）．?假如∠C=60°，那么∠ B 的度数是 ________．12．如图 3，假如 AB ∥CD，∠1=65°，那么∠2=第 13题图 AD 78 EE 第 11题图°A D 第 14题图124第 12题图BC OB C13、如图，已知 AB ∥ CD， AD ∥ BC，∠ B＝60°，∠ EDA ＝ 50°，则∠CDO＝.14、如图， DAE是一条直线， DE∥ BC，则∠ BAC =_____.15、如图， D、E、F 分别是△ ABC三边上的点，且∠ 1=∠B，∠2=∠C，?则图中与∠A 相等的角有 _________ ．（所有写出）A第 15题F E2 1B D C第16题第17题16．如图，假如∠1=∠2=30°，要使图中 DE∥BC且 EF∥BD，则应补上的一个条件是 __________．17．如图，把一张长方形纸片 ABCD沿 EF 折叠后，点 C，D 分别落在 C ′， D′的地点上， EC′交 AD于点 G，已知∠ EFG=58° , 那么∠ BEG =_______度．三：解答题18、填空（填上原因，增补完好）如图， AB∥CD， BF∥CE，则∠ B 与∠ C 有什么关系？请说明原因。

2023年浙教版七下数学第一章平行线章节复习（教师版）一、知识梳理知识点1：平行线的定义1．定义：在同一平面内，不相交的两条直线叫做平行线，如果直线a与b平行，记作a ∥b．注意：(1)平行线的定义有三个特征：一是在同一个平面内；二是两条直线；三是不相交，三者缺一不可；(2)有时说两条射线平行或线段平行，实际是指它们所在的直线平行，两条线段不相交并不意味着它们就平行．(3)在同一平面内，两条直线的位置关系只有相交和平行两种．特别地，重合的直线视为一条直线，不属于上述任何一种位置关系．知识点2：同位角、内错角和同旁内角两条直线被第三条线所截，可得八个角，即“三线八角”，如图6所示。

（1）同位角：可以发现∠1与∠5都处于直线l的同一侧，直线a、b的同一方，这样位置的一对角就是同位角。

图中的同位角还有∠2与∠6，∠3与∠7，∠4与∠8。

（2）内错角：可以发现∠3与∠5都处于直线l的两旁，直线a、b的两方，这样位置的一对角就是内错角。

图中的内错角还有∠4与∠6。

（3）同旁内角：可以发现∠4与∠5都处于直线l的同一侧，直线a、b的两方，这样位置的一对角就是同旁内角。

图中的同旁内角还有∠3与∠6。

知识点3：平行公理及推论1．平行公理：经过直线外一点，有且只有一条直线与这条直线平行．2．推论：如果两条直线都与第三条直线平行，那么这两条直线也互相平行．记作：如果a∥b，a∥c，那么a∥c注意：(1)平行公理特别强调“经过直线外一点”，而非直线上的点，要区别于垂线的第一性质．（2）“平行公理的推论”也叫平行线的传递性知识点4：平行线判定判定方法（1）：两条直线被第三条直线所截，如果同位角相等，那么这两条直线平行简单说成：同位角相等，两直线平行。

几何语言：∵∠1＝∠2∴ AB∥CD（同位角相等，两直线平行）判定方法（2）：两条直线被第三条直线所截，如果内错角相等，那么这两条直线平行．简单说成：内错角相等，两直线平行。

上课用---新浙教版七年级下数学知识点汇总(期末复习宝典)第1章平行线在同一平面内，两条直线的位置关系只有两种：相交与平行。

平行线的定义为：在同一平面内，不相交的两条直线叫做平行线，用符号“∥”表示。

为什么要有“在同一平面内”这个条件？因为平行线只存在于同一平面内，如果不在同一平面内，两条直线可能会相交。

平行线的基本事实是：经过直线外一点，有且只有一条直线与这条直线平行。

为什么要经过“直线外”一点？因为如果经过直线上的点，会有无数条直线与这条直线平行。

用三角尺和直尺画平行线的方法是：一贴，二靠，三推，四画。

需要注意的是，作图题要写出结论。

同位角、内错角、同旁内角是判断平行线关系的重要概念。

在判断过程中，需要画出给定的两个角的边（共三条边），公共边就是截线，剩下两条边就是被截线。

同位角在截线的同旁，被截线的同一侧；内错角在截线的异侧，被截线之间；同旁内角在截线的同旁，被截线之间。

练时需要填写正确的角对应关系。

平行线的判定有多种方法：同位角相等、内错角相等、同旁内角互补、平行线的定义、平行于同一条直线的两条直线平行、在同一平面内，垂直于同一条直线的两条直线互相平行。

在练中需要根据给定条件判断两条直线是否平行。

平行线的性质包括同位角相等、内错角相等、同旁内角互补。

在练中需要根据已知条件计算未知角度。

图形的平移是指一个图形沿某个方向移动，在XXX的过程中，原图形上所有的点都沿同一个方向移动相等的距离，这样的图形运动叫做图形的平移。

平移不改变图形的形状、大小和方向，且一个图形和它经过平移所得的图形中，两组对应点的连线平行（或在同一条直线上）且相等。

在描述一个图形的平移时，必须指出平移的方向和距离。

练：已知△ABC和其平移后的△DEF，点A的对应点是D，点B的对应点是E，线段AC的对应线段是DF，线段AB的对应线段是DE，平移的方向是从△ABC到△DEF的方向，平移的距离是未知。

若AC＝AB＝5，BC＝4，平移的距离是3，则CF＝4，DB＝5，AE＝3，四边形AEFC的周长是14.折叠问题：1）如图，将一张纸条ABCD沿EF折叠，若折叠角∠XXX°，则∠1＝64°。

江苏省数学七年级下学期期末复习专题1 平行线姓名:________ 班级:________ 成绩:________一、单选题 (共15题；共30分)1. （2分） (2021八上·彭州开学考) 下列说法（1）两条不相交的直线是平行线；（2）过一点有且只有一条直线与已知直线平行；（3）在同一平面内两条不相交的线段一定平行；（4）过一点有且只有一条直线与已知直线垂直；（5）两点之间，直线最短；其中正确个数是（）A . 0个B . 1个C . 2个D . 3个2. （2分） (2021七下·曾都期末) 如图，下列说法不正确的是（）A . ∠1与∠3是对顶角B . ∠2与∠6是同位角C . ∠3与∠4是内错角D . ∠3与∠5是同旁内角3. （2分）(2020·遵化期中) 如图，四个图形中，∠1 和∠2不是同位角的是（）A .B .C .D .4. （2分） (2020七下·深圳期中) 如图，下列条件中不能判定AB∥CD的是（）A . ∠1＋∠4＝180°B . ∠2＝∠6C . ∠5＋∠6＝180°D . ∠3＝∠55. （2分） (2020七下·硚口期中) 如图，点在的延长线上，下列条件中不能判定的是（）A .B .C .D .6. （2分） (2019七下·江门期末) 下列命题错误的是（）A . 如果，那么B . 如果，那么C . 如果，那么D . 如果，那么7. （2分）(2018·宣化模拟) 如图，直线∥ ，直线与、都相交，如果∠1=50°，那么∠2的度数是（）A . 50°B . 100°C . 130°D . 150°8. （2分） (2019八上·桂林期末) 下列命题：①若，则；②两直线平行，内错角相等；③对顶角相等.它们的逆命题一定成立的有（）A . 0个B . 1个C . 2个D . 3个9. （2分） (2021八上·杭州期末) 在下列命题中，为真命题的是（）A . 相等的角是对顶角B . 平行于同一条直线的两条直线互相平行C . 同旁内角互补D . 垂直于同一条直线的两条直线互相平行10. （2分）(2021·禅城模拟) 如图，则的度数为（）A .B .C .D .11. （2分）数轴上一点A表示的有理数为﹣2，若将A点向右平移3个单位长度后，A点表示的有理数应为（）A . 3B . ﹣1C . 1D . ﹣512. （2分） (2020八下·余干期末) 将一次函数的图像沿轴向左平移4个单位长度后，得到的新的图像对应的函数关系式为（）A .B .C .D .13. （2分）如图，直线a，b都与直线c相交，给出的下列条件：①∠1=∠7；②∠3=∠5；③∠1+∠8=180°；④∠3=∠6．其中能判断a∥b的是（）A . ①③B . ②③C . ③④D . ①②③14. （2分）如图．已知直线a ， b被直线c所截，且a∥b ，∠1＝48°，那么∠2的度数为（）A . 42°B . 48°C . 52°D . 132°15. （2分）(2018·遵义模拟) 如图，已知直线AB,CD被直线AC所截，AB∥CD，E是平面内任意一点（点E 不在直线AB,CD,AC上），设∠BAE=α，∠DCE=β．下列各式：①α+β，②α﹣β，③180°﹣α﹣β，④360°﹣α﹣β，∠AEC的度数可能是（）A . ①②③B . ①②④C . ①③④D . ①②③④二、填空题 (共5题；共5分)16. （1分） (2017七下·嵊州期中) 如图，请添加一个条件：，使DE∥BC.17. （1分）(2018·海陵模拟) 如图，AB∥CD， AF＝EF，若∠C＝62°，则∠A＝度．18. （1分）(2020·青海) 如图，将周长为8的沿BC边向右平移2个单位，得到，则四边形的周长为.19. （1分）在同一平面内L1与L2没有公共点，则L1L2 ．20. （1分）如图，与∠C是直线BC与被直线AC所截的同位角，与是直线AB与AC被直线DE所截的内错角，与∠A是直线AB与BC被直线所截的同旁内角．三、解答题 (共7题；共58分)21. （5分） (2019七下·金寨期末) 已知：如图所示，和的平分线交于，交于点，．（1）求证：；（2）试探究与的数量关系．22. （8分） (2020七下·北京期中) 动手操作题：如图，点A在∠O的一边OA上．按要求画图并填空：（1）过点A画直线AB⊥OA，与∠O的另一边相交于点B；（2）过点A画OB的垂线段AC，垂足为点C；（3）过点C画直线CD∥OA，交直线AB于点D；（4）∠CDB=°；（5）图中，与∠O相等的角有．23. （7分） (2019九上·南岗期中) 如图，在边长为1个单位长度的小正方形组成的网格中，给出了格点三角形（顶点是网格线的交点）．（1）先将竖直向上平移6个单位，再水平向右平移3个单位得到△ ，请画出△ ；（2）将△ 绕点顺时针旋转，得△ ，请画出△ ；（3）连接，直接写出的长．24. （10分） (2019七下·吉林期中) 如图,已知∠1＝∠2,∠3＋∠4＝180°.求证：AB∥EF25. （5分） (2020八下·新蔡期末) 如图所示，已知点E，F在 ABCD的对角线BD上，且BE=DF.求证：（1）△ABE≌△CDF；（2）AE∥CF.26. （10分） (2020七下·云梦期中) 如图，在平面直角坐标系xOy中，已知，将线段平移至，点D在x轴正半轴上，，且 .连接OC，AB，CD，BD.（1）写出点C的坐标为；点B的坐标为；（2）当的面积是的面积的3倍时，求点D的坐标；（3）设，，，判断、、之间的数量关系，并说明理由.27. （13分）如图所示，在∠AOB内有一点P．①过P画L1∥OA；②过P画L2∥OB；③用量角器量一量L1与L2相交的角与∠O的大小有怎样关系？参考答案一、单选题 (共15题；共30分)答案：1-1、考点：解析：答案：2-1、考点：解析：答案：3-1、考点：解析：答案：4-1、考点：解析：答案：5-1、考点：解析：答案：6-1、考点：解析：答案：7-1、考点：解析：考点：解析：答案：9-1、考点：解析：答案：10-1、考点：解析：考点：解析：答案：12-1、考点：解析：答案：13-1、考点：解析：答案：14-1、考点：解析：答案：15-1、考点：解析：二、填空题 (共5题；共5分)答案：16-1、考点：解析：答案：17-1、考点：解析：答案：18-1、考点：解析：答案：19-1、考点：解析：答案：20-1、考点：解析：三、解答题 (共7题；共58分)答案：21-1、答案：21-2、考点：解析：答案：22-1、答案：22-2、答案：22-3、答案：22-4、答案：22-5、考点：解析：答案：23-1、答案：23-2、答案：23-3、考点：解析：答案：24-1、考点：解析：答案：25-1、答案：25-2、考点：解析：答案：26-1、答案：26-2、答案：26-3、考点：解析：答案：27-1、考点：解析：。

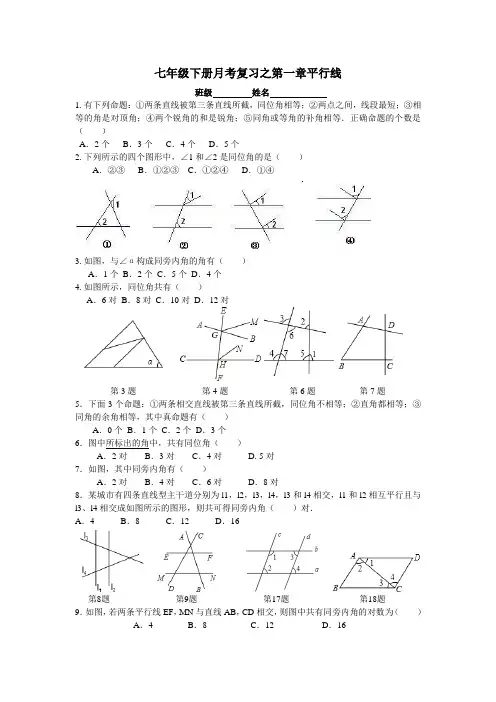
七年级下册月考复习之第一章平行线班级姓名1.有下列命题：①两条直线被第三条直线所截，同位角相等；②两点之间，线段最短；③相等的角是对顶角；④两个锐角的和是锐角；⑤同角或等角的补角相等．正确命题的个数是（）A．2个B．3个C．4个D．5个2.下列所示的四个图形中，∠1和∠2是同位角的是（）A．②③B．①②③C．①②④D．①④3.如图，与∠α构成同旁内角的角有（）A．1个B．2个C．5个D．4个4.如图所示，同位角共有（）A．6对B．8对C．10对D．12对第3题第4题第6题第7题5．下面3个命题：①两条相交直线被第三条直线所截，同位角不相等；②直角都相等；③同角的余角相等，其中真命题有（）A．0个B．1个C．2个D．3个6．图中所标出的角中，共有同位角（）A．2对B．3对C．4对D.5对7．如图，其中同旁内角有（）A．2对B．4对C．6对D．8对8．某城市有四条直线型主干道分别为l1，l2，l3，l4，l3和l4相交，l1和l2相互平行且与l3、l4相交成如图所示的图形，则共可得同旁内角（）对．A．4 B．8 C．12 D．16第8题第9题第17题第18题9．如图，若两条平行线EF，MN与直线AB，CD相交，则图中共有同旁内角的对数为（）A．4 B．8 C．12 D．1610．下列说法不正确的是（）A．过任意一点可作已知直线的一条平行线B．同一平面内两条不相交的直线是平行线C．在同一平面内，过直线外一点只能画一条直线与已知直线垂直D．平行于同一直线的两直线平行11．下列语句中：①一条直线有且只有一条垂线；②不相等的两个角一定不是对顶角；③两条不相交的直线叫做平行线；④若两个角的一对边在同一直线上，另一对边互相平行，则这两个角相等；⑤不在同一直线上的四个点可画6条直线；⑥如果两个角是邻补角，那么这两个角的平分线组成的图形是直角．其中错误的有（）A．2个B．3个C．4个D．5个12．下列语句：①同一平面上，三条直线只有两个交点，则其中两条直线互相平行；②如果两条平行线被第三条截，同旁内角相等，那么这两条平行线都与第三条直线垂直；③过一点有且只有一条直线与已知直线平行，其中（）A．①、②是正确的命题B．②、③是正确命题C．①、③是正确命题D．以上结论皆错13．下列说法中可能错误的是（）A．过一点有且只有一条直线与已知直线平行B．过一点有且只有一条直线与已知直线垂直C．两条直线相交，有且只有一个交点D．若两条直线相交成直角，则这两条直线互相垂直14．下列选项中正确的是（）A．相等的角是对顶角B．两直线平行，同旁内角相等C．直线外一点到这条直线的垂线段，叫点到直线的距离D．经过直线外一点，有且只有一条直线与这条直线平行15．过一点画已知直线的平行线（）A．有且只有一条B．不存在C．有两条D．不存在或有且只有一条16．某人在广场上练习驾驶汽车，两次拐弯后，行驶方向与原来相同，这两次拐弯的角度可能是（）A．第一次左拐30°，第二次右拐30°B．第一次右拐50°，第二次左拐130°C．第一次右拐50°，第二次右拐130°D．第一次向左拐50°，第二次向左拐120°17．如图，要得到a∥b，则需要条件（）A．∠2=∠4 B．∠1+∠3=180°C．∠1+∠2=180°D．∠2=∠318．如图，下列说法中，正确的是（）A．因为∠2=∠4，所以AD∥BCB．因为∠BAD+∠D=180°，所以AD∥BCC．因为∠1=∠3，所以AB∥CDD．因为∠BAD+∠B=180°，所以AD∥BC19．在同一个平面内，不相邻的两个直角，如果它们有一条边共线，那么另一边互相（）A．平行B．垂直C．共线D．平行或共线20．下列与垂直相交的说法：①平面内，垂直于同一条直线的两条直线互相平行；②一条直1FC E B A DA BEDC线如果它与两条平行线中的一条垂直，那么它与另一条也垂直；③平面内，一条直线不可能与两条相交直线都垂直，其中说法错误的个数有（ ）A ．3个B ．2个C ．1个D ．0个 21．如图，下列条件①∠1=∠2；②∠3=∠4；③∠3+∠4=180°；④∠1+∠2=180°； ⑤∠1+∠2=90°；⑥∠3+∠4=90°；⑦∠1=∠4中，能判断直线l1∥l2的条件有（ ） A ．②④ B ．①②⑦ C ．③④ D ．②③⑥第21题 第22题 第23题 第24题 22.如图，直线a ∥b,∠1=40°，∠2=50°，则∠3= .23.如图，将一块直角三角板和一把直尺如图放置，则∠1与∠2的关系是 . 24.如图，AB ∥CD ∥EF ，则∠1，∠2，∠3的关系是 . 25.∠BAF=50°，∠ACE=140°，CD⊥CE,证明：AB∥CD26．如图，AD ⊥BC,EF ⊥BC ，∠F=∠1，AD 平分∠BAC 吗？并说明理由。

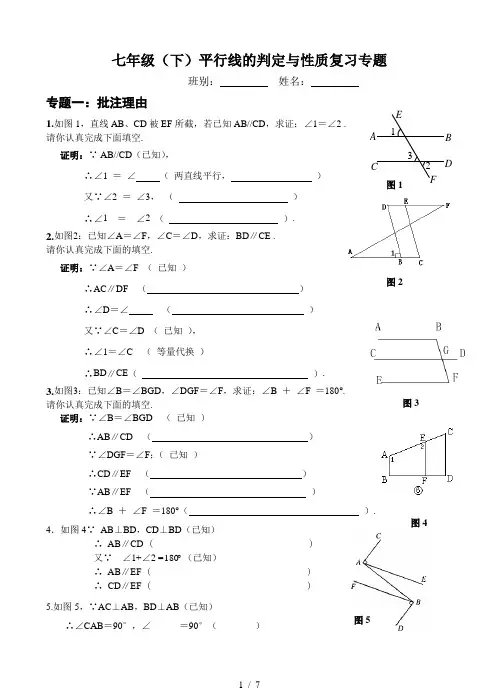
B DE 13A CF2 七年级（下）平行线的判定与性质复习专题班别： 姓名：专题一：批注理由1.如图1，直线AB 、CD 被EF 所截，若已知AB//CD ，求证：∠1＝∠2 .请你认真完成下面填空. 证明：∵ AB//CD （已知），∴∠1 ＝ ∠ （ 两直线平行， ） 又∵∠2 ＝ ∠3， （ ） ∴∠1 ＝ ∠2 （ ）.2.如图2：已知∠A ＝∠F ，∠C ＝∠D ，求证：BD ∥CE .请你认真完成下面的填空.证明：∵∠A ＝∠F （ 已知 ）∴AC ∥DF （ ） ∴∠D ＝∠ （ ） 又∵∠C ＝∠D （ 已知 ）， ∴∠1＝∠C （ 等量代换 ）∴BD ∥CE （ ）.3.如图3：已知∠B ＝∠BGD ，∠DGF ＝∠F ，求证：∠B ＋ ∠F ＝180°. 请你认真完成下面的填空.证明：∵∠B ＝∠BGD （ 已知 ）∴AB ∥CD （ ） ∵∠DGF ＝∠F ；（ 已知 ）∴CD ∥EF （ ） ∵AB ∥EF （ ）∴∠B ＋ ∠F ＝180°（ ）.4．如图4∵ AB ⊥BD ，CD ⊥BD （已知）∴ AB ∥CD ( ) 又∵ ∠1+∠2 = 180（已知）∴ AB ∥EF ( ) ∴ CD ∥EF ( ) 5.如图5，∵AC ⊥AB ，BD ⊥AB （已知）∴∠CAB ＝90°，∠______＝90°（ ）图1图2图3 图4 图5∴∠CAB＝∠______（）∵∠CAE＝∠DBF（已知）∴∠BAE＝∠______∴_____∥_____（）4.如图6，推理填空：（1）∵∠A =∠（已知），∴AC∥ED（）；（2）∵∠2 =∠（已知），∴AC∥ED（）；（3）∵∠A +∠= 180°（已知），∴AB∥FD（）；（4）∵∠2 +∠= 180°（已知），∴AC∥ED（）；5.如图7，AB∥DE，试问∠B、∠E、∠BCE有什么关系．解：∠B＋∠E＝∠BCE过点C作CF∥AB，则B∠=∠____（）又∵AB∥DE，AB∥CF，∴____________（）∴∠E＝∠____（）∴∠B＋∠E＝∠1＋∠2即∠B＋∠E＝∠BCE．6.阅读理解并在括号内填注理由：如图8，已知AB∥CD，∠1＝∠2，试说明EP∥FQ．证明：∵AB∥CD，∴∠MEB＝∠MFD（）又∵∠1＝∠2，∴∠MEB－∠1＝∠MFD－∠2，即∠MEP＝∠______∴EP∥_____．（）专题二：求角度大小123AFCDBE图6图7图81．如图9，DE∥BC，∠D∶∠DBC = 2∶1，∠1 =∠2，求∠DEB的度数．2.如图10，已知AB、CD、EF相交于点O，AB⊥CD，OG平分∠AOE，∠FOD＝28°，求∠COE、∠AOE、∠AOG的度数．3．如图11 ，已知AB∥CD，∠ABE和∠CDE的平分线相交于F，∠E = 140º，求∠BFD的度数？4. 如图，一条公路修到湖边时，需拐弯绕湖而过，如果第一次拐的角A是120°，第二次拐的角B是150°，第三次拐的角是∠C，这时的道路恰好和第一次拐弯之前的道路平行，问∠C是多少度？说明你的理由．图921B CED图10图125.（1）如图，若AB ∥DE ，∠B=135°，∠D=145°，你能求出∠C 的度数吗？（2）在AB ∥DE 的条件下，你能得出∠B 、∠C 、∠D 之间的数量关系吗？并说明理由．6.已知如图，四边形ABCD 中，AB ∥CD ，BC ∥AD ，那么∠A 与∠C ，∠B 与∠D 的大小关系如何？请说明你的理由．7．如图，∠1∶∠2∶∠3 = 2∶3∶4， ∠AFE = 60°，∠BDE =120°，写出图中平行的直线，并说明理由．8． 已知DB ∥FG ∥EC ，A 是FG 上一点，∠ABD ＝60°，∠ACE ＝36°，AP 平分∠BAC ，求：⑴∠BAC 的大小；⑵∠P AG 的大小.13 2A E CD B F专题三：证明题1. 如图，已知∠EFB+∠ADC=180°，且∠1=∠2，试说明DG∥AB.12ABCDFEG2. 已知:如图2-96,DE⊥AO于E,BO⊥AO,FC⊥AB于C，∠1=∠2,求证：DO⊥AB.3. 如图2-97,已知：∠1=∠2=，∠3=∠4，∠5=∠6.求证:AD∥BC.4. 如图2—101，若要能使AB∥ED，∠B、∠C、∠D应满足什么条件?5．已知：如图∠1=∠2，∠C=∠D，问∠A与∠F相等吗？试说明理由．6．已知：如图⑿，CE平分∠ACD，∠1=∠B，求证：AB∥CE7．如图：∠1=︒53，127，∠3=︒53，∠2=︒试说明直线AB与CD，BC与DE的位置关系。