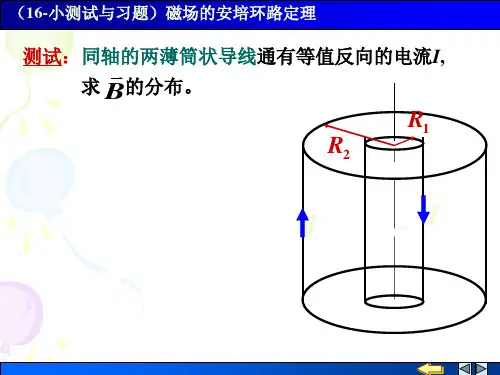
大学物理练习题 安培环路定理
- 格式:pdf
- 大小:187.31 KB
- 文档页数:4




习题10]10.1选择题(1) 对于安培环路定理的理解,正确的是:(A )若环流等于零,则在回路L 上必定是H 处处为零; (B )若环流等于零,则在回路L 上必定不包围电流;(C )若环流等于零,则在回路L 所包围传导电流的代数和为零; (D )回路L 上各点的H 仅与回路L 包围的电流有关。
[答案:C](2) 对半径为R 载流为I 的无限长直圆柱体,距轴线r 处的磁感应强度B () (A )内外部磁感应强度B 都与r 成正比;(B )内部磁感应强度B 与r 成正比,外部磁感应强度B 与r 成反比; (C )内外部磁感应强度B 都与r 成反比;(D )内部磁感应强度B 与r 成反比,外部磁感应强度B 与r 成正比。
[答案:B](3)质量为m 电量为q 的粒子,以速率v 与均匀磁场B 成θ角射入磁场,轨迹为一螺旋线,若要增大螺距则要() (A ) 增加磁场B ;(B )减少磁场B ;(C )增加θ角;(D )减少速率v 。
[答案:B](4)一个100匝的圆形线圈,半径为5厘米,通过电流为0.1安,当线圈在1.5T 的磁场中从θ=0的位置转到180度(θ为磁场方向和线圈磁矩方向的夹角)时磁场力做功为() (A )0.24J ;(B )2.4J ;(C )0.14J ;(D )14J 。
[答案:A]10.2 填空题(1)边长为a 的正方形导线回路载有电流为I ,则其中心处的磁感应强度 。
[答案:aIπμ220,方向垂直正方形平面](2)计算有限长的直线电流产生的磁场 用毕奥——萨伐尔定律,而 用安培环路定理求得(填能或不能)。
[答案:能, 不能](3)电荷在静电场中沿任一闭合曲线移动一周,电场力做功为 。
电荷在磁场中沿任一闭合曲线移动一周,磁场力做功为 。
[答案:零,正或负或零](4)两个大小相同的螺线管一个有铁心一个没有铁心,当给两个螺线管通以 电流时,管内的磁力线H 分布相同,当把两螺线管放在同一介质中,管内的磁力线H 分布将 。

习题版权属西南交大物理学院物理系《大学物理AI 》作业No.10安培环路定律 磁力 磁介质班级 ________ 学号 ________ 姓名 _________ 成绩 _______一、选择题:1.若空间存在两根无限长直载流导线,空间的磁场分布就不具有简单的对称性,则该磁场分布[ ](A) 不能用安培环路定理来计算 (B) 可以直接用安培环路定理求出 (C) 只能用毕奥-萨伐尔定律求出 (D) 可以用安培环路定理和磁感强度的叠加原理求出解:空间的磁场分布不具有简单的对称性,不能直接用安培环路定理求出空间的磁场分布,但可以由安培环路定理分别求出每根长直载流导线的磁场分布,再由磁场叠加原理求出空间总的磁场分布。
故选D2.无限长载流空心圆柱导体的内外半径分别为a 、b ,电流在导体截面上均匀分布,则空间各处B的大小与场点到圆柱中心轴线距离r 的关系定性地如图所示。
正确的图是:[ ]解:由安培环路定理有无限长载流空心圆柱导体各区域磁感应强度为:a r <时,02d =⨯=⋅⎰r B l B Lπ0=B b r a <<时,)()(2d 22220a r ab I r B l B L--=⨯=⋅⎰ππμπr a r a b IB 22220)(2-⋅-=πμ)1()(2d d 22220r a a b I r B +⋅-=πμ 由此知:随着r 的增加,B ~r 曲线的斜率将减小b r >时, I r B l B L02d μπ=⨯=⋅⎰rr I B 120∝=πμ故选B3导线固定不动,则载流三角形线圈将: [ ] (A) 向着长直导线平移 (B) (C) 转动 (D) 不动 解:建立如图所示的坐标轴,无限长直载流导线在x >0处产生的磁感应强度为:xIB πμ201=方向⊗由安培定律可得不同位置a 处三角形线圈的三个边受力大小分别为:l a II AB a I I F AB πμπμ22210210==)231ln(330cos d 2d 21030cos 2102a lI I x x I I l BI F F l a aCABC AC +=︒⋅===⎰⎰︒+πμπμ 式中l 为三角形边长,各力方向如图所示,则载流三角形线圈所受合力为:令)0(>=λλal,有 0)23111(2]231233321[2d )(d 210210<+--=+⨯--=∑λπμλπμλI I I I F x 又0|0==∑λx F(无穷远处),所以载流线圈所受合力始终向着长直电流,可见载流三角形线圈不可能转动,只能向着长直导线平动。

第五版普通物理习题 11-4,11-5安培环路定理及其应用1.选择题1若空间存在两根无限长直载流导线,空间的磁场分布就不具有简单的对称性,则该磁场分布(A )不能用安培环路定理来计算 (B )可以直接用安培环路定理求出 (C )只能用毕奥-萨伐尔定律求出(D )可以用安培环路定理和磁感应强度的叠加原理求出[ ]答案:(D )2在图(a )和(b )中各有一半径相同的圆形回路L 1和L 2,圆周内有电流I 1和I 2,其分布相同,且均在真空中,但在(b )图中L 2回路外有电流I 3,P 2、P 1为两圆形回路上的对应点,则:(A )2121,P P L L B B l d B l d B =⋅=⋅⎰⎰ (B )2121,P P L L B B l d B l d B ≠⋅≠⋅⎰⎰(C )2121,P P L L B B l d B l d B ≠⋅=⋅⎰⎰ (D )2121,P P L L B B l d B l d B =⋅≠⋅⎰⎰[ ]答案:(C )3一载有电流I 的导线分别均匀密绕在半径为R 和r 的长直圆筒上形成两个螺线管(R=2r ),两螺线管单位长度上的匝数相等,两螺线管中的磁感应强度大小B R 和B r 应满足(A )B R =2B r (B )B R =B r (C )2B R =B r (D )B R =4B r [ ] 答案:(B )4无限长载流空心圆柱导体的内外半径分别为a 、b ,电流在导体截面上均匀分布,则空间各处的B的大小与场点到圆柱中心轴线的距离r 的关系定性地如图所示。
正确的图是(A) (B) (C) (D)[ ] 答案:(B)5如图所示,六根无限长导线互相绝缘,通过电流均匀为I,区域Ⅰ、Ⅱ、Ⅲ、Ⅳ均为相等的正方形,哪一个区域指向纸内的磁通量最大(A)Ⅰ区域(B)Ⅱ区域(C)Ⅲ区域(D)Ⅳ区域[ ]答案:(B)6如图所示,流出纸面的电流为2I,流进纸面的电流为I,则下述式中哪一个是正确的(A)Il dBL12μ=⋅⎰(B)Il dBL2μ=⋅⎰(C)Il dBL3μ-=⋅⎰(D)Il dBL4μ-=⋅⎰[ ] 答案:(D)7在一圆形电流I所在的平面内,选取一个同心圆形闭合回路L,则由安培环路定理可知(A)0=⋅⎰l dBL,且环路上任意一点B=0(B)0=⋅⎰l dBL,且环路上任意一点B≠0(C)0≠⋅⎰l dBL,且环路上任意一点B≠0(D)0≠⋅⎰l dBL,且环路上任意一点B=常量[ ]8如图,两根直导线ab 和cd 沿半径方向被接到一个截面处处相等的铁环上,稳恒电流I 从a 端流入而从d 端流出,则磁感强度B 沿图中包围铁环截面的闭合路径L 的积分ld B L⋅⎰等于(A )I 0μ (B )3/0I μ (C )4/0I μ (D )3/20I μ[ ]答案:D9无限长直圆柱体,半径为R ,沿轴向均匀流有电流。


《大学物理》作业 No.6 磁场的安培环路定理班级 ___________ 学号 __________ 姓名 ____________ 成绩 __________说明:字母为黑体者表示矢量内容提要:安培环路定理 ∑⎰=⋅I l d B L0μ1. 安培环路定理的理解:①B是环路上各点的磁感应强度,是环路内外所有电流共同激发的磁场。
②∑I 只是被环路包围的电流的代数和。
③不被环路包围的电流在环路上激发的磁场在环路的线积分中抵消掉了。
④环路上各点0=B 时,必有0=∑I ;但0=∑I 时,未必环路上各点的B 一定都为零。
⑤对于电流的正负的规定:当电流的方向与环路积分的方向符合右手螺旋关系时,电流为正,否则为负。
⑥安培环路定理中的电流应该是闭合(或无限长)恒定电流,对于一段恒定电流的磁场,安培环路定理不成立。
2. 安培环路定理的应用:①只有在磁场具有较好的对称性时才能用安培环路定理求解B ,但安培环路定理是普遍成立的,不具有较好对称性的磁场不能用安培环路定理求解B ,但定理依然成立。
②利用安培环路定理求磁场分布一般包含两步:首先依据电流的对称性分析磁场分布的对称性,然后再利用安培环路定理计算磁感应强度的数值和方向。
此过程中决定性的技巧是选取合适的闭合路径L (环路),以便⎰⋅Ll d B 中的B 能以标量形式从积分号内提出来。
基本要求:1.掌握安培环路定理:2.掌握安培环路定理分析计算磁感应强度的条件和方法,并能熟练运用。
一、选择题1.如图6.1所示,有两根无限长直载流导线平行放置,电流分别为I 1和I 2, LI 1在L 内,I 2在L 外,P 是L 上的一点,今将I 2 在L 外向I 1移近时,则有 [ ] (A)l B d ⋅⎰L与B P同时改变. (B) l B d ⋅⎰L与B P都不改变. (C) l B d ⋅⎰L不变,B P改变.(D)l B d ⋅⎰L改变,BP不变.2.对于某一回路l ,积分l B d ⋅⎰l等于零,则可以断定I 图6.1[ ] (A) 回路l 内一定有电流. (B) 回路l 内可能有电流.(C) 回路l 内一定无电流. (D) 回路l 内可能有电流,但代数和为零.3. 如图6.2所示,两根直导线ab 和cd 沿半径方向被接到一个截面处处相等的铁环上,稳恒电流I 从a 端流入而从d 端流出,则磁感应强度B 沿图中闭合路径L 的积分l B d ⋅⎰l等于[ ] (A) I u 0(B) I u 031(C)I u 041(D) I u 0324. 用相同细导线分别均匀密绕成两个单位长度匝数相等的半径为R 和r 的长直螺线管(R =2r ),螺线管长度远大于半径.今让两螺线管载有电流均为I ,则两螺线管中的磁感强度大小B R 和B r 应满足:[ ] (A) B R = 2B r . (B) B R = B r . (C) 2B R = B r . (D) B R = 4B r .二、填空题1.在安培环路定理中iLI∑=⋅⎰0d μl B , 其中∑I i 是指 ;B 是由 的电流产生的.2. 两根长直导线通有电流I ,图6.3所示有三种环路,对于环路a ,=⋅⎰a L l B d ;对于环路b , =⋅⎰b L l B d 。
习题版权属西南交大物理学院物理系《大学物理AI 》作业No.10安培环路定律 磁力 磁介质班级 ________ 学号 ________ 姓名 _________ 成绩 _______一、选择题:1.若空间存在两根无限长直载流导线,空间的磁场分布就不具有简单的对称性,则该磁场分布[ ](A) 不能用安培环路定理来计算 (B) 可以直接用安培环路定理求出 (C) 只能用毕奥-萨伐尔定律求出 (D) 可以用安培环路定理和磁感强度的叠加原理求出解:空间的磁场分布不具有简单的对称性,不能直接用安培环路定理求出空间的磁场分布,但可以由安培环路定理分别求出每根长直载流导线的磁场分布,再由磁场叠加原理求出空间总的磁场分布。
故选D2.无限长载流空心圆柱导体的内外半径分别为a 、b ,电流在导体截面上均匀分布,则空间各处B的大小与场点到圆柱中心轴线距离r 的关系定性地如图所示。
正确的图是:[ ]解:由安培环路定理有无限长载流空心圆柱导体各区域磁感应强度为:a r <时,02d =⨯=⋅⎰r B l B Lπ0=B b r a <<时,)()(2d 22220a r ab I r B l B L--=⨯=⋅⎰ππμπr a r a b IB 22220)(2-⋅-=πμ)1()(2d d 22220r a a b I r B +⋅-=πμ 由此知:随着r 的增加,B ~r 曲线的斜率将减小b r >时, I r B l B L02d μπ=⨯=⋅⎰rr I B 120∝=πμ故选B3导线固定不动,则载流三角形线圈将: [ ] (A) 向着长直导线平移 (B) (C) 转动 (D) 不动 解:建立如图所示的坐标轴,无限长直载流导线在x >0处产生的磁感应强度为:xIB πμ201=方向⊗由安培定律可得不同位置a 处三角形线圈的三个边受力大小分别为:l a II AB a I I F AB πμπμ22210210==)231ln(330cos d 2d 21030cos 2102a lI I x x I I l BI F F l a aCABC AC +=︒⋅===⎰⎰︒+πμπμ 式中l 为三角形边长,各力方向如图所示,则载流三角形线圈所受合力为:令)0(>=λλal,有 0)23111(2]231233321[2d )(d 210210<+--=+⨯--=∑λπμλπμλI I I I F x 又0|0==∑λx F(无穷远处),所以载流线圈所受合力始终向着长直电流,可见载流三角形线圈不可能转动,只能向着长直导线平动。
练习十二 安培环路定理一、选择题1. 电流I 1穿过一回路l ,而电流I 则在回路的外面,于是有2l B l v v d ⋅∫B v(A ) l 上各点的都只与I 有关。
及积分1l B l v v d ⋅∫B v只与I 与I 、I (B ) l 上各点的有关。
有关,积分112l B l v v d ⋅∫B v与I 、I 与I (C ) l 上各点的无关。
12有关,积分2l B l v v d ⋅∫B v都与I 、I (D ) l 上各点的及积分12有关。
l B l vv d ⋅∫2. 对于某一回路l ,积分等于零,则可以断定。
(A ) 回路l 内一定有电流。
(B ) 回路l 内可能有电流。
(C ) 回路l 内一定无电流。
(D ) 回路l 内可能有电流,但代数和为零。
3. 无限长直电流产生磁场的公式为B = μI /(2πr ),以下说法正确的是 0(A ) 此公式中只要求导线为直导线。
(B ) 此公式中只要求导线为无限长,且截面必须为圆形。
(C ) 当r = 0时,此公式不适用,因为磁感强度B 为无限大。
(D ) 当r = 0时,此公式不适用,因为此时场点到导线的距离不是远大于导线的截面尺寸,导线不能看成无限细。
l B l vv d ⋅∫4. 安培环路定律=μI 中的电流I0(A ) 必须穿过回路l 所圆的曲面,且必须为无限长的直线。
(B ) 必须穿过回路l 所圆的曲面,但可以为有限长的直线。
(C ) 不必穿过回路l 所圆的曲面,但必须闭合。
(D ) 必须穿过回路l 所圆的曲面,且必须闭合。
5. 用相同细导线分别均匀密绕成两个单位长度匝数相等的半径为R 和r 的长直螺线管(R = 2r ),螺线管长度远大于半径。
今让两螺线管载有电流均为I ,则两螺线管中的磁感强度大小B R 和B r 应满足: (A ) B R = 2B r 。
(B ) B R = B r 。
(C ) 2B R = B r 。
安培环路定律、运动电荷的磁场9.如图,两根直导线ab 和cd 沿半径方向被接到一个截面处处相等的铁环上,稳恒电流I 从a 端流入而从d 端流出,则磁感应强度B 沿图中闭合路径L 的积分⎰⋅l d B等于(A )I 0μ (B )3/0I μ (C )I 0μ/4 (D )2I 0μ/310.在图(a )和(b )中各有一半径相同的圆形回路1L 、2L ,圆周内有电流1I 、2I ,其分布相同,且均在真空中,但在(b )图中2L 回路外有电流3I ,1P 、2P 为两圆形回路上的对应点,则(A )⎰⎰⋅=⋅12L L l d B l d B ,21P P B B = (B )⎰⎰⋅≠⋅12L L l d B l d B,21P P B B = (C )⎰⎰⋅=⋅12L L l d B l d B,21P P B B ≠ (D )⎰⎰⋅≠⋅12L L l d B l d B,21P P B B ≠11.在安培环路定理∑⎰=⋅i I l d B 0μ中,∑i I 是指__ ,B是指 ,它是由 决定的。
12.如图,平行的无限长直载流导线A和B ,电流强度为I ,垂直纸面向外,两载流导线之间相距为a ,则(1)AB 中点(P 点)的磁感应强度PB =,(2)磁感应强度B 沿图中环路L 的积分⎰⋅l d B= 。
13.一根半径为R 的长直导线载有电流I ,做一宽为R ,长为L 的假想平面S ,如图所示。
若假想平面S 可在导线直径与轴OO ’所定的平面内离开OO ’轴移动至远处,试求当通过S 面的磁通量最大时S 面的位置(设直导线内电流分布是均匀的)。
I 3L 1 L 2 2P 1(b)(a)14.有一无限长圆柱形导体和一无限长薄圆桶形导体,都通有沿轴向均匀分布的电流I,它 ,外半径都为R。
今取长L、宽为2R的矩形平面ABCD和A’B’C’D’,们的磁导率都为AD及A’D’正好在圆柱的轴线上,如图所示,问通过ABCD的磁通量为多少?通过A’B’C’D’的磁通量为多少?15.两平行长直导线相距d =40cm ,每根导线载有电流A I I 2021==,如图,求: (1)两导线所在平面内与该两导线等距的一点A 处的磁感应强度, (2)通过图中斜线所示面积的磁通量(cm r r 1021==,cm L 25=)。
20XX年复习资料大学复习资料专业:班级:科目老师:日期:安培环路定理 磁力一 选择题[ C ]2.如图所示,一固定的载流大平板,在其附近,有一载流小线框能自由转动或平动。
线框平面与大平板垂直,大平板的电流与线框中电流方向如图所示,则通电线框的运动情况从大平板向外看是: (A)靠近大平板AB (B)顺时针转动 (C)逆时针转动(D)离开大平板向外运动。
[ A ]3.如图,一无限长直载流导线与正三角形载流线圈在同一平面内,若长直导线固定不动,则载流三角形线圈将:(A) 向着长直导线平移 (B) 离开长直导线平移 (C) 转动(D) 不动二 填空题1.两根长直导线通有电流I ,在图示三种环路中,l B d ⋅⎰分别等于:I 0μ (对于环路a )。
0 (对于环路b )。
I02μ (对于环路c )。
2.一带电粒子平行磁力线射入匀强磁场,则它作______匀速直线________运动。
一带电粒子垂直磁力线射入匀强磁场,则它作_____匀速率圆周_________运动。
一带电粒子与磁力线成任意交角射入匀强磁场,则它作_____等距螺旋___运动。
4.空间某处有互相垂直的两个水平磁场 1B 和 2B , 1B 向北,2B 向东,现在该处有一段载流直导线,只有当这段导线____水平面内___放置时,才有可能使两磁场作用在它上面的合力为零。
当这段导线与2B 的夹角为60°时,欲使导线所受合力为零。
则两个水平磁场1B 与2B 的大大小必须满足的关系为 321=B B 。
7.如图所示的空间区域内,分布着方向垂直于纸面的匀强磁场,在纸面内有一正方形边框abcd (磁场以边框为界),而a 、b 、c 三个角顶处开有很小的缺口,今有一束具有不同速度的电子由a 缺口沿ad 方向射入磁场区域,若b 、c 两缺口处分别有电子射出,自此两处I 2I bIcc IaBmP 2I 1I A ab⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯B电子的速率之比=cb v v 21。
练习十二 安培环路定理一、选择题1. 电流I 1穿过一回路l ,而电流I 则在回路的外面,于是有2l B l v v d ⋅∫B v(A ) l 上各点的都只与I 有关。
及积分1l B l v v d ⋅∫B v只与I 与I 、I (B ) l 上各点的有关。
有关,积分112l B l v v d ⋅∫B v与I 、I 与I (C ) l 上各点的无关。
12有关,积分2l B l v v d ⋅∫B v都与I 、I (D ) l 上各点的及积分12有关。
l B l vv d ⋅∫2. 对于某一回路l ,积分等于零,则可以断定。
(A ) 回路l 内一定有电流。
(B ) 回路l 内可能有电流。
(C ) 回路l 内一定无电流。
(D ) 回路l 内可能有电流,但代数和为零。
3. 无限长直电流产生磁场的公式为B = μI /(2πr ),以下说法正确的是 0(A ) 此公式中只要求导线为直导线。
(B ) 此公式中只要求导线为无限长,且截面必须为圆形。
(C ) 当r = 0时,此公式不适用,因为磁感强度B 为无限大。
(D ) 当r = 0时,此公式不适用,因为此时场点到导线的距离不是远大于导线的截面尺寸,导线不能看成无限细。
l B l vv d ⋅∫4. 安培环路定律=μI 中的电流I0(A ) 必须穿过回路l 所圆的曲面,且必须为无限长的直线。
(B ) 必须穿过回路l 所圆的曲面,但可以为有限长的直线。
(C ) 不必穿过回路l 所圆的曲面,但必须闭合。
(D ) 必须穿过回路l 所圆的曲面,且必须闭合。
5. 用相同细导线分别均匀密绕成两个单位长度匝数相等的半径为R 和r 的长直螺线管(R = 2r ),螺线管长度远大于半径。
今让两螺线管载有电流均为I ,则两螺线管中的磁感强度大小B R 和B r 应满足: (A ) B R = 2B r 。
(B ) B R = B r 。
(C ) 2B R = B r 。
(D ) B R = 4B r 。
6. 无限长直圆柱体,半径为R ,沿轴向均匀流有电流。
设圆柱体内(r < R )的磁感强度为B 1,圆柱体外(r >R )的磁感强度为B 2,则有: (A ) B 1、B 均与r 成正比。
2(B ) B 、B 12均与r 成反比。
(C ) B 与r 成正比,B 12与r 成反比。
(D ) B 1与r 成反比,B 2与r 成正比。
7. 在图(a )和(b )中各有一半径相同的圆形回路L P 1 L (a )3 P 2 (b )和L ,圆周内有电流I 和I 1222,其分布相同,且均在真空中,但在图(b )中,L 回路外有电流I 23,P 1、P 2为两圆形回路上的对应点,则:l B l B L L vv v v d d 21⋅∫=⋅∫21P P B B v v =(A ) 。
,l B l B L L vv v v d d 21⋅∫≠⋅∫21P P B B v v =(B ) 。
,l B l B L L vv v v d d 21⋅∫=⋅∫21P P B B v v ≠。
(C ) ,l B l B L L vv v v d d 21⋅∫≠⋅∫21P P B B v v ≠。
(D ) ,8. 如图所示,两根直导线ab 和cd 沿半径方向被接到一个截面处处相等的铁环上,恒定电流I 从a 端流入而从d 端流出,则磁感强度B vl B L v v d ⋅∫等于: 沿图中闭合路径的积分(A ) μI 。
0(B ) μI /3。
0(C ) μI /4。
0(D )2μI /3。
09. 如图所示,在一圆形电流I 所在的平面内,选取一个同心圆形闭合回路L ,则由安培环路定理可知0d =⋅∫l B L vv ,且环路上任意点B ≠ 0。
(A ) 0d =⋅∫l B L vv ,且环路上任意点B = 0。
(B ) 0d ≠⋅∫l B L vv ,且环路上任意点B ≠ 0。
(C ) 0d≠⋅∫l B L vv ,且环路上任意点B = 0。
(D ) 10. 如图所示,有两根无限长直载流导线平行放置,电流分别为I I 和I ,L 是空间一闭曲线,I 在L 内,I 1212在L 外,P 是L 上的一点,今将I 在L 外向I 移近时,则有21l B L v v d ⋅∫P B v(A ) 同时改变。
与l B L v v d ⋅∫P B v都不改变。
(B ) 与l B L v v d ⋅∫P B v改变。
(C ) 不变,l B L v v d ⋅∫P B v不变。
(D ) 改变,l B l vv d ⋅∫11. 如图所示,一环形电流I 和一回路l ,则积分应等于 (A ) 0。
(B ) 2I 。
(C ) −2μI 。
0(D ) 2μI 。
0l B l vv d ⋅∫12. 对于某一回路l ,积分= μI ≠ 0,则可以肯定0B v可能为零,有些可能不为零,或所有点可能全不为零。
(A ) 回路上有些点的B v一定不为零。
(B ) 回路上所有点的B v一定为零。
(C ) 回路上有些点的(D ) 回路上所有点的可能都为零。
B v13. 载流空心圆柱导体的内外半径分别为a 和b ,电流在导体截面上均匀分布,则空间各点的B -r 曲线应为图中的哪一图?(A )(B )(C )(D )二、填空题21.如图所示,真空中有两圆形电流I 和I 和三个环路L 、L 、L 12123,则安培环路定律的表达式为=⋅∫l B L vv d 1 ,=⋅∫l B L vv d 2,=⋅∫l B L v v d 3 。
i L I l B Σμ0d =⋅∫v v 2.在安培环路定理中,其中∑I i 是指 ;是指 B v,B 是由环路 v的电流产生的。
3. 两根长直导线通有电流I ,图所示有三种环路,=⋅∫l B a L v v d 对于环路a , ;=⋅∫l B b L vv d 对于环路b , ; =⋅∫l B c L vv d 对于环路c , 。
4. 圆柱体上载有电流I ,电流在其横截面上均匀分布,一回路L 通过圆柱内部,将圆柱体横截面分为两部分,其面积大小分别为S 1和S 2,如图所示,则=⋅∫l B L vv d 。
5. 长度为L ,半径为R 的有限长载流圆柱,电流为I ,用安培环路定律 (填能或不能)计算此电流产生的磁场。
设想此有限长载流圆柱与其它导线组成电流为I 的闭合电路,如以此圆柱轴线为心作一圆形回路l ,l 的半径为r (r <R ),回路平面垂直电流轴线,则积分l B l vv d ⋅∫应等于 。
6. 如图所示,两条平行的半径为a 的无限长直载流导线A 、B 相距为d ,电流为I ,P 、P 、P 123分别距电流A 为x 1、x 2、x 3,它们与电流A 、B 的轴线共面,则它们的磁感应强度的大小分别为B P1 = ,B P2 = ,B P3 = 。
7. 有—长直金属圆简,沿长度方向有稳恒电流I流通,在横截线上电流均匀分布。
筒内空腔各处的磁感应强度为 ,筒外空间中离轴线r 处的磁感应强度为。
8. 如图,平行的无限长直载流导线A 和B ,电流强度均为I ,垂直纸面向外,两根载流导线之间相距为a ,则P B vAB 中点(P 点)的磁感应强度(1) = 。
B v沿图中环路L 的线积分(2)磁感应强度∫⋅Ll B vv d = 。
9. 在磁场空间分别取两个闭合回路,若两个回路各自包围载流导线的根数不同,但电流的代数和相同。
则磁感应强度沿各闭合回路的线积分;两个回路的磁场分布 。
(填:相同、不相同)10. 如图16.5所示,将半径为R 的无限长导体薄壁管(厚度忽略)沿轴向割去一宽度为h (h <<R )的无限长狭缝后,再沿轴向均匀地流有电流,其面电流的线密度为i ,则管轴线上磁感强度的大小是 。
练习十二答案一、1. C ,2. D ,3. D ,4. D ,5. B ,6. C ,7. C ,8. D ,9. A ,10. C ,11. D ,12,A ,13. B 二、1. −μI 01;μ(I +I 012);0,2. 环路L 所包围的电流;环路L 上的磁感应强度;内外,3. μI ;0;2μI , 004. −μIS 01/(S 1+S 2), 225. 不能;μIr /R ,06. μ0Ix 1/(2πa 2)−μ0I /[2π(d −x 1)];μ0I /(2πx 2)−μ0I /[2π(d −x 2)];μ0I /(2πx 3)−μ0I (d −x 3)/[2πa 2]。
7. 0;μI /(2πr ), 08. 0;-μI , 09. 相同;不相同, Rih π20μ10.。