大学物理安培定律
- 格式:ppt
- 大小:1.17 MB
- 文档页数:3


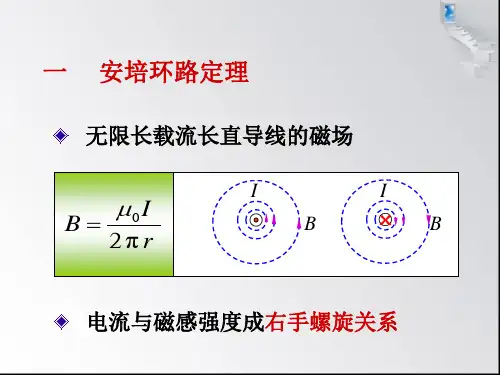
10-4 安培环路定理静电场的一个重要特征是电场强度E 沿任意闭合路径的积分等于零,即0d =⋅⎰l E l,那么,磁场中的磁感强度B 沿任意闭合路径的积分⎰⋅ld lB 等于多少呢?可以证明:在真空的稳恒磁场中,磁感强度B 沿任一闭合路径的积分(即B 的环流)的值,等于0μ乘以该闭合路径所包围的各电流的代数和,即∑⎰==⋅ni lI10 d il B μ (10-8)安培环路定理与静电场环路定理的比较 讨论:安培环路定理的证明如图(a)所示,有一通有电流I 的长直载流导线垂直于屏幕平面,且电流流向垂直屏幕平面向内. 在屏幕平面上取两个闭合路径1C 和2C ,其中闭合路径1C 内包围的电流为I ,而在闭合路径2C 内没有电流. 从图(b )可以看出,由于磁感强度B 的方向总是沿着环绕直导线的圆形回路的切线方向,所以对闭合路径1C 或2C 上任意一线元l d ,磁感强度B 与l d 的点积为ϕαd cos d d Br l B ==⋅l B式中r 为载流导线至线元l d 的距离. 由第10-2节二中例1的式(2),上式可写成ϕμϕμd π2d π2d 00Ir rI==⋅l B (1)对于图(a )的闭合回路1C ,ϕ将由0增至π2. 于是,磁感强度B 沿闭合路径1C 的环流为这就是真空中磁场的环路定理,也称安培环路定理。
它是电流与磁场之间的基本规律之一。
在式(10-8)中,若电流流向与积分回路呈右螺旋关系,电流取正值;反之则取负值。
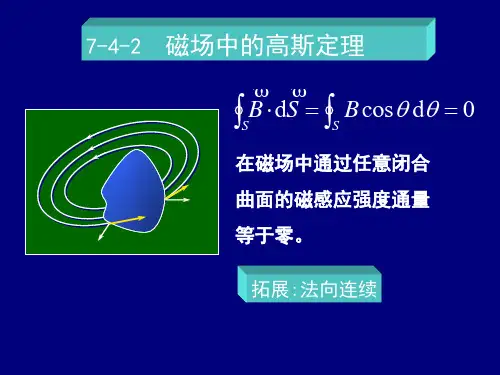
⎰⎰===⋅1000π2π2d π2d CIIIμμϕμl B (2)可见,真空中磁感强度B 沿闭合路径的环流等于闭合路径所包围的电流乘以0μ,而与闭合路径的形状无关.然而,对于图(a )中的闭合路径2C ,将得到不同的结果,当我们从闭合路径2C 上某一点出发,绕行一周后,角ϕ的净增量为零,即⎰=0d ϕ于是,由式(1)可得⎰=⋅20d c l B (3)比较式(2)和式(3)可以看出,它们是有差别的. 这是由于闭合路径1C 包围了电流,而闭合路径2C 却未包围电流. 于是我们可以得到普遍的安培环路定理:沿任意闭合路径的磁感强度B 的环流为⎰∑=⋅20d c I μl B式中∑I 是该闭合路径所包围电流的代数和 人物简介:安培简介安培(Andre Marie Ampere,1775-1855),法国物理学家,对数学和化学也有贡献,他在电磁理论的建立和发展方面建树颇丰。



大学常用的物理公式(二)引言概述:大学物理是大多数理工科专业学生所学的一门基础课程。
在学习物理过程中,常用的物理公式是不可或缺的工具。
本文将介绍大学常用的物理公式(二)。
根据其应用领域,这些公式可分为五个大点:力学、热学、电磁学、光学和量子物理。
每个大点都包含了几个小点,总共提供了全面的物理公式知识。
正文:一、力学1. 速度公式:速度(v)等于物体位移(s)除以物体经过的时间(t),即v = s/t。
2. 加速度公式:加速度(a)等于物体速度(v)变化的量除以时间(t),即a = Δv / t。
3. 牛顿第二定律:力(F)等于物体质量(m)乘以物体加速度(a),即F = ma。
4. 动能公式:物体的动能(K)等于质量(m)乘以速度(v)的平方的一半,即K = 1/2 mv²。
5. 万有引力公式:物体间的引力(F)等于物体质量(m₁)乘以另一物体质量(m₂),再除以二者间的距离(r)的平方,即F = G(m₁m₂)/r²。
(G为万有引力常数)二、热学1. 热传导公式:热传导(Q)等于热传导系数(k)乘以温度差(ΔT)除以物体的厚度(d),即Q = kΔT / d。
2. 热容量公式:物体的热容量(C)等于物体的质量(m)乘以物体的比热容(c),即C = mc。
3. 理想气体状态方程:理想气体的压强(P)等于气体物质的摩尔数(n)乘以气体的温度(T)除以气体的体积(V),即P = nRT/V。
(R为气体常数)4. 熵变公式:系统的熵变(ΔS)等于系统吸收的热量(Q)除以温度(T),即ΔS = Q/T。
5. 热力学第二定律:热不会自发从低温物体传递到高温物体,即熵在自然过程中总是增加的。
三、电磁学1. 电场力公式:电场力(F)等于电荷(q)乘以电场强度(E),即F = qE。
2. 磁场力公式:磁场力(F)等于带电粒子的电荷(q)乘以其速度(v)乘以磁场(B)的正弦角(θ),即F = qvBsinθ。


一、教学目标1. 理解安培环路定律的基本概念和原理。
2. 掌握安培环路定律的应用方法。
3. 培养学生的逻辑思维能力和分析问题的能力。
二、教学重点1. 安培环路定律的基本概念和原理。
2. 安培环路定律的应用方法。
三、教学难点1. 理解安培环路定律中的积分运算。
2. 掌握安培环路定律在不同情况下的应用。
四、教学过程一、导入1. 介绍安培环路定律的背景和意义。
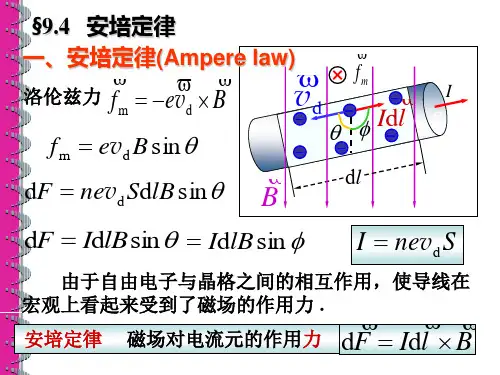
2. 提出问题:如何计算载流导线产生的磁场?二、讲解安培环路定律1. 介绍安培环路定律的基本概念和原理,包括磁感应强度B、闭合路径l、微小线元素dl、磁常数μ0、闭合路径所包围的电流I等。
2. 解释安培环路定律的表达式:∮B·dl = μ0I3. 分析安培环路定律的物理意义:在稳恒磁场中,磁感应强度B沿任何闭合路径的线积分等于闭合路径所包围的电流乘以磁导率。
三、讲解安培环路定律的应用方法1. 应用安培环路定律计算载流导线产生的磁场。
2. 应用安培环路定律分析复杂电流分布产生的磁场。
3. 通过实例讲解如何确定闭合路径和计算积分。
四、讲解安培环路定律的局限性1. 介绍安培环路定律的适用范围:仅适用于稳恒磁场。
2. 说明安培环路定律在含时电场中的局限性。
五、课堂练习1. 列举安培环路定律的典型应用实例。
2. 分析并解决相关计算问题。
六、总结与拓展1. 总结安培环路定律的基本概念和原理。
2. 拓展安培环路定律在电磁学领域的应用。
七、作业1. 完成课后习题,巩固所学知识。
2. 查阅资料,了解安培环路定律在工程和科研中的应用。
八、教学反思1. 分析学生在学习安培环路定律过程中的难点和困惑。
2. 优化教学方法和手段,提高学生的学习效果。

《大学物理》作业 No.6 磁场的安培环路定理班级 ___________ 学号 __________ 姓名 ____________ 成绩 __________说明:字母为黑体者表示矢量内容提要:安培环路定理 ∑⎰=⋅I l d B L0μ1. 安培环路定理的理解:①B是环路上各点的磁感应强度,是环路内外所有电流共同激发的磁场。
②∑I 只是被环路包围的电流的代数和。
③不被环路包围的电流在环路上激发的磁场在环路的线积分中抵消掉了。
④环路上各点0=B 时,必有0=∑I ;但0=∑I 时,未必环路上各点的B 一定都为零。
⑤对于电流的正负的规定:当电流的方向与环路积分的方向符合右手螺旋关系时,电流为正,否则为负。
⑥安培环路定理中的电流应该是闭合(或无限长)恒定电流,对于一段恒定电流的磁场,安培环路定理不成立。
2. 安培环路定理的应用:①只有在磁场具有较好的对称性时才能用安培环路定理求解B ,但安培环路定理是普遍成立的,不具有较好对称性的磁场不能用安培环路定理求解B ,但定理依然成立。
②利用安培环路定理求磁场分布一般包含两步:首先依据电流的对称性分析磁场分布的对称性,然后再利用安培环路定理计算磁感应强度的数值和方向。
此过程中决定性的技巧是选取合适的闭合路径L (环路),以便⎰⋅Ll d B 中的B 能以标量形式从积分号内提出来。
基本要求:1.掌握安培环路定理:2.掌握安培环路定理分析计算磁感应强度的条件和方法,并能熟练运用。
一、选择题1.如图6.1所示,有两根无限长直载流导线平行放置,电流分别为I 1和I 2, LI 1在L 内,I 2在L 外,P 是L 上的一点,今将I 2 在L 外向I 1移近时,则有 [ ] (A)l B d ⋅⎰L与B P同时改变. (B) l B d ⋅⎰L与B P都不改变. (C) l B d ⋅⎰L不变,B P改变.(D)l B d ⋅⎰L改变,BP不变.2.对于某一回路l ,积分l B d ⋅⎰l等于零,则可以断定I 图6.1[ ] (A) 回路l 内一定有电流. (B) 回路l 内可能有电流.(C) 回路l 内一定无电流. (D) 回路l 内可能有电流,但代数和为零.3. 如图6.2所示,两根直导线ab 和cd 沿半径方向被接到一个截面处处相等的铁环上,稳恒电流I 从a 端流入而从d 端流出,则磁感应强度B 沿图中闭合路径L 的积分l B d ⋅⎰l等于[ ] (A) I u 0(B) I u 031(C)I u 041(D) I u 0324. 用相同细导线分别均匀密绕成两个单位长度匝数相等的半径为R 和r 的长直螺线管(R =2r ),螺线管长度远大于半径.今让两螺线管载有电流均为I ,则两螺线管中的磁感强度大小B R 和B r 应满足:[ ] (A) B R = 2B r . (B) B R = B r . (C) 2B R = B r . (D) B R = 4B r .二、填空题1.在安培环路定理中iLI∑=⋅⎰0d μl B , 其中∑I i 是指 ;B 是由 的电流产生的.2. 两根长直导线通有电流I ,图6.3所示有三种环路,对于环路a ,=⋅⎰a L l B d ;对于环路b , =⋅⎰b L l B d 。
安培定律计算公式如何计算
安培定律是电磁学中的基本定律之一,用来描述电流对磁场的作用。
根据安培定律,电流元产生的磁场可以通过以下公式计算:
B = (μ0/4π) * (I * dl * sinθ) / r^2
其中
B表示磁场强度,单位为特斯拉(T);
μ0表示真空中的磁导率,其数值为4π*10^-7特斯拉·米/安培;
I表示电流强度,单位为安培(A);
dl表示电流元的长度;
θ表示电流元与观察点的夹角,一般取为电流元与径向的夹角;
r表示观察点到电流元的距离。
根据这个公式,可以计算出特定电流元产生的磁场强度。
如果需要计算复杂电流分布的磁场,可以通过对整个电流路径进行积分来得到磁场。
需要注意的是,安培定律适用于静电场情况下的电流分布。
如果电流随时间变化,则需要结合法拉第定律和麦克斯韦方程组,采用更复杂的数学方法进行计算。