大学物理安培环路定理

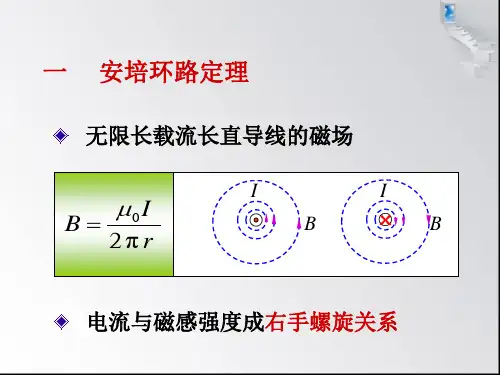
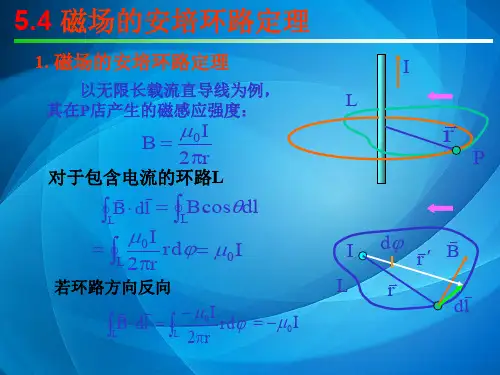
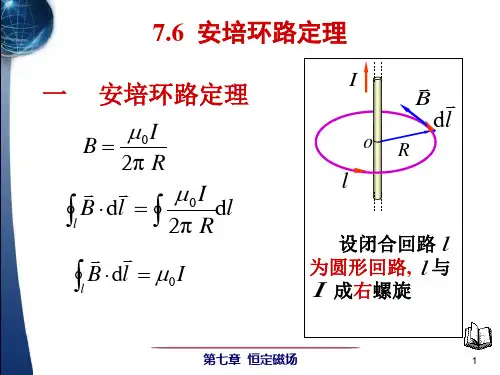
10-4 安培环路定理
静电场的一个重要特征是电场强度E 沿任意闭合路径的积分等于零，即0
d =⋅⎰l E l
，那么，
磁场中的磁感强度B 沿任意闭合路径的积分⎰⋅l
d l
B 等于多少呢？可以证明：在真空的稳恒磁场
中，磁感强度B 沿任一闭合路径的积分（即B 的环流）的值，等于0μ乘以该闭合路径所包围的
各电流的代数和，即
∑⎰==⋅n
i l
I
1
0 d i
l B μ （10-8）
安培环路定理与静电场环路定理的比较 讨论：安培环路定理的证明
如图(a)所示，有一通有电流I 的长直载流导线垂直于屏幕平面，且电流流向垂直屏幕平面向内. 在屏幕平面上取两个闭合路径
1C 和2C ，其中闭合路径1C 内包围的电流为I ，而在闭合路径
2C 内没有电流. 从图（b ）可以看出，由于磁感
强度B 的方向总是沿着环绕直导线的圆形回路的切线方向，所以对闭合路径
1C 或2C 上任意一线元l d ，磁感强度B 与l d 的点积为
ϕαd cos d d Br l B ==⋅l B
式中r 为载流导线至线元l d 的距离. 由第10-2节二中例1的式（2），上式可写成
ϕ
μϕμd π
2d π2d 00I
r r
I
=
=
⋅l B （1）
对于图（a ）的闭合回路1C ，ϕ将由0增至π2. 于是，磁感强度B 沿闭合路径1C 的环流
为
这就是真空中磁场的环路定理，也称安培环路定理。

它是电流与磁场之间的基本规律之一。

在式（10-8）中，若电流流向与积分回路呈右螺旋关系，电流取正值；反之则取负值。

⎰⎰
==
=
⋅1
000π2π
2d π
2d C
I
I
I
μμϕμl B （2）
可见，真空中磁感强度B 沿闭合路径的环流等于闭合路径所包围的电流乘以0μ，而与闭合
路径的形状无关.
然而，对于图（a ）中的闭合路径2C ，将得到不同的结果，当我们从闭合路径2C 上
某一点出发，绕行一周后，角
ϕ的净增量为零，即
⎰=0d ϕ
于是，由式（1）可得
⎰=⋅2
0d c l B （3）
比较式（2）和式（3）可以看出，它们是有差别的. 这是由于闭合路径1C 包围了电流，而
闭合路径
2C 却未包围电流. 于是我们可以得到普遍的安培环路定理：沿任意闭合路径的磁感强
度B 的环流为
⎰∑=⋅2
0d c I μl B
式中∑I 是该闭合路径所包围电流的代数和 人物简介：安培简介
安培(Andre Marie Ampere,1775-1855)，法国物理学家，对数学和化学也有贡献，他在电磁理论的建立和发展方面建树颇丰。

1820年9月提出了物质磁性起源的分子电流假设，并在1821—1825年精巧实验的基础上导出两电流元间相互作用力的公式，后来人们结合毕奥—萨伐尔定律而将该公式写成现在通用的安培力公式，即安培定律。

讨论：安培环路定理与静电场环路定理的比较
静电场环流为零说明静电场是保守场，并由此引入了电势能的概念，静电场环流定理是描述静电
B d⋅显然并不代表磁场力的功，定理只是表明磁场性质的基本定理。

对于安培环路定理，其中l
场中存在环流，它用数学形式表述了磁场环流与电流的关系。

恒稳磁场的环流不为零，因此磁场不是保守场，磁场是无源的涡旋场，磁场的安培环路定理是描述稳恒磁场性质的重要定理。

一、例1载流长直螺线管内的磁场
处于真空中的载流长直螺线管内外的磁场分布情况与管上各匝线圈的疏密程度及管的尺寸有关。

对于线圈较稀疏的载流螺线管，它的磁感线分布如下图所示。

由图可以看出，在螺线管内中间部分靠近管轴处的磁感线趋于与管轴平行；而导线附近的磁感线几乎是一些以导线为轴的同心圆。

这样，管外中间部分贴近外管壁的区域里，存在着磁场，磁感强度不为零。

然而对于绕得非常密集的直螺线管，它的磁感线分布如上图所示。

由图可以看出，在螺线管内中部，从管壁到管轴的区域里，磁感线可看成是趋于与管轴平行；而管外中部
l比管的直径贴近外管壁附近的磁场很弱，磁感强度趋于零。

当螺线管绕得很密，而且管的长度
d大得很多时（d
l>>）。

可将此螺线管当成无限长的螺线管。

右图是一个密绕的无限长螺线管中间的一段，在单位长度上绕有n 匝线圈，通过的电流为I 。

管内的磁感强度B 的方向处处与管轴平行，且大小均相等；在管外贴近管壁处的磁感强度可视为零。

下面我们用安培环路定理来讨论管内的磁感强度。

在图中作一矩形闭合路径MNOPM 。

则
⎰⎰⎰⎰⎰⋅+⋅+⋅+⋅=⋅PM
OP
N O
MN
l
d d d d d l B l B l B l B l B
其中，⎰=⋅OP d 0l B 。

0
=⋅=⋅⎰⎰PM N O d d l B l B 。

而在MN 段，磁感强度B 的大小均相同，且B 的
方向与l d 相同，所以上式为
MN B l d =⋅⎰l B
根据安培环路定理，有
nI
MN MN B l
d 0 μ==⋅⎰l B
得
nI
B 0μ=
上式表明，无限长载流螺线管内中部，任意点磁感强度的大小与通过螺线管的电流和单位长度线圈的匝数成正比。

讨论：载流螺绕环内的磁场
图示为一螺绕环，环内为真空。

环上均匀地密绕有N 匝线圈，线圈中的电流为I 。

由于环上的线圈绕得很密集，环外的磁场很微弱，可以略去不计，磁场几乎全部集中在螺绕环内，此时，呈对称分布的电流使磁场也具对称性，导致环内的磁感线形成同心圆，且同一圆周上各点的磁感强度B 的大小相等，方向处处和环面平行。

现通过环内点P ，以半径R 作一圆形闭合路径, 如图所示。

显然闭合路径上各点的磁感强度方向都和闭合路径相切，各点B 的值都相等，并且圆形闭合路径内电流的流向和此圆形闭合路径构成右螺旋关系。

这样，根据安培环路定理有
⎰==⋅l
NI R B 0
π2d μl B
可得
R NI B π20μ=
如果L 表示螺绕环中心线所在的圆形闭合路径的长度，那么，圆环中心线上一点处的磁感强度为
L NI B 0
μ=
当螺绕环中心线的直径比线圈的直径大得多，即d 2>>R 时，管内的磁场可近似看成是均匀的，管内任意点的磁感强度均可用上式表示。

二、无限长载流圆柱体的磁场
设在半径为R 的圆柱形导体中，电流沿轴向流动，且电流在截面积上的分布是均匀的。

如果圆柱形导体很长，那么在导体的中部，磁场的分布可视为是对称的。

下面先用安培环路定理来求圆柱体外的磁感强度。

如下图(右)所示，设点P 离圆柱体轴线的垂直距离为r ，且R r >。

通过P 作半径为r 的圆，圆面与圆柱体的轴线垂直，由于对称性，在以r 为半径的圆周上，B 的值相等，方向都是沿圆的切线，故l B d d =⋅l B 。

于是根据安培环路定理有
I
r B l B l
l
π2d d μ
===⋅⎰⎰l B
得
)
(π20R r r
I
B >=
μ
由此可见，无限长载流圆柱体外的磁感强度与无限长载流直导线的磁感强度是相同的。

现在来计算圆柱体内距轴线垂直距离为r 处（R r <）的磁感强度。

如上图(左)所示，通过点P 作半径为r 的圆，圆面与圆柱体的轴线垂直。

由于磁场的对称性，圆周上各点B 的值相等，方向均与圆周相切。

故根据安培环路定理有
⎰
∑==⋅i
I r B 0π2d μl B
式中∑
i
I
是以r 为半径的圆所包围的电流。

如果在圆柱体内电流密度是均匀的，有2
π/R I j =，那么，通过
截面积2πr 的电流222/πR Ir r j I i ==∑。

于是上式为
22
0 π2d R Ir r B l μ==⋅⎰l B
得
)
(π22
0R r R Ir
B <=
μ
三、思考题
1. 在下面三种情况下，能否用安培环路定律来求磁感强度？为什么？
（1）有限长载流直导线产生的磁场； （2）圆电流产生的磁场；
（3）两无限长同轴载流圆柱面之间的磁场。

2. 如下图所示在一个圆形电流的平面内取一个同心的圆形闭合回路，并使这两个圆同轴，且互相平行。

由于此闭合回路内不包 含电流，所以把安培环路定理用于上述闭合回路，可得 ⎰=⋅l 0
d l B 由此结果
能否说在闭合回路上各点的磁感强度为零？。