数字PID及其参数整定方法

pid参数的整定过程
PID（比例-积分-微分）控制器是一种常用的反馈控制器，用于调节和稳定系统。

PID控制器的参数整定过程通常包括以下几个步骤：
1.初始参数设定：根据系统的性质和需求，设置PID控制器的初
始参数。

通常情况下，可以将三个参数（比例增益Kp、积分时
间Ti、微分时间Td）都设为一个较小的初始值。

2.比例增益调整：从零开始逐步增加比例增益Kp的数值，观察
系统响应的变化。

如果Kp过小，系统响应可能过慢；如果Kp
过大，系统可能会出现超调或不稳定的情况。

通过不断调整Kp
的数值，直到找到一个合适的值，使得系统响应快速且稳定。

3.积分时间调整：在找到合适的Kp之后，开始调整积分时间Ti
的数值。

增大Ti会增加积分作用的影响，降低控制器对于持续
偏差的敏感度。

然而，过大的Ti可能导致系统响应的延迟和振
荡。

通过逐步调整Ti的数值，找到一个使系统响应稳定且快速
的值。

4.微分时间调整：在完成比例增益和积分时间的调整后，可以开
始调整微分时间Td的数值。

微分作用可以抑制系统响应中的
过冲和振荡，并提高系统的稳定性。

然而，过大的Td可能会引
入噪声的放大。

通过逐步调整Td的数值，找到一个能够平衡系
统响应速度和稳定性的值。

5.反复迭代：整定PID参数是一个迭代的过程。

一旦完成了上述
步骤，需要对整个系统进行测试和观察，以确定参数的最佳组合。

如果发现系统仍然存在问题，可以根据实际情况再次进行参数调整，直到达到满意的控制效果。

PID控制器的参数整定PID控制器是一种常用的闭环控制器，可以根据系统的输入和输出之间的误差来调整控制器的参数，从而实现对系统的稳定控制。

PID控制器的参数整定是指确定控制器的比例系数Kp、积分时间Ti和微分时间Td的过程。

下面将详细介绍PID控制器的参数整定方法和相关的考虑因素。

一、参数整定方法：1.经验整定法：根据经验将控制器的参数进行初步设定。

经验整定法通常通过试验或先验知识来确定参数，根据具体的应用场景不断调整，以达到较好的控制效果。

该方法常用与简单的控制系统或者无法获得系统数学模型的情况下。

2. Ziegler-Nichols整定法：Ziegler-Nichols整定法是一种基于试验的整定方法。

该方法首先暂时关闭积分和微分控制，只调整比例控制系数Kp，使系统达到临界稳定状态。

然后测量临界增益Ku和临界周期Pu，根据不同类型的控制系统（比例型、积分型和微分型），采用不同的参数整定公式确定Kp、Ti和Td的初始值，再根据系统的实际响应实时调整。

3. Ziegler-Nichols改进整定法（Chien-Hrones-Reswich法）：该方法是对Ziegler-Nichols整定法的改进，可以更精确地测定控制器参数。

该方法同样通过测量系统的临界增益Ku和临界周期Pu，但是对参数的计算公式进行了修正，提高了参数整定的准确性。

4. 极点配置法（Pole Placement）：极点配置法是一种基于系统数学模型的整定方法。

通过分析系统的传递函数，确定控制器的极点位置，从而使系统的闭环响应满足所需的性能指标。

该方法需要对系统的数学模型有较详细的了解，适用于相对复杂的控制系统。

5.自整定法：自整定法是一种自动寻优的整定方法，常用于智能控制器中。

该方法通过观察系统的动态性能，通过迭代寻找最优的参数组合。

自整定法通常采用优化算法（如遗传算法、粒子群算法等）来最优参数，在一定的性能和收敛速度之间进行权衡。

二、参数整定的考虑因素：1.系统的稳定性：控制器的参数整定应确保系统的闭环响应稳定。

PID控制原理与参数整定方法PID控制是一种常用的反馈控制方法，它通过测量控制系统的输出与期望输入之间的差异，计算出一个控制信号来调节控制系统的行为。

PID 控制器的主要参数有比例增益（Proportional），积分时间（Integral）和微分时间（Derivative）。

通过调节这些参数，可以实现对控制系统的动态响应和稳定性的优化。

首先，我们来了解一下PID控制器的工作原理。

PID控制器是基于控制误差和误差的变化率来计算输出控制信号的，它包含三个部分：比例控制项、积分控制项和微分控制项。

比例控制项（P项）以控制误差的比例关系来计算输出信号。

它的计算公式为：P=Kp*e(t)，其中Kp为比例增益，e(t)为控制误差。

比例增益越大，控制器对误差的纠正力度越大，但过大的比例增益会引起震荡。

积分控制项（I项）以控制误差的累积值来计算输出信号。

它的计算公式为：I = Ki * ∫e(t)dt，其中Ki为积分时间，∫e(t)dt为控制误差的累积值。

积分控制项主要用于消除稳态误差，但过大的积分时间会引起超调和不稳定。

微分控制项（D项）以控制误差的变化率来计算输出信号。

它的计算公式为：D = Kd * de(t)/dt，其中Kd为微分时间，de(t)/dt为控制误差的变化率。

微分控制项主要用于抑制系统的震荡和快速响应，但过大的微分时间会引起噪声放大。

接下来，我们来介绍一下PID参数整定的方法。

在实际应用中，PID 参数的选择通常需要经验和试验。

以下是常用的PID参数整定方法。

1.经验设置法：根据经验设置PID参数的初始值，然后根据实际系统的响应进行调整。

这种方法需要经验和实践的积累，适用于经验丰富的控制工程师。

2. Ziegler-Nichols方法：这是一种基于实验步骤响应曲线的整定方法。

该方法通过观察控制系统的临界点，确定比例增益、积分时间和微分时间的初始值，然后通过试探法逐步调整，直到系统达到所需的动态响应。

PID参数自整定的方法及实现近年来出现的各种智能型数字显示调节仪，一般都具有PID参数自整定功能。

仪表在初次使用时，可通过自整定确定系统的最佳P、I、D调节参数，实现理想的调节控制。

在自整定启动前，因为系统在不同设定值下整定的参数值不完全相同，应先将仪表的设定值设置在要控制的数值（如果水电站或是中间值）上。

在启动自整定后，仪表强制系统产生扰动，经过2~3个振荡周期后结束自整定状态。

仪表通过检测系统从超调恢复到稳态（测量值与设定值一致）的过度特性，分析振荡的周期、幅度及波形来计算仪表的最佳调节参数。

理想的调节效果是，设定值应与测量值保持一致，可从动态（设定值变化或扰动）合稳态（设定值固定）两个方面来评价系统调节品质，通过PID参数自整定，能够满足大多数的系统。

不同的系统由于惯性不同，自整定时间有所不同，从几分钟到几小时不等。

我单位有一台DYJ-36-2型油加热器。

该油加热器是由加热炉体、载体传输通道、膨胀系统及电控装置构成，与用热设备组成了一个循环加热系统。

热载体（导热油）在炉体内被电热管加热后，用热油泵通过管路传送到用热设备，放热后再次回到炉体内升温，实现连续循环过程。

控制油温的调节仪表时日本SHIMADEN（岛电）公司的SR73型PID自整定温控仪。

温度控制系统为闭环负反馈系统。

由热电偶检测的油温信号对应的mV信号，传送至调节仪的信号输入端，调节仪输出DC15V、20mV的高电平信号，传送至SSR固态继电器，驱动晶闸管过零触发开关电路，改变固定期内的输出占空比，从而控制电热器的输出功率。

在系统投入运行前，我们对调节仪进行PID参数的自整定工作。

首先把它的设定值（SV）调至工艺常用温度90℃。

仪表提供了一组PID参数：比例带P=0.1%~999.9%积分时间I=1~6000s微分时间D=0~3600s再进入功能彩旦，把P、I、D参数分别按经验值设定为：P=3.0；I=120；D=30；超调抑制系数SF=0.4。

PID控制原理与参数整定方法一、概述PID是比例-积分-微分控制的简称，也是一种控制算法，其特点是结构改变灵活、技术成熟、适应性强。

对一个控制系统而言，由于控制对象的精确数学模型难以建立，系统的参数经常发生变化，运用控制理论综合分析要耗费很大的代价，却不能得到预期的效果，所以人们往往采用PID调节器，根据经验在线整定参数，以便得到满意的控制效果。

随着计算机特别是微机技术的发展，PID控制算法已能用微机简单实现，由于软件系统的灵活性，PID算法可以得到修正而更加完善。

我们阳江基地有数以千计的采用PID控制的调节器，用于温度控制、压力控制、流量控制，在塑杯及灌装生产过程中，发挥着重要的作用。

因此，学习PID控制的基本原理，合理的设计PID控制系统，用好、维护好这些调节器，对提高产品质量，降低废品率，节约能源具有十分重要的意义。

本课程从系统的角度，采用多种分析方法，详细讲解经典PID控制的基本原理和PID参数的整定方法，简介现代数字PID控制思想，希望对大家使用PID调节器有所帮助。

二、调节系统的品质和特性一个调节系统的品质可以用静态品质和动态品质来衡量。

所谓静态品质就是系统稳定后，被控参数与给定值间的差值的大小。

偏差愈大则静差愈大，静差愈小静态品质愈好。

当系统受到扰动后或整定在一个新值时需要在较短时间内过渡到稳定，不发生振荡和发散，这便是衡量系统动态特性的指标。

一个好的调节系统应该二个品质都好。

但动静态品质往往是相互矛盾的，要静差小，系统的放大倍数就要大，系统放大倍数愈大则系统愈不稳定，即动态品质不好。

图1-1收敛型1图1-2收敛型2图1-3发散型落图1-4振荡型图1-1至1-4是几种典型的控制曲线，只有图1-1表示动静态品质都好。

一般的调节系统都具有惯性和滞后两种特性/只是大小不同而已。

这两个特性应从控制对象，控制作用这两个方面去理解。

弄懂以上关于调节系统的几个基本概念，对于理解PID控制的原理有很大的帮助。

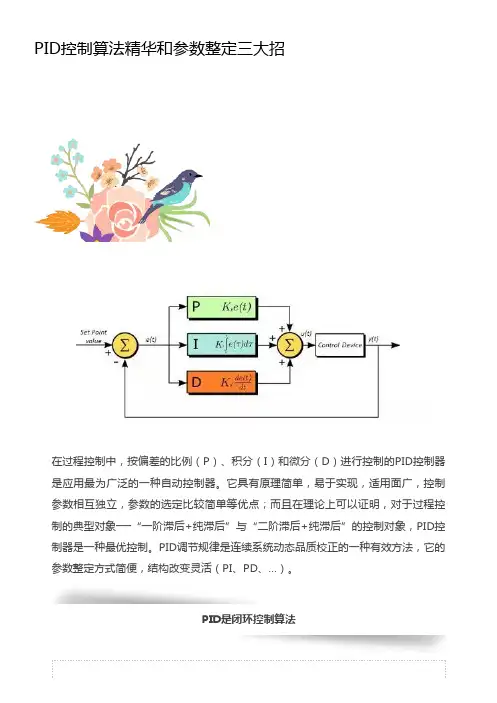
PID控制算法精华和参数整定三大招PID是闭环控制算法在过程控制中，按偏差的比例（P）、积分（I）和微分（D）进行控制的PID控制器是应用最为广泛的一种自动控制器。

它具有原理简单，易于实现，适用面广，控制参数相互独立，参数的选定比较简单等优点；而且在理论上可以证明，对于过程控制的典型对象──“一阶滞后+纯滞后”与“二阶滞后+纯滞后”的控制对象，PID控制器是一种最优控制。

PID调节规律是连续系统动态品质校正的一种有效方法，它的参数整定方式简便，结构改变灵活（PI、PD、…）。

因此要实现PID算法，必须在硬件上具有闭环控制，就是得有反馈。

比如控制一个电机的转速，就得有一个测量转速的传感器，并将结果反馈到控制路线上，下面也将以转速控制为例。

PID是比例(P)、积分(I)、微分(D)控制算法但并不是必须同时具备这三种算法，也可以是PD,PI,甚至只有P算法控制。

我以前对于闭环控制的一个最朴素的想法就只有P控制，将当前结果反馈回来，再与目标相减，为正的话，就减速，为负的话就加速。

现在知道这只是最简单的闭环控制算法。

PID控制器结构PID控制系统原理结构框图对偏差信号进行比例、积分和微分运算变换后形成一种控制规律。

“利用偏差，纠正偏差”。

模拟PID控制器模拟PID控制器结构图PID控制器的输入输出关系为：比例(P)、积分(I)、微分(D)控制算法各有作用比例，反应系统的基本(当前)偏差e(t)，系数大，可以加快调节，减小误差，但过大的比例使系统稳定性下降，甚至造成系统不稳定;积分，反应系统的累计偏差，使系统消除稳态误差，提高无差度，因为有误差，积分调节就进行，直至无误差;微分，反映系统偏差信号的变化率e(t)-e(t-1)，具有预见性，能预见偏差变化的微分，反映系统偏差信号的变化率e(t)-e(t-1)，具有预见性，能预见偏差变化的趋势，产生超前的控制作用，在偏差还没有形成之前，已被微分调节作用消除，因此可以改善系统的动态性能。

PID控制原理与参数的整定方法PID控制器是一种常用的自动控制器，在工业控制中广泛应用。

它的原理很简单，即通过不断调节控制信号来使被控制物体的输出接近给定值。

PID控制器由比例（P）、积分（I）和微分（D）三个控制参数组成。

下面将详细介绍PID控制的原理和参数整定方法。

一、PID控制原理1.比例（P）控制比例控制根据被控制量的偏差的大小，按照一定比例调节控制量的大小。

当偏差较大时，调节量增大；当偏差较小时，调节量减小。

此项控制可以使系统快速响应，并减小系统稳态误差。

2.积分（I）控制积分控制根据被控制物体的偏差的积分值来调节控制量。

积分控制的作用主要是消除系统的稳态误差。

当偏差较小但持续较长时间时，积分量会逐渐增大，以减小偏差。

3.微分（D）控制微分控制根据被控制物体的偏差的变化率来调节控制量。

当偏差的变化率较大时，微分量会增大，以提前调整控制量。

微分控制可以减小系统的超调和振荡。

综合比例、积分和微分控制，PID控制器可以通过不同的控制参数整定来适应不同的被控制物体的特性。

二、PID控制参数整定方法1.经验整定法经验整定法是根据对被控制系统的调试经验和运行情况来选择控制参数的方法。

它是通过实际试验来调整控制参数，通过观察系统的响应和稳定性来判断参数的合理性。

2. Ziegler-Nichols整定法Ziegler-Nichols整定法是根据系统的临界响应来选择PID控制参数的方法。

在该方法中，首先将I和D参数设置为零，然后不断提高P控制参数直到系统发生临界振荡。

根据振荡周期和振荡增益的比值来确定P、I和D的参数值。

3.设计模型整定法设计模型整定法是根据对被控系统的数学建模来确定PID控制参数的方法。

通过建立被控系统的数学模型，分析其频率响应和稳态特性，从而设计出合理的控制参数。

4.自整定法自整定法是通过主动调节PID控制器的参数，使被控系统的输出能够接近给定值。

该方法可以通过在线自整定或离线自整定来实现。

PID参数的整定方法PID控制器是目前最常用的控制算法之一，其调节参数（也称为PID 参数）的合理设置对控制系统的性能起着关键作用。

下面将介绍几种常用的PID参数整定方法。

1.经验法：经验法是最为简单直接的方法，通常由经验工程师根据自身经验来设定PID参数。

这种方法适用于一些简单的控制系统，但是对于复杂的系统来说，由于经验法不能提供具体的参数值，容易出现性能较差的情况。

2. Ziegler-Nichols 整定法：Ziegler-Nichols 整定法是PID参数整定中较为经典的方法，其步骤如下：-首先将PID控制器的I和D参数设置为零。

-逐渐增大比例参数（P）直到系统出现持续且稳定的振荡。

-记录此时的比例参数为Ku。

- 根据不同的控制对象类型，Ziegler-Nichols方法会有不同的参数整定公式，常见的有：-P型系统：Kp=0.50Ku，Ti=0.50Tu，Td=0.125Tu-PI型系统：Kp=0.45Ku，Ti=0.83Tu，Td=0.125Tu-PID型系统：Kp=0.60Ku，Ti=0.50Tu，Td=0.125Tu其中Ku为临界增益值，Tu为临界周期。

3. Chien-Hrones-Reswick (CHR) 整定法：CHR整定法基于频域设计方法，通过系统的频率响应曲线来确定PID参数。

其步骤如下：-绘制系统的频率响应曲线（一些软件和仪器可以直接测量）。

-根据曲线的特征，确定比较慢的过程的时间常数τ和极点频率ωp。

-根据以下公式得到PID参数：-P参数：Kp=2/（ωpτ）-I参数：Ti=τ/2-D参数：Td=τ/8不能掉进方法的误区，如超调范围不合适，调节周期过大或周期过小时，传递函数为微分型等。

4.设计优化法：设计优化法是基于性能指标的优化算法，通过对系统的模型进行优化，得出最佳的PID参数。

这种方法较复杂，通常使用数学工具或计算机软件进行参数优化。

常见的优化算法有遗传算法、粒子群算法等。

PID控制器参数整定的一般方法：PID控制器的参数整定是控制系统设计的核心内容。

它是根据被控过程的特性确定PID控制器的比例系数、积分时间和微分时间的大小。

PID控制器参数整定的方法很多，概括起来有两大类：一是理论计算整定法。

它主要是依据系统的数学模型，经过理论计算确定控制器参数。

这种方法所得到的计算数据未必可以直接用，还必须通过工程实际进行调整和修改；二是工程整定方法，它主要依赖工程经验，直接在控制系统的试验中进行，且方法简单、易于掌握，在工程实际中被广泛采用。

PID控制器参数的工程整定方法，主要有临界比例法、反应曲线法和衰减法。

三种方法各有其特点，其共同点都是通过试验，然后按照工程经验公式对控制器参数进行整定。

但无论采用哪一种方法所得到的控制器参数，都需要在实际运行中进行最后调整与完善。

现在一般采用的是临界比例法。

利用该方法进行 PID控制器参数的整定步骤如下：(1)首先预选择一个足够短的采样周期让系统工作；(2)仅加入比例控制环节，直到系统对输入的阶跃响应出现临界振荡，记下这时的比例放大系数和临界振荡周期；(3)在一定的控制度下通过公式计算得到PID控制器的参数。

PID参数的设定：是靠经验及工艺的熟悉，参考测量值跟踪与设定值曲线，从而调整P、I、D的大小。

书上的常用口诀：参数整定找最佳，从小到大顺序查；先是比例后积分，最后再把微分加；曲线振荡很频繁，比例度盘要放大；曲线漂浮绕大湾，比例度盘往小扳；曲线偏离回复慢，积分时间往下降；曲线波动周期长，积分时间再加长；曲线振荡频率快，先把微分降下来；动差大来波动慢。

微分时间应加长；理想曲线两个波，前高后低4比1；一看二调多分析，调节质量不会低。

个人认为PID参数的设置的大小，一方面是要根据控制对象的具体情况而定；另一方面是经验。

P是解决幅值震荡，P大了会出现幅值震荡的幅度大，但震荡频率小，系统达到稳定时间长；I是解决动作响应的速度快慢的，I大了响应速度慢，反之则快；D是消除静态误差的，一般D设置都比较小，而且对系统影响比较小。

PID参数整定方式为了使PID控制器能够在实际控制过程中具有较好的性能，需要对PID参数进行合理的整定。

PID参数整定方法有很多种，下面将介绍几种常见的整定方法。

1.试-误整定法：试-误整定法是最常见的整定方法之一，通过不断试验和观察系统的响应，调整PID参数，直到满足控制要求。

这种方法的优点是简单易行，但由于需要进行大量试验，整定过程较为繁琐，而且可能造成系统过度振荡或不稳定。

2.经验法整定：经验法是基于经验公式进行PID参数整定的方法。

常用的经验公式有：Ziegler-Nichols方法、Chien-Hrones-Reswick方法等。

这些公式通过对系统的开环和闭环响应进行分析，得出相应的参数整定公式。

这种方法的优点是较为简单和直观，缺点是不适用于不同的系统和工况。

3.频率响应法整定：频率响应法是通过对系统的频率特性进行分析，来确定PID参数的方法。

常用的方法有：奈奎斯特曲线法、波特曼图法等。

这些方法借助于系统的频率特性图形，通过观察曲线的形状和特点，确定PID参数。

这种方法的优点是适用范围广，适用于不同的系统类型和工况，但缺点是需要一定的专业知识和技巧。

4.优化算法整定：优化算法包括遗传算法、粒子群算法、模拟退火算法等。

这些算法通过不断优化PID参数，使系统响应达到最优或接近最优。

这种方法的优点是较为灵活和智能化，能够得到较好的参数整定结果，但缺点是计算复杂度较大，需要较高的计算资源和时间。

综上所述，PID参数整定是针对特定系统和工况而进行的调整过程，不同的整定方法适用于不同的控制要求和应用场景。

在实际应用过程中，可以根据系统特点和控制要求选择合适的整定方法，并通过试验和优化来调整PID参数，以实现最佳控制效果。

PID控制及参数整定PID控制是一种常用的控制器设计方法，广泛应用于各种自动控制系统中。

PID控制器基于被控对象的误差信号，通过比例、积分和微分三个部分进行加权计算，生成控制量来驱动被控对象，使其输出接近设定值。

参数整定是指通过调整PID控制器的比例系数、积分时间和微分时间等参数，使得控制系统性能最佳化。

本文将详细介绍PID控制及参数整定的相关内容。

一、PID控制原理F(t) = Kp * e(t) + Ki * ∫e(t)dt + Kd * de(t)/dt其中，Kp、Ki和Kd分别是比例增益、积分时间和微分时间，e(t)为被控系统目标值与实际值之间的误差，de(t)/dt为误差的变化速率。

-比例作用：比例增益Kp使得控制器能够对误差进行直接补偿，其作用是使系统更快地接近目标值。

当比例增益增大时，系统响应速度更快，但可能引起过冲或稳定性问题。

-积分作用：积分时间Ki使得控制器能够记录误差的累积量，并对其进行补偿。

积分作用可以消除稳态误差，提高系统的精度。

但积分时间过长可能引起系统的振荡或不稳定。

-微分作用：微分时间Kd使得控制器对误差的变化率进行补偿，以避免系统过冲或振荡。

微分作用可以提高系统的稳定性和抗干扰能力。

但微分时间过大可能引起系统的噪声放大或响应迟滞。

二、PID参数整定方法PID参数整定是为了找到合适的Kp、Ki和Kd值，以获得最佳的控制系统性能。

常用的PID参数整定方法有以下几种：1.经验调整法：根据经验公式或类似系统的参数进行估计。

这种方法简单易行，但精度较低，适用于对控制精度要求不高的系统。

2. Ziegler-Nichols方法：这是一种经典的PID参数整定方法，通过系统的临界增益和临界周期来确定合适的参数。

具体步骤是先将系统增益逐渐增大，直到系统开始振荡，记录振荡的周期和振幅。

然后根据临界周期和振幅计算出Kp、Ki和Kd值。

这种方法相对简单，但对系统的稳定性有一定要求。

3.调整法：根据控制系统的特性和需求进行逐步调整。

2.3 PID参数整定方法2.3.1 工程整定法PID数字调节器的参数，除了比例系数K p，积分时间T i和微分时间T d外，还有1个重要参数即采样周期T。

1．采样周期T的选择确定从理论上讲，采样频率越高，失真越小。

但是，对于控制器，由于是依靠偏差信号来进行调节计算的，当采样周期T 太小，偏差信号也会过小，此时计算机将失去调节作用；若采样周期T太长，则将引起误差。

因此采样周期T必须综合考虑。

采样周期的选择方法有两种，一种是计算法，另一种是经验法。

计算法由于比较复杂，特别是被控对象各环节时间常数难以确定，工程上较少用。

经验法是一种凑试法，即根据人们在控制工作实践中积累的经验以及被控对象的特点，先选择一个采样周期T，进行试验，再反复改变T，直到满意为止。

2．K p，T i，T d的选择方法1）扩充临界比例度法扩充临界比例度法是简易工程整定方法之一，用它整定K p，T i，T d的步骤如下。

选择最短采样周期T min，求出临界比例度S u和临界振荡周期T u。

具体方法是将T min输入计算机，只有P环节控制，逐渐缩小比例度，直到系统产生等幅振荡。

此时的比例度即为临界比例度S u，振荡周期称为临界振荡周期T u。

选择控制度为：（2-15）通常当控制度为1.05时，表示数字控制方式与模拟方式效果相当。

根据计算度，查表2-1可求出K p，T i，T d。

表2-1 扩充临界比例度法整定参数表控制度控制规律参数T K p T i T d1.05PIPID0.03T u0.014T u0.53S u0.63S u0.88T u0.49T u/0.14T u1.2PIPID 0.05T u0.43T u0.49S u0.47S u0.91T u0.47T u/0.16T u1.5PIPID 0.14T u0.09T u0.42S u0.34S u0.99T u0.43T u/0.20Tu2.0PIPID 0.22T u0.16T u0.36S u0.27S u1.05T u0.4T u/0.22T u2）扩充响应曲线法若已知系统的动态特性曲线，可以采用和模拟调节方法一样的响应曲线法进行整定，其步骤如下。

PID-采样周期及参数整定方法数字PID控制器控制参数的选择，可按连续-时间PID参数整定方法进行。

在选择数字PID参数之前，首先应该确定控制器结构。

对允许有静差（或稳态误差）的系统，可以适当选择P或PD控制器，使稳态误差在允许的范围内。

对必须消除稳态误差的系统，应选择包含积分控制的PI或PID控制器。

一般来说，PI、PID和P控制器应用较多。

对于有滞后的对象,往往都加入微分控制。

控制器结构确定后，即可开始选择参数。

参数的选择，要根据受控对象的具体特性和对控制系统的性能要求进行。

工程上，一般要求整个闭环系统是稳定的，对给定量的变化能迅速响应并平滑跟踪，超调量小；在不同干扰作用下，能保证被控量在给定值；当环境参数发生变化时，整个系统能保持稳定，等等。

这些要求，对控制系统自身性能来说，有些是矛盾的。

我们必须满足主要的方面的要求，兼顾其他方面，适当地折衷处理。

PID控制器的参数整定，可以不依赖于受控对象的数学模型。

工程上，PID控制器的参数常常是通过实验来确定，通过试凑，或者通过实验经验公式来确定。

采样周期的选择采样周期：采样一数据控制系统中，设采样周期为T S，采样速率为1/T S，采样角频率为采样周期T S是设计者要精心选择的重要参数，系统的性能与采样周期的选择有密切关系。

需要考虑的因素：采样周期的选择受多方面因素的影响,主要考虑的因素分析如下。

（1）香农（Shannon）采样定理（Wmax--被采样信号的上限角频率）给出了采样周期的上限。

满足这一定理，采样信号方可恢复或近似地恢复为原模拟信号，而不丢失主要信息。

在这个限制范围内，采样周期越小，采样-数据控制系统的性能越接近于连续-时间控制系统。

（2）闭环系统对给定信号的跟踪，要求采样周期要小。

（3）从抑制扰动的要求来说，采样周期应该选择得小些。

（4）从执行元件的要求来看，有时要求输入控制信号要保持一定的宽度。

（5）从计算机精度考虑，采样周期不宜过短。

PID控制原理及参数整定方法PID控制是一种经典的控制策略，广泛应用于各种工业自动化系统。

其通过比较设定值与实际输出值，根据误差及其变化趋势，实时调整控制器的参数，以达到期望的控制效果。

本文将详细介绍PID控制原理及参数整定方法，旨在帮助读者更好地理解和应用PID控制。

PID控制模型是由比例（P）、积分（I）和微分（D）三个环节组成的。

在工业自动化中，PID控制器作为一种核心组件，用于维持系统输出值与设定值之间的误差为最小。

PID控制器具有结构简单、稳定性好、易于实现等优点，因此被广泛应用于各种工业控制系统中。

PID控制原理基于控制系统的稳态误差，通过比例、积分和微分三个环节的作用，达到减小误差的目的。

比例环节根据误差信号的大小，产生相应的控制输出；积分环节根据误差信号的变化率，进一步调整控制输出；微分环节则根据误差信号的变化趋势，提前进行控制调整，以迅速消除误差。

PID参数整定的目的是选择合适的控制器参数，以满足系统的动态性能和稳态性能要求。

整定过程中，需要合理调整比例系数、积分时间和微分增益等参数。

其中，比例系数主要影响系统的稳态误差；积分时间用于控制积分环节的灵敏度；微分增益则决定了微分环节的作用强度。

针对不同的控制对象和系统要求，需要灵活调整这些参数，以获得最佳的控制效果。

以某化工生产线的液位控制为例，说明PID控制原理及参数整定的应用。

在此案例中，液位控制器通过比较设定值与实际液位值的误差，实时调整进料泵的转速，以维持液位稳定。

选择一个合适的比例系数Kp，使得系统具有较快的响应速度；调整积分时间Ti，以避免系统出现稳态误差；适当微分增益Kd的设定，可以改善系统的动态性能。

通过合理的参数整定，液位控制系统可以取得良好的控制效果。

然而，若比例系数过大，系统可能会出现振荡现象；若积分时间过长，系统可能无法达到预期的稳态性能；若微分增益过强，系统可能会对噪声产生过度反应。

因此，在参数整定过程中，需要根据实际情况进行反复调整，以达到最佳的控制效果。

PID参数整定方法PID（Proportional-Integral-Derivative，比例积分微分控制）是一种常用的控制算法，它通过调整输出信号，使得被控对象的输出变量尽可能地接近设定值。

为了实现良好的控制效果，需要对PID参数进行合理的整定。

下面将介绍几种常用的PID参数整定方法。

1.经验整定法：经验整定法是一种经验性的参数整定方法，根据工程经验和试错原则来确定PID参数。

具体步骤如下：-初始设定PID参数为Kp=1，Ki=0，Kd=0。

-逐渐增加Kp的值，直到系统开始出现超调现象。

-根据系统的超调量，逐渐减小Kp的值，直到系统的超调量满足要求。

-根据系统的超调时间，逐渐增加Ki的值，使得系统的超调时间减小。

-根据系统的响应速度，逐渐增加Kd的值，使得系统的响应速度增加。

2. Ziegler-Nichols指标整定法：Ziegler-Nichols指标整定法是一种基于系统阶跃响应的参数整定方法，通过测量系统的阶跃响应特性来确定PID参数。

该方法分为三种整定方式：- Ziegler-Nichols开环法：-将系统设置为开环控制。

-逐渐增大Kp的值，直到系统开始出现持续振荡的现象。

-记录该时刻的Kp值（Ku）和持续振荡的周期（Tu）。

-根据Ku和Tu计算出PID参数：Kp=0.6Ku，Ki=1.2Ku/Tu，Kd=3KuTu/40。

- Ziegler-Nichols闭环法：-将系统设置为闭环控制。

-逐渐增大Kp的值，直到系统的输出响应快速但不超调。

-记录该时刻的Kp值（Ku）。

-根据系统的临界增益（Ku）计算出PID参数：Kp=0.33Ku，Ki=0.33Kp/Tu，Kd=0.33KpTu。

- Ziegler-Nichols两点法：-将系统设置为闭环控制。

-记录系统输出值最初变化的瞬间（T1）和最终变化的瞬间（T2）。

-根据T1和T2计算出PID参数：Kp=(4/Tu)(1/T1+1/T2)，Ki=2/Tu，Kd=KpTu/83. Chien-Hrones-Reswick方法：Chien-Hrones-Reswick方法是一种基于系统阶跃响应曲线形状的参数整定方法。