异步时序逻辑电路分析方法案例说明

分析图所示电平异步时序逻辑电路
电平异步时序逻辑电路的竞争
电平异步时序逻辑电路是利用反馈回路 的时间延迟实现记忆功能。前面对电路 进行分析时，没有对各反馈回路之间时 间延迟的长短进行讨论，也就说，是在 假定各回路之间延迟时间相同的情况下 对电路的工作进程进行分析的。事实上， 反馈回路的延迟往往各不相同。
从激励表中可知，在要求触发器状态不变 时，有两种不同的处理方法。一是令CP 为d，输入端取相应值；二是令CP为0， 输入端取任意值。
例 6.3 用T触发器作为存储元件，设计一 个异步模8加1计数器，该电路对输入端x 出现脉冲进行计数，当收到八个脉冲时， 输出端Z产生一个进位输出脉冲。
用D触发器作为存储元件，设计一个“x1x2-x2”序列检测器。该电路有两个输入x1 和x2 ，一个输出Z。仅当x1输入一个脉冲 后， x2连续输入两个脉冲时，输出端Z由 0变为1，该1信号将一直维持到输入端x1 或x2再出现脉冲时才由1变为0。
脉冲异步时序逻辑电路的分析
脉冲异步时序逻辑电路的分析与同步时序 逻辑电路大致相同。 1.写出电路的输出函数和激励函数表达式； 2.列出电路次态真值表； 3.作出状态表和状态图； 4.画出时间图并用文字描述电路的逻辑功 能。
与同步时序逻辑电路分析的区别主要表现在 两点： 第一，当存储元件采用时钟控制触发器时， 对触发器的时钟控制应作为激励函数处理。 分析时应特别注意触发器时钟端何时有脉冲 作用，仅当时钟端有脉冲作用时，才根据触 发器的输入确定状态转移方向，否则，触发 器状态不变。若采用非时钟控制触发器，则 应注意作用到触发器输入端的脉冲信号
这里所谓的竞争，是指当输入信号变化引 起电路中两个或两个以上状态变量发生变 化时，由于各反馈回路延迟时间的不同， 使状态变量的变化有先有后而导致不同状 态响应过程的现象。若竞争中各种可能最 终能到达预定的稳定，则称为非临界竞争。 反之，若使电路到达不同的稳态，既状态 转移不可预测，则称为临界竞争。

第六章 异步时序逻辑电路
6.1 脉冲异步时序逻辑电路
6.1.1 概
一、结 构
述
脉冲异步时序电路的一般结构如下图所示。
图中，存储电 路可由时钟控制触 发器或非时钟控制 触发器组成。
第六章 异步时序逻辑电路
二、输入信号的形式与约束 1.输入信号为脉冲信号; 2.输入脉冲的宽度必须保证触发器可靠翻转; 3.输入脉冲的间隔必须保证前一个脉冲引起的电路响 应完全结束后，后一个脉冲才能到来; 4.不允许两个或两个以上输入端同时出现脉冲。 对n个输入端的电路，其一位输入只允许出现n+1种取 值组合，其中有效输入种取值组合为n种。
x1 x2 Z
第六章 异步时序逻辑电路
例2
X2
A/0 X2
X1 X2 X1 X2
B/0 X1
D/1
X1
C/0
第六章 异步时序逻辑电路
例2
X2
A/0 X2 X1 X2 X1 X2 B/0 X1 X1 Present Next state output state X1 X2
D/1
C/0
Y1
Y2
0
1 D C
D2
& ≥1
Q2 C2
Q2
D1 X1
≥1 C1
Q1
X2
Q1
第六章 异步时序逻辑电路
例2 用T触发器作为存储元件，设计一个异步模8加1计数 器，电路对输入端x出现的脉冲进行计数，当收到第八个脉冲 时，输出端Z产生一个进位输出脉冲。 解 由题意可知，该电路模型为Mealy型。由于状态数目 和状态转换关系非常清楚，可直接作出二进制状态图和状态表。 ⑴作出状态图和状态表 设电路初始状态为“000”，状态变量用y2、y1、y0表示， 可作出二进制状态图如下。

X=1 Z
X Q1n
n Q2 1Q1n1
Z
0 0 1 1
0 1 0 1
0 1 0 1
0 1 1 0
1 0 1 0
0 0 0 1
1 0 1 0
1 0 0 1
1 0 1 0
0 0 0 1
状态图
n Qn1Q1 1 / Z 2 X=0 X=1
QQ
0 0 0 1 1 0 1 1
n 2
n 1
X/Z Q2Q1 0/0 00 00
4. 确定和说明电路的逻辑功能
5.2.2 同步时序逻辑电路的分析举例1
先介绍相对简单的Moore型时序逻辑电路，再介绍相对复 杂的Mealy型时序逻辑电路
例1 试分析下图所示时序电路的逻辑功能。
解：由电路图可知，此为同步时序逻辑电路，无输入信号
所以，属Moore型 1.写出各触发器的驱动方程和输出方程。
D0 Q2 Q0
D1 Q1
n1

D 2= Q 0 Q 1
Q
Q
n 1 0 n 2 n 0
D
n 0
Q Q CP0 Q CP0
Q
n1 1
n1 2
Q CP1 Q CP1
n 1 n 1
n 1 n 0 n 2


Q
Q Q CP2 Q CP2

(3)列电路状态转换真值表
Y 输出方程： 1 Q1 , Y2 Q2
驱动方程：
1J ＞C1
Y1
Q1
1J ＞C1 1K
Y2
Q2
J1 Q2 , K1 1 J 2 Q1 , K2 1
CP
1K
5.2.2 同步时序逻辑电路的分析举例1

(2) 将驱动方程代入相应 触发器的特性方程，求出
各触发器的状态方程：
(3) 列状态表、画状态图 和时序图：
例6.2.5 分析图6.2.12所示异步时序逻辑电路
（QQAnD+负发 这1 =跳器十由Q时从个分A此Q0状0析B式态0Q可0有C是～见效每1，0）来0触1一
QBn个 一+1 C个=P异递QB步加十1，进所制以加是法
解：(1)各触发器的
触发脉冲方程：
CPD = CP
CPA = CPC = QD CPB = QC
驱动方程:
JD = KD = 1 JC = QA , KC = 1 JB = KB = 1 JA = QBQC , K A = 1
QAn+1 = QAQBQC（QD负跳时此式有效） QBn+1 = QB （QC负跳时此式有效） QCn+1 = QAQC （QD负跳时此式有效） QDn+1 = QD （CP负跳时此式有效）
例6.2.5 分析图6.2.12所示异步时序逻辑电路
CPD = CP
CPA = CPC = QD
CPB = QC
驱动方程:
解：(1) 写出各触发器的触发脉冲方程 和驱动方程：
JD = KD = 1
JC = QA , KC = 1 JB = KB = 1 JA = QBQC , K A = 1
例6.2.5 分析图6.2.12所示异步时序逻辑电路
状态图
QAQBQCQD
1111 1110
1010 1011
1100 1101
0000 0001 0010 0011 0100
10 0 0 0 0
1001 1000 0111 0110 0101

状态不确定
例2 分析如图所示异步时序逻辑电路.
& CLK ≥ CP0 ＞ C FF0 Q0 CP1 ＞C FF1 Q1
≥ ≥ CP2 ＞ C FF2 Q2
Q0
Q1
Q2
& CLK 何时出现触 ≥ CP0 ＞ C FF0 Q0 CP1 ＞C FF1 Q1
≥ ≥ CP2 ＞ C FF2 Q2
发沿？
解 (1) 列出各逻辑方程组 时钟方程
同步时序电路——所有触发器同时转换状态 异步时序电路——各个触发器之间的状态转换存在一定的延迟， 在此期间，电路的状态是不确定的。只有当全部触发器状态转 换完毕，电路才进入新的“稳定”状态，即次态Sn+1。
二.
异步时序逻辑电路的分析举例
FF0 CLK 1D ＞C1 FF1 1D ＞C1 & Z
例1 分析如图所示异步电路 1. 写出电路方程式 ① 时钟方程 CP0=CLK CP1=Q0 ②输出方程 ③激励方程
Q
n 2
Q
0
n 1
Q
n 0
cp2
0
cp1
0
cp0
1
Q2n 1 Q1n 1 Q0n 1
0 0 1
0
00ຫໍສະໝຸດ 0 0 1 1 101 1 0 0 1
1
0 1 0 1 0
0
0 1 1 1 1
1
0 1 0 0 0
1
1 1 0 0 0
0
0 1 0 0 0
1
1 0 0 0 1
0
1 0 0 1 0
1
1
1
1
0
0
0
1
1 0
1 0
1 0 1 0 1

脉冲异步时序逻辑电路的输出信号可以是脉冲 信号也可以是电平信号。
若电路结构为Mealy型，则输出为脉冲信号。 因为输出不仅是状态变量的函数，而且是输入 的函数，而输入为脉冲信号，所以，输出一定是脉 冲信号。 若电路结构为Moore型，则输出是电平信号。 因为输出仅仅是状态变量的函数，所以，输出 值被定义在两个间隔不定的输入脉冲之间，即由两 个输入脉冲之间的状态决定。
高位触发器次态不仅与触发器的现态有关，而且与触发 器的次态有关。在填写状态时，通常要由低位向高位依次填 写。
000 1/0 111 1/0 110 1/0 101
Q1(n+1)＝Q1 x
1/0
1/0
Q2(n+1)＝Q2 Q1+Q2Q1 001 1/0 010 1/0 011 1/0 100
Q3(n+1)＝Q3 Q2Q1+Q3Q2Q1+Q3Q2
• 电路中除可以使用带时钟的触发器外，还可以 使用不带时钟的触发器和延迟元件作为存储元 件；
•电路中没有统一的时钟； •电路状态的改变由外部输入的变化直接引起。
根据外部输入是脉冲信号还是电平信号，
可将异步时序逻辑电路分为脉冲异步时序电路 和电平异步时序电路。
x1
Z1
x1
Z1
组合
组合
xn
逻辑
Zm
xn
1
CP0
(Q
2nQ
n 0
0
Q
n 0
)
Q
2nQ
n 0
Q n1 1
CP1
Q1n
CP1
Q1n
Q1nQ0n
Q1nQ0n
Q n1 2
CP2
Q2n
CP2
Q2n

x1x2x3 y2y1 100 010 001
00 1 01 d 11 d 10 0 0 d 0 0
x1x2x3
y2y1 100 010 001 00 0 d d 0 1 d 1 1 d 11 0 10 d
R1 01 0
由上面的卡诺图，可得 S1＝x1x2x3y2 R1= x1x2x3y2＋x1x2x3
例：分析下图所示的脉冲异步时序电路 z & Q3 Q2 Q1
K3 C J3 “ 1” CP3
K2 C J2 CP2
K1 C J1
x(CP1)
解：
写出输出函数和激励函数表达式 Z＝ Q1n Q2nQ3nx J1=K1=1, J2=K2=1, CP1=x CP2= Q1n
J3=K3=1,
CP3= Q2n
x1
xn
Z1 组合
逻辑 y1 Y1 存储电路
Δ t1
Zm Yr
Y1 存储电路 触发器
触发器
yr
延迟元件
延迟元件
Δ tr
脉冲异步时序逻辑电路
对输入脉冲信号的两点限制： • 在两个或两个以上的输入线上不允许同时出现 脉冲信号；
• 第二个输入脉冲的到达，必须在第一个输入脉
冲所引起的整个电路响应结束之后。
写出电路的状态方程
J－K触发器的次态方程为
Qn+1=(JQn+KQn)CP 该式表明当CP为逻辑1时，触发器的状态才 能发生变化，而只有当时钟出现有效跳变时， CP才为逻辑1。
将3个触发器的激励函数代入触发器的次态方程，
Q1n+1=(J1Q1n+K1Q1n)CP＝Q1 n x Q2n+1=(J2Q2n+K2Q2n)CP＝Q2n Q1n Qn+1=(J3Q3n+K3Q3n)CP＝Q3n Q2n

7．2．2异步时序逻辑电路的分析方法异步时序逻辑电路的分析方法和同步时序逻辑电路的基本相同，但在异步时序逻辑电路中，只有部分触发器由计数脉冲信号源CP触发，而其它触发器则由电路内部信号触发。

在分析异步时序逻辑电路时，应考虑各个触发器的时钟条件，即应写出时钟方程。

这样，各个触发器只有在满足时钟条件后，其状态方程才能使用。

这也是异步时序逻辑电路在分析方法上与同步时序逻辑电路的根本不同点，应引起足够的重视。

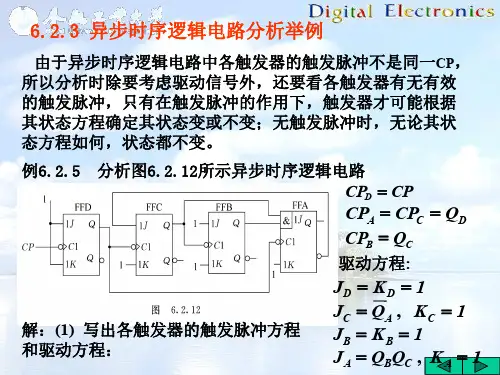
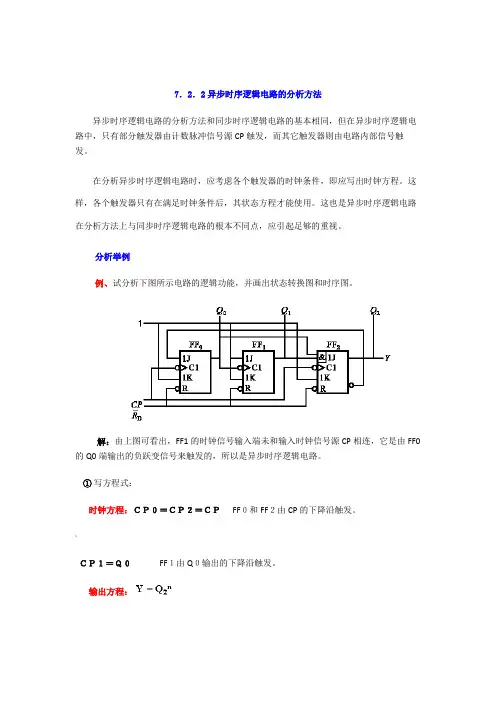
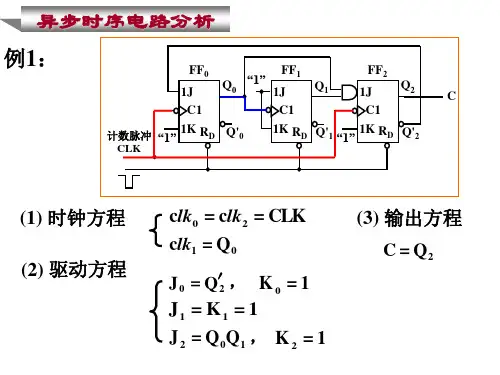
分析举例例、试分析下图所示电路的逻辑功能，并画出状态转换图和时序图。

解：由上图可看出，FF1的时钟信号输入端未和输入时钟信号源CP相连，它是由FF0的Q0端输出的负跃变信号来触发的，所以是异步时序逻辑电路。

①写方程式：时钟方程：ＣＰ０＝ＣＰ２＝ＣＰ FF０和FF２由CP的下降沿触发。

~ＣＰ１＝Ｑ０ FF１由Q０输出的下降沿触发。

输出方程：驱动方程：状态方程：②列状态转换真值表：状态方程只有在满足时钟条件后，将现态的各种取值代入计算才是有效的。

设现态为＝000，代入输出方程和状态方程中进行计算，可以得出该逻辑电路的状态转换真值表：现态次态输出`时钟脉冲Y CP2CP1$CP00000010》0010100《0100110?0111000\ 1000001…表中的第一行取值，在现态＝000时，先计算次态为＝01，由于CP１＝Q０，其由0跃到1为正跃变，故FF１保持0态不变，这时＝001。

表中的第二行取值，在现态为＝001时，得＝00，这时CP１＝Ｑ０由1跃到0为负跃变，FF１由0态翻到1态，这时＝010。

其余依此类推。

③逻辑功能说明：由上表可看出，该电路在输入第5个计数脉冲时，返回初始的000状态，同时输出端Y 输出一个负跃变的进位信号，因此，该电路为异步五进制计数器。

④状态转换图和时序图。

根据状态转换真值表可画出该电路的状态转换图和时序图，如下图所示。

！。

Q* 0 = Q′ 0clk0 ′′ Q* 1 = (Q3Q1 )clk1 Q* 2 = Q′ 2clk 2
Q* 3 = Q1Q2Q′ 3clk3
clk0 = clk0 clk1 = clk3 = Q0 clk2 = Q1
当时钟脉冲 跳变沿 到来时，方程成立 无时钟，保持原态
Q* =( JQ′ + K′ Q )CLK
′ ′ ′ clk1 = (Q′ Q* 3Q1 )clk1 1 = ( J1Q1 + K1Q1 ) ′ ′ Q* 2 = ( J 2Q2 + K 2Q2 ) clk2 = Q′ 2clk 2
′ ′ Q* 3 = ( J 3Q3 + K 3Q3 ) clk3 = Q1Q2Q′ 3clk3
(3) 输出方程
C = Q2
J1 = K1 = 1 J 2 = Q0Q1 ， K 2 = 1
异步时序电路分析 例 1：
(4) 特性方程 (5) 状态方程
当时钟脉冲 跳变沿 到来时，方程成立 无时钟，保持原态
Q* =( JQ′ + K′ Q )CLK
′ ′ ′ Q* 0 = (J 0Q0 + K 0Q0 ) clk0 = (Q′ 2Q0 )CLK
J0 = K0 = 1 J1 = Q′ 3 , K1 = 1 J2 = K2 = 1
(3) 输出方程
C = Q0Q3
(2) 驱动方程
J 3 Q2Q1 ，K 3 = 1
异步时序电路分析 例 2：
(4) 特性方程 (5) 状态方程 ′ ′ Q* 0 = (J 0Q0 + K 0Q0 ) clk0 = Q′ 0clk0
计数脉冲 CLK 0 1 2 3 4 5
C = Q2

第二十三讲 基于SSIC的时序逻辑电路的设计
10 32
10 32
10 32
10 32
《数字电子技术基础》
第二十三讲 于SSIC的时序逻辑电路的设计
Q3n1
Q2n1
Q1n1
Q0n1
《数字电子技术基础》
第二十三讲 基于SSIC的时序逻辑电路的设计
即可得电路的状态方程如下：
Q3n1 Q3nQ1nQ1n Q1nQ1n Q3n 1 Q3n
cp1
cp2
cp3
cp0
图5 【例5】电路图
至此，逻辑设计完毕。
《数字电子技术基础》
第二十三讲 基于SSIC的时序逻辑电路的设计
█ 异步时序逻辑电路的特点 ◆ 工作频率范围相对较窄，即工作频率 不 宜过高；
◆ 工作不稳定，容易产生竞争－冒险； ◆ 所设计的电路一般较同步时序逻辑电 路 简单。
《数字电子技术基础》
Qcc Q3nQ0n 《数字电子技术基础》
第二十三讲 基于SSIC的时序逻辑电路的设计
（五）自启动检测； 电路完整的状态转换图如下：
图4 【例5】状态转换图 《数字电子技术基础》
第二十三讲 基于SSIC的时序逻辑电路的设计
（六）根据（四）所得的驱动方程、输出方程和时钟 信号画出逻辑电路图如下：
Q2n1 Q2n
Q1n1 Q1n Q3nQ2n 1 Q1n Q3nQ2n Q1n
Q0n1
Qn 0
∵JK-FF的特性方程为：Qn1 JQn KQn
∴各JK-FF的驱动方程为：
JJ23
Q2nQ1n 1 K2
K3 1
1
J1 1
K QnQn
1
32
J0 1 K0 1

Q n1 n1
1
0
00 0
001
0
0
1
00 1
011
0
1
0
01 0
001
0
1
1
01 1
111
1
0
0
10 0
100
0
0
0
10 1
100
0
0
1
11 0
100
0
1
0
11 1
100
0
1
1
状态图
Q2n
Q1n Q0n
cp cp cp Q Q n1 2
Q n1
1
n1 0
2
1
0
000 0 0 1 0 0 1
001 0 1 1 0 1 0
010 0 0 1 0 1 1
011 1 1 1 1 0 0
100 1 0 0 0 0 0
101 1 0 0 0 0 1
110 1 0 0 0 1 0
111 1 0 0 0 1 1
Q2Q1Q0
000
001
101
100
4、拟定逻辑功能
011
电路是一种异步五进制加计数电路。
010
110
111
Q 2
CLK
Q Q Q Q CLK (Q Q Q )CLK
01
2
01
2
状态方程
Q n+1 Q ncp Q n cp
0
0
0
0
0
Q n+1 Q ncp Q n cp
1
1
1
1
1
Q n+1 Q ncp Q n cp

J 3 Q3
CP 3
&
C
K0
K1
K2
K3
•写方程： 输出方程： C Q3Q0 驱动方程： J 0 K 0 1 时钟方程： CP0 外部 状态方程：
n 1 Q0 Q0 (CP0 )
n 1 Q2 Q2 (CP2 )
J1 Q3 , K1 1
CP 1 CP 3 Q0
D2 Q2
D3 Q3
D2 Q2
D1 Q3 Q1
CP
C
CP 1
CP2
CP3
时钟方程： CP 1 CP 3 CP 状态方程:
CP2 Q1
Q3n 1 Q2Q1 (CP3 )
n 1 Q2 Q2 (CP2 )
Q1n 1 Q3 Q1 (CP 1 )
状态转移表：
CP
CP2 Q1 ,
J1 Q3 , K1 1
CP 1 CP 3 Q0
n 1 1
J 2 K 2 1 J 3 Q2Q1 , K 3 1
CP2 Q1
Q0 (CP0 )
Q
Q3 Q1 (CP 1 )
n 1 Q2 Q2 (CP2 )
Q3n 1 Q1Q2 Q3 (CP3 )
J 2 K 2 1 J 3 Q2Q1 , K 3 1
CP2 Q1
Q1n1 Q3 Q1 (CP 1 )
Q3n 1 Q1Q2 Q3 (CP3 )
输出方程： C Q3Q0 驱动方程： J 0 K 0 1 时钟方程： CP0 外部 状态方程： Q
n 1 0
6.3 异步时序电路的分析方法
异步时序电路的分析步骤，和同步时序电路分析步骤相同， 但需注意两点： 1、写方程：输出、激励、状态方程﹑时钟方程 2、各触发器翻转的时间和条件。

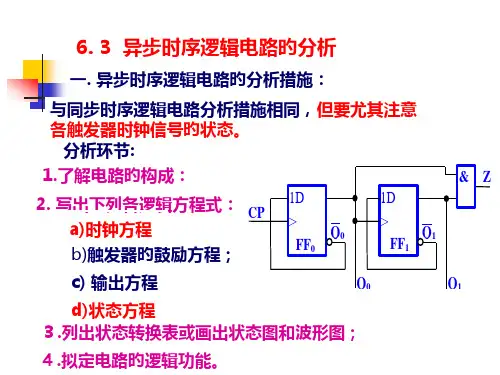
5.3异步时序逻辑电路的分析异步时序逻辑电路的分析一.分析的目的：得出时序电路的逻辑功能。

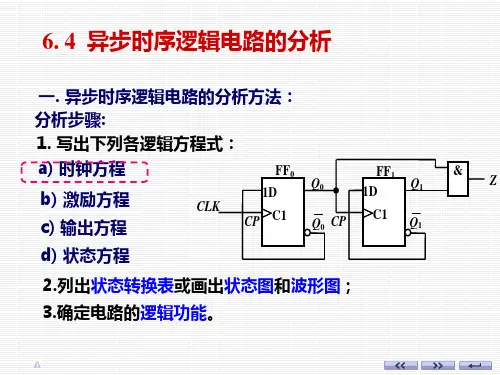
二.分析的方法(步骤)：1、写方程式：（1）时钟方程；（2）输出方程；（3）驱动方程；（4）状态方程。

2、列状态表；3、画状态转换图；4、画时序图；5、逻辑功能说明；6、检查电路能否自启动。

注意：异步时序电路的状态改变时，电路中要更新状态的触发器，有的先翻转，有的后翻转，是异步进行的。

因为在这种时序电路中，有的触发器的信号就是输入时钟脉冲，有的触发器则不是，而是其他触发器的输出。

异步时序电路的分析举例例1 试分析图示的时序电路的逻辑功能。

C解：（1）写方程式脉冲方程： CP CP CP ==20，01Q CP=驱动方程： nnQ Q D 020=，nQ D11=，nnQ Q D 012=状态方程：D触发器的特性方程：DQn =+1把驱动方程代入特性方程，可得状态方程：nn n Q Q Q 021=+ CP 上升沿有效nn Q Q 111=+ 0Q 上升沿有效nnn Q Q Q 0112=+ CP 上升沿有效（2）列状态表在依次设定的电路现态nn n Q Q Q12，代入状态方程式进行计算，求出次态。

特别注意的是每一个方程式的时钟条件，只有当其中条件具备时，触发器才会按照方程式的规定更新状态，否则只有保持原来的状态不变。

计算结果状态表状态表（3）画状态图0 0 1 1 1 01 1 1 1 0 1Q 001000000001111111Q 010001（5）电路功能说明该电路为一个异步五进制加法计数器。

（6）检查电路能否自启动：能自启动。

例2 试分析如图电路的逻辑功能。

C解：（1）写方程式脉冲方程： CP CP =0，nQ CP1=，nQ CP2=驱动方程： nQ D=nQ D 11= nQ D22=输出方程： nn n Q Q Q C 210=状态方程D触发器的特性方程：DQn =+1把驱动方程代入特性方程得各个触发器的状态方程：nn Q Q 010=+ （）nn Q Q 1=+ （） nn Q Q 212=+ （）（2）列状态表（3）画出状态图。

C0 = x
； T0 = 1
Z = xy2y1y0
第六章 异步时序逻辑电路
⑶画出逻辑电路图
根据激励函数和输出函数表达式，可画出实现给定要求的 逻辑电路如下图所示。
第六章 异步时序逻辑电路
6.2 电 平 异 步 时 序 逻 辑 电 路
6.2.1 概述
前面所述同步时序电路和脉冲异步时序电路有两个共同 的特点：
引起的，工作速度较高；
⑵电路的二次状态和激励 状态仅仅相差一个时间延迟。
二次状态y是激励状态Y经过 延迟Δt后的“重现”。
第六章 异步时序逻辑电路
⑶ 输入信号的一次变化可能引起二次状态的 多次变化。
⑷电路在状态转换过程中存在稳定状态和 非稳定状态。
稳 定 状 态： Y=y 非稳定状态 ：Y≠y
第六章 异步时序逻辑电路
输入脉冲 现 态
x
y2 y1 y0
1
000
1
001
1
010
1
011
1
100
1
101
1
110
1
111
次态 y2(n+1)y1(n+1) y0(n+1)
001 010 011 100 101 110 111 000
激励函数
C2 T2 C1 T1 C0 T0
0 d 0 d 11 0 d 1 1 11 0 d 0 d 11 1 1 1 1 11 0 d 0 d 11 0 d 1 1 11 0 d 0 d 11 1 1 1 1 11
&
第六章 异步时序逻辑电路
& 解:该电路由两个J-K
触发器和一个与门组成，
有一个输入端x和一个输 出端Z，输出是输入和状 态的函数，属于Mealy型 脉冲异步时序电路。

寄存器的工作原理
寄存器是由多个触发器组成的组合逻辑电路，能 够存储多位二进制信息。
寄存器在时钟脉冲的驱动下，将输入信号依次存 储在触发器中，实现数据的串行输入和输出。
寄存器具有并入、并出、串入、串出等多种工作 模式，可根据实际需求进行选择。
异步时序逻辑电路的设计步骤
01
确定电路的功能需求和性能参数。
总结词
状态方程是描述电路状态转换关系的数学模型，通过解状态方程可以得出电路的输出和状态转移规律 。
详细描述
状态方程是一个非线性方程组，描述了电路的状态变量和输入变量之间的关系。通过解状态方程，可 以得出电路的输出和状态转移规律，进而分析电路的逻辑功能和性能指标。
波形图分析法
总结词
波形图是一种直观的表示方法，可以 描述电路的输入输出信号随时间的变 化情况。
异步时序逻辑电路 的分析知识
contents
目录
• 异步时序逻辑电路的基本概念 • 异步时序逻辑电路的分析方法 • 异步时序逻辑电路的设计原理 • 异步时序逻辑电路的实例分析
01
CATALOGUE
异步时序逻辑电路的基本概念
定义与特点
定义：异步时序逻辑电路是一种数字电 路，其状态变化依赖于输入信号的改变 ，而不是统一的时钟信号。
详细描述
复杂异步时序逻辑电路包含多个触发器和记忆元件，这些元件之间相互作用，实现更复 杂的逻辑功能。状态转换图用于描述电路的状态转换过程和逻辑功能，通过分析状态转
换图可以确定电路的逻辑功能和性能。
实例三：实际应用中的异步时序逻辑电路分析
总结词
实际应用中的异步时序逻辑电路具有广泛的 应用领域，如计算机、通信、自动化等。
异步时序逻辑电路的应用场景

异步时序电路的分析步骤与同步时序电路大体一致，也分为读图、带入、计算、转换和总结等几步，分析流程与图8.2.3所示结构基本相同。

两者的主要差异在于，由于异步时序电路中，各个触发器的工作点（动作时刻）是不一样的，因此，在求出电路的状态方程时，必须同时标明各触发器的工作点，随后在列写状态表（依旧是整体分析法）时，往往需要分层次进行。

写出状态表后，转换为状态图和总结功能的过程就基本一致了。

以下，通过具体例题，详细讲解异步时序电路的分析过程。

【例8.2.6】分析图8.2.28所示的时序逻辑电路，说明该电路的逻辑功能。

图8.2.28 例8.2.6的电路图解：（1）判断：根据电路图可知，这是一个异步时序逻辑电路。

（2）读图：电路使用了3个下降沿工作，高有效的 触发器，共有8种状态迁移关系； 三个触发器的激励方程（驱动方程）为（3）带入：将上述激励方程带入激励端高有效的 触发器的特征方程，得到电路中3个触发器的状态方程，并对应标明各触发器的时钟工作点。

（4）根据状态图，得到表8.2.9所示的状态表（重点内容）：1:FF ; 11:FF ; 1:FF 201221110200⎩⎨⎧==⎩⎨⎧==⎩⎨⎧==K Q Q J K J K Q J nn n :FF :FF :FF 0122222122011111111020000100⎪⎩⎪⎨⎧↓=+=↓=+=↓=+=+++CLK Q Q Q Q K Q J Q Q Q Q K Q J Q CLK Q Q Q K Q J Q nn n n n n nn n n n n n nn n JK JK nQ CLK CLK CLK CLK 0120 ===、表8.2.9 例8.2.6的状态表★ 列写状态表，仍应遵循整体分析法进行，尽量避免带入运算；★ 分层次进行；首先列写受外部时钟工作点控制的 和； 由此得到的全部8个迁移关系，作为 的时钟信号，状态表的8行中，出现的情况时，表示此时出现了下降沿（共4个工作点，如表中所示），则此时；其余4行中， （没有出现工作点，则的状态保持不变）。