表上作业法的源代码
- 格式:doc
- 大小:44.50 KB
- 文档页数:10


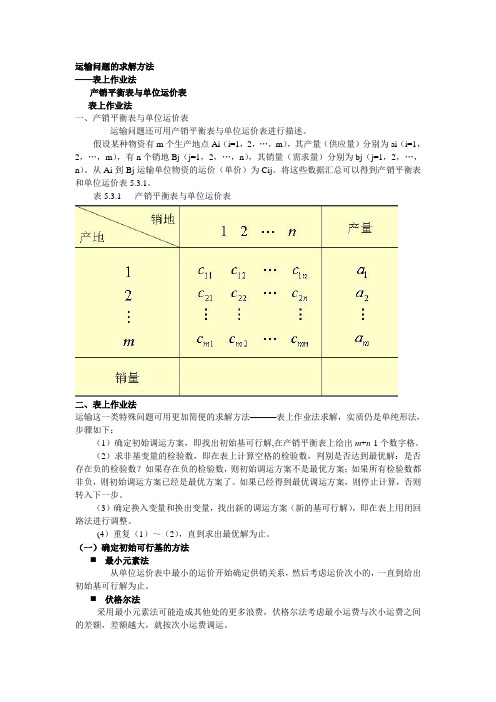
运输问题的求解方法——表上作业法产销平衡表与单位运价表表上作业法一、产销平衡表与单位运价表运输问题还可用产销平衡表与单位运价表进行描述。
假设某种物资有m个生产地点Ai(i=1,2,…,m),其产量(供应量)分别为ai(i=1,2,…,m),有n个销地Bj(j=1,2,…,n),其销量(需求量)分别为bj(j=1,2,…,n)。
从Ai到Bj运输单位物资的运价(单价)为Cij。
将这些数据汇总可以得到产销平衡表和单位运价表5.3.1。
表5.3.1 产销平衡表与单位运价表二、表上作业法运输这一类特殊问题可用更加简便的求解方法———表上作业法求解,实质仍是单纯形法,步骤如下:(1)确定初始调运方案,即找出初始基可行解,在产销平衡表上给出m+n-1个数字格。
(2)求非基变量的检验数,即在表上计算空格的检验数,判别是否达到最优解:是否存在负的检验数?如果存在负的检验数,则初始调运方案不是最优方案;如果所有检验数都非负,则初始调运方案已经是最优方案了。
如果已经得到最优调运方案,则停止计算,否则转入下一步。
(3)确定换入变量和换出变量,找出新的调运方案(新的基可行解),即在表上用闭回路法进行调整。
(4)重复(1)~(2),直到求出最优解为止。
(一)确定初始可行基的方法⏹最小元素法从单位运价表中最小的运价开始确定供销关系,然后考虑运价次小的,一直到给出初始基可行解为止。
⏹伏格尔法采用最小元素法可能造成其他处的更多浪费,伏格尔法考虑最小运费与次小运费之间的差额,差额越大,就按次小运费调运。
(二)最优解的判别计算非基变量(空格)的检验数,当所有的检验数时,为最优解。
求空格检验数的方法有:⏹闭回路法以某一空格为起点找一条闭回路,用水平或垂直线向前划,每碰到一数字格转900后,继续前进,直到回到起始空格为止。
闭回路如图5.3.1的(a)、(b)、(c)等所示。
从每一个空格出发一定存在并且可以找到唯一的闭回路。
因为,m+n-1个数字格(基变量)对应的系数向量是一个基,任一空格(非基变量)对应的系数向量是这个基的线性组合。
![[物流管理]表上作业法](https://img.taocdn.com/s1/m/3bd49cf75ff7ba0d4a7302768e9951e79b89690e.png)
表上作业法什么是表上作业法表上作业法是指用列表的方法求解线性规划问题中运输模型的计算方法。
是线性规划一种求解方法。
当某些线性规划问题采用图上作业法难以进行直观求解时,就可以将各元素列成相关表,作为初始方案,然后采用检验数来验证这个方案,否则就要采用闭合回路法、位势法等方法进行调整,直至得到满意的结果。
这种列表求解方法就是表上作业法。
表上作业法的步骤1、找出初始基本可行解(初始调运方案,一般m+n-1个数字格),用西北角法、最小元素法;(1)西北角法:从西北角(左上角)格开始,在格内的右下角标上允许取得的最大数。
然后按行(列)标下一格的数。
若某行(列)的产量(销量)已满足,则把该行(列)的其他格划去。
如此进行下去,直至得到一个基本可行解。
(2)最小元素法:从运价最小的格开始,在格内的右下角标上允许取得的最大数。
然后按运价从小到大顺序填数。
若某行(列)的产量(销量)已满足,则把该行(列)的其他格划去。
如此进行下去,直至得到一个基本可行解。
注:应用西北角法和最小元素法,每次填完数,都只划去一行或一列,只有最后一个元例外(同时划去一行和一列)。
当填上一个数后行、列同时饱和时,也应任意划去一行(列),在保留的列(行)中没被划去的格内标一个0。
2、求出各非基变量的检验数,判别是否达到最优解。
如果是停止计算,否则转入下一步,用位势法计算;运输问题的约束条件共有m+n个,其中:m是产地产量的限制;n是销地销量的限制。
其对偶问题也应有m+n个变量,据此:σij = c ij− (u i + v j) ,其中前m个计为,前n个计为由单纯形法可知,基变量的σij = 0c ij− (u i + v j) = 0因此u i,v j可以求出。
3、改进当前的基本可行解(确定换入、换出变量),用闭合回路法调整;(因为目标函数要求最小化)表格中有调运量的地方为基变量,空格处为非基变量。
基变量的检验数σij = 0,非基变量的检验数。

表上作业法中初始方案均为哎呀,说起表上作业法,这可真是个让人又爱又恨的家伙!咱今天就好好聊聊这其中初始方案的事儿。
表上作业法呀,就像是我们解决运输问题的一把神奇钥匙。
而初始方案呢,那就是打开这扇神奇大门的第一步。
你想想,就好比你要去一个陌生的地方探险,出发的第一步是不是特别关键?这初始方案也是一样的道理。
在实际生活中,我曾经碰到过这么一件事儿。
有一家小工厂,要把生产的货物运到各个销售点去。
老板愁眉苦脸地找到我,说运输成本太高啦,快撑不住啦!我一看他们的运输计划,好家伙,这哪有什么合理的方案呀,完全是瞎搞。
我就决定用表上作业法来帮帮他。
一开始的初始方案,那真是乱得像一团麻。
比如说,从工厂 A 到销售点 B 的运输量,居然是随意定的,一点依据都没有。
这就像是闭着眼睛走路,能不栽跟头嘛!咱们来说说这初始方案到底为啥这么重要。
初始方案就像是盖房子的地基,如果地基打得歪歪扭扭,那这房子能牢固吗?同样的道理,如果初始方案不合理,后面的调整优化那可就费劲啦,甚至可能越搞越糟糕。
那初始方案都有哪些类型呢?常见的有西北角法、最小元素法等等。
就拿西北角法来说吧,先从表格的西北角开始填数,听起来是不是有点神奇?其实就是按照一定的规则,先从最开始的位置入手,逐步填满整个表格。
比如说,还是那个小工厂的例子。
用西北角法来制定初始方案,先从工厂 A 和销售点 D 的交叉位置开始,看看能运多少货物。
然后再按照顺序,一步一步来,这样就能得到一个初步的方案。
虽然这个方案不一定是最优的,但至少是一个有章可循的开始。
再说说最小元素法。
这个方法呢,是先找出运价最小的单元格,优先满足它的运输需求。
这就像是先解决最容易解决的问题,把简单的搞定了,再去攻克那些难的。
还回到那个小工厂,用最小元素法的时候,先找到运价最低的那个运输路径,比如说从工厂 C 到销售点 B,然后根据需求确定运输量。
这样一轮一轮下来,初始方案也就有了个模样。
但是要注意哦,不管用哪种方法得到的初始方案,都只是一个开头,后面还需要不断地检验、调整,才能找到最优方案。

《表上作业法》《表上作业法》是一种求解指派问题的优化算法。
这种算法通过在表格中进行标记和计算,找出最优解或可行解,使得分配问题得到最优质的解决方案。
以下是关于《表上作业法》的详细介绍。
1.背景和目的《表上作业法》是一种针对指派问题的优化算法,旨在寻找最优解或可行解,使得分配问题得到最优质的解决方案。
它是一种常见的数学优化方法,适用于各种类型的分配问题,如任务分配、资源分配和决策制定等。
通过使用《表上作业法》,可以在给定的一组选项中,为每个任务或资源选择最佳的分配方案,以达到最优的效果或目标。
2.方法和步骤《表上作业法》的核心思想是将指派问题转化为表格形式,通过在表格中进行标记和计算,找出最优解或可行解。
《表上作业法》可以在一个给定的任务集合中选择一个任务来完成,使得选择的每个任务的综合评估值最大。
它包括以下步骤:(1)定义问题:首先,要明确指派问题的具体目标、任务集合、每个任务的评估值和约束条件等。
(2)建立表格:根据指派问题的任务集合和评估值,建立一个合适的表格。
表格的行代表各个任务,列代表可用的资源或选择方案。
在表格中,每个单元格表示某个任务在某个资源或选择方案下的评估值。
(3)填表:根据问题的约束条件和每个任务的评估值,填写表格中的各个单元格。
填表过程中要确保表格的可行性,即满足所有约束条件。
(4)寻找最优解:在填好表格后,通过一定的搜索策略,找出使得综合评估值最大的任务分配方案。
(5)输出结果:输出找到的最优解或可行解,分析每个任务被分配的情况以及对应的评估值。
3.应用和优势《表上作业法》适用于各种类型的指派问题,如任务分配、资源分配和决策制定等。
它具有以下优势:(1)直观易懂:《表上作业法》通过表格形式展示问题,使得问题更加直观易懂。
(2)容易实现:《表上作业法》算法流程清晰明了,容易实现,不需要太多的编程技巧。
(3)可扩展性强:《表上作业法》可以扩展到处理大型复杂的问题,可以有效地处理大规模问题。
表上作业法中初始方案均为关键信息项:1、表上作业法的定义和适用范围2、初始方案的生成方式3、初始方案的优化原则4、优化过程中的约束条件5、结果评估与验证方法1、引言表上作业法是一种用于解决运输问题、分配问题等线性规划问题的有效方法。
在运用表上作业法时,初始方案的确定至关重要,它直接影响到后续的优化过程和最终的解决方案。
11 表上作业法的基本概念表上作业法是通过在表格上进行运算和调整,以求得最优解的一种方法。
它将实际问题转化为表格形式,便于直观分析和操作。
111 适用场景适用于物资调运、生产任务分配、人员安排等多种资源分配问题。
2、初始方案的生成21 最小元素法优先满足单位运价最小的供销关系,逐步填充运量,从而得到初始方案。
211 操作步骤依次选择单位运价最小的单元格,确定其运量,同时要满足供应和需求的限制条件。
22 西北角法从表格的西北角开始分配运量,逐行或逐列进行,直至满足所有的供应和需求。
221 具体流程先从表格的左上角开始分配,按照先列后行或先行后列的顺序进行。
23 伏格尔法通过计算每行和每列的罚数,选择罚数最大的行或列进行运量分配,以得到更接近最优解的初始方案。
231 罚数的计算方法罚数等于次小运价与最小运价之差。
3、初始方案的优化原则31 闭回路调整法通过构建闭回路,对运量进行调整,以降低运输总成本。
311 闭回路的构建规则从一个空格出发,沿水平或垂直方向前进,遇到有数字的格转向,最终回到起始空格。
32 调整运量的原则选择调整量为闭回路上偶数顶点运量的最小值。
321 调整后的检验调整后需要重新计算总运输成本,判断是否达到更优的方案。
4、优化过程中的约束条件41 供应约束各供应点的供应量必须得到满足,不能超额供应。
411 需求约束各需求点的需求量必须得到满足,不能出现缺货情况。
42 非负约束运量必须为非负数。
421 整数约束在某些实际问题中,运量可能要求为整数。
5、结果评估与验证51 目标函数值计算总运输成本,作为评估方案优劣的主要指标。
/* 表上作业法的源代码 */#include ""#include ""#include ""/* #define debug */#define a(j) (*(C+(M-1)*N+j)) /*销量数组*/#define b(i) (*(C+i*N+N-1)) /*产量数组*/#define c(i,j) (*(C+i*N+j)) /*运价数组*/#define x(i,j) (*(X+i*(N-1)+j)) /*运量数组 *//*(<:基本解,>=:运量为0) */#define s(i,j) (*(S+i*(N-1)+j)) /*检验数数组Sij */ #define u(i) (*(U+i)) /*位势数组Ui*/#define v(i) (*(V+i)) /*位势数组Vi*/#define cpi(k) ((CP+k)->i) /*闭回路点i标*/#define cpj(k) ((CP+k)->j) /*闭回路点i标*/#define cpf(k) ((CP+k)->f) /*闭回路点i标*//* f=0:j++; f=2:j--;f=1;i--; f=3:i++; *//*void TP(int M,int N,double *C,double *X); */10 6 300 20 30 40 50 6012 7 14 16 9 10 9 13 8 14183 185 119 162 137 102 179 118 114189 107 169 161 179 169 140 135 112184 149 128 106 165 178 199 183 194127 184 173 124 125 151 127 178 160162 105 150 185 179 153 174 121 142108 163 157 138 189 171 114 131 165150 159 131 155 135 165 124 167 107109 107 149 175 162 108 182 135 181106 136 183 134 179 188 136 131 189166 158 159 180 162 104 116 159 111void main(){int M,N,i,j;double *C; /*存储运价,产量及销量 */double *X; /*存储运量分配方案 */float z;FILE *fp;char fn[80];double sum;void TP(int M,int N,double *C,double *X);printf("please input the data file name: ");scanf("%s",fn);if((fp=fopen(fn,"r"))==NULL){printf("Cannot open the data file!");}fscanf(fp,"%d%d",&M,&N);M++; N++;X=(double *)malloc(sizeof(double)*(M-1)*(N-1));C=(double *)malloc(sizeof(double)*M*N);/* 把运价,供应量和需求量的数据读入到数组c(i,j); *//*---高太光:这里可以直接定义固定的数组c(i,j),也可以从文件读取for(i=0;i<M;i++){for(j=0;j<N;j++){fscanf(fp,"%f",&z);c(i,j)=z;}printf("\n");}fclose(fp);/* output c(i,j); */printf("\n=============Data File================\n");for(i=0;i<M;i++){for(j=0;j<N;j++){printf("%10.3f",c(i,j));}printf("\n");}getch();TP(M,N,C,X);/* 输出产销分配方案; */printf("\n=============Best Solution===================\n"); sum=0;for(i=0;i<M-1;i++){for(j=0;j<N-1;j++){if(x(i,j)>=printf("%10s","******");else{printf("%10.3f",x(i,j));sum+=(x(i,j)*c(i,j));}}printf("\n");}printf("\n\n\tThe min Cost is: %-10.4f\n",sum);getch();}struct PATH{int i,j,f;}; /*记录闭回路点结构*/void TP(int M,int N, double *C,double *X){double *U,*V,*S;int MN1,m,n;struct PATH *CP;int k,i,j,l,k1,l1,ip;double Cmin,sum;int I0,J0,Imin,Jmin;int fi,fj,fc,f;MN1=(M-1)+(N-1)-1;m=M-1;n=N-1;S=(double *)malloc(sizeof(double)*(M-1)*(N-1));U=(double *)malloc(sizeof(double)*M);V=(double *)malloc(sizeof(double)*N);CP=(struct PATH *)malloc(sizeof(struct PATH)*(MN1+1)); #ifdef debugprintf("\nM=%d,N=%d,m=%d,n=%d\n",M,N,m,n);printf("\nb(i)is following:\n");for(i=0;i<m;i++)printf("%8.4f\t",b(i));printf("\na(j)is folowing:\n");for(j=0;j<n;j++)printf("%8.4f\t",a(j));printf("\n");getch();#endif/*解初始化Xij=; */for(i=0;i<m;i++)for(j=0;j<n;j++)x(i,j)=;/*最小元素法求初始可行解 */for(k=0;k<MN1;k++){Cmin=;for(i=0;i<m;i++){fi=0;for(l=0;l<k;l++){/* 去除已经用过的行; */if(i==cpi(l)){fi=1;break;}}if(fi==1)continue;for(j=0;j<n;j++){fj=0;for(l=0;l<k;l++){/* 去除已经用过的列; */if(j==cpj(l)){fj=1;break;}}if(fj==1) continue;if(Cmin>c(i,j)){Cmin=c(i,j);I0=i;J0=j;#ifdef debugprintf("\n now c(i,j)=%8.4f\n",c(i,j));#endif}} /*end for j */}/* end for i *//*得到了未划去的最小运价所在格的坐标(I0,J0)和最小运价Cmin */if(k>0){if(Cmin==&&cpi(k-1)==0){for(l1=0;l1<m;l1++)if(x(l1,cpj(k-1))=={x(l1,cpj(k-1))=0;}}else if(Cmin==&&cpi(k-1)!=0){for(l1=0;l1<n;l1++)if(x(cpi(k-1),l1)=={x(cpi(k-1),l1)=0;}}}if(b(I0)<a(J0)){cpi(k)=I0;cpj(k)=-1;x(I0,J0)=b(I0);#ifdef debugprintf("I0=%d,J0=%d,x(I0,J0)=%8.4f,k=%d,cpi(k)=%d,cpj(k)=%d\n",I0,J0,x(I0,J0),k,cpi(k),cpj(k)); #endifa(J0)-=b(I0);b(I0)=0;}else{cpi(k)=-1;cpj(k)=J0;x(I0,J0)=a(J0);#ifdef debugprintf("I0=%d,J0=%d,x(I0,J0)=%8.4f,k=%d,cpi(k)=%d,cpj(k)=%d\n",I0,J0,x(I0,J0),k,cpi(k),cpj(k)); #endifb(I0)-=a(J0);a(J0)=0;}} /*END FOR K 用最小元素法求得了初使可行解*//*输出初始可行解*/printf("\n=============init Solution===================\n");sum=0;for(i=0;i<M-1;i++){for(j=0;j<N-1;j++){if(x(i,j)>=printf("%10s","******");else{printf("%10.3f",x(i,j));sum+=(x(i,j)*c(i,j));}}printf("\n");}printf("\n\n\tThe Cost is: %-10.4f\n",sum);getch();/***************循环换入换出,直到检验数为非负数*****************************//*循环决定换入变量 */while(1){/*位势置初值Ui,Vi= */for(i=0;i<m;i++)u(i)=;for(j=0;j<n;j++)v(j)=;/*求位势*/l=0;u(0)=0;for(i=0;i<m;i++){for(j=0;j<n;j++){if(u(i)>=&&v(j)>=&&x(i,j)<{cpi(l)=i;cpj(l)=j;l++; /*记录未求过位势的位置*/}else if(x(i,j)<&&u(i)<{v(j)=c(i,j)-u(i);}else if(x(i,j)<&&v(j)<{u(i)=c(i,j)-v(j);}}/*end for j */}/*end for i *//*按记录位置求其余位势*/if(l>0){while(1){ip=0;for(k=0;k<l;k++){i=cpi(k);j=cpj(k);if((u(i)>=&&(v(j)>=&&(x(i,j)<){cpi(ip)=i;cpj(ip)=j;ip++; /*记录未求过位势的位置*/ }else if(x(i,j)<&&u(i)<{v(j)=c(i,j)-u(i);}else if(x(i,j)<&&v(j)<{u(i)=c(i,j)-v(j);}}/*end for k */if(ip==0)break;l=ip;}/*end for while */} /*end if l */#ifdef debugprintf("\nU(i):");for(i=0;i<m;i++){printf("%10.2f",u(i));}printf("\nV(j):");for(j=0;j<n;j++){printf("%10.2f",v(j));}printf("\n");#endif/*求检验数*/for(i=0;i<m;i++){for(j=0;j<n;j++){ s(i,j)=;if(x(i,j)>= s(i,j)=c(i,j)-u(i)-v(j);}}/*求最小检验数*/Cmin=;for(i=0;i<m;i++){for(j=0;j<n;j++){if(Cmin>s(i,j)){Cmin=s(i,j);I0=i;J0=j;}}}#ifdef debugprintf("\ncheck number:\n");for(i=0;i<m;i++){for(j=0;j<n;j++){printf("s(%d,%d)=%-10.2f\n",i,j,s(i,j));}printf("\n");}printf("Smin=%-10.2f",Cmin);getch();#endifif(Cmin>=0) return; /*已经得到最优解,返回主程序*/ /*此时找到了入基变量X(I0,J0) *//*求闭回路*/for(k=0;k<MN1;k++){cpf(k)=-1;}/*end for k */cpi(0)=I0;cpj(0)=J0;k=0;while(1){f=cpf(k);/*设置闭回路搜索方向*/while(1){i=cpi(k);j=cpj(k);fc=0;f++;cpf(k)=f;if(f>=4)break;/*避免反向搜索*/if(k>0){if(f==0&&cpf(k-1)==2) continue;else if(f==1&&cpf(k-1)==3)continue;else if(f==2&&cpf(k-1)==0)continue;else if(f==3&&cpf(k-1)==1)continue;}if(f==0){/*沿J+方向搜索*/while(1){j++;if(j>=n){fc=2;break;}if((i==I0)&&(j==J0)){fc=1;break;}if(s(i,j)>={fc=3;break;}}}/*end j+ */else if(f==1){ /*沿i-方向搜索*/while(1){ i--;if(i<0){fc=2;break;}if((i==I0)&&(j==J0)){fc=1;break;} if(s(i,j)>={fc=3;break;}}}/*end if=1 */else if(f==2){/*沿J-方向搜索*/while(1){j--;if(j<0){fc=2;break;}if((i==I0)&&(j==J0)){fc=1;break;} if(s(i,j)>={fc=3;break;}}} /*end f==2 */else if(f==3){/*沿I+方向搜索*/while(1){i++;if(i>=m){fc=2;break;}if((i==I0)&&(j==J0)){fc=1;break;} if(s(i,j)>={fc=3;break;}}}/*end f==3 */if((fc==1)||(fc==3))break;}/*end while flag 2 */if(fc==0){/*沿些方向搜索失败,退回回到前一点*/ k--;}else if(fc==1)break; /*搜索完成*/else if(fc==3){/*沿此方向搜索成功,前进一点*/k++;cpi(k)=i;cpj(k)=j;#ifdef debugprintf("\n");printf("k=%d,cpi(k)=%d,cpj(k)=%d,cpf(k)=%d,x(i,j)=%8.4f\n",k,cpi(k),cpj(k),cpf(k),x(cpi(k),cpj(k))); getch();#endifcpf(k)=-1;}}/*end while *//*去除闭回路中的非转折点*/l=0;while(l<k-1){ i=l+1;while(i<=k){if(cpf(l)==cpf(i)) i++;else break;}if(i>(l+1)){j=l+1;k1=k-(i-j);/*如果某些点前进方向相同,则去除中间各点*/while(i<=k){cpi(j)=cpi(i);cpj(j)=cpj(i);cpf(j)=cpf(i);i++;j++;}l+=2;k=k1;}else l++;}/*end while l<k-1 *//*查找闭回路上基本解的最小值*/Cmin=x(cpi(1),cpj(1));Imin=cpi(1);Jmin=cpj(1);for(i=3;i<=k;i+=2){if(Cmin>x(cpi(i),cpj(i))){Cmin=x(cpi(i),cpj(i));Imin=cpi(i);Jmin=cpj(i);}}/*换入基变量*/x(I0,J0)=Cmin;for(i=1;i<=k;i+=2){x(cpi(i),cpj(i))-=Cmin;if((i+1)<=k) x(cpi(i+1),cpj(i+1))+=Cmin;}x(Imin,Jmin)=;}free(CP);free(V);free(U);free(S);QUIT: return;}================END====================。