表上作业法

运输问题的求解方法(过程)——表上作业法的解题思路和原理、具体步骤。

运输问题是一种常见的工业应用问题,涉及到如何安排运输工具和货物,以最小化总成本或最大化利润。

表上作业法(Tableau Programming)是解决运输问题的一种有效方法,其解题思路和原理、具体步骤如下:1. 确定问题的状态在表上作业法中,我们需要先确定问题的状态。

状态是指某个特定时间段内,某个运输问题需要满足的条件。

例如,在一个例子中,我们可以将运输问题的状态定义为“需要从A城市运输货物到B城市,运输工具数量为3,运输距离为100公里”。

2. 定义状态转移方程接下来,我们需要定义状态转移方程,以描述在不同状态下可能采取的行动。

例如,在这个问题中,我们可以定义一个状态转移方程,表示当运输工具数量为2时,货物可以运输到B城市,而运输距离为80公里。

3. 确定最优解一旦我们定义了状态转移方程,我们就可以计算出在不同状态下的最优解。

例如,在这个问题中,当运输工具数量为2时,货物可以运输到B城市,运输距离为80公里,总成本为200元。

因此,该状态下的最优解是运输距离为80公里,运输工具数量为2,总成本为200元。

4. 确定边界条件最后,我们需要确定边界条件,以确保问题的状态不会无限制地变化。

例如,在这个问题中,当运输工具数量为3时,运输距离为120公里,超过了B城市的运输距离范围。

因此,我们需要设置一个限制条件,以确保运输工具数量不超过3,且运输距离不超过120公里。

表上作业法是一种简单有效的解决运输问题的方法,其原理和具体步骤如下。

通过定义状态转移方程、确定最优解、确定边界条件,我们可以计算出问题的最优解,从而实现最小化总成本和最大化利润的目标。

土石方调配--表上作业法一、土方调配原理土方调配是场地平整施工设计的一个重要容。

土方调配的目的是在使土方总运输量最小或土方运输成本最小的条件下，确定填挖方区土方的调配方向和数量，从而达到缩短工期和降低成本的目的。

（一）土方调配区的划分，平均运距和土方施工单价的确定1、调配区的划分原则进行土方调配时，首先要划分调配区。

划分调配区应注意下列几点：（1）调配区的划分应该与工程建（构）筑物的平面位置相协调，并考虑它们的开工顺序、工程的分期施工顺序；（2）调配区的大小应该满足土方施工主导机械（铲运机、挖土机等）的技术要求；（3）调配区的围应该和土方工程量计算用的方格网协调，通常可由若干方格组成一个调配区；（4）当土方运距较大或场地围土方不平衡时，可根据附近地形，考虑就近取土或就近弃土，这时一个取土区或弃土区都可作为一个独立的调配区。

2、平均运距的确定调配区的大小和位置确定之后，便可计算各填、挖方调配区之间的平均运距。

当用铲运机或推土机平土时，挖土调配区和填方调配区土方重心之间的距离，通常就是该填、挖方调配区之间的平均运距。

当填、挖方调配区之伺距离较远，采用汽车、自行式铲运机或其他运土工具沿工地道路或规定线路运土时，其运距应按实际情况进行计算。

3、土方施工单价的确定如果采用汽车或其他专用运土工具运土时，调配区之间的运土单价，可根据预算定额确定。

当采用多种机械施工时，确定土方的施工单价就比较复杂，因为不仅是单机核算问题，还要考虑运、填配套机械的施工单价，确定一个综合单价。

（二）用“线性规划”方法进行土方调配时的数学模型表是土方平衡与施工运距（单价）表。

此表格说明了整个场地划分为个挖方区，，…，，其挖方量应为，，…，；有个填方区，，，…，，其填方量相应为，，…，；用表示由挖方区到填方区的土方调配数，由填挖方平衡，即：（1-1-6）若从到的价格系数（平均运距，或单位土方运价、或单位土方施工费用）为，一般地，从到的价格系数为，于是土方调配问题可以用下列数学模型表达：求一组的值、使目标函数：（1-l-7）为最小值，并满足下列约束条件：（=1，2，…，）（=1，2，…，）据约束条件知道，未知量有X个，而方程数为+个。

表上作业法的基本步骤1. 简介表上作业法（Tabletop Exercise，TTE）是一种用于组织和管理应急响应演练的方法。

它通过模拟真实情景来评估组织的应急计划、流程和资源准备情况，以提高应对突发事件的能力和效率。

本文将介绍表上作业法的基本步骤，并探讨如何有效地进行表上作业。

2. 基本步骤步骤一：确定目标和范围在进行表上作业之前，首先需要明确目标和范围。

目标是指希望通过此次演练达到什么样的效果，例如测试应急计划的可行性、评估团队协作能力等。

范围则是指演练涉及的主题、参与人员、时间限制等。

步骤二：制定剧本剧本是表上作业的核心部分，它描述了演练中所模拟的事件场景、参与者角色以及事件发展过程。

制定剧本时需要考虑真实性和复杂性，以使演练更具挑战性和可信度。

步骤三：确定参与者确定参与者是表上作业的重要一步。

参与者包括应急响应团队成员、管理层代表、外部合作伙伴等。

根据演练目标和剧本，确定参与者的角色和责任，并确保他们具备相应的知识和技能。

步骤四：准备材料为了顺利进行表上作业，需要准备相关的材料，如演练手册、应急计划、流程图等。

这些材料可以帮助参与者了解演练的目标、规则和流程，提供必要的信息支持。

步骤五：组织演练在进行表上作业之前，需要确定演练的时间、地点和形式。

通常情况下，表上作业可以通过线下会议或在线视频会议进行。

组织方需要确保参与者按照预定时间和地点参加演练，并提供必要的技术支持。

步骤六：实施演练在实施演练时，可以按照事先设定的剧本逐步展开。

参与者根据自己的角色扮演，并在模拟事件发生后采取相应的行动。

组织方可以通过观察、记录或评估工具来监控演练的进展，并及时提供反馈和指导。

步骤七：总结评估演练结束后，需要进行总结评估。

参与者可以就演练过程中的问题、挑战和经验进行交流和讨论。

组织方可以收集参与者的反馈意见，并根据演练结果提出改进建议。

步骤八：改进计划根据总结评估的结果，制定改进计划以提升应急响应能力。

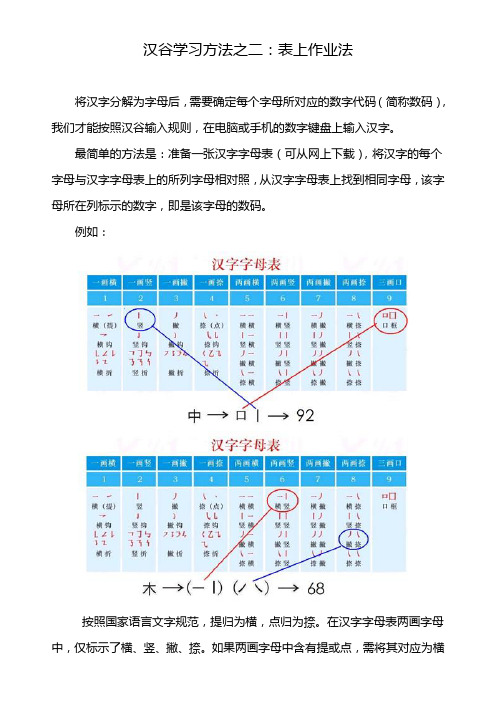
汉谷学习方法之二：表上作业法
将汉字分解为字母后，需要确定每个字母所对应的数字代码（简称数码），我们才能按照汉谷输入规则，在电脑或手机的数字键盘上输入汉字。

最简单的方法是：准备一张汉字字母表（可从网上下载），将汉字的每个字母与汉字字母表上的所列字母相对照，从汉字字母表上找到相同字母，该字母所在列标示的数字，即是该字母的数码。

例如：
按照国家语言文字规范，提归为横，点归为捺。

在汉字字母表两画字母中，仅标示了横、竖、撇、捺。

如果两画字母中含有提或点，需将其对应为横
或捺，再按上述方法进行作业。

例如：
表上作业法只是初学者入门的一根拐棍，经过多次作业后，汉字字母表已经烂熟于心，您就完全可以甩掉这根拐棍。

很熟练后，只要一看到字母，您根本用不着思考，脑子里条件反射式地跳出相应数码。

到那时，汉谷输入法好似您与生俱来的本能，时刻为您所用，永远不会忘记。

用表上作业法求解指派问题的方法指派问题是一类经典的优化问题，其目标是找到最佳的任务分配方案，使得总成本或总利益最小或最大化。

其中，指派问题的目标是将一系列任务分配给一组人员或资源，使得总成本最小化。

表上作业法（Hungarian algorithm）是解决指派问题的一种有效方法。

它的基本思想是利用矩阵的行和列的减法和加法运算，在保证每行每列至多只有一个0的条件下，找到最优的任务分配方案。

具体来说，表上作业法的步骤如下：1. 创建一个n x n的矩阵，其中n表示任务和人员或资源的数量。

矩阵的每个元素表示将某个任务分配给某个人员或资源的成本或利益。

2. 对矩阵进行行减法和列减法，使得每行和每列至少有一个0。

行减法和列减法的目的是找到一个初始解。

3. 在矩阵中找到一个0，标记该0为“*”。

如果该0位于独立的行或列中，则找到最优解，算法结束。

4. 如果该0位于非独立的行或列中，找到与该0同行或同列的其他0，并标记为“*”。

然后，以标记的0为新的起点，重复步骤3和4，直到找到最优解或无法找到更多的0。

5. 如果无法找到更多的0，则进行列减法和行加法，找到一个最小的非标记元素，并将其减去该行的最小非标记元素。

然后，将矩阵中所有的标记元素去除，回到步骤3。

通过重复执行步骤3至步骤5，直到找到最优解为止。

最优解是指在保证每行和每列至多只有一个0的条件下，使得总成本最小化或总利益最大化的任务分配方案。

表上作业法是解决指派问题的一种经典算法，其时间复杂度为O(n^3)，能够快速找到最优解。

因此，它在实际应用中被广泛使用，如任务分配、人员调度、作业调度等领域。